How powerful are summary-based methods for identifying expression-trait associations under different genetic architectures?

Abstract

Transcriptome-wide association studies (TWAS) have recently been employed as an approach that can draw upon the advantages of genome-wide association studies (GWAS) and gene expression studies to identify genes associated with complex traits. Unlike standard GWAS, summary level data suffices for TWAS and offers improved statistical power. Two popular TWAS methods include either (a) imputing the cis genetic component of gene expression from smaller sized studies (using multi-SNP prediction or MP) into much larger effective sample sizes afforded by GWAS –- TWAS-MP or (b) using summary-based Mendelian randomization –- TWAS-SMR. Although these methods have been effective at detecting functional variants, it remains unclear how extensive variability in the genetic architecture of complex traits and diseases impacts TWAS results. Our goal was to investigate the different scenarios under which these methods yielded enough power to detect significant expression-trait associations. In this study, we conducted extensive simulations based on 6000 randomly chosen, unrelated Caucasian males from Geisinger’s MyCode population to compare the power to detect cis expression-trait associations (within 500 kb of a gene) using the above-described approaches. To test TWAS across varying genetic backgrounds we simulated gene expression and phenotype using different quantitative trait loci per gene and cis-expression /trait heritability under genetic models that differentiate the effect of causality from that of pleiotropy. For each gene, on a training set ranging from 100 to 1000 individuals, we either (a) estimated regression coefficients with gene expression as the response using five different methods: LASSO, elastic net, Bayesian LASSO, Bayesian spike-slab, and Bayesian ridge regression or (b) performed eQTL analysis. We then sampled with replacement 50,000, 150,000, and 300,000 individuals respectively from the testing set of the remaining 5000 individuals and conducted GWAS on each set. Subsequently, we integrated the GWAS summary statistics derived from the testing set with the weights (or eQTLs) derived from the training set to identify expression-trait associations using (a) TWAS-MP (b) TWAS-SMR (c) eQTL-based GWAS, or (d) standalone GWAS. Finally, we examined the power to detect functionally relevant genes using the different approaches under the considered simulation scenarios. In general, we observed great similarities among TWAS-MP methods although the Bayesian methods resulted in improved power in comparison to LASSO and elastic net as the trait architecture grew more complex while training sample sizes and expression heritability remained small. Finally, we observed high power under causality but very low to moderate power under pleiotropy.

1. Introduction

Genome-wide association studies (GWAS) have discovered a large number of variants associated with a host of complex traits and diseases¹. However, these GWAS-significant variants explain a very limited proportion of the overall trait heritability, a phenomenon that is widely referred to as “missing heritability”². Moreover, traditional GWAS have also largely ignored the relationship that exists between genetic variants, DNA functional elements (e.g. gene expression/protein levels) and complex traits and diseases. eQTL studies can help identify the extent of influence that a variant can have on gene expression. However, the extent to which this variant can modulate gene expression to also influence complex traits and diseases remains a topic of great interest in the genetics and public health community.

One way to address this question is to conduct studies in which both gene expression and trait measurements are available on the same set of individuals. However, such studies are extremely limited in number and are hampered by small sample sizes owing to the costs involved in data collection. Alternatively, one could combine the features of eQTL studies and GWAS (performed on different populations) to illuminate gene-trait relationships using a transcriptome-wide association study (TWAS). Such a study exploits the relationship between a genetic variant and gene expression as well as the large sample sizes afforded by GWAS to help identify novel gene-trait associations in a powerful manner.

Many “flavors” of TWAS have been published already^3–8. These approaches include determining whether GWAS-significant variants are also enriched for eQTLs^3,4, detecting co-localization of expression signals at known GWAS loci⁷, performing Mendelian Randomization using summary-statistics for gene expression-genotype and genotype-phenotype associations⁹, and performing multi-SNP prediction (MP) analysis that can more explicitly model linkage disequilibrium (LD) when causal variants are not genotyped^5,8. Additionally, TWAS-MP methods also use different regression models to “impute” cis-gene expression into much larger GWAS datasets; for instance, Gusev et al.⁵ use the best linear unbiased predictor (BLUP) while PrediXcan⁸ applies elastic net regression to achieve the same goal.

The type of data required by each of these approaches is also different; for instance, some methods require individual-level genotype and phenotype as well as gene expression data [e.g. TWAS-MP (elastic net) in PrediXcan⁸], while others only need summary-level data at one or both levels (e.g. TWAS-MP (elastic net) in MetaXcan¹⁰, TWAS-MP (BLUP)⁸, summary-based Mendelian Randomization or TWAS-SMR⁹, and COLOC⁷). At the expense of introducing some bias, summary-based approaches can vastly improve computation efficiency. Some approaches also attempt to incorporate distinctions between different kinds of genetic models in their model assumptions. For instance, while TWAS-MP assumes either direct/indirect causality (when expression mediates between genotyped/non-genotyped SNP and trait) or pleiotropy (when the genetic variant has direct and independent effects on gene expression as well as the phenotype), TWAS-SMR distinguishes pleiotropy from linkage (in effect, when two causal variants that are in LD with each other independently influence either gene expression or phenotype) using a post-hoc method called heterogeneity in dependent instruments (HEIDI)⁹.

Thus far, no study has compared the power (to detect gene-trait associations) of these methods under a range of complex genetic architectures. In this study, we compare the statistical power afforded by TWAS-MP and TWAS-SMR in hitherto unexplored scenarios. This work can help us recognize genetic patterns underlying complex trait variation. We consider two different genetic models: causality and pleiotropy (as described above). We also investigate the influence on power of trait heritability, expression heritability, number of quantitative trait loci (QTL), sample size for training the imputation algorithm (relevant to TWAS-MP methods) and finally, the GWAS sample sizes. We compare different variable selection and shrinkage-based methods that can perform TWAS-MP (e.g. BLUP/Bayesian Ridge Regression, Bayesian LASSO, Bayesian spike-slab, elastic net and LASSO) to TWAS-SMR, GWAS, and eQTL-based GWAS (eGWAS). We have integrated Bayesian LASSO with TWAS for the first time in this study. Under the assumption of causality, TWAS-MP methods yielded the highest (and consistently identical) power under different simulation scenarios while TWAS-SMR, eGWAS and GWAS yielded consistently lower power. For TWAS-MP, Bayesian methods were at least as powerful as elastic net and LASSO, and surpassed their power as trait complexity increased, expression heritability remained low, and training sample size was small. Interestingly, we observed that traditional GWAS resulted in higher power than TWAS under the assumption of pleiotropy, although there was a massive overall loss in power from before.

2. Methods

In this section, we describe the data structure and quality control procedures, the simulation pipeline (modified from Gusev et al.⁵) as well as the statistical methods employed for calculating the power of detecting gene-trait associations.

2.1. Genotype Data

Individuals included in this simulation study came from a patient cohort in the MyCode^® Community Health Initiative of Geisinger Health System¹¹. We used participants that were genotyped using the Illumina Human Omni Express plus exome beadchip in the DiscovEHR study (a collaboration between Geisinger Health System and Regeneron Genetics Center). The genetic data was imputed using the Haplotype Reference Consortium panel and the dataset contained 60,000 individuals and approximately 600K variants after some initial quality control measures. For this analysis, we removed any related samples (up to 1^st cousins) as well as those that did not pass a sample call rate filter of 90%. We filtered variants that did not pass a genotype call rate filter of 99% and a minor allele frequency filter of 1% (so as to restrict ourselves to common variants only). We finally selected at random 6000 males of European American ancestry to ensure as much homogeneity in the population as possible.

2.2. Simulation pipeline

2.2.1. Simulating gene expression

We started with 6000 randomly chosen unrelated European American males from the MyCode^® population. We then sampled 100 genes at random from across the genome, each of length between 100 and 200 SNPs, as annotated using Biofilter¹². We selected the region 100 kb upstream and downstream of each chosen gene. We chose 5 different seeds per gene, giving us a total of 500 replications in the power simulation.

In each replication, we divided the total sample size into two sets: training (100, 250, 500, 1000 individuals each) and testing (5000 individuals). In each training set, we first simulated gene expression under an additive genetic model at each of four levels of causal variants per gene (number of QTL = 5%, 10%, 25% and 50%) as well as three levels of cis-expression heritability ( $\mathit{\text{cis}}-h_e^2=50\%$, 17% and 30%). The $\mathit{\text{cis}}-h_e^2$ levels were chosen based on their published distributions for significant (i.e. $\mathit{\text{cis}}-h_e^2>>0$ by likelihood ratio test) cis-eQTLs in three different SNP-expression cohorts⁵.

Let the sample size be represented by n, the number of SNPs by p and the number of QTL by m. The model to simulate gene expression can be expressed as follows:

$$E=X\beta +\epsilon$$ (1)

where E is the n×1 vector of standardized gene expression values for the n individuals in the training set, β is the m×1 vector of marker effects for the m QTL in the gene and is drawn from a normal distribution with mean zero and variance $\mathit{\text{cis}}-h_e^2$, X is the n×m matrix of genotypes and ε is the vector of the normally distributed errors with mean zero and variance $1-\mathit{\text{cis}}-h_e^2$.

2.2.2. Simulating phenotype

We simulated the phenotype in the testing set (5000 individuals) under eight different levels of trait heritability per gene (h² = 0%, 0.005%, 0.001%, 0.025%, 0.05%, 0.1%, 0.5%, 1%), wherein h² = 0 corresponded to the null model. In the testing set, two genetic models were used to simulate the phenotype: causality (when expression mediates the relationship between SNP and phenotype) and pleiotropy (when gene expression and phenotype independently share the same causal variant). Phenotypes using either genetic model were simulated under an additive genetic model as follows:

(1) Causality

$$Y={\mathit{\text{Eb}}}_1+{\epsilon }_1$$ (2)

where Y is the 5000×1 vector of the standardized response for the 5000 individuals in the testing set, E is the 5000×1 vector of gene expression values for testing set, b₁ is transcript effect drawn with zero mean and variance h², and ε₁ is vector of the normally distributed errors with mean zero and variance 1−h².

(1) Pleiotropy

$$Y={\mathit{\text{Xb}}}_2+{\epsilon }_2$$ (3)

where Y is the 5000×1 vector of the standardized response for the 5000 individuals in the testing set, X is the 5000×m matrix of genotypes (same as those used to simulate gene expression), b₂ is the m×1 vector of marker effects drawn from a normal distribution with mean zero and variance h², and ε₂ is vector of the normally distributed errors with mean zero and variance 1−h².

To reach precision corresponding to a large-sized GWAS, we repeated the phenotype generation with different environmental noise terms: 10 iterations resulted in a GWAS sample size of 50,000, 30 iterations resulted a GWAS sample size of 150,000 and 60 iterations resulted in a GWAS sample size of 300,000.

2.2.3. Power analysis

The following were the null and alternative hypotheses in this study:

• H₀: There is no association between gene and phenotype; i.e. $\text{cis}-h_e^2=0$ or h² = 0

• H₁: There is a non-zero association between gene and phenotype; i.e. $\text{cis}-h_e^2>0$ and h² > 0

In this study, we only considered the h² = 0 scenario as our null model. We first conducted eQTL analysis on the training set to identify the p×1 vector of z-scores (Z_eQTL) by regressing gene expression on the p SNPs in the chosen gene. Subsequently, we obtained p-values corresponding to expression-trait associations from 8 different models:

• 1GWAS: For each GWAS set (50K, 150K, or 300K individuals), we conducted meta-analysis across the smaller sets to obtain a p×1 vector of z-scores (Z_GWAS) and corresponding p-values for all SNP-trait associations. The gene was considered to be detected if at least one SNP in the gene had a p-value < 5E-8.
• 2eGWAS: In this eQTL-based GWAS, we used the GWAS p-value of the single most significant SNP from eQTL analysis. The gene was considered to be detected if this p-value < 0.05/15,000 (where 15,000 corresponds to the number of genes across the genome).
• 3TWAS-MP: This approach involves imputation of expression-trait association statistics directly into GWAS summary statistics and involves three different steps:

Obtaining weights

The first step here was to obtain estimated coefficients (weights obtained on regressing gene expression on SNPs) on the training set using five different penalized regression/Bayesian regularization approaches; elastic net, LASSO, Bayesian ridge regression (BRR), Bayesian LASSO (BL) and Bayesian spike slab or BayesC (BC). LASSO and elastic net are penalized regression methods that differ in the choice of the penalty function; LASSO¹³ uses the L1 norm as the penalty function whereas elastic net¹⁴ uses the weighted average of the L1 and L2 norms. While both methods perform a combination of variable selection and shrinkage on marker effects, elastic net also accounts for correlated predictors better than LASSO. BRR, BL and BC are Bayesian shrinkage estimators that use a Gaussian prior, thick-tailed (double-exponential) prior and spike-slab (point-of-mass at zero and Gaussian slab) prior, respectively, for marker effects. BRR and BL perform homogeneous and differential shrinkage respectively, whereas BC performs a combination of variable selection and homogeneous shrinkage on marker effects¹⁵. The weights W for LASSO and elastic net were obtained using the glmnet¹⁶ package in R while those for BRR, BL and BC were obtained using the BGLR¹⁷ package in R.

Accounting for LD

Irrespective of the training sample size used to obtain weights, the covariance matrix among all the chosen SNPs in the gene Σ was obtained using the full training set of 1000 individuals. This is reasonable because, [i] in practice, publicly available human genotype data (e.g. 1000 genomes data¹⁸) can be used for this purpose and [ii] we wanted to keep the influence of LD consistent between training sets.

Imputing the weights into GWAS

TWAS was conducted by imputing the weights W obtained using each of the five above-described penalized/Bayesian regularized regression approaches into the GWAS summary statistics. The single imputed z-score (normally distributed with zero mean and unit variance) of cis-genetic effect on the phenotype can be obtained as follows:

$$z_{\mathit{\text{TWAS}}-\mathit{\text{MP}}}=W\prime Z_{\mathit{\text{GWAS}}}/{(W\prime \sum W)}^{\frac{1}{2}}$$ (4)

Similar to eGWAS, the gene was considered to be detected if its p-value < 0.05/15,000.

• 4
  TWAS-SMR: For the given gene, we obtained the TWAS-SMR-based z-score by combining the z-score of the single most significant SNP from eQTL analysis (z_eQTL = min (Z_eQTL)) with the z-score of the corresponding SNP from GWAS (z_eGWAS), which can be expressed as follows:

  $$z_{\mathit{\text{TWAS}}-\mathit{\text{SMR}}}\approx (z_{\mathit{\text{eQTL}}}\ast z_{\mathit{\text{eGWAS}}})/\sqrt{(z_{\mathit{\text{eQTL}}}^2+z_{\mathit{\text{eGWAS}}}^2)}$$ (5)

  Similar to eGWAS and TWAS-MP, the gene was considered to be detected if its p-value < 0.05/15,000.

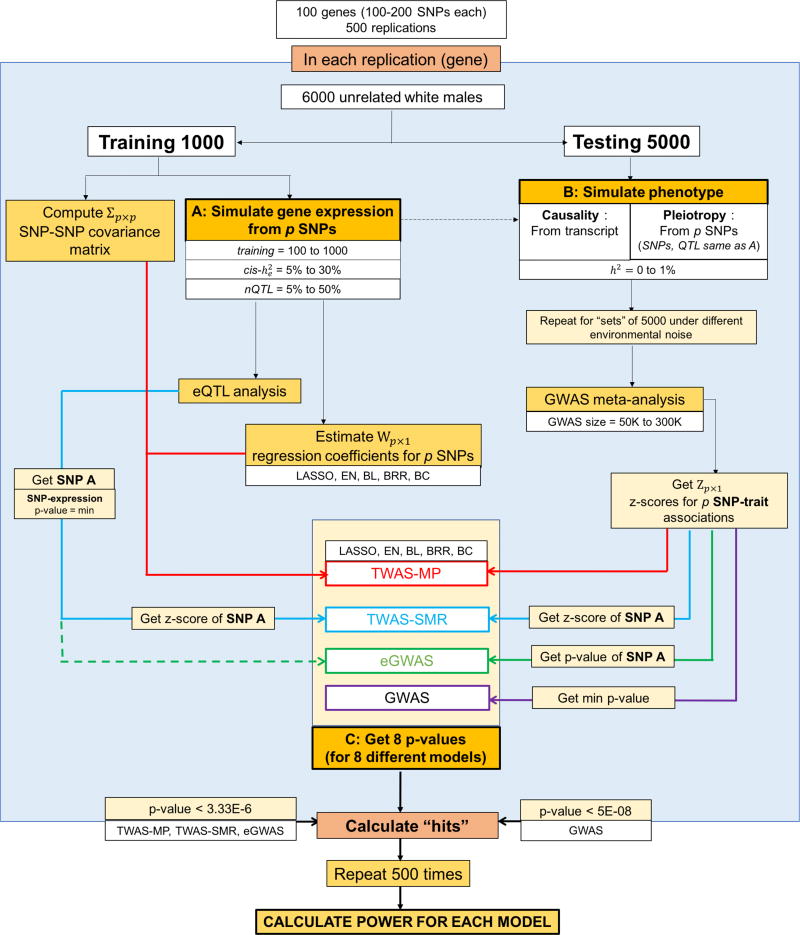
The entire procedure was repeated 500 times and power was calculated as the fraction of instances where the given gene was detected. A summarized version of the power analysis pipeline is given in Figure 1. All models were fit using the 3.2.1 version of software R.

Figure 1. Simulation pipeline per gene for power analysis.

3. Results

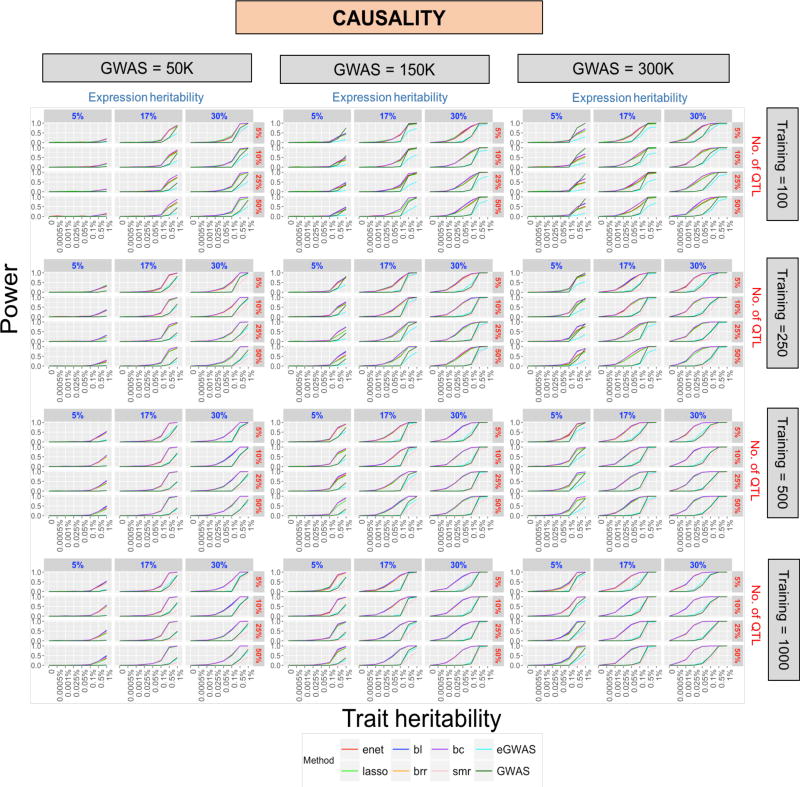
We observed that the power of detecting an expression-trait association varied not only with the genetic architecture of the trait but also with the sample size. Let’s first consider the genetic model corresponding to causality (Figure 2). Broadly, power was observed to increase with: (1) the sample size used for training the TWAS imputation algorithm and for eQTL analyses, (2) the sample size used to conduct GWAS meta-analysis, (3) the trait heritability as well as (4) the expression heritability. We observed that GWAS sample size had a bigger effect on power than the training sample size (we only considered realistic GWAS and training sample sizes).

Figure 2. Power distributions under causality (full).

Power (y-axis) across trait heritability (x-axis) under varying levels of expression heritability (in blue—subplot columns), no. of QTL (in red—subplot rows), training sample size (main plot rows) and GWAS sample size (main plot columns). Each plot represents power from 8 different models; TWAS-MP (LASSO, elastic net, BL, BC, BRR), TWAS-SMR, eGWAS, and GWAS. Enlarged views of this plot can help identify differences between methods. Relevant differences between TWAS-MP methods can be seen in Figure 2.

Across all cases, we observed that a trait heritability of less than 0.001% resulted in low to zero power, irrespective of the considered sample sizes. For a GWAS sample size as large as 150,000 individuals, trait heritability less than 0.025% yielded low to zero power across all methods (even when the expression heritability was as high as 30%). In addition, eGWAS and TWAS-SMR did significantly worse than all other considered methods, except when trait heritability, expression heritability and GWAS sample size were very high (~ 1%, ~30% and >=150,000, respectively).

TWAS-SMR achieved peak performance and offered power comparable to eGWAS and GWAS (across all levels of trait heritability) when the expression heritability, training sample size and GWAS sample sizes were all at their highest levels (30%, 1000 and 300,000 respectively). However, its performance was still worse than that of eGWAS and GWAS, especially when expression heritability was low. Although eGWAS’s performance was also poor under low expression heritability, it made up for this loss as GWAS sample size increased. As expected, power afforded by GWAS was unaffected by expression heritability and training sample size; it increased only with trait heritability and GWAS sample size. Interestingly, GWAS resulted in marked improvement in power over all other methods when expression heritability, number of QTL, and training sample sizes were at their lowest levels and GWAS sample size was high (see first subplot column under top right main plot panel in Figure 2; GWAS is in dark green).

TWAS-MP always resulted in the highest power, except when expression heritability and training sample sizes were at their lowest (Figure 2). For instance, given an expression heritability of 17% and a trait heritability of 0.1%, moderate sample sizes for training and GWAS (250 and 150,000 respectively) were sufficient to achieve >=75% power using any of the TWAS imputation methods. Also, genes with average to high expression heritability were found to have very high power of detecting a significant gene-trait association even when GWAS and training sample sizes were low; the power ranged from approximately 0% at $h_e^2=5\%$ to approximately 100% at $h_e^2=30\%$ for a gene that had a trait heritability of greater than 0.5% (see top- and left-most panel in Figure 2). In general, the TWAS-MP methods yielded almost identical power. However, Bayesian methods performed better than LASSO and elastic net when the expression heritability was low to moderate (5%–17%), number of QTL was high (>=25%) and training sample size was low to moderate (<=500) (Figure 2). In particular, when the expression heritability is low (5%), BL achieved a maximum improvement in power (~ 17%–18%) as compared to the elastic net and LASSO under a trait heritability of at least 0.5% and using a GWAS sample size of 150K (Table 1).

Table 1. Comparison of power of TWAS-MP methods under causality (reduced).

Power using 5 TWAS-MP approaches (elastic net, LASSO, BL, BRR, BC) at training sample sizes of 100, 250, 500, 1000, GWAS sample size of 150K, expression heritability of 5% and trait heritability of 0.5% and 1%, respectively.

TWAS-MP	Training sample size
	100				250				500				1000
	nQTL				nQTL				nQTL				nQTL
	25%		50%		25%		50%		25%		50%		25%		50%
	h2		h2		h2		h2		h2		h2		h2		h2
	0.50%	1%	0.50%	1%	0.50%	1%	0.50%	1%	0.50%	1%	0.50%	1%	0.50%	1%	0.50%	1%
ENET	0.207	0.352	0.196	0.585	0.313	0.848	0.312	0.370	0.635	0.592	0.514	0.787	0.945	0.994	0.908	0.982
LASSO	0.179	0.317	0.185	0.578	0.304	0.808	0.289	0.339	0.591	0.525	0.509	0.791	0.934	0.992	0.893	0.988
BL	0.250	0.484	0.258	0.748	0.498	0.938	0.484	0.488	0.734	0.768	0.672	0.932	0.988	1.000	0.984	0.998
BRR	0.258	0.444	0.242	0.722	0.472	0.910	0.452	0.468	0.706	0.736	0.664	0.918	0.968	1.000	0.960	0.998
BC	0.256	0.458	0.234	0.732	0.486	0.930	0.468	0.462	0.716	0.716	0.660	0.898	0.974	0.998	0.986	0.998

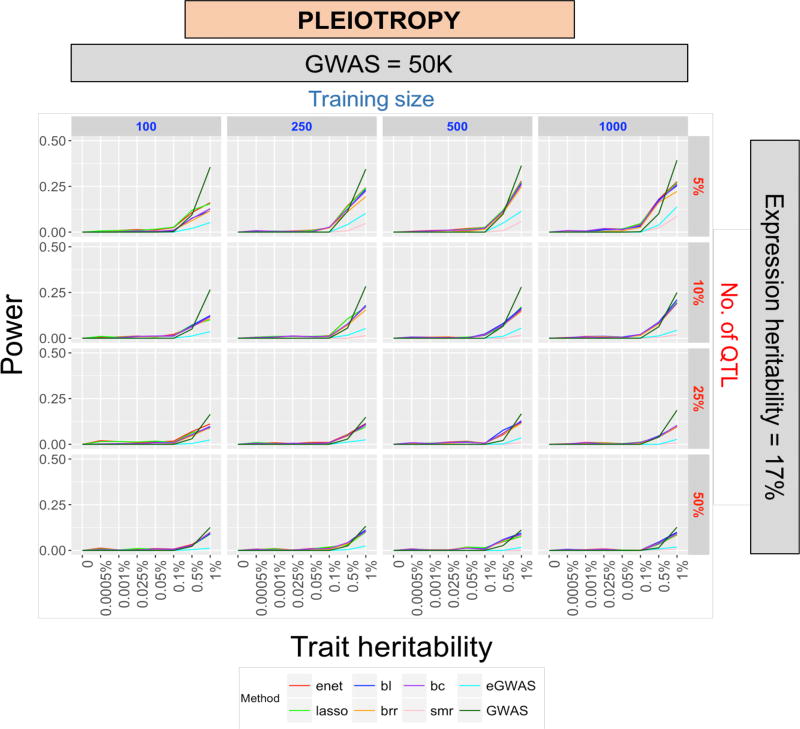
Under pleiotropy, GWAS always resulted in the best power among all the other methods considered (Figure 4) and the trend was consistent across training and GWAS sample sizes as well as levels of expression heritability (data not shown). Accordingly, the power peaked when number of causal variants was small. Interestingly, even with a trait heritability as high as 1%, we could only achieve a maximum power of approximately 40% with GWAS.

Figure 4. Power distributions under pleiotropy (reduced).

Power (y-axis) across trait heritability (x-axis) under varying levels of training sample sizes (in blue-columns) and no. of QTL (in red-rows), at GWAS sample size of 50K and expression heritability of 17%. Each plot represents power from 8 different models; TWAS-MP (LASSO, ENet, BL, BC, BRR), TWAS-SMR, eGWAS, and GWAS.

4. Discussion

TWAS have been introduced as a way to combine SNP-expression information and GWAS to identify genes whose expression levels are associated with a trait. A recent study has applied TWAS to over 30 different complex human traits to identify functional signatures in pleiotropic traits¹⁹. However, the scenarios under which different flavors of TWAS can achieve improved power as compared to eQTL-based GWAS and GWAS have not yet been explored. In this study, we examine the influence of complex genetic architectures and sample size on power afforded by different TWAS-based approaches (five TWAS-MP methods and TWAS-SMR), eGWAS and GWAS. We vary several simulation parameters including the number of QTL, the training sample size, the GWAS sample size, the trait heritability and the expression heritability under two genetic models (causality and pleiotropy) and examine the influence of each on power.

4.1 Training sample size

Training sample size is important since eQTL studies are typically limited in sample size. The NIH Common Fund project called Genotype Tissue Expression Project (GTEx²⁰) is assembling a database of SNP-expression associations spanning 43 different tissues. However, for any given tissue, the sample size is fairly low, ranging from approximately 77 (small intestine terminal ileum) to 161 (muscle skeletal). Other currently available SNP-expression studies are also limited in size, e.g. the Netherlands Twin Register (1,247 peripheral blood samples), the Metabolic Syndrome in Men study (563 adipose samples^21–23), the Genetic European Variation in Health and Disease (460 lymphoblastoid cell lines^8,24), Depression Genes and Network (922 whole blood samples²⁵), and Braineac (130 individuals with brain region samples²⁶). Accordingly, we explored training sample sizes ranging from 100 to 1,000 in this study. Under the assumption of causality, we see that even a sample size as small as 100 is sufficient to achieve 100% power for a gene with moderate expression heritability (17%) as long as the GWAS sample size is at least 150,000. Training sample size was not observed to have a marked influence under pleiotropy (Figure 4).

4.2 GWAS sample size

GWAS sample sizes have been increasing over the years using meta-analyses across multiple cohorts and a multitude of common variants have been detected for a host of complex traits and diseases. We observe that GWAS sample size plays a crucial role in also detecting gene-trait associations, especially under the assumption of causality. A high GWAS sample size can help detect genes with low expression heritability (and moderate to high trait heritability) even when the training sample size is small, especially under the assumption of causality (Figure 2).

4.3. Number of QTL

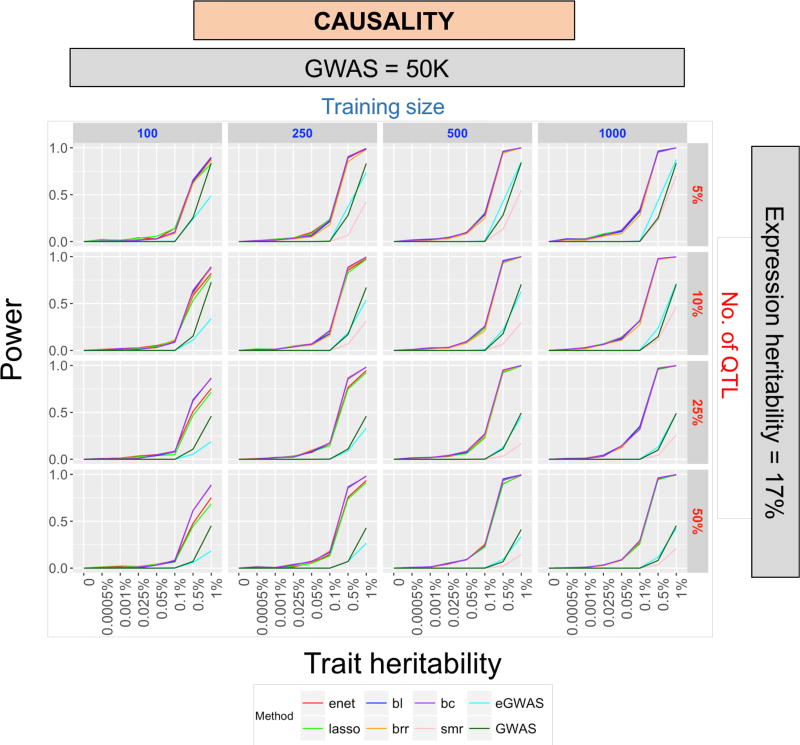
We chose genes with of sizes between 100 and 200 SNPs and included the region 500 kb upstream and downstream of the gene into our analyses to investigate the impact of the number of causal variants as well as the extent of LD between markers and causal variants on statistical power. It is known that these factors affect the prediction accuracy of a trait in whole-genome regression based studies^27,28. Under the assumption of causality (Figures 2 and 3), the number of QTL had a noticeable impact on power obtained using eGWAS, GWAS, and TWAS-SMR while that obtained from TWAS-MP was not significantly affected. This is understandable given that eQTL-guided GWAS, GWAS and TWAS-SMR only choose the top-most significant SNP/eQTL in the gene and lose a considerable portion of the genetic signal when the number of QTL forms a large proportion of the gene. This behavior, albeit muted, was also observed under pleiotropy (Figure 4).

Figure 3. Power distributions under causality (reduced).

Power (y-axis) across trait heritability (x-axis) under varying levels of training sample sizes (in blue-columns) and no. of QTL (in red-rows), at GWAS sample size of 50K and expression heritability of 17%. Each plot represents power from 8 different models; TWAS-MP (LASSO, ENet, BL, BC, BRR), TWAS-SMR, eGWAS, and GWAS.

4.4. Expression heritability

Few studies have thus far shed light on the average heritability of gene expression across different cohorts and tissues. This parameter refers to the proportion of variation in gene expression that can be explained by genotype. Under the genetic model of causality (Figures 2 and 3) we observe that expression heritability has a profound influence on power, especially when training sample size and GWAS sample sizes are moderate to low (e.g. top left-most panel in Figure 2). Under the genetic model of pleiotropy, expression heritability only has a slight influence on TWAS-MP but no effect on the other methods (eGWAS, GWAS and TWAS-SMR), irrespective of training and GWAS sample sizes (data not shown). This intuitive result confirms that even a gene with very high expression heritability is not likely to have high power to detect a gene-trait association when gene expression does not mediate between the SNP and the phenotype.

4.5. Trait heritability

Complex traits have widely varying heritability measures ranging from ~80–90% for height²⁹ to between 30%–70% for lipid traits³⁰. We chose an upper limit of 1%, which would correspond to a large-effect gene that explains almost 1% of the overall trait heritability. Under causality, we observed that TWAS-MP methods were powerful in detecting genes even with moderate trait heritability (17%) as long as the sample sizes were high (Figures 2 and 3). Under pleiotropy, we observed that a gene needed to have very high trait heritability (>1%) to be detected with moderate power (<40%) at best (Figure 4).

4.6. Genetic model

We only considered two genetic models in this study. The power obtained under pleiotropy was significantly lower than that obtained under causality, which demonstrates the weaknesses of TWAS methods when genes operate under non-causal genetic models (Figures 3–4).

4.7. Statistical model

In general, all TWAS-MP methods (LASSO, elastic net, BC, BRR, and BL) performed uniformly well and achieved high power under the assumption of causality. However, in particular, Bayesian methods performed better than LASSO and elastic net as the trait architecture grew more complex, expression heritability remained low and training sample sizes were small (Figure 2 and Table 1). This shows that LASSO and elastic net are more conducive for variable selection than BL, BRR, and BC and their performance worsens as a greater number of predictors in the model carry genetic signal. On the other hand, TWAS-SMR did much worse than TWAS-MP under all considered simulation scenarios. As expected, eGWAS, GWAS and TWAS-SMR had better power when the number of QTL was small although their performance still lagged behind that of TWAS-MP methods. As expression mediated weakly between SNP and trait, performance of TWAS worsened and assuming no mediation at all (pleiotropy), GWAS performed better than TWAS-MP, TWAS-SMR and eGWAS (which had uniformly poor power).

A limitation of this work is that our GWAS “meta-analysis” only comprised Caucasian males, which is likely to have resulted in a sample with far more homogeneous LD patterns than what can be expected in reality. Also, our meta-analysis (sampling with replacement) is likely to have resulted in inflated power due to sample relatedness. We will exploit more heterogeneous GWAS samples in the future and will also conduct type I error experiments to ensure type I error is well controlled. Also, we assumed that all causal variants were included in our model whereas in reality we might only have SNPs tagged to the causal variants. Finally, it is a worthwhile future exercise to compare power of TWAS-MP to TWAS-SMR when both eQTL and GWAS data have summary-level data.

In conclusion, we have presented a comprehensive power analysis for detecting gene-trait associations under a range of complex genetic architectures using approaches based on individual-level and/or summary-level data. In future, these methods could also be applied to integrate GWAS with other kinds of “omic” information aside from gene expression (e.g. metabolomics, methylation). This is a starting step to better understand methods that can illuminate genetic patterns and functional mechanisms underlying complex trait variation in a powerful yet computationally efficient manner.