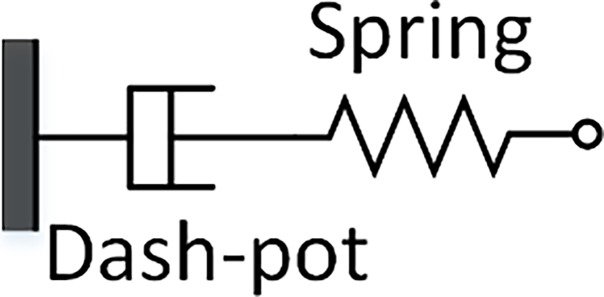Abstract
Viscoelasticity of soft tissue is often related to pathology, and therefore, has become an important diagnostic indicator in the clinical assessment of suspect tissue. Surgeons, particularly within head and neck subsites, typically use palpation techniques for intra-operative tumor detection. This detection method, however, is highly subjective and often fails to detect small or deep abnormalities. Vibroacoustography (VA) and similar methods have previously been used to distinguish tissue with high-contrast, but a firm understanding of the main contrast mechanism has yet to be verified. The contributions of tissue mechanical properties in VA images have been difficult to verify given the limited literature on viscoelastic properties of various normal and diseased tissue. This paper aims to investigate viscoelasticity theory and present a detailed description of viscoelastic experimental results obtained in tissue-mimicking phantoms (TMPs) and ex vivo tissues to verify the main contrast mechanism in VA and similar imaging modalities. A spherical-tip micro-indentation technique was employed with the Hertzian model to acquire absolute, quantitative, point measurements of the elastic modulus (E), long term shear modulus (η), and time constant (τ) in homogeneous TMPs and ex vivo tissue in rat liver and porcine liver and gallbladder. Viscoelastic differences observed between porcine liver and gallbladder tissue suggest that imaging modalities which utilize the mechanical properties of tissue as a primary contrast mechanism can potentially be used to quantitatively differentiate between proximate organs in a clinical setting. These results may facilitate more accurate tissue modeling and add information not currently available to the field of systems characterization and biomedical research.
Introduction
Evaluation of viscoelastic properties of targets plays a crucial role in material science and medical diagnosis. Specifically, a target’s elastic modulus (i.e. stiffness) and long term shear modulus (i.e. viscosity, resistance to flow) can be determined from the resultant displacement from an applied force. The viscoelasticity of soft tissues is often associated with pathological state, and therefore can be utilized as a diagnostic tool for resections, amongst other operations, to reduce the morbidity associated with the disease at hand. Such a tool can particularly assist surgeons with tumor excision procedures, which could potentially improve clinical outcome [1–3]. Based on recent studies, tumorous tissues are typically characterized by an elastic modulus that differs from surrounding healthy tissue by several orders of magnitude [4, 5]. Such tissue contrast has been leveraged to delineate tissue margins between diseased and normal regions [4, 5]. Currently, standard clinical practice, especially in head and neck subsites, relies heavily on palpation in determining relative tissue stiffness [1, 2]. This method is based on a qualitative assessment of the region, and in many cases, the size and/or the location of the lesion makes this technique an insufficient method for medical diagnosis. A non-invasive, accurate, and high-resolution technique that uses viscoelastic properties of tissue to generate contrast may be more appropriate to detect small tissue abnormalities that are otherwise occult in palpation assessment.
Over the last decade, there has been growing interest in studying viscoelastic properties of soft tissues. The relation between tissue feature and tissue pathology has primarily been explored by vibroacoustography (VA) and acoustic radiation force in combination with various imaging modalities (i.e. Magnetic Resonance (MR) and Optical Coherence Tomography (OCT)). While both VA and similar techniques are relatively new research imaging approaches that are used to investigate and reconstruct mechanical properties of tissue, VA has gained more attention due to its relatively high resolution, minimal cost, and potential real-time imaging capabilities [6]. In comparison to palpation, the spatial resolution of VA is in the sub-millimeter range and the depth of penetration is in the sub-centimeter range, making the technique more suitable for high-resolution detection and imaging of tissue abnormalities [7].
In VA, the target absorbs an applied oscillating force and produces an acoustic emission field at the beat frequency, which is detected by a nearby, highly sensitive hydrophone [8]. Our group has previously reported on a novel VA imaging system that has been used to generate high contrast maps of tissues in response to a localized acoustic radiation force in both TMPs and ex vivo human squamous cell carcinoma tissues [3, 9, 10]. Although multiple studies have investigated VA to detect abnormal from healthy tissue regions with enhanced boundaries [7, 9, 11, 12], a direct correlation has yet to be established between acoustic signal and mechanical measurements [3]. Steps towards confirming viscoelasticity as the main contrast mechanism of VA require quantification of the major components of viscoelasticity, elastic modulus, long term shear modulus, and relaxation time constant (i.e. decay time), in clinically relevant models [3, 13]. To maintain clinical relevance, these models must incorporate static values of viscoelasticity to best mimic standard clinical practices, particularly palpation, which rely on static evaluation of tissue.
Moreover, existing imaging modalities and their respective theoretical models either fail to include significant mechanical tissue properties (i.e. elastic modulus, long term shear modulus, or relaxation time constant) or oversimplify the model with too many theoretical assumptions [14, 15]. Therefore, there is a need for an imaging modality with a complete model that more accurately characterizes the properties of tissue. Current models have been explored, and while each pose significant findings, none are yet suitable for tumor delineation in viscoelastic imaging modalities, such as VA. Phase-domain photoacoustic sensing is able to calculate absorption constants using temporally-delayed laser pulses by chirping modulation. This optical absorption constant is dependent on the mechanical properties of the sample, more specifically density and heat capacity, as the sample thermally expands upon exposure to laser [16]. Modeling using photoacoustics has also led way to quantitative photoacoustic tomography (qPAT), which generates a map of tissue response to light energy absorption. Although conventional models of qPAT, particularly diffusion approximation and radiation transport, have shortcomings, a novel model utilizing Monte Carlo simulations proves promising, as generated images possess high contrast [17]. Both photoacoustic models place emphasis on optical absorbance of tissue, which suits the respective technologies very well, and serve as paradigms for future modeling. However, these models do not incorporate viscoelastic properties (i.e. elasticity, long term shear modulus, and time constant) to the extent that must be quantitatively determined for applications in intra-operative surgical procedures and development of viscoelastic imaging modalities such as VA.
Personalized cardiac biomechanical modeling, in relating kinematics to dynamics through patient-specific modeling, is an additional area that has been explored for mechanical modeling of tissue pathology. Simulated mechanical characterization of the left ventricle has presented novel surrogates for rheological and non-invasive imaging measurements. Accurate modeling of the left ventricle’s cardiac cycle using a Holzapfel-Ogden model was successfully implemented with paralleled MR images as validation [18]. The simulated measurements were calculated from sample-specific data including fiber orientations, ventricle cavity volume, and overall geometry of the ventricle. However, this model explicitly assumed that the myocardial tissue behaved as incompressible hyper-elastic material, and mandated robust model selection and parameterization that did not include viscoelastic-specific parameters.
Utilizing energy-based cost function to identify biomechanical frameworks of biological tissue is yet another promising approach in material characterization. However, this method has not yet demonstrated the ability to quantitatively characterize parameters of interest, particularly long term shear modulus and time constant, in more relevant clinical settings [19].
On the contrary, shear wave elastography developments by Kazemirad et al. may provide promising techniques in quantitative viscoelastic characterization. Loss modulus (i.e. viscosity) and storage modulus (i.e. elasticity), are calculated through this method, which indirectly provides estimation of mechanical properties of soft biological tissues for characterizations in medical applications [20]. Unfortunately, the current proposed model is frequency-dependent and is in terms of propagation distance when analyzing the cylindrical shear wave field produced by the homogeneous tissue. This further demonstrates that a more thorough methodology is still needed to provide valid and accurate mechanical characterization of tissue.
The work presented in this paper originates from our previous studies that correlated elastic properties of TMPs with radiation force intensity measurements from a VA system to develop a model to explore the observed behavior of targets under the acoustic radiation force [7]. Based on this previous correlational study between VA signal intensity and elastic moduli in TMPs, we concluded that additional parameters, specifically long term shear modulus and relaxation time constant, should be considered for more accurate modeling of viscoelastic properties of tissues. Herein, we use static rheological models, specifically the Hertzian model (see Appendix), to characterize mechanical properties of pre-clinical targets. This model was used in conjunction with micro-indentation technique to acquire absolute measurements of mechanical properties of TMPs and ex vivo animal tissues. Mechanical measurements were acquired in three types of TMPs, specifically agar, gelatin, and polyvinyl alcohol (PVA), at concentrations that mimic the acoustic properties of human tissue. A total of 10 measurements, 5 for each depth, were conducted on each phantom type.
Liver and gallbladder tissue from a porcine model and liver tissue from a rat model were also chosen to more closely mimic human tissues. A total of 13 liver samples and two gallbladder samples from two different porcine subjects were examined. Ex vivo indentation measurements consisted of a total of 34 porcine liver indentation measurements, 17 for each depth, and 7 measurements of porcine gallbladder tissue at one depth due to the tissue’s small thickness. This viscoelastic characterization test was also performed on 14 samples of rat liver tissue from three different subjects, resulting in 38 total measurements, 19 for each depth. A static, spherical-tip micro-indentation technique produced elastic modulus, long term shear modulus, and time constant values for ex vivo animal tissue and TMPs. The results were then compared and assessed for statistical significance. These results could be used in future studies that investigate the contrast mechanism of dynamic imaging techniques like VA and similar acoustic radiation techniques.
Modeling and methods
Biological tissues are modeled as viscoelastic materials due to the manifestation of hysteresis in their stress relaxation behavior [21, 22]. The word viscoelastic is a combination of viscous fluidity and elastic solidity, and thus, biological materials under stress and strain exhibit both viscous and elastic behavior. In modeling of materials, such as biological tissues, the linear elastic Hookean spring, which describes elasticity behavior, and the linear viscous Newtonian Dash-pot, which describes long term shear modulus behavior, are used in conjunction to examine and understand the performance of these materials under spring force and displacement. Fig 1 shows the linear elastic spring and linear viscous Dash-pot [21, 22].
Fig 1. Viscous Dash-pot and linear spring lumped element model connected in series.
The linear elastic spring relates stress, defined as the exerted force per unit area, to strain, defined as changes in length with respect to initial length, in a linear fashion by the elastic modulus (E). During this mechanical process, the material undergoes an instantaneous deformation upon loading and an instantaneous de-straining upon un-loading. Eq 1 illustrates the simplified relationship in a one-dimensional (1D) case:
| (1) |
where σ and ε represent stress and strain in 1D, respectively.
The linear viscous Dash-pot contains a piston-cylinder filled with a viscous fluid and, by definition, it linearly relates stress and strain by the long term shear modulus of the material (η). Eq 2 represents the linear elastic spring and linear viscous Dash-pot:
| (2) |
Multiple models, such as Maxwell Dash-pot, Kelvin-Voigt, and Hertzian, have been used to characterize the mechanical properties of biological tissues [21]. Of these three models considered for this paper, the Hertzian model was chosen to analyze the acquired data because a spherical-tip micro-indenter was used. As shown by Oyen, Hertzian model offers a versatile, depth-sensing indentation technique with spherical-tip indenters to predict accurate viscoelastic mechanical behavior of biological tissues [23]. Moreover, in this model, linear elastic deformation of both shapes is assumed with a quadratic pressure distribution along the area of contact and assumes only elastic deformation [24]. It also has previously been used for other biological spherical-tip micro-indentation experiments, including characterizing bovine ocular tissues [25]. The derivation of the model is included in the appendix.
Target preparations and experimental setup
Three TMP types, agar, polyvinyl alcohol (PVA), and gelatin, were fabricated and investigated. These materials were chosen to mimic relevant human anatomical structures (i.e. prostate, oral cavity, liver, and breast) in terms of acoustic and mechanical properties [10–12, 18–21]. The homogeneous TMPs were synthesized in molds with defined geometries. Due to the controlled phantom synthesis, the mean phantom thickness, measuring ~18 mm, did not vary among each phantom.
Fresh ex vivo liver and bile ducts were harvested from porcine and male Dewey rats shortly after each animal was euthanized under protocols #2009-094-23 for rat tissues and #2003–093 for porcine tissues. Since the ex vivo tissues were freshly excised, their thicknesses and geometrical arrangements were not identical to one another. The thicknesses were measured as the following: ~11 mm for porcine liver, ~6 mm for rat liver, and ~1 mm for porcine gallbladder. These excised samples were relatively flat and of similar lateral dimensions to avoid collection/slippage error. The fabrication process, rationale, and procedure for the TMPs and ex vivo tissues are attached in the appendix. Fig 2 illustrates the experimental set-up for ex vivo animal specimen undergoing micro-indentation.
Fig 2. Fig 2A displays an excised porcine liver sample placed in a petri dish prior to indentation, while Fig 2B illustrates the same porcine liver specimen undergoing the micro-indentation test.
Fig 2C illustrates the porcine gallbladder specimen undergoing the micro-indentation. Spherical tip diameter was adjusted due to the thickness of the specimen.
A 100 nm precision linear stepper motor and controller (LNR50 Series, Thorlabs, Newton, NJ) were synchronized with a 100 μg precision analytical balance (ML Model, Mettler-Toledo, Columbus, OH) to perform the viscoelastic measurements on the targets [25]. The stepper motor was connected to an acrylic rod that displaces a stainless steel sphere. A 2 mm diameter sphere was used to create an indentation depth of 300 μm and 400 μm for ex vivo porcine liver samples, 200 μm and 300 μm for ex vivo rat liver, and 100 μm for porcine gallbladder. Porcine gallbladder was only indented at one depth due to its very small thickness. A slightly larger, 4 mm diameter sphere was used to create indentation depths of 600 μm and 800 μm for all TMP targets. Two indentation depths were utilized to accurately compute viscoelastic behavior of each target and to further illustrate the stability and consistency of the measurement parameters.
For all micro-indentation measurements, the indentation depth was much less than the radius of the sphere to be in the theoretical regime of contact mechanics between sphere and flat surface. These indentation distances were also chosen based on the thickness of the targets to stay within the linear regime, ~3% strain rate, of the samples [24, 26]. The Hertzian model assumes indentation of up to 3% of the specimen’s thickness to be negligible in comparison to sample thickness, so that the substrate does not influence the calculations [27]. Every indentation was performed in a different location; therefore, pre-stress and timing constraint between consecutive indentations were not considered. The displacement depth for all targets, except gallbladder tissues, was less than the radius of the indenter to avoid any subsequent errors in the recordings.
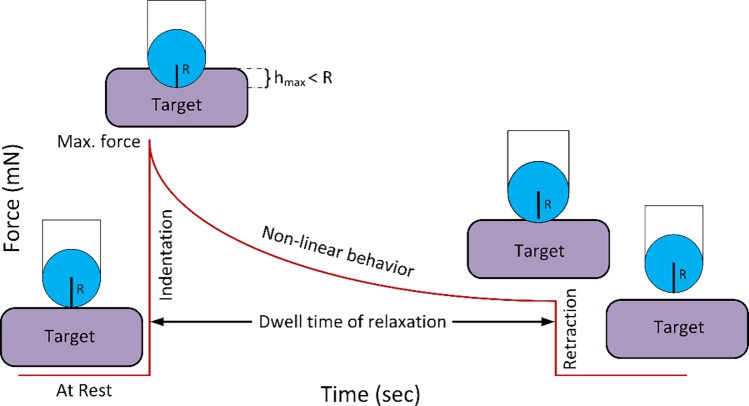
The indenter displaced downward against the targets, which were placed on an analytical balance pan. This balance served to record the force measurements. Prior to each measurement, the balance was zeroed to avoid surface tension errors, which are transiently negative values upon initial contact of the probe with the liquid layer of the tissue [25]. Shortly after, the target was indented by the sphere, at 2 mm/sec motor speed, generating a positive force by the target, conveying that contact has begun. Once the given displacement was reached, the indenter remained fixed in position, and the target was allowed to relax for approximately 300 seconds. During this period, the balance beneath the target recorded the applied force from the target to the sphere. Specimens were periodically moisturized using Ringer’s lactate solution throughout the entire experimental procedure. Moreover, in order to minimize changes in load due to evaporation of water surrounding the specimen, the load cell was surrounded by a glass closed-chamber on all sides except for a small slit for the indenter shaft. Fig 3 illustrates the experimental setup that was used to acquire measurements.
Fig 3. Spherical-tip micro-indentation experimental set-up.
As illustrated in the figure, the sphere induces indentation, smaller than its radius, into the target (Indentation period). After it reaches the maximum depth, it allows the target to relax, with regards to exerted force, in a period of 300 seconds (dwell time of relaxation period). After completion of the process, the sphere is moved away from the target (Retraction period).
Results
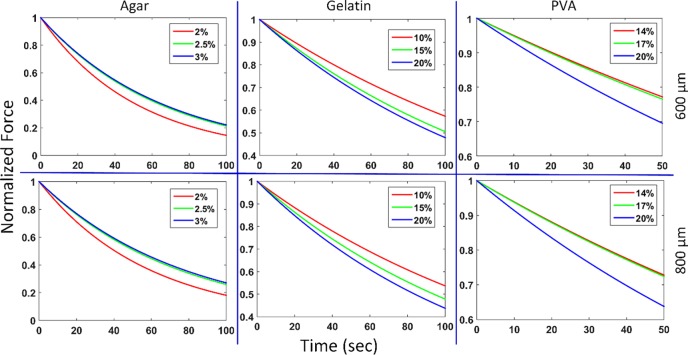
The viscoelastic behavior of TMPs and ex vivo porcine and rat tissues were examined by a micro-indentation technique using a stainless steel sphere. Fig 4 illustrates the relaxation plots for all TMPs and Table 1 shows the instantaneous elastic modulus, analogous to Young’s modulus, long term shear modulus, and time constants with standard deviation of the mean for all TMPs at the two different indentation depths. Elastic modulus and long term shear modulus values were calculated by fitting the collected data to a first order exponential decay [3]. From this function, the time constants were calculated using the single relaxation curve in MATLAB. The relatively small standard deviation of the mean for elastic modulus and long term shear modulus measurements of each phantom type shows a very small deviation from the mean in both indentation depths for all phantoms.
Fig 4. Mean elastic relaxation behavior plots of agar, gelatin, and PVA TMPs as a function of time.
The top and bottom rows illustrate the 600 μm and 800 μm indentation behaviors, respectively. As shown, gelatin and PVA have the same relaxation behavior, but the opposite is observed for agar TMPs.
Table 1. Mean elastic modulus, long term shear modulus, and time constant data, including standard deviation of the mean, for each type of TMP: PVA, gelatin, and agar.
| Phantom Type | Elastic Modulus (kPa) | Mean (kPa) | Standard Deviation | Long term Shear Modulus (MPa sec) | Mean (MPa sec) | Standard Deviation | Time Constant (sec) | ||
|---|---|---|---|---|---|---|---|---|---|
| 600 μm | 800 μm | 600 μm | 800 μm | ||||||
| 14% PVA | 5.722 | 5.598 | 5.660 | 0.158 | 1.105 | 0.883 | 0.994 | 0.040 | 175.657 |
| 17% PVA | 9.552 | 9.319 | 9.435 | 0.200 | 1.785 | 1.467 | 1.626 | 0.075 | 172.330 |
| 20% PVA | 33.563 | 33.866 | 33.715 | 1.015 | 4.693 | 3.824 | 4.259 | 0.273 | 126.317 |
| 10% Gelatin | 15.823 | 16.873 | 16.348 | 0.897 | 2.830 | 2.710 | 2.770 | 0.128 | 169.424 |
| 15% Gelatin | 43.518 | 46.903 | 45.210 | 2.243 | 6.390 | 6.358 | 6.374 | 0.309 | 140.988 |
| 20% Gelatin | 62.010 | 69.907 | 65.959 | 3.087 | 8.649 | 8.957 | 8.803 | 0.445 | 133.458 |
| 2% Agar | 106.497 | 102.778 | 104.638 | 3.911 | 5.595 | 6.000 | 5.797 | 0.210 | 55.405 |
| 2.5% Agar | 137.034 | 133.918 | 135.476 | 4.647 | 9.122 | 10.045 | 9.583 | 0.607 | 70.737 |
| 3% Agar | 199.049 | 191.284 | 195.166 | 4.281 | 13.575 | 14.913 | 14.244 | 0.840 | 72.984 |
As shown by the calculations in Table 1 and Fig 4, as the concentration of gelatin and PVA TMPs increases, the calculated time constant decreases, but in the case of agar TMPs, the exact opposite was observed. This result may be due to the structural properties as well as the structural cross-linking of the agar substituents within the phantom.
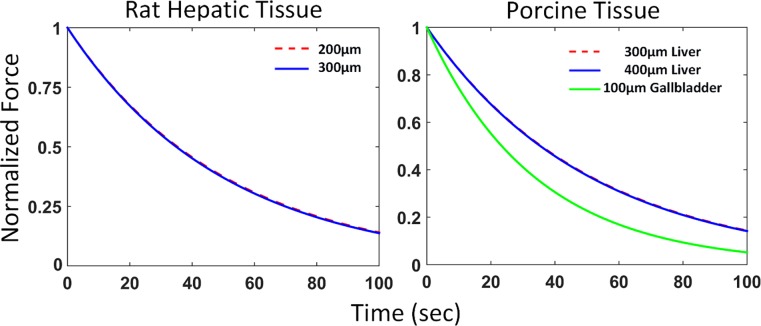
Fig 5 illustrates the relaxation plots and Table 2 shows the instantaneous elastic modulus, long term shear modulus, and time constant for ex vivo porcine liver, porcine gallbladder, and rat liver. All ex vivo tissues had small variations, as shown by their respective standard deviation of the mean in Table 2.
Fig 5. Mean elastic relaxation behavior plots of ex vivo animal tissues.
The liver tissues for both rat and porcine models decay exponentially in a similar fashion for both indentation depths. The relaxation behaviors of the porcine gallbladder and liver tissue are very distinct, illustrating their unique viscoelastic characteristics.
Table 2. Ex vivo porcine liver, porcine gallbladder, and rat liver elastic modulus, long term shear modulus, and time constant are calculated.
Standard deviation of the mean for each tissue is also computed.
| Tissue Type | Depth | Elastic Modulus (kPa) | Mean (kPa) | Standard Deviation | Long term Shear Modulus (MPa sec) | Mean (MPa sec) | Standard Deviation | Time Constant (sec) |
|---|---|---|---|---|---|---|---|---|
| Porcine Liver | 300 μm | 2.575 | 2.553 | 0.085 | 0.138 | 0.135 | 0.006 | 52.879 |
| 400 μm | 2.531 | 0.132 | ||||||
| Rat Liver | 200 μm | 2.890 | 2.758 | 0.094 | 0.154 | 0.147 | 0.007 | 53.299 |
| 300 μm | 2.626 | 0.140 | ||||||
| Porcine Gallbladder | 100 μm | 4.730 | 4.730 | 0.735 | 0.176 | 0.176 | 0.033 | 37.209 |
During gallbladder tissue preparation, excess bile was removed from the tissue to avoid slippage of the sphere indenter, which could have potentially affected the viscoelastic measurements. The standard deviation of the mean for both rat and porcine liver were very small due to consistency of the data; however, that error value was a bit higher for the gallbladder. This could be due to the remnants of bile that could not be removed, and the small tissue thickness of the gallbladder samples. In comparison to the liver tissues, the porcine gallbladder tissues demonstrate a smaller time constant, though a higher elastic modulus and long term shear modulus. Two-tailed unequal variance (heteroscedastic) T-tests were conducted for TMPs and ex vivo tissues, the results of which are illustrated in Table 3.
Table 3. Two-tailed T-test statistical analysis of elastic modulus and long term shear modulus of TMPs and ex vivo tissue specimen (α = 0.05).
The Small Depth corresponds to the lower indentation depth measurement of each tissue, while the Long Depth corresponds to the higher. Porcine gallbladder was only indented at one depth due to its small thickness.
| Subject Type | Depth | P-Value (α = 0.05) | |
|---|---|---|---|
| Elastic Modulus | Long Term Shear Modulus | ||
| 14% vs. 17% PVA | 600 μm | 0.00002 | 0.00005 |
| 800 μm | 0.00001 | 0.00343 | |
| 17% vs. 20% PVA | 600 μm | 0.00013 | 0.00091 |
| 800 μm | 0.00002 | 0.00040 | |
| 14% vs. 20% PVA | 600 μm | 0.00013 | 0.00188 |
| 800 μm | 0.00002 | 0.00044 | |
| 2% vs. 2.5% Agar | 600 μm | 0.01038 | 0.01720 |
| 800 μm | 0.00553 | 0.00145 | |
| 2.5% vs. 3% Agar | 600 μm | 0.00017 | 0.03186 |
| 800 μm | 0.00001 | 0.00582 | |
| 2% vs. 3% Agar | 600 μm | 0.00001 | 0.00318 |
| 800 μm | 0.00001 | 0.00082 | |
| 10% vs. 15% Gelatin | 600 μm | 0.00017 | 0.00043 |
| 800 μm | 0.00008 | 0.00011 | |
| 15% vs. 20% Gelatin | 600 μm | 0.00826 | 0.02962 |
| 800 μm | 0.00037 | 0.00560 | |
| 10% vs. 20% Gelatin | 600 μm | 0.00011 | 0.00035 |
| 800 μm | 0.00001 | 0.00005 | |
| Rat Liver vs. Porcine Liver | Small | 0.10364 | 0.27704 |
| Long | 0.57440 | 0.53586 | |
| Rat Liver vs. Poricne Gallbladder | Small | 0.04657 | 0.54677 |
| Porcine Liver vs. Porcine Gallbladder | Small | 0.02604 | 0.29875 |
The elastic modulus and long term shear modulus were significantly different among varying concentrations for each type of TMP. Hence, our mechanical testing methodology is evidently capable of producing distinct results for different types of viscoelastic material. Furthermore, there was no statistical significant difference between rat and porcine liver in both elastic and long term shear modulus, illustrating that liver possesses similar viscoelastic properties despite being from different species. Within the same animal, different organs were distinguished in terms of viscoelastic properties, as seen by the statistical significant difference between porcine liver and gallbladder elastic modulus. However, the long term shear modulus between the liver and gallbladder tissues were not significantly different.
Discussion
This paper characterizes the viscoelastic properties of TMPs and ex vivo animal tissues by examining elastic modulus, long term shear modulus, and relaxation time constant in a unique fashion. The Hertzian mathematical model and spherical-tip micro-indentation were used to analyze the observed relaxation curves. The generated relaxation curves were fitted to a first order exponential fit with a relatively high R2 value (i.e. > 0.9) for all cases. Based on our results and statistical analysis, elasticity, long term shear modulus, and relaxation time constant should be considered for mechanical modeling of biological tissue with viscoelastic behaviors.
The TMP elasticity measurements show three unique elastic moduli ranges: PVA: 1–40 kPa (low), gelatin: 10–100 kPa (medium), and agar: 100–200 kPa (high). Along with their corresponding long term shear modulus values, the TMPs were examined to cover a wide range of viscoelasticity for soft tissues, also previously shown by Wells and Liang [4]. The similarity in acoustic property trends between the selected TMPs and human tissues (see Appendix) makes this study a crucial stepping stone for imaging modalities like VA. Moreover, due to our unique experimental set-up and measurement calculations, direct comparisons are not forthright for each aspect of the TMP study. However, similar approaches have been made. Hamhaber et al. completed a quantitative comparison of a shear wave MR elastography technique with mechanical compression tests on agar-agar gel phantoms. This was done by comparing strain-generated wave amplitudes from shear-wave MR elastography to computed shear modulus, and performing dynamic mechanical compression tests in the range of 125–400 Hz [28]. They computed the elastic modulus of their 2% agar-agar elastic modulus by making an assumption of Poisson ratio of incompressible materials. Their results were within the same range of ours. Furthermore, Pavan et al. examined non-linear elastic behavior of gelatin and agar phantoms by using Bose Endura TEC 3200 ELF system [29]. They used large oscillatory deformations (~25% strain rate) on 2-month-old phantoms samples, whereas the phantoms used in our study were freshly made and experiments were conducted on the same day with a strain rate of ~3%. They reported higher values than those in this study, which could be due to the age of their phantoms along with their high deformation rates. However, the overall trend demonstrated in our study showed higher concentrations lead to higher elastic modulus values, similar to the trend generated from the study by Pavan et al. Additionally, elasticity measurements on TMPs performed by Chen et al. were conducted using uniaxial compression, though the accompanied rheological model was not specified, which may explain discrepancies in results. The group reported significantly higher elastic moduli for 2% agar, with values varying between 250–650 kPa depending on strain rate [30]. This may be because the group applied extreme strains of up to 1.0 on their samples, and utilized measurements from regions of up to 0.4 strain, whereas the strain utilized in our study was 0.03 to remain within the linear regime of the specimens.
Long term shear modulus and time constant characterization were other features that were analyzed. To the best of our knowledge, there are no straightforward comparisons with the literature, but there are related works on long term shear modulus of soft tissues and solids characterizations. Catheline et al. performed measurements of viscoelastic properties of bovine muscle using transient elastography by comparing Maxwell Dash-pot to Voigt model [31]. Kobayashi et al. also performed a similar study on viscoelastic solids with high long term shear modulus by uniform shear stress deformation method in a temperature controlled setting [32]. However, the long term shear modulus values reported by Catheline et al. are orders of magnitude smaller, while Kobayashi et al. presents values that are orders of magnitude higher, than the ones reported on TMPs in this paper. The different deformation methods along with different implemented assumptions could be reasons for these discrepancies. Kobayashi et al. used pure shear and mainly tensile (extensional) deformation mode, while Catheline et al. used transient elastography with frequency ranges 50–350 Hz in 25 Hz step sizes. Although both methods may be valid in their own respects, they do not seem ideal for applications in characterizing tissue pathology. Unlike the aforementioned studies, our p-values were below 0.05 among all TMP paired T-tests, for both elasticity as well as long term shear modulus. Our study is one of few to demonstrate reliability and precision in all viscoelastic characterizations. Moreover, spherical-tip micro-indentation may be the step forward for correlating tissue viscoelasticity and acoustic response.
Porcine liver and gallbladder tissues, along with rat livers, were tested using the same technique that was used for TMPs. The tissues were excised fresh, immediately after the animals were euthanized, and kept in a saline solution during transport to maintain tissue integrity. Many scientists use pre-conditioning techniques with cyclic deformations for their ex vivo sample preparations. However, this technique was not used in this study because the generated results were already in steady-state mode and the elastic modulus, long term shear modulus, and time constant calculations were consistent with very low standard deviation of the mean [33]. Moreover, the duration of examination for each sample was relatively short, ~15 minutes per sample, demonstrating the perseverance of the physiological conditions throughout the span of the measurement.
Similar to our TMP viscoelasticity results, there is no direct comparison for our generated ex vivo porcine and rat tissue viscoelasticity data within the literature, but some methodologies have been developed. Kerdok et al. characterized the effects of perfusion on the viscoelastic characteristics of porcine liver by using indentation devices to measure the organ’s creep response to applied loads [34]. Their calculated time constants for both porcine and rat liver were very similar to the ones calculated in this study, demonstrating similarity in physiological structure as well the accuracy of our measurements. Elastic modulus and long term shear modulus were not directly calculated in their study, but the calculated time constant can alone be a precursor to the viscoelastic measurements since in theory, the time constant is the product of elastic modulus and long term shear modulus, as seen in Eq 13 of the Appendix.
Venkatesh et al. and Chen et al. reported healthy in vivo human parenchyma, rat parenchyma, and porcine liver shear modulus and long term shear modulus values using Magnetic resonance elastography for human and rat parenchyma liver and Shear wave Dispersion Ultrasound Vibrometry for the porcine liver [35, 36]. For comparison with these studies, since liver is assumed as an incompressible material, the Poisson ratio was estimated to be 0.50 [4], and the calculated elastic moduli using the relationship in Eq 3 was ~6.16 kPa for human, ~6.58 kPa for porcine, and ~5.26 kPa for rat.
| (3) |
However, both our calculated elastic modulus and long term shear modulus values for porcine and rat livers are smaller than the values reported by Venkatesh et al. and Chen et al. One reason for this discrepancy could be due to the assumptions (i.e. tissue homogeneity, density, the implemented model (Voigt model)), as well as the detection scheme they used for calculating these values. Since micro-indentation was used in this study, some of these assumptions, particularly density and homogeneity, can be ignored, even though liver tissues are not homogeneous [37]. Moreover, placing a tissue on a hard surface induces external forces (i.e. stress) that are not present in the in vivo state. Other factors, such as capsules, blood flow, cellular association, amongst other in vivo conditions, need to be taken into account for accurate measurements. However, our measurements, for both rat and porcine liver, were free of these potentially confounding in vivo factors. As depicted in Table 3, there was no statistical significant difference between rat and porcine liver in both elastic and long term shear modulus. This further illustrates that liver possesses similar viscoelastic properties despite being from different animals. Also, the time constants and relaxation curves for both rat liver and porcine liver were very similar, and statistically insignificant (i.e. p-value >0.05), conveying that the viscoelasticity of liver is generally similar between these two animals.
Porcine gallbladder was the third tissue type characterized in this study. We sought to use the viscoelastic properties of the gallbladder to differentiate it among other close organs, particularly the porcine liver. As presented in Table 2, the elastic modulus was ~2 kPa higher than the liver and there was a difference of ~20 seconds in the time constants. The p-value is also significant when comparing elastic modulus of porcine gallbladder to that of both rat liver and porcine liver. Thus, there exists a distinct difference in viscoelastic properties between the two porcine tissue types, liver and gallbladder. Even though the two organs are relatively close to one-another, their respective viscoelastic properties can be used to differentiate the two, highlighting clear boundary distinction between the two tissue types. However, the long term shear modulus between the liver and gallbladder tissues were not significantly different, likely due to the relatively limited sample size of gallbladder specimen, small thickness of gallbladder, and remnants of excess bile on gallbladder tissues. Aside from the future work needed to fully characterize gallbladder long term shear modulus, our mechanical testing methodology is capable of producing distinct viscoelastic characterizations with statistical significance for different tissue types. Future studies will include comparison between static (i.e. micro-indentation) and dynamic measurements of viscoelasticity properties of tissues.
These results can be used to facilitate validation studies of viscoelastic imaging techniques with the aim of investigating mechanical properties of tissue as the primary source of image contrast to develop a mathematical model. Furthermore, complete dynamic mechanical characterization, particularly those which assess stress and strain rates that bring the tissue to failure, in both in vivo and ex vivo cases, are critical for establishing mathematical models. These properties can then be used in conjunction with imaging modalities (i.e. VA) to accurately and precisely describe viscoelastic mechanical behavior of targets for accurate identification, border detection, and system characterization in the field of medicine.
Conclusion
Accurate characterization and modeling of tissue still requires clinically relevant TMPs and fresh biological tissues. Given that biological tissues behave as viscoelastic materials, long term shear modulus, relaxation time constant, and elasticity must be considered in their evaluation. This study focuses on characterization of the viscoelastic properties of TMPs and ex vivo animal tissues; however, direct characterization and evaluation with ex vivo and possible in vivo biological organs in a dynamic fashion is still a necessity for further validation of mechanical properties. The experimental results in this study may bolster the possibility of using tissue mechanical properties, particularly viscoelasticity, as the primary contrast mechanism for developing new imaging modalities, like vibroacoustography (VA) and similar techniques. To this end, insights gained from assessment of animal tissues have helped researchers better understand the underlying mechanical behavior of biological tissue, but better ex vivo experimental setting (i.e. closer replication to non-homogeneous in vivo physiological parameters) must be implemented for optimal viscoelastic characterizations. Nevertheless, characterization and evaluation of ex vivo animal hepatic and gallbladder tissues under micro-indentation techniques, among other mechanical techniques, may furnish additional information that can guide researchers and scientists in modeling and investigative approaches for tissue response under a static force in target imaging (i.e. VA and similar techniques) and material characterization.
Appendix
Hertzian model
The solution for the viscoelastic spherical indentation relates the exerted force, F, from a rigid sphere with a radius, R, to the elastic modulus, E, and the Poisson ratio, ν, of an incompressible material at a given displacement, h, shown by Eq 4, where the viscoelastic counterpart of the Hertzian problem in elasticity is deduced from the elastic solution proposed by Hertz [38]. In this solution, the viscoelastic operators are substituted for elastic constants in the elastic solution, which allows for an identification of relaxation time constant behavior of specimens in terms of elastic modulus, Poisson ratio, indentation depth, and short and long-term shear elastic moduli. This solution is based on a single relaxation curve fit and utilizes a “ramp correction factor” (RCF) approach to correct the difference between ramp and step loading cycles for each exponential decay.
| (4) |
The Poisson ratio, the ratio of the transverse contracting strain to the elongation strain, of incompressible biological materials is assumed to be between 0.45 to 0.50. However, Poisson ratio was chosen to be 0.50, a common approximation used in literature for all TMPs and ex vivo animal tissues in this study [39, 40].
The relaxation response of a step-load (i.e. ideal), rigid, spherical-tip indenter to the material as a function of time and shear modulus, G (t), is illustrated by Eq 5:
| (5) |
where time-dependent shear relaxation modulus, G(t), is equal to E(t)/3. The observed rise time (tR) in real instances is not an instantaneous step loading process, as opposed to the ideal cases; hence the ramp correction factor (RCF) is used. Therefore, the viscoelastic integral operator for relaxation, where u is a strain function in terms of τ is used and is shown by Eq 6:
| (6) |
By combing Eqs 5 and 6, the real exerted force as a function of time, Freal (t) is:
| (7) |
As shown by Mattice et al.[41], the Boltzmann integral method is used to solve Eq 7 and for ramp-loading rate, k, displacement for ramp-hold relaxation can be written as:
| (8) |
| (9) |
Since the load, F(t), exponentially decays during the process, the solution is expressed as the step-loading relaxation solution adjusted by an RCF due to non-instantaneous ramp loading. Only the first two terms are considered for simplicity in calculations, as shown in Eqs 10 and 11 [23, 42]:
| (10) |
| (11) |
Where τ1 rpresents the time constant for the first exponential decay. A0 and A1, and B0 and B1 represent the fitting constants and the relaxation coefficients, respectively. Only the first term of both the fitting constants and relaxation coefficients (i.e. A0 and B0) are computed to compare the material relaxation in terms of applied force with the Wiechert theoretical model [43]. Once all the fitting parameters, A0 and A1, have been determined, they are converted to relaxation parameters, B0 and B1, using Eqs 12, 13 and 14, where tr is time that it takes for the force to reach its maximum value:
| (12) |
| (13) |
| (14) |
Instantaneous modulus, E(0), can be computed from the fitted relaxation coefficients using Eq 15:
| (15) |
The long term shear modulus, η, for each type of material can be calculated with Eq 16 [21]:
| (16) |
Target preparation
The target preparation was divided into two parts: an investigation of 1) TMPs and 2) ex vivo hepatic and bile duct tissues in pre-clinical animal models. For the first part of this study, certain physical geometries and sizes of phantoms were used to satisfy homogeneity and isotropy assumptions for viscoelastic calculations. Additionally, flat, ideal-sized samples of animal tissues were chosen to avoid slippage of the indenter and to reduce any generated noise from the measurements for the second part of the study.
Three TMP types, agar, polyvinyl alcohol (PVA), and gelatin, were fabricated and investigated. These materials were chosen to mimic relevant human anatomical structures (i.e. prostate, oral cavity, liver, and breast) in terms of acoustic and mechanical properties [10–12, 18–21]. These water-based gels particularly satisfy the acoustic properties of human tissues, including the speed of sound (about 1540 m/s), attenuation (~0.5 dB-1 cm-1 MHz-1), and backscatter coefficient (between 10−5 and 10−2, between 2 and 7 MHz) [4].
These phantoms were also selected due to their distinguished elasticity ranges: PVA falls in the lower end of the elastic moduli spectrum at 1–40 kPa; gelatin is slightly higher at 10–100 kPa, and agar occupies the highest range at 100–200 kPa. In particular, 15% gelatin, 3% agar, and 17% PVA were fabricated due to their respective similarities to the acoustic velocity, acoustic impedance, and acoustic attenuation of ideal, healthy human tissue [4, 44–49].
For instance, the acoustic velocity in the PVA phantoms were shown to vary from 1520–1540 m/s, which is within the typical range for human soft tissue. Furthermore, PVA phantoms ranging between 14% to 20% are characterized by acoustic impedances similar to those of human breast and skin tissue. Agar TMPs, particularly within the range of 2% to 4%, match the acoustic properties of human prostate tissues. Lastly, the selected gelatin phantom concentrations mimic the acoustic attenuation of human tissues, specifically breast, liver, head and neck, and prostate [45–47, 50].
Agar (Agar, Sigma-Aldrich, St. Louis, MO) blocks of varying deionized water/agar concentrations were fabricated in a ~20 x 20 x 18 mm3 plastic mold. Three separate rectangular blocks of agar containing 2, 2.5, and 3%wt of agar were mixed and heated above their gel point (~90 oC) to maximize cross-linking between the polymers. Increasing the amount of powdered extract in the mixtures was predicted to result in a corresponding increase in the elastic modulus of the phantom.
Gelatin (Porcine Gelatin, Sigma-Aldrich, St. Louis, MO) blocks of 10, 15, and 20%wt were used as a second type of TMP. Similar procedures as agar phantoms were used in the preparations of gelatin phantoms; however, the final mixture was placed in a centrifuge at a rotation speed of two rcf (relative centrifugal force) for a period of ~25 seconds to remove air bubbles from the solution.
Finally, a third type of TMP, PVA (99% hydrolyzed, Sigma-Aldrich, St. Louis, MO), was fabricated using the same procedure as stated above. Three cubic blocks (same dimensions as agar and gelatin phantoms) containing 14, 17, and 20%wt of PVA were synthesized. Unlike agar and gelatin phantoms, the final PVA mixtures were left at room temperature to cool down for ~two hours and then placed in a freezer at -20 0C for a period of 24 hours. The phantoms were then taken out of the freezer and allowed to thaw at room temperature for ~two hours, completing one freezing-thawing cycle. All phantoms, agar, gelatin, and PVA, were made at least 90 minutes prior to measurements to avoid any confounding errors (i.e. dryness and degradation) in the collected data.
Fresh ex vivo liver and bile ducts were harvested from porcine and male Dewey rats shortly after each animal was euthanized with Isofluorane (5–30%, vapor only, no direct contact for rat) and intravenous injection of pentobarbital per weight for porcine. Approval was granted by UCLA institutional animal care and use committee (IACUC), protocols #2009-094-23 for rat tissues and #2003–093 for porcine tissues. The samples were stored in saline solution to avoid tissue dryness and degradation and maintain ideal physiological conditions during transportation to the measurement laboratory. Prior to measurements, the tissues were taken out of the saline solution and cut into smaller pieces measuring ~15 x 15 x 10 mm3 for porcine liver and slightly thinner for the other tissue types. After sectioning the samples, they were placed in a petri dish on a balance for viscoelastic measurements. Specimens were periodically moisturized using Ringer’s lactate solution to coat the specimen with isotonic fluid during the entire experimental procedure.
Acknowledgments
The authors would like to thank UCLA Vivarium for their help and contributions.
Data Availability
All relevant data are within the paper.
Funding Statement
This work is supported by U.S. Public Health Service, National Eye Institute: grants EY008313 and EY000331 to Andrew Shin. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Vigneswaran N, Williams MD. Epidemiological trends in head and neck cancer and aids in diagnosis. Oral and maxillofacial surgery clinics of North America. 2014;26(2):123 doi: 10.1016/j.coms.2014.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Epstein JB, Güneri P, Boyacioglu H, Abt E. The limitations of the clinical oral examination in detecting dysplastic oral lesions and oral squamous cell carcinoma. The Journal of the American Dental Association. 2012;143(12):1332–42. [DOI] [PubMed] [Google Scholar]
- 3.Maccabi A, Taylor Z, Bajwa N, Clair JM-S, John MS, Sung S, et al. An examination of the elastic properties of tissue-mimicking phantoms using vibro-acoustography and a muscle motor system. Review of Scientific Instruments. 2016;87(2):024903 doi: 10.1063/1.4942049 [DOI] [PubMed] [Google Scholar]
- 4.Wells PN, Liang H-D. Medical ultrasound: imaging of soft tissue strain and elasticity. Journal of the Royal Society Interface. 2011;8(64):1521–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Streitberger K-J, Reiss-Zimmermann M, Freimann FB, Bayerl S, Guo J, Arlt F, et al. High-resolution mechanical imaging of glioblastoma by multifrequency magnetic resonance elastography. PloS one. 2014;9(10):e110588 doi: 10.1371/journal.pone.0110588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Urban MW, Alizad A, Aquino W, Greenleaf JF, Fatemi M. A review of vibro-acoustography and its applications in medicine. Current medical imaging reviews. 2011;7(4):350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fatemi M, Manduca A, Greenleaf JF. Imaging elastic properties of biological tissues by low-frequency harmonic vibration. Proceedings of the IEEE. 2003;91(10):1503–19. [Google Scholar]
- 8.Fatemi M, Greenleaf JF. Vibro-acoustography: An imaging modality based on ultrasound-stimulated acoustic emission. Proceedings of the National Academy of Sciences. 1999;96(12):6603–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Maccabi A, Arshi A, Garritano J, Saddik G, Kohanbash E, Tajudeen B, et al. Ultrasound-stimulated vibro-acoustography for high-resolution differentiation based on viscoelastic properties of tissue mimicking phantoms. Studies in health technology and informatics. 2014;196:262 [PubMed] [Google Scholar]
- 10.Maccabi A, Garritano J, Arshi A, Saddik G, Tajudeen BA, John MS, et al. , editors. Ex vivo viscoelastic characterization of head and neck tissue abnormalities using ultrasound-stimulated vibro-acoustography (USVA). SPIE Medical Imaging; 2014: International Society for Optics and Photonics. [Google Scholar]
- 11.Alizad A, Fatemi M, Wold LE, Greenleaf JF. Performance of vibro-acoustography in detecting microcalcifications in excised human breast tissue: A study of 74 tissue samples. Medical Imaging, IEEE Transactions on. 2004;23(3):307–12. [DOI] [PubMed] [Google Scholar]
- 12.Alizad A, Whaley DH, Greenleaf JF, Fatemi M. Critical issues in breast imaging by vibro-acoustography. Ultrasonics. 2006;44:e217–e20. doi: 10.1016/j.ultras.2006.06.021 [DOI] [PubMed] [Google Scholar]
- 13.Aguiló M, Aquino W, Brigham JC, Fatemi M. An inverse problem approach for elasticity imaging through vibroacoustics. Medical Imaging, IEEE Transactions on. 2010;29(4):1012–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fatemi M, Greenleaf JF. Probing the dynamics of tissue at low frequencies with the radiation force of ultrasound. Physics in medicine and biology. 2000;45(6):1449 [DOI] [PubMed] [Google Scholar]
- 15.Fatemi M, Greenleaf JF. Imaging the viscoelastic properties of tissue Imaging of Complex Media with Acoustic and Seismic Waves: Springer; 2002. p. 257–76. [Google Scholar]
- 16.Gao F, Zhang R, Feng X, Liu S, Ding R, Kishor R, et al. Phase-domain photoacoustic sensing. Applied Physics Letters. 2017;110(3):033701. [Google Scholar]
- 17.Liu Y, Jiang H, Yuan Z. Two schemes for quantitative photoacoustic tomography based on Monte Carlo simulation. Medical physics. 2016;43(7):3987–97. doi: 10.1118/1.4953185 [DOI] [PubMed] [Google Scholar]
- 18.Asner L, Hadjicharalambous M, Chabiniok R, Peresutti D, Sammut E, Wong J, et al. Estimation of passive and active properties in the human heart using 3D tagged MRI. Biomechanics and modeling in mechanobiology. 2016;15(5):1121–39. doi: 10.1007/s10237-015-0748-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nasopoulou A, Shetty A, Lee J, Nordsletten D, Rinaldi CA, Lamata P, et al. Improved identifiability of myocardial material parameters by an energy-based cost function. Biomechanics and Modeling in Mechanobiology. 2017;16(3):971–88. doi: 10.1007/s10237-016-0865-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kazemirad S, Bernard S, Hybois S, Tang A, Cloutier G. Ultrasound shear wave viscoelastography: Model-independent quantification of the complex shear modulus. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2016;63(9):1399–408. doi: 10.1109/TUFFC.2016.2583785 [DOI] [PubMed] [Google Scholar]
- 21.Roylance D. Engineering viscoelasticity. Department of Materials Science and Engineering–Massachusetts Institute of Technology, Cambridge MA. 2001;2139:1–37. [Google Scholar]
- 22.Kelly P. Solid Mechanics. Part. 2008;1:301–13. [Google Scholar]
- 23.Oyen ML. Spherical indentation creep following ramp loading. Journal of Materials Research. 2005;20(8):2094–100. [Google Scholar]
- 24.Johnson KL. Contact mechanics Cambridge university press, Cambridge New York; 1985. [Google Scholar]
- 25.Yoo L, Reed J, Shin A, Kung J, Gimzewski JK, Poukens V, et al. Characterization of ocular tissues using microindentation and hertzian viscoelastic models. Investigative ophthalmology & visual science. 2011;52(6):3475–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Popov V. Contact mechanics and friction: physical principles and applications: Springer Science & Business Media; 2010. [Google Scholar]
- 27.Yoo L, Reed J, Shin A, Demer JL. Atomic force microscopy determination of Young׳ s modulus of bovine extra-ocular tendon fiber bundles. Journal of biomechanics. 2014;47(8):1899–903. doi: 10.1016/j.jbiomech.2014.02.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hamhaber U, Grieshaber F, Nagel J, Klose U. Comparison of quantitative shear wave MR‐elastography with mechanical compression tests. Magnetic Resonance in Medicine. 2003;49(1):71–7. doi: 10.1002/mrm.10343 [DOI] [PubMed] [Google Scholar]
- 29.Pavan TZ, Madsen EL, Frank GR, Carneiro AAO, Hall TJ. Nonlinear elastic behavior of phantom materials for elastography. Physics in medicine and biology. 2010;55(9):2679 doi: 10.1088/0031-9155/55/9/017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen AI, Balter ML, Chen MI, Gross D, Alam SK, Maguire TJ, et al. Multilayered tissue mimicking skin and vessel phantoms with tunable mechanical, optical, and acoustic properties. Medical physics. 2016;43(6):3117–31. doi: 10.1118/1.4951729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Catheline S, Gennisson J-L, Delon G, Fink M, Sinkus R, Abouelkaram S, et al. Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: an inverse problem approach. The Journal of the Acoustical Society of America. 2004;116(6):3734–41. [DOI] [PubMed] [Google Scholar]
- 32.Kobayashi H, Hiki Y, Takahashi H. An experimental study on the shear viscosity of solids. Journal of applied physics. 1996;80(1):122–30. [Google Scholar]
- 33.Brouwer I, Ustin J, Bentiey L, Dhruv A, Tendick F, editors. Measuring in vivo animal soft tissue properties for haptic modeling in surgical. Medicine meets virtual reality; 2001. [PubMed] [Google Scholar]
- 34.Kerdok AE, Ottensmeyer MP, Howe RD. Effects of perfusion on the viscoelastic characteristics of liver. Journal of Biomechanics. 2006;39(12):2221–31. doi: 10.1016/j.jbiomech.2005.07.005 [DOI] [PubMed] [Google Scholar]
- 35.Venkatesh SK, Yin M, Ehman RL. Magnetic resonance elastography of liver: technique, analysis, and clinical applications. Journal of Magnetic Resonance Imaging. 2013;37(3):544–55. doi: 10.1002/jmri.23731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen S, Urban MW, Pislaru C, Kinnick R, Zheng Y, Yao A, et al. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on. 2009;56(1):55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang MH, Palmeri ML, Guy CD, Yang L, Hedlund LW, Diehl AM, et al. In vivo quantification of liver stiffness in a rat model of hepatic fibrosis with acoustic radiation force. Ultrasound in medicine & biology. 2009;35(10):1709–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee EH, Radok JRM. The contact problem for viscoelastic bodies. Journal of Applied Mechanics. 1960;27(3):438–44. [Google Scholar]
- 39.Krouskop TA, Wheeler TM, Kallel F, Garra BS, Hall T. Elastic moduli of breast and prostate tissues under compression. Ultrasonic imaging. 1998;20(4):260–74. doi: 10.1177/016173469802000403 [DOI] [PubMed] [Google Scholar]
- 40.Kruse S, Smith J, Lawrence A, Dresner M, Manduca A, Greenleaf JF, et al. Tissue characterization using magnetic resonance elastography: preliminary results*. Physics in medicine and biology. 2000;45(6):1579 [DOI] [PubMed] [Google Scholar]
- 41.Mattice JM, Lau AG, Oyen ML, Kent RW. Spherical indentation load-relaxation of soft biological tissues. Journal of Materials Research. 2006;21(8):2003–10. [Google Scholar]
- 42.Chua WK, Oyen ML. Viscoelastic properties of membranes measured by spherical indentation. Cellular and Molecular Bioengineering. 2009;2(1):49–56. [Google Scholar]
- 43.Shin A, Yoo L, Demer JL. Viscoelastic Characterization of Extraocular Z-MyotomyBiomechanics of Z-Myotomy. Investigative ophthalmology & visual science. 2015;56(1):243–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cao R, Huang Z, Varghese T, Nabi G. Tissue mimicking materials for the detection of prostate cancer using shear wave elastography: A validation study. Medical physics. 2013;40(2):022903 doi: 10.1118/1.4773315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dunmire B, Kucewicz JC, Mitchell SB, Crum LA, Sekins KM. Characterizing an agar/gelatin phantom for image guided dosing and feedback control of high-intensity focused ultrasound. Ultrasound in medicine & biology. 2013;39(2):300–11. [DOI] [PubMed] [Google Scholar]
- 46.Madsen EL, Hobson MA, Shi H, Varghese T, Frank GR. Tissue-mimicking agar/gelatin materials for use in heterogeneous elastography phantoms. Physics in medicine and biology. 2005;50(23):5597 doi: 10.1088/0031-9155/50/23/013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jiang S, Liu S, Feng W. PVA hydrogel properties for biomedical application. Journal of the mechanical behavior of biomedical materials. 2011;4(7):1228–33. doi: 10.1016/j.jmbbm.2011.04.005 [DOI] [PubMed] [Google Scholar]
- 48.Cournane S, Cannon L, Browne J, Fagan A. Assessment of the accuracy of an ultrasound elastography liver scanning system using a PVA-cryogel phantom with optimal acoustic and mechanical properties. Physics in medicine and biology. 2010;55(19):5965 doi: 10.1088/0031-9155/55/19/022 [DOI] [PubMed] [Google Scholar]
- 49.Zell K, Sperl J, Vogel M, Niessner R, Haisch C. Acoustical properties of selected tissue phantom materials for ultrasound imaging. Physics in medicine and biology. 2007;52(20):N475 doi: 10.1088/0031-9155/52/20/N02 [DOI] [PubMed] [Google Scholar]
- 50.Hall TJ, Bilgen M, Insana MF, Krouskop T. Phantom materials for elastography. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on. 1997;44(6):1355–65. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.