A model for cooperative gating of L-type Ca²⁺ channels and its effects on cardiac alternans dynamics

Abstract

In ventricular myocytes, membrane depolarization during the action potential (AP) causes synchronous activation of multiple L-type Ca_V1.2 channels (LTCCs), which trigger the release of calcium (Ca²⁺) from the sarcoplasmic reticulum (SR). This results in an increase in intracellular Ca²⁺ (Ca_i) that initiates contraction. During pulsus alternans, cardiac contraction is unstable, going from weak to strong in successive beats despite a constant heart rate. These cardiac alternans can be caused by the instability of membrane potential (V_m) due to steep AP duration (APD) restitution (V_m-driven alternans), instability of Ca_i cycling (Ca²⁺-driven alternans), or both, and may be modulated by functional coupling between clustered Ca_V1.2 (e.g. cooperative gating). Here, mathematical analysis and computational models were used to determine how changes in the strength of cooperative gating between LTCCs may impact membrane voltage and intracellular Ca²⁺ dynamics in the heart. We found that increasing the degree of coupling between LTCCs increases the amplitude of Ca²⁺ currents (I_CaL) and prolongs AP duration (APD). Increased AP duration is known to promote cardiac alternans, a potentially arrhythmogenic substrate. In addition, our analysis shows that increasing the strength of cooperative activation of LTCCs makes the coupling of Ca²⁺ on the membrane voltage (Ca_i→V_m coupling) more positive and destabilizes the V_m-Ca_i dynamics for V_m-driven alternans and Ca_i-driven alternans, but not for quasiperiodic oscillation. These results suggest that cooperative gating of LTCCs may have a major impact on cardiac excitation-contraction coupling, not only by prolonging APD, but also by altering Ca_i→V_m coupling and potentially promoting cardiac arrhythmias.

Author summary

Recent experimental studies have suggested that clusters of L-type Ca_V1.2 channels (LTCCs) can open and close in unison (i.e., cooperative or coupled gating) and that this gating modality may regulate excitation-contraction coupling in the heart. However, whether amplification of Ca²⁺ influx by cooperative gating of LTCCs promotes alternans is unknown. In this study, we developed a novel computational model of cooperative gating of LTCCs from experimental data. We incorporate the model into a physiologically detailed action potential (AP) model and investigated how changes in coupling strength of LTCCs may impact dynamics of AP and Ca²⁺ alternans. Our data suggest that increasing coupling strength of LTCCs prolongs AP duration and leads to Ca²⁺ overload. In addition, our theoretical and computational approaches elucidate that increasing coupling strength of LTCCs promotes positive Ca_i→V_m coupling, which could lead to V_m-driven and Ca²⁺-driven alternans.

Introduction

L-type Ca_V1.2 channels (LTCC) play a critical role in triggering cardiac muscle contraction during the action potential (i.e., excitation-contraction (EC) coupling) [1]. LTCCs are distributed in small clusters of about 10–12 [2–5] channels along the sarcolemma of these cells [1]. At the membrane potential reached during the plateau phase of the ventricular action potential (AP), LTCCs open, allowing Ca²⁺ ions to enter the cell. This Ca²⁺ signal is amplified via Ca²⁺-induced Ca²⁺ release through opening of ryanodine receptors (RyRs) from the sarcoplasmic reticulum (SR), which causes a cell-wide increase in Ca²⁺ that triggers cell contraction [6, 7].

Recent experimental studies [2, 8, 9, 28] have suggested that clusters of LTCCs can open and close in unison (i.e., cooperative or coupled gating). Functional coupling between LTCCs requires Ca²⁺ for the induction of physical interactions between adjacent channels that ultimately leads to amplification of Ca²⁺ influx. This suggests the intriguing hypothesis that cooperative gating of LTCCs may impact membrane voltage (V_m) and intracellular Ca²⁺ (Ca_i) cycling dynamics.

In cardiac myocytes, the dynamics of V_m are highly nonlinear. The LTCC current (I_CaL) is one of the major currents, which determines the plateau membrane potential and regulates V_m dynamics. For example, a slower recovery of LTCC steepens the action potential duration (APD) restitution curve and promotes APD alternans [10–12]. Also, reactivation of LTCC during the plateau phase can cause early afterdepolarizations [13–15]. Furthermore, intracellular Ca²⁺ cycling also has its own nonlinear dynamics [12, 16]. In fact, AP clamp experiments showed that the unstable Ca_i cycling can induce Ca_i transient alternans without APD alternans [16]. The dynamics of Ca_i cycling is primary regulated by a steep SR Ca²⁺ release vs. SR Ca²⁺ load relationship [17–19] and thus RyR sensitization or Ca²⁺ overload often leads to Ca²⁺ alternans.

In this study, we generated a novel computational model of I_CaL based on experimental data and APs that incorporates cooperative gating of LTCCs and used it in physiologically detailed AP models to investigate the effects of varied degrees of LTCC coupling on Ca²⁺ entry, APD, and the likelihood of promoting voltage and Ca²⁺ alternans.

Materials and methods

We developed two computational models. One is a totally stochastic model of cooperative gating (hereafter, we call it ‘stochastic model’). In this model, we simulated individual LTCCs described by a stochastic Markov model. Using this model, we investigated I_CaL properties by comparing with experimental observations. The other is a deterministic model based on the stochastic model (hereafter, we call it ‘ionic model’). Since simulation of the stochastic model is highly computationally intensive and thus time-consuming, we developed the ionic model to permit the investigation of steady state alternans within a practical time frame.

Stochastic model

We used a physiologically detailed subcellular Ca²⁺ cycling model as in our previous studies [20–22], which is based on the rabbit ventricular myocyte model by Restrepo et al. [23]. Whereas the main structure of our model is similar to the Restrepo model, a key difference in our model is the open probability of RyRs. We reduced the number of RyRs opening during a spark from nearly 100 in the Restrepo model to only 5–10 to fit the experimental observation [20].

Cell geometry

The dimension of this model is 121 μm × 25 μm × 11 μm and there are 19,305 (65×27×11) Ca²⁺ release units (CRUs). The separations of CRU are 1.84 μm and 0.9 μm in the longitudinal direction and transverse direction, respectively. Experimental observations indicate that each CRU contains about 10 LTCCs [24, 25]. Each CRU in this model contains at least 1 LTCC, but no more than 25. The cluster size obeys Gaussian distribution with a mean of 10 and standard deviation of 3. One CRU contains 100 RyRs, thus yielding ~1,930,500 RyRs in the cell. In each CRU, there are 5 compartments for Ca²⁺; cytosolic Ca²⁺ ([Ca²⁺]_i, c_i in equations), sub-membrane Ca²⁺ ([Ca²⁺]_s, c_s in equations), cleft space Ca²⁺ ([Ca²⁺]_Cleft, c_p in equations), network SR Ca²⁺ ([Ca²⁺]_SR, c_NSR in equations), and junctional SR Ca²⁺ ([Ca²⁺]_JSR, c_JSR in equations). CRUs are connected by Ca²⁺ diffusion in the cytosol and the network SR. The RyR is described by a four-state Markovian model and each RyR also opens stochastically depending on cleft space Ca²⁺ concentration ([Ca²⁺]_Cleft) and junctional SR Ca²⁺ concentration ([Ca²⁺]_JSR). SERCA pumps are distributed equally over the cell.

Ca²⁺ cycling

Intracellular Ca²⁺ cycling is governed by the following equations:

$$\begin{array}{c}\frac{d{c}_i^n}{dt}={\beta }_i\left(c_i^n\right)\left(I_{dsi}\frac{v_s}{v_i}-I_{up}-I_{TCi}+I_{ci}\right),\\ \frac{d{c}_s^n}{dt}={\beta }_s\left(c_s^n\right)\left(I_{dps}\frac{v_p}{v_s}+I_{NCX}-I_{dsi}-I_{TCs}+I_{cs}-I_{cabk}-I_{slcap}\right),\\ \frac{d{c}_p^n}{dt}={\beta }_p\left(c_p^n\right)\left(I_r+I_{CaL}-I_{dps}\right),\\ \frac{d{c}_{NSR}^n}{dt}=\left(I_{up}\frac{v_i}{v_{NSR}}-I_{tr}\frac{v_{JSR}}{v_{NSR}}+I_{cNSR}\right),\\ \frac{d{c}_{JSR}^n}{dt}={\beta }_{JSR}\left(c_{JSR}^n\right)\left(I_{tr}-I_r\frac{v_p}{v_{JSR}}\right),\end{array}$$

where v_i is the local cytosolic volume, v_s is the local submembrane space volume, v_p is the local proximal space volume, v_JSR is the local JSR volume, β_i is the instantaneous buffer function for c_i, β_s is the instantaneous buffer function for c_s, β_p is the instantaneous buffer function for c_p, β_JSR is the instantaneous buffer function for c_JSR, I_TCi is time-dependent buffering to Troponin C for c_i, I_TCs is time-dependent buffering to Troponin C for c_s, I_dsi is the diffusive current between c_s and c_i, I_up is the uptake current, I_ci is the nearest-neighbor diffusive current for c_i, I_cs is the nearest-neighbor diffusive current for c_s, I_dps is the diffusive current between c_p and c_s, I_NCX is the sodium-calcium exchange current, I_CaBk is the background sarcolemmal membrane Ca flux, I_SLCaP is the sarcolemmal membrane Ca pump, I_r is the release current, I_CaL is the L-type Ca current, I_tr is the JSR refilling current, I_cNSR is the nearest-neighbor diffusive current for c_NSR, superscript n shows the n-th compartment.

The diffusive currents between different compartments are the same as those previously employed by Restrepo et al. [23].

$$\begin{array}{l}{I}_{dsi}=\frac{c_s-c_i}{{\tau }_{si}}\\ I_{tr}=\frac{c_{NSR}-c_{JSR}}{{\tau }_{tr}}\\ I_{dps}=\frac{c_p-c_s}{{\tau }_p}\end{array}$$

Cooperative gating of LTCCs and L-type Ca current

As stated above, each CRU contains between 1 and 25 LTCCs. I_CaL is described by

$$I_{CaL}=i_{Ca}{N}_L$$

$$i_{CaL}=4P_{Ca}zF\frac{{0.001\gamma }_i{c}_p{e}^{2z}-{\gamma }_o{\left[Ca\right]}_O}{e^{2z}-1}$$

where i_CaL is the single channel current, N_L is the number of open channels from 0 to 25, z = VF/(RT). LTCC activity is described by a Markov model with stochastic openings (Fig 1). N_L is determined by the number of open states of the Markov model within the CRU. Channel coupling and its [Ca²⁺]_Cleft dependence were incorporated in the LTCC model as follows. α in Fig 1 was replaced with α∙γ₁ where

$${\gamma }_1=1+w_1\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(-15(N_L/3-p{o}_x\left)\right)}\bullet \frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(-1.0(c_p-c{p}_x\left)\right)}$$

and r₁ in Fig 1 was replaced with r₁∙γ₂ where

$${\gamma }_2=1+w_2\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(-15(N_L/3-p{o}_x\left)\right)}\bullet \frac{1}{1+\exp \left(-1.0\left(c_p-c{p}_x\right)\right)}.$$

po_x and cp_x are parameters, which control the sensitivity of the coupling, w₁ and w₂ are the coupling strength. Other rates in Fig 1 are given by:

$$\begin{array}{l}\alpha =p_o^{\mathrm{\infty }}/{\tau }_{po}\\ \mathrm{\beta }=\frac{1-p_o^{\mathrm{\infty }}}{{\tau }_{po}}\\ p_o^{\mathrm{\infty }}=\frac{1}{1+e^{-V/8}}\\ s_1=0.02f\left(c_p\right)\\ k_1=0.03f\left(c_p\right)\\ s_2=s_1\left(k_2/k_1\right)/(r_1/r_2)\\ s_2^{\prime }=s_1^{\prime }\left(k_2^{\prime }/k_1^{\prime }\right)/{(r}_1/r_2)\\ f\left(c_p\right)=\frac{1}{1+{\left(\widetilde{c_p}/c_p\right)}^3}\\ k_3=\frac{e^{-\frac{\left(V+40\right)}{3}}}{3\left(1+e^{-\left(V+40\right)/3}\right)}\\ k_3^{\prime }=k_3\\ k_4=k_3\left(\alpha /\beta \right)\left(k_1/k_2\right)\left(k_5/k_6\right)\\ k_4^{\prime }=k_3^{\prime }\left(\alpha /\beta \right)\left(k_1^{\prime }/k_2^{\prime }\right)\left(k_5^{\prime }/k_6^{\prime }\right)\\ k_5=\frac{1-P_s}{{\tau }_{Ca}}\\ k_6=f\left(c_p\right)P_s/{\tau }_{Ca}\\ k_5^{\prime }=\frac{1-P_s}{{\tau }_{Ba}}\\ k_6^{\prime }=P_s/{\tau }_{Ba}\\ {\tau }_{Ca}=\left(R\left(V\right)-T_{Ca}\right)P_r+T_{Ca}\\ {\tau }_{Ba}=\left(R\left(V\right)-T_{Ba}\right)P_r+T_{Ba}\\ T_{Ca}=\frac{114}{1+{\left(c_p/\stackrel{-}{c_p}\right)}^4}\\ R\left(V\right)=10+4954e^{V/15.6}\\ P_r=\frac{e^{-\left(V+40\right)/4}}{1+e^{-\left(V+40\right)/4}}\\ P_s=\frac{e^{-\left(V+40\right)/11.32}}{1+e^{-\left(V+40\right)/11.32}}\end{array}$$

Fig 1. 7-state Markov model of the L-type Ca channel.

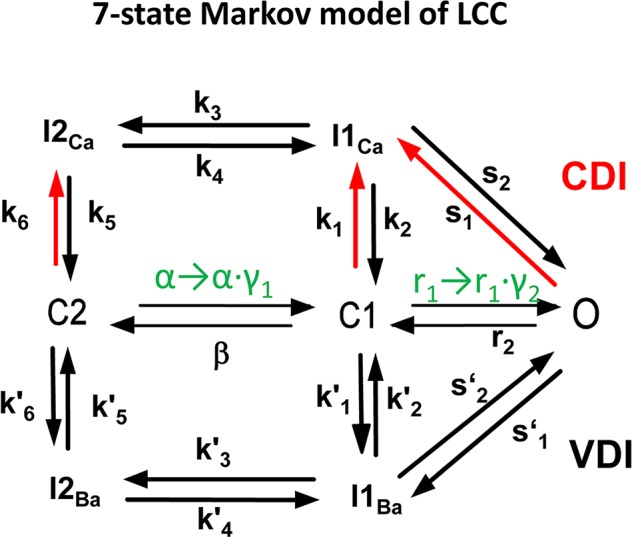
γ₁ and γ₂ are Ca²⁺ and the number of open channels dependent.

Note that the notations employed here are the same as those used by Mahajan et al. in [26]. A table of constants and the detailed formulation for other current fluxes to reproduce our results can be found in the supplemental material section.

Ionic model

In order to investigate physiological and dynamic regulation of alternans by cooperative gating of LTCCs, we use the action potential (AP) and Ca_i cycling model of the ventricular myocyte by Shiferaw et al. [12] since we know which parameters control V_m and Ca²⁺ dynamics in this model.

The dynamics of membrane voltage (V_m) are described by the equation:

$$\frac{d{V}_m}{dt}=-\frac{1}{C_m}\left(I_{ion}+I_{stim}\right),$$

where I_ion is the total membrane current density, I_stim is the stimulus current, and where C_m is the cell membrane capacitance. The total membrane current is given by:

$$I_{ion}=I_{Na}+I_{to}+I_{Kr}+I_{Ks}+I_{Kp}+I_{K1}+I_{NaCa}+I_{CaL},$$

where I_Na is the fast sodium current, I_to is the transient outward potassium current, I_Kr is the rapid component of the delayed rectifier potassium current, I_Ks is the slow component of the delayed rectifier potassium current, I_Kp is the plateau potassium current, I_K1 is the inward rectifier potassium current, I_NaCa is the sodium-Ca²⁺ exchanger, and I_CaL is the L-type Ca²⁺ current.

Ca²⁺ cycling was modeled by following Shiferaw et al. [19]. This model describes Ca²⁺ released from the SR as a summation of local release fluxes distributed throughout the cell. The equations for Ca²⁺ cycling are:

$$\begin{array}{l}\frac{d{c}_s}{dt}=\frac{{\beta }_s{v}_i}{v_s}\left[J_{rel}-\frac{c_s-c_i}{{\tau }_s}+J_{Ca}+J_{NaCa}\right],\\ \frac{d{c}_i}{dt}={\beta }_i\left[\frac{c_s-c_i}{{\tau }_s}-J_{up}\right],\\ \frac{d{c}_j}{dt}=-J_{rel}+J_{up},\\ \frac{d{c}_j^{\prime }}{dt}=\frac{c_j-c_j^{\prime }}{{\tau }_a},\\ \frac{d{J}_{rel}}{dt}=g{J}_{Ca}\bullet Q\left(c_j^{\prime }\right)-\frac{J_{rel}}{{\tau }_r},\end{array}$$

where c_s, c_i and c_j are the average concentrations of free Ca²⁺ in a thin layer just below the cell membrane, in the cytosol, and the SR, with volumes v_s, v_i and v_sr respectively. Here the SR volume includes both JSR and NSR. Also $c_j^{\prime }$ is the average JSR Ca²⁺ concentration within dyadic junctions in the whole cell. The factors β_i and β_s describe instantaneous buffering to Calmodulin, the SR membrane, and Troponin C.

All Ca fluxes are divided by v_i and have units of μM/ms, which can be converted to units of μA/μF using the conversion factor nFv_i/C_m, where n is the ionic charge of the charge carrier, and where F is Faraday's constant. Therefore, ionic fluxes can be converted to currents by:

$$I_{Ca}=-2\alpha J_{Ca},I_{NaCa}=\alpha J_{NaCa},$$

where α = Fv_i/C_m, and where the ion currents are in units of μA/μF.

The L-type Ca²⁺ current flux (J_CaL):

J_CaL is given by

$$J_{CaL}={-g}_{Ca}\bullet d\bullet f\bullet f_{Ca}\bullet i_{Ca},$$

where g_Ca is the maximum conductance of J_CaL, d is activation, f is voltage-dependent inactivation and f_Ca is the Ca²⁺ dependent inactivation, i_Ca is the single channel current.

To replicate the Markov model shown above, cooperative gating and its Ca²⁺ dependence were incorporated in the LTCC model as follows:

$$\begin{array}{l}\frac{d\left(d\right)}{dt}={\alpha }_d{\gamma }_d\left(1-d\right)-{\beta }_{d}d,\\ d_{\mathrm{\infty }}=\frac{1}{1+\exp \left(\frac{-\left(V_m+5\right)}{6.24}\right)}\\ {\alpha }_d=\frac{d_{\mathrm{\infty }}}{{\tau }_d}\\ {\beta }_d=\frac{1-d_{\mathrm{\infty }}}{{\tau }_d}\end{array}$$

$${\gamma }_d=1+0.01\bullet w\bullet \frac{1}{1+\exp \left(-15\left(p{o}_{Ca}-p{o}_x\right)\right)}\bullet \frac{1}{1+\exp \left(-1.0\left(cs-c{s}_x\right)\right)},$$

where γ_d is the coupling, which depends on the open probability of LTCC (po_Ca = d ∙ f ∙ f_Ca) and submembrane [Ca²⁺] (c_s), po_x and cs_x are parameters, which control the sensitivity of the coupling, w is the coupling strength.

Voltage-dependent inactivation and the Ca²⁺ dependent inactivation are given by

$$\begin{array}{l}\frac{df}{dt}=\frac{f_{\mathrm{\infty }}-f}{{\tau }_f}\\ f_{\mathrm{\infty }}=\frac{1}{1+\exp \left(\frac{V_m+35}{8.6}\right)}\\ \frac{d{f}_{Ca}}{dt}=\frac{f_{Ca}^{\mathrm{\infty }}-f_{Ca}}{{\tau }_{fca}}\\ f_{Ca}^{\mathrm{\infty }}=\frac{1}{1+{\left(\frac{c_s}{\widehat{c_s}}\right)}^{\gamma }}\end{array}$$

The single channel current is given by

$$i_{Ca}=\frac{4V_m{F}^2}{RT}\left(\frac{c_s{e}^{2a}-0.34{\left[C{a}^{2+}\right]}_O}{e^{2a}-1}\right)$$

with a = V_mF/RT.

We varied the recovery time constant (τ_f) of the inactivation gate (f) of LTCCs to control the stability of the V_m system since it is known that the steepness of APD restitution is sensitive to it. In order to control the stability of the Ca²⁺ system, we varied the steepness of the slope (u) of the SR Ca²⁺ release function, which controls the sensitivity of release to SR load. The degree of Ca²⁺ dependent inactivation (γ) was varied to obtain positive Ca_i→V_m coupling (γ = 0.7) and negative Ca_i→V_m coupling (γ = 1.5).

Tables of constants and the detailed formulation for other current fluxes and buffers can be found in the supplemental material section. All programs were written in C++ and run on a 24-node High-Performance Computing cluster and Amazon Cloud Computing Services. An expanded section with all equations can be found in the supplemental material section. The C++ code is available via our website.

Results and discussion

Model of cooperative gating (Stochastic model)

We built a stochastic model of cooperative gating of LTCCs and incorporated this gating modality into the subcellular Ca²⁺ cycling model, which has realistic Ca²⁺ compartments and diffusion. In this model, LTCC and RyR activity depends on the V_m, [Ca²⁺]_Cleft, the degree of LTCC coupling within a cluster as well as [Ca²⁺]_Cleft and [Ca²⁺]_JSR (RyR).

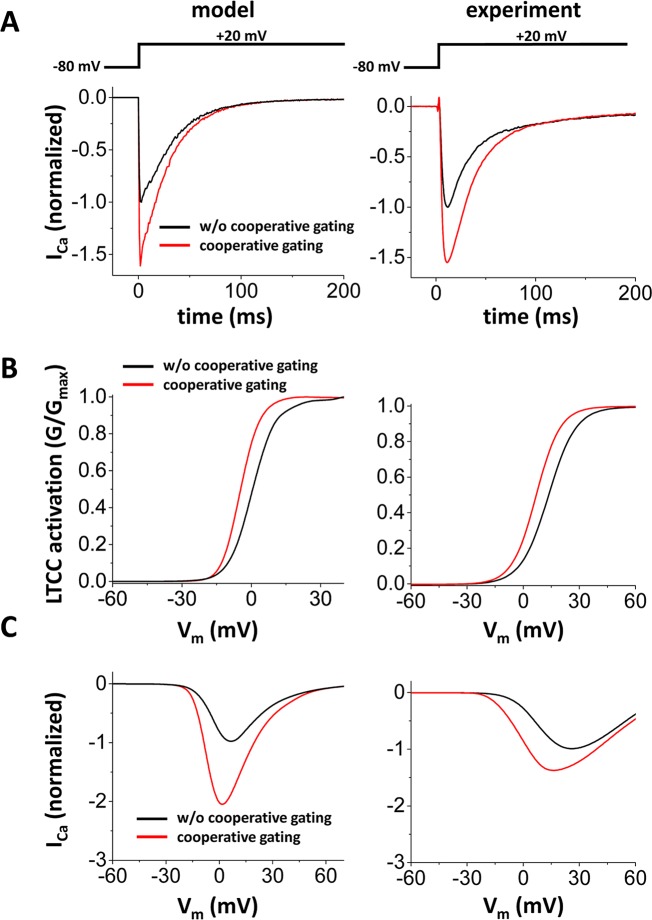
Validation of the model involved the use of experimental data. When LTCCs are coupled, simultaneous opening events occurred more often (Fig 2A). Without cooperative gating, events of simultaneous opening of >2 channels are rare. On the other hand, with cooperative gating, events of simultaneous opening of 2 to 6 channels often occurred. Also, open dwell time of the LTCC cluster becomes longer with cooperative gating of LTCCs (Fig 2B vs 2C). We also measured the current-voltage relationship of I_CaL and the activation curve. To measure these curves, we used the same protocol used in the experimental study by Dixon et al. [9]. To be more specific, the membrane potential was depolarized from a holding potential of -80 mV to a specified test potential. Fig 3A shows one example of I_CaL vs time when V_m is depolarized from -80 mV to +20 mV. When cooperative gating is introduced, the peak of I_CaL was about 1.5 times larger than that of I_CaL without coupling. Cooperative gating of LTCCs shifted the activation curve to the left about 5 or 6 mV (Fig 3B) and nearly doubled the peak I_CaL (Fig 3C). Activation occurs at slightly lower voltage in the model. This discrepancy could be due to species differences as the model is built based on rabbit experiments [26] yet the experimental data collected by Dixon et al. was obtained from mouse cardiomyocytes [9]. Regardless of this, our in silico results are generally consistent with the previously reported experimental observations [9, 27]. Furthermore, they support the use of this model to examine the effects of LTCC coupling on Ca²⁺ entry, APD, and voltage and Ca²⁺ alternans.

Fig 2. The stochastic model of cooperative gating of LTCCs.

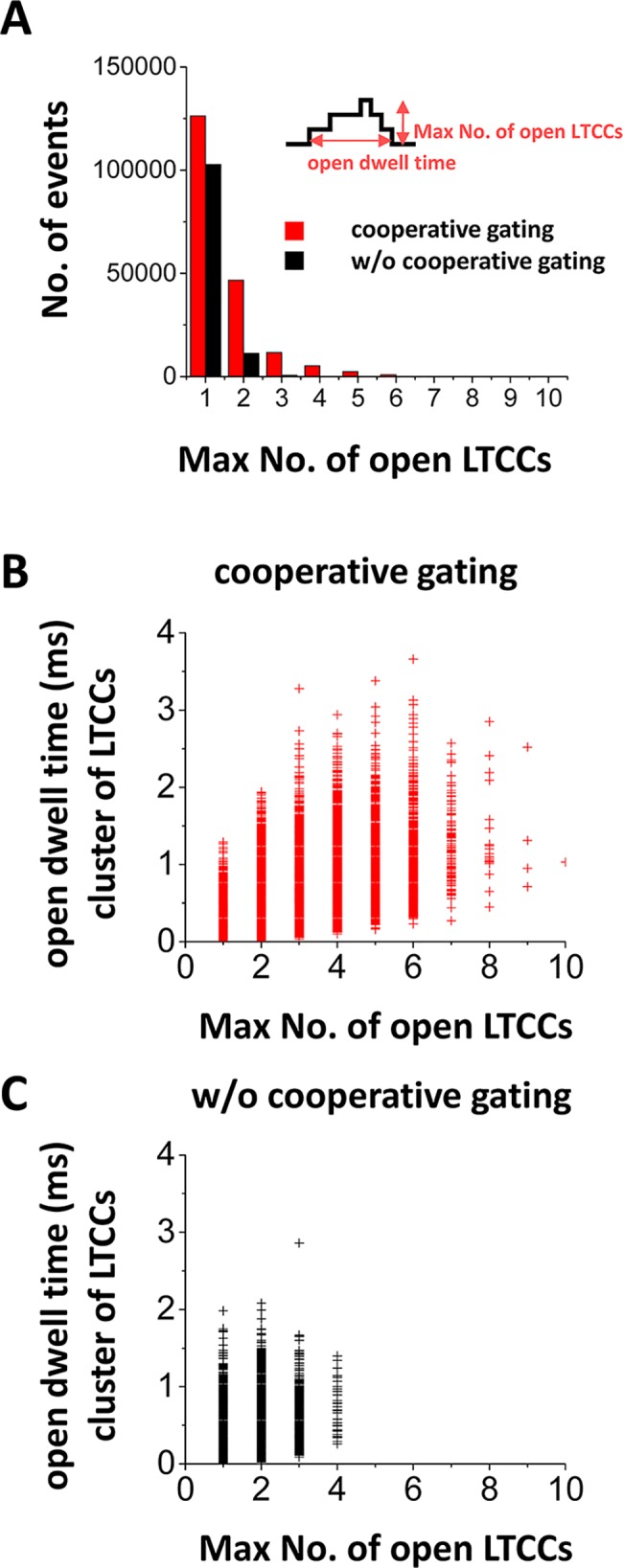
In this model, LTCCs and RyRs open stochastically. (A) The histogram of the maximum number of open LTCCs. Cooperative gating promotes simultaneous opening. (B) open dwell time of the cluster of LTCCs with coupling gating of LTCCs. (C) open dwell time of the cluster of LTCCs without coupling gating of LTCCs. In these simulations, the CRU contains 10 LTCCs.

Fig 3. The stochastic model of cooperative gating of LTCCs (properties of I_CaL).

Left panels: Model results Right panels: Experimental results reconstructed from ref [9]. (A) I_CaL vs time when V_m is depolarized from -80 mV to +20 mV. (B) Activation curve of LTCC without cooperative gating (black) and with cooperative gating (red). (C) I-V curve of I_CaL without cooperative gating (black) and with cooperative gating (red).

To test if cooperative gating promotes alternans, the cell was paced with and without cooperative gating at fast rates. Fig 4 shows the development of alternans and its steady states. The cell was paced at pacing cycle length (PCL) = 300 ms. Without cooperative gating, alternans was not observed (black traces in each panel). However, when cooperative gating was introduced, alternans was developed within 100 beats (Fig 4A: voltage and Fig 4B: Ca²⁺). It reached the steady state after ~30 beats (Fig 4C & 4D). APD alternans amplitude (ΔAPD) is defined as

$$\mathrm{\Delta }APD={\left(-1\right)}^n\left({\mathrm{A}\mathrm{P}\mathrm{D}}_{n+1}-{\mathrm{A}\mathrm{P}\mathrm{D}}_n\right).$$

Fig 4. Cooperative gating promotes alternans.

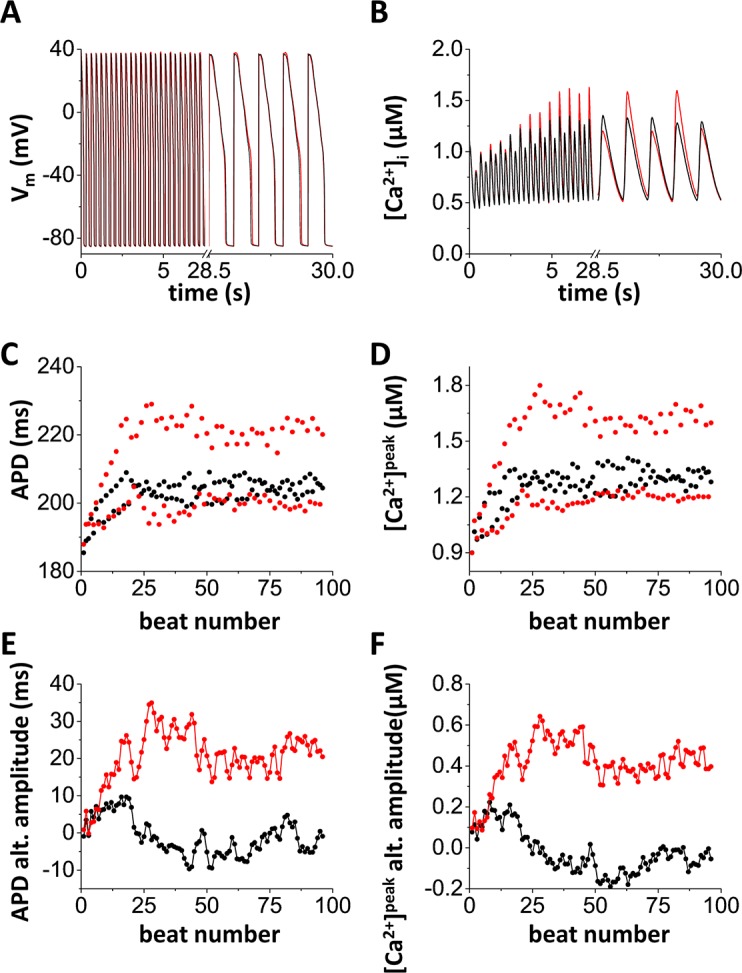
The cell with (red) /without (black) cooperative gating was paced at PCL = 300 ms. The initial conditions are the same in both cases. Alternans was developed within 100 beats only if cooperative gating was introduced. (A) The membrane potential vs time. (B) cytosolic [Ca²⁺] vs time. (C) APD vs the beat number. (D) peak cytosolic [Ca²⁺] vs the beat number. (E) APD alternans amplitude vs the beat number. (C) peak cytosolic [Ca²⁺] alternans amplitude vs the beat number.

Ca²⁺ transient alternans amplitude (ΔCa²⁺) is defined as

$$\mathrm{\Delta }{\mathrm{C}\mathrm{a}}^{2+}={\left(-1\right)}^n\left(\right[{\mathrm{C}\mathrm{a}}_{n+1}^{peak}+{\mathrm{C}\mathrm{a}}_n^{peak}).$$

Without cooperative gating, alternans amplitudes fluctuate around zero. On the other hand, if cooperative gating is introduced, alternans amplitudes stay and fluctuate around certain values (Fig 4E & 4F). When the cell is paced at a faster rate (PCL = 290 ms), alternans occurred in both cases. However, APD and Ca²⁺ transient alternans amplitudes were much larger when LTCCs were coupled (S1 Fig). These results are consistent with experimental results [9]. Ca²⁺ transient alternans was observed when the cell was paced at PCL = 300 ms using a clamped AP waveform. This implies that Ca²⁺ cycling is unstable and contributes development of alternans.

Functional effects of cooperative gating on alternans: Mathematical analysis

Alternans can be caused by instability of V_m due to steep APD restitution or instability of Ca_i cycling due to steep SR Ca²⁺ release vs. SR Ca²⁺ load relationship, or both [11, 12] (Fig 5A). The V_m dynamics and Ca²⁺ dynamics are coupled via Ca²⁺-sensitive currents such as I_CaL and the Na⁺-Ca²⁺ exchanger (NCX). When the Ca_i transient becomes larger, NCX prolongs the APD, whereas the I_CaL shortens the APD due to Ca²⁺-induced inactivation of the channel. Therefore, if NCX dominates, APD becomes longer as the Ca_i transient becomes larger. In our previous study [12], we defined this as positive coupling of Ca²⁺ on V_m (positive Ca_i→V_m coupling, Fig 5B left). On the other hand, if I_CaL dominates, APD becomes shorter as the Ca²⁺ transient becomes larger. We defined this as negative coupling of Ca²⁺ on V_m (negative Ca_i→V_m coupling, Fig 5B right). The stability of the coupled system is determined by the eigenvalues of a two dimensional map (see ref. [12] for details). The eigenvalues are:

$${\lambda }_{\pm }=\frac{1}{2}\left(-{\lambda }_v-{\lambda }_c\pm \sqrt{{\left({\lambda }_c-{\lambda }_v\right)}^2+4C}\right),$$

where λ_v is the eigenvalue associated with the map of the voltage system and λ_c is the eigenvalue associated with the map of the Ca²⁺ system, and C is coupling of Ca²⁺ on the membrane voltage. If V_m and Ca_i are uncoupled (C = 0), the system becomes unstable (i.e. alternans occurs) when λ_v or λ_c exceeds unity in absolute value. Black lines in Fig 6A and 6B show stability boundaries (|λ| = 1) when the Ca_i→V_m coupling is positive (C = 0.1, Fig 6A) and negative (C = -0.1, Fig 6B) from our previous study [12].

Fig 5. Cell dynamics and positive and negative Ca_i→V_m coupling.

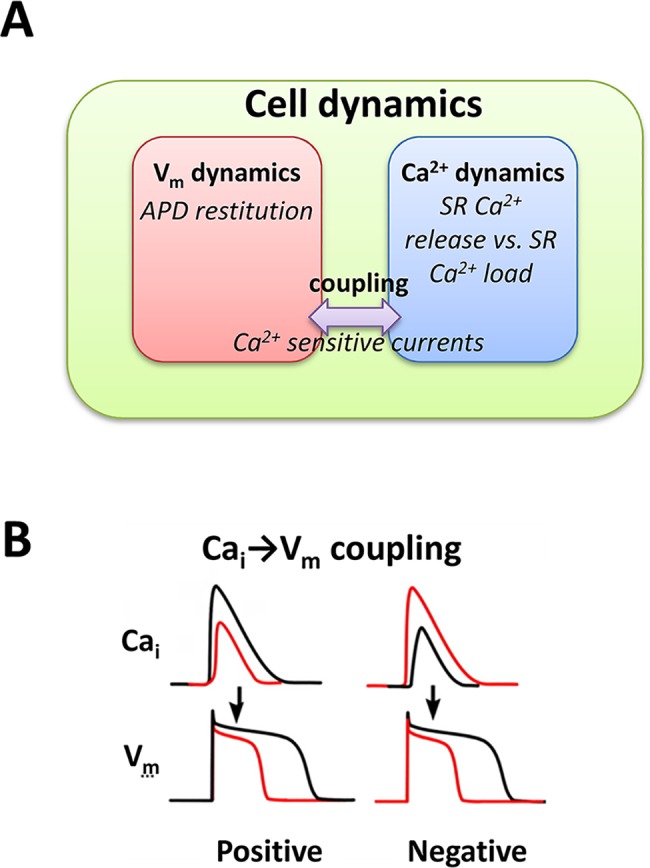
(A) Coupled dynamics of V_m and Ca²⁺. The V_m dynamics is governed by APD restitution. Ca²⁺ dynamics is governed by SR Ca²⁺ release vs. SR Ca²⁺ load relationship. The V_m dynamics and Ca²⁺ dynamics are coupled via Ca²⁺-sensitive currents. (B) Positive and negative Ca_i→V_m coupling.

Fig 6. Theoretical analysis of the effects of coupled gating of LTCCs.

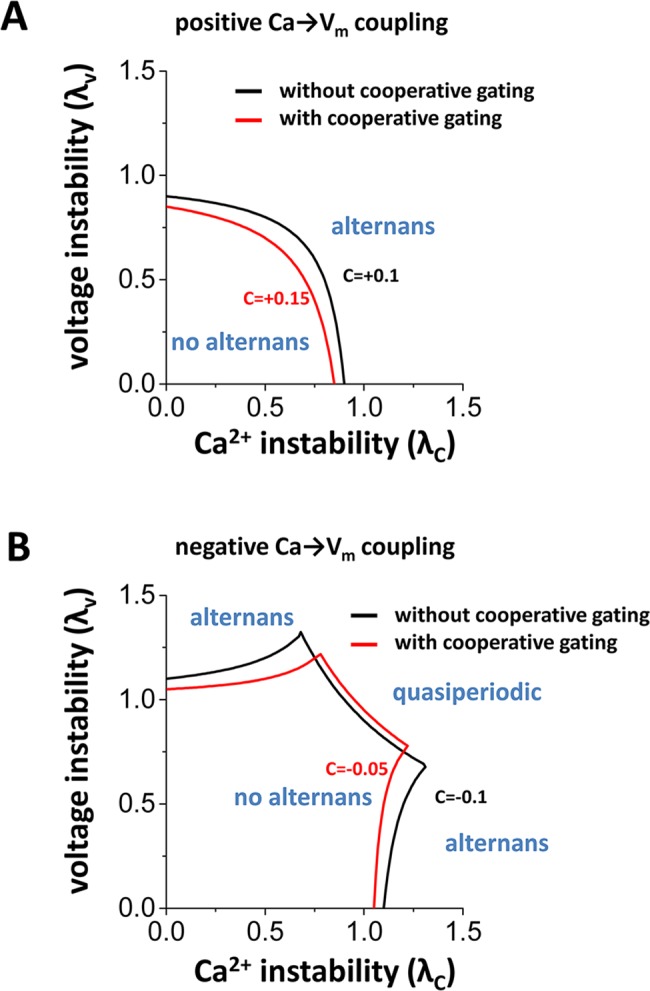
(A) Stability boundary in the case of positive Ca_i→V_m coupling. Black line C = 0.1 (without cooperative gating). Red line C = 0.15 (with cooperative gating). (B) Stability boundary in the case of negative Ca_i→V_m coupling. Black line C = -0.1 (without cooperative gating). Red line C = -0.05 (with cooperative gating).

It is also known that Ca²⁺ is required for the process of cooperative gating of LTCCs [2, 29]. Therefore, larger Ca²⁺ transients could tend to prolong APD due to increased strength of cooperative gating of LTCCs. In other words, cooperative gating of LTCCs may promote positive Ca_i→V_m coupling. Consistent with this, red lines in Fig 6A and 6B show the stability boundary of alternans when Ca_i→V_m coupling became more positive (C = 0.15, Fig 6A) and less negative (C = -0.05, Fig 6B). An increase in the strength of cooperative gating of LTCCs prolongs APD, which promotes steep APD restitution and increases Ca²⁺ influx, which may destabilize Ca²⁺ cycling. In addition, this analysis suggests that cooperative gating of LTCCs may destabilize the system (the stable areas became smaller) and promotes alternans except for the quasiperiodic regime.

Functional effects of cooperative gating on alternans: Simulation (ionic model)

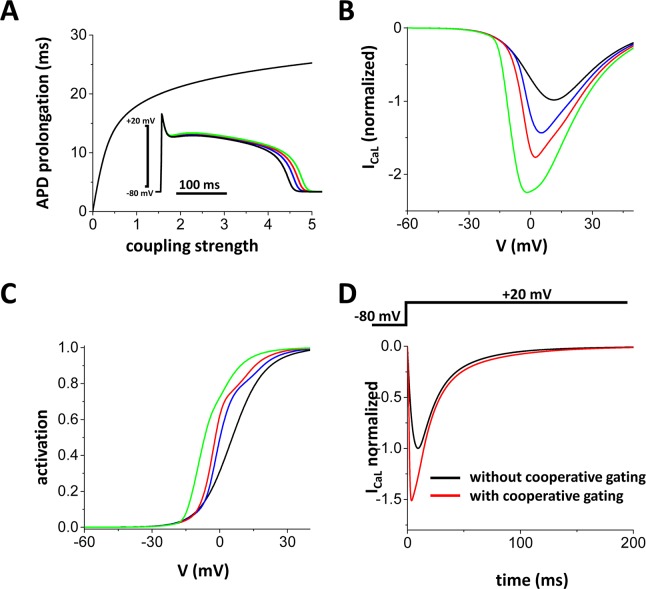
To test our theoretical predictions above, we simulated alternans with the ionic model as described in the Methods section. Fig 7A shows that as the coupling strength became larger, APDs became longer. In this simulation, the cell was paced until it reaches the steady state. We chose parameters that do not cause alternans (τ_f = 45 ms, u = 3 s^-1) without coupling (w = 0). Subsequently, the coupling strength was varied and the APD prolongation was measured. The inset shows the action potentials with w = 0.3 and 1.0. When the coupling strength is increased to 1.0, The peak of the current-voltage curve of I_CaL was almost doubled (Fig 7B). Increased coupling strength of LTCCs also shifts the activation curve to the left (Fig 7C). In Fig 7D, I_CaL vs time is shown when V_m is depolarized from -80 mV to 20 mV. Cooperative gating resulted in a 1.5-fold increase in peak I_CaL. These data are consistent with the results with the stochastic model (Fig 3) and experimental observations [9, 27].

Fig 7. The deterministic model of cooperative gating of LTCCs.

(A) Coupling gating of LTCCs prolongs APs. Inset: V_m vs time. Black: w = 0, Blue: w = 0.3, Red: w = 1, Green: w = 5. (B) I-V curve of I_CaL. Black: w = 0, Blue: w = 0.3, Red: w = 1, Green: w = 5. (C) Activation curve of LTCC. Black: w = 0, Blue: w = 0.3, Red: w = 1, Green: w = 5. (D) I_CaL vs time when V_m is depolarized from -80 mV to +20 mV. w = 1.

We also measured the stability boundary to test if increased strength of cooperative gating of LTCCs alters the stability as we predicted in the mathematical analysis (Fig 6). To investigate the effect of the change in channel cooperativity on alternans, we perturbed the cell by changing the coupling strength from w = 0 to w = 0.03. Fig 8A shows the stability boundary when Ca_i→V_m coupling is positive and Fig 8B shows the stability boundary when Ca_i→V_m coupling is negative. In both cases, V_m-driven alternans and Ca²⁺-driven alternans are promoted with increased coupling strength of LTCCs. On the other hand, quasiperiodic oscillations are not affected. These results are consistent with the theoretical prediction (Fig 6A vs Fig 8A & Fig 6B vs Fig 8B). We note that this is not due to APD prolongation but due to Ca_i→V_m coupling. In fact, unlike Fig 8B, simple prolongation of APD by the reduced potassium current stabilizes Ca²⁺-driven alternans when the coupling is negative (S3 Fig). If the coupling strength is within the physiological range, cooperative gating can change the sign of Ca_i→V_m coupling from negative to positive (S4 Fig).

Fig 8. Coupling gating of LTCCs promotes positive Ca_i→V_m coupling.

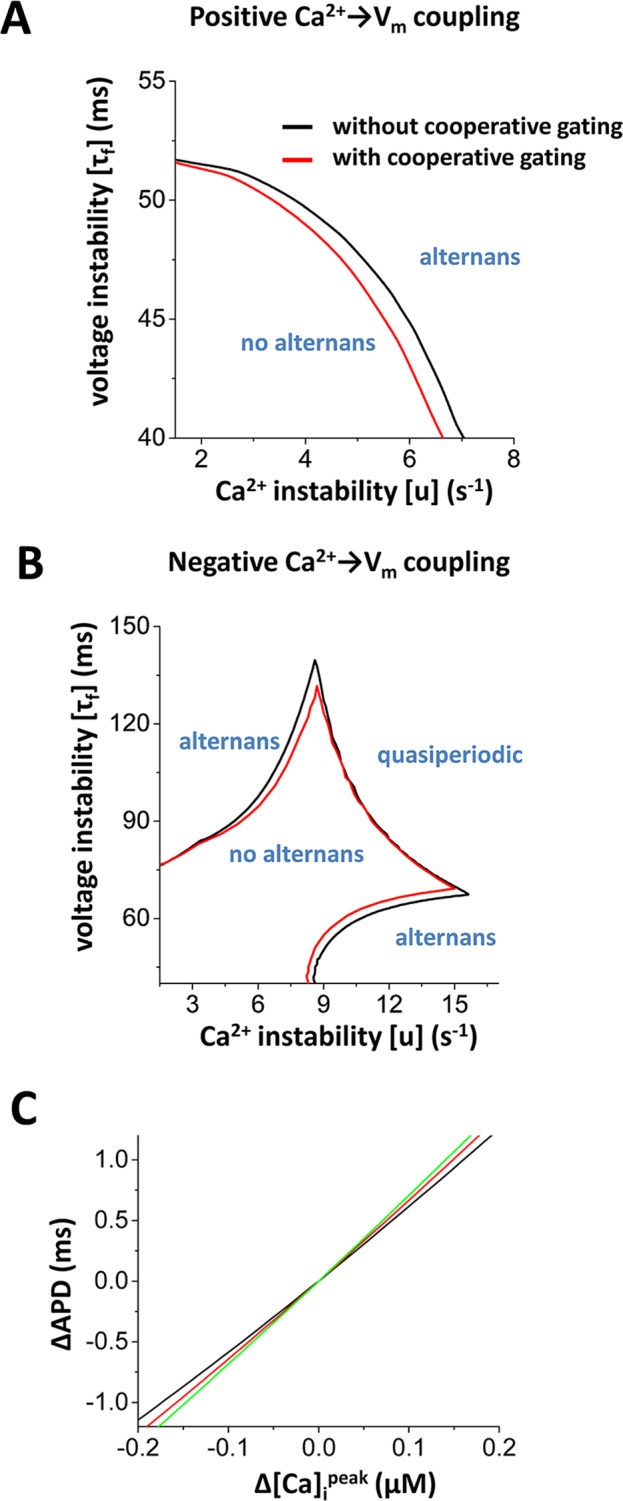
(A) Stability boundary in the case of positive Ca_i→V_m coupling. The coupling strength is 0.03. (B) Stability boundary in the case of negative Ca_i→V_m coupling. The coupling strength is 0.03. (C) Coupling gating of LTCCs promotes positive Ca_i→V_m coupling. The original Ca_i→V_m coupling is positive. The slope became steeper with cooperative gating of LTCCs. The coupling strength is 0 (black), 0.05 (red), and 0.1 (green).

Fig 8C shows that as the coupling strength became larger, Ca_i→V_m coupling became more positive. In this simulation, after reaching the steady state, initial [Ca²⁺]_SR was varied to change the amplitude of the Ca²⁺ transients and then the cell was paced once and the change in the APD was measured. The slope of Δ Ca²⁺ vs ΔAPD shows Ca_i→V_m coupling. In Fig 8C, the slope became more positive as the coupling strength becomes larger, thus indicating that cooperative gating of LTCCs promotes positive Ca_i→V_m coupling.

Cooperative gating, excitation-contraction coupling, and arrhythmias

Cooperative gating of LTCCs facilitates synchronized opening of LTCCs, which may have a major impact on cardiac excitation-contraction coupling due to Ca²⁺ signal amplification. In this study, we built stochastic and deterministic computational models of cooperative gating of LTCCs and investigated how this gating modality may affect dynamics of the V_m and Ca_i cycling system, especially focusing on alternans, which is the arrhythmogenic substrate.

The novelty of our work is three-fold. Firstly, we model cooperative gating of LTCCs for the first time and add the complexity of this gating phenomenon to the existing models, bringing it more in-line with current thinking on Ca²⁺ signaling. We have thus generated a computational model encompassing cooperative gating of LTCCs, which has not been done before. Secondly, we model the effects of cooperative gating on alternans, finding that, in agreement with previously published experimental data [9], aberrant levels of cooperative gating can lead to Ca²⁺ alternans. Our theoretical and computational approaches suggest that increases in the strength of cooperative gating of LTCCs promotes positive Ca_i→V_m coupling and thus promotes V_m-driven and Ca-driven alternans. Finally, we confirmed that our model could reproduce experimental data, by specifically examining the effects of changes in the strength of cooperative gating of LTCCs on L-type Ca²⁺ currents. The degree of LTCC cooperativity can vary depending on physiological and pathological conditions. Our model provides an in silico means to explore the effects of LTCC cooperative gating under various conditions. In addition, Ca_i→V_m coupling at the cellular level has been linked to mechanisms of spatially discordant alternans in tissue [30–32]. These findings underscore the importance of cooperative gating of LTCCs in excitation-contraction coupling and cardiac arrhythmias.

Supporting information

S1 Fig. The cell with (red) /without (black) cooperative gating was paced at PCL = 290 ms.

The initial conditions are the same in both cases. Alternans was developed within 100 beats in both cases. (A) The membrane potential vs time. (B) cytosolic [Ca²⁺] vs time. (C) APD vs the beat number. (D) peak cytosolic [Ca²⁺] vs the beat number. (E) APD alternans amplitude vs the beat number. (C) peak cytosolic [Ca²⁺] alternans amplitude vs the beat number.

(TIFF)

S2 Fig. The cell with cooperative gating was paced at PCL = 300 ms using a clamped AP waveform.

Ca²⁺ transient alternans was observed. This demonstrate Ca²⁺ cycling is unstable and contributes development of alternans.

(TIFF)

S3 Fig. Simple AP prolongation does not promote Ca-driven alternans when Ca_i→V_m coupling is negative.

G_Kr was reduced by 50%. (A) positive Ca_i→V_m coupling (B) negative Ca_i→V_m coupling.

(TIFF)

S4 Fig. When the coupling strength is within physiological values (w = 0.3~1), negative Ca_i→V_m coupling (black) became positive Ca_i→V_m coupling (red).

Black: w = 0, Red: w = 1.

(TIFF)

Data Availability

All relevant data are within the paper and its Supporting Information files. The mathematical model is available via our website (http://www.ucdmc.ucdavis.edu/pharmacology/).

Funding Statement

This work was supported by National Institutes of Health (https://www.nih.gov/) grant R00-HL111334, American Heart Association (http://www.heart.org/) Grant-in-Aid 16GRNT31300018, and Amazon (https://aws.amazon.com/) AWS Cloud Credits for Research (DS), American Heart Association (http://www.heart.org/) Scientist Development Grant 15SDG25560035 (RED), National Institutes of Health grant R01-HL085686 and R01-HL085870 (LFS) and National Institutes of Health grant R01-HL121059 and R01-HL098200 (MFN). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.