Abstract
We created a metastasis imaging, analysis platform consisting of software and multi-spectral cryo-imaging system suitable for evaluating emerging imaging agents targeting micro-metastatic tumor. We analyzed CREKA-Gd in MRI, followed by cryo-imaging which repeatedly sectioned and tiled microscope images of the tissue block face, providing anatomical bright field and molecular fluorescence, enabling 3D microscopic imaging of the entire mouse with single metastatic cell sensitivity. To register MRI volumes to the cryo bright field reference, we used our standard mutual information, non-rigid registration which proceeded: preprocess → affine → B-spline non-rigid 3D registration. In this report, we created two modified approaches: mask where we registered locally over a smaller rectangular solid, and sliding organ. Briefly, in sliding organ, we segmented the organ, registered the organ and body volumes separately and combined results. Though sliding organ required manual annotation, it provided the best result as a standard to measure other registration methods. Regularization parameters for standard and mask methods were optimized in a grid search. Evaluations consisted of DICE, and visual scoring of a checkerboard display. Standard had accuracy of 2 voxels in all regions except near the kidney, where there were 5 voxels sliding. After mask and sliding organ correction, kidneys sliding were within 2 voxels, and Dice overlap increased 4%–10% in mask compared to standard. Mask generated comparable results with sliding organ and allowed a semi-automatic process.
Keywords: Micro-metastases imaging, cryo-imaging, MRI contrast agent, parameters optimization, sliding organ registration
1. INTRODUCTION
Cancer is the second major cause of death. A primary tumor mass can often be clinically controlled, but over 90% of cancer deaths are due to metastases. There are increasing efforts to image, advance therapeutic targets, improve understanding of biology, and develop clinical treatments for metastatic cancer [1]. An insidious aspect is that tumor cells can remain dormant and activate years later. Medical imaging is limited in its ability to detect small metastases. Clinical limit of Positron Emission Tomography (PET) is about 7mm [2]. While specialized with high Gadolinium (Gd), high resolution, Magnetic Resonance Imaging (MRI) scanning gets to about 2–3 mm in the brain [3]. Only larger tumors are reliably detected in body scans. Improved detection will only be possible with targeted imaging agents. Preclinical research on micro-metastasis (<2mm), and larger, scattered throughout the body is limited because histology is impractical and because traditional in vivo imaging has insufficient resolution and contrast for reliable detection.
We are developing a system for analyzing preclinical studies of metastatic cancer, which can be applied to advance pipelines of technologies like imaging agents, imaging methods, therapeutics, tumor models, etc. Here we report methods to help increase accuracy in analyzing a new MR molecular imaging agent, CREKA-Gd [4]. Key to our strategy is cryo-imaging (CryoVizTM, BioInVision Inc., Cleveland, OH), which provides microscopic 3D color and fluorescence imaging with single cell detection over vast volumes, as large as a mouse [5], [6], [7]. Mice were sent for in vivo MRI scanning first and then were embedded in a histological medium called optimal cutting temperature (OCT) for cryo imaging. Typically, the very high resolution cryo bright field, green and red fluorescence volumes were about 120G for each mouse.
To enable evaluation of CREKA-Gd, we have developed 3D image registration between CREKA-Gd MRI and cryo volumes. The bright field of the cryo-imaging was used as the reference volume and the 3D CREKA-Gd MRI was registered to it. Though we used a mold for cryo-imaging to minimize the mouse body movement, there was still deformation between the MRI volume and the frozen mouse in the cryo-image volume.
Most of the sliding organ algorithms aim to register lung images. M. P. Heinrich et al. imposed an Lp norm regularization term instead of the quadratic norm regularization term [8]. Anisotropic diffusive regularization method was based on decomposing the deformation field into normal and tangential components and applying different smoothness constraints [9]. Subanatomical region segmentation was utilized so that registration was performed on each subregion independently [10]. From our experiments, kidneys were not only sliding tangential to the organ boundary but also expanding perpendicular to the organ boundary in the cryo images compared to MRI. Therefore, the sliding effects cannot be simply solved with anisotropic regularization. We will compare three methods (standard, mask, and sliding organ) for performing non-rigid sliding kidney registration.
2. 3D REGISTRATION ALGORITHM
We evaluated three non-rigid registration algorithms. They were: (a) standard which proceeded as preprocess, affine, B-spline non-rigid registration and we used the same registration parameters for the entire mouse; (b) mask where we applied a cuboid binary mask around the kidney region and registration parameters were working inside the mask volume; (c) sliding organ where we registered sliding organs and the rest body volume separately and combined the results. We first describe the standard registration process. Other approaches build on it.
Preprocessing
Color bright field images were firstly converted to gray scale using Equation (1) below. High resolution cryo bright field images were down sampled to 0.1×0.1×0.1mm using anti-aliasing Lanczos filter to make the resolution closer to MRI resolution, which was 0.1172×0.0977×0.1406mm. OCT background was segmented out using a semi-automated method. The 16 bit MRI images were then mapped to 8 bit range. This is to ensure the bins for the joint histogram in mutual information are appropriately scaled. We very roughly registered the cryo and MRI volumes before automatic registration so that they were well overlapped and similarly oriented. As long as they were roughly matched up, automatic registration was deemed successful.
| (1) |
Standard Registration
After preprocessing, we firstly performed affine registration. The algorithm we employed is described in [12]. In general, the algorithm was based on a block matching strategy which utilized the highest 50% variance displacement vectors calculated with normalized cross correlation between reference and floating images, and then used the least trimmed squares to get the global transform estimates. Although normalized cross correlation was used as the similarity measure instead of the normalized mutual information for multimodality data, it is effective since it finds the local high variance features such as edges within corresponding blocks. For whole mouse torso registration, a block size of 20×20×20 voxels performs well.
Next we applied non-rigid registration to the affine registered mouse using free form deformation (FFD) algorithm [13]. FFD uses a lattice of control points superimposed on the reference volume to estimate a transformation T in Equation (2) between the reference and the floating volumes. FFD used a pyramidal approach that the resolution of the control point grid increases with the image resolution, in a coarse to fine fashion. The deformation at each voxel in the transformed floating image is calculated using a cubic B-spline interpolation of each of the coordinates in the surrounding n×n×n control points; n was 2 voxels in the standard method. Mathematically, each voxel in the floating image x= [x1, x2, x3], is mapped to the reference position location x̅ = [x̅1, x̅2, x̅3] in the reference image by T(x) where T(x) = [T1(x), T2(x), T3(x)] and is defined by
| (2) |
Ba, Bb, Bc: 1D B-spline basis functions of order 3
Ca,b,c: the mesh of control points locations
r=[ri, rj, rk]: relative position of a voxel with respect to the closest point and is found using
The transformation value of each voxel in each direction was interpolated with 2 control points below and 2 control points above with the 1D spline basis functions (Ba, Bb, Bc). The cost function which consists of the normalized mutual information (NMI) value and two regularization terms in Equation (3) was iteratively optimized. The bending energy (BE) smoothness constraint in Equation (4) is based on the second spatial derivative of the deformation field. It penalizes unrealistic deformations. The determinant of the Jacobian in Equation (5) measures local volume change. A value greater or less than one means expansion or compression, respectively. In Equation (6) it is the absolute value of the determinant of the Jacobian (JL).
| (3) |
| (4) |
| (5) |
| (6) |
The FFD spline parameter of control point grid size was 2×2×2 voxels. The number of bins for NMI calculation was 256. The number of maximum iteration per level was 10000 to ensure convergence before stop.
Mask registration
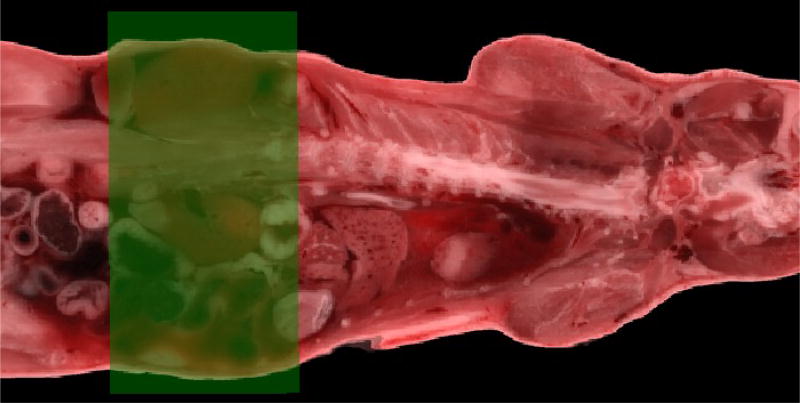
Mask has the same whole body affine registration as standard. For the non-rigid FFD, we used a 3D binary cuboid reference mask such that NMI was calculated and optimized inside the mask region. A 2D illustration of the kidney mask in one slice was shown in figure 1. The FFD parameters were same as standard.
Figure 1.
An illustration of the kidney mask in one slice with the green transparent rectangle being the mask.
Sliding organ registration
The kidneys were considered as one subregion and other parts of the mouse body were considered as another subregion. Segmentation was done by a person experienced in identifying MRI and cryo-imaging organs. Masks were created for each subregion and the subregions were registered separately. The masks were used to modify the voxel intensities: voxels belong to the mask subregion maintained their values and voxels outside the mask subregion were assigned to zero. The zero values helped match the boundaries of the subregions by imposing a penalty. Kidneys had an affine registration with block size of 5×5×5 voxels, and no-kidney body volume used a block size of 20×20×20 voxels. Both kidneys and no-kidney volume used the same non-rigid FFD parameters including the control point grid size, the number of bins and the maximum iteration as the standard and mask. After registration of the two subregions with modified intensities, they were combined to give a whole body view.
Through mask registration, we can achieve an automatic process by simply giving a cuboid volume of interest. In sliding organ registration, manual segmentation was always required, but we expected it to give us a good standard to measure other registration methods.
3. EXPERIMENTAL METHODS
We developed experimental methods and image analysis software for evaluation of a new molecular MR imaging agent. Three mice for registration were from an experiment to assess the molecular imaging agent CREKA-Gd [4]. All the mice experiment were performed in accordance with the animal protocol approved by the CWRU Institutional Animal Care and Use Committee (IACUC). Briefly, we injected 4T1-GFP-Luc2 breast cancer cells in the mammary fat pad for tumor induction in seven-to-eight-week-old female mice. The MRI study was performed using a Bruker Biospec 7T MRI scanner (Bruker Corp., Billerica, MA, USA) with a volume radio frequency coil. For MR and cryo-imaging combined study, mice were pre-settled in a mold. During MRI we captured two volumes: an in vivo scan using a 3D fat suppression sequence optimized for Gadolinium, and then a high resolution sequence after mouse death to be used in 3D registration. After MRI, mice were prepared for cryo-imaging. Frozen mice were imaged at 10.472 × 10.472 µm in-plane resolution, and sectioned at 50 µm slice thickness using cryo. Bright field, GFP, and Cy5 images were acquired using a liquid crystal RGB filter and a monochrome camera. The MRI high resolution scan was registered to the bright field cryo-image data. The GFP and Cy5 image volumes were concurrently obtained with bright field images so they were perfectly registered. The ultimate goal is to achieve tumors and metastases unambiguous correspondence in CREKA-Gd MRI and cryo-imaging, which means the misregistration should be within 2 voxels. NiftyReg software [11] was used in our experiment to perform affine and non-rigid free form deformation (FFD).
Experiments to optimize registration parameters
We designed a method to find optimal regularization parameters weights of the FFD cost function by varying them from 0 to 0.1 with a step of 0.005. The weights grid search was utilized in the standard and mask registration methods. We held the FFD control point grid size same for two methods as 2×2×2 voxels, the maximum number of iteration as 1000 and the number of bins for normalized mutual information calculation as 256. In standard and mask registration, the weights were specifically optimized for kidneys. We obtained the deformed MRI kidney volumes by applying the deformation fields from different sets of parameters to the affine registered kidney volume. Highest Dice overlap result of deformed MRI kidney volumes and cryo kidney volume in Equation (7) indicated the best set of parameters.
| (7) |
Experiments to compare algorithms
We compared optimal Dice overlap and checkerboard visualization in kidney area from standard, mask, and sliding organ registration.
4. RESULTS
4.1 Registration results
Standard registration result
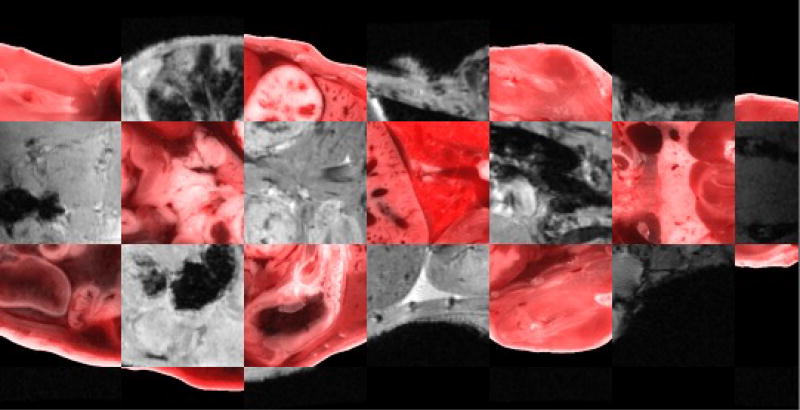
Organ movement is not only due to the body deform, but also the organ tissue and interstitial fluid expansion after freezing. In our experiment, we found both of the two regularization terms BE and JL were necessary. The checkerboard view of cryo and MRI from one mouse standard registration was shown in figure 2. The registration accuracy in the mouse torso was within 2 voxels except for kidneys, where there were 5 voxels misregistration. We have no ambiguity in matching up most of the parts in the corresponding MRI and cryo volumes. However, we still need better kidney correspondence.
Figure 2.
A slice of standard registration checkerboard view of cryo bright field color image and MRI.
Standard and mask comparison
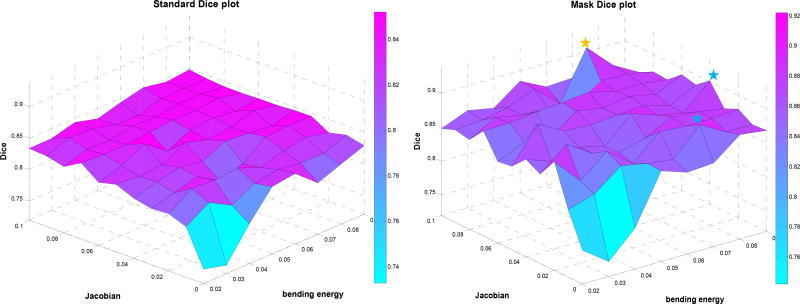
For mouse 1, the standard and mask weights grid search result of Dice overlap is shown in figure 3. The results are displayed at 0.01 step size for BE and JL weights for better visualization. The yellow star represented the peak in mask Dice plot, and the blue stars showed the next highest two values. The best Dice overlap in mask increased by 6% to 92% compared to standard 86% overlap. In other two mice, the Dice overlap increased 10% and 4% respectively. The overall performance of mask increased compared to standard. When applying a mask, the NMI value was calculated only inside the mask, and therefore the displacements outside of the mask came only from the B-spline interpolation. Figure 4 shows a slice of the displacement field generated from the mask, where the green rectangle was a slice of the cuboid mask. We can observe that the interpolation has a rather long range effect: the displacement value decreased to a half voxel when reaching liver and a tenth of a voxel when reaching lung. In the standard, control points in the spleen, liver, stomach, digestive tube etc. could have affected the kidney movement. Mask avoided the interpolation effect from the other parts of the mouse body. Therefore it is feasible to get regularization parameters that specifically work for kidneys.
Figure 3.
Mouse 1 standard registration (left) and mask registration (right) Dice plots of BE ranging from 0.02 to 0.09 and JL from 0 to 0.1.
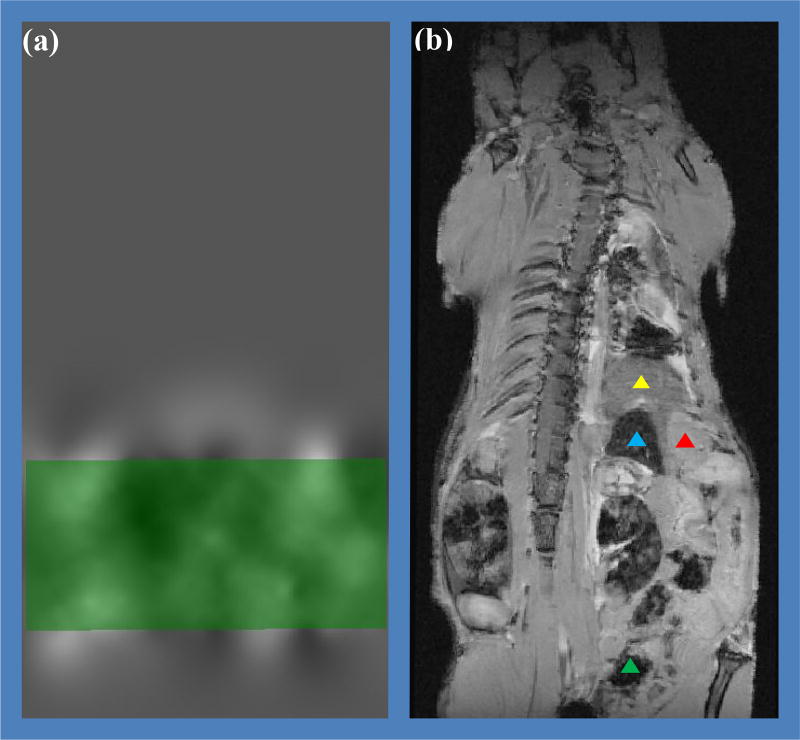
Figure 4.
Mouse 1 mask registration: (a) a slice of the displacement field where the green rectangle is a slice of the mask; (b) the MRI affine result as non-rigid registration input (yellow triangle is the liver, blue is the spleen, red is the stomach and green is the digestive tract). The B-spline interpolation has a rather long range effect.
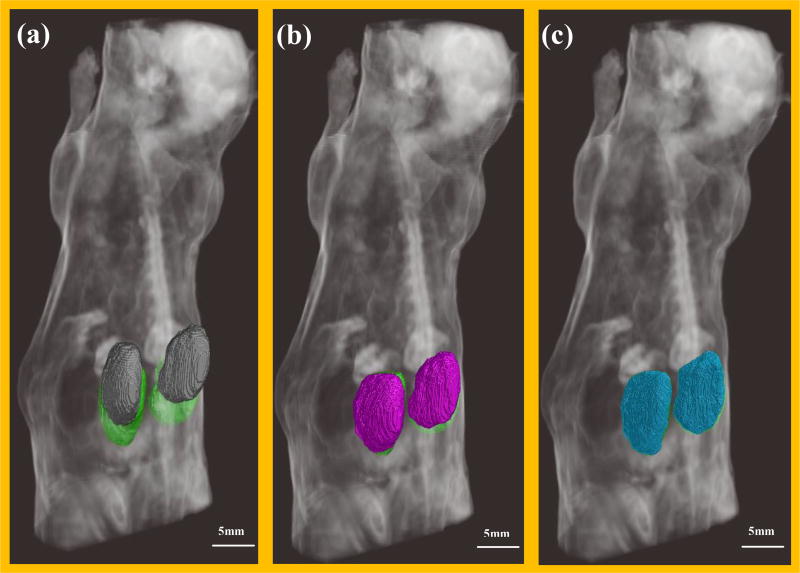
Applying the optimal regularization parameters, 3D volume rendering before registration and after standard and mask registration is shown in figure 5. The white part in three sub-figures represented the volume rendering of cryo mouse body. The cryo kidneys contour were rendered with green, the non-registered MRI kidneys contour were rendered with gray, the standard registered MRI kidneys contour were rendered with cyan and the mask registered MRI kidneys contour were rendered with blue. Before registration (a), there was great sliding and volume difference. After standard registration (b), the kidney volumes were better aligned but there were still around 5 voxels sliding along head-tail direction. Whereas in the mask registered result (c), the two volumes were well overlapped.
Figure 5.
3D rendering of mouse body and kidney volumes. (a) Gray volumes were MRI kidney before registration; (b) cyan volumes were MRI kidneys after standard registration; (c) blue volumes were MRI kidneys after mask registration. In all three renderings, kidneys from the cryo-image were shown in green.
Standard, mask and sliding organ visual comparison
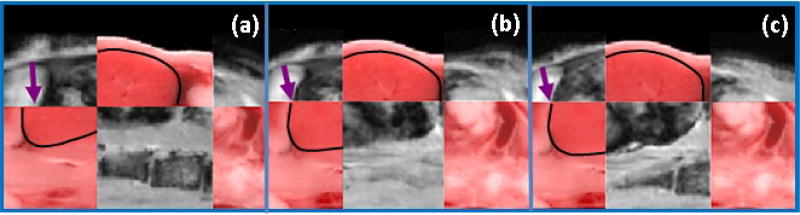
A checkerboard view of standard, mask and sliding organ registration in one kidney is shown in figure 6. The black lines indicate the kidney contour in cryo. And the arrows points out the difference in three methods where we can identify the registration quality was sliding organ >mask > standard. Qualitatively, mask and sliding organ improved kidney registration and gave comparable result. We then quantitatively compared the mask and sliding organ methods on three mice.
Figure 6.
One kidney checkerboard view of (a) standard (b) mask (c) sliding organ registration result and cryo. The arrows pointed at the sliding place in (a) and correction in (b) and (c), respectively.
Mask and sliding organ quantitative comparison
The regularization parameters (BE and JL) and Dice results of all the three mice are shown in table 1. High values are desirable for Dice. The Dice overlap in mouse 2 sliding organ was slightly smaller than mask, which was due to unprecise manual segmentation of kidneys in MRI.
Table 1.
Mask and sliding organ registration result comparison on three mice.
| Mask and sliding organ comparison | ||||
|---|---|---|---|---|
| BE | JL | Dice | ||
|
|
||||
| mouse1 | mask | 0.07 | 0.09 | 0.92 |
| sliding organ | 0.92 | |||
| mouse2 | mask | 0.015 | 0.01 | 0.89 |
| sliding organ | 0.88 | |||
| mouse3 | mask | 0.065 | 0.01 | 0.90 |
| sliding organ | 0.94 | |||
The BE and JL parameters for three mice were not the same. It was due to different registration results after whole body affine registration. However, we can give a pool of the two weighting parameters that could be used for future tests which shrinks the searching space.
4.2 Technology application
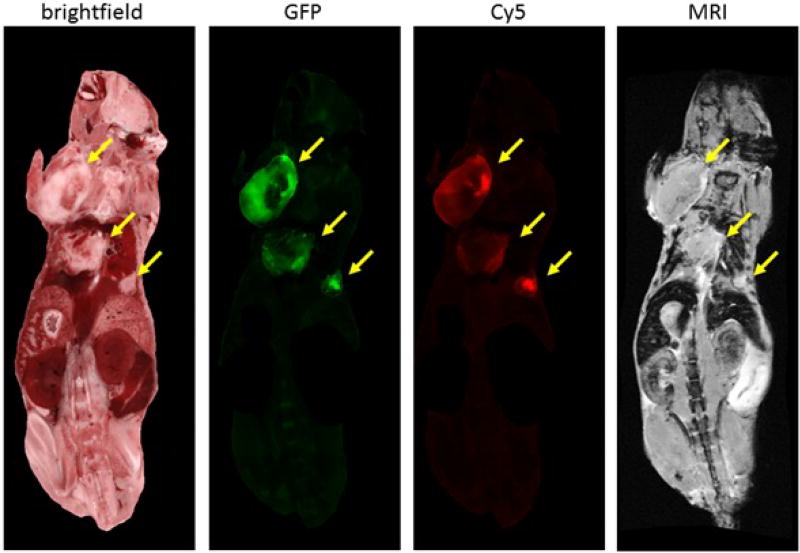
In our mouse cancer models, we aim to achieve no ambiguity for tumors and metastases detection in the registered color anatomy bright field, GFP, CREKA-Cy5 peptide and CREKA-Gd MRI volumes. We visually examined the peptide targeting results by locating the GFP signal in the Cy5 and MRI volumes to assess the signal intensity and labeling potential. From figure 7, a multi-modality view of a slice in the mouse after standard registration is shown. We observed good correspondence of tumors in cryo bright field, GFP, Cy5 and MRI images. CREKA-Gd and CREKA-Cy5 tends to label the edges of bigger tumors and label the whole area of smaller metastases. The tumors diameters are 7.5 mm, 6.3 mm, and 2.5 mm respectively.
Figure 7.
Multi-modality view of a slice in the mouse. From left to right: color anatomy bright field, green GFP tumors, red CREKA-Cy5 peptide tumors, CREKA-Gd MRI. The yellow arrows points to three big tumors. We masked the area outside these tumors in GFP and Cy5.
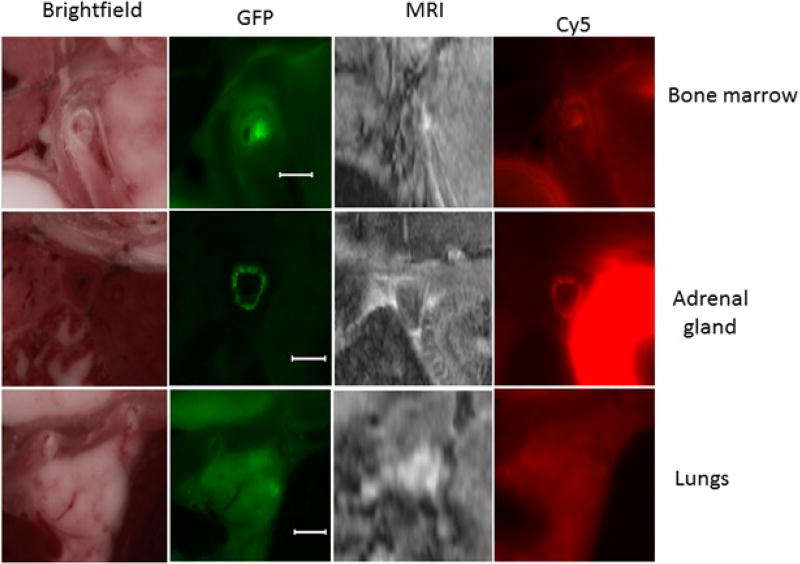
Given the four registered volumes, we further inspected the micro-metastasis (0.2 mm – 2mm) targeting. From figure 8, examples of micro-metastases in cryo bright field, GFP, MRI and Cy5 were found in upper shoulder bone marrow, adrenal glands, and lungs. The diameters of the metastases are 0.3, 1, and 2mm respectively. Many of other micro metastases were also found in CREKA-Gd and CREKA-Cy5 images. Our method proves the CREKA-Gd detectability over micro-metastasis and is robust for imaging agents testing.
Figure 8.
Examples of micro-metastases in cryo bright field, GFP, MRI, Cy5. From up to down: bone marrow, adrenal glands, and lungs. Reference bar is 1mm.
5. DISCUSSION AND CONCLUSION
Our system of cryo-imaging and registration software allows one to evaluate molecularly-targeted imaging agents and nano-therapeutics for cancer. Utilizing this technique, Zhou Z. et al. [4] found the MRI with CREKA-Gd was able to detect 91% of the GFP labelled metastases with size>0.5mm3. And a preliminary free response receiver operating characteristic (FROC) analysis to validate the human observer blind detection of the metastases indicated that the observer could blindly identify 83% metastatic tumors at a rate of 0.22 false positives per examination. This robust platform should be readily applicable to other usage such as different tumor types, other diseases, peptides, nanoparticle designs, etc.
The standard FFD registration method works well in nearly every region of the mouse. That is, registration errors are less than 2 voxels, allowing one to unambiguously compare signals seen in MRI to the presence of metasteses in cryo-imaging. This was not the case in the kidneys. Because the kidneys move (about 20 voxels) and expand (about 8%) with freezing, we have the classic problem of sliding organ registration.
When registering the kidney region, we evaluated three registration methods (standard, mask, and sliding organ) and finally preferred mask. The sliding organ registration method, requiring segmentation of both the reference and moving volumes, worked well. However, it required accurate manual segmentation of the kidneys, a tedious task and one prone to potential error. Sliding organ does provide a good standard for comparisons to other algorithms. Mask with grid search worked well and gave results as good as sliding organ. It worked much better than standard, presumably because deformations outside the mask volume did not affect deformation in the kidney region. The downside to mask is that registration quality is very sensitive to the choice of weights of the regularization parameters, bending energy and Jacobian, and that a grid evaluation of these parameters reveals multiple locally optimum values (Fig 3). Mask registration is reasonably quick (< 2 min), allowing an experienced operator to manually optimize the regularization parameters based on experimental prior knowledge about the candidate parameters. A potential option is to use a semi-automated approach whereby one launches multiple registrations, each with a different set of regularization parameters. The operator could then choose the best result.
References
- 1.Sleeman J, Steeg PS. Cancer metastasis as a therapeutic target. European Journal of Cancer. 2010;46(7):1177–1180. doi: 10.1016/j.ejca.2010.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Erdi YE. Limits of Tumor Detectability in Nuclear Medicine and PET. Molecular imaging and radionuclide therapy. 2012;21(1):23–28. doi: 10.4274/Mirt.138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Engh JA, Flickinger JC, NIranjan A, Min DV, Kondziolka DS, Lunsford LD. Optimizing intracranial metastasis detection for stereotactic radiosurgery. Stereotactic and functional neurosurgery. 2007;85(4):162–168. doi: 10.1159/000099075. [DOI] [PubMed] [Google Scholar]
- 4.Zhou Z, Qutaish M, Han Z, Schur RM, Liu Y, Wilson DL, Lu Z. MRI detection of breast cancer micrometastases with a fibronectin-targeting contrast agent. Nature Communication. 2015;6:7984. doi: 10.1038/ncomms8984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wilson DL, Roy D, Steyer G, Gargesha M, Stone M, Mckinley E. whole mouse Cryo-imaging. Proceedings of SPIE – the International Socienty for Optical Engineering. 2008;6916 doi: 10.1117/12.772840. 691611-691611-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Roy D, Steyer GJ, Gargesha M, Wilson DL. 3D cryo-imaging: a very high-reslution view of the whole mouse. Anatomical record (Hoboken, NJ: 2007) 2009;292(3):342–351. doi: 10.1002/ar.20849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Qutaish M, Sullivant KE, Burden-Gulley SM, Lu H, Roy D, Wang J, Basilion J, Brady-Kalnay SM, Wilson DL. Cryo-imaging analysis of tumor cell migration, invasion, and dispersal in a mouse Xenograft model of human Glioblastoma Multiforme. Molecular Imaging and Biology. 2012;14(5):572–583. doi: 10.1007/s11307-011-0525-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heinrich MP, Jenkinson M, Brady M, Schnabel J. Discontinuity preserving regularization for variational optical-flow registration using the modified Lp norm. Medical Image Analysis for the Clinic: A Grand Challenge, Workshop MICCAI. 2010:185–194. [Google Scholar]
- 9.Pace DF, Enquobahrie A, Yang H, Aylward SR, Niethammer M. Deformable image registration of sliding organs using anisotropic diffusive regularization. Proc IEEE Int Symp Biomed Imaging. 2011:407–413. doi: 10.1109/ISBI.2011.5872434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu Z, Rietzel E, Boldea V, Sarrut D, Sharp GC. Evaluation of deformable registration of patient lung 4DCT with subanatomical region segmentations. Medical Physics. 2008;35(2):775–781. doi: 10.1118/1.2828378. [DOI] [PubMed] [Google Scholar]
- 11.Modat M, Ridgway G, Taylor Z, Lehmann Manja, Barnes J, Hawkes DJ, Fox NC, Ourselin S. Fast free-form deformation using graphics processing units. Computer Methods and Programs in Biomedicine. 2010;98(3):278–284. doi: 10.1016/j.cmpb.2009.09.002. [DOI] [PubMed] [Google Scholar]
- 12.Ourselin S, Roche A, Subsol G, Pennec X, Ayache N. Reconstructing a 3D structure from serial histological sections. Image and Vision Computing. 2001;19(1–2):25–31. [Google Scholar]
- 13.Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Transaction on Medical Imaging. 1999;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]