Automated Detection of Post-ictal Generalized EEG Suppression

Abstract

Although there is no strict consensus, some studies have reported that Post-ictal generalized EEG suppression (PGES) is a potential Electroencephalographic (EEG) biomarker for risk of Sudden Unexpected Death in Epilepsy (SUDEP). PGES is an epoch of EEG inactivity after a seizure, and the detection of PGES in clinical data is extremely difficult due to artifacts from breathing, movement and muscle activity that can adversely affect the quality of the recorded EEG data. Even clinical experts visually interpreting the EEG will have diverse opinions on the start and end of PGES for a given patient. The development of an automated EEG suppression detection tool can assist clinical personnel in the review and annotation of seizure files, and can also provide a standard for quantifying PGES in large patient cohorts, possibly leading to further clarification of the role of PGES as a biomarker of SUDEP risk. In this paper, we develop an automated system that can detect the start and end of PGES using frequency domain features in combination with boosting classification algorithms. The average power for different frequency ranges of EEG signals are extracted from the pre-filtered recorded signal using the Fast Fourier Transform (FFT) and are used as the feature set for the classification algorithm. The underlying classifiers for the boosting algorithm are linear classifiers using a logistic regression model. The tool is developed using 12 seizures annotated by an expert then tested and evaluated on another 20 seizures that were annotated by 11 experts.

I. Introduction

Sudden Unexpected Death in Epilepsy (SUDEP) is the sudden, unexpected, witnessed or un-witnessed, non-traumatic and non-drowning death of people with epilepsy with or without evidence of a seizure and excluding status epilepticus, where the autopsy does not reveal another cause of death [1]. SUDEP is responsible for approximately 5,000 deaths annually in the US. Although there is no consensus on the role that PGES may play in SUDEP, some studies speculate that PGES is a SUDEP risk biomarker [2][20][23], through association with peri-ictal autonomic dysfunction [3], while other studies were unable to confirm a direct link between PGES and SUDEP [21][22], leaving the possibility that PGES may play a role as biomarker for SUDEP risk but may not represent the initiating event in a terminal cascade leading to respiratory and cardiac dysfunction and thus SUDEP. According to [2]: (1) the odds of SUDEP with PGES duration longer than 50 seconds are significantly elevated (p < 0.05), and (2) beyond 80 seconds, the odds are quadrupled (p < 0.005). Each 1-second increase in PGES duration results in the odds of SUDEP increasing by a factor of 1.7% (p<0.005). PGES is currently quantified solely by visual analysis that relies on the expertise of clinicians reviewing the EEG patterns. In our study, we observe that different clinicians can interpret and annotate PGES from the same EEG patterns very differently, significantly increasing the complexity in using PGES as a biomarker for SUDEP, and possibly suggesting why there is no consensus as to the relationship between PGES and SUDEP.

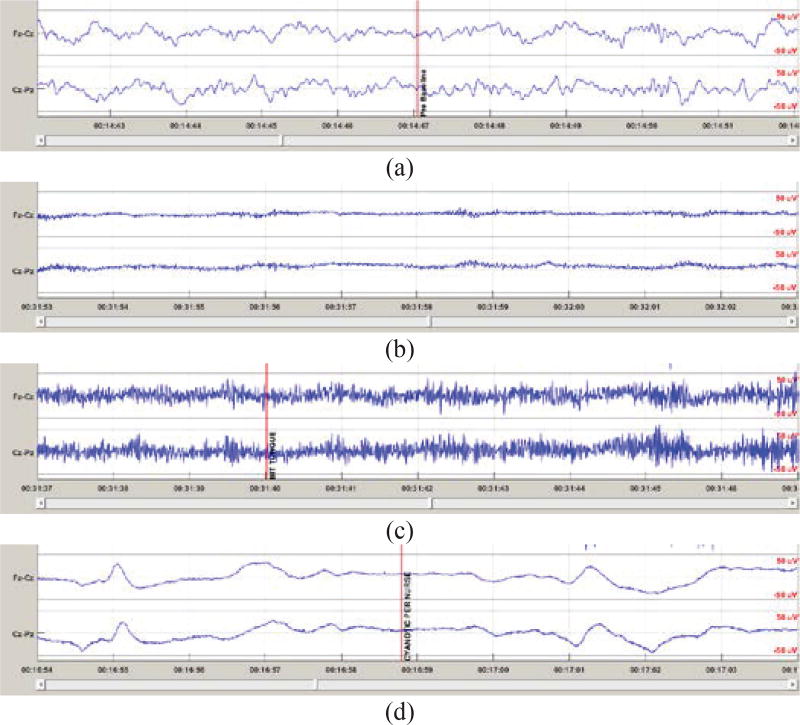
PGES is a period of inactivity of the brain after a seizure. In noise free data, the EEG amplitude should be relatively flat with magnitude close to zero microvolts. Due to electrical noise and other artifacts in the recoded EEG, PGES is defined as an epoch in the postictal period where the EEG amplitudes from all recorded electrodes are within the 10μV peak-to-peak range [2] as shown in Figure 1(b). At the end of PGES, there is an EEG waveform in one or more channels that does not satisfy the PGES amplitude criteria. After the PGES period, the EEG can either return immediately to a normal (rhythmic) EEG pattern or enter a generalized postictal EEG slowing state [2] before returning to the normal pattern. Detecting PGES should be relatively straightforward since by definition we only need to identify an epoch after the seizure (postictal period) in which EEG amplitudes are within ±5μV. In most clinical data from Epilepsy Monitoring Units (EMU), there are various high (in comparison to μV level EEG signals) amplitude artifacts, such as breathing, movement and muscle artifact that cause the EEG amplitudes to far exceed ±5μV during PGES as shown in Figure 1(c)(d). Some artifacts. such as muscle movement, can be easily recognized by most clinicians as shown in Figure 1(c). However, some artifacts may look like rhythmic EEG patterns as shown in Figure 1(d). In the EMU, clinicians generally use both EEG patterns and video recording to identify high amplitude artifacts that are not real EEG activities since external interventions from clinical personnel can generate rhythmic-like patterns in the EEG signal. Thus, the classification of EEG suppression is far more complex than applying the amplitude criteria for detection indicates.

Figure 1.

EEG patterns from Fz-Cz and Cz-Pz. The data is scaled to ±50μV for a consistent display of multiple EEG patterns with different amplitude. (a) Pattern of regular rhythmic EEG. (b) EEG pattern during PGES with relatively clean (artifact-free) signals. (c) EEG pattern during PGES with muscle artifact that is easily recognized by clinicians. (d) EEG pattern during PGES with artifact that could be difficult to identify as artifact.

Automated detection algorithms using Neural Networks have been developed for EEG time series analysis including the detection of burst-suppression and seizures in [4][5] and an Adaptive Neuro-Fuzzy Inference System (ANFIS) approach is proposed by Jang in [6]–[8]. The simplified line-length algorithm for calculating short time energy has been shown to be an effective feature extraction method [9][10] to detect seizure onset. With a variety of feature extraction methods available for time series data, it is necessary to determine which features are the most useful in a given application. Approaches using the genetic algorithm (GA) to obtain the “optimal” feature set for a specific classification problem are described in [11]–[14].

Although many techniques have been proposed for seizure detection, there has been little discussion focused on automated PGES detection. Clinically, periods of suppressed EEG are determined through visual analysis of the EEG time series data by human experts, with mixed results in terms of inter-rater agreement between different scorers. Automated EEG suppression detection and reviewing tools could greatly reduce the clinical workload and would also provide a consistent scoring approach across different clinical cohorts and centers. Identifying quantifiable factors for scoring the suppression period are important to provide objective references for further studies and for comparison of clinical cases across different medical centers and from different patient groups. Thus it is important to develop a tool that can be effectively integrated into the clinical workflow and that can assist clinicians with annotating PGES.

Classifying an EEG epoch with specific time duration as suppressed or non-suppressed consists of two tightly coupled problems, feature extraction and classification. In the first problem, selection of the signal and associated features of the signal are included. In this paper, we use the “same” EEG signals as clinicians since one of our goals is to create an automated tool that assist clinicians and reduce the workload during the annotating process. We refrain from using sophisticated features and use average power in different EEG bands (Gamma, Delta, Theta and Alpha) as the features to imitate human annotators. Thus, interpretation of the classification should be “similar” to clinicians. Instead of classifying all features from all EEG signals or statistically combining the classification results from different EEG signals, we use the boosting algorithm for multi-channel EEG signals for PGES classification.

The paper is organized as follows. Section II contains basic knowledge for classification and the boosting algorithm. Implementation of the boosting algorithm for PGES detection is fully explained in section III. The pre-processing of EEG signals including feature extraction and post processing is presented in section IV. PGES detection on EEG recordings from clinical patients and comparison of the results from auto-detection and visual annotation by clinicians is detailed in Section V. Conclusions are given in Section VI.

II. TECHNICAL BACKGROUND

A. Logistic Regression

For both rule-based and probabilistic systems, a hyperplane originally introduced in Linear Algebra, can be used to separate real-valued, D-dimensional data into groups. A linear, D-dimensional hyperplane can be represented by a set of weights, w ∈ R^D, that defines a normal to the hyperplane in D-dimension space. Any D-dimensional point x on the hyperplane satisfies w^Tx + b = 0, where both w and x are D-dimensional real-valued vectors, w^Tx is the dot (inner) product between w and x, and b is a scalar offset value. We define the classifier F(x) = I(w^Tx + b > 0) where I(·) is the indicator function and equal to 1 when its argument is true and 0 when it is false. Any point on one side of the hyperplane satisfies w^Tx ≤ 0 (F(x) = 0) while points on the other satisfy w^Tx + b > 0 (F(x) = 1). To simplify notation, we assume that w is defined to include a bias term w₀ (the offset b) and x is defined to include the unity term, w and x are then (D + 1)-dimensional vectors.

In probabilistic systems, we can extend the notion of separating groups by modeling the degree to which a particular data point x belongs in either group. Generalized Linear Models (GLMs) are a family of models model that relate the target distribution Y|x ~ f_Y|X(y|x) with uncertainty to a data sample x via a link function g(·) and the assumption that g(μ_Y|x) = w^Tx. Logistic regression is a particular GLM for modeling real-valued data that belongs to two groups. Here, the target distribution Y|x ~ f_Y|X(y|x) is Bernoulli or f_Y|X(y; p) = p^y (1 − p)^{(1 − y)}. Where g(·) is the logit function, logit(p) = log(p) − log(1 − p) for some scalar value p ∈ (0, 1), and its inverse is the sigmoid function $\mathrm{\sigma }(\mathrm{s})=\frac{1}{1+\text{exp}(-\mathrm{s})}$ for some scalar value s ∈ R, and p has the interpretation as the probability that x belongs to one group while 1 − p is the probability it belongs to the other group [15]–[17]. Note that for p = 0.5, we have g(p) = logit(p) = 0. Also note that p = σ(w^Tx), so we can now have F(x) = I(σ (w^Tx) > 0.5) as an equivalent rule-based classifier. Logistic Regression also provides the interpretation that, with Y ~ Bern(x; p), we have E[y|x] = μ_Y|x = p, so the expected value of class y will be 1 with probability p = σ(w^Tx).

Based on the idea of a soft threshold, logistic regression models a set of N Bernoulli random variables y that depends on continuous, real-valued inputs, x and a parameter p according to:

$$\mathrm{Y}|\mathrm{X}~\prod _{\mathrm{n}=1}^{\mathrm{N}}\text{Bern}({\mathrm{y}}_{\mathrm{n}};{\mathrm{p}}_{\mathrm{n}})=\prod _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{p}}_{\mathrm{n}}^{{\mathrm{y}}_{\mathrm{n}}}{(1-{\mathrm{p}}_{\mathrm{n}})}^{(1-\mathrm{n})}$$

where p_n = σ(w^Tx_n). The logistic regression parameters w can be determined using the maximum likelihood technique in which the optimization is over the log probability of all the examples in the dataset {(y₁, x₁), (y₂, x₂), …, (y_N, x_N)}. Each of these examples is assumed to be independent and identically distributed (i.i.d.). The optimal classifier weight vector w* is determined by

$${\mathrm{w}}^{\ast }=\text{arg }\underset{\mathrm{w}}{\text{max}}{\sum }_{\mathrm{n}=1}^{\mathrm{N}}\text{log }\mathrm{p}({\mathrm{y}}_{\mathrm{n}}|{\mathrm{x}}_{\mathrm{n}};\mathrm{w})$$

B. Boosting Algorithm

In practice, it is common to use an ensemble method to combine the results from multiple classifiers in order to increase performance, and there are two basic types of ensemble methods [19]. The first type is a simple method based on classification averaging where the results from each classifier are combined through a weighted average to yield the final classification. The second type of ensemble method modifies the training process of the classifiers then combines the results from each classifier to give the ensemble labels. The Boosting algorithm is one of the most widely used ensemble techniques of the second type and there are several variations and implementations of the Boosting algorithm that can be found in [18], with AdaBoost being the most popular algorithm in this category.

For N training examples {(x₁, y₁), (x₂, y₂), …, (x_N, y_N)} where x_n and y_n are the feature vector and label of the n^th sample, the training protocol for AdaBoost with logistic regression is as follows [17]. First we define m classifiers ${\mathrm{F}}_{\mathrm{m}}(\mathrm{x})=\mathrm{I}(\mathrm{\sigma }({\mathrm{w}}_{\mathrm{m}}^{\mathrm{T}}\mathrm{x})>0.5)$ for m = 1, 2, …, M. Then the algorithm proceeds with following steps.

1. Initialize weight coefficients $\{{\mathrm{\beta }}_1^{(1)},{\mathrm{\beta }}_2^{(1)},\dots {\mathrm{\beta }}_{\mathrm{N}}^{(1)}\}$ for each training example by setting ${\mathrm{\beta }}_{\mathrm{n}}^{(1)}=\frac{1}{\mathrm{N}}$ for n = 1, 2, …, N.

2. For the m^th classifier where m = 1, 2, …, M:

   1. Fit a classification result, F_m(x), to the training data by minimizing the weighted error function ${\mathrm{J}}_{\mathrm{m}}={\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}\mathrm{I}({\mathrm{F}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}})\ne {\mathrm{y}}_{\mathrm{n}})$ where I(F_m(x_n) ≠ y_n) is equal to 1 when F_m(x_n) ≠ y_n and 0 otherwise.
   2. Evaluate the weighted classification error for the current classifier ${\mathrm{\epsilon }}_{\mathrm{m}}=\frac{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}\mathrm{I}({\mathrm{F}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}})\ne {\mathrm{y}}_{\mathrm{n}})}{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}}$ then compute ${\mathrm{\alpha }}_{\mathrm{m}}=\text{ln}\left\{\frac{1-{\mathrm{\epsilon }}_{\mathrm{m}}}{{\mathrm{\epsilon }}_{\mathrm{m}}}\right\}$
   3. For n = 1,2, …, N, update the weights ${\mathrm{\beta }}_n^{(\mathrm{m})}$ for the next classifier by ${\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m}+1)}={\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}\text{ exp}\{{\mathrm{\alpha }}_{\mathrm{m}}\mathrm{I}({\mathrm{F}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}})\ne {\mathrm{y}}_{\mathrm{n}})\}$

3. The final boosted ranking function is ${\mathrm{p}}_{\mathrm{M}}(\mathrm{x})={\sum }_{\mathrm{m}=1}^{\mathrm{M}}{\mathrm{\alpha }}_{\mathrm{m}}\mathrm{\sigma }({\mathrm{w}}_{\mathrm{m}}^{\mathrm{T}}\mathrm{x})$ where α_m has been normalized to $\frac{{\mathrm{\alpha }}_{\mathrm{m}}}{{\sum }_{\mathrm{m}\prime =1}^{\mathrm{M}}{\mathrm{\alpha }}_{\mathrm{m}\prime }}$. The final rule-based classifier is ${\mathrm{F}}_{\mathrm{M}}(\mathrm{x})=\mathrm{I}({\mathrm{p}}_{\mathrm{M}}(\mathrm{x})>\frac{1}{2})$.

C. Receiver Operating Characteristic (ROC)

ROC curves are used to evaluate the performance of binary classifiers in datasets where Type-I (false positive) or Type-II (false negative) errors are not equally likely or are not equally important. First, we define $\mathrm{T}={\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{y}}_{\mathrm{n}}$ as the number of data points of class 1 or that are “true” in the dataset. The True Positive (TP) count $\text{TP}={\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{y}}_{\mathrm{n}}\mathrm{F}({\mathrm{x}}_{\mathrm{n}})$ is the number of true examples that are classified correctly. The True Negative (TN) in a dataset is $\text{TN}={\sum }_{\mathrm{n}=1}^{\mathrm{N}}(1-{\mathrm{y}}_{\mathrm{n}})(1-\mathrm{F}({\mathrm{x}}_{\mathrm{n}}))0$ and represents the number of data points correctly classified as “false” in the dataset. The True Positive Rates (TPR) and True Negative Rates (TNR) for a classifier F represents the accuracies of the classifier on positive and negative examples only with $\text{TPR}=\frac{\text{TP}}{\mathrm{T}}$ and $\text{TNR}=\frac{\text{TN}}{\mathrm{N}-\mathrm{T}}$.

The Area Under the Curve (AUC) of a classifier is the calculated area (in [0, 1]) under the TPR and FPR (False Positive Rate) response curves and characterizes how well the classifier has learned the class probabilities of a dataset. The AUC curve is computed using a continuous, scalar-valued ranking function that orders examples in the dataset. Logistic regression based models provide the probability parameter as a ranking function, p_M(x) = σ(w^Tx_n). For a dataset with N examples, let the ranking function be the probability that 0 < p_M(x_n) < 1, sorted based on the output of the classifier so that 0 < p_M(x₁) … <= F(x_N) < 1. In the case of logistic regression this ordering is invariant to w₀. An AUC of 1, ½, and 0 describe a perfect classifier on the dataset, random guessing, and a perfect classifier on the dataset with the labels flipped, respectively.

III. IMPLEMENTATION OF CLASSIFICATION ALGORITHM

A. Regularization

To prevent overfitting of the model to the data, we use a form of MAP inference by specifying that the logistic regression weights are sampled from a normal distribution with a density, p(w) ~ Normal(w| μ, σ²I), having mean μ and isotropic covariance σ²I. For a single logistic regression classifier, the new fitting procedure is

$${\mathrm{w}}^{\ast }=\text{arg }\underset{\mathrm{w}}{\text{max}}{\sum }_{\mathrm{n}=1}^{\mathrm{N}}\text{log }\mathrm{p}({\mathrm{y}}_{\mathrm{n}}|{\mathrm{x}}_{\mathrm{n}},\mathrm{w})\mathrm{p}(\mathrm{w}|\mathrm{\mu },\mathrm{I}{\mathrm{\sigma }}^2).$$

In practice, this instance of MAP inference is equivalent to the L2 cost of the parameters, λw^Tw, with $\mathrm{\lambda }=\frac{1}{2{\mathrm{\sigma }}^2}$. The w₀ in w is not given any L2 regularization [15][16]. In our approach, μ was set to 0 and σ was selected by cross validation.

B. Imbalanced classes and AUC Optimization

For the PGES classification problem, suppression periods can last from seconds to minutes in duration, followed by intermittent and continuous slow EEG patterns that can last on the order of tens of minutes. If we consider EEG epochs of constant duration, this creates imbalanced class sizes with the majority of the epoch samples being continuous slow. Application of naïve maximum likelihood optimization will yield a classifier that maximizes the prediction to the most dominant class.

Our solution to deal with the imbalance in class sizes is to perform approximate AUC optimization for bias selection only after each additional boosted classifier is trained. That is, after the calculation of the weights w_m for the m^th logistic regression model in Adaboost, the bias term is determined to maximize an approximate form of the AUC, ${\widehat{\text{AUC}}}_{\mathrm{m}}$, in order to make TNR_m and TPR_m equal. The approximate AUC form we use is ${\widehat{\text{AUC}}}_{\mathrm{m}}={\text{TPR}}_{\mathrm{m}}{\text{TNR}}_{\mathrm{m}}$ and although this may be considered a rather poor approximation of AUC_m, our results suggest this approximation was sufficient in distinguishing between the two classes. For differentiability considerations, we replace the rule-based classifier F_m(·) with the differentiable ranking function p_m(·) as follows:

$${\widehat{\text{TPR}}}_{\mathrm{m}}=\frac{{\widehat{\text{TP}}}_{\mathrm{m}}}{{\mathrm{T}}_{\mathrm{m}}}=\frac{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{p}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}}){\mathrm{y}}_{\mathrm{n}}}{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{y}}_{\mathrm{n}}}\text{and}$$

$${\widehat{\text{TNR}}}_{\mathrm{m}}=\frac{{\widehat{\text{TN}}}_{\mathrm{m}}}{\mathrm{N}-{\mathrm{T}}_{\mathrm{m}}}=\frac{{\sum }_{\mathrm{n}=1}^{\mathrm{m}}(1-{\mathrm{p}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}}))(1-{\mathrm{y}}_{\mathrm{n}})}{{\sum }_{\mathrm{i}=1}^{\mathrm{m}}(1-{\mathrm{y}}_{\mathrm{n}})}.$$

We maximize $\text{log}({\widehat{\text{AUC}}}_{\mathrm{M}})$ rather than ${\widehat{\text{AUC}}}_{\mathrm{M}}$ directly:

$$b_m^{\ast }=\text{arg log}({\widehat{\text{AUC}}}_{\mathrm{M}})=\text{log}\left(\frac{{\widehat{\text{TP}}}_{\mathrm{m}}}{{\mathrm{T}}_{\mathrm{m}}}\right)+\text{log}\left(\frac{{\widehat{\text{TN}}}_{\mathrm{m}}}{\mathrm{N}-{\mathrm{T}}_{\mathrm{m}}}\right),$$

$$b_m^{\ast }=\text{log}({\widehat{\text{TP}}}_{\mathrm{m}})+\text{log}({\widehat{\text{TN}}}_{\mathrm{m}})+\text{const}.$$

Since the goal is to classify *sequences* of epochs that make up a particular suppression sequence for a particular record, it may appear to be a weakness that our model considers all EEG epochs for all records to be i.i.d. In practice, however, we found that we were able to achieve good results despite this simplification using a modified training objective, discussed in the next section.

C. Regularized Adaboost

We relaxed the representation of the ROC to be continuous in the model parameters, and use a similar relaxation approach for the cost function. While training an individual classifier, F_m(x_n; w), we use a modified cost function for Adaboost so that rather than maximizing

$${\mathrm{\epsilon }}_{\mathrm{m}}=\frac{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}\mathrm{I}({\mathrm{F}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}})\ne {\mathrm{y}}_{\mathrm{n}})}{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}}=\frac{{\sum }_{\{\mathrm{n}:{\mathrm{F}}_{\mathrm{m}}({\mathrm{x}}_{\mathrm{n}})\ne {\mathrm{y}}_{\mathrm{n}}\}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}}{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}},$$

we instead maximize by gradient descent

$${\mathrm{w}}_{\mathrm{w}}^{\ast }={\text{argmax}}_{\mathrm{w}}({\mathrm{\epsilon }}_{\mathrm{m}}^{\prime })$$

where

$${\mathrm{\epsilon }}_{\mathrm{m}}^{\prime }\approx -\frac{{\sum }_{\mathrm{n}=1}^{\mathrm{M}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}\text{log}(\mathrm{p}({\mathrm{y}}_{\mathrm{n}}|{\mathrm{x}}_{\mathrm{n}},{\mathrm{w}}_{\mathrm{m}})\mathrm{p}({\mathrm{w}}_{\mathrm{m}}|\mathrm{\mu },\mathrm{I}{\mathrm{\sigma }}^2))}{{\sum }_{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m})}}.$$

This modified cost ensures that all individual logistic regression ranking functions include all examples, as opposed to traditional boosting in which the m^th classifier is only trained on misclassified examples from the previous iteration. Once ${\mathrm{w}}_{\mathrm{m}}^{\ast }$ is obtained, error ${\mathrm{\epsilon }}_{\mathrm{m}}^{\prime }$ is used to update w_m, α_m, and ${\mathrm{\beta }}_{\mathrm{n}}^{(\mathrm{m}+1)}$.

IV. CLINICAL DATA AND FEATURES EXTRACTION

A. Clinical Datasets

Fourteen non-invasive EEG recordings with seizures from 12 patients are used for training the boosting classifier. All of the data has more than 30 minutes of recording during the postictal period. The clinical annotations for start and end of PGES for training data are obtained from a clinical expert for consistency in the training dataset. The classifier only uses the scalp (non-invasive) electrode recordings for both training and classification based on the standard bipolar 10–20 EEG (double banana) montage.

Twenty non-invasive EEG recordings with seizures from 20 patients are used as a testing data set. EEG recordings for testing are independent of the EEG recordings used for training the boosting classifier. Annotations from 11 clinicians that independently annotated the 20 EEG recordings in the testing set are used as a benchmark for evaluating the performance of the PGES detection algorithm. It is important to note that the detection algorithm only uses EEG data to annotate PGES while 10 out of 11 of the clinicians also used video recordings to annotate PGES from the data files.

B. EEG Preprocessing and Feature Extraction

EEG recordings from clinical units are usually very noisy and often require some preprocessing before that data can be used effectively. Because filtering can increase the difficulty in differentiating between artifact and EEG when determining the end of PGES, the characteristics of the filter most be chosen carefully. In this application, a 2nd order Butterworth low pass filter with 70 Hz cutoff, a 1st order Butterworth high pass filter with 1.6 Hz cutoff and notch filter at 50 (and 60) Hz are used.

For each EEG signal in the 10–20 montage, frequency domain features are extracted from 1-second epochs using the FFT. The features associated with each 1-second epoch are the average power of the EEG within the following frequency bands: 1–4 Hz, 4–7 Hz, 7–12 Hz and 30–70 Hz. These frequency bands correspond to the traditional Delta, Theta, Alpha and Gamma bands, respectively. We limited the range of frequencies included in the Alpha band based explorations on training data that indicated excluding data in the 13–15 Hz frequency range improved the classification results. In general, the peak-to-peak amplitude of the EEG is lower than 10 μV during the suppression period. However, we do not explicitly enforce this rule but rely on the boosting classifier to both discover this rule and separate artifact and real EEG patterns from the training data.

C. Post Processing of Classification Result

The result of the Boosting Algorithm is a sequence of real numbers in the range [0,1]. This sequence represents the posterior probability of epoch-by-epoch suppression and the determination of PGES needs to be derived from this sequence. We use a threshold of 0.5 to convert the sequence of probabilities into a binary sequence that represents epoch-by-epoch suppression where a value of one represents suppression and a value of zero represents non-suppression. In theory, these sequences should only interchange from zero to one (and one to zero) at the actual transitions between suppressed and non-suppressed epochs. This includes both the PGES period and the period of slowing before the EEG pattern returns to its normal state. Due to imperfect classification on the clinical data, the interchange of the values in the sequence also occurs when there is any misclassification. Thus, post processing of the results of the classification algorithm is necessary to produce the final result. At the current stage of development, the following rules are used to generate the final auto-detection for PGES. First, all suppression epochs that do not have two adjacent epochs labeled as suppression are re-labeled as not suppressed. All one-second non-suppressed epochs surrounded by suppressed epochs are re-labeled as suppressed. The first contiguous collection of suppressed epochs is labeled as PGES and is the final result from our algorithm.

V. Results And Discussion

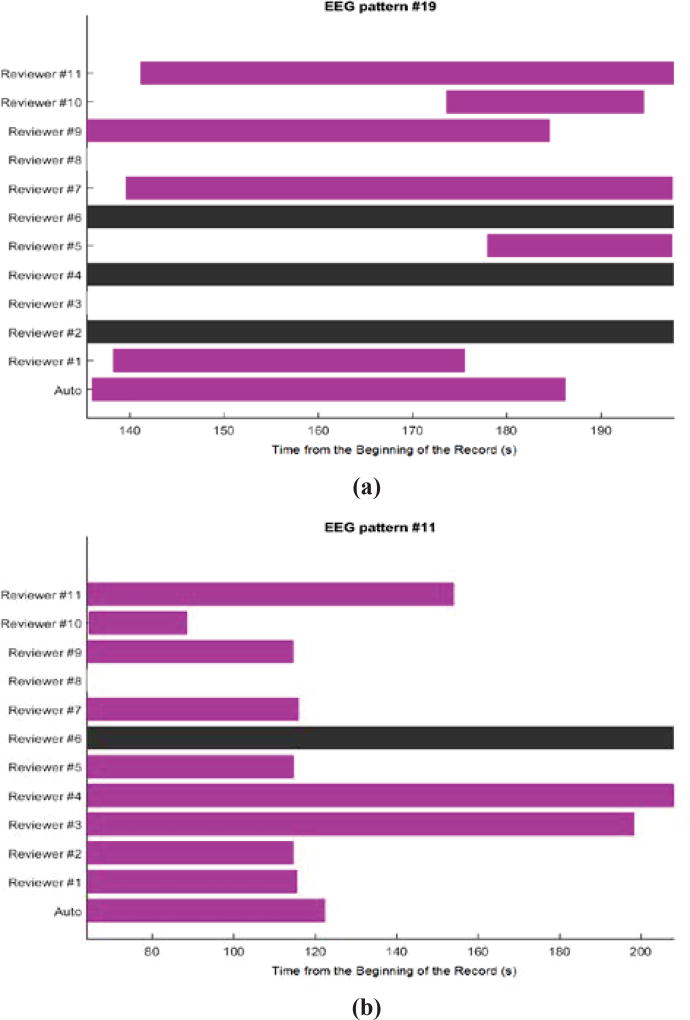
Twenty EEG patterns that are not included in our training data are used as a benchmark for evaluating the performance of our algorithm. For each EEG pattern, because there is no gold standard for annotating PGES, we use annotations from 11 independent clinical scorers in the validation protocol. From these 20 EEG patterns, the PGES annotations from the clinicians are diverse and majority consensus cannot be determined in half data files. In some of these data, opinions are split into two to three major groups. Even when majority consensus exists, some clinicians might not agree with the majority agreement. Sample PGES annotation results from these two groups can be seen in Figure 2(a) and Figure 2(b) respectively. In addition, the start and end time of PGES can vary among clinicians even if they are mostly in agreement. For these reasons, performance comparisons between clinical scorers and between clinical scorers and an automated algorithm are extremely difficult and challenging. We emphasize that our objective is to show that the PGES annotations derived from our algorithm are comparable to most clinical annotations. The automated PGES classification algorithm requires the end of seizure annotations in the data files along with the EEG signal data to score PGES while the clinical scorers used video in addition to the EEG data during the annotation of the PGES period. The video is used by the clinicians to clearly identify the end of the seizure period, the beginning PGES, and also to examine certain segments of the EEG data during the suppression period to determine if the visual changes in the EEG are due to a transition out of PGES (end of the PGES period) or from artifact. Common sources of artifact include breathing and movement during the post-ictal period after a seizure and/or external interference from clinical personnel, and the video provides useful information, not available to the automated algorithm, for making a final decision related to the extent of PGES in any given record. The fact that the clinicians have access to video and that there is such variability in PGES annotations among different clinicians complicates the performance comparisons between the clinical and algorithm annotations, but the approach we have taken is reasonable and provides useful information on the automated annotations of PGES.

Figure 2.

Annotations of PGES from 11 reviewers and auto-detection on two EEG patterns. The beginning of each bar indicates the start of PGES and the end of each bar indicates the end of PGES from a corresponding rater on the same row. (a) Annotations on an EEG pattern that does not have majority consensus. (b) Annotations on an EEG pattern that has majority consensus. The black bar on any row indicates that the clinicians decided not to annotate the EEG pattern. Any row without a color bar implies that the clinicians believe that there is no PGES on that EEG pattern. Auto-detection is on the last row.

For validation, we use the EEG data from the first occurrence of an end of seizure annotation or the beginning of suppression annotation from clinical reviewers to the last annotation of the end of suppression from all clinical reviewers to define the data analysis period. The EEG signal data during this period is then divided into non-overlapping epochs and for each epoch, if the rater considers more than 60% of that epoch as being suppressed EEG, the epoch is labeled as suppressed for that corresponding rater. As a result, PGES annotations from each clinician generate a binary vector for each EEG signal. This binary vector is used to compute Cohen-Kappa statistics for all pairs of clinicians including the PGES auto-detection algorithm using the same EEG signal data. Afterward, we set the threshold for Cohen-Kappa statistic at 0.6 and pairs with a Cohen-Kappa statistic above the threshold are considered to be in agreement.

It is difficult to make conclusions from Cohen-Kappa statistics represented in Table I and Table II. The numbers in each table can range from 0–11 and indicate the number of clinicians that agree on PGES for that EEG pattern. The results are divided into two groups, Group 1 consists of EEG patterns where there is no clinical consensus (reported in Table I), and Group 2 consists of EEG patterns where there is clinical consensus (reported in Table II). From these results, we observe that the performance of the algorithm is indistinguishable from some raters, e.g., R1 and R11, and we can further aggregate results for comparison by comparing the data in Table I and Table II against the average for each EEG pattern, reported in Table III. Data that are above the average are marked as pass and the percentages that pass from each of the raters for difficult EEG patterns (Table I) and normal EEG patterns (Table II) are computed and compared separately. The summary shown in Table III indicates that our algorithm is better in more challenging EEG patterns when compared to normal EEG patterns which is contrary to what is expected and to what occurs with the human scorers. The algorithm has better overall performance than 2/11 clinicians, R3 and R8, and is better than 5/11 clinicians on difficult EEG patterns, while only 2/11 raters are better than the automated algorithm on this cohort. The weak point of our algorithm is the lack in precision on some EEG patterns resulting in decreased performance of our algorithm by 20% on normal EEG patterns (Group2 in Table III). It is worth mentioning that two clinicians, R5 and R7, have very high performance on both normal and difficult EEG patterns while two other clinicians, R2 and R9, are the best in scoring normal EEG patterns. These four clinicians, R2, R5, R7 and R9, have the highest overall performance among raters while our algorithm is comparable to the rest of clinicians.

Table I.

The Number of Clinicians (and Auto-Detection) that are in Agreement (Using Threshold on Kappa Statistic at 0.6) on Difficult EEG Patterns that do not Hhve Majority Consensus

EEG#	A	R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11
2	1	3	-	2	-	1	2	2	2	1	3	3
4	4	1	-	4	-	4	4	3	4	3	2	1
5	4	5	5	1	-	3	1	4	3	3	1	3
8	3	2	2	1	-	3	2	3	2	2	2	1
9	2	1	1	2	-	1	-	2	2	2	1	2
10	6	6	-	1	-	6	6	6	6	1	1	1
13	1	5	4	5	-	1	5	4	5	4	5	4
14	3	3	2	3	-	5	4	4	3	1	1	4
16	1	4	-	4	-	3	1	3	4	3	4	1
19	2	1	-	2	-	2	-	2	2	2	2	2
AVG	3	3	3	3	-	3	3	3	3	2	2	2

Table II.

The Number of Clinicians (and Auto-Detection) that are in Agreement (Using Threshold on Kappa Statistic at 0.6) on Normal EEG Patterns that have Majority Consensus

EEG#	A	R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11
1	5	2	5	2	-	5	1	2	1	5	5	2
3	4	4	-	2	-	4	4	4	2	4	4	4
6	2	7	7	2	-	7	1	7	1	7	7	7
7	7	7	7	2	-	1	2	7	7	7	7	1
11	7	6	6	1	1	6	-	6	1	6	1	2
12	1	6	-	2	-	6	-	6	2	6	6	6
15	1	10	10	10	9	10	10	9	9	10	1	7
17	3	3	6	1	-	3	6	1	6	6	6	6
18	3	3	7	1	-	7	7	7	3	7	7	7
20	7	2	7	1	-	7	7	7	2	7	1	7
AVG	4	5	7	2	5	6	5	6	3	7	5	5

The first column contains identification numbers of EEG the patterns. The second column shows agreement of clinicians with a result from auto-detection algorithm on each EEG pattern. The rest of the columns show agreement of specific clinicians with other results on the same EEG pattern. The last rows in TABLES I and II are the average number of agreement across 10 EEG patterns. These values show on the average how many raters agree with a rater in each column for difficult EEG patterns (TABLE I) and for normal EEG patterns (TABLE II).

Table III.

The Percentage of EEGs Pattern in a Group that Raters have the Number of Agreement above the Average Number of Agreement

Group	A	R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11
1	70	60	40	70	-	70	63	100	90	60	40	60
2	50	60	100	10	50	80	63	80	30	100	70	60
All	60	60	77	40	50	75	63	90	60	80	55	60

The numerical value in i^th column and j^th row (omitting first row and first column) corresponds to the percentage of EEG patterns for which the j^th rater in a given group has more agreement compared to other raters.

Group 1 includes “difficult” EEG patterns in which majority consensus does not exist.

Group 2 includes “easy” EEG patterns in which majority consensus exists.

VI. Conclusion

From analysis of the clinical annotations, we conclude that identifying PGES is a complicated problem and there is disagreement among different clinicians for almost all EEG patterns in this study. There is no single EEG pattern for which all 11 clinicians agree on the start and end of the PGES period. Even for EEG signal recordings that most clinicians agree on the PGES annotation, other clinicians will have totally different opinions. Without a definitive gold standard, it is difficult to make a clear-cut decision on the correctness and accuracy of annotations from each clinician. The best we can do is to use pairwise comparisons to quantify the agreement among clinicians, and we proposed such a procedure to benchmark PGES detection, from our algorithm, by using the agreement of our algorithm with the clinicians. Using this benchmark, four clinicians have much better performance than the rest of reviewers and overall our algorithm is comparable with the performance of most of the clinicians and is better than two of the human raters. While the proposed PGES detection method needs further improvement on regular EEG patterns, it performs surprisingly well on difficult EEG patterns. This could be due to the EEG patterns that were selected for use in the training dataset.

Future work on this algorithm will include: (C1) Improving algorithm performance on classifying PGES for normal EEG patterns while maintaining or improving performance on difficult EEG patterns. (C2) Developing a graphical user interface (GUI) tool for clinicians to use and evaluate the algorithm in the Epilepsy Monitoring Unit (EMU) as part of the clinical workflow. This process will significantly improve the future development of PGES detection so that, at a minimum, it can be used as a training platform for new clinicians who will work on annotating PGES. (C3) We are currently developing a new mathematical model that will more fully describe EEG suppression and will include data from PGES as well as the intermittent and continuous slow periods of EEG recovery during the postictal period. This development will use full probabilistic modeling of time-series data. For example, a non-stationary hidden Markov model is one of the approaches currently being investigated. In addition, we are currently collaborating with a group of clinical experts to create a dataset with broad consensus across the clinical group to serve as a gold standard dataset. Clinical annotations will be derived from the consensus of these experts who examine each EEG pattern as a group while sharing their opinions and expertise. This dataset will not only be useful for the development and improvement of our future algorithm, it also can serve to assist new clinicians in annotating PGES.