Abstract
The 2013 Nobel Prize in Chemistry was awarded to the authors of the first two publications utilizing the concept of combined quantum mechanical and molecular mechanical (QM/MM) methods. In celebrating this great event in computational chemistry, we review the early development of combined QM/MM techniques and the associated events that took place through the mid-1990s. We also offer some prospects for the future development of quantum mechanical techniques for macromolecular systems.
Keywords: biomolecular interactions, computational chemistry, electronic structure, molecular mechanics, quantum mechanics
1. Introduction
The idea of combining electronic structure theory and empirical force fields to model complex chemical processes was first described in 1972 in a study of the potential energy surfaces of the ground and excited states of conjugated molecules.[1] In that work, a hydrocarbon system was separated into a σ framework, approximated by an empirical potential function, and a π-electronic structure component, represented by the semiempirical Pariser-Parr-Pople (PPP) theory. Subsequently, in 1976, this approach was used to include an all-valence electron semiempirical method and was applied to the modeling of carbocation stabilization in the active site of lysozyme.[2] This technique has become what is known as the combined quantum mechanical and molecular mechanical (QM/MM) method, which is a class of multiscale models, for which the authors of these two publications were awarded the 2013 Nobel Prize in Chemistry.[3] In retrospect, the idea of a combined QM/MM approach was far ahead of its time, as the method was not used by others until ten years later.[4,5] It took another ten years before combined QM/MM methods finally emerged as a method of choice for studying chemical and photochemical processes in condensed phases, including biological macromolecules.[6,7] In this article, we trace back the early developments and applications of combined QM/MM techniques for studying complex chemical and enzymatic reactions.
The present review is restricted to studies that explicitly employed electronic structure theories in combination with molecular mechanics, i.e., electronic structural QM/MM approaches; we do not include investigations that used empirical potential functions parameterized to fit quantum chemical results or that were dressed in a quantum chemical framework. Furthermore, we focus on the literature covering the first twenty years of QM/MM development through to 1996. In the following, we first provide a chronological summary of the key studies and events that stimulated the methodological development and application of combined QM/MM methods. We next highlight some QM/MM studies of chemical and biological problems, and then conclude with a summary of prospects for the future development of quantum mechanical techniques for macromolecular systems.
2. Method
The two articles highlighted in the introduction[1,2] presented an idea that had a far-reaching impact in theoretical and computational chemistry, and also in other areas of computational science. The first study[1] was stimulated by the need to have a description of both the ground and excited state potential energy surfaces when modeling the isomerization dynamics between the 11-cis and all-trans conformations of retinal in the visual pigment during light excitation.[8,9] However, at that time, it was not computationally tractable to produce accurate results with an ab initio electronic structure method, even for molecules as simple as ethene. To avoid introducing different parameter sets for different electronic states in an empirical potential function,[10] the authors assumed that the σ and π electrons in a conjugated system were fully separable, and that the σ electrons could be modeled by an empirical potential and the π electrons by the very successful, semiempirical PPP theory.[11,12] The total energy for such a hybrid system was written as the sum of empirical potential energy for the σ bonds and the electronic energy of the conjugated π system:
| (1) |
where was the empirical potential, i.e., molecular mechanical,[13,14] energy of the σ framework, was the electronic energy of the π electrons in the ground state, and was the excitation energy of the Nth excited state from a configuration interaction (CI) treatment within PPP theory. A detailed description of the theoretical approximations inherent to this approach are beyond the scope of this review;[1] suffice it to say, the idea presented in Eq. 1 provided a computationally efficient and, with appropriate parametrization, an accurate procedure for yielding the potential energy of a molecular system. It also enabled calculation of the atomic forces– the derivatives of the potential energy with respect to the atomic coordinates, R– which permitted geometry optimizations and dynamics simulations to be carried out. The method introduced in Eq. 1 was later extended to include the effects of σ electrons on π polarization in molecules containing heteroatoms.[15]
The complete separation of σ and π electrons in Eq. 1 ignored the electrostatic coupling between the two regions of the system.[15] Although this is a very reasonable assumption for hydrocarbons, the electrostatic interactions between the QM and MM regions are no longer negligible for polar systems such as reactions in the active sites of enzymes. As a result, these interactions were included in the second paper,[2] which studied carbonium ion stabilization by lysozyme. The revised combined QM and MM energy expression was:
| (2) |
where VQM/MM was the QM/MM coupling, and VMM and VQM had the same meanings as the first two terms in Eq. 1, except that they now referred to distinct groups of atoms, as an all-valence electron QM method was employed. The QM/MM interaction energy was approximated as follows:[2]
| (3) |
where the index i specified QM atoms and j ran over the MM atoms, and the four terms in Eq. 3 described, respectively, van der Waals interactions represented by the Lennard-Jones potential, electrostatic, induction, and long-range dielectric polarization modeled by the Langevin formula .[2] The inclusion of the environmental electrostatic terms in the diagonal elements of the Fock matrix allowed polarization of the electronic wave function of the QM region, i.e., the atomic charges of the QM atoms {Qi}, whereas the polarization of the MM subsystem was modeled by a first-order, i.e., non-self-consistent, approximation in which , with αj being the atomic polarizability, and ε(rij) being a dielectric screening factor, approximated by a constant value of 1.36.
The decade following the publication of the lysozyme paper saw a lull in the development of QM/MM methods. One of the Nobel Prize recipients continued to explicitly work on enzyme catalysis, but to do so, an alternative, simpler approach, namely the empirical valence bond model, was used and is championed to this day, producing a voluminous body of work. Discussion of this approach is outside the scope of this review; the interested reader may find details in numerous review articles, including Ref. [16].
The next major developments in the QM/MM area occurred in the mid-1980s. In 1986, Singh and Kollman described the QUEST program that merged the Gaussian-82 package with the AMBER force field,[4] and used it to model the SN2 reaction between chloride ions and chloromethane in water. Their work was stimulated by the Monte Carlo simulation of the potential of mean force for the same reaction by Jorgensen and coworkers,[17] who used QM results to construct empirical potential functions in condensed-phase simulations (QM+MM). In their calculations, Singh and Kollman iteratively optimized the geometries of the MM and QM subsystems, separately, by holding the other region rigid. They also omitted the electrostatic interactions between QM and MM atoms during the optimization steps, but included them to obtain the final energies.[4] A similar study by the same group, of a model peptide hydrolysis reaction in water, was reported a year earlier.[18] In both studies, the computed energies of the optimized solute-solvent, or active site-protein, system were found to be in agreement with free energy simulation results[17] or experimental data, although, as the authors pointed out, configuration sampling and entropic contributions were not included.
Interestingly, one of the lasting contributions of the work of Singh and Kollman[4] was the introduction of connection or link atoms to saturate the valencies of the molecular QM fragments covalently bonded to the MM region. The link-atom approach remains one of the most popular strategies in combined QM/MM applications today, because of its simplicity and the fact that it can be implemented without modifications to the electronic structure software.
During the time of the above study, Paul Bash was collaborating with Chandra Singh and Peter Kollman on free energy simulations and protein-ligand interactions.[19] After completing his Ph.D. in 1986, Bash moved to the east coast and joined the Karplus group at Harvard. There, he started to collaborate with one of the authors, MJF, who was also in the group, and together they implemented a combined QM/MM model in the program CHARMM,[20] to study chemical reactions in complex systems. This collaborative effort resulted in the first statistical mechanical simulation employing a combined QM/MM potential, with which the free energy difference between the transition state (TS) and an ion-dipole complex (IDC) for the methyl chloride-chloride ion exchange reaction in aqueous solution was determined.[5] A dual-topology approach was introduced, in which the IDC (state A) and the TS (state B) species co-existed in a common solvent environment, but with no interaction between them. The dynamics simulations were carried out by using the mixed potential surface
| (4) |
The free energy difference between the two states was determined by free energy perturbation (FEP) theory,[21] through a series of simulations that gradually transformed the system from A to B, by varying the coupling parameter, λ, from 0 to 1. The dual-topology approach circumvented a difficulty in FEP simulations between two different molecules represented by an electronic structure theory: while it is simple to “mutate” one molecule into another in molecular mechanics,[22] it is not possible to change the number of electrons in QM calculations in a continuous fashion. Eq. 4 provided a smooth potential energy surface for FEP simulations.
The use of reaction field approaches in quantum chemistry to model solvent effects has a long history, and in principle, the procedures are very similar to those employed in an explicit treatment with combined QM/MM.[23] Extending a direct reaction field (DRF) version of the self-consistent reaction field (SCRF) method developed classically for a point charge/atomic polarizability representation,[24] Rullmann et al. incorporated the DRF Hamiltonian into Hartree-Fock (HF) self-consistent field (SCF) calculations to investigate ligand-protein interactions in the active site of papain.[25] The DRF Hamiltonian involves a direct inversion of the matrix describing the polarization response in the medium (protein and solvent), rather than iteratively converging the polarization field. Furthermore, in addition to induction effects, the method incorporates a dispersion-like term, corresponding to a second-order perturbation theory between the QM and MM regions. However, this semi-classical approach over-estimates dispersion interactions by a factor of at least 2.[26] Despite many interesting features in the DRF approach,[25] it appears that the method was not widely used in later applications.
Although the concept of combining electronic structure theory with a classical force field offered great promise for treating large molecular systems, it is sobering to notice that less than a dozen publications employing combined QM/MM approaches appeared in the 19-year interval between 1972 and 1990.[4, 5, 15, 18, 25, 27–29] If the studies in the early 1970s introduced the basic ideas of combined QM/MM methods, it was the 1990 publication by Field, Bash, and Karplus that had the greatest impact in the field,[29] by describing how the approach could be implemented into electronic structure theory and integrated with molecular mechanics software for geometry optimization and dynamics simulation. Here, the electrostatic QM/MM interaction energy was directly determined from electronic structure calculations, instead of the Coulomb approximation highlighted in Eq. 3. It used an interaction Hamiltonian of the form
| (5) |
where Pμν is an element of the density matrix of the QM region, is the one-electron integral due to charges on MM site j, and is the Coulomb energy between QM nuclei and MM charges. Eq. 5 allows analytic gradients to be exactly and conveniently determined, producing dynamic trajectories that conserved energy, without complications due to the neglect or the approximation of the derivatives of the partial atomic charges of QM atoms {Qi} in Eq. 3.
The study published by Gao and Xia in Science in 1992[6] marked the transition to a period of rapid increase in the development and application of combined QM/MM methods.[30] In this work, the reliability of the QM/MM technique in free energy simulations was established.[6] In addition, it demonstrated that the non-bonded van der Waals terms between QM and MM regions depended on the electronic structure method and basis set used, as well as its combination with a particular MM force field, and it highlighted a procedure to optimize these unavoidable parameters for a given QM and MM combination in order to achieve computational accuracy.[6,31,32] Importantly, an interaction-energy decomposition procedure was also introduced, which illustrated some of the unique features that a combined QM/MM method could offer, but which were not readily available from simulations employing an MM force field.[6]
Unlike the energy expression in Eq. 2, the total energy of the system is written in terms of the electronic energy of the QM subsystem in vacuum ( ), and the transfer energy of the QM subsystem from the gas phase into the MM environment, ΔVQM/MMM:
| (6) |
The last two terms in Eq. 6 have different meanings from those in Eq. 2; and correspond, respectively, to the electronic energy of the QM subsystem in the hybrid system (ΨQM) and in the gas phase ( ), whereas ΔVQM/MM (Eq. 6) and VQM/MM (Eq. 2) differ by the term . Eq. 6 offers a convenient dual-level approach[33,34] for combining separate gas-phase and condensed-phase calculations, in which a high-level QM method is used to determine the energy of the QM subsystem for greater accuracy, whereas a lower level QM model is used to construct the QM/MM potential with greater computational efficiency for the more time-consuming, condensed-phase simulations.
In QM/MM interaction energy decomposition,[6] the total interaction energy, ΔVQM/MM, was decomposed into components with well-defined physical interpretations, which proved to be useful for understanding intermolecular interactions in solution, as well as for developing polarizable empirical potentials:[35,36]
| (7) |
In Eq. 7, is the “permanent” QM/MM interaction energy, with the QM electron density fixed to that in the gas , and ΔVpol is the total polarization energy of the QM subsystem by the MM environment, which includes contributions from the ΔVdist term. The latter is the energy needed to polarize the wave function of the QM subsystem by the MM external field, and it is the quantum chemical analog of the self-energy in classical polarization theory that has been used to justify the SPC-E model for water.[37]
The treatment of the mutual polarization between the QM region and the MM subsystem in a consistent way was presented by Thompson and Schenter,[38,39] and the many-body effects and energy terms were analyzed by Gao.[30,40] Of particular interest are the two equalities in Eqs. 8 and 9 that relate the interaction energies between the QM and MM regions, and which can be used to numerically validate the consistency of the polarization field in a hybrid QM and MM simulation. The equations are
| (8) |
and
| (9) |
where HQM/MM(qMM) and HQM/MM(μMM) are the Hamiltonians for the potentials due to the static point charges and induced dipoles on the MM atoms, respectively, and and are the potential and electric field due to the QM subsystem (ΦQM) at the jth MM site. Eqs. 8 and 9 correspond to the interaction energies of the atomic charges and induced dipoles of the MM subsystem with the QM charge density (wave function). The two equalities are the consequence of classical (the left-hand sided of the equations) and quantum (the right-hand side of the equations) representations of the same quantities, and they are used, respectively, in the MM-SCF and QM-SCF iterations.[38,40] Eq. 9 is only valid when the entire coupled MM and QM SCF is fully converged. As noted by Thompson and Schenter,[38] the development that expressed the electronic charge density in terms of scaled atomic charges in the QM region (Eq. 3)[41,42] formally violated Eq. 9, and at best, it approximately satisfied Eq. 9, but only if the charges (Qi) were fitted to the QM electrostatic potential everywhere in space.
In 1995, an integrated molecular orbital and molecular mechanics (IMOMM) model was described by the Morokuma group for molecular geometry optimization,[43,44] and this was immediately extended to an IMOMO model.[45,46] The latter article formally featured an energy addition and subtraction scheme, which has evolved to the currently used acronym, ONIOM (our[47] own n-layered integrated molecular orbital and molecular mechanics). The ONIOM model is available in the Gaussian package, which has been widely used. These early layered addition-subtraction models did not include electrostatic effects between the higher level QM region and the rest of the system, although they have been introduced in later implementations. To describe the different ways in which groups used to integrate QM and MM methods, Bakowies and Thiel summarized three combination levels.[48] These comprised a simple “mechanical embedding” of the QM subsystem that omitted electrostatic interactions with the surrounding, an “electrostatic embedding” that included these terms, and a third level that consistently treated polarization interactions.
One of the main issues in combined QM/MM methods is the way in which covalent bonds between QM and MM atoms are treated. Simple truncation of covalent bonds in a molecular system is inappropriate as it causes major perturbation to the electronic structure. This subject continues to be an active area of research.[49,50] In general, methods for treating the QM and MM covalent boundary can be grouped into two categories:[51] methods that do not introduce or eliminate any degrees of freedom, including atomic charges; and those that employ additional pseudo-atoms to satisfy the free valencies of the QM fragment. In Ref. [2], a minimal set of semiempirical hybrid orbitals was used to represent a covalent bond across the QM-MM boundary.[2] A rigorous formulation of this approach is the local self-consistent field (LSCF) method that was developed by Rivail and coworkers.[49,52–55] In particular, if Cb and CM are the boundary atoms that connect the QM and MM fragment (Figure 1), the Cb−CM covalent bond is described by a strictly localized bond orbital |l>, which can be predefined for common bonds in the relevant basis set, or can be extracted from a full quantum chemical calculation on a model compound that contains the bond of interest, followed by orbital localization.[49,56] The LSCF method was extended in a procedure called the generalized hybrid orbital (GHO) approach (Figure 1),[51,57] in which the orbital was hybridized on the fly during a dynamics simulation, eliminating the need to predefine and parameterize frozen bond orbitals for specific cases. Importantly, it provides a smooth transition from the QM region into the MM subunit without deleting or adding new degrees of freedom, nor altering atomic charges in close proximity to the QM atoms.
Figure 1.
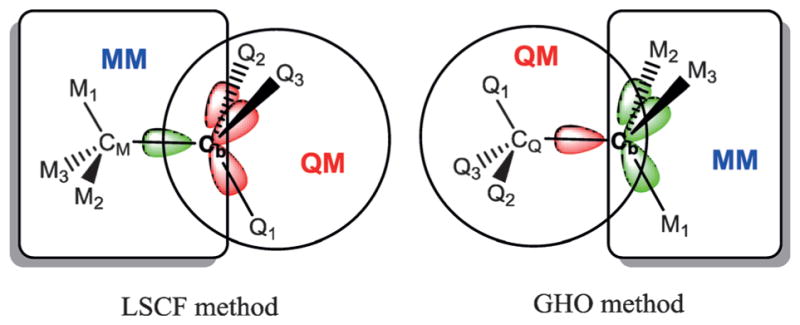
Illustrations depicting the difference between the local self-consistent field and the generalized hybrid orbital methods. In the LSCF method, one (green) hybrid orbital points to the MM subsystem and is kept frozen in the QM/MM calculation, whereas the other three (red) orbitals are optimized. In the GHO method, only one hybrid orbital, dependent on the instantaneous geometry at the boundary carbon (Cb), is optimized in the SCF procedure, whereas the other three are kept frozen.
The second category of QM-MM covalent boundary methods includes the link-atom method described above and the substitution of the MM atom of the broken bond with a fictitious monovalent replacement.[4,29] The latter is usually hydrogen, but pseudo-halogen atoms that mimic the MM atom that it replaces have also been used.[58–60] Numerous variants of the link-atom approach have been developed, including the dummy group,[61] connection atom,[58] pseudobond,[62] frozen density, quantum capping,[ 63] double link,[64] add-and-remove,[65] and redistributed charge methods.[50]
The early years of the 1990s saw a rapid increase in the application of combined QM/MM methods to a wide range of chemical and biomolecular systems (Figure 2). These studies were reviewed in two publications,[7,30] and included solvation and solvent effects on chemical reactions, free energy simulations of enzymatic processes, heterogeneous catalysis and the electronic spectra of organic molecules in solution. By the mid-1990s, it became clear that combined QM/MM approaches were the method of choice for studying complex chemical processes in condensed phases and in biological systems.[66]
Figure 2.
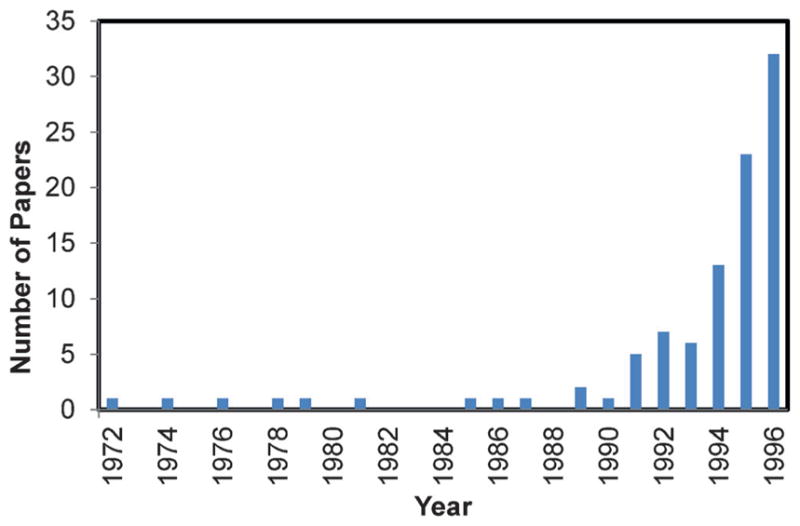
Papers published between 1972 and 1996 that utilized the concept of combined quantum mechanics and molecular mechanics.
Before closing this section, we note that equally important to the progress of combined QM/MM methods were a series of scientific meetings solely devoted to the subject, which have been documented through edited books, special journal issues and conference proceedings. In 1995, two of the authors (MJF and JG) organized a joint CECAM-NSF planning meeting[67] on Hybrid Quantum and Classical Methods for Simulation of Biopolymers in Solution in Lyon, France, which was coordinated with another conference on Quantum Mechanical Simulation Methods for Studying Biological Systems[68] in Les Houches at the foot of Mont Blanc. The CECAM-NSF meeting was supported by grants from the National Science Foundation and the Centre Européen de Calcul Atomique et Moléculaire, enabling 39 participants,[67] including one of the recipients of the 2013 Nobel Prize, from ten countries working on various aspects of QM/MM methods to travel to the two conferences.[67] Among the participants was Michael Zerner who contributed enthusiastically to the scientific discussion and development of QM/MM models, particularly for simulations of electronic spectroscopy in solution.[69,70] In fact, soon after the 1992 publication,[6] he invited one of the authors (JG) to present a plenary talk on QM/MM methods at the 33rd Sanibel Symposium in Florida.[71] The advice that he had provided, on both personal and professional levels, proved to be extremely valuable to the young scientist who had just begun venturing into a competitive, but rewarding field.
The CECAM-NSF meeting was followed by a symposium co-organized by Field, Gao and Thompson in 1996 on Combined QM/MM Methods at the Pacific Symposium on Biocomputing in Hawaii,[72] and a four-day symposium co-organized by Gao and Thompson in 1997 on Hybrid Quantum Mechanical and Molecular Mechanical Methods at the 214th American Chemical Society (ACS) National Meeting in Las Vegas. The conference proceedings of this symposium were developed into a volume in the ACS Symposium Series (No. 712),[66] which featured nineteen chapters covering all aspects of QM/MM methods and applications at that time. A sequel to the ACS conference was again followed by a symposium co-organized by Gao and York on Combined Quantum Mechanical and Molecular Mechanical Method at the 221st ACS National Meeting in Chicago in 2001, which capped ten years of progress since the JCC publication by Field, Bash, and Karplus.[29] The conference proceedings were published in a special issue in Theoretical Chemistry Accounts.[73] It was observed of the conference that “The past decade saw remarkable progress in the development of combined quantum mechanical and molecular mechanical (QM/MM) methods and in the scope of their applications. … In a short period of 5 years (since the 214th ACS meeting), the field has grown to a much more sophisticated level, ranging from technical issues, such as the treatment of the QM and MM boundary, to wider applications, such as enzyme catalysis”.[73] Since 1998, there have been numerous CECAM workshops and tutorials devoted to the topics of combined QM/MM simulations.
3. Applications
3.1 Free Energy Simulations and pKas of Organic Acids
One of the greatest achievements in computer simulation in the 1980s was the ability to accurately compute the difference in the free energy of solvation, for different solute molecules, using free energy perturbation theory (FEP).[19,21,22,74,75] Aside from its chemical and biochemical significance, the FEP method also provided a way of assessing the accuracy of the underlying potential energy function. The FEP procedure involves a gradual transformation of the potential energy function from that for one solute into that for another. This is conveniently done using empirical potential functions, but it is not straight-forward using a combined QM/MM potential. The dual-level approach is a viable procedure,[5] particularly between molecules of similar size and shape, but it suffers from convergence difficulties at the end-points in the alchemical mutation.
An alternative QM-to-MM procedure, which transformed the combined QM/MM interaction Hamiltonian into a purely empirical potential function between the solute and solvent molecules, was proposed in 1992.[76] In this approach, the classical force field served as a conduit to bridge two solute molecules with a different number of atoms and electrons through a thermodynamic cycle (Figure 3). The method was used to determine the absolute free energies of solvation for a range of organic compounds and ions representing amino acid side chains, and excellent agreement with experimental results was obtained, demonstrating the accuracy of combined QM/MM methods.[6] A similar approach, which combined the MNDO (modified neglect of diatomic overlap) and AM1 (Austin Model 1) semiempirical methods with the Langevin dipole (LD) model, was published in the same year.[42] It was reported that both the LD model and the all-atom simulation approach yielded similar results for the free energies of transfer of polar molecules from non-polar solvent into water and the solvation of hydrophobic ions.[42] Merz and coworkers implemented the QM-to-MM FEP strategy in a combined DFT/MM simulation, and the solvation free energies of several monovalent ions in water were computed.[77]
Figure 3.
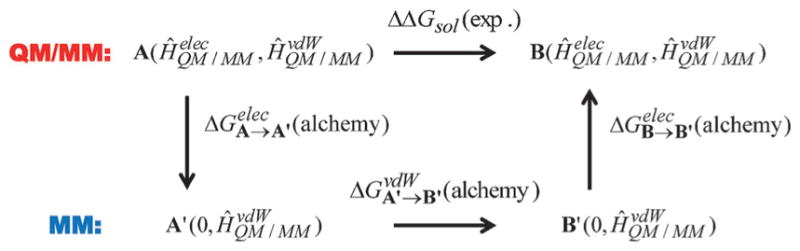
Thermodynamic cycle illustrating the alchemical transformation to determine the difference in free energy of solvation between molecules A and B, represented by a QM/MM potential, through pure MM conduits, A′ and B′, consisting of van der Waals terms. The MM conduits could also include Coulomb terms, if desired.
As a bold alternative, Merz and coworkers directly perturbed the electronic Hamiltonian in free energy simulations. Two approaches were reported. The first involved changing the identity of the nucleus (its charge), but keeping the number of valence electrons constant. This method was used in the test study of relative free energies of solvation between F− and Cl−, and between ammonium ions and methane in water.[78] The second approach was to introduce a variable to directly change the number of electrons in a QM/MM potential as well.[79] However, despite the appeal of being able to directly carry out alchemical mutations like that using an empirical force field, the large change in electronic energy made the calculation of the small free energy difference in interaction energies in solution difficult to converge, and so, these methods have not been widely used.[80]
The success of combined QM/MM potentials in free energy simulations was attributed to careful consideration and calibration of the van der Waals parameters in the QM/MM Hamiltonian.[6,29] An optimal strategy involves parametrization of the van der Waals parameters of a QM atom for a given QM (level of theory and basis set) and MM (force field) combination versus high-level ab initio results or experimental data for bimolecular complexes containing different functional groups interacting with water. Hydrogen-bonding energies for a range of neutral and charged systems were examined by Vasilyev et al. using the semiempirical MNDO, AM1 and PM3 (parameterized model number 3) Hamiltonians for the QM region and the OPLS (optimized potentials for liquid simulations) potential for the MM fragment.[81] It was found that a limited number of parameters were sufficient, dependent only on the atomic number and sometimes, also on the hybridization state for heteroatoms.[6,31,32,82] It is worth emphasizing that the performance of optimized QM/MM models in describing intermolecular interactions is often better than that obtained by a pure QM treatment, unless an extremely high level of theory (CCSD(T)) and large basis sets (aug-cc-pVTZ) are used.[6,81] Thus, it is not necessarily true that a larger QM region would lead to better performance in QM/MM calculations.
Accurate free energy simulations permitted the estimation of aqueous acidity constants and the pKa values of organic acids. For example, the relatively higher basicity of the syn lone pair of a carboxylate, compared with that of the anti-form has been used to explain the frequent observation of the syn-orientation in the His-Asp (histidine-aspartate) couple in protein structures.[83] However, other experiments indicated that the basicity difference was rather small,[84] and this was confirmed by QM/MM free energy simulations of acetic acid in the syn- and anti-conformations, revealing that the basicity difference was less than 1 pKa unit.[33] Electronic polarization effects on the relative tautomeric equilibria in 2- and 4-hydroxypyridine/pyridone pairs were analyzed via Monte Carlo simulations in organic and aqueous solutions, and differential polarization between the hydroxyl and oxo forms was found to contribute as much as 68% of the total solvation effect.[85] In another study, the keto-enol tautomeric equilibrium constants in acetic acid and acetate ion were determined from dual-level QM/MM free energy simulations, and the pKas for the ionization at the α-carbon site and for the enol were determined to be 26.6 and 7.3, respectively.[86]
The ground and excited state pKas of phenol were determined from a combination of QM/MM free energy simulations of solvent effects on the ground and excited state species (employing a CI wave function), and the vertical and equilibrium excitation energies in the gas phase using CASPT2 (complete active space perturbation theory) with an atomic natural orbital basis set.[87] Photochemical excitation of phenol significantly increased its acidity, lowering the pKa from 10 in the ground state to a value of 1.4 pKa units in the excited state, if equilibrium solvation of the excited state was considered. However, following a Foster cycle analysis, an excited state pKa of about 5 was predicted with non-equilibrium solvation, which was in reasonable agreement with the experimental estimate of about 4.[87]
3.2 Intermolecular Interactions
Combined QM/MM methods provided the unique opportunity of understanding solvent polarization effects directly from electronic structure calculations. Statistically averaged, induced molecular dipole moments for a variety of organic compounds were obtained from Monte Carlo simulations,[6] and molecular polarization was examined using the Langevin dipole-MNDO combination.[16,42] Wei and Salahub carried out a dynamics simulation of a QM-represented water molecule, using both local and nonlocal density functionals, with the TZVP+ basis set in a bath of TIP3P water molecules,[88] and found good agreement between the computed molecular dipole moment and previous results. The concept of atomic partial charges is useful for understanding chemical reactivity as well as for developing quantitative empirical force fields, although these quantities are not experimental observables. A particularly useful method for deriving them is by fitting electrostatic potentials from quantum chemical calculations. Monte Carlo simulations using a combined QM/MM potential were performed to obtain the average electrostatic potentials outside the van der Waals radius of organic molecules, from which partial atomic charges were fitted, incorporating the average solvent effects.[89] This was extended to investigate polarization contributions to computed solvation free energies in aqueous solution[90] and in chloroform,[91] and an excellent correlation was found with results obtained from continuum SCRF calculations.
To model QM/MM electrostatic interactions, Bakowies and Thiel described a parametrization of semiempirical electrostatic potentials using MNDO and AM1 integrals fitted to those determined from HF/6-31G(d) calculations, and a semiempirical procedure to obtain partial charges based on the principle of electronegativity equalization.[92] To efficiently determine the forces between QM and MM interactions, Bala et al. developed an extended Hellmann-Feynman theorem for non-stationary states in coupled quantum-classical molecular dynamics simulations.[93]
The potential of mean force for a model cation-π complex between tetramethyl ammonium (TMA) ions and benzene, in water, was determined using a mixed AM1 representation for the solutes and the TIP4P water model for the solvent.[94] A free energy barrier of about 3 kcal mol−1 was predicted between the contact pair and the solvent-separated species. Importantly, it was found that TMA has a greater affinity for benzene than for chloride ions, with a binding constant of 0.8 M−1.[94]
Host-guest systems are one of the favorite targets for combined QM/MM simulations. Thompson et al. carried out a molecular dynamics simulation of K+ complexed with dimethyl ether (DME) and 18-crown 6 (18c6) in aqueous solution.[95–97] In these studies, the hosts were included in the QM region modeled by the AM1 method, whereas the cation and solvent molecules were treated by force fields. QM-MM interactions were fitted to MP2 results, giving rise to a highly accurate model for such a complex system. It was found that the most probable position of the cation is near the center of 18c6, and an interaction energy of −82.6 kcalmol−1 was obtained by treating the crown ether flexibility with a fitted torsion potential. This work was extended by decorating 18c6 with six exocyclic carbon rings, two of which had a carbon replaced by either an oxygen or a sulfur atom (s18c6). Combined QM/MM simulations revealed that the newer model s18c6 was more suitable for ion transport and more selective in binding Na+ and K+, as a result of reduced cavity size.
Ion solvation was studied by Kerdcharoen et al. who described a “hot spot” approach, treating the inner solvation layer of Li+ quantum chemically, using a Hartree-Fock/DVZ+P QM method.[98] It was found that the lithium ion was coordinated with four water molecules. Stanton et al. examined the performance of an ab initio HF/MM model for describing hydrogen-bonded complexes and the free energies of solvation of several ions in water; the effects of basis set size and the inclusion of correlation were considered.[99] Treboux described an approach that coupled Huckel theory to a molecular mechanical potential to determine geometry and vibrational frequencies of conjugated molecules.[100] Tunon et al. developed a hybrid density functional molecular dynamics simulation procedure to study ion solvation in water.[101] The same procedure was used to model a quantum-mechanically treated water molecule with a non-local functional and triple-zeta basis set in liquid water, and they found significant fluctuations in the instantaneous molecular dipole on the QM water.[102] A combined DFT/MM method was also applied to model solvent effects on the geometry of water in liquid water, and the vibrational frequency shifts of carbonyl compounds in water.[103] A perturbative approach for Monte Carlo simulations employing an ab initio QM/MM potential was described by Truong and Stefanovich, in which the wave function for the QM solute was not optimized when solvent moves were made,[104] and the method was applied to Monte Carlo simulations of chloride ions in water.[105]
3.3 Chemical Reactions in Solution
Combined QM/MM methods have their greatest appeal when studying chemical reactions in condensed phases and in enzymes (see the next section). This is because quantum chemical methods are necessary for modeling bond-forming and -breaking processes, but are intractable for explicit condensed phase simulations. By contrast, the approximate representation of the solvent environment by a classical MM model, which does not directly participate in the chemical reaction, but provides critical effects on the chemical reactivity of the solutes, offers the efficiency needed to carry out statistical mechanical simulations.[106] This has been the main motivation in developing mixed QM and MM models.[4,5,7,27,28]
Roughly speaking, the use of QM/MM potentials for studying chemical reactions, and the enzymatic reactions discussed next, falls into two categories: (a) energy minimizations to locate the energy reaction path; and (b) free energy simulations to determine the potential of mean force along a predefined reaction coordinate. Both approaches have strengths and weaknesses. The use of geometry optimization techniques to locate minimum energy paths can be useful for exploring the potential energy landscape, and can be insightful to understand the mechanism and chemical reactivity in heterogeneous catalysis and enzyme catalysis involving transition metal centers. However, the results from energy minimization in an enzyme active site strongly depend on the initial structure used, as it has been observed that small variations of a few tenths of an angstrom in the positions of key residues can result in energy changes that are greater than the reaction barrier itself. The entropic contributions from protein dynamics fluctuations can also be critical to the proper understanding of enzyme catalysis. The most relevant approach is free energy simulations of chemical processes in condensed phases and enzymes,[107] in which entropic contributions from the environment are included. On the other hand, statistical mechanical free energy simulations are time demanding, requiring hundreds of millions of energy and gradient calculations, using electronic structure theory with a combined QM/MM potential. The use of a mixed QM and MM approach to model chemical processes was illustrated in early studies.[4,27,28] Statistical mechanical simulation of the free energy difference between the solvent-separated ion pair and the transition state for the SN2 reaction between Cl− and CH3Cl in water was carried out in 1987.[5]
Subsequently, a series of free energy simulations with combined QM/MM potentials, mainly employing semiempirical quantum chemical models to gain the needed computational efficiency in condensed-phase simulations, were performed in Gao’s group to determine the potentials of mean force and solvent polarization effects on chemical reactions in solution.[7,30] These studies included: the dependence of free energy barrier height on donor-acceptor distance for the model proton transfer reaction between NH4+ and NH3 in water by computing a two-dimensional free energy surface;[71] the striking solvent effects on the Menschutkin reaction between NH3 and CH3Cl in water, which significantly shifted the transition state and stabilized the product by more than 150 kcal mol−1;[108] the differential polarization effects on the reactant and transition states for the isomerization about amide bonds in water and in chloroform;[34,109] solvent effects on the Claisen rearrangement of allyl vinyl ether and the substituent effect that enhances aqueous polarization;[110–112] and the aqueous acceleration of the Diels-Alder reaction.[106,113] In addition, an automated procedure that incorporated solvent effects over gas-phase intrinsic reaction paths for organic reactions was developed, and was employed in the study of the enormous solvent effects on the reaction rate of decarboxylaton of 3-carboxybenzisoxazole.[114] Later, a catalytic antibody was found to catalyze a similar decarboxylation reaction.
Solvent effects on the internal rotation barrier of formamide bonds were studied by an ab initio continuum solvation model, and by Monte Carlo simulations employing a mixed QM/MM potential, with both semiempirical and ab initio representations.[115] It was emphasized that solvent polarization effects significantly change the transition-state structure in water, compared with that in the gas phase.
In addition to the seminal work of Singh and Kollman,[4] and Bash, Field, and Karplus[5] on the SN2 reaction of Cl− and CH3Cl in water, many research groups have made important contributions to the QM/MM field. Weiner et al. performed a mechanical embedding optimization of formamide hydrolysis by the hydroxide ion in water, followed by an electrostatic embedding energy correction.[18] Liu and Shi employed the AM1 semiempirical QM method to determine the potential of mean force for the nucleophilic addition of an hydroxide ion to formamide in water.[116] The authors found that the reaction paths for the reaction in water and in the gas phase were very different due to solvation. This technique was extended to investigate solvation effects on the conformational equilibrium of dimethoxyethane in water.[117] It was found that the gauche conformation was more favored from MNDO-QM/MM simulations than that from continuum reaction field calculations. The proton transfer between water and a hydroxide ion was modeled using HF/6-31G** embedded in an all-atom solvent model for water.[118] Employing a semiempirical Hamiltonian, Merz and coworker determined the potential of mean force for the SN1 ionization reaction of t-BuCl in water.[119] The authors noted that agreement with experiment in computed barrier height was only obtained when long-range electrostatic effects were included in the QM/MM interaction Hamiltonian.
Williams and coworkers used a combined QM/MM potential to model the transition state geometries for several reactions in solution.[120] The theoretical modeling featured a novel methodology to determine kinetic isotope effects for the acid-catalyzed glycoside hydrolysis in water. It was found that although both stepwise and concerted mechanisms are possible, the computed kinetic isotope effects are only in agreement with experiment for the stepwise process.[120] This approach has been applied to characterize the transition state and mechanism of the reaction catalyzed by the enzyme sialidase.[121]
To increase the reliability of semiempirical methods in QM/MM applications, Bash and coworkers decided to re-optimize the NDDO-type Hamiltonian specifically for the target reactions being studied, using experimental and high-level ab initio QM data. A series of papers were published detailing studies of various proton transfer reactions.[122,123]
3.4 Biological Systems
Early studies of enzyme-catalyzed reactions focused on energy minimizations and reaction path characterizations using combined QM/MM models. Rullmann et al. studied the reaction path for peptide bond cleavage by papain, employing a direct reaction field Hamiltonian coupled to the semiempirical AM1 model.[25] The researchers focused on the proton transfer between the catalytic Cys (cysteine) residue and a neighboring His, and concluded that the zwitterionic form, which is optimal for nucleophilic attack in the bond cleavage step, was the preferred form in the active site, due to electrostatic stabilization from the helix dipole.[25] The direct reaction field method has been implemented in the HONDO program.[124] The reaction pathway of triosephosphate isomerase (TIM), involving proton abstraction by a Glu (glutamic acid) residue and recombination with the substrate intermediate, was determined by Karplus and coworkers.[125–127] This study introduced an extremely useful analysis technique, which was the gradual annihilation of the partial atomic charges away from the active site, to gain insight into the energetic contributions to substrate (transition state) stabilization or destabilization. This technique has been widely used in later studies of enzymatic reactions. Later studies of the TIM reaction were also undertaken by the Karplus group and others to characterize in more detail the mechanism and to quantify protein dynamical effects.
Hillier and coworkers made effective use of the combined QM/MM method to model a number of enzyme-catalyzed reactions, including the potential energy surface[128–130] for the inhibition[131] of the ester hydrolysis by phospholipase A2, and the transition structure for the amide hydrolysis catalyzed by papain.[132] Vasilyev described a combined PM3/OPLS optimization of the tetrahedral intermediate in the acylation step of the acetylcholine esterase reaction that involved the catalytic triad Ser220-His440-Glu327 in the active site.[133] The interaction of the substrate with the “oxyanion hole” of the enzyme was demonstrated to lower the barrier height to formation of the tetrahedral intermediate. Employing a combined AM1/MM strategy, Harrison et al. optimized the transition state structure for the amide bond cleavage catalyzed by the enzyme papain.[132] The authors found that the reaction proceeded via a concerted mechanism, without the formation of a tetrahedral intermediate.
The Claisen rearrangement of chorismate to prephenate catalyzed by the enzyme chorismate mutase has been a favorite target of computational studies employing combined QM/MM models. Davidson et al. docked the HF/3-21G reaction pathway into the enzyme active site, and found that hydrogen bonding interactions are maximal at the transition state leading to rate enhancement.[134,135] Results from Richards and coworkers revealed that chorismate mutase does not chemically catalyze the reaction, but rather selectively binds a strained conformation of chorismate.[136] The effect of solvation on the chorismate conformation population shift was examined by Carlson and Jorgensen, who employed ab initio fitted charges in Monte Carlo simulations to show that the pseudodiaxial conformation is enhanced in water relative to that in methanol solution.[137] This conformational shift was attributed to be solely responsible for the observed rate enhancement. Subsequent to 1996, there have been at least 50 publications employing QM and QM/MM simulations that have probed the chorismate mutase reaction and the related reactions catalyzed by catalytic antibodies. A comprehensive listing of these studies is beyond the scope of this review, which is mainly limited to work performed until 1996.
By 1995, the field of combined QM/MM methods had matured enough to witness a flush of publications aimed at understanding catalytic mechanisms in biological systems. Elcock et al. studied the sequence preference of DNA cross linking by nitrous acid with six DNA duplex models.[138] The Merz group performed several QM/MM studies of carbonic anhydrase II, including an investigation of conformational change in the zinc binding site,[139] and the active-site binding of an azide ligand as a result of electrostatic complementarity.[140] Brooks and coworkers addressed a number of practical issues relevant to QM/MM simulations of enzymatic reactions, including the construction of starting structures for the protein-substrate complex, the selection of an appropriate QM method, the partition of QM and MM regions, and the technique for coupling QM and MM subsystems.[141]
3.5 Excited States and Spectroscopy
The study of electronically excited states played a critical role in the development of combined QM/MM methods. In fact, the first QM/MM study was motivated by the construction of the ground and excited state potential energy surfaces for conjugated compounds, using a single set of semiempirical parameters in the PPP theory, rather than employing different parameters in the MM force fields for different electronic states.[1] That method was used to determine the excited state conformations and vibronic structure of retinal.[9,15,142] Microscopic calculations of absorption spectra of conjugated molecules in solution was examined using the Langevin dipole model mentioned above and an all-atom solvent model.[41] Notably, the use of the time-dependent excitation energies during molecular dynamics simulations allowed the obtention of the absorption line shape. One of the key approximations in that study included an energy expression for the excited states similar to Eq. 3.[41] Statistical mechanical Monte Carlo simulations, employing a CI single wave function, were carried out to investigate the blue shifts in the n→π* excitation energy of acetone in water and several organic solvents.[143] In that work, the TIP4P model for water was employed, without allowing the mutual solvent polarization response to the electronic excitation of the solute. Consistent polarization effects were added a few years later in the study of the π→π* transition of pyrimidine in water using a polarizable solvent model,[144] and acetone in ambient and supercritical conditions.[145] Thompson championed the importance of a consistent treatment between solute (QM) and solvent (MM) polarizations compared to the point-charge approximation,[39] and applied his QM/MMpol method to formaldehyde, acetaldehyde, and acetone in water. Employing a semiempirical INDO/S Hamiltonian, Thompson and Schenter studied the spectra of the bacteriochlorophyll b dimer of the photosynthetic reaction center of Rhodopseudomonas viridis, in which 325 atoms were included in the QM region embedded in 20,158 polarizable atoms of the rest of the protein and solvent molecules.[38] It was found that only when both the protein-solvent permanent charges and induced polarization are included in the QM/MM model, can the charge transfer asymmetry and experimental Stark effects can be fully explained.[38]
The Monte Carlo statistical mechanical simulation approach was used to examine the excited state pKa of phenol, a weak organic acid in the ground state, which changes to a strong acid in the excited state.[87] This required the calculations of solvent effects on the adsorption and emission energy for both the acid and its conjugated base, and a dual-level approach employing CASPT2/ANO computation of the ground and excited states in the gas phase, and semiempirical QM-CI/MM simulation in aqueous solution, was employed. The article addressed the interplay of equilibrium solvation that is needed to estimate acidity and non-equilibrium solvation effects involved in Foster cycle analysis, based on experimental absorption and emission spectra.[87]
The use of the electrostatic Hamiltonian alone in a combined QM/MM treatment of electronic absorption and emission spectra is not sufficient to account for dispersion contributions to the observed spectral shifts, which tend to stabilize the excited states more than that of the ground state. Zerner and coworkers proposed a perturbation approach based on the Thomas-Reiche-Kuhn sum rule to model the dispersion red-shifts for conjugated compounds.[69,70,146] The method makes use of separate calculations for solute and solvent molecules, and was shown to yield excellent results for a range of conjugated compounds.
The vibrational frequency shifts for the 12 modes of methanol from the gas phase into the liquid were investigated by Wang et al.,[147] who employed three different QM/MM coupling schemes, including mechanical embedding, a Coulomb approximation to QM/MM interactions, and explicit treatment of QM/MM integrals. It was found that the weakest QM/MM coupling yielded the best agreement with experiment on the overall vibrational frequency shift. However, it was a model that employed the exact QM/MM electronic coupling that correctly produced the frequency shift for the O-H stretching mode, emphasizing the importance of correctly treating electrostatic interactions between QM and MM regions.[147]
4. Summary
The authors of the first two publications utilizing combined quantum mechanical and molecular mechanical methods were awarded the 2013 Nobel Prize in Chemistry. In celebrating this great event in computational chemistry, we have reviewed the early development of this computational technique. In retrospect, the idea of combining electronic structure theory with a classical force field was clearly far ahead of its time when it was introduced in 1972.[1] The concept offered great promise for treating chemical processes in large molecular systems, but combined QM/MM methods were only used in less than a dozen publications in the 19-year period from 1972 through 1990, including a calculation of the carbocation stabilization in the active site of lysozyme,[2] and the simulation of an SN2 reaction between chloromethane and chloride ions in water.[4,5] It was the 1990 publication by Field, Bash, and Karplus that had the greatest impact in the field,[29] by providing details of the way in which electronic structure theory could be integrated with molecular mechanics software. And, it was the 1992 study by Gao and Xia that provided the essential validation of computational accuracy and showed the many unique features from a combined QM/MM approach, compared with pure MM calculations.[6] These studies established free energy perturbation procedures that bridged QM/MM and pure MM potentials, and decomposed the interaction energy terms to gain further understanding of polarization effects in solution. The consistent treatment of the mutual polarization between the QM wave function and the MM electric field was rigorously described by Thompson,[39] and the interaction energy terms were analyzed by Gao,[40] highlighting two equalities that relate the interaction energies between the QM and MM regions. The work carried out in the early 1990s[27,28] stimulated a flood of applications utilizing combined QM/MM simulations, such as the study of complex processes in chemistry and the mechanisms of heterogeneous catalysis, including enzymatic reactions, and the calculation of solvent effects on electronic and vibrational spectra of organic molecules (see Ref. [30]). By the mid-1990s, it became clear that combined QM/MM approaches were the method of choice for studying complex chemical processes in condensed phases and in biological systems.[7]
Equally important to the development of combined QM/MM method were a series of scientific conferences dedicated to QM/MM simulations of macromolecular systems. In this regard, the CECAM program played a critical role, as it hosted the first joint NSF-CECAM workshop on combined QM/MM methods and has since supported numerous equivalent meetings and tutorials. The American Chemical Society’s National Meetings have also included frequent symposia featuring combined QM/MM techniques, two of the early ones taking place in 1997 and 2001, respectively. The earlier gatherings offered a chance to hear about up-to-date QM/MM results and permitted the free exchange of ideas and advice among the participants without worrying about individual credit. It is safe to say that many publications in that period had traces of the ideas discussed at these conferences.
Looking ahead, there is still a great need for increased accuracy and predictability in computational studies of the mechanisms, assemblies and binding interactions of biological processes. Combined QM/MM approaches are just the beginning towards this goal, and there is much to improve. On the one hand, it is desirable to model even larger systems with longer temporal scales than the unbelievable work carried out by Schulten and coworkers on the HIV-1 capsid,[148] consisting of 64 million atoms. Eventually, a certain level of multiscale coarse graining will be necessary, for which sophisticated approaches are becoming available. On the other hand, in order to develop truly predictable models in biomolecular simulations, it is essential to gain an understanding of complex chemical and biological processes on the basis of first principles physics. This requires the complete treatment of a biological macromolecule and solvent system by quantum chemical electronic structural theory.
Currently, many research groups are actively developing a class of fragment-based QM models to treat large molecules, by partitioning the system into smaller fragments to increase computational efficiency. One of these approaches is the explicit polarization (X-Pol) theory,[149–151] in which electronic polarization and charge transfer effects are explicitly modeled by electronic structural theory. Its feasibility for molecular dynamic simulations of a fully solvated protein, the bovine pancreatic trypsin inhibitor (BPTI) in a box of water,[152] was demonstrated a few years ago, and its accuracy for modeling condensed phase systems, such as liquid water, has recently been presented.[153] We anticipate that even more accurate and predictive methods will be available for modeling biomolecular interactions in the near future.
Acknowledgments
The work on the development and applications of combined QM/MM methods has been generously supported by the National Institutes of Health (Grant No. GM46376).
Biographies

Meiyi Liu received her B.A. at Jilin Normal University in 2011. She is currently a Ph.D. student in the State Key Laboratory of Theoretical and Computational Chemistry, Jilin University (China). Her research focuses on molecular dynamics simulations of biological molecules under the guidance of Professor Jiali Gao.

Yingjie Wang obtained his B.S. (2009) from Nanjing University. He is currently a graduate student at the University of Minnesota. He has been working on developing fragment quantum mechanical methods, including the explicit polarization (X-Pol) and the block-localized molecular orbital method. He is also engaged in developing new QM/MM schemes.

Yakun Chen obtained his Ph.D. (2010) from the University of British Columbia and remained there as a postdoctoral fellow until 2013. He is currently an Associate Professor at the State Key Laboratory of Theoretical and Computational Chemistry, Jilin University. His research interest lies in the development and application of combined QM/MM methods.

Martin Field has been a team leader at the Institute of Structural Biology (IBS) in Grenoble since 1992. His research has centered upon the development, implementation (in pDynamo), and application of hybrid QM/MM simulation techniques. He was a postdoctoral fellow with Martin Karplus at Harvard (1985–1989) and a research scientist at the NIH (1990–1991).

Jiali Gao studied at Beijing University, followed by graduate work at Purdue and postdoctoral research at Harvard. He was on the faculty of SUNY, Buffalo (1990–1999), where his studies laid the groundwork for QM/MM applications in chemistry and biology. He is currently a Professor with partial appointments at the University of Minnesota and Jilin University.
References
- 1.Warshel A, Karplus M. J Amer Chem Soc. 1972;94:5612–5625. [Google Scholar]
- 2.Warshel A, Levitt M. J Mol Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 3.The Nobel Foundation. [Accessed on January 13, 2014];2013 Nobel Prize in Chemistry. http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2013/
- 4.Singh UC, Kollman PA. J Comput Chem. 1986;7:718–730. [Google Scholar]
- 5.Bash PA, Field MJ, Karplus M. J Am Chem Soc. 1987;109:8092–8094. [Google Scholar]
- 6.Gao J, Xia X. Science. 1992;258:631–635. doi: 10.1126/science.1411573. [DOI] [PubMed] [Google Scholar]
- 7.Gao J. Acc Chem Res. 1996;29:298–305. [Google Scholar]
- 8.Honig B, Karplus M. Nature. 1971;229:558–560. doi: 10.1038/229558a0. [DOI] [PubMed] [Google Scholar]
- 9.Honig B, Warshel A, Karplus M. Acc Chem Res. 1975;8:92–100. [Google Scholar]
- 10.Allinger NL, Sprague JT. J Am Chem Soc. 1973;95:3893–3907. [Google Scholar]
- 11.Pariser R, Parr RG. J Chem Phys. 1953;21:466–471. [Google Scholar]
- 12.Pople JA. Trans Faraday Soc. 1953;49:1375–1385. [Google Scholar]
- 13.Bixon M, Lifson S. Tetrahedron. 1967;23:769–784. [Google Scholar]
- 14.Lifson S, Warshel A. J Chem Phys. 1968;49:5116–5129. [Google Scholar]
- 15.Warshel A, Lappicirella A. J Am Chem Soc. 1981;103:4664–4673. [Google Scholar]
- 16.Aqvist J, Warshel A. Chem Rev. 1993;93:2523–2544. [Google Scholar]
- 17.Chandrasekhar J, Smith SF, Jorgensen WL. J Am Chem Soc. 1984;106:3049–3050. [Google Scholar]
- 18.Weiner SJ, Singh UC, Kollman PA. J Am Chem Soc. 1985;107:2219–2229. [Google Scholar]
- 19.Bash PA, Singh UC, Langridge R, Kollman PA. Science. 1987;236:564–568. doi: 10.1126/science.3576184. [DOI] [PubMed] [Google Scholar]
- 20.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 21.Zwanzig R. J Chem Phys. 1954;22:1420–1426. [Google Scholar]
- 22.Jorgensen WL, Ravimohan C. J Chem Phys. 1985;83:3050–3054. [Google Scholar]
- 23.Tapia O. J Math Chem. 1992;10:139–181. [Google Scholar]
- 24.Thole BT, Vanduijnen PT. Theor Chim Acta. 1980;55:307–318. [Google Scholar]
- 25.Rullmann JAC, Bellido MN, Vanduijnen PT. J Mol Biol. 1989;206:101–118. doi: 10.1016/0022-2836(89)90527-5. [DOI] [PubMed] [Google Scholar]
- 26.Angyan JG, Jansen G. Chem Phys Lett. 1990;175:313–318. [Google Scholar]
- 27.Warshel A. Chem Phys Lett. 1978;55:454–458. [Google Scholar]
- 28.Warshel A. J Phys Chem. 1979;83:1640–1652. [Google Scholar]
- 29.Field MJ, Bash PA, Karplus M. J Comput Chem. 1990;11:700–733. [Google Scholar]
- 30.Gao J. In: Rev Comput Chem. Lipkowitz KB, Boyd DB, editors. VCH; New York: 1995. pp. 119–185. [Google Scholar]
- 31.Gao J. ACS Symp Ser. 1994;569:8–21. [Google Scholar]
- 32.Freindorf M, Gao J. J Comput Chem. 1996;17:386–395. [Google Scholar]
- 33.Gao J, Pavelites JJ. J Am Chem Soc. 1992;114:1912–1914. [Google Scholar]
- 34.Gao J. Proc Indiana Acad Sci. 1994;106:507–519. [Google Scholar]
- 35.Gao J, Habibollazadeh D, Shao L. J Phys Chem. 1995;99:16460–16467. [Google Scholar]
- 36.Gao J, Pavelites JJ, Habibollazadeh D. J Phys Chem. 1996;100:2689–2697. [Google Scholar]
- 37.Berendsen HJC, Grigera JR, Straatsma TP. J Phys Chem. 1987;91:6269–6271. [Google Scholar]
- 38.Thompson MA, Schenter GK. J Phys Chem. 1995;99:6374–6386. [Google Scholar]
- 39.Thompson MA. J Phys Chem. 1996;100:14492–14507. [Google Scholar]
- 40.Gao J. J Comput Chem. 1997;18:1062–1971. [Google Scholar]
- 41.Luzhkov V, Warshel A. J Am Chem Soc. 1991;113:4491–4499. [Google Scholar]
- 42.Luzhkov V, Warshel A. J Comput Chem. 1992;13:199–213. [Google Scholar]
- 43.Maseras F, Morokuma K. J Comput Chem. 1995;16:1170–1179. [Google Scholar]
- 44.Matsubara T, Maseras F, Koga N, Morokuma K. J Phys Chem. 1996;100:2573–2580. [Google Scholar]
- 45.Froese RDJ, Morokuma K. Chem Phys Lett. 1996;263:393–400. [Google Scholar]
- 46.Svensson M, Humbel S, Morokuma K. J Chem Phys. 1996;105:3654–3661. [Google Scholar]
- 47.Svensson M, Humbel S, Froese RDJ, Matsubara T, Sieber S, Morokuma K. J Phys Chem. 1996;100:19357–19363. [Google Scholar]
- 48.Bakowies D, Thiel W. J Phys Chem. 1996;100:10580–10594. [Google Scholar]
- 49.Monari A, Rivail JL, Assfeld X. Acc Chem Res. 2012;46:596–603. doi: 10.1021/ar300278j. [DOI] [PubMed] [Google Scholar]
- 50.Wang B, Truhlar DG. J Chem Theory Comput. 2013;9:1036–1042. doi: 10.1021/ct300935m. [DOI] [PubMed] [Google Scholar]
- 51.Gao J, Amara P, Alhambra C, Field MJ. J Phys Chem A. 1998;102:4714–4721. [Google Scholar]
- 52.Ferenczy GG, Rivail JL, Surjan PR, Narayszabo G. J Comput Chem. 1992;13:830–837. [Google Scholar]
- 53.Thery V, Rinaldi D, Rivail JL, Maigret B, Ferenczy GG. J Comput Chem. 1994;15:269–282. [Google Scholar]
- 54.Assfeld X, Rivail JL. Chem Phys Lett. 1996;263:100–106. [Google Scholar]
- 55.Monard G, Loos M, Thery V, Baka K, Rivail JL. Int J Quantum Chem. 1996;58:153–159. [Google Scholar]
- 56.Murphy RB, Philipp DM, Friesner RA. J Comput Chem. 2000;21:1442–1457. [Google Scholar]
- 57.Amara P, Field MJ, Alhambra C, Gao J. Theor Chem Acc. 2000;104:336–343. [Google Scholar]
- 58.Antes I, Thiel W. J Phys Chem A. 1999;103:9290–9295. [Google Scholar]
- 59.Cummins PL, Gready JE. J Phys Chem B. 2000;104:4503–4510. [Google Scholar]
- 60.Xiao C, Zhang Y. J Chem Phys. 2007;127:124102. doi: 10.1063/1.2774980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ranganathan S, Gready JE. J Phys Chem B. 1997;101:5614–5618. [Google Scholar]
- 62.Zhang Y, Lee TS, Yang W. J Chem Phys. 1999;110:46–54. [Google Scholar]
- 63.DiLabio GA, Hurley MM, Christiansen PA. J Chem Phys. 2002;116:9578–9584. [Google Scholar]
- 64.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodoscek M, Brooks BR. J Chem Phys. 2002;117:10534–10547. [Google Scholar]
- 65.Swart M. Int J Quantum Chem. 2003;91:177–183. [Google Scholar]
- 66.Gao J, Thompson MA, editors. Combined Quantum Mechanical and Molecular Mechanical Methods. Vol. 712. American Chemical Society; Washington, DC: 1998. [Google Scholar]
- 67.Field M, Gao J. Int J Quantum Chem. 1996;60:1093–1096. [Google Scholar]
- 68.Bicout DJ, Field MJ, editors. Quantum Mechanical Simulation Methods for Studying Biological Systems. Vol. 4. Les Houches Workshop and EDP Science; Les Ulis, France: 1996. [Google Scholar]
- 69.Broo A, Pearl G, Zerner MC. J Phys Chem A. 1997;101:2478–2488. [Google Scholar]
- 70.Canuto S, Coutinho K, Zerner MC. J Chem Phys. 2000;112:7293–7299. [Google Scholar]
- 71.Gao J. Int J Quantum Chem Quantum Chem Symp. 1993;27:491–499. [Google Scholar]
- 72.Field MJ, Gao J, Thompson MA. In: Pacific Symposium on Biocomputing. Hunter L, Klein TE, editors. World Scientific; New Jersey: 1996. [Google Scholar]
- 73.Gao J, York D. Theor Chem Acc. 2003;109:99–99. [Google Scholar]
- 74.Postma JPM, Berendsen HJC, Haak JR. Faraday Symp Chem Soc. 1982:55–67. [Google Scholar]
- 75.Tembe BL, Mccammon JA. Comput Chem. 1984;8:281–283. [Google Scholar]
- 76.Gao J. J Phys Chem. 1992;96:537–540. [Google Scholar]
- 77.Stanton RV, Hartsough DS, Merz KM., Jr J Phys Chem. 1993;97:11868–11870. [Google Scholar]
- 78.Stanton RV, Little LR, Merz KM., Jr J Phys Chem. 1995;99:483–486. [Google Scholar]
- 79.Stanton RV, Dixon SL, Merz KM., Jr J Phys Chem. 1995;99:10701–10704. [Google Scholar]
- 80.Stanton RV, Dixon SL, Merz KM., Jr ACS Symp Ser. 1996;629:142–153. [Google Scholar]
- 81.Vasilyev VV, Bliznyuk AA, Voityuk AA. Int J Quantum Chem. 1992;44:897–930. [Google Scholar]
- 82.Gao JL. Biophys Chem. 1994;51:253–261. doi: 10.1016/0301-4622(94)00046-8. [DOI] [PubMed] [Google Scholar]
- 83.Gandour RD. Bioorg Chem. 1981;10:169–176. [Google Scholar]
- 84.Tadayoni BM, Rebek J. Bioorg Med Chem Lett. 1991;1:13–16. [Google Scholar]
- 85.Gao J, Shao L. J Phys Chem. 1994;98:13772–13779. [Google Scholar]
- 86.Gao JL. J Mol Struct: THEOCHEM. 1996;370:203–208. [Google Scholar]
- 87.Gao J, Li N, Freindorf M. J Am Chem Soc. 1996;118:4912–4913. [Google Scholar]
- 88.Wei D, Salahub DR. Chem Phys Lett. 1994;224:291–296. [Google Scholar]
- 89.Gao J, Luque FJ, Orozco M. J Chem Phys. 1993;98:2975–2982. [Google Scholar]
- 90.Orozco M, Luque FJ, Habibollahzadeh D, Gao J. J Chem Phys. 1995;102:6145–6152. [Google Scholar]
- 91.Luque FJ, Zhang Y, Aleman C, Bachs M, Gao J, Orozco M. J Phys Chem. 1996;100:4269–4276. [Google Scholar]
- 92.Bakowies D, Thiel W. J Comput Chem. 1996;17:87–108. doi: 10.1002/(SICI)1096-987X(199608)17:11<1318::AID-JCC4>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 93.Bala P, Lesyng B, McCammon JA. Chem Phys Lett. 1994;219:259–266. [Google Scholar]
- 94.Gao J, Chou LW, Auerbach A. Biophys J. 1993;65:43–47. doi: 10.1016/S0006-3495(93)81031-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Thompson MA, Glendening ED, Feller D. J Phys Chem. 1994;98:10465–10476. [Google Scholar]
- 96.Thompson MA. J Phys Chem. 1995;99:4794–4804. [Google Scholar]
- 97.Thompson MA. J Am Chem Soc. 1995;117:11341–11344. [Google Scholar]
- 98.Kerdcharoen T, Liedl KR, Rode BM. Chem Phys. 1996;211:313–323. [Google Scholar]
- 99.Stanton RV, Little LR, Merz KM., Jr J Phys Chem. 1995;99:17344–17348. [Google Scholar]
- 100.Treboux G. J Phys Chem. 1994;98:10054–10062. [Google Scholar]
- 101.Tunon I, Martinscosta MTC, Millot C, Ruizlopez MF. Chem Phys Lett. 1995;241:450–456. [Google Scholar]
- 102.Tunon I, MartinsCosta MTC, Millot C, Ruiz Lopez MF. J Mol Model. 1995;1:196–201. [Google Scholar]
- 103.Alhambra C, Byun K, Gao J. ACS Symp Ser. 1998;712:35–49. [Google Scholar]
- 104.Truong TN, Stefanovich EV. Chem Phys Lett. 1996;256:348–352. [Google Scholar]
- 105.Truong TN, Stefanovich EV. Chem Phys. 1997;218:31–36. [Google Scholar]
- 106.Gao J, Furlani TR. IEEE Comput Sci Eng. 1995;Fall:24–33. [Google Scholar]
- 107.Gao J, Ma S, Major DT, Nam K, Pu J, Truhlar DG. Chem Rev. 2006;106:3188–3209. doi: 10.1021/cr050293k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Gao J, Xia X. J Am Chem Soc. 1993;115:9667–9675. [Google Scholar]
- 109.Gao J. J Am Chem Soc. 1993;115:2930–2935. [Google Scholar]
- 110.Gao J. J Am Chem Soc. 1994;116:1563–1564. [Google Scholar]
- 111.Gao J, Xia X. ACS Symp Ser. 1994;568:212–228. [Google Scholar]
- 112.Sehgal A, Shao L, Gao J. J Am Chem Soc. 1995;117:11337–11340. [Google Scholar]
- 113.Furlani TR, Gao J. J Org Chem. 1996;61:5492–5497. [Google Scholar]
- 114.Gao J. J Am Chem Soc. 1995;117:8600–8607. [Google Scholar]
- 115.Craw JS, Guest JM, Cooper MD, Burton NA, Hillier IH. J Phys Chem. 1996;100:6304–6309. [Google Scholar]
- 116.Liu HY, Shi YY. J Comput Chem. 1994;15:1311–1318. [Google Scholar]
- 117.Liu H, Mueller-Plathe F, van Gunsteren WF. J Chem Phys. 1995;102:1722–1730. [Google Scholar]
- 118.Muller RP, Warshel A. J Phys Chem. 1995;99:17516–17524. [Google Scholar]
- 119.Hartsough DS, Merz KM., Jr J Phys Chem. 1995;99:384–390. [Google Scholar]
- 120.Barnes JA, Williams IH. Chem Commun. 1996:193–194. [Google Scholar]
- 121.Barnes JA, Williams IH. Biochem Soc Trans. 1996;24:263–268. doi: 10.1042/bst0240263. [DOI] [PubMed] [Google Scholar]
- 122.Bash PA, Ho LL, MacKerell AD, Jr, Levine D, Hallstrom P. Proc Natl Acad Sci USA. 1996;93:3698–3703. doi: 10.1073/pnas.93.8.3698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Ho LL, MacKerell AD, Bash PA. J Phys Chem. 1996;100:4466–4475. [Google Scholar]
- 124.De Vries AH, Van Duijnen PT, Juffer AH, Rullmann JAC, Dijkman JP, Merenga H, Thole BT. J Comput Chem. 1995;16:37–55. [Google Scholar]
- 125.Davenport RC, Bash PA, Seaton BA, Karplus M, Petsko GA, Ringe D. Biochemistry. 1991;30:5821–5826. doi: 10.1021/bi00238a002. [DOI] [PubMed] [Google Scholar]
- 126.Bash PA, Field MJ, Davenport RC, Petsko GA, Ringe D, Karplus M. Biochemistry. 1991;30:5826–5832. doi: 10.1021/bi00238a003. [DOI] [PubMed] [Google Scholar]
- 127.Karplus M, Evanseck JD, Joseph D, Bash PA, Field MJ. Faraday Discuss. 1992;93:239–248. doi: 10.1039/fd9929300239. [DOI] [PubMed] [Google Scholar]
- 128.Waszkowycz B, Hillier IH, Gensmantel N, Payling DW. J Chem Soc Perkin Trans 2. 1989;1795–1800 [Google Scholar]
- 129.Waszkowycz B, Hillier IH, Gensmantel N, Payling DW. J Chem Soc Perkin Trans. 1991;2:225–231. [Google Scholar]
- 130.Waszkowycz B, Hillier IH, Gensmantel N, Payling DW. J Chem Soc Perkin Trans 2. 1991:2025–2032. [Google Scholar]
- 131.Waszkowycz B, Hillier IH, Gensmantel N, Payling DW. J Chem Soc Perkin Trans 2. 1991:1819–1832. [Google Scholar]
- 132.Harrison MJ, Burton NA, Hillier IH, Gould IR. Chem Commun. 1996:2769–2770. [Google Scholar]
- 133.Vasilyev VV. J Mol Struct THEOCHEM. 1994;110:129–141. [Google Scholar]
- 134.Davidson MM, Gould IR, Hillier IH. J Chem Soc Chem Commun. 1995:63–64. [Google Scholar]
- 135.Davidson MM, Gould IR, Hillier IH. J Chem Soc Perkin Trans 2. 1996:525–532. [Google Scholar]
- 136.Lyne PD, Mulholland AJ, Richards WG. J Am Chem Soc. 1995;117:11345–11350. [Google Scholar]
- 137.Carlson HA, Jorgensen WL. J Am Chem Soc. 1996;118:8475–8484. [Google Scholar]
- 138.Elcock AH, Lyne PD, Mulholland AJ, Nandra A, Richards WG. J Am Chem Soc. 1995;117:4706–4707. [Google Scholar]
- 139.Hartsough DS, Merz KM., Jr J Phys Chem. 1995;99:11266–11275. [Google Scholar]
- 140.Merz KM, Jr, Banci L. J Phys Chem. 1996;100:17414–17420. [Google Scholar]
- 141.Eurenius KP, Chatfield DC, Brooks BR, Hodoscek M. Int J Quantum Chem. 1996;60:1189–1200. [Google Scholar]
- 142.Warshel A, Karplus M. J Am Chem Soc. 1974;96:5677–5689. doi: 10.1021/ja00825a001. [DOI] [PubMed] [Google Scholar]
- 143.Gao J. J Am Chem Soc. 1994;116:9324–9328. [Google Scholar]
- 144.Gao J, Byun K. Theor Chem Acc. 1997;96:151–156. [Google Scholar]
- 145.Lin YL, Gao J. J Chem Theory Comput. 2007;3:1484–1493. doi: 10.1021/ct700058c. [DOI] [PubMed] [Google Scholar]
- 146.Roesch N, Zerner MC. J Phys Chem. 1994;98:5817–5823. [Google Scholar]
- 147.Wang J, Boyd RJ, Laaksonen A. J Chem Phys. 1996;104:7261–7269. [Google Scholar]
- 148.Zhao G, Perilla JR, Yufenyuy EL, Meng X, Chen B, Ning J, Ahn J, Gronenborn AM, Schulten K, Aiken C, Zhang P. Nature. 2013;497:643–646. doi: 10.1038/nature12162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Gao J. J Phys Chem B. 1997;101:657–663. [Google Scholar]
- 150.Xie W, Gao J. J Chem Theory Comput. 2007;3:1890–1900. doi: 10.1021/ct700167b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Field MJ. Mol Phys. 1997;91:835–845. [Google Scholar]
- 152.Xie W, Orozco M, Truhlar DG, Gao J. J Chem Theory Comput. 2009;5:459–467. doi: 10.1021/ct800239q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Han J, Mazack MJM, Zhang P, Truhlar DG, Gao J. J Chem Phys. 2013;139:054503. doi: 10.1063/1.4816280. [DOI] [PMC free article] [PubMed] [Google Scholar]


