Evaluation of intensity drift correction strategies using MetaboDrift, a normalization tool for multi-batch metabolomics data

Abstract

In recent years, mass spectrometry-based metabolomics has increasingly been applied to large-scale epidemiological studies of human subjects. However, the successful use of metabolomics in this context is subject to the challenge of detecting biologically significant effects despite substantial intensity drift that often occurs when data are acquired over a long period or in multiple batches. Numerous computational strategies and software tools have been developed to aid in correcting for intensity drift in metabolomics data, but most of these techniques are implemented using command-line driven software and custom scripts which are not accessible to all end users of metabolomics data. Further, it has not yet become routine practice to assess the quantitative accuracy of drift correction against techniques which enable true absolute quantitation such as isotope dilution mass spectrometry. We developed an Excel-based tool, MetaboDrift, to visually evaluate and correct for intensity drift in a multi-batch liquid chromatography -mass spectrometry (LC-MS) metabolomics dataset. The tool enables drift correction based on either quality control (QC) samples analyzed throughout the batches or using QC-sample independent methods. We applied MetaboDrift to an original set of clinical metabolomics data from a mixed-meal tolerance test (MMTT). The performance of the method was evaluated for multiple classes of metabolites by comparison with normalization using isotope-labeled internal standards. QC sample-based intensity drift correction significantly improved correlation with IS-normalized data, and resulted in detection of additional metabolites with significant physiological response to the MMTT. The relative merits of different QC-sample curve fitting strategies are discussed in the context of batch size and drift pattern complexity. Our drift correction tool offers a practical, simplified approach to drift correction and batch combination in large metabolomics studies.

1 Introduction

As metabolomics has matured as a member of the ‘omics sciences, its application to large-scale studies, including epidemiological studies of human subjects, has undergone substantial growth. Unlike experiments using cell culture or animal models in which carefully controlled conditions allow modest sample numbers to achieve sufficient statistical power, studies of human subjects require analysis of hundreds or thousands of samples to overcome natural variability and detect subtle biological effects. However, due to the extended nature of some protocols in clinical research, metabolomics data may be acquired in multiple batches over the course of weeks, months or years. In mass-spectrometry based metabolomics studies, instrument response frequently changes over the short-term (within a batch) and long-term (between batches), leading to a phenomenon termed intensity drift [1] that adds variability to the data and may limit the ability to detect biologically significant effects [2]. Thus, the difficulty of achieving reliable quantitation is a great barrier to successful completion of large-scale metabolomics studies.

The need for robust normalization techniques for large sets of MS-based metabolomics data has long been apparent; various approaches have been implemented previously and the subject has been the topic of a recent review [3]. The simplest option is to normalize data to total metabolite signal intensity or median signal intensity [4, 5]. However, this approach assumes that all metabolites experience the same pattern of drift over the course of the analyses and that the sum or median metabolite abundance is approximately the same in all samples, which is often not the case [6]. A second option is to use internal standards (IS), added at a uniform concentration to all samples, to monitor or correct for intensity drift. This is most effective when stable isotope-labeled versions of the exact metabolites to be quantitated are used, (e.g., isotope dilution mass spectrometry) [7, 8] but in most cases, it is impractical or impossible to include an isotope-labeled IS for all metabolites of interest. To enable more comprehensive metabolomics profiling with IS normalization, computational techniques have been proposed to aid in selection of an internal standard from the available subset that most optimally corrects for drift or matrix effects in each metabolite [6]. While superior to ad-hoc internal standard selection, it is not possible to ensure the drift correction is valid for each compound, as the pattern of intensity drift often varies significantly from metabolite to metabolite, even within a class of compounds.

The other major drift correction strategy, which has become the most widely cited approach in recent metabolomics literature, is to use a quality control (QC) sample analyzed once or repeatedly with each batch of samples as the basis for performing drift correction [2, 9-14]. This technique adds some effort to a metabolomics study, as it requires an ample supply of a suitable QC sample to be prepared in advance for use over multiple batches, and it increases the amount of instrument time needed due to the addition of QC sample runs interspersed regularly throughout the queue. In return for this effort, it allows correction for intensity drift in each individual metabolite, regardless of whether an appropriate internal standard is available, making it suited for both targeted and untargeted metabolomics studies. One of the most widely cited variants of this strategy was described by Dunn et al., who used locally estimated scatterplot smoothing (LOESS) to correct for peak area drift based upon observed intensity drift in a QC sample [9], although other curve-fitting strategies have also been proposed [15].

The most widely-used tools for metabolomics data analysis such as XCMS Online and MetaboAnalyst offer basic methods such as total signal or median signal correction for automated normalization of metabolomics data [16, 17], but do not support QC-sample based intensity drift correction. Most QC-based drift correction of metabolomics data has been performed using command-line driven software, often using scripts written in individual research laboratories. This allows flexibility for customization to specific data analysis workflows and permits automation of the process, but limits the application of the tool to researchers familiar with programming, or at least operating, such software. Recently, several software packages which allow QC-sample based drift correction or similar strategies either as a part of a complete data analysis workflow or for stand-alone use have been described in the literature [18-23]. Most of these tools are designed as packages for R, which offers a highly flexible data analysis environment but usually requires familiarity with command-line driven software. Many of these tools are not specifically designed to treat between-batch drift in a distinct manner from within-batch drift, and/or do not perform integrated visualization of the pre- and post-correction data. In this manuscript, we present a Microsoft Excel based tool, MetaboDrift, which allows metabolomics data acquired on any platform to be easily visualized and assessed for within and between-batch intensity drift. The tool performs within-batch drift correction as a distinct step from between-batch normalization. Intensity drift correction is based on QC sample data and uses quadratic regression, cubic splines fitting, or LOESS smoothing to model and correct for drift. MetaboDrift also includes options for total-signal, median-signal, and internal standard-based data normalization. MetaboDrift is suitable for both targeted and untargeted metabolomics data, and includes support for input and output of data files generated by the popular metabolomics data analysis platforms including XCMS [24] and MetaboAnalyst [25].

We demonstrate the use of MetaboDrift on an original set of LC-MS-based metabolomics data from a study of metabolic response to a mixed-meal tolerance test (MMTT) in human subjects [26-28]. The data are used to compare the effectiveness of several drift correction and data normalization strategies. For a subset of metabolites, the drift-corrected metabolomics data are also validated against stable-isotope-normalized data, often considered the gold-standard method for quantitation in LC-MS metabolomics. We assess the impact of drift correction on interpretation of the MMTT study data, and present a simple workflow for drift correction of multi-batch LC-MS-based metabolomics data.

2 Materials and Methods

2.1 Human subjects

All participants gave written informed consent for inclusion before participation in the study. The study was conducted in accordance with the Declaration of Helsinki [29], and the protocol was approved by the Institutional Review Board of the University of Michigan Medical School (HUM00030088). Plasma samples used in this study were collected as part of the ongoing clinical Weight Management Program at the University of Michigan, Ann Arbor, MI (NIH Clinicaltrials.gov NCT 02043457), which has been previously described in detail [30, 31]. In brief, samples were collected from 16 non-obese and 35 obese subjects. The non-obese group consisted of 6 male and 10 female subjects, mean age 48 y. (range 27-60), and mean BMI 23.1 (range 19.2-26.0); the obese group consisted of 20 male and 15 female subjects, mean age 50 y. (range 30-63), and mean BMI 39.8 (range 30.5-50.6). Obese subjects underwent a MMTT at baseline and following ∼15% weight loss; non-obese subjects only underwent a single MMTT. Samples from this particular program were selected for evaluation of drift correction techniques as it represents ‘typical’ collection patterns of clinical studies analyzed by metabolomics – i.e., samples were collected from multiple subjects over a period of several years at different locations, and samples were analyzed by LC-MS in multiple non-contiguous batches over the course of an extended period of time.

2.2 Mixed meal tolerance test and blood sampling

To limit the effect of the most recent meal and exercise, participants were asked to consume a prescribed isocaloric diet and to refrain from exercise for three days prior to the MMTT. Following an overnight fast blood was collected from a peripheral venous catheter placed in either in the arm (antecubital) or hand; this was considered the baseline timepoint (0 min). Each participant then consumed a liquid mixed meal (237 ml of Ensure^® Original Therapeutic Nutrition, containing 250 kcal total energy, 22% fat, 64% carbohydrate and 14% protein) within 10 min. Venous blood was sampled again at 15, 30, 60 and 120 min after meal consumption. Samples were collected in EDTA vacutainers, inverted, and placed immediately on ice. Within 15 minutes following collection, samples were centrifuged at 2000 g for 10 min at 4 °C to separate plasma, aliquoted and then frozen at -80 °C until analysis.

2.3 Sample preparation and LC-MS metabolomics

Targeted metabolomics was used to quantitate 122 plasma metabolites (a complete list is provided in Supplementary Table S1). Due to limitations in the available quantity of some plasma samples from the MMTT, a pooled human plasma sample obtained from the American Red Cross was used as the QC sample for the study. Before beginning the study, LC-MS analysis was performed to confirm that the QC sample contained detectable levels of all 122 metabolites included in our targeted metabolomics method. The pooled sample was separated into 50 μL aliquots and stored at -80 °C. Individual aliquots were thawed and extracted along with each analytical batch. To precipitate proteins and extract metabolites, 200 μL of extraction solvent (1:1:1 methanol: acetonitrile: acetone) containing a mixture of isotope-labeled internal standards (Supplementary Table S2) was added to 50 μL of plasma. The samples were vortexed for 10 sec., allowed to rest on ice for 5 min, and then centrifuged at 16,000 g for 10 min at 4 °C. The supernatant was transferred to an autosampler vial for liquid chromatography-mass spectrometry (LC-MS) analysis using an Agilent 1200 LC with an Agilent 6220 time-of-flight MS (Santa Clara, CA). All solvents and reagents used were LC-MS grade and were obtained from Sigma-Aldrich (St. Louis, MO).

As we have done previously [32], three LC-MS analyses were performed per sample: negative ion mode hydrophilic interaction chromatography – electrospray ionization mass spectrometry (HILIC-ESI-MS) and both positive and negative ion mode reversed phase liquid chromatography (RPLC-ESI-MS). This approach provides good coverage of major plasma metabolite classes (organic acids, amino acids, free fatty acids, phospholipids and acylcarnitines) while keeping total run time under 1 hour per sample. As our HILIC method is well-suited to retention of acidic (negatively-charged) but not basic (positively charged) metabolites, addition of positive mode ESI to the HILIC analysis would only slightly improve metabolite coverage at a cost of substantially increased analysis time; therefore, positive-mode HILIC was not used in this study. HILIC was performed using a Phenomenex Luna NH2 column, 3 μm particle size, 150 mm × 1 mm inner diameter (i.d.) (Torrance, CA), similar to previous work [33, 34]. Mobile phase A was 5 mM ammonium acetate in water adjusted to pH 9.9 using ammonium hydroxide, and mobile phase B was acetonitrile (no additives) [35]. The gradient consisted of a 15-min linear ramp from 80 to 0 % B, 5 min at 0 % B, and 15 min of re-equilibration at 80 % B. The flow rate was 0.07 mL/min from 0-27 min, 0.08 mL/min from 27-32 min and 0.09 mL/min from 32-35 min; the column temperature was 25 °C. Electrospray ionization MS parameters were as follows: full-scan MS1 detection (m/z 50 to 1,200), acquisition rate 1 spectrum/sec, capillary voltage 3500 V, gas temperature 350 °C, drying gas 10 L/min, nebulizer pressure 20 psig, reference mass correction enabled. RPLC in both negative and positive ion modes was performed using a Waters Acquity HSS T3 column, 1.8 μm particle size, 2.1 × 100 mm i.d., with a flow rate of 0.2 mL/min (Milford, MA). Mobile phase A was 0.1% formic acid and 0.028% of ammonium hydroxide in water and mobile phase B was 0.1% formic acid and 0.028% ammonium hydroxide in 8:2 isopropanol: methanol. The gradient consisted of 6-min linear ramp from 0 to 100 % B, 4 min at 100 % B, and 5 min of re-equilibration at 0 % B. The column temperature was held at 45°C throughout the run. MS parameters were the same as HILIC except the acquisition rate was 2 spectra/sec and the nebulizer pressure was 40 psig.

A total of 418 human subject sample injections and 66 QC sample injections were performed in HILIC and RPLC methods to generate the data used in this study. The runs were performed over 14 batches. A QC sample was analyzed approximately every 8^th run within each batch. To improve data quality and eliminate the runs prone to the most extreme drift, the QC sample prepared with each batch was injected and analyzed 3 times (for HILIC) or 5 times (for RPLC) before starting analysis of each new batch, and data from all these QC pre-injections were not analyzed or used for drift correction. Targeted metabolomics data analysis was performed using Agilent MassHunter Quantitative Analysis software. Peaks were identified by comparison of accurate mass and retention time with those of authentic standards analyzed using the same method. Peaks were quantitated by peak area using the “Agile2” peak integrator, and were validated by visual inspection of all chromatograms.

2.4 Peak area drift correction

To correct for peak area drift within and between each sample batch, we developed a custom macro-enabled Excel spreadsheet called MetaboDrift, which is included with this manuscript as Supporting Information; an up-to-date version of MetaboDrift will also be maintained at https://github.com/evanscr/MetaboDrift. Detailed instructions for using MetaboDrift are provided within the worksheet itself; the user interface is illustrated in Figure 1. The user inputs metabolite names, sample names, and peak area data generated by any software into the worksheet. Alternatively, these data can be automatically imported from a standard XCMS “diffreport” file [24]. The user then assigns each sample to a batch number and marks QC samples to enable their use for drift correction. Samples are then sorted by batch number and run order number, and peak intensity profile plots are generated for each metabolite using in-cell plots (Excel “Sparklines”) for QC samples and all other samples. These plots, as well as automatically-calculated percent relative standard deviation (% RSD) values for QC samples, help the user evaluate whether intensity drift exists in the data set, and whether its pattern is consistent or differs across metabolites. Six options are available for drift correction or normalization of metabolomics data. The first three methods, quadratic fit (QUAD), cubic splines fit (CUBSPL), and LOESS, use QC samples to correct for within- and between-batch drift. QC-sample-based drift correction is performed by adjusting raw peak area according to the equation [36, 37]:

Figure 1. MetaboDrift user interface.

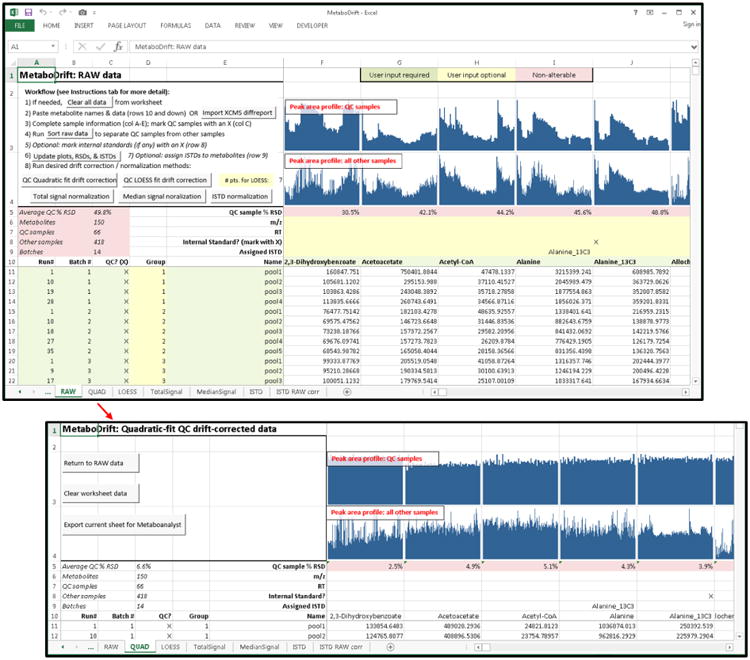
Raw data are input or imported into the worksheet. Using automated scripts, data are sorted, visualized, and the desired normalization method(s) are applied to the data. Resulting output are displayed as additional worksheets within the workbook and can be exported for further analysis.

$${{\mathrm{X}}^{\prime }}_{p,b,i}={\mathrm{X}}_{\mathrm{p},\mathrm{b},\mathrm{i}}\frac{R_p}{C_{\mathrm{p},\mathrm{b},\mathrm{i}}}$$

in which X_p,b,i is the intensity of peak p for sample i within batch b, and X′_p,b,i is the adjusted intensity after application of a correction factor C_p,b,i, with a rescaling factor R_p (set as the average peak intensity across all samples and batches), which is added to maintain the relative intensity of the peak. The correction factor C_p,b,i is determined by the drift correction method. QUAD applies a least-squares quadratic regression to the QC sample data. The resulting regression equation is used to compute the correction factor (C_p,b,i) for each run number (i), which is set as the ratio of the first QC peak area in the batch to the peak area predicted by the equation for run (i). The correction factor (C_p,b,i) is computed similarly for CUBSPL and LOESS regression fits, except that the regression equation is calculated using natural cubic splines regression for CUBSPL [38] and a locally-estimated polynomial smoothing procedure, as described by Dunn et al., for LOESS [9]. Our implementation of both CUBSPL and LOESS fitting in Excel use publicly available Excel Visual Basic (VBA) functions, accessible at (https://newtonexcelbach.wordpress.com/2009/07/02/cubic-splines/) and (http://peltiertech.com/loess-smoothing-in-excel); both are included in MetaboDrift. CUBSPL requires no additional user input, whereas LOESS allows specification of a smoothing parameter, α, which determines the fraction of the data used for each LOESS fit [8]. MetaboDrift allows α to be set between 0.1 and 1; lower values result in tighter fitting of the QC data, but too low of an α value may result in fitting of random noise from the QC sample data, and thus degrade drift correction performance. The default parameter of α = 0.5 often yields acceptable results, but can be adjusted to optimize the LOESS smoothing if desired [9]. For QUAD, CUBSPL, and LOESS, the drift correction procedure is applied individually to each batch, and batches are then normalized to one another by correction to the same rescaling factor (R_p).

Median and total signal normalization are carried out by dividing the peak area of each metabolite by the median or sum of all peak areas for all metabolites within the same sample. IS normalization is performed by calculating the ratio of metabolite peak area to the selected IS, multiplied by the rescaling factor R_p. In MetaboDrift, the data resulting from drift correction or normalization are placed in separate worksheets, which allows comparison of the raw data with the corrected data, or comparison between multiple correction methods. If the normalized data does not meet acceptable user-determined criteria (e.g., a particular % RSD value for corrected peak area in QC samples), the metabolite can be dropped from further analysis or an alternate drift correction strategy can be considered.

2.5 Statistics

All data are reported as average +/- standard error of mean (SEM). Statistical comparisons of metabolite levels between baseline and later timepoints of the MMTT (e.g., t=0 vs. t=60 min) were performed in Excel 2013 using a paired student's t-test with Benjamini-Hochburg correction for multiple comparisons using a false discovery rate (FDR) of 0.05 [39]. FDR-corrected p-values < 0.05 were considered statistically significant. For batch effect analysis, PCA was performed using the rda function in the vegan Package in R on both pre-corrected and post- intensity drift-corrected data.

3 Results and Discussion

3.1 Peak area drift assessment in MMTT metabolomics data

As has been reported previously, within- and between-batch metabolite peak area drift interferes significantly with quantitation in large metabolomics data sets [9, 10]. In our study of the response of the human plasma metabolome to a MMTT, LC-MS data was acquired in multiple batches run over the course of weeks on a shared-use instrument. Although contiguous runs of all samples in a study is preferable to minimize the impact of instrumental drift, division of runs into batches is an unavoidable scenario in many busy laboratories. Moreover, some study designs in lengthy clinical trials require that subsets of samples be run before collection of all samples are complete. In the MMTT data, peak area drift was prominent in all classes of metabolites, as evidenced by the substantial variation in QC sample peak areas (Supplementary Table S3), which averaged 45.7% RSD for IS compounds and 49.8% across all metabolites. Intensity shifts between batches were generally more prominent than within-batch drift. Within each batch, most metabolite peak areas declined or were near constant with increasing run number; however, for some metabolites, the peak area increased with additional runs, or a more complex pattern of intensity drift was observed. In contrast to the observed peak area drift, retention times and peak shapes were relatively stable for the vast majority of metabolites (average retention time RSDs were 0.28%, 0.26% and 1.22% for RPLC +, RPLC – and HILIC –, respectively). Targeted peak detection was performed with manual validation of peak integration, and no missing peak area data were observed in the data set. These observations suggest that deterioration in chromatography or issues with peak alignment were not responsible for the observed intensity drift. Remaining possible causes include fouling of the instrument ion source, contamination or charging of ion optics and/or detectors, and variable degradation or interconversion of labile metabolites in solution. Although cleaning the source and ion optics of the mass spectrometer can help restore sensitivity and reduce the impact of drift, it is often impractical to perform such maintenance frequently enough to eliminate its impact on the data. Given the large magnitude of the between- and within-batch intensity drift observed in this data set, it was essential to correct the data to allow useful quantitative comparisons to be made between groups. Furthermore, the inclusion of a stable-isotope internal standard mixture spanning multiple metabolite classes in the sample extraction procedure made this data set an ideal test-case for study of the effectiveness and quantitative accuracy of distinct drift correction and normalization approaches.

3.2 Evaluation of drift correction and normalization strategies

In the context of the MMTT data, we applied MetaboDrift as described in Section 2.4 to evaluate three data normalization approaches based on QC sample drift correction, two QC-sample independent normalization strategies, and IS normalization for metabolites with exact-matching stable-isotope IS. The three QC-sample curve-fitting strategies (QUAD, CUBSPL and LOESS) are illustrated for a single batch from the MMTT data (Figure 2A) and an alternate data set with larger batch size (Figure 2B) described in Section 3.2.1. MetaboDrift automatically applies the selected curve-fitting method for each metabolite within each batch and subsequently normalizes each batch for intensity and generates a table with corrected peak areas for each metabolite and sample. The result of drift correction on the MMTT data is a dramatic reduction in within- and between-batch intensity drift, illustrated for select metabolites in Supplementary Figure S1. As a measure of how tightly the three drift-correction methods fit the QC data, the average % RSD of the peak areas in the QC samples decreased from 49.8% before correction to 6.6%, 0.0%, and 6.1% following correction using QUAD, CUBSPL, and LOESS methods, respectively. Notably, CUBSPL always gives 0.0% RSD for post-correction QC sample peak area because it uses each QC sample as a lock point for curve fitting; the advantages and disadvantages of this attribute are discussed further below. For the biological samples, as a measure of data spread before and after normalization, the % RSD of the metabolites in the biological samples decreased from 59.6% in the raw data to 31.7%, 30.9%, and 31.0% using QUAD, CUBSPL, and LOESS. Residual variation in the biological samples is expected due to natural variability of the samples and changes induced by physiological response to the MMTT. These results are comparable to those obtained by other published descriptions of QC-sample based drift correction of metabolomics data {Dunn, 2011; Brunius, 2016}. Total signal normalization and median signal normalization lead to less reduction in the data spread, to 59.5% and 50.5% RSD, respectively, suggesting these methods perform poorly compared to QC-based drift correction for complex, multi-batch datasets. One further issue observed was that LOESS drift correction failed to properly correct data when there were insufficient QC samples in a batch. In a batch with only two QC samples, attempting to apply LOESS drift correction resulted in a gap in the drift-corrected data; therefore, this batch was omitted from comparisons between drift-correction strategies. For small batch size, QUAD (which acts as a linear fit when only two QC points are present) or CUBSPL are more likely to successfully model and correct for drift.

Figure 2. Curve fitting of QC sample data to correct for intensity drift.

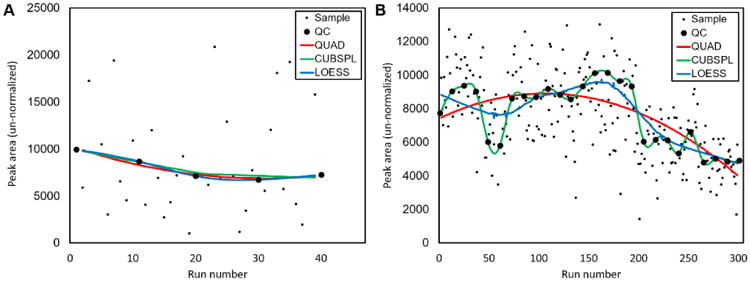
Three curve fitting methods, QUAD, CUBSPL, and LOESS (described in Methods 2.4) were applied to model drift of an individual metabolite within a single batch of metabolomics data from (a) the MMTT study described in section 2.4 and (b) an additional, publicly-accessible metabolomics dataset described in section 3.2.

Though all drift correction methods appeared to improve data quality, an objective assessment of performance is best achieved by comparing drift-corrected data to known metabolite levels or concentrations. Relatively few studies have tested the accuracy of drift-corrected metabolomics data in this manner [40]. To this end, peak areas of select metabolites in the MMTT data were normalized to matching stable-isotope internal standards (Supplementary Table S2), which serves as a gold-standard method for metabolite quantitation [41]. Pearson's correlation coefficients were then calculated for drift-corrected peak areas versus internal standard-normalized peak areas, which are illustrated in Figure 3A and listed in Supplementary Table S3. QUAD, CUBSPL, and LOESS performed nearly equally well for almost all of the MMTT data, as indicated by the nearly overlapping profile of correlation coefficients. The average Pearson's correlation coefficient for all metabolites with a matching IS increased from 0.56 for the raw data to 0.79, 0.81, and 0.79 for the QUAD, CUBSPL, and LOESS drift-corrected data. Total signal and median signal normalization resulted in small to no improvement in correlation for most metabolites. The effect of the various drift correction strategies on correlation with IS-normalized abundance is illustrated using scatter plots for a representative metabolite, malic acid, in Figure 3B-G. Although QC-based drift correction was effective for most metabolites, some metabolites (L-carnitine, His, Ser, Gly, C3-carnitine) showed relatively poor correlation even after drift correction, and few metabolites had correlation coefficients greater than 0.9. The lowest values may be partly explained by insufficient concentration of some internal standards to allow reliable normalization, but the imperfect correlations also likely occur because drift correction cannot correct for all sources of variability in LC-MS metabolomics data, including differential ion suppression between samples. As another metric of normalization performance, we also evaluated the effect of drift correction on % RSD of the isotopically-labeled internal standards in the non-QC samples before and after drift-correction. The results, included in Supplementary Table S3, again indicated that the three drift-correction strategies produced similar results, with average % RSD values for IS compounds of 15.6%, 14.1% and 14.4% for QUAD, CUBSPL, and LOESS, respectively, compared to 45.2% for the raw, uncorrected data.

Figure 3. Comparison of quantitation after drift-correction versus internal standard normalization.

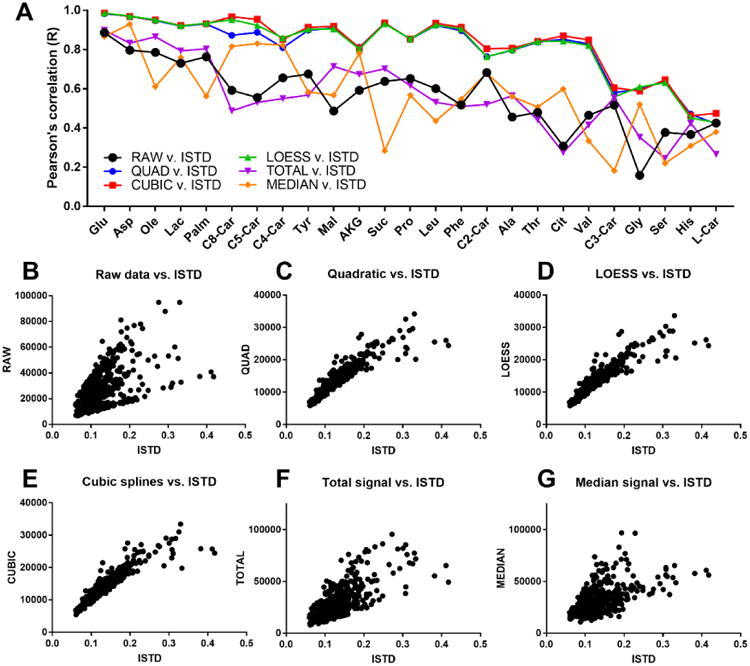
(a) Pearson's correlation coefficients between IS-normalized peak area and peak areas normalized by other strategies were calculated in Excel for metabolites with matching isotopic standards using all biological samples from the MMTT study. (b-g) Scatter plots illustrating correlation between IS-normalization and other strategies for a single representative metabolite, malic acid.

3.2.1 Effect of batch size on selection of drift correction method

Although some individual metabolites illustrated better performance with one drift correction method over another, on a global level QUAD, CUBSPL, and LOESS performed similarly for drift-correction for the MMTT data. One explanation is that the batch size in the MMTT study was small, with 5 or fewer QC samples and 40 or fewer biological samples in each batch, which likely enabled all three methods to successfully correct for the relatively simple patterns of drift in the data. To test our drift correction strategies on data with a larger batch size, we downloaded a publicly-accessible dataset from the Metabolomics Workbench (Project ID: PR000303, http://www.metabolomicsworkbench.org/data/DRCCMetadata.php?Mode=Project&ProjectID=equals;PR000303). This data set consists of 250 test samples and 26 QC samples analyzed in a single batch. We used only the positive ion mode data that consists of 708 features including both identified and unidentified metabolites. Since these data did not contain isotopic internal standards, every 3rd QC sample was left out of the drift correction calculations to create an independent set of QC samples to assess the effectiveness of the normalization methods, as previously described by Brunius et al. [14]. The average % RSD of each metabolite's peak area for the independent QC samples (n=8) were: raw data, 13.6%; QUAD, 13.1%; CUBSPL, 19.0%, LOESS, 12.2%, total signal 12.6%, median signal 13.0%. These data suggest that total drift in the raw data was relatively mild, and that drift correction resulted in only modest reductions in data spread. Among drift-correction methods, LOESS provided the best result for this data set by a small margin. Notably, CUBSPL drift correction resulted in higher average % RSD for the QC samples than no drift correction at all. The likely explanation is overfitting, a phenomenon in which fitting of random noise in the QC sample data results in introduction of additional noise into the corrected data. This phenomenon has been observed previously by others in this and similar contexts [9, 42] and is visually illustrated in Figure 2B, in which the CUBSPL curve perfectly fits the profile of the QC sample intensity, in spite of the fact that much of the sample-to-sample variation is likely due to noise. A similar effect is likely to occur for LOESS curve fitting when the smoothing parameter, α, is set too low. Conversely, for data with large batch size, coarse fitting methods such as QUAD are likely to underfit the data, failing to correct for more complex patterns of drift, also illustrated in Figure 2B. Thus, drift-correction strategy should be selected in light of batch size and drift pattern complexity; due to its tuneable smoothing parameter, LOESS may offer the best flexibility for data sets with larger batch size and/or complex patterns of drift. A flow-chart to aid selection of an appropriate drift-correction or normalization strategy is included in Supplementary Figure S2.

3.2.2 Drift correction and batch effects

In addition to improving quantitative accuracy, a major goal of any metabolomics data normalization strategy is to reduce batch effects in the data. Batch effects are differences in measured metabolite levels between analytical batches mask real differences between biologically relevant sample groups. Several reports pertaining to correction of batch effects in MS-based metabolomics data are found in recent literature [35-38]; an effective visual method for detection of batch effects is principal component analysis (PCA) [39]. To assess the effectiveness of our QC-based drift correction to reduce batch effects, we performed PCA to visualize the MMTT metabolomics data before and data drift correction using QUAD (Figure 4). Two-dimensional score plots were generated and post drift-correction data were projected onto the same principal component axes as the pre-correction data. The pre-correction data shows clear separation of batches into groups in the 2D score plots, confirming that the existence of substantial batch effects in the data. Post drift-correction, the separation between batches is no longer apparent, and the data cluster more tightly. This confirms that the approach MetaboDrift uses, correcting for within-batch and between-batch drift using separate mathematical steps, is effective for reducing batch effects and undesired scatter in the data. This result is comparable to a recent report which also emphasizes the advantage of separate between- and within-batch drift correction for mitigation of batch effects in metabolomics data [14].

Figure 4. Principal component analysis of MMTT data before and after drift correction.

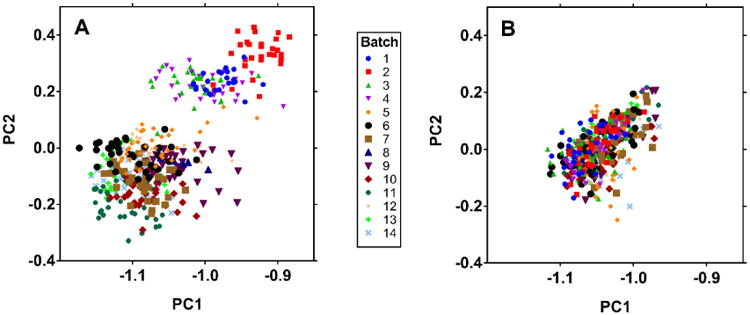
PCA 2D score plots illustrate prominent batch effects before correction (a) and elimination of most batch effects post-correction (b). Data before and after drift correction are projected onto the same principal component axes. Samples are colored by batch number (1-14).

3.3 Effect of drift correction on quantitative analysis of biological metabolomics data

Ultimately, the utility of intensity drift correction is determined by whether it enables more biologically meaningful information to be derived from metabolomics data. Since only 26 of the 122 metabolites quantitated in the MMTT data were matched to internal standards, and batch size was too small to leave select QC samples out of the normalization as was done for the alternate data set described in Section 3.2.1, the best means of assessing the effect of normalization strategies for compounds without IS was to observe the effect of normalization strategy on biological interpretation of metabolic response to the MMTT. Focusing on the non-obese subjects (n=16), we investigated the number of metabolites significantly altered in response to the MMTT between the t=0 and t=60 min. timepoints. As listed in Supplementary Table S1, using the raw, non-drift-corrected data, 40 metabolites were statistically different between t=0 and t=60. Following QUAD drift correction, the number of significantly different features increased to 50. Additional features which the drift-corrected data, but not the raw data, revealed to be altered by MMTT included several amino acids (valine, tryptophan, asparagine, glutamine), TCA cycle intermediates (citrate, α-ketoglutarate), and products of branched-chain amino acid catabolism (C3- and C5-carnitine, keto-leucine and keto-isoleucine). These metabolites are closely associated with nutrient intake and catabolism, which is expected to be directly affected by a MMTT, validating that drift correction of this data set produced conclusions congruent with expected biological effects. The importance of intensity drift correction may be greater for studies with smaller sample group size, as under these conditions randomization of injection order becomes less effective to compensate for compensate for intensity drift on its own. As a simple validation of this concept, when half of the subjects were removed at random from the MMTT data set to yield n=8, the drift-corrected data retained 35 significantly altered metabolites between t=0 and 60 min, whereas the raw data only showed 20.

We also compared whether QC-sample drift correction produced quantitative results consistent with internal standard normalization, the gold-standard approach for quantitation, in the context of the biological study. Average fold-change values in metabolite levels between t=0 and t=60 in the MMTT were calculated for each metabolite with a matching IS using both QUAD drift-corrected and IS-normalized data. The result, summarized in Table 1, indicates that the fold-change values measured by QC-drift-corrected and IS normalized data were generally consistent. Only 4 of 28 metabolites showed a statistically significant difference in fold-change (p<0.05) between QUAD and IS methods, and of these, only palmitic acid showed a major difference (1.6 fold change for QC drift correction vs. 2.2 fold change for IS normalization). This difference might be caused by increased self-ion suppression of palmitate at higher concentrations, a phenomenon which would not be expected to be compensated for by drift correction. Thus, although IS normalization remains a preferred strategy for absolute quantitation, in our study QC-based drift correction produced generally accurate relative quantification of biologically significant trends. However, it is remains advisable to use internal standards representative of major metabolite classes to assess the accuracy of metabolomics data in large biological studies relying on drift-corrected peak areas for relative quantitation.

Table 1.

Average metabolite peak fold change from 0 to 60 min during MMTT, computed using internal standard normalization and QC sample drift correction methods described in the text.

	Fold change 0 v. 60 min (IS normalization)	Fold change 0 v. 60 min (QC-sample drift correction)	p-value
Free fatty acids
Oleic acid	↓ 2.27	↓ 2.27	0.478
Palmitic acid	↓ 2.27	↓ 1.64	<0.001$
Acylcarnitines
L-carnitine	↑ 1.07	↑ 1.07	0.840
C2 carnitine	↓ 1.22	↓ 1.27	0.295
C3 carnitine	↑ 1.05	↑ 1.12	0.054
C4 carnitine	↓ 1.03	↓ 1.05	0.635
C5 carnitine	↑ 1.14	↑ 1.16	0.619
C8 carnitine	↓ 1.69	↓ 1.59	0.321
C14:0 carnitine	↓ 1.18	↓ 1.18	0.968
C16:0 carnitine	↓ 1.04	↓ 1.01	0.680
Amino acids
Alanine	↑ 1.35	↑ 1.35	1.000
Aspartic acid	↑ 1.08	↑ 1.07	0.783
Isoleucine+leucine	↑ 1.26	↑ 1.28	0.030$
Glutamic acid	↓ 1.11	↓ 1.11	0.928
Glycine	↑ 1.12	↑ 1.10	0.253
Histidine	↑ 1.17	↑ 1.12	0.051
Methionine	↑ 1.27	↑ 1.22	0.019$
Phenylalanine	↑ 1.18	↑ 1.19	0.518
Proline	↑ 1.39	↑ 1.36	0.285
Serine	↑ 1.09	↑ 1.10	0.466
Threonine	↑ 1.16	↑ 1.16	0.635
Tyrosine	↑ 1.20	↑ 1.25	0.005$
Valine	↑ 1.13	↑ 1.14	0.950
Glycolysis/TCA
Citrate	↑ 1.14	↑ 1.14	0.604
Alpha-ketoglutarate	↑ 1.14	↑ 1.12	0.344
Malate	↑ 1.24	↑ 1.27	0.161
Succinate	↑ 1.14	↑ 1.10	0.012$
Lactate	↑ 1.63	↑ 1.58	0.223

^$= p-value <0.050.

The final, drift-corrected profile of non-obese subjects in response to the MMTT for the 122 metabolites quantitated in this study is illustrated as a heatmap in Figure 5. Interpretation of the biological significance of our findings was not the focus of this work; however, the data are consistent with the expected appearance and clearance of nutrients and other metabolites following a meal [43, 44]. For instance, free fatty acids and long-chain acylcarnitines decreased postprandially and reached a minimum at 60 min, consistent with the known insulin-induced suppression of lipolysis which occurs in the transition from fasting to fed-state [38]. Several amino acids show modest increases in concentration over the duration of the postprandial period, likely due to influx of these nutrients into the bloodstream following consumption of the meal. More detailed analysis of these and other biological findings involving non-obese and obese sub-groups will be the subject of a future work.

Figure 5. Heatmap of plasma metabolome response to MMTT.

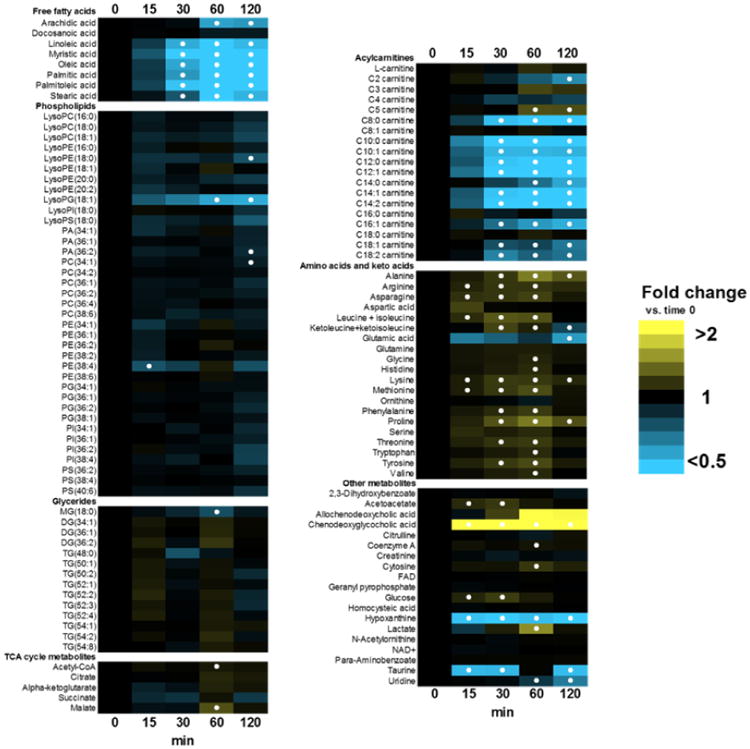
Data are expressed as fold-change vs. time 0 (pre-MMTT fasting state). Solid circles represent p < 0.05 vs. t=0.

4 Conclusion

Our strategy for metabolomics data analysis allows drift correction of data from large, multi-batch studies to be implemented with a minimum of prior data manipulation using a simple Excel worksheet. Selection of Excel as the platform for MetaboDrift has distinct advantages and disadvantages. On one hand, Excel is a familiar data analysis environment with a small learning curve, and thus should be accessible to both experienced and novice users interested in evaluating and correcting intensity drift in metabolomics data; other metabolomics data analysis tools have previously been developed in Excel for these reasons [45]. Additionally, the spreadsheet-based environment with integrated graphics enables rapid visualization of metabolite peak area drift for the entire data set, allowing trends to be observed and abnormalities in trends for individual metabolites to be detected and flagged for further assessment. However, Excel is generally less computationally efficient than environments such as R or Matlab, which may increase analysis time for large data sets, and may not be as versatile for automation or incorporation into a high-throughput data analysis workflow. Further, a scripted programming language such as R facilitates better tracking of data processing steps and thus could help ensure data integrity compared to spreadsheet-based software. Many statisticians and bioinformaticians are likely to prefer R-based or similar tools over MetaboDrift for these reasons [18-23]. However, as the metabolomics community continues to expand to a wider diversity of researchers, approachable, non-command-line tools for data analysis become increasingly necessary to help solve common challenges such as intensity drift. Our data support the use of drift-corrected metabolomics data as a means of improving accuracy of relative quantitation in large multi-batch metabolomics data sets, and highlight the fact that the characteristics of each data set, including drift severity, batch size and drift pattern complexity, should be considered when selecting an appropriate drift correction strategy.

Highlights.

• A tool for drift correction and visualization of metabolomics data was developed.

• Quantitation by drift correction compared favorably to isotope standard normalization.

• Optimal drift correction strategy was shown to depend on batch size and drift pattern complexity

• Drift correction was evaluated in the context of biological interpretation of metabolic response to a mixed meal tolerance test.