Fluid Dynamic Aspects of Ejection in Hypertrophic Cardiomyopathy

Hypertrophic cardiomyopathy (HCM) is a fascinating and polymorphic cardiac disease. Its impact on cardiac function¹ retains intense clinical interest as it is one of the most common inherited cardiac diseases, affecting about 1 in 500 people.² According to the prevalent view, HCM is a predominantly obstructive disease compromising systolic left ventricular (LV) ejection.^3–21 Then again, impeded left ventricular orthograde emptying is not an invariable finding.^22–30 Diastolic dysfunction associated with the abnormal hypertrophy patterns and their sequelae may also be responsible for impaired LV pumping performance.^31–36 The diastolic peculiarities of LV dynamics in HCM were the focus of a companion survey.³¹ Additionally, the myocyte disorganization typifying HCM probably creates systolic contraction inefficiencies,³⁷ and may be implicated in marked mechanical functional limitation in some HCM patients.

As ejection flow characteristics became clinically measurable diagnostic features—with conventional and multisensor left heart catheterization, echocardiography, Doppler velocimetry, and MRI—details have been sought with a view to localizing LV outflow obstruction and characterizing the role of the systolic anterior motion (SAM) of the mitral valve.^38–41 Mitral leaflet coaptation is disrupted by SAM, resulting in significant mitral regurgitation and impairing forward cardiac output;^42–43 there can be an apparent “normalization” of the Doppler mitral inflow pattern, associated with the orthograde surge of the regurgitant volume ensuing in early filling.³³

The many-sided phenotypic abnormalities of HCM

The complexity of the underlying diverse and interacting abnormalities in HCM is epitomized in the more than 80 individual names given to it by different investigators in the past.⁴⁴ No theory focusing on a “single culprit” pathophysiologic mechanism could possibly be generally applicable. Being fully cognizant of this, after an overview of systolic ejection pressure gradients in HCM, I aim at conveying a new physiologic understanding and clinical awareness of important, selected fluid dynamic phenomena.

These phenomena underlie imaging and multisensor catheterization dynamic geometry and flow patterns of LV systolic function that are more likely to be seen in HCM patients than in others. However, it should be recognized that similar LV fluid dynamics can prevail in certain circulatory states characterized by hyperdynamic ventricular contraction with low venous return and greatly diminished end-systolic volumes.⁴⁵ Such states are typified by powerful activation of the sympathoadrenal system, in a reflex compensatory response to severe hypovolemia accruing from hemorrhage, burns, dehydration from gastrointestinal losses, diabetic ketoacidosis, or excessive sweating, or in response to a drastically impeded venous return or mitral inflow caused by a tension pneumothorax, pulmonary embolism, cardiac tumor, or cardiac tamponade.

The protean fluid dynamics of HCM

Most cardiologists appreciate that fluid dynamics are central in gaining insight into systolic LV function in this clinically protean and fascinating disease. Lurking behind the adjective “protean,” meaning variable or inconsistent, stands the sea-god Proteus from Greek mythology. When confronted, Proteus shape-shifts to a new identity; he escapes by “morphing.” I have previously⁴⁶ applied the term “polymorphic” HCM systolic pressure gradients in a similar sense, akin to that in polymorphic DNA: DNA sequences that are relatively variable between different individuals. Protean and polymorphic are the complicated fluid dynamics of HCM. Fortunately, a qualitative appreciation of their nature and implications and of their expressions in catheterization and noninvasive measurements is within the command of interested clinical cardiologists.

Flow-associated early- and mid-systolic non-obstructive pressure gradients

The total acceleration of a fluid particle is the time rate of change of its velocity along its path. Therefore, the total acceleration is the sum of two quantities: the local acceleration, or time rate of change of the velocity at any given point in the flow, and the convective acceleration, which is the change in velocity of a particle due to change in position and relates to velocity non-uniformity in space (e.g. converging or diverging instantaneous streamlines). Inertial forces associated with local and convective accelerations of intraventricular blood dominate early ejection.⁴⁷ Inertia is the tendency of a body to preserve its present state of motion, whether it is at rest or moving uniformly forward in a straight line. Due to its inertia, it takes application of some force to compel a fluid such as blood to be accelerated, or alter its state of motion. The early phase of ejection in HCM is characterized by increasing deep and outflow tract left ventricular and aortic root pressures, while aortic root flow velocity briskly attains and transiently remains near its peak (Figure 1).⁴⁶ We can analyze early ejection dynamics by the Euler equation and its integral, the unsteady Bernoulli equation, familiar to cardiologists, which incorporates only pressure and inertial effects, rather than the unwieldy Navier-Stokes equations, which also encompass viscous (“frictional”) effects.⁴⁸

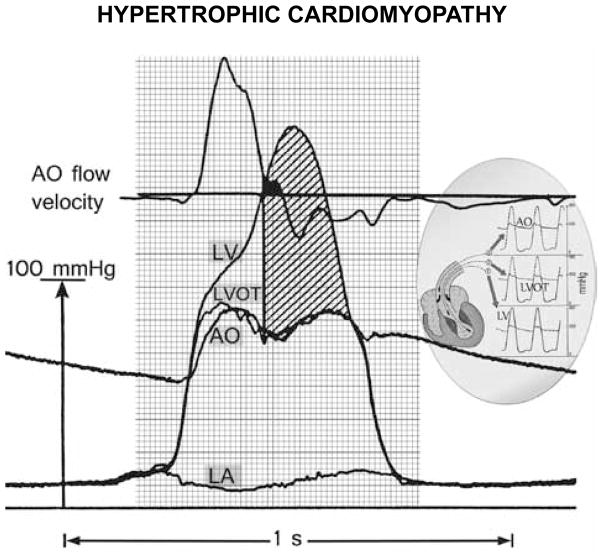
Figure 1.

Pressure-flow relation with large early- and huge mid- and late-systolic pressure gradients in hypertrophic cardiomyopathy. From top downward: aortic velocity, and deep left ventricular (LV), LV outflow tract (LVOT), and aortic root (AO) micromanometric signals, by retrograde triple-tip pressure-plus-velocity left-heart catheter. The left atrial (LA) micromanometric signal was measured simultaneously by transseptal catheter. The vertical line identifies onset of SAM-septal contact, from a simultaneous M-mode mitral echocardiogram (not shown); most of the ejection is already completed by then, in this patient. The huge mid- and late-systolic gradient (hatched area) is maintained despite minuscule remaining forward or even negative aortic velocities. Inset: continuous lines designate the LV, LVOT, and AO signals, superposed on interrupted-line tracings from the other sites. AO – aortic; SAM – systolic anterior motion of the mitral valve. Reproduced with permission of PMPH-USA from Pasipoularides A. Heart’s vortex: intracardiac blood flow phenomena. Shelton, CT: People’s Medical Publishing House, 2010.

It is the interaction of flow-field geometry—outflow tract narrowing by subaortic septal hypertrophy—with enhanced early ejection velocities and accelerations that underlies the augmentation of the early intraventricular and aortic transvalvular ejection pressure gradients.^1,46 The term Bernoulli effect pertains to this phenomenon of pressure reduction with increasing velocity. Fluid dynamic analysis, using multisensor-catheter ejection velocities and pressure gradients and angiographic measurements,⁴⁹ suggests that ordinary convective acceleration (“Bernoulli”) effects are accentuated preeminently in early ejection in HCM; thus, at peak aortic root flow acceleration, they account for over half the instantaneous intraventricular pressure gradient, whereas under normal conditions, they may contribute less than one-quarter of its magnitude.^1,46 Greatly intensified Bernoulli effects in a narrowed subaortic region can engender spectacular intraventricular and transvalvular flow-associated early- and mid-ejection pressure gradients.^1,46,50–52

Systolic anterior motion of the mitral leaflets and apposition to the septum

The intensified Bernoulli gradients in the outflow tract region that is narrowed by upper septal hypertrophy may regularly give rise to a Venturi mechanism, whereby the high-velocity flow entrains the neutrally buoyant mitral leaflets, drawing them anteriorly, and lifts them toward the interventricular septum.^1,12,46 That LV outflow velocities at the level of the mitral leaflets are elevated at the onset of SAM is compatible with such a Venturi action, but does not prove that this mechanism is predominantly or invariably responsible for SAM in HCM. SAM may also implicate a concomitant papillary muscle displacement. Anterior and inward displacement of the papillary muscles in HCM can alter the effectiveness of chordal support, so that the relatively slack leaflets are readily displaced anteriorly. Moreover, the leaflet-coaptation point may be displaced closer to the septum than normal, and this might allow the protruding leaflets to extend into the oncoming stream⁵³ and be shoved (rather than sucked) by the flow against the septum. A classic continuous-wave Doppler sign is the late peaking so-called “lobster-claw”¹⁷ or “dagger-shaped”⁵⁴ profile, which is accompanied by a pressure gradient escalation while the mitral valve moves closer to the septum as the chamber shrinks; these findings are exaggerated by the Valsalva maneuver.

Whether mitral leaflet-septal contact is the cause of the huge mid- and late-systolic intraventricular gradient remains somewhat controversial. It is noteworthy that, as highlighted in Figure 1, this gradient rises to its peak levels and maintains them in the face of diminutive forward or even negative aortic root velocities recorded by the multisensor-catheter. Mitral regurgitation invariably accompanies SAM. Open-heart ventriculo-myectomy or transaortic septal myectomy, by trimming the septum and widening the outflow tract, eliminate the abnormal leaflet motion and mitral regurgitation.⁵⁵

Dissipative structures preclude significant pressure recovery in aortic root

The diminutive forward or reversed aortic root velocities recorded by the catheter-mounted electromagnetic sensor late in systole and exemplified in Figure 1 probably represent coherent turbulent flow structures or vortices^1,46,47,56 with recirculating retrograde velocity components. Coherent turbulent eddies representing “dissipative structures”^1,47 are also seen in the ascending aorta in conjunction with the jet issuing from a stenosed aortic valve.^{1,46,47,50,51}

Because of the intense turbulence, there is no significant pressure rise by Bernoulli interconversion in the wide flow area of the ascending aorta;¹ this is easily verified by comparing the LV outflow tract and aortic pressure signals in Figure 1. It implies negligible pressure loss recovery^1,46,57 or insignificant conversion of flow kinetic energy into pressure in the ascending aorta, where flow area re-expands beyond the confluent-streamline subvalvular region; there is instead a transfer of flow kinetic energy to turbulent eddies that dissipate mechanical energy into heat in the eddy cascade.⁴⁷ The polymorphic late-systolic ascending aortic velocity signals in HCM, with eddy-related secondary positive/negative velocity fluctuations, have also been demonstrated by Doppler velocimetry.⁵⁸

Mid- and late-systolic intraventricular gradients

In addition to augmented inertial forces, viscous (“frictional”) shear forces⁵⁹ impact the enormous mid- and late-systolic intraventricular gradients.¹ The continuing importance of inertial forces is obvious from the sharp accelerations and rising confluent velocities demonstrated by Doppler recordings in the outflow tract as echocardiographic dimensions shrink.^46,58 Previous analyses have revealed how viscous effects grow rapidly with shrinking size in the receding late-systolic flow passageway in HCM,^1,46 as the intraventricular flow regime transforms its quasi-inviscid (negligible frictional effects) early- to mid-ejection character. This transformation greatly complicates matters. Because viscous forces are no longer negligible, the Euler equation and all Bernoulli variants, which are predicated on inviscid behavior,⁵⁹ become inapplicable. Accordingly, a solution to the Navier-Stokes equations⁵⁹ encompassing pressure, inertial, and viscous forces is necessary in analyzing these mid- and late-systolic gradients.¹

The Navier-Stokes equations arise from applying Newton’s Second Law to fluid motion to describe fluid dynamics. They govern velocity rather than position. A solution of the partial differential Navier-Stokes equations is termed a velocity- or flow-field, and describes the fluid velocity in space and time. Once the velocity-field is resolved, other quantities of interest (such as volumetric flow rate) may be found and one can visualize various trajectories, such as instantaneous streamlines for laminar flow. As a general rule, explicit solutions for the Navier-Stokes equations, such as that for Poiseuille tube flow, cannot be given. However, with the help of mathematical and computational methods we can construct similarity transformations,^1,46 which by taking into account the rotational symmetry of the approximately cylindrical flow-field can reduce the Navier-Stokes equations to ordinary differential equations⁶⁰ that can be solved numerically to derive computer simulations of the mid- and the late-systolic intraventricular flow-fields.

Computer simulations: “experiments” conducted in silico

Computer simulation is a method for studying complex systems with applications in almost every field of scientific study.⁶⁰ Over the last fifty years, its exploitation to gain insight into complex dynamic phenomena not readily amenable to conventional experimentation has grown to encompass medical fields, including cardiology. Among clinicians it remains relatively unexploited, although it has been demonstrated^61–65 to play a role as informative and creative as the conventional approach to scientific inquiry that entails measuring and experimenting in the clinical and basic settings.

Having features superior to those of modern instrumentation and imaging modalities, including high spatiotemporal resolutions in studies of time-varying intracardiac flow-fields, simulations offer superb investigatory power.^60–66 There are indeed some problems, such as the detailed fluid dynamics of the empirically observed, in a subset of HCM patients and others, phenomenon of “cavity obliteration,”^23,45 for which simulations provide unobtrusive and much more reliable and detailed answers than any experiment or clinical instrumentation, which are limited by practical constraints of spatiotemporal resolution.⁶⁷

Computer simulations must be used to address problems that cannot be feasibly addressed through empirical studies: to wit, catheter-mounted transducers should but cannot always cause only insignificant interference with the flow quantities being measured. Besides, there is routinely a tradeoff between the temporal and spatial resolutions of a technique—cf. speckle-tracking echocardiography and tagged MRI.³¹ And we should make no mistake about it: simulation is a process of data creation, and is a deeply creative source of urgently needed knowledge and understanding in this area. More and more scientific “experiments” are being carried out in silico, and a great variety of simulation techniques have been developed against a backdrop of well-established fluid dynamic theory.

Simulations are a useful tool for sharpening our understanding of HCM and other diseases and their management.⁶⁶ They reveal features of phenomena for which conventional data are sparse. In this context, consider a) the interference with the flow-field of late-systolic cavity obliteration stemming from catheter placement within this narrow cylindrical field, and b) the more or less unavoidable “catheter entrapment”⁶⁸ vitiating catheter-placement within this contracting late-systolic field. Such considerations demonstrate the importance of simulations in analyzing the fluid dynamics of cavity obliteration, as seen not only in selected cases of HCM but also in circulatory states characterized by hyperdynamic LV contraction with low venous return and greatly diminished end-systolic volumes.

Simulation of large intraventricular gradient production without obstruction

To a fluid dynamicist, the argument that large flow-associated intraventricular and aortic transvalvular ejection pressure gradients in HCM are always synonymous with an “obstruction” would be equivalent to arguing with an astronaut that the Earth is flat. In this and subsequent sections, we will examine prominent gradients associated with flow without any localized obstruction, employing fluid dynamic computer simulation results.

Computer simulation visualizations can make the abstract concrete, and provide virtually tangible access to mathematical relationships that reveal the essential nature of phenomena not amenable to direct detailed measurement.^61,66 The graphs that follow enliven our process of understanding the dynamics of cavity obliteration in HCM. Vision provides insight and plays a central role in developing both scientific understanding and theories.⁶⁶ Indeed, “theory” has roots in the Greek verb theorein (to look at) and the noun theoria (both sight and theory).

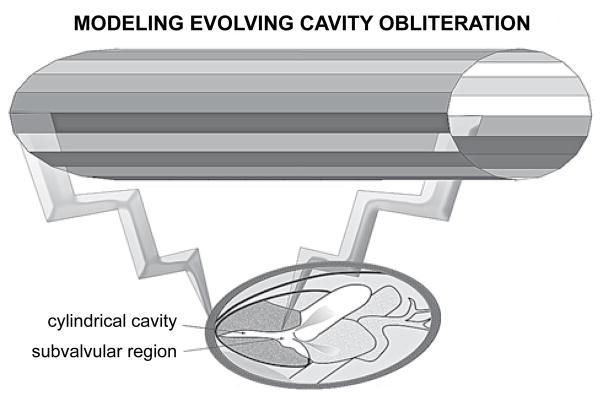
HCM illustrates palpably the principle, enunciated and thoroughly elaborated by Aristotle in several of his works, that form and function go together; anatomy and physiology are coupled.⁶⁹ Figure 2 depicts the geometry of a model I developed to simulate late-systolic dynamics in HCM with cavity obliteration.^1,46 The “obliterating” chamber is represented as a narrow tube with contracting walls, assuming a small constant volumetric outflow rate consistent with the late-systolic signals in Figure 1. Local and dynamic (associated with uniform wall-contraction displacing sequentially cumulative flow increments from apex to outlet) convective inertial as well as viscous effects are important in the flow-field. A solution to the Navier-Stokes equations is derived using a similarity transformation,^1,46–48 and clinically important insightful results are presented graphically in the following figures and computer-created diagrams.

Figure 2.

Geometry of model simulating late-systolic fluid dynamics in hypertrophic cardiomyopathy with “cavity obliteration.” The shrinking late-systolic left ventricular chamber is represented as a narrow tube with contracting walls. Local and especially convective (associated with wall collapse, which displaces sequentially increasing flow increments from apex to outlet) inertial as well as powerful viscous effects are salient. Note the wider subvalvular region.

Radial contraction-associated convective acceleration

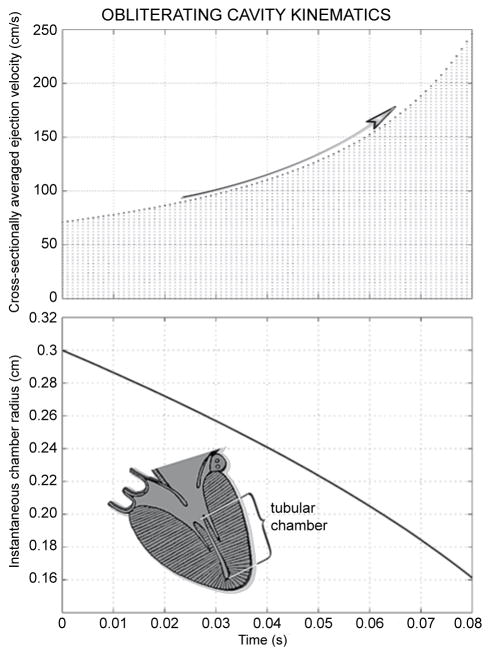
Figure 3 illustrates cavity-obliteration kinematics assuming a late-systolic “starting” radius of 0.3 cm and a constant late-systolic volumetric outflow rate of 20 ml/s. As displayed in the top panel, the cross-sectionally averaged linear outflow velocity increases at an increasing rate with advancing cavity shrinkage and, as shown in the lower panel, by the time the effective radius falls to 0.16 cm, only slightly more than half its starting value, the outflow velocity attains nearly 2.5 m/s.

Figure 3.

Fluid dynamic computer simulation results; inset depicts geometry. As demonstrated in the top panel, the cross-sectionally averaged outlet velocity increases at an increasing rate with advancing cavity shrinkage, attaining nearly 2.5 m/s by the time the effective radius falls to 0.16 cm, only slightly more than half its starting value, shown in the lower panel.

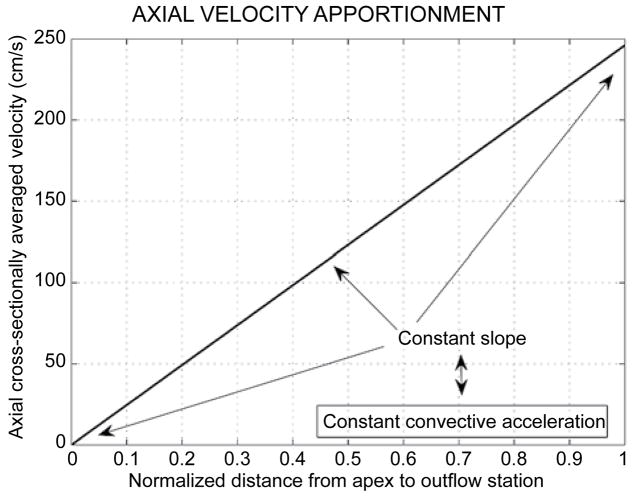
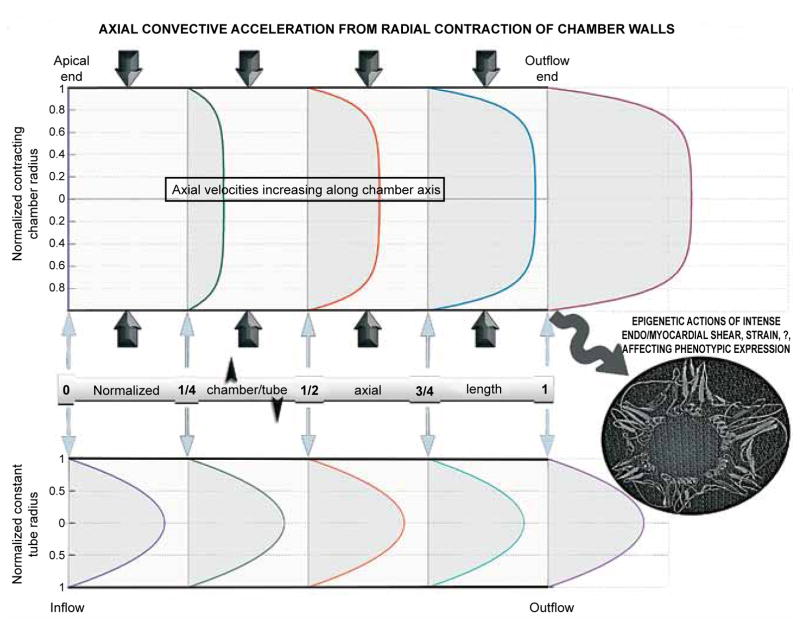
Figure 4 displays the linear increase of the axial cross-sectionally averaged velocity along the chamber axis, resulting from the uniform pattern of radial contraction along the chamber length (cf. Figure 2 and inset of Figure 3). The constant slope reflects the uniform dynamic convective acceleration produced by the radial contraction of the walls; this contraction engenders dynamic convective acceleration despite the uniform cross-section!

Figure 4.

The linear increase of the axial cross-sectionally averaged velocity along the chamber axis accruing from the uniform radial contraction pattern (cf. Figure 2). The constant slope reflects the constant dynamic convective acceleration along the cylinder axis. The radial contraction of the walls engenders forceful dynamic convective acceleration despite the uniform cross-section.

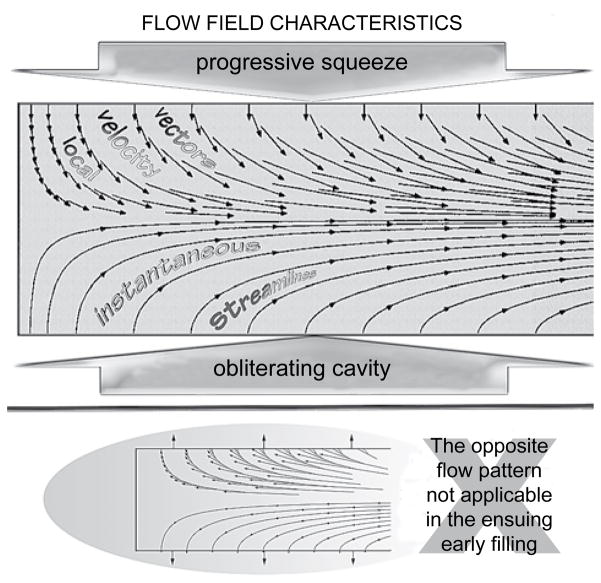
The elucidation of this radial contraction-associated dynamic convective acceleration is provided in the top panel of Figure 5, in which a computational example of the simulated intraventricular ejection flow-field is shown graphically. Representative velocity vectors are shown on the top half of the diametral cross-section of the axisymmetric flow-field. Each such vector has two components: one normal to the cavity walls associated with their radial contraction; and another along the chamber axis. Representative streamlines are shown on the bottom half of the diametral cross-section. Observe that, for this realistic simulation that encompasses not only inertial but also viscous flow forces, all streamlines originate perpendicularly to the “endocardial” surface. Thus the viscous-flow condition of “no-slip” of fluid relative to the wall is satisfied;^{46,47,56,61,63} this is corroborated by the velocity vector plot: the fluid velocity at the wall equals the wall collapse velocity.

Figure 5.

Late-systolic ejection flow-field kinematics in hypertrophic cardiomyopathy with cavity obliteration. The strong convective acceleration of the flow is reflected in converging streamlines toward the downstream outlet and in the concomitant elongation of the axial velocity-vector components. The zero axial components of the velocity vectors at the endocardial surface satisfy the “no-slip” condition. The opposite flow pattern is not applicable in the ensuing early filling because highly decelerated flows are unstable.

Streamlines are everywhere parallel to the local velocity vector. Accordingly, no flow crosses a streamline. Streamlines are lines of constant stream-function, ψ, a mathematical idea embodying the principle of mass conservation. The difference in the stream-function values of any two streamlines represents the volumetric flow rate between them.^59–61,63 In view of these considerations, the depictions on the two halves of the diametral cut through the axisymmetric field portray vividly the strong dynamic convective acceleration between apex and outflow orifice of the cavity, as it is squeezed by myocardial contraction.

In Figure 5, not only does the axial velocity vector component increase, but also the cross-stream distance between streamlines diminishes greatly closer to the outflow orifice. Confluence of streamlines implies a convective increase in velocity; conversely, diffluence or divergence of streamlines implies a convective decrease in velocity, i.e., convective deceleration, as is hinted on the bottom panel.^{46,59–61,63} As signposted on the bottom panel, such decelerated flows are inherently unstable, tending to break down into vortical patterns under the action of the corresponding adverse (Bernoulli) pressure gradient.^56,61,70,71

Convective acceleration effects on mid- and late-ejection velocity profiles

Figure 6 illustrates the effects of the myocardial contraction-induced dynamic convective acceleration on mid- and late-ejection velocity profiles. Profiles are plotted along the cylinder axis at values of the normalized tubular chamber length (distance from apex/axis length) corresponding to 0 (apical end), ¼, ½ (middle), ¾, and 1 (outflow end). The augmentation of the velocities and of the radial slope of the velocity at the wall at successive stations is conspicuous. In view of the uniform radial contraction rate, the cross-sectionally averaged value of the plotted velocity profiles increases from 0 (apical closed end), to ¼, ½, ¾ and 1 times the outflow-end value. The parabolic profiles for Poiseuille tube flow, distributed uniformly along the axis, are plotted for comparison.

Figure 6.

The effects of myocardial contraction-induced convective acceleration on the development of axial mid-to-late ejection velocity profiles. Blunt profiles corresponding to the computed fluid dynamic solution are plotted at successive normalized tubular chamber lengths (distance from apex/axis length). Note the progressive sharp increase in the slope of the velocity profile at the endocardial surface; this slope is proportional to the shear stress exerted by ejected blood locally at the endocardial surface. High shear stress may have important epigenetic influences in hypertrophic cardiomyopathy. The axially uniform parabolic Poiseuille profiles are plotted for comparison.

Observe the progressive sharp increase in the slope of the velocity profile at the cylinder wall; this slope is proportional to the shear stress exerted by flowing blood locally at the endocardial surface.⁵⁹ Its sharp intensification may beget important epigenetic influences,⁶⁹ affecting cardiac structure and function in HCM in as yet unknown ways. Ambitious genotypic studies in patients with HCM, pursued without due attention to the modulating influences of such fluid dynamic epigenetic factors that are in play in any given case, may not be the most efficient approach in this emerging era of pharmacogenomics and personalized therapeutics.⁶⁹

Remarkable intraventricular gradient production without obstruction

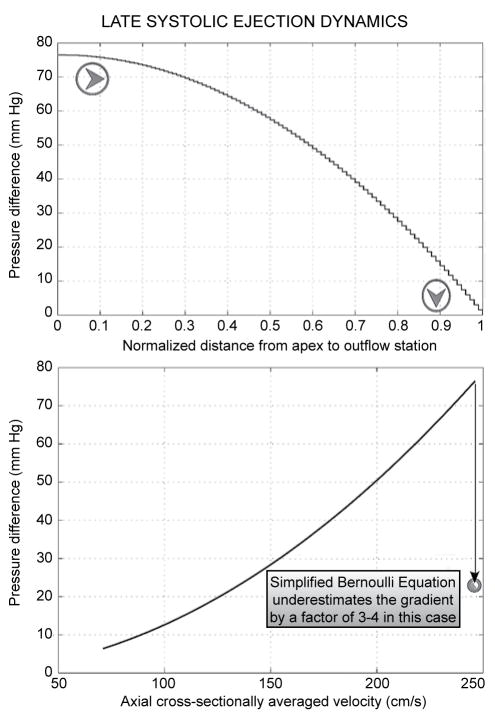
Figure 7 exemplifies the giant intraventricular gradient production without static or dynamic obstruction in the cylindrical model of late-stage systolic ejection with cavity obliteration. The top panel of Figure 7 shows the axial apportionment of the gradient along the normalized distance from apex to outlet orifice. Observe that the gradient intensifies closer to the outlet;^{1,46,50,61–65,70–72} this is revealed to best advantage by the stairstep graph plot—note also the orientation of the arrowheads.

Figure 7.

Enormous intraventricular gradient production without static or dynamic obstruction in the fluid dynamic model of “cavity obliteration.” Top panel: axial pressure gradient apportionment, highlighting gradient intensification nearer the outlet. Bottom panel: the pressure drop (ΔP) from the upstream closed end of the contracting cylinder to progressively increasing distances, from apex to outflow orifice, along its entire length (8 cm in this simulation) plotted against the corresponding local value of the cross-sectionally averaged velocity. Application of the “simplified Bernoulli formula” to the highest velocity (nearly 2.5 m/s) shown would predict ΔP≈25 mmHg—too low compared to the huge late gradients of hypertrophic cardiomyopathy and to the simulated gradient of almost 80 mmHg. This stems from neglecting the potent viscous (frictional) hydrodynamic shear forces in the simplified Bernoulli formula.

Consider now the anatomic relationship between the model cylinder representing the obliterating LV cavity on the one hand and the adjacent subaortic LV outflow tract region, also depicted in Figures 2 and 3, on the other. Referring to this fluid-dynamically most salient topography, I suggest that at least some cases of HCM that appear to be without a prominent transvalvular pressure gradient may be accounted for by a technical cause: the placement of the upstream micromanometric sensor in the subvalvular region, beyond the obliterating cavity across whose length the flow-associated gradient actually develops (cf. lower panel). This is a worthwhile clinical point to remember.

The bottom panel of Figure 7 shows the pressure drop, or gradient, from the apical end of the contracting cavity to progressively increasing distances along its entire length (8 cm in this simulation), plotted against the corresponding rapidly increasing local value of the cross-sectionally averaged velocity. Note that applying the popular “simplified Bernoulli formula” (ΔP = 4v², where “gradient” is in mmHg and velocity in m/s) to the highest velocity (nearly 2.5 m/s) shown in Figure 7 would predict a ΔP of about 25 mmHg; too low in comparison to the huge late-systolic gradients of HCM with cavity elimination and to the simulated gradient of almost 80 mmHg.^1,46 This results from ignoring the viscous hydrodynamic shear forces, powerful in this geometric setting, in the simplified Bernoulli formula, which allows for only convective acceleration inertial effects (and only implicitly at that).

Tiny volumes may be ejected by huge mid- and late-ejection intraventricular gradients

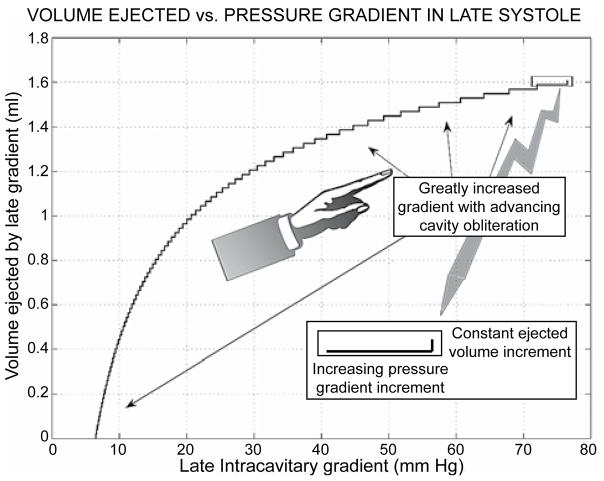
Figure 8 illustrates the tiny cumulative volumes that are ejected by the huge driving intraventricular late-systolic gradients in HCM with cavity elimination.^{1,22,26,46,59} Again, this is demonstrated to great advantage by the stairstep graph plot (cf. arrows, too), which shows that the progressively explosive augmentation of the successive pressure gradient increments ensues in the face of minuscule ejected volume increments in late systole. Such late-systolic gradients are not accompanied by any beneficial stroke volume effect. They do, however, have considerable deleterious effects: they raise substantially subendocardial myocardial stresses and metabolic energy demands, while impeding subendocardial blood perfusion and metabolic supply, thus exacerbating further cardiac hypertrophy-induced impairments of relaxation and diastolic function.^{32,33,46,47,73–78}

Figure 8.

Stairstep graph plot demonstrating to best advantage the progressively explosive augmentation of the pressure gradient increments, which ensues in the face of minuscule ejected volume additions in late systole (cf. arrows, too).

Conclusions and clinical implications

Computer simulation visualizations can reveal the essential nature of phenomena not amenable to direct detailed measurement, including the multifaceted, protean manifestations of morpho-mechanical abnormalities in HCM. They can be relied upon to address problems that cannot be tackled through conventional instrumentation, because it interferes with the quantities being measured. Having features superior to those of modern instrumentation and imaging modalities, including high spatiotemporal resolutions in studies of time-varying intracardiac flow-fields, simulations offer superb investigatory power. In problems such as the detailed fluid dynamics of the phenomenon of “cavity obliteration,” simulations provide unobtrusive, reliable, and much more detailed answers than available laboratory or clinical instrumentation. They demonstrate that large flow-associated intra-ventricular and aortic transvalvular ejection pressure gradients are not synonymous with an obstruction.

Clinically, it is important that only tiny volumes may be ejected by huge mid- and late-ejection intra-ventricular gradients, which are not accompanied by any beneficial stroke volume effect. Nevertheless, these gradients can raise substantial subendocardial stresses and metabolic energy demands, while impeding subendocardial blood perfusion and metabolic supply, thus exacerbating impairments of relaxation and diastolic function.

Considering the anatomic contiguity of the model cylinder representing the obliterating LV cavity and the adjacent subaortic LV outflow tract region, I propose that at least some cases of HCM that appear to be non-obstructive (viz. without a prominent transvalvular pressure gradient) may be accounted for by the placement of the upstream pressure sensor in the subvalvular region, beyond the obliterating cavity across whose length the flow-associated gradient actually develops. This is a clinically vital point. So is the fact that the popular “simplified Bernoulli formula” severely underestimates the huge late-systolic gradients of HCM with cavity elimination because it ignores powerful viscous hydrodynamic shear forces.

Dynamic (associated with wall-contraction displacing sequentially cumulative flow increments from apex to outlet) convective acceleration as well as viscous effects are important under circumstances of cavity obliteration in HCM. The cross-sectionally averaged value of the velocity increases along the LV-axis, accompanied by a progressive sharp increase in the radial slope of the velocity profile at the cavity wall; this slope is proportional to the shear stress exerted by flowing blood locally at the endocardial surface. Its sharp intensification may beget important epigenetic influences, affecting cardiac structure and function in HCM in as yet unknown ways. Ambitious genotypic studies in patients with HCM should pay due attention to the modulating influences of such fluid dynamic epigenetic factors, in this emerging era of pharmacogenomics and personalized therapeutics.^69,79