Simultaneous tumor and surrogate motion tracking with dynamic MRI for radiation therapy planning

Abstract

Respiration-induced tumor motion is a major obstacle for achieving high-precision radiotherapy of cancers in the thoracic and abdominal regions. Surrogate-based estimation and tracking methods are commonly used in radiotherapy, but with limited understanding of quantified correlation to tumor motion. In this study, we propose a method to simultaneously track the lung tumor and external surrogates to evaluate their spatial correlation in a quantitative way using dynamic MRI, which allows real-time acquisition without ionizing radiation exposure. To capture the lung and whole tumor, four MRI-compatible fiducials are placed on the patient’s chest and upper abdomen. Two different types of acquisitions are performed in the sagittal orientation including multi-slice 2D cine MRIs to reconstruct 4D-MRI and two-slice 2D cine MRIs to simultaneously track the tumor and fiducials. A phase-binned 4D-MRI is first reconstructed from multi-slice MR images using body area as a respiratory surrogate and groupwise registration. The 4D-MRI provides 3D template volumes for different breathing phases. 3D tumor position is calculated by 3D-2D template matching in which 3D tumor templates in the 4D-MRI reconstruction and the 2D cine MRIs from the two-slice tracking dataset are registered. 3D trajectories of the external surrogates are derived via matching a 3D geometrical model of the fiducials to their segmentations on the 2D cine MRIs. We tested our method on ten lung cancer patients. Using a correlation analysis, the 3D tumor trajectory demonstrates a noticeable phase mismatch and significant cycle-to-cycle motion variation, while the external surrogate was not sensitive enough to capture such variations. Additionally, there was significant phase mismatch between surrogate signals obtained from the fiducials at different locations.

1. Introduction

Radiotherapy for thoracoabdominal sites, including the lung, liver, and pancreas, are affected by breathing motion. Such respiration-induced tumor motion is a major obstacle for achieving high-precision dosimetry and radiotherapy. Motion variability in the lung, liver, and pancreas over longer durations consistent with radiotherapy treatments has been demonstrated in numerous studies (Ozhasoglu and Murphy 2002, Seppenwoolde et al 2002, Gierga et al 2004, Shirato et al 2004, von Siebenthal et al 2007b). Additional treatment margins are typically added to the clinical target volume (CTV) to adequately treat the target tumor considering the setup uncertainty and the patient motion, which causes toxicity to healthy tissues (ICRU 1993; ICRU 1999). Therefore, significant resources have been focused at developing pre-treatment and intra-treatment motion management methods over the last decade (Hanley et al 1999, Shirato et al 2000, Remouchamps et al 2003, Hashimoto et al 2005, Berbeco et al 2006, Gibbs 2006, Kupelian et al 2007, Cerviño et al 2011).

In the pre-treatment stage, computed tomography (CT) is the reference image modality for radiotherapy planning and dose computation. Accordingly, respiration-correlated CT or 4D-CT is considered an effective tool to characterize tumor and normal tissue motion during radiotherapy. 4D-CT has become the gold standard for radiotherapy treatment planning in the context of breathing motion, and a pre-treatment 4D-CT scan is typically obtained to approximate the internal target volume (ITV), which is the extended volume by motion and geometric uncertainty from the gross target volume (GTV), for radiotherapy planning. 4D-CT is an approximation, though, because it only samples a limited number of tidal volumes. The sampled tumor excursion is then assumed to represent tumor motion over the course of a treatment session. (ICRU 1993, 1999). Additionally, CT deposits additional radiation dose to the patient, thus hindering its extension into acquiring information over timescales consistent with a treatment session.

During treatment, common motion management strategies currently used in radiotherapy include respiration gating (Li et al 2006, Berbeco et al 2005a, 2005b), real-time tumor tracking (Shirato et al 2000), and breath-hold techniques (Mah et al 2000, Rosenzweig et al 2000, Wong et al 1999) where external or internal surrogates are typically used to derive the patient and tumor position. While these methods may yield an improved treatment with reduced margins, they have inherent limitations. Tracking techniques often expose patients to ionizing radiation and an invasive procedure may be necessary for internal surrogate marker placement (Ionascu et al 2007). In addition, anatomic motion due to breathing is significantly variable between breathing cycles, treatment fractions, individual patients, and tumor location, and the respiratory motion can exhibit non-periodic, irregular patterns (Korin et al 1992, Stevens et al 2001). However, surrogate-based motion management strategies are widely used in clinics despite limited understanding of their limitations. Furthermore, tracking using implanted markers (Ionascu et al 2007, Korreman et al 2008) carry sub-sampled spatial information of the tumor, which may not be enough to represent tumor shape, size or the relational position of the tumor location in the organ.

Compared to current pre-treatment and intra-treatment approaches, magnetic resonance imaging (MRI) is advantageous due to its capability of visualizing the target tumor in contextual anatomy with excellent soft tissue contrast. MRI poses minimal risk to patients because it delivers non-ionizing radiation, making it highly suitable for longer duration and repeated scans (Cerviño et al 2011, Paganelli et al 2015a). Recent advances in dynamic MR imaging technologies enable MRI-guided radiation therapy (Liu et al 2004, Plathow et al 2004, Cai et al 2008, Bjerre et al 2013), which may better characterize organ motion. Dynamic MRI can improve 4D radiation therapy by giving continuous, rather than sample based data on tumor motion throughout a prolonged period of respiratory movement, either during a single treatment session or over a course of radiation treatment.

There have been studies to track tumor motion with 2D cine MR images (Sheng et al 2007, Feng et al 2009, Bjerre et al 2013, Tryggestad et al 2013), and more recently to predict the tumor motion by dynamic MRI (Seregni et al 2016). However, only a few groups have analyzed the correlation between the tumor motion and surrogate using 2D dynamic MR imaging techniques (Koch et al 2004, Feng et al 2009). These studies suggest that tumor positioning based on surrogates should be used with caution and imply that dynamic MRI is an attractive solution to address breathing motion and tumor tracking obstacles in radiotherapy. In this study, we propose a novel method to simultaneously track the 3D position of the tumor and external surrogates with dynamic MRI, which allows us to evaluate the correlation between the tumor motion and external surrogate signal for radiation therapy.

2. Methods

To simultaneously track the 3D tumor and external fiducial motions, we acquired 2D multi-slice and two-slice sagittal cine MR images as shown in Figure 1, with a slice acquisition frequency of approximately 4 Hz on average. Four MRI-compatible fiducials were placed on the thorax and upper abdominal regions to provide external surrogate signals. The sagittal slice was preferred because the tumor and fiducial motions are occurring mainly along superior-inferior (SI) and anterior-posterior (AP) directions with much smaller lateral motion. Multi-slice 2D cine MR images were acquired in an interleaved fashion to avoid signal cross-talk between adjacent slices. The total number of slices was set to ensure coverage of the whole tumor, and was therefore variable between patients. This group of slices was then repeatedly acquired to fully sample the respiratory cycle. This data allowed us to retrospectively reconstruct a 4D-MRI volume that provides a representative depiction of one-cycle respiration motion, somewhat analogous to 4D-CT (von Siebenthal et al 2007a, Paganelli et al 2015b). However, this 4D-MRI cannot fully represent the tumor and fiducial motions over a long period of time. To simultaneously track the motions of both tumor and external fiducials, a two-slice 2D cine MR scan was performed; the reduced number of slices compared to the multi-slice technique provided the necessary temporal resolution to adequately sample breath-to-breath variations in the respiratory cycle. Two images were obtained at the fixed positions of π^R and π^L in an alternating and repetitive way as shown in Figure 1(c). In this scan, one slice was positioned to capture both the tumor and two fiducials located on the tumor side, while the other slice was positioned to capture the remaining two fiducials on the non-tumor side as shown in Figure 1(a).

Figure 1.

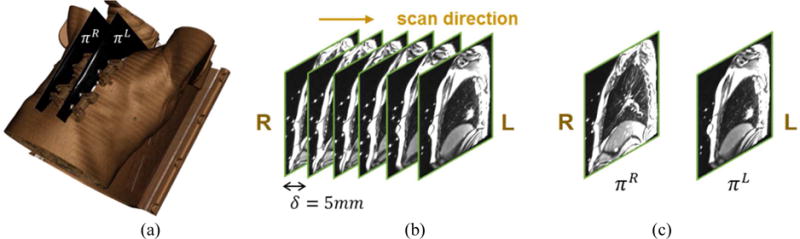
Image acquisition. (a) Volume rendering of the chest and four fiducials overlaid with two-slice scan planes. (b) Multi-slice 2D images represented from the right to the left. (c) Two-slice scan images at locations π^R and π^L.

2.1. 4D-MRI reconstruction and tumor template

4D-MRI volumes are reconstructed from the multi-slice MR images. 4D-MRI reconstruction was useful for obtaining not only representative volumes for one breathing cycle, but also 4D tumor templates. The obtained 4D tumor templates were later used to track the 3D tumor motion from 2D MR images. Figure 2 describes our 4D-MRI reconstruction workflow. The patient’s respiratory signal was extracted by computing body area on each 2D image (Liu et al 2014). Each respiration cycle was divided into N=10 breathing phases and the collected multi-slice MR images are sorted into these N breathing phases. Each phase bin contained multiple MR images that were roughly at similar breathing phase but with variations due to uncertainties in phase binning. To reconstruct a 2D image from multiple sorted images at each slice location and each bin, we performed groupwise registration between the sorted images (Farah et al 2015). Groupwise registration is a technique to mitigate uncertainties in multiple images (usually images in population) by incorporating them through registration process (Balci et al 2007, Yushkevich et al 2012). As shown in Figure 2(b), we performed groupwise registration between multiple sorted images to compute a 2D slice image at each slice location and bin. We repeated this process across different slice locations and breathing phases. The reconstructed slices per breathing phase were then slice-stacked to form a representative 4D image. The final outcome was a series of N=10 reconstructed volumes, Ψ = (V₀, …, V_N−1) each of which represented a 3D volume at each breathing phase. Tumor volumes were segmented from the 4D-MRI reconstruction volumes by region-growing from user-selected points. The segmented tumors were served as the reference templates for 3D motion tracking in the next step.

Figure 2.

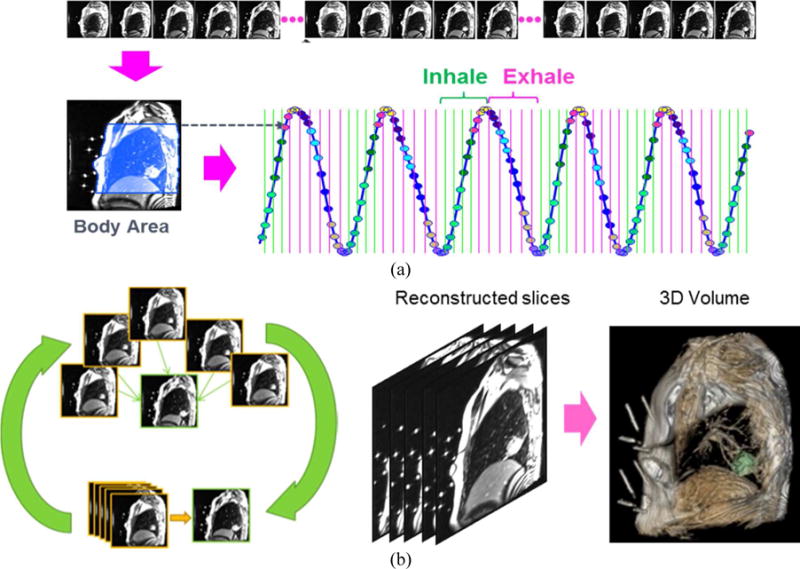
The 4D-MRI reconstruction process. (a) Phase binning based on body area. The blue region on the left image shows the automatically computed body area including the lung. (b) 4D-MRI reconstruction by groupwise registration. For each breathing phase, each slice image is reconstructed by groupwise registration of multiple sorted images (left). Slice reconstruction is repeated for all slices, and a 3D reconstruction at each breathing phase is computed by stacking the reconstructed slice images (middle). Tumor is then segmented from the reconstructed 4D-MRI to form a tumor template (right, green indicates the segmented tumor).

2.2. Tumor tracking

3D tumor motion was determined from the two-slice cine MRI acquisition. We calculated the 3D motion from the 2D scan by 3D (tumor template volumes in 4D-MRI) to 2D (cine MRI) registration. Because the 2D tracking images and 4D-MRI are defined in the same MR coordinate system, their relative geometry is a known a priori. Given the 3D MRI volume V_i at the i^th phase, let us denote the segmented tumor volume as R_i ⊂ V_i and the centroid of R_i as c_i. To match the tumor region, the sequential 2D cine MR images ${\pi }_t^S(t=1,2,\dots ,S\in [R,L])$ were sorted by the same phase-binning approach based on body area as used for 4D-MRI reconstruction. For each time stamp, t, a rigid transformation T_t between the 3D tumor template in the same phase and the target 2D image was estimated by 3D template to 2D image registration. We assume that there was no tumor shape change between the 3D template and the 2D slice image that were obtained at the same breathing phase. We maximized normalized cross-correlation (NCC) between the 2D slice image and cross-section of the 3D tumor template on the 2D slice image plane. To reduce computation time, NCC was computed only within a region-of-interest (ROI) expanded from R_i. Image intensity was used for NCC computation and we represented the tumor motion by the series of the transformed center locations T_t(c_i). The rigid transformation included six parameters, consisting of xyz-translation and Euler angles, and the optimal T_t which maximizes NCC was found by the quasi-Newton method(Press et al 2007). An example of tumor tracking is shown in Figure 3.

Figure 3.

Tumor tracking by 3D-2D registration. (a) 3D volume, V_i, in the same phase for a particular time point, t, of ${\pi }_t^S$. (b) ROI from R_i on the matched plane (white plane) to ${\pi }_t^S$. (c) ROI from ${\pi }_t^S$.

2.3. Fiducial tracking

The MRI-compatible fiducial designed for our study consists of four cylinders filled with 0.9% sodium chloride (normal saline) that were mounted on the top and bottom side of a V-shaped acrylic body with the bounding box size of 8.2×7.6×2.4 cm³ (width × height × thickness). When imaged sagittally or quasi-sagittally, it produces a unique 2D slice cut as shown in Figure 4(d–e). The 3D motion of the fiducial is calculated by matching its 3D geometrical model to 2D cine images. A 3D geometrical model of the fiducial was derived from its CT scan where center lines of the four cylinders and centroid of the fiducial body were computed. In each 2D MR image, the four cylinders from each fiducial are clearly visible as bright ellipses. The fiducial ellipses were individually segmented and indexed in each of the two-slice MR images. The 3D location and orientation of the fiducial in the MRI coordinate frame is thus calculated by matching its 3D geometrical model to 2D cine images.

Figure 4.

Fiducial tracking. (a) The photograph of the fiducial, composed of 4 cylinders filled with normal saline. (b) Volume rendering of the fiducial (cylinders only). (c) Locations of four fiducials on volumetric rendering. (d) Fiducial segmentation in 2D MR image (colored boxes). (e) 3D fiducial tracking by matching 3D fiducial model (4 line segments) to the segmented fiducial markers shown in (d).

A line segment connecting the two end points p, q ∈ ℝ³ can be written as l(t) = p+(q−p)t in parametric form with t ∈ ℝ (0 < t < 1). Since there are 4 cylinders in a fiducial, the fiducial geometry can be defined by an ordered set of four line segments F = (l₁, l₂, l₃, l₄). The fiducial features, as shown in Figure 4(d), were segmented by thresholding and morphological filtering and subsequently indexed by their locations. Fiducial tracking was then realized by a rigid registration, determined by fitting the CT-based fiducial model F to its MR segmentation. Formally, the image plane is defined as n·(x−o) = 0, where o is the origin of the plane and n is the plane normal vector. The intersection point x between the line segment and the plane can be computed by

$$\mathbf{x}=\mathbf{p}+\frac{\mathbf{n}\cdot (\mathbf{o}-\mathbf{p})}{\mathbf{n}\cdot \mathbf{d}}\mathbf{d}=\frac{(\mathbf{n}\cdot \mathbf{o})\mathbf{d}+\mathbf{n}\times (\mathbf{p}\times \mathbf{d})}{\mathbf{n}\cdot \mathbf{d}}$$ (1)

where d = (q−p)/║q−p║. Let T (x): ℝ³ → ℝ³ the rigid transformation of the line segment to the image plane. To estimate the 3D center of the fiducial markers from the 2D MR images, we find the optimal transformation which minimizes the following cost function

$$E={\displaystyle \sum _{i=1}^4{\Vert {\mathbf{c}}_i-T({\mathbf{x}}_i)\Vert }^2}$$ (2)

where c_i. is the center of the segmented marker in 2D MRI as shown in Figure 4(e) and T(x) is computed as

$$T(\mathbf{x})=\frac{(\mathbf{n}\cdot \mathbf{o})T(\mathbf{d})+\mathbf{n}\times (T(\mathbf{p})\times T(\mathbf{d}))}{\mathbf{n}\cdot T(\mathbf{d})}$$ (3)

The rigid transformation T has six degrees of freedom in this model ([x, y, z] translation and Euler angles). To find an optimal solution of this non-linear least squares problem of (2), we used the well-known Levenberg-Marquardt algorithm (Press et al 2007), and the initial solution was estimated from the trapezoidal geometry of the fiducial image in 2D MR images. Finally, the fiducial centroid trajectory of each fiducial was computed based on the estimated transformation, yielding a surrogate signal.

2.4. Simulations

To evaluate the accuracy of the proposed dynamic MRI-based tumor tracking, we simulated 2D dynamic MR image acquisition process using 4D-MR images reconstructed from our multi-slice MR scan. We then applied our tumor tracking algorithm to the simulated 2D dynamic MR images. This simulation study is useful as we know the 3D ground truth position of the tumor at the time of 2D MRI acquisition, therefore can quantitatively assess the accuracy of our tracking. To estimate and simulate the lung and tumor motions during breathing, we first segmented only lung region L_i ⊂ ℝ³ (i=0, …, n−1) from each phase volume. We registered all 10 lung regions (equivalent to 10 breathing phases) in the 4D-MRI and performed principal components analysis (PCA) on the computed deformation fields. We used the 50% phase as the reference, $\widehat{\mathbf{L}}$, and deformably registered the other phases L_j (j=1, …, n−1, ${\mathbf{L}}_j\ne \widehat{\mathbf{L}}$) to $\widehat{\mathbf{L}}$ using the demons registration method (Park et al 2017). Deformation vector fields d_j were obtained for each registration between L_j and $\widehat{\mathbf{L}}$ from which the breathing cycle can be represented as $\mathbf{L}=\widehat{\mathbf{L}}+{\displaystyle {\sum }_{j=1}^{n-1}{w}_j{\mathbf{d}}_j}$ To simulate virtual respiration volume, we extracted principal modes of variation of the deformation. From the matrix D = [d₁ ⋯ d_n−1], principal components of the deformation can be computed by singular vector decomposition (SVD) as shown

$$\mathbf{D}={\displaystyle {\sum }_{i=1}^r{\lambda }_i\cdot {\mathbf{u}}_i\cdot {{\mathbf{v}}_i}^T}$$ (4)

where r (< n) is the rank of D, {λ_i} are non-negative and eigenvalues in decreasing order, {u_i} are corresponding eigenvectors in space domain, and {v_i} are eigenvectors in temporal domain. By selecting K (K ≪ r) eigenvectors from {u_i} and associated weights w_k (t), we can calculate the 3D spatial transformation for each voxel based on a small set of major modes of variation

$$\mathbf{L}(t)\approx \widehat{\mathbf{L}}+{\displaystyle {\sum }_{k=1}^K{\mathbf{u}}_k{w}_k(t)}$$ (5)

3. Experiments and Results

We tested our method on 10 lung cancer patients under an IRB (Institutional Review Board) approved protocol. MR images were acquired using Siemens Magnetom Espree 1.5T scanner (Siemens Medical Solutions, Malvern, PA) with a balanced steady-state free precession sequence (TrueFISP, TR≈3 ms, TE=1.22 ms, flip angle=77–79°). Multi-slice MR images for 4D-MRI reconstruction were first acquired; subsequently, two-slice cine MRI for tracking was acquired. The patient breathed normally during both scans. Acquired images were corrected for geometric distortion using the Siemens distortion correction function provided within Syngo platform (Siemens AG, Erlangen, Germany). The obtained 2D MR images had a spatial resolution of 2×2 mm² with slice thickness and spacing of 5 mm. The slice acquisition frequency was approximately 4 Hz. The number of slices in the multi-slice MR scan varied between 10 and 15 depending on the tumor size. Five minutes of multi-slice and each two-slice MR image acquisition were used to derive the 4D-MRI in this study. Therefore, at each slice location, about 600 MR images were acquired for two-slice scan, and 80-120 images were acquired for multi-slice scan depending on the tumor size. Given that we sorted multi-slice MR images into 10 breathing phases, there were approximately 8-12 images obtained at each breathing phase and slice location.

We tracked motions of the target tumor and 4 fiducial markers (i.e., surrogate signals) using the two-slice 2D MR images. We analyzed the correlation between the tumor and each fiducial motion, and also assessed the sensitivity of 4D-CT-driven ITV using the estimated tumor motion. 4D-CT images of 10 phases for each patient were obtained by Philips Brilliance Big Bore scanner (Philips Medical Systems, Cleveland, OH, USA) with spatial resolutions of [0.98, 1.27]×[0.98, 1.27] mm² and 3mm slice thickness.

3.1. Evaluation by simulation

Based on (5), we generated 4D motion of randomly selected five cases among total 10 cases. The overall target registration errors (TREs) of the deformable image registration showed 2.38±1.03mm for the whole five cases with 30 feature points from each case. To account for irregularity in real patient’s breathing, we added random noise to w_k (t) with Gaussian distribution N(0, 0.05σ_k), where σ_k is the standard deviation of k^th eigenvector. A series of 2D slice images were obtained by cutting L(t) at the same slice location with the same frequency as our 2D MR image acquisition. The same tumor tracking process described in Section 2.2 was performed to the simulated 2D slice images. Note that the ground truth tumor location was known for each simulated 2D slice image; therefore, the tumor tracking accuracy was computed by measuring the Euclidean distance between the estimated tumor centroid and the ground truth.

In our experiments, K=2 in (5) was selected because more than 90% of lung motion could be described by the first two eigenvectors, which is consistent with other studies (Li et al 2011, Stemkens et al 2016). Figure 5 shows the plot of normalized eigenvalues for two test cases.

Figure 5.

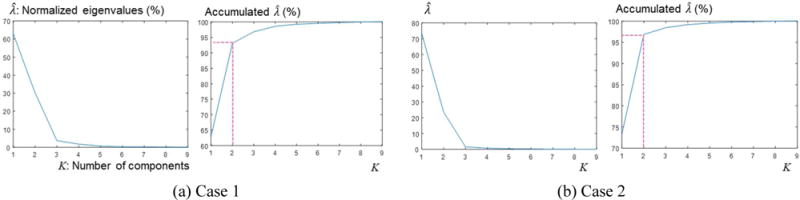
Plots of normalized percentage eigenvalues of D

Table 1 shows the tumor tracking errors for 5 simulation cases. Since the rotational tracking error was very small compared with the translation error for all 5 cases, here we report errors in tumor centroid tracking in Table 1. The overall mean error in 3D shows 1.63 mm (< 2mm) with 2×2×5mm resolution MR slice, which is acceptable to analyze the successive patient data. The major errors are from right-left (RL) direction in most cases, which is reasonable considering only sagittal planes are acquired in our experiments. During the registration iteration, 3D tumor template volume keeps being resampled based on the currently estimated transformation along the 2D image plane, from which sub-voxel registration accuracy can be achieved (Tian and Huhns 1986, Debella-gilo and Kääb 2011, Karybali et al 2008). The 3D-2D registration handles not only the in-plane alignment but also out-of-plane alignment altogether.

Table 1.

Tumor tracking accuracy. Mean ± standard deviation (max) in mm. SI: superior-inferior, AP: anterior-posterior, RL: right-left.

Case	SI	AP	RL	3D
1	0.64 ± 0.31	0.97 ± 0.64	1.03 ± 0.75	1.52 ± 1.09 (3.02)
2	1.01 ± 0.51	1.08 ± 0.69	1.12 ± 1.01	1.93 ± 1.21 (3.57)
3	0.57 ± 0.48	0.88 ± 0.75	1.23 ± 0.79	1.56 ± 1.02 (3.31)
4	0.51 ± 0.41	1.02 ± 0.79	1.32 ± 0.87	1.73 ± 1.04 (3.15)
5	0.45 ± 0.39	0.91 ± 0.63	1.03 ± 0.73	1.43 ± 1.21 (2.97)

3.2. In-vivo experiments

3.2.1. Tumor vs surrogate motion

Since external fiducial and tracking systems are used to extract breathing signal in clinical practice, we extracted a 3D surrogate motion signal from the largest motion direction of each fiducial while tumor motion was analyzed by breaking into the three orthogonal directions (AP, SI, RL). Figure 6 shows two examples of the tumor motion and surrogate signal comparison under normal breathing. In general, the surrogate signal correlated well with the tumor motion, but often showed significant phase mismatch.

Figure 6.

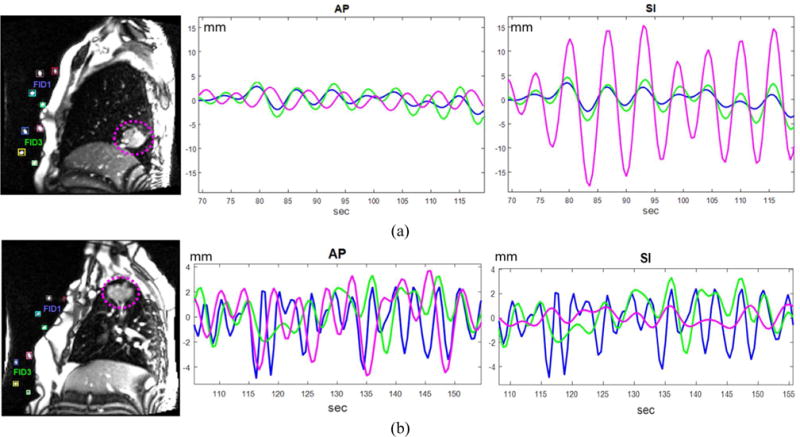
Tumor motion and surrogate signal estimated from fiducials. The magenta dotted circles in the left images indicate the tumors. The magenta, blue, and green colors in the middle and right images represent the tumor, fiducial 1 and fiducial 3, respectively. (a) The tumor locates at lower lobe of the right lung and shows major motion in the SI direction. (b) The tumor locates at upper lobe of the right lung and shows major motion in the AP direction.

Cross-correlation (CC) between each fiducial and the tumor motion signals is described in Table 2. Overall CC values for the ten cases showed 16.60±7.55, 14.14±8.20, and 8.75±3.00 for SI, AP, and RL directions, respectively. Note that cross-correlation is a global comparison of two signals for the whole scanning time and therefore does not show the local mismatch. In addition, there is significant amplitude variation in the tracking signals of the tumor and fiducials, which makes a proper interpretation of the presented values hard. To better measure the local phase mismatch, we also measured the mean and standard deviations of phase differences between the tumor and fiducial motion signals (also shown in Table 2). To compute the phase differences, we identified all the peaks in both tumor motion and fiducial signals, and computed time differences between the matched peaks.

Table 2.

Comparison between the tumor motion signal and fiducial motion signals: cross-correlation and phase differences.

	Tumor location*	Tumor motion	Cross-correlation				Phase difference in seconds (mean ± standard deviation)
			Fid 1	Fid 2	Fid 3	Fid 4	Fiducial 1	Fiducial 2	Fiducial 3	Fiducial 4
Case 01	RL	SI	36.14	36.14	38.00	36.23	0.043 ± 0.14	0.108 ± 0.21	0.108 ± 0.21	0.409 ± 0.44
		AP	37.92	37.73	37.71	36.65	0.301 ± 0.29	0.215 ± 0.39	0.452 ± 0.47	0.925 ± 0.54
		RL	15.31	16.14	16.73	16.92	1.469 ± 1.10	1.405 ± 1.04	1.405 ± 0.93	1.389 ± 1.03
Case 02	RU	SI	16.52	9.48	16.62	14.42	0.559 ± 0.47	0.655 ± 0.55	0.575 ± 0.52	0.607 ± 0.58
		AP	9.44	9.50	11.59	11.48	0.999 ± 0.74	0.942 ± 0.80	0.747 ± 0.52	0.878 ± 0.81
		RL	9.24	9.43	8.13	9.14	0.527 ± 0.49	0.463 ± 0.60	0.942 ± 0.81	0.527 ± 0.61
Case 03	LU	SI	15.91	22.39	20.14	14.21	0.763 ± 0.72	0.634 ± 0.69	0.699 ± 0.72	0.826 ± 0.79
		AP	12.67	18.48	17.32	15.43	0.603 ± 0.67	0.587 ± 0.56	0.604 ± 0.58	0.731 ± 0.74
		RL	9.32	11.24	11.02	9.21	0.463 ± 0.44	0.383 ± 0.42	0.399 ± 0.45	0.575 ± 0.76
Case 04	RM	SI	11.57	16.81	8.00	7.45	0.447 ± 0.63	0.447 ± 0.48	0.591 ± 0.63	0.607 ± 0.68
		AP	8.82	9.58	9.99	9.02	0.575 ± 0.54	0.543 ± 0.60	0.543 ± 0.60	0.583 ± 0.60
		RL	5.13	4.96	5.22	5.01	1.421 ± 1.07	1.693 ± 0.99	1.341 ± 1.06	1.469 ± 1.11
Case 05	LM	SI	16.31	15.47	15.21	14.04	0.247 ± 0.33	0.314 ± 0.31	0.359 ± 0.43	0.507 ± 0.48
		AP	13.48	14.30	12.96	12.51	0.375 ± 0.42	0.319 ± 0.40	0.451 ± 0.40	0.531 ± 0.52
		RL	7.73	8.16	8.52	9.01	0.543 ± 0.36	0.399 ± 0.32	0.335 ± 0.32	0.255 ± 0.44
Case 06	RU	SI	14.23	16.89	15.76	13.97	0.447 ± 0.33	0.314 ± 0.31	0.359 ± 0.43	0.507 ± 0.48
		AP	11.98	12.09	12.21	10.31	0.375 ± 0.42	0.319 ± 0.40	0.451 ± 0.40	0.531 ± 0.52
		RL	8.43	8.96	9.01	8.89	0.469 ± 1.10	0.405 ± 1.04	0.405 ± 0.93	1.389 ± 1.03
Case 07	LM	SI	13.51	14.96	13.04	13.33	0.347 ± 0.33	0.314 ± 0.31	0.459 ± 0.43	0.407 ± 0.38
		AP	12.13	12.94	12.08	11.29	0.375 ± 0.42	0.319 ± 0.40	0.351 ± 0.40	0.531 ± 0.52
		RL	7.31	7.85	7.99	8.41	0.469 ± 0.30	0.405 ± 0.34	0.405 ± 0.33	0.389 ± 0.23
Case 08	RM	SI	11.98	11.31	11.56	10.39	0.803 ± 0.40	0.821 ± 0.52	0.764 ± 0.52	0.721 ± 0.52
		AP	10.26	9.31	9.88	9.76	0.826 ± 0.46	0.737 ± 0.48	0.617 ± 0.54	0.622 ± 0.58
		RL	6.12	6.89	5.98	6.35	0.413 ± 0.34	0.349 ± 0.26	0.445 ± 0.48	0.127 ± 0.22
Case 09	RU	SI	15.73	11.21	10.57	9.48	0.247 ± 0.33	0.314 ± 0.31	0.359 ± 0.43	0.507 ± 0.48
		AP	9.32	10.36	8.11	7.05	0.375 ± 0.42	0.319 ± 0.40	0.451 ± 0.40	0.531 ± 0.52
		RL	5.93	6.13	6.18	6.84	1.469 ± 1.10	1.405 ± 1.04	1.405 ± 0.93	1.389 ± 1.03
Case 10	LL	SI	20.13	21.14	17.31	15.61	0.373 ± 0.50	0.328 ± 0.54	0.421 ± 0.52	0.473 ± 0.50
		AP	13.21	13.04	12.89	12.56	0.226 ± 0.35	0.237 ± 0.48	0.317 ± 0.54	0.326 ± 0.35
		RL	8.91	9.34	9.41	9.58	0.413 ± 0.34	0.345 ± 0.48	0.315 ± 0.54	0.413 ± 0.34

^*Tumor locations - RU: right upper, RM: right middle, RL: right lower, LU: left upper, LM: left middle, LL: left lower.

Figure 7 summarize the phase differences in each direction as a box plot which visualizes the range of mean phase differences between 4 fiducial markers.

Figure 7.

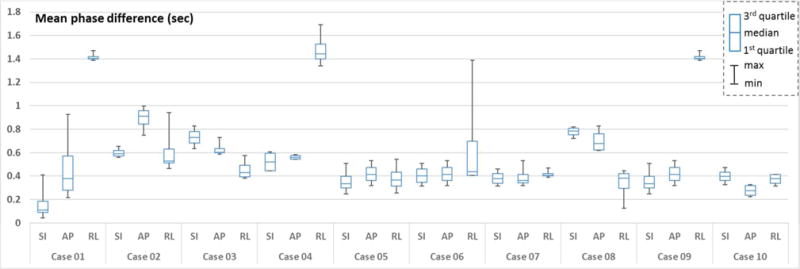
Box plots of the mean phase differences between four fiducial motions and the tumor motion along each direction - SI: superior-inferior, AP: anterior-posterior, RL: right-left.

3.2.2. Tumor motion vs ITV

We compared the tracked tumor motion with the standard 4D-CT-based estimate of ITV by first rigidly registering the 4D-CT volumes to 4D-MR volumes. We used the spine and posterior lung boundary as the landmarks since the patient was scanned in the supine position for both CT and MRI, and was also treated in this position. We assessed the sensitivity of the CT-based ITV by computing the percentage of time the MR-estimated tumor volume was contained within the CT-ITV over the course of the 5 minute MR-tracking scan. We also computed the volume percentage within the ITV corresponded to normal tissues on average during the 5-minute scan and the results are described in Table 3. On average, the tumor volumes were within ITV for 85.1% (81.6-89.1%), and 44.8% (38.2-53.1%) of ITV corresponded to normal tissues. These results imply that the 4D-CT-driven ITV may not accurately represent the actual long-duration tumor motion occurring during a radiation treatment session, which has been shown by other studies (Minn et al 2009).

Table 3.

Comparison between tumor motion and ITV for normal breathing scan.

ITV comparison (%)	Case 01	Case 02	Case 03	Case 04	Case 05	Case 06	Case 07	Case 08	Case 09	Case 10
Sensitivity	82.4 ± 10.7	89.1 ± 5.5	88.3 ± 6.4	87.9 ± 8.3	85.6 ± 9.4	85.1 ± 8.9	82.3 ± 7.2	83.5 ± 9.4	85.4 ± 9.3	81.6 ± 5.4
Normal tissue	53.1 ± 6.1	38.2 ± 7.4	39.6 ± 6.3	43.9 ± 8.4	44.2 ± 5.6	43.1 ± 7.1	48.2 ± 6.4	45.4 ± 7.3	43.2 ± 8.1	49.1 ± 5.6

Considering that the planning target volume (PTV) is determined by adding a margin to ITV, we performed the same comparison of the tracked tumor motion to PTV. While PTV covered the tumor motions well for all cases, on average 67.12 ± 8.7 % of PTV D95 corresponded to normal tissues, implying that a significant portion of normal tissues received unnecessary radiation exposure.

4. Discussion

As shown in Figure 6 and 7, the phase mismatch was often systematic, but there existed significant transient phase mismatches, which may pose significant problems in external surrogate-based tumor motion tracking during radiotherapy. We also observed significant phase difference between the upper (placed to the upper chest) and lower (placed to the lower chest close to abdomen) fiducials. This is due to the variation of the patient’s surface motion around the upper and lower chest areas depending on breathing patterns. This suggests that the position of the external fiducial should be carefully chosen and the tumor location also has to be considered when estimating its motion based on the surrogate signal. This gives the observations from our experiments that the differences in tumor and surrogate motion signals along SI direction were small in general as shown in (Ionascu et al 2007), but not for all ten cases, and also different signal correlation patterns were observed depending on the fiducial locations as shown in Table 2 and Figure 7.

Compared with internal/external marker-based approaches (Ionascu et al 2007, Korreman et al 2008), our image-driven motion management has advantage to provide more quantitative information about ITV coverage. In our 4D-CT based ITV comparison, on average 15% of tumor region was not covered by CT-based ITV and corresponding normal tissues were included into ITV. Although 4D-CT-driven PTV covered tumor motion for all 10 cases examined in this study, over 65% of PTV corresponded to normal tissues. This implies that the proposed 4D-MRI-based tumor motion tracking method can be a very useful tool to analyze the tumor motion for long duration that is equivalent to the fractionated radiation therapy and adjust the treatment margin. Taken together, these data suggest that the surrogate-based tumor motion estimation may have significant amount of uncertainties to manage the tumor motion during radiotherapy. Based on the proposed framework, additional quantitative analysis such as tracking error or correlation according to the tumor location and size is possible with larger cohort of patients.

There are several prior studies which tracked 3D tumor motion using orthogonal, e.g., sagittal and coronal, 2D dynamic MRI (Bjerre et al 2013, Tryggestad et al 2013). In our study, we scanned the patient only at sagittal orientation to simultaneously track both tumor and 4 external fiducials. Since the external fiducials were placed in 4 different locations, it was not possible to capture the motions of the tumor and all 4 fiducials using an orthogonal scan protocol. Instead, we tracked their 3D motions from two sagittal scans using image processing techniques: 4D tumor template to 2D MR image matching for the tumor, and 3D model to 2D MR image matching for the fiducials. In this method, tumor tracking error in RL direction is likely to be larger than the other directions. However, major tumor motion occurs along SI and AP directions and the motion in RL direction is relatively smaller. As shown in our simulation study (Table 1), the proposed method showed reasonable accuracy in all three directions as well as in 3D with only slightly larger error in RL direction than the other directions. Additionally, one may concern that rigid 3D-2D registration may not be sufficient enough to account for potential tumor deformation. We observed that deformation of the tumor shape was negligible in all of our patients. Since our 3D tumor template is extracted from 4D-MRI volume reconstructed at the same breathing phase as the 2D tracking MR image, potential tumor deformation, although usually small, is already captured in our approach. The robustness of the tacking algorithm may be further improved if a breathing guide system is combined, e.g., audiovisual biofeedback (Lee et al 2016) which has proven to improve intra- and inter-fraction tumor motion consistency measured in MRI compared with free-breathing.

It is also important to note that there exist artifacts in 4D-MRI reconstruction due to retrospective image sorting. Most notable artifact of retrospective 4D-MRI reconstruction is inconsistent reconstruction along the through-plane direction, i.e., lateral direction in our case as our images were acquired at (semi)sagittal orientation. Such inconsistency may result in inconsistent 3D tumor template, leading to erroneous tumor tracking by the proposed 3D tumor template to 2D image registration. In order to minimize such inconsistency, our 4D-MRI reconstruction process takes multiple measured 2D images at each breathing phase and slice location, and performs groupwise registration of all sorted images, requiring high correlation between reconstructed slices. The groupwise registration finds a slice reconstruction that mitigates uncertainties and biases between the multiple measured images, therefore produces smoother reconstruction along the through-plane direction with higher signal to noise ratio compared to conventional averaging approaches. However, improved 4D-MRI reconstruction would further improve the tumor tracking accuracy of the proposed method.

Unlike the simulation, there could be large motion deviations in real patients caused by a significant breathing pattern change, gross patient motion, or coughing. Such a large deviation may result in images with missing tumor or fiducials (since tumor or fiducials could move out of plane). However, this motion is transient, and unobserved tumor or fiducial locations were interpolated using adjacent time frames.

In this study, our tracking was performed offline after the MRI scan. Tumor tracking for each time frame takes approximately 800ms in our current Matlab implementation. Although real-time tumor tracking is not the goal of this study, the computation time can be further reduced by incorporating a motion prediction algorithm (Verma et al 2011) into the tracking and optimizing the algorithm. Tracking with motion prediction may better cope with the missing data problem than simple interpolation. A robust and fast 3D tumor tracking algorithm based on 2D dynamic MRI will enable intrafractional tracking of target tumor when used with recently developed MR-LINAC’s. Combined with motion adaptive planning and treatment approaches (Keall et al 2001, Niu et al 2017), it can allow for margin reduction in PTV with high tumor tracking accuracy.

5. Conclusions

We proposed a novel method to simultaneously track tumor and external fiducial motions with dynamic MRI, and quantitatively measured the correlation between the external surrogate signals and internal tumor motions. 4D-MRI reconstruction from multi-slice dynamic MRI scan allows us to build a 4D tumor template which is then used to track 3D tumor motion from 2D dynamic MR images by 3D(tumor template)-2D MR image registration. MR-compatible fiducials with a unique configuration enables 3D fiducial motion tracking from 2D MR images by model to 2D image matching. Using the proposed methods, we simultaneously tracked both tumor and 4 fiducials placed at different locations on the patient’s chest. The tumor motion and surrogate signal correlated well in general, but often showed systemic and/or transient variations in phase. Additionally, the ITV derived from 4D-CT, which is a single snapshot of one breathing cycle, was not sensitive enough to capture the tumor motion for longer time durations. Although tested on a limited number of patients, our results suggest that surrogate-based lung tumor motion management in radiation therapy should be used with caution. Furthermore, the proposed method showed its utility to enable patient-specific analysis of tumor motion that is monitored for long duration of time equivalent to the treatment, thus helping us determine the best motion management method at the time of radiotherapy planning.