Abstract
Path-integral free energy perturbation (PI-FEP) theory is presented to directly determine the ratio of quantum mechanical partition functions of different isotopologs in a single simulation. Furthermore, a double averaging strategy is used to carry out the practical simulation, separating the quantum mechanical path integral exactly into two separate calculations, one corresponding to a classical molecular dynamics simulation of the centroid coordinates, and another involving free-particle path-integral sampling over the classical, centroid positions. An integrated centroid path-integral free energy perturbation and umbrella sampling (PI-FEP/UM, or simply, PI-FEP) method along with bisection sampling was summarized, which provides an accurate and fast convergent method for computing kinetic isotope effects for chemical reactions in solution and in enzymes. The PI-FEP method is illustrated by a number of applications, to highlight the computational precision and accuracy, the rule of geometrical mean in kinetic isotope effects, enhanced nuclear quantum effects in enzyme catalysis, and protein dynamics on temperature dependence of kinetic isotope effects.
1. INTRODUCTION
Although the dominant factor in enzyme catalysis is the lowering of the free energy barrier of a catalyzed reaction (Garcia-Viloca, Gao, Karplus, & Truhlar, 2004; Schowen, 1978), it is of great interest to understand the detailed mechanism of transition state stabilization and the connection between protein dynamics and rate acceleration. Kinetic isotope effects (KIEs) provide a direct probe of the transition state, and a comparison of experimental KIEs for the enzymatic and uncatalyzed reactions in water can reveal surprising differences. KIEs are not only significant for proton, hydride, and hydrogen-atom transfer reactions due to their small mass, but also they are important for reactions involving heavy atoms as illustrated by the work of Schramm (2003), who used the experimental KIE to develop transition state models for inhibitor design. KIEs are of quantum mechanical origin, including contributions from zero-point energy and tunneling (Pu, Gao, & Truhlar, 2006). A challenging question is whether enzymes have evolved to enhance nuclear quantum effects in rate acceleration (Major et al., 2009), and another intriguing question is by what means amino acid mutations that alter protein dynamics affect the measured KIE (Klinman & Kohen, 2014). To rationalize the experimental findings (Gao et al., 2006; Garcia-Viloca et al., 2004; Kohen & Limbach, 2005; Layfield & Hammes-Schiffer, 2014; Wang, Fried, Boxer, & Markland, 2014; Wong, Xu, & Xu, 2015), computational studies are often necessary, and quantum mechanics is essential for modeling enzymatic mechanism and kinetics (Gao et al., 2006; Gao & Truhlar, 2002). In this chapter, we present methods that have been developed in our group for studying enzymatic reactions, with a particular emphasis on accurate computation of primary and secondary KIEs.
Quantum mechanics is essential in enzyme kinetics modeling, and there are two major challenges to accurately determine the rate constant and KIEs (Gao & Truhlar, 2002). First, it is necessary to construct an accurate potential energy surface (PES) to model enzymatic reactions in aqueous solution (Gao et al., 2006). To this end, combined quantum mechanical and molecular mechanical (QM/MM) methods (Liu, Wang, Chen, Field, & Gao, 2014), in which the active site is modeled by an electronic structural theory and the surrounding solvent and protein environment is represented by a force field, provide an effective procedure to treat the bond-forming and bond-breaking processes (Gao, 1995a, 1996; Senn & Thiel, 2009). Such a combined QM/MM approach offers both accuracy and computational efficiency (Gao, 1996), and methods that can treat the entire protein–solvent system with a quantum mechanical representation are being actively pursued by a number of research groups (Gao, Truhlar, Wang, et al., 2014; Gao, Zhang, & Houk, 2014; Merz, 2014; Xie, Orozco, Truhlar, & Gao, 2009).
The second challenge to theory is to explicitly incorporate nuclear quantum effects, including quantum mechanical treatment of vibrational motions and tunneling (Pu et al., 2006). A variety of methods are available to treat nuclear quantum effects for gas-phase reactions (Fernandez-Ramos, Miller, Klippenstein, & Truhlar, 2006). In principle, these techniques can be directly extended to condensed-phase systems; however, the size and complexity of enzyme systems make it intractable computationally. One approach successfully applied to enzymatic reactions is the ensemble-averaged variational transition state theory with QM/MM sampling (EA-VTST-QM/MM) (Gao & Truhlar, 2002; Pu et al., 2006). This technique extends the VTST method developed for gas-phase reactions into condensed-phase reactions through ensemble averaging over configurations sampled through dynamics simulations (Alhambra et al., 2001). In another work, a grid-based hybrid approach was used to model nuclear quantum effects by numerically solving the vibrational wave function of the quantized nucleus (Layfield & Hammes-Schiffer, 2014). Recently, transition path sampling was used with normal model centroid molecular dynamics to determine KIE for enzymatic reactions (Dzierlenga, Antoniou, & Schwartz, 2015).
The theoretical framework in our study of enzymatic KIE is discrete path-integral simulation, in which the ratio of the quantum mechanical partition functions between different isotopic systems is determined in a single simulation, providing the necessary precision required for computing KIEs (Major & Gao, 2007). In particular, our method makes use of free energy perturbation (FEP) theory (Zwanzig, 1954) by carrying out path-integral simulation of one isotopolog, eg, the light (L) isotope, and by treating the difference in another isotope distribution, eg, the heavy (H) isotope, as a perturbation. Thus,
| (1) |
where β = 1/kB T, is the difference in the quantum mechanical (qm) effective potential (Feynman & Hibbs, 1965) between the light and heavy isotopes, and the average 〈⋯〉L is carried out based on the effective potential for the light particle. In principle, the average of Eq. (1) can be obtained from path-integral simulations directly, or using various other procedures such as centroid molecular dynamics (Cao & Voth, 1996; Hernandez, Cao, & Voth, 1995) and ring-polymer dynamics. Importantly, an even more efficient method is to separate the direct quantum mechanical average into two separate steps (Major & Gao, 2007). In particular, using a free-particle reference state, the quantum mechanical average of a property, A, can be rigorously obtained through path-integral free-particle sampling over classical configurations from molecular dynamics or Monte Carlo simulations:
| (2) |
where the inner average 〈⋯〉FP represents free-particle sampling over classical atomic coordinates as the centroids of the discrete paths, and the outer average 〈⋯〉cm represents a classical mechanical ensemble average.
The double averaging strategy was given by Feynman (Feynman & Hibbs, 1965) and used by Sprik et al. in Monte Carlo simulations for a system consisting of one electron embedded in random hard spheres (Sprik, Klein, & Chandler, 1985). It was also called quantized classical path and pointed out that the expression of Eq. (2) is particularly useful (Hwang & Warshel, 1993, 1996; Major & Gao, 2007) because the quantum free energy of the system (here, in Eq. (1), the difference between two isotopic systems) can be obtained through two separate simulations: first by carrying out a Newtonian simulation to determine generate the classical ensemble, and then, by evaluating quantum contributions through free-particle sampling in a path-integral simulation.
The rest of the chapter focuses on discussion of treatment of the PES U(r̄), and the technical details of using Eqs. (1) and (2) to compute free energies of activation and nuclear quantum effects in enzymatic reactions.
2. METHODS
Almost all enzyme reactions can be well described by the Born–Oppenheimer approximation (exceptions include, for example, photochemical processes), in which the sum of the electronic energy and the nuclear repulsion provides a potential energy function, or PES, governing the interatomic motions. Therefore the molecular modeling problem breaks into two parts: the PES and the dynamics simulations.
2.1 Potential Energy Surface
The potential energy function describes the energetic changes as a function of the variations in atomic coordinates, including thermal fluctuations and rearrangements of the chemical bonds. The accuracy of the potential energy function used to carry out molecular dynamics simulation directly affects the reliability of the computational results (Truhlar et al., 2002). Although it is possible to treat an entire enzyme–solvent system by QM methods (Car & Parrinello, 1985; Gao, Zhang, et al., 2014; Rohrig, Guidoni, & Rothlisberger, 2005; Stewart, 1996; Titmuss, Cummins, Rendell, Bliznyuk, & Gready, 2002), the computational costs are still too large to be practical for free energy simulations of enzymatic reactions. The most effective approach to model chemical reactions both in condensed phases and in enzymes is QM/MM methods (Liu et al., 2014), which offer the advantage of both computational efficiency and accuracy (Gao, 1995a).
In QM/MM methods, a system is divided into a QM region and an MM region (Field, Bash, & Karplus, 1990; Gao, 1992, 1995a; Gao & Xia, 1992; Liu et al., 2014; Singh & Kollman, 1986; Warshel & Levitt, 1976). The QM region typically includes atoms that are directly involved in the chemical step and they are treated explicitly by an electronic structure method, whereas the MM region consists of the rest of the system that is approximated by an MM force field. The QM/MM potential is given by Field et al. (1990) and Gao (1995a):
| (3) |
where is the Hamiltonian of the QM-subsystem (the substrate and key amino acid residues), Umm is the classical (MM) potential energy of the remainder of the system, and Hqm/mm(S) represents the interactions between the two regions. Ψ(S) is the molecular wave function of the QM-subsystem optimized for .
It is most convenient to rewrite Eq. (3) as follows (Gao, 1992; Gao & Xia, 1992):
| (4) |
where is the energy of the QM-subsystem in the gas phase, and ΔEqm/mm(S) is the energy change of transfer to bring the QM-subsystem from the gas phase into the enzyme. The latter, which is also called QM–MM interaction energy, is defined by
| (5) |
Eq. (4) is especially useful in that the total energy of a hybrid QM and MM system is separated into two “independent” terms—the gas-phase energy and the interaction energy—which can now be evaluated using different QM methods. Here, we have identified the energy terms involving electronic degrees of freedom by E and those purely empirical functions by U. First, the high accuracy needed to describe the intrinsic chemical reactivity of the QM-subsystem must be obtained by using an accurate quantum chemical model. This typically prevents its use in statistical mechanical simulations, especially for macromolecular systems, because of the high computation cost. Fortunately, the required accuracy is primarily associated with the first term in Eq. (4), , in the gas phase, and it typically does not demand for extensive configurational sampling. Thus, it is possible to use methods such as coupled-cluster theory CCSD(T), complete active space self-consistent field with perturbation theory CASPT2, or density functional theory with a well-tested functional along with large basis functions. In other cases, it is also possible to reparameterize semiempirical methods to fit experimental data or high-level QM results. To emphasize the use of a high-level (HL) theory to substitute the term, which could be different from the QM/MM interaction term (Eq. 5), we have
| (6) |
This substitution of QM models can be made on the fly during a dynamics simulation, or post priori.
For condensed-phase systems such as enzymatic reactions, the most critical issue is adequate configuration sampling, and this affects the accuracy in the calculation of the ΔEqm/mm(S) term. It was recognized early on, when QM/MM simulations were first carried out that combined QM/MM potential is an empirical model, which contains empirical parameters and should be optimized to describe QM/MM interactions (Freindorf & Gao, 1996; Gao, 1994a; Gao & Xia, 1992). By systematically optimizing the associated van der Waals parameters for the “QM-atoms,” both semiempirical and ab initio (Hartree–Fock) QM/MM potentials can yield excellent results for hydrogen-bonding and dispersion interactions in comparison with experimental data. The use of semiempirical methods (Cui, Elstner, Kaxiras, Frauenheim, & Karplus, 2001; Dewar, Zoebisch, Healy, & Stewart, 1985; Gaus, Cui, & Elstner, 2011; Stewart, 1989) in QM/MM simulations has been validated through extensive studies of a variety of properties and molecular systems, including computations of free energies of solvation and polarization energies of organic compounds (Gao & Xia, 1992; Orozco, Luque, Habibollahzadeh, & Gao, 1995), the free energy profiles for organic reactions (Gao, 1995b, 1996; Major, York, & Gao, 2005), and the effects of solvation on molecular structures and on electronic transitions (Gao, 1994b; Gao & Byun, 1997; Lin & Gao, 2007). Importantly, these relatively lower-level (LL) methods for QM/MM interactions (but with a high degree of accuracy) offer an opportunity to perform adequate configuration sampling essential for understanding the contributions of protein dynamics to catalysis.
| (7) |
It should be noted that unlike the use of a preoptimized reaction path and the associated empirical parameters including partial charges in subsequent MM simulations, the prescription of Eqs. (5) and (7) includes the instantaneous electronic polarization of the QM-subsystem due to the thermal fluctuations of the enzyme and solvent environment (Garcia-Viloca, Truhlar, & Gao, 2003). The latter is essential for enzymes.
The approach described above represents a highly accurate dual-level (DL) total energy for enzymatic systems (Byun, Mo, & Gao, 2001):
| (8) |
The DL QM/MM approach is akin to the ONIOM model developed by Maseras and Morokuma (1995), but physically and conceptually different in that it is not an energy subtraction–addition scheme, and it is a gas-phase and condensed-phase separation algorithm.
The QM/MM PES combines the generality of quantum mechanical methods for treating chemical processes with the computational efficiency of molecular mechanics for large molecular systems. The use of an explicit electronic structure method to describe the enzyme active site is important because understanding the changes in electronic structure along the reaction path can help design inhibitors and novel catalysts. It is also important because the dynamic fluctuations of the enzyme and aqueous solvent system have a major impact on the polarization of the species involved in the chemical reaction, which, in turn, affects the chemical reactivity (Gao et al., 2006; Gao & Xia, 1992).
2.2 Potential of Mean Force
The rate constant in our study of enzymatic reactions is determined using path-integral quantum transition state theory (QTST) (Voth, Chandler, & Miller, 1989a, 1989b), which was derived by writing the rate expression analogous to classical transition state theory (TST) (Fernandez-Ramos et al., 2006).
| (9) |
where h is Planck’s constant, and is the free energy of activation, which can be obtained from path-integral or quantum mechanical potential of mean force (PMF), wqm(z̄), as a function of the centroid reaction coordinate denoted as z̄. As in classical TST, the quantum free energy of activation can then be obtained from the PMF:
| (10) |
where the symbol z̄≠ specifies the value of the centroid reaction coordinate, at which wqm(z̄) has the maximum value, and z̄R is the coordinate at the reactant state.
Feynman path-integral simulation provides a convenient procedure to determine wqm(z̄), incorporating quantum effects on tunneling and nuclear vibrations (Feynman & Hibbs, 1965). In this approach, ensemble averages for the quantum system are obtained from a classical simulation in which the quantized particles are represented by ring polymers of classical particles. To determine the PMF, the average positions, or centroids, of the quantized particles are used as classical variable to define a corresponding reaction coordinate z̄ (Cao & Voth, 1994; Gillan, 1988; Messina, Schenter, & Garrett, 1993; Voth et al., 1989a). Practical methods include centroid molecular dynamics (Jang & Voth, 2000; Makarov & Topaler, 1995; Messina, Schenter, & Garrett, 1995; Mills, Schenter, Makarov, & Jonsson, 1997) and ring-polymer molecular dynamics (Habershon, Manolopoulos, Markland, & Miller, 2013). We employ an alternative approach, in which the quantum mechanical PMF wqm(z̄) is determined through a double averaging procedure. This approach has been used in simple applications and has been applied to enzymatic reactions, and it has been called quantized classical path (Hwang & Warshel, 1993, 1996; Major & Gao, 2007; Villa & Warshel, 2001).
In the discrete path-integral method, each quantized nucleus is represented by a ring of P quasi-particles called beads. The coordinates for the M-quantized particles are collectively denoted as , with the definition of rP + 1 = r1. Each bead associated with a given quantized particle is connected to its two neighbors via harmonic springs and is subjected to a fraction, 1/P, of the full classical potential, , where S represents all classical protein–solvent coordinates. In centroid path integral, the centroid positions {r̄} are used as the principle variable and the canonical QM partition function of the hybrid system can be written as follows:
| (11) |
where Veff(r, S) is the effective quantum mechanical potential, ∫ dR = ∫ dr1⋯ ∫ drPδ(r̄), the centroid coordinates {r̄} of the quasi-particles is defined as , and the de Broglie thermal wavelength λq of a particle of mass mq is .
The quantum partition function of Eq. (11) can be exactly rewritten as a double average (Hwang & Warshel, 1993, 1996; Major & Gao, 2005, 2007; Major, Garcia-Viloca, & Gao, 2006; Sprik et al., 1985):
| (12) |
where is the classical partition function (Feynman & Hibbs, 1965). As noted above, the average 〈⋯〉U is obtained according the potential U(r̄, S), which is of QM/MM type, but purely classical in nuclear degrees of freedom, and the inner average 〈⋯〉FP,r̄ represents free-particle sampling, constrained to match the path-integral centroid coordinates with the classical atomic positions. The average differential potential energy in Eq. (12) is given as follows:
| (13) |
and the free-particle sampling is carried out according to the distribution , or
| (14) |
where Δri = ri − ri + 1.
The double averaging procedure yields the exact path-integral centroid density, thereby, the centroid quantum mechanical PMF:
| (15) |
where wqm(z̄) and wcm(z = z̄) are the centroid quantum mechanical and classical mechanical PMF, respectively.
2.3 KIEs and the PI-FEP Method
KIE is defined as the ratio of the rate constants between light and heavy isotopic reactions, which can be computed simply by applying QTST as follows:
| (16) |
where and are the centroid PMF for the reactions with light and heavy isotopologs, respectively. Eq. (16) indicates that KIEs may be determined by computing the potentials of mean force separately for the L and H isotopes (whether or not using path-integral simulations) (Hwang & Warshel, 1993, 1996; Major & Gao, 2007; Major et al., 2006), and this indeed is typically the procedure used in many applications. However, statistical fluctuations in the actual simulations for computing the potentials of mean force are typically of similar, or even greater, magnitude as the free energy difference in isotope effects (Major & Gao, 2007). Thus, it is extremely difficult to obtain meaningful results for heavy atom and especially for secondary KIE using this strategy.
KIEs can also be expressed in terms of the ratio of partial partition functions at the centroid reactant and transition state:
| (17) |
This expression is particularly useful because it transforms two separate calculations of the PMF for different isotopic reactions in Eq. (16) into evaluation of the relative probabilities of the light and heavy isotopes at the transition state and in the reactant state region. As highlighted in Eq. (1), the ratio of the quantum partition functions for different isotopes can be determined directly through FEP theory by perturbing the mass from one isotope into the other (Ceriotti & Markland, 2013; Major & Gao, 2007; Marsalek et al., 2014). Therefore, only one path-integral simulation of a given isotopic reaction is needed to yield the free energy difference, ie, the ratio to the partition function of anther isotope. This method is called path-integral free energy perturbation (PI-FEP) theory (it seems that the SC-FEP scheme in Ceriotti and Markland (2013) is the same as the PI-FEP method, but the authors were apparently not aware of the earlier work), which results in a major improvement in precision for KIE calculations such that not only H/D primary KIE can be computed, but also heavy atom and secondary KIEs can be determined accurately.
In PI-FEP, we further separate the PI quantum average into a hybrid classical molecular dynamics and path-integral simulation with free-particle sampling. The theory is exact, but the separate procedures of classical MD and PI-free-particle sampling are especially advantageous because it allows an extensive sampling of the protein–solvent (bath) conformational space, and the free-particle sampling scheme avoids the discrete-bead distribution being trapped in a local minimum. Specifically, the ratio of the distribution functions for a system with light and heavy isotope substitutions is given as follows:
| (18) |
where the subscripts L specifies that the ensemble averages are done using the light isotope, ΔŪL is the difference (Eq. 13) between the average potential of the P-discrete beads of the light particle and that of the centroid {r̄}, and ΔΔUH←L = ΔŪH − ΔŪL. One may recall the reweighting expression of umbrella sampling (UM) of Valleau and Torrie (1977); thus, our method really is an integrated PI-FEP and UM approach.
A practical difficulty in path-integral simulations is to obtain converged results for the computed PMF within a tolerable amount of simulation time, especially at a precision needed for computing KIE. To this end, we have developed a bisection sampling technique, called BQCP (Major & Gao, 2005; Major et al., 2006). The method was based on the approach developed by Ceperley for free-particle sampling in which the initial and final beads are not connected (Ceperley, 1995; Pollock & Ceperley, 1984). In our implementation, the bisection sampling was made as originally proposed (Ceperley, 1995; Pollock & Ceperley, 1984), but we enforce the first and last beads to be identical to enclose the ring particles. We then impose the condition that the centroid position matches the corresponding atomic coordinates by rigid-body translocation (Major & Gao, 2005; Major et al., 2006). Since free-particle distribution is known exactly at a given temperature, each discrete-bead distribution is generated according to this distribution and thus 100% accepted. Furthermore, in this construction, each new configuration is created independently, starting from a single initial bead position, allowing the ring-polymer configurations to move into completely different regions of configurational space, independent of previous beads distribution. This latter point is especially important to enhance convergence by avoiding being trapped in a local minimum of the classical potential in the path-integral sampling. Using this sampling technique, the PI-FEP method has been applied to a range of condensed-phase and enzymatic systems (Fan, Cembran, Ma, & Gao, 2013; Gao, Wong, & Major, 2008; Lin, Gao, Rubinstein, & Major, 2011; Major & Gao, 2005, 2007; Major et al., 2006, 2009, 2005).
In the bisection sampling scheme, the perturbed heavy isotope positions are related to the lighter ones by
| (19) |
where and are the coordinates for bead i of the corresponding light and heavy isotopes of the classical atom q, mq,L, and mq,H are the masses for the light and heavy nuclei, and is a position vector with respect to the position of the centroid, or classical atomic coordinates in the bisection sampling scheme (Major & Gao, 2005). In our PI-FEP (or PI-FEP/UM) simulation scheme, the position vectors for the perturbed beads, eg, the heavy isotope, are made identical to the reference (ie, light) isotope distribution. As a result, beads positions of the perturbed mass are solely determined by the square root of mass ratio (Eq. 19).
3. ILLUSTRATIVE EXAMPLES
In the following, I have carefully selected a few illustrative examples to highlight applications of the PI-FEP method. These include (1) the computation of primary and secondary KIEs for heavy elements, (2) the rule of geometric mean (RGM) and Swain–Schaad exponents, (3) an enzyme that has been optimized to enhance nuclear quantum effects over the uncatalyzed process, and (4) the effect of protein dynamics on temperature dependence of KIE.
3.1 Primary and Secondary KIE for Non-Hydrogen Atoms
It is straightforward to compute H/D primary KIE, which typically have reasonably large values that can be determined from separate PMF calculations of the hydrogen and deuterium systems. However, the calculation of primary KIE for heavy isotopologs as well as secondary KIEs (hydrogen and non-hydrogen) presents a major challenge because the relative free energies of activation associated with these isotope changes are too small to be adequately treated by separate simulations. To illustrate the computational precision of the PI-FEP method, we first present a study of the primary and secondary KIEs involving heavy atoms in the decarboxylation reaction of N-methyl picolinate in water (Major & Gao, 2007; Rishavy & Cleland, 2000). We first performed Newtonian molecular dynamics simulations to obtain the (classical) PMF along the C2 − CO2 distance reaction coordinate for N-methyl picolinate in a box of 888 water molecules (Major & Gao, 2007). Combined QM/MM potential was used, in which the N-methyl picolinate ion was treated by the semiempirical AM1 Hamiltonian and water by the TIP3P model. Then, centroid path-integral free-particle sampling was carried out on the classical ensemble of configurations to yield the ratio of the quantum mechanical partition functions for different isotopes (12C, 13C, 14N, and 15N) associated with the decarboxylation reaction. Note that the classical PMF is independent of atomic masses. Also, in addition to the isotopically substituted nucleus, the immediately adjacent atoms were also quantized, and each quantized atom was described by 32 beads.
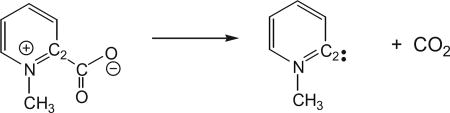
Solvent effects are significant, increasing the free energy barrier by 15.2 kcal/mol to a value of 26.8 kcal/mol. The large solvent effect is due to the presence of a positive charge on the pyridine nitrogen, which is annihilated in the decarboxylation reaction. There is only about 2 kcal/mol of CO2 recombination barrier, which would post difficulty for computing KIEs using only a single transition structure.
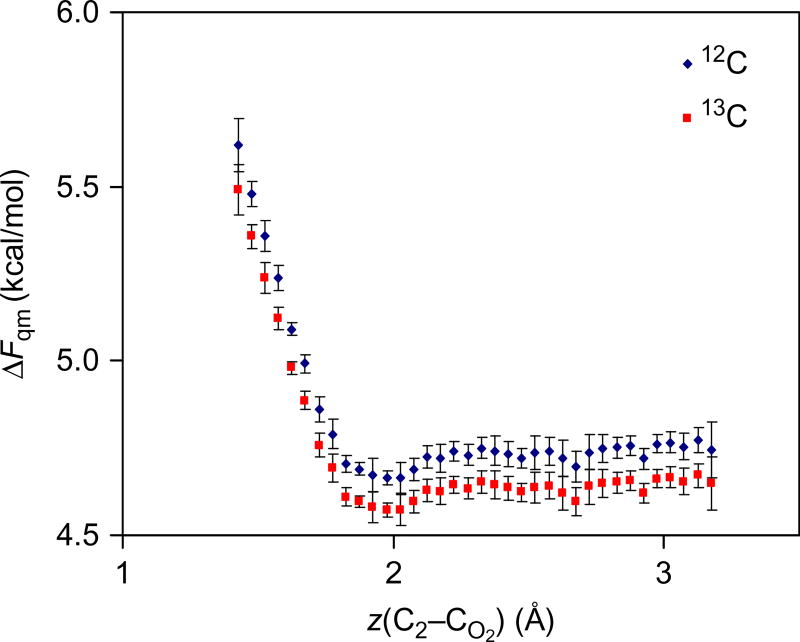
The computed 12C/13C primary KIE at the carboxyl carbon position and the 14N/15N secondary KIE are listed in Table 1. Figs. 1 and 2 depict the difference in computing KIE by (1) using two separate PMF simulations for different isotopes (QTST) and (2) using the single-simulation PI-FEP method. In the first approach (denoted by QTST, although KIE calculations using PI-FEP are also based on QTST), one needs to take difference of two quantities with large fluctuations illustrated by the error bars along the PMFs (Fig. 1), resulting in large standard errors in the computed KIE (Table 1). On the other hand, the standard error for KIE from the PI-FEP method is simply that of a single simulation (Fig. 2). The computed intrinsic 13C primary KIE is 1.0345 ± 0.0028 from PI-FEP at 25°C for the decarboxylation of N-methyl picolinate in water. Although the standard deviation is greater than the accuracy of experimental measurement (Table 1), the confidence level is much higher than that from separate PMF calculations, even though the same beads configurations were used in PI simulations. To emphasize the sensitivity of the computational result, the computed KIE is equivalent to a free energy difference of merely 0.0187 kcal/mol. For the secondary 15N KIE, the PI-FEP simulation yields an average value of 1.0083 ± 0.0016, which may be compared with experiment (1.0070 ± 0.0003) (Rishavy & Cleland, 2000).
Table 1.
Computed and Experimental Primary 12C/13C and Secondary 14N/15N Kinetic Isotope Effects for the Decarboxylation Reaction of N-Methyl Picolinate in Water at 25°C
| 12k/13k | 14k/15k | |
|---|---|---|
| Exp (25°C) | 1.0281 ± 0.0003 | 1.0070 ± 0.0003 |
| PI-QTST | 1.0346 ± 0.8773 | 1.0067 ± 0.8862 |
| PI-FEP | 1.0345 ± 0.0028 | 1.0083 ± 0.0016 |
Fig. 1.
Computed nuclear quantum effects along the potential of mean force for the decarboxylation reaction of N-methyl picolinate ion in water. 13C denotes isotope substitution at the carboxyl carbon position.
Fig. 2.
Computed ratio of quantum partition function between 12C and 13C isotope substitutions at the carboxyl carbon position along the centroid reaction coordinate for the decarboxylation of N-methyl picolinate in water.
This example shows that both the accuracy and the precision of the computed KIE using the PI-FEP method are of similar magnitude in comparison with experiment. This cannot be said with alternative simulation approaches applied to enzyme systems.
3.2 The RGM and Swain–Schaad Exponent
Tunneling in chemical reactions is of great interest both for chemical processes and for enzyme catalysis. However, it is not easy to separate tunneling from other nuclear quantum effects such as zero-point energy. The effect of a second isotope substitution on KIE, also called the rule of geometric mean (RGM), is often used to provide insights on tunneling contributions to a chemical process:
| (20) |
where the superscripts indicate secondary sites, and the subscripts denote primary positions. It was originally derived at high temperature limit with small quantum tunneling contribution (Bigeleisen, 1955 #6990), and it has been shown to have negligible deviations on model systems using semiclassical TST (Saunders, 1985). If , it implies that there is no isotope effect from a second site on the measured KIE at the first site, and Eq. (20) can be rearranged as follows
| (21) |
or equivalently,
| (22) |
Eq. (22) shows that if RGM holds, the total KIE will be the product of the individual primary and secondary KIEs, or the change in activation free energy is additive. Deviation or the observation of RGM breakdown is often used as a measure of the extent of tunneling in a given system (Huskey, 2006).
Another widely used indicator for tunneling is the so-called Swain–Schaad exponent (Swain, Stivers, Reuwer, & Schaad, 1958), which is expressed below using the notation of Huskey (2006),
| (23) |
| (24) |
These equations assume that the isotope effects are determined solely by the change in the zero-point energy from the mode corresponding to the reaction coordinate without tunneling. Studies have shown that the value of nHD for primary KIEs is typically in the range of 1.43–1.45 (Huskey, 2006). Deviations from these values are thought to be indicative of presence of tunneling (Cha, Murray, & Klinman, 1989).
The Swain–Schaad exponent in Eqs. (23) and (24) are restricted to isotope substitutions on a single site, primary KIEs as indicated (but certainly possible using secondary KIEs). It turns out that mixed Swain–Schaad exponents from both primary and secondary isotope substitutes are more sensitive which have been generally favored for assessing tunneling (Swain et al., 1958).
| (25) |
| (26) |
The first equation is the primary Swain–Schaad exponent, which reflects the secondary isotope effects on primary KIEs. The use of different primary KIEs, H/T vs D/T is to increase the magnitude of the exponent. The second equation describes a similar relationship for the secondary KIEs. Semiclassical arguments dictate that values of the mixed Swain–Schaad exponents greater than 3.3 are strong indication that tunneling contribution is significant (Cha et al., 1989).
Here, we use the proton abstraction reaction of nitroalkane by acetate ion in aqueous solution to illustrate the above phenomena or tunneling indicators. Interestingly, the reaction itself is a classic example that shows an unusual Brønsted relationship in water, known as the nitroalkane anomaly (Bernasconi, 1992; Bordwell & Boyle, 1972; Kresge, 1974). This process is also catalyzed by the nitroalkane oxidase (NAO) in the initial step of the oxidation of nitroalkanes (Valley & Fitzpatrick, 2003), which will be addressed in Section 3.3.
Summarized in Table 2 are the computed primary and secondary KIEs for D and T substitutions (Gao et al., 2008; Major & Gao, 2007; Major et al., 2005). The computed H/D primary and secondary intrinsic KIEs are and , respectively. Experimentally, only the total effects where both primary and secondary hydrogen atoms are replaced by deuterium were determined (7.8 ± 0.1) (Valley & Fitzpatrick, 2004); the PI-FEP result is (Valley & Fitzpatrick, 2004). Interestingly, the RGM of Eq. (22) yields a value of 8.88 (6.63 × 1.34). This gives a ratio of over the actual computed value (8.31). Another way of interpreting the results is that there is a secondary KIE of 1.07 on the primary KIEs according to Eq. (20). These values are reasonably close to unity, therefore, there is a rather small nonadditive effect (in free energy terms), or tunneling contribution, in the proton abstraction in solution.
Table 2.
Computed Primary (1 degree) and Secondary (2 degree) Kinetic Isotope Effects, and Computed and Experimental Total Deuterium Isotope Effects for the Proton Transfer from Nitroethane to Asp402 in NAO and to Acetate Ion in Water
| Primary KIE |
|
|
|
|||
| H2O | 6.63 ± 0.31 | 13.0 ± 1.0 | 2.17 ± 0.04 | |||
| NAO | 8.36 ± 0.58 | 18.1 ± 2.4 | 2.38 ± 0.05 | |||
| Secondary KIE |
|
|
|
|||
| H2O | 1.340 ± 0.132 | 1.375 ± 0.183 | 1.096 ± 0.048 | |||
| NAO | 1.213 ± 0.150 | 1.229 ± 0.209 | 1.050 ± 0.025 | |||
|
Total
|
Calc. | Expt. | ||||
| H2O | 8.3 ± 1.1 | 7.8 ± 0.1 | ||||
| NAO | 10.1 ± 1.4 | 9.2 ± 0.4 |
Subscripts and superscripts are used to specify the rate constant for isotope substitutions at the primary and secondary position, respectively.
Alternatively, single-site Swain–Schaad exponents can be calculated for primary KIE at a value of , and for secondary KIE at ; these values are close to the semiclassical limits. It is interesting to note that the exponents, and , for D/T ratios are rather large, at values of 3.8 and 12.3, respectively, which exhibit a significant deviation from the semiclassical limit, particularly on secondary KIEs. The latter tends to have greater computational errors because of the small free energy difference. Mixed-site Swain–Schaad exponents, which is favored by experimentalists, can also be determined using the data in Table 2, for a primary exponent of , and for a secondary exponent of . These results are again close to the semiclassical limit, suggesting also small tunneling contributions in the proton abstraction of nitroethane in aqueous solution.
3.3 NAO: An Enzyme Enhancing Nuclear Quantum Effects
The proton abstraction of nitroethane is catalyzed by the flavoenzyme NAO, which accelerates the proton transfer by a factor of 109 relative to the uncatalyzed reaction in water (Valley & Fitzpatrick, 2004). Valley and Fitzpatrick reported a KIE of 9.2 for the dideuterated substrate [1,1-2H] nitroethane by NAO, noticeably greater than that in water (7.8) (Valley & Fitzpatrick, 2004; Valley, Tichy, & Fitzpatrick, 2005). Here, we provide an example, revealing that the enzyme NAO has been optimized to enhance nuclear quantum effects relative to that of the identical, uncatalyzed process in water.
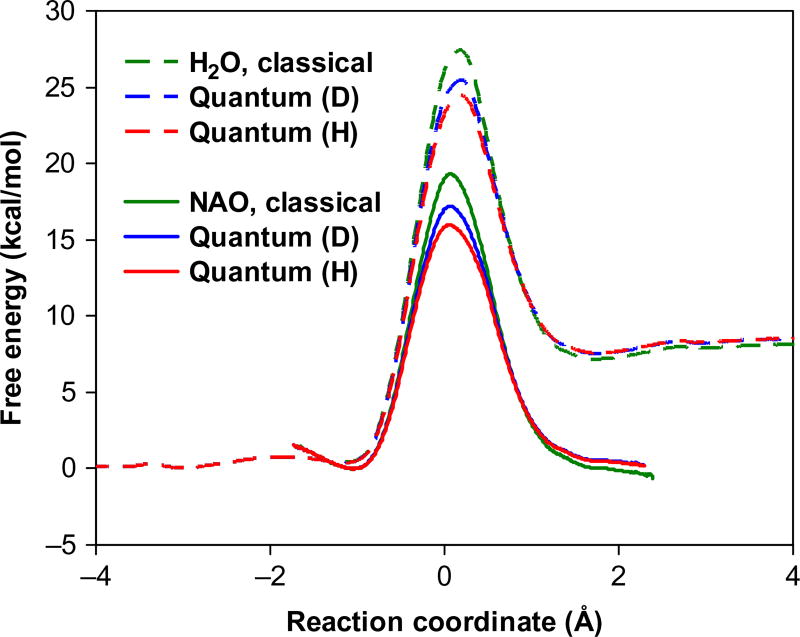
The same combined QM/MM PES for the aqueous reaction described in Section 3.2 was used to model the NAO catalysis (Gao & Xia, 1992; Major et al., 2005), and the PI-FEP approach was applied to model the corresponding nuclear quantum effects. Thus, both the electronic structure of the reacting system and the nuclear dynamics are treated at an equal footing by quantum mechanics. It is interesting to note that a parallel computational and X-ray crystallographic study resulted in an identical Michaelis complex structure, which was used in the enzyme simulation (Major et al., 2009). The computed centroid PMFs from PI-FEP coupled with UM simulations in NAO and in water are shown in Fig. 3. The centroid reaction coordinate is defined as the difference between the breaking (C–H) and forming (H–O) bond distances. The computed free energies of activation are 15.9 and 24.4 kcal/mol for the enzymatic and the uncatalyzed reaction in water, respectively, in agreement with experimental results (14.0 and 24.8 kcal/mol) (Valley & Fitzpatrick, 2004).
Fig. 3.
Classical (blue) and quantum mechanical potential of mean force for the proton (red) and deuteron (green) transfer from nitroethane to acetate ion in water (dashed curves), and to Asp402 (solid curves) in the active site of nitroalkane oxidase.
The results in Table 2 and Fig. 3 reveal a number of findings, supporting the conclusion that the NAO-catalyzed process has greater nuclear quantum effects that the corresponding uncatalyzed reaction in water (Major et al., 2009). First, the double averaging strategy in the PI-FEP method allows us to determine both classical and quantum mechanical free energy barriers. Fig. 3 shows that the classical barrier in the enzyme active site is lowered more (−3.4 kcal/mol) than that of the uncatalyzed reaction in water (−3.0 kcal/mol), due to nuclear quantum effects (Major et al., 2009). Second, the difference in quantum effects between proton and deuteron transfer is more significant for the enzymatic reaction than the uncatalyzed one as indicated by the primary H/D KIE (8.4 vs 6.6). Third, both experiment (9.2 vs 7.8) and computation (10.1 vs 8.3) show enhanced total KIEs in the enzyme over that in water. Fourth, the mixed Swain–Schaad exponent for the enzymatic reaction is greater than the semiclassical limit without tunneling and it is increased for the enzyme process (4.3 vs 3.5 in water). Finally, the tunneling transmission coefficient was found to be about three times greater for the enzyme reaction than the model reaction in water from another analysis employing an entirely different approach, namely EA-VTST/MT (Alhambra et al., 2001; Gao & Truhlar, 2002; Pu et al., 2006) (ensemble-averaged variational TST with multidimensional tunneling).
Analyses of the tunneling paths in EA-VTST revealed that the origin for the difference is due to a narrowing effect in the effective potential for tunneling in the enzyme than that in aqueous solution (Major et al., 2009). These studies demonstrate that differential quantum tunneling contributions are utilized in certain enzymatic catalysis as illustrated by NAO.
3.4 Protein Dynamics on Enzymatic KIEs
The connection between protein dynamics and enzyme activity is an intriguing question that has been actively debated. Of course, it is clear that protein dynamic fluctuations are essential for their biological functions; it is of interest to understand the mechanism by which protein dynamics affects enzyme kinetics. In this example, we show the effect of amino acid mutations that quench protein dynamic fluctuations in going from the Michaelis complex to the transition state on enzyme kinetics.
Dihydrofolate reductase (DHFR) is a small, flexible protein with a relatively large cofactor, nicotinamide adenine dinucleotide phosphate (NADPH), and a rather large substrate, 7,8-dihydrofolate (DHF). This interesting combination results in a protein ternary complex that is dynamically flexible. For example, NMR experiments established that conformational changes of several flexible loops in the protein play critical roles in ligand specificity and catalytic turnover (Bhabha et al., 2011; Boehr, McElheny, Dyson, & Wright, 2006, 2010; Oyeyemi et al., 2011, 2010). The double amino acid mutation of M42W and G121V as well as other replacements, which are remote from the catalytic center, can have profound, nonadditive effects on reaction rate, activation parameters, and the temperature dependence of KIE (Carroll et al., 2012; Loveridge, Behiry, Guo, & Allemann, 2012; Mauldin & Lee, 2010; Mauldin, Sapienza, Petit, & Lee, 2012; Rajagopalan, Lutz, & Benkovic, 2002; Swanwick, Shrimpton, & Allemann, 2004; Wang, Goodey, Benkovic, & Kohen, 2006; Watney, Agarwal, & Hammes-Schiffer, 2003; Wong, Selzer, Benkovic, & Hammes-Schiffer, 2005).
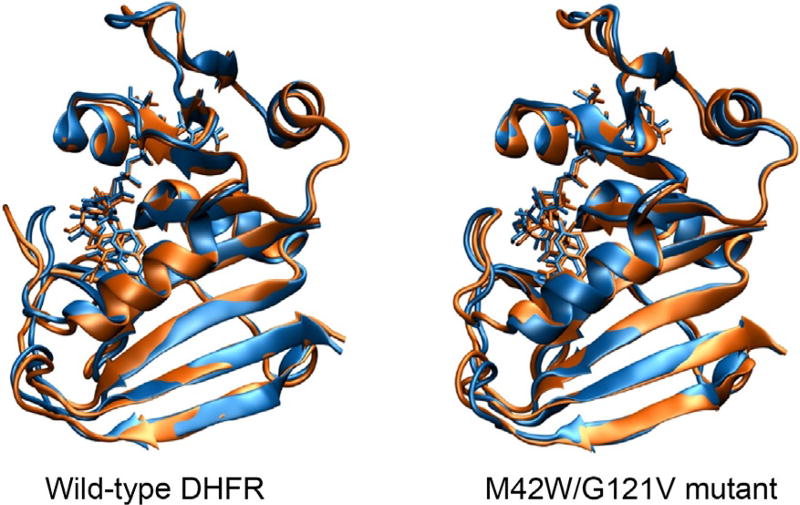
Using a QM/MM methodology established for the DHFR reaction (Garcia-Viloca et al., 2004, 2003; Pu, Ma, Gao, & Truhlar, 2005; Truhlar et al., 2002), we obtained the potentials of mean force for the hydride transfer from NADPH to DHF catalyzed by wild-type (wt)-DHFR and the M42W/G121V double mutant (dm)-DHFR at 5°C, 25°C, and 45°C. We obtained a free energy of activation of 16.4 kcal/mol for the hydride transfer in wt-DHFR, in agreement with experiment (16.7 kcal/mol) (Wang et al., 2006), whereas the activation free energy is increased by 1.2 kcal/mol in the M42W/G121V mutant, somewhat smaller than the corresponding experimental value (2.3 kcal/mol). Decomposition of the activation free energies into enthalpy and entropy contributions reveals that the double mutation significantly lowers the entropy of activation by −18.2 cal/K mol from computation and −13.2 cal/K mol from experiment (Fan et al., 2013). Analyses of the dynamic fluctuations and structural changes, we attribute the decreased dynamic flexibility during the catalyzed process, as expressed in kinetic parameters, to the annihilation of the Met20 loop motions at the transition state and the product state in the double mutant (Fig. 4).
Fig. 4.
Superposition comparison of snapshots of the Michaelis complex (blue) and transition state (brown) structures for the wild-type enzyme dihydrofolate reductase (left) and the M42W/G121V double mutant (right).
The altered Met20 loop dynamics, resulting in decreased entropy of activation in the G121V/M42W double mutation, is also reflected in the measured and computed KIEs. Wild-type Escherichia coli DHFR exhibits a temperature-independent KIE for the hydride transfer step (Sikorski et al., 2004). However, it becomes temperature dependent for the hydride transfer in M42W/G121V dm-DHFR (Wang et al., 2006). In fact, a large number of enzymes have been found to show temperature independence of KIEs in their optimal operating temperature range, but the KIEs are changed to temperature-dependent outside this temperature range, or as a result of mutations (Nagel & Klinman, 2006, 2009). Several studies have proposed that the wild-type enzyme has evolved to optimize the average donor– acceptor distance for tunneling, resulting in mass-independent thermal activation (Nagel & Klinman, 2006, 2009; Roston, Cheatum, & Kohen, 2012; Stojkovic, Perissinotti, Willmer, Benkovic, & Kohen, 2012; Wang et al., 2006).
Our study showed that there are two major contributions to the overall nuclear quantum effects, responsible for the observed KIEs: the change in quantum vibrational free energy, predominantly zero-point effects, and tunneling (Gao & Truhlar, 2002; Pu et al., 2006, 2005; Truhlar et al., 2002). For the hydride transfer catalyzed by DHFR where the observed intrinsic primary KIE is only about 3 both in the wt-DHFR and in mutants (Loveridge et al., 2012; Sikorski et al., 2004; Wang et al., 2006), it would be important for a mechanism to also account for the change in zero-point vibrational energy. Using EA-VTST/MT (Alhambra et al., 2001; Gao & Truhlar, 2002), we identified two general features responsible for the observed temperature independence of KIEs in wt-DHFR (Pu et al., 2005). First, we found that the location of the transition state for the hydride transfer coordinate is slightly shifted at different temperatures (Pu et al., 2005). Consequently, the difference in vibrational energy between H-transfer and D-transfer is increased at a higher temperature, resulting in a nearly temperature invariant Boltzmann factor. Second, the tunneling potential becomes narrower at higher temperature and a small increase in the tunneling transmission factor, also giving rise to a temperature insensitive effect.
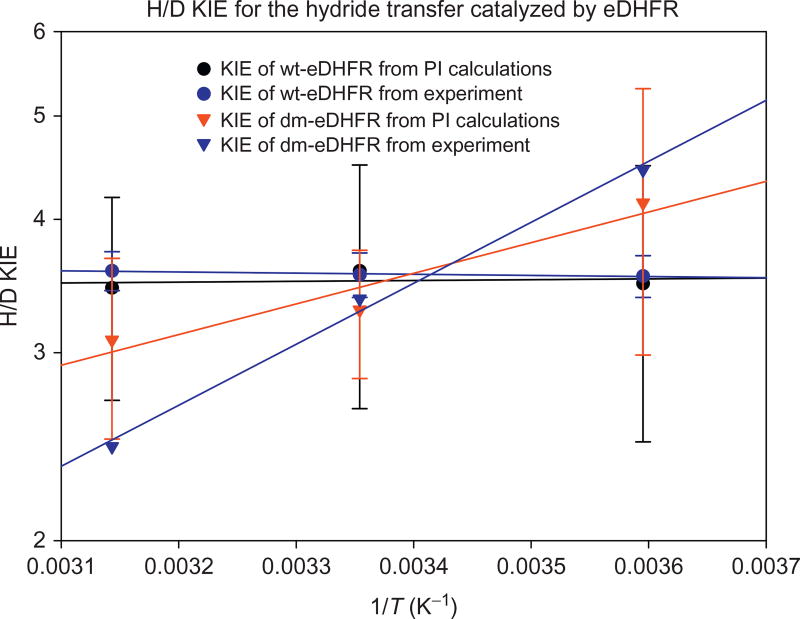
The temperature dependence of the H/D primary KIE for the hydride transfer in the M42W/G121 dm-DHFR was examined using PI-FEP simulations (Fan et al., 2013). Unlike the EA-VTST approach (Pu et al., 2005), vibrational free energy and nuclear tunneling are not separable in path-integral simulations, but the total nuclear quantum effects as well as KIE are obtained directly from dynamics simulations. Arrhenius plots of the calculated and experimental H/D KIEs are shown in Fig. 5. Good accord was obtained for the wild-type DHFR both in the absolute value of KIEs and in the temperature-independent behavior. The agreement for the M42W/G121V double mutant is also good, although the slope of the temperature dependence plot is smaller than that measured experimentally. Since the average donor–acceptor distances are not different between wt-DHFR and the M42W/G121V mutant, suggesting similar zero-point effects, we attribute the change is temperature dependence of the KIEs in the double mutant to altered PES for tunneling. This is consistent with structural analyses and computed change in entropy of activation for the wild-type and double mutant DHFR.
Fig. 5.
Computed and experimental H/D primary kinetic isotope effects for the hydride transfer process catalyzed by wild-type and M42W/G121V mutant dihydrofolate reductase at different temperatures.
4. CONCLUDING REMARKS
We presented a method for incorporating quantum mechanics into enzyme kinetics modeling, in which (1) the PES is represented by combined QM/MM methods to describe bond forming and breaking processes and (2) PI-FEP theory is used to directly determine the ratio of quantum mechanical partition functions for different isotopologs in a single simulation. In the latter simulation approach, we further employ a double averaging strategy, separate the quantum mechanical path-integral simulation exactly into two separate calculations, one corresponding to classical molecular dynamics simulation of the centroid coordinates, and another involving free-particle path-integral sampling over the classical, centroid positions. An integrated centroid path-integral free energy perturbation and umbrella sampling (PI-FEP/UM, or simply, PI-FEP) method along with a bisection sampling procedure was summarized, which provides an accurate, fast convergent method for computing KIEs for chemical reactions in solution and in enzymes. These methods are illustrated by applications to the decarboxylation reaction of N-methyl picolinate in water to highlight the precision of the PI-FEP method contrasted to conventional approaches, the deprotonation process of nitroethane in water to highlight the RGM and Swain–Schaad exponent for assessing tunneling, the same deprotonation process catalyzed by NAO to reveal an enzyme that has been evolved to enhance nuclear quantum effects, and the effects of protein dynamics on temperature dependence of KIEs in DHFR. These examples show that the incorporation of quantum mechanical effects is essential for enzyme kinetics simulations, and our computational approaches provided insights on the importance of nuclear quantum effects.
Acknowledgments
This work has been supported by the National Institutes of Health. The author wishes to thank his coworkers whose name are shown in references cited.
References
- Alhambra C, Corchado J, Sanchez ML, Garcia-Viloca M, Gao J, Truhlar DG. Canonical variational theory for enzyme kinetics with the protein mean force and multidimensional quantum mechanical tunneling dynamics. Theory and application to liver alcohol dehydrogenase. The Journal of Physical Chemistry. B. 2001;105:11326–11340. [Google Scholar]
- Bernasconi CF. The principle of nonperfect synchronization: More than a qualitative concept? Accounts of Chemical Research. 1992;25:9–16. [Google Scholar]
- Bhabha G, Lee J, Ekiert DC, Gam J, Wilson IA, et al. A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science. 2011;332:234–238. doi: 10.1126/science.1198542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigeleisen J. Statistical mechanics of isotopic systems with small quantum corrections. I. General considerations and the rule of the geometric mean. The Journal of Chemical Physics. 1955;23:2264. [Google Scholar]
- Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- Boehr DD, McElheny D, Dyson HJ, Wright PE. Millisecond timescale fluctuations in dihydrofolate reductase are exquisitely sensitive to the bound ligands. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:1373–1378. doi: 10.1073/pnas.0914163107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bordwell FG, Boyle WJ., Jr Acidities, Broensted coefficients, and transition state structures for 1-arylnitroalkanes. Journal of the American Chemical Society. 1972;94:3907–3911. [Google Scholar]
- Byun K, Mo Y, Gao J. New insight on the origin of the unusual acidity of Meldrum’s acid from ab initio and combined QM/MM simulation study. Journal of the American Chemical Society. 2001;123:3974–3979. doi: 10.1021/ja001369r. [DOI] [PubMed] [Google Scholar]
- Cao J, Voth GA. The formulation of quantum statistical mechanics based on the Feynman path centroid density. V. Quantum instantaneous normal mode theory of liquids. The Journal of Chemical Physics. 1994;101:6184–6192. [Google Scholar]
- Cao J, Voth GA. A unified framework for quantum activated rate processes. I. General theory. The Journal of Chemical Physics. 1996;105:6856–6870. [Google Scholar]
- Car R, Parrinello M. Unified approach for molecular dynamics and density-functional theory. Physical Review Letters. 1985;55:2471–2474. doi: 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
- Carroll MJ, Mauldin RV, Gromova AV, Singleton SF, Collins EJ, Lee AL. Evidence for dynamics in proteins as a mechanism for ligand dissociation. Nature Chemical Biology. 2012;8:246–252. doi: 10.1038/nchembio.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceperley DM. Path integrals in the theory of condensed helium. Reviews of Modern Physics. 1995;67:279–355. [Google Scholar]
- Ceriotti M, Markland TE. Efficient methods and practical guidelines for simulating isotope effects. The Journal of Chemical Physics. 2013;138:014112. doi: 10.1063/1.4772676. [DOI] [PubMed] [Google Scholar]
- Cha Y, Murray CJ, Klinman JP. Hydrogen tunneling in enzyme reactions. Science. 1989;243:1325–1330. doi: 10.1126/science.2646716. [DOI] [PubMed] [Google Scholar]
- Cui Q, Elstner M, Kaxiras E, Frauenheim T, Karplus M. AQM/MM implementation of the self-consistent charge density functional tight binding (SCC-DFTB) method. The Journal of Physical Chemistry. B. 2001;105:569–585. [Google Scholar]
- Dewar MJS, Zoebisch EG, Healy EF, Stewart JJP. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. Journal of the American Chemical Society. 1985;107:3902–3909. [Google Scholar]
- Dzierlenga MW, Antoniou D, Schwartz SD. Another look at the mechanisms of hydride transfer enzymes with quantum and classical transition path sampling. Journal of Physical Chemistry Letters. 2015;6:1177–1181. doi: 10.1021/acs.jpclett.5b00346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Y, Cembran A, Ma S, Gao J. Connecting protein conformational dynamics with catalytic function as illustrated in dihydrofolate reductase. Biochemistry. 2013;52:2036–2049. doi: 10.1021/bi301559q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Ramos A, Miller JA, Klippenstein SJ, Truhlar DG. Modeling the kinetics of bimolecular reactions. Chemical Reviews. 2006;106:4518–4584. doi: 10.1021/cr050205w. [DOI] [PubMed] [Google Scholar]
- Feynman RP, Hibbs AR. Quantum mechanics and path integrals. New York: McGraw-Hill; 1965. [Google Scholar]
- Field MJ, Bash PA, Karplus M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. Journal of Computational Chemistry. 1990;11:700–733. [Google Scholar]
- Freindorf M, Gao J. Optimization of the Lennard-Jones parameters for a combined ab initio quantum mechanical and molecular mechanical potential using the 3–21G basis set. Journal of Computational Chemistry. 1996;17:386–395. [Google Scholar]
- Gao J. Absolute free energy of solvation from Monte Carlo simulations using combined quantum and molecular mechanical potentials. The Journal of Physical Chemistry. 1992;96:537–540. [Google Scholar]
- Gao J. Computation of intermolecular interactions with a combined quantum mechanical and classical approach. ACS Symposium Series. 1994a;569:8–21. [Google Scholar]
- Gao J. Monte Carlo quantum mechanical-configuration interaction and molecular mechanics simulation of solvent effects on the n.fwdarw.pi.* blue shift of acetone. Journal of the American Chemical Society. 1994b;116:9324–9328. [Google Scholar]
- Gao J. Methods and applications of combined quantum mechanical and molecular mechanical potentials. In: Lipkowitz KB, Boyd DB, editors. Reviews in computational chemistry. New York: VCH; 1995a. pp. 119–185. [Google Scholar]
- Gao J. An automated procedure for simulating chemical reactions in solution. Application to the decarboxylation of 3-carboxybenzisoxazole in water. Journal of the American Chemical Society. 1995b;117:8600–8607. [Google Scholar]
- Gao J. Hybrid quantum mechanical/molecular mechanical simulations: An alternative avenue to solvent effects in organic chemistry. Accounts of Chemical Research. 1996;29:298–305. [Google Scholar]
- Gao J, Byun K. Solvent effects on the n->pi* transition of pyrimidine in aqueous solution. Theoretical Chemistry Accounts. 1997;96:151–156. [Google Scholar]
- Gao J, Ma S, Major DT, Nam K, Pu J, Truhlar DG. Mechanisms and free energies of enzymatic reactions. Chemical Reviews. 2006;106:3188–3209. doi: 10.1021/cr050293k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J, Truhlar DG. Quantum mechanical methods for enzyme kinetics. Annual Review of Physical Chemistry. 2002;53:467–505. doi: 10.1146/annurev.physchem.53.091301.150114. [DOI] [PubMed] [Google Scholar]
- Gao JL, Truhlar DG, Wang YJ, Mazack MJM, Loffler P, et al. Explicit polarization: A quantum mechanical framework for developing next generation force fields. Accounts of Chemical Research. 2014;47:2837–2845. doi: 10.1021/ar5002186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J, Wong K-Y, Major DT. Combined QM/MM and path integral simulations of kinetic isotope effects in the proton transfer reaction between nitroethane and acetate ion in water. Journal of Computational Chemistry. 2008;29:514–522. doi: 10.1002/jcc.20810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J, Xia X. A prior evaluation of aqueous polarization effects through Monte Carlo QM-MM simulations. Science. 1992;258:631–635. doi: 10.1126/science.1411573. [DOI] [PubMed] [Google Scholar]
- Gao JL, Zhang JZH, Houk KN. Beyond QM/MM: Fragment quantum mechanical methods. Accounts of Chemical Research. 2014;47:2711. doi: 10.1021/ar500293u. [DOI] [PubMed] [Google Scholar]
- Garcia-Viloca M, Gao J, Karplus M, Truhlar DG. How enzymes work: Analysis by modern rate theory and computer simulations. Science. 2004;303:186–195. doi: 10.1126/science.1088172. [DOI] [PubMed] [Google Scholar]
- Garcia-Viloca M, Truhlar DG, Gao J. Importance of substrate and cofactor polarization in the active site of dihydrofolate reductase. Journal of Molecular Biology. 2003;327:549–560. doi: 10.1016/s0022-2836(03)00123-2. [DOI] [PubMed] [Google Scholar]
- Gaus M, Cui QA, Elstner M. DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB) Journal of Chemical Theory and Computation. 2011;7:931–948. doi: 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillan MJ. The quantum simulation of hydrogen in metals. Philosophical Magazine A. 1988;58:257–283. doi: 10.1103/PhysRevLett.58.563. [DOI] [PubMed] [Google Scholar]
- Habershon S, Manolopoulos DE, Markland TE, Miller TF. Ring-polymer molecular dynamics: Quantum effects in chemical dynamics from classical trajectories in an extended phase space. Annual Review of Physical Chemistry. 2013;64:387–413. doi: 10.1146/annurev-physchem-040412-110122. [DOI] [PubMed] [Google Scholar]
- Hernandez R, Cao J, Voth GA. On the Feynman path centroid density as a phase space distribution in quantum statistical mechanics. The Journal of Chemical Physics. 1995;103:5018–5026. [Google Scholar]
- Huskey WP. Multiple-isotope probes of hydrogen tunneling. In: Hynes JT, Klinman JP, Limbach HH, Schowen RL, editors. Hydrogen-transfer reactions. Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA; 2006. p. 1285. [Google Scholar]
- Hwang JK, Warshel A. A quantized classical path approach for calculations of quantum mechanical rate constants. The Journal of Physical Chemistry. 1993;97:10053–10058. [Google Scholar]
- Hwang J-K, Warshel A. How important are quantum mechanical nuclear motions in enzyme catalysis? Journal of the American Chemical Society. 1996;118:11745–11751. [Google Scholar]
- Jang S, Voth GA. A relationship between centroid dynamics and path integral quantum transition state theory. The Journal of Chemical Physics. 2000;112:8747–8757. Erratum: 2001. 114: 1944. [Google Scholar]
- Klinman JP, Kohen A. Evolutionary aspects of enzyme dynamics. The Journal of Biological Chemistry. 2014;289:30205–30212. doi: 10.1074/jbc.R114.565515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohen A, Limbach HH, editors. Isotope effects in chemistry and biology. New York: Taylor & Francis Group, CRC Press; 2005. [Google Scholar]
- Kresge A. The nitroalkane anomaly. Canadian Journal of Chemistry. 1974;52:1897–1903. [Google Scholar]
- Layfield JP, Hammes-Schiffer S. Hydrogen tunneling in enzymes and biomimetic models. Chemical Reviews. 2014;114:3466–3494. doi: 10.1021/cr400400p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y-L, Gao J. Solvatochromic shifts of the n->pi* transition of acetone from steam vapor to ambient aqueous solution: A combined configuration interaction QM/MM simulation study incorporating solvent polarization. Journal of Chemical Theory and Computation. 2007;3:1484–1493. doi: 10.1021/ct700058c. [DOI] [PubMed] [Google Scholar]
- Lin Y-L, Gao J, Rubinstein A, Major DT. Molecular dynamics simulations of the intramolecular proton transfer and carbanion stabilization in the pyridoxal 5′-phosphate dependent enzymes l-dopa decarboxylase and alanine racemase. Biochimica et Biophysica Acta (BBA)—Proteins and Proteomics. 2011;1814:1438–1446. doi: 10.1016/j.bbapap.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu MY, Wang YJ, Chen YK, Field MJ, Gao JL. QM/MM through the 1990s: The first twenty years of method development and applications. Israel Journal of Chemistry. 2014;54:1250–1263. doi: 10.1002/ijch.201400036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loveridge EJ, Behiry EM, Guo JN, Allemann RK. Evidence that a ‘dynamic knockout’ in Escherichia coli dihydrofolate reductase does not affect the chemical step of catalysis. Nature Chemistry. 2012;4:292–297. doi: 10.1038/nchem.1296. [DOI] [PubMed] [Google Scholar]
- Major DT, Gao J. Implementation of the bisection sampling method in path integral simulations. Journal of Molecular Graphics & Modelling. 2005;24:121–127. doi: 10.1016/j.jmgm.2005.04.002. [DOI] [PubMed] [Google Scholar]
- Major DT, Gao J. An integrated path integral and free-energy perturbation-umbrella sampling method for computing kinetic isotope effects of chemical reactions in solution and in enzymes. Journal of Chemical Theory and Computation. 2007;3:949–960. doi: 10.1021/ct600371k. [DOI] [PubMed] [Google Scholar]
- Major DT, Garcia-Viloca M, Gao J. Path integral simulations of proton transfer reactions in aqueous solution using combined QM/MM potentials. Journal of Chemical Theory and Computation. 2006;2:236–245. doi: 10.1021/ct050257t. [DOI] [PubMed] [Google Scholar]
- Major DT, Heroux A, Orville AM, Valley MP, Fitzpatrick PF, Gao J. Differential quantum tunneling contributions in nitroalkane oxidase catalyzed and the uncatalyzed proton transfer reaction. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:20736–20739. doi: 10.1073/pnas.0911416106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Major DT, York DM, Gao J. Solvent polarization and kinetic isotope effects in nitroethane deprotonation and implications to the nitroalkane oxidase reaction. Journal of the American Chemical Society. 2005;127:16374–16375. doi: 10.1021/ja055881u. [DOI] [PubMed] [Google Scholar]
- Makarov DE, Topaler M. Quantum transition-state theory below the crossover temperature. Physical Review E: Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics. 1995;52:178–188. doi: 10.1103/physreve.52.178. [DOI] [PubMed] [Google Scholar]
- Marsalek O, Chen PY, Dupuis R, Benoit M, Meheut M, et al. Efficient calculation of free energy differences associated with isotopic substitution using path-integral molecular dynamics. Journal of Chemical Theory and Computation. 2014;10:1440–1453. doi: 10.1021/ct400911m. [DOI] [PubMed] [Google Scholar]
- Maseras F, Morokuma K. IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. Journal of Computational Chemistry. 1995;16:1170–1179. [Google Scholar]
- Mauldin RV, Lee AL. Nuclear magnetic resonance study of the role of M42 in the solution dynamics of Escherichia coli dihydrofolate reductase. Biochemistry. 2010;49:1606–1615. doi: 10.1021/bi901798g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauldin RV, Sapienza PJ, Petit CM, Lee AL. Structure and dynamics of the G121V dihydrofolate reductase mutant: Lessons from a transition-state inhibitor complex. PloS One. 2012;7:e33252. doi: 10.1371/journal.pone.0033252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merz KM. Using quantum mechanical approaches to study biological systems. Accounts of Chemical Research. 2014;47:2804–2811. doi: 10.1021/ar5001023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messina M, Schenter GK, Garrett BC. Centroid-density, quantum rate theory: Variational optimization of the dividing surface. The Journal of Chemical Physics. 1993;98:8525–8536. [Google Scholar]
- Messina M, Schenter GK, Garrett BC. A variational centroid density procedure for the calculation of transmission coefficients for asymmetric barriers at low temperature. The Journal of Chemical Physics. 1995;103:3430–3435. [Google Scholar]
- Mills G, Schenter GK, Makarov DE, Jonsson H. Generalized path integral based quantum transition state theory. Chemical Physics Letters. 1997;278:91–96. [Google Scholar]
- Nagel ZD, Klinman JP. Tunneling and dynamics in enzymatic hydride transfer. Chemical Reviews. 2006;106:3095–3118. doi: 10.1021/cr050301x. [DOI] [PubMed] [Google Scholar]
- Nagel ZD, Klinman JP. A 21(st) century revisionist’s view at a turning point in enzymology. Nature Chemical Biology. 2009;5:543–550. doi: 10.1038/nchembio.204. [DOI] [PubMed] [Google Scholar]
- Orozco M, Luque FJ, Habibollahzadeh D, Gao J. The polarization contribution to the free energy of hydration. The Journal of Chemical Physics. 1995;103:9112. Erratum to document cited in CA122:299891. [Google Scholar]
- Oyeyemi OA, Sours KM, Lee T, Kohen A, Resing KA, et al. Comparative hydrogen-deuterium exchange for a mesophilic vs thermophilic dihydrofolate reductase at 25°C: Identification of a single active site region with enhanced flexibility in the mesophilic protein. Biochemistry. 2011;50:8251–8260. doi: 10.1021/bi200640s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oyeyemi OA, Sours KM, Lee T, Resing KA, Ahn NG, Klinman JP. Temperature dependence of protein motions in a thermophilic dihydrofolate reductase and its relationship to catalytic efficiency. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:10074–10079. doi: 10.1073/pnas.1003678107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollock EL, Ceperley DM. Simulation of quantum many-body systems by path-integral methods. Physical Review B. 1984;30:2555–2568. [Google Scholar]
- Pu J, Gao J, Truhlar DG. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chemical Reviews. 2006;106:3140–3169. doi: 10.1021/cr050308e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pu J, Ma S, Gao J, Truhlar DG. Small temperature dependence of the kinetic isotope effect for the hydride transfer reaction catalyzed by Escherichia coli dihydrofolate reductase. Journal of Physical Chemistry B. 2005;109:8551–8556. doi: 10.1021/jp051184c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajagopalan PT, Lutz S, Benkovic SJ. Coupling interactions of distal residues enhance dihydrofolate reductase catalysis: Mutational effects on hydride transfer rates. Biochemistry. 2002;41:12618–12628. doi: 10.1021/bi026369d. [DOI] [PubMed] [Google Scholar]
- Rishavy MA, Cleland WW. Determination of the mechanism of orotidine 5′-monophosphate decarboxylase by isotope effects. Biochemistry. 2000;39:4569–4574. doi: 10.1021/bi000376p. [DOI] [PubMed] [Google Scholar]
- Rohrig UF, Guidoni L, Rothlisberger U. Chem Phys Chem. 2005;6:1836. doi: 10.1002/cphc.200500066. [DOI] [PubMed] [Google Scholar]
- Roston D, Cheatum CM, Kohen A. Hydrogen donor-acceptor fluctuations from kinetic isotope effects: A phenomenological model. Biochemistry. 2012;51:6860–6870. doi: 10.1021/bi300613e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders WH., Jr Calculations of isotope effects in elimination reactions. New experimental criteria for tunneling in slow proton transfers. Journal of the American Chemical Society. 1985;107:164–169. [Google Scholar]
- Schowen RL. Catalytic power and transition-state stabilization. In: Gandour RD, Schowen RL, editors. Transition states of biochemical processes. New York: Plenum Press; 1978. pp. 77–114. [Google Scholar]
- Schramm VL. Enzymatic transition state poise and transition state analogues. Accounts of Chemical Research. 2003;36:588–596. doi: 10.1021/ar0200495. [DOI] [PubMed] [Google Scholar]
- Senn HM, Thiel W. QM/MM methods for biomolecular systems. Angewandte Chemie International Edition. 2009;48:1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- Sikorski RS, Wang L, Markham KA, Rajagopalan PTR, Benkovic SJ, Kohen A. Tunneling and coupled motion in the Escherichia coli dihydrofolate reductase catalysis. Journal of the American Chemical Society. 2004;126:4778–4779. doi: 10.1021/ja031683w. [DOI] [PubMed] [Google Scholar]
- Singh UC, Kollman PA. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: Applications to the CH3Cl + Cl− exchange reaction and gas phase protonation of polyenes. Journal of Computational Chemistry. 1986;7:718–730. [Google Scholar]
- Sprik M, Klein ML, Chandler D. Staging: A sampling technique for the Monte Carlo evaluation of path integrals. Physical Review B. 1985;31:4234–4244. doi: 10.1103/physrevb.31.4234. [DOI] [PubMed] [Google Scholar]
- Stewart JJP. Optimization of parameters for semiempirical methods I. Method. Journal of Computational Chemistry. 1989;10:209–220. [Google Scholar]
- Stewart JJP. Application of localized molecular orbitals to the solution of semiempirical self-consistent field equations. International Journal of Quantum Chemistry. 1996;58:133–146. [Google Scholar]
- Stojkovic V, Perissinotti LL, Willmer D, Benkovic SJ, Kohen A. Effects of the donor-acceptor distance and dynamics on hydride tunneling in the dihydrofolate reductase catalyzed reaction. Journal of the American Chemical Society. 2012;134:1738–1745. doi: 10.1021/ja209425w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swain CG, Stivers EC, Reuwer JF, Schaad LJ. Use of hydrogen isotope effects to identify the attacking nucleophile in the enolization of ketones catalyzed by acetic acid. Journal of the American Chemical Society. 1958;80:5885–5893. [Google Scholar]
- Swanwick RS, Shrimpton PJ, Allemann RK. Pivotal role of Gly 121 in dihydrofolate reductase from Escherichia coli: The altered structure of a mutant enzyme may form the basis of its diminished catalytic performance. Biochemistry. 2004;43:4119–4127. doi: 10.1021/bi036164k. [DOI] [PubMed] [Google Scholar]
- Titmuss SJ, Cummins PL, Rendell AP, Bliznyuk AA, Gready JE. Comparison of linear-scaling semiempirical methods and combined quantum mechanical/molecular mechanical methods for enzymic reactions. II. An energy decomposition analysis. Journal of Computational Chemistry. 2002;23:1314–1322. doi: 10.1002/jcc.10122. [DOI] [PubMed] [Google Scholar]
- Truhlar DG, Gao J, Alhambra C, Garcia-Viloca M, Corchado J, et al. The incorporation of quantum effects in enzyme kinetics modeling. Accounts of Chemical Research. 2002;35:341–349. doi: 10.1021/ar0100226. [DOI] [PubMed] [Google Scholar]
- Valleau JP, Torrie GM. A guide to Monte Carlo for statistical mechanics: 2. Byways. In: Berne BJ, editor. Modern theoretical chemistry. New York: Plenum Press; 1977. pp. 169–194. [Google Scholar]
- Valley MP, Fitzpatrick PF. Reductive half-reaction of nitroalkane oxidase: Effect of mutation of the active site aspartate to glutamate. Biochemistry. 2003;42:5850–5856. doi: 10.1021/bi034061w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valley MP, Fitzpatrick PF. Comparison of enzymatic and non-enzymatic nitroethane anion formation: Thermodynamics and contribution of tunneling. Journal of the American Chemical Society. 2004;126:6244–6245. doi: 10.1021/ja0484606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valley MP, Tichy SE, Fitzpatrick PF. Establishing the kinetic competency of the cationic imine intermediate in nitroalkane oxidase. Journal of the American Chemical Society. 2005;127:2062–2066. doi: 10.1021/ja043542f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villa J, Warshel A. Energetics and dynamics of enzymatic reactions. The Journal of Physical Chemistry. B. 2001;105:7887–7907. [Google Scholar]
- Voth GA, Chandler D, Miller WH. Rigorous formulation of quantum transition state theory and its dynamical corrections. The Journal of Chemical Physics. 1989a;91:7749–7760. [Google Scholar]
- Voth GA, Chandler D, Miller WH. Time correlation function and path integral analysis of quantum rate constants. The Journal of Physical Chemistry. 1989b;93:7009–7015. [Google Scholar]
- Wang L, Fried SD, Boxer SG, Markland TE. Quantum delocalization of protons in the hydrogen-bond network of an enzyme active site. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:18454–18459. doi: 10.1073/pnas.1417923111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Goodey NM, Benkovic SJ, Kohen A. Coordinated effects of distal mutations on environmentally coupled tunneling in dihydrofolate reductase. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:15753–15758. doi: 10.1073/pnas.0606976103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel A, Levitt M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. Journal of Molecular Biology. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- Watney JB, Agarwal PK, Hammes-Schiffer S. Effect of mutation on enzyme motion in dihydrofolate reductase. Journal of the American Chemical Society. 2003;125:3745–3750. doi: 10.1021/ja028487u. [DOI] [PubMed] [Google Scholar]
- Wong KF, Selzer T, Benkovic SJ, Hammes-Schiffer S. Impact of distal mutations on the network of coupled motions correlated to hydride transfer in dihydrofolate reductase. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:6807–6812. doi: 10.1073/pnas.0408343102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong KY, Xu Y, Xu L. Review of computer simulations of isotope effects on biochemical reactions: From the Bigeleisen equation to Feynman’s path integral. Biochimica et Biophysica Acta. 2015;1854:1782–1794. doi: 10.1016/j.bbapap.2015.04.021. [DOI] [PubMed] [Google Scholar]
- Xie W, Orozco M, Truhlar DG, Gao J. X-Pol potential: An electronic structure-based force field for molecular dynamics simulation of a solvated protein in water. Journal of Chemical Theory and Computation. 2009;5:459–467. doi: 10.1021/ct800239q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwanzig R. High-temperature equation of state by a perturbation method. I. Non-polar gases. The Journal of Chemical Physics. 1954;22:1420–1426. [Google Scholar]