Quantile causal mediation analysis allowing longitudinal data

Abstract

Mediation analysis has mostly been conducted with mean regression models. With this approach modeling means, formulae for direct and indirect effects are based on changes in means, which may not capture effects that occur in units at the tails of mediator and outcome distributions. Individuals with extreme values of medical endpoints are often more susceptible to disease and can be missed if one investigates mean changes only. We derive the controlled direct and indirect effects of an exposure along percentiles of the mediator and outcome using quantile regression models and a causal framework. The quantile regression models can accommodate an exposure-mediator interaction and random intercepts to allow for longitudinal mediator and outcome. Because DNA methylation acts as a complex “switch” to control gene expression and fibrinogen is a cardiovascular factor, individuals with extreme levels of these markers may be more susceptible to air pollution. We therefore apply this methodology to environmental data to estimate the effect of air pollution, as measured by particle number, on fibrinogen levels through a change in interferon-gamma (IFN-γ) methylation. We estimate the controlled direct effect of air pollution on the q^th percentile of fibrinogen and its indirect effect through a change in the p^th percentile of IFN-γ methylation. We found evidence of a direct effect of particle number on the upper tail of the fibrinogen distribution. We observed a suggestive indirect effect of particle number on the upper tail of the fibrinogen distribution through a change in the lower percentiles of the IFN-γ methylation distribution.

1. Introduction

Mediation analysis aims to identify a direct effect of an exposure on an outcome and an indirect effect between the same exposure and outcome via a change in a mediator [1]. Scientists have recently developed and used mediation analysis tools in many disciplines, such as causal inference [2–6], social sciences [7,8], and epidemiological research [9–12]. The total effect decomposition (i.e., into a indirect effect via a mediator and a direct effect not through this mediator) allows one to investigate biological pathways and thus, disease mechanisms [13–15].

Mediation analysis has largely focused on mean regression models to define controlled direct, natural direct, and natural indirect effects. These estimands may not reflect effects that occur primarily in the tails of the distributions of the mediator and the outcome. We have illustrated that standard regression models for the outcome mean could miss effects in susceptible subgroups, that is, individuals with already extreme levels of mediator and/or outcome that are risk factors for disease [12, 16, 17]. Quantile regression is an estimation method that addresses this issue. If one chooses regression coefficients that minimize the sum of the absolute values of the residuals instead of the sum of squared residuals, the result is an estimate of covariate effects on the median, instead of the mean, of the outcome distribution. Quantile regression generalizes this approach by weighting the positive and negative residuals differently, which forces the regression line to other percentiles of the distribution, which is useful to examine the exposure-outcome relationship at different locations of the outcome distribution, especially when this relationship is not homogenous across quantiles of the outcome. This distribution-free approach, modeling quantiles of a distribution instead of the mean, has already been used successfully to describe: 1) how air pollution effects on cardiovascular markers are different across the distribution of these same cardiovascular markers [17], and 2) how air pollution and temperature exposures change the shape of DNA methylation distributions, an epigenetic outcome [12, 16]. In these recent papers, the authors identified susceptible subgroups and therefore allows one to provide more precise results for risk assessment in biomedicine.

Recent research has also identified epigenetics as an important molecular response to environmental pollutants [18–20]. Epigenetics refers to chromosome changes that influence gene expression without modifying the genetic code. The most frequently studied epigenetic mechanism is DNA methylation which involves methylation of cytosine in CpG pairs. Because DNA methylation often acts as a complex “switch” to control gene expression, individuals with extreme methylation level may be more susceptible to environmental exposures. This result has been suggested recently with air pollution [12] and temperature [16]. DNA methylation has been related to cardiovascular and pulmonary outcomes [21,22], that have, in turn, been associated with exposure to air pollution [23]. These findings raised interest for examining DNA methylation as an intermediate player in air pollution adverse responses [24,25].

The motivation of this paper is to study the mediated effects of air pollution on an cardiovascular marker via DNA methylation, but across the distributions of: 1) the mediator and 2) the outcome. To estimate these effects, we need to expand standard mediation methods and consider quantiles of mediators and outcomes as dependent variables. Mediation formulae based on quantiles of the outcome distribution have been derived [14, 26]. However, these formulae focuses mostly on mean changes in the mediator [14] or do not explicitly define the causal estimands as functions of potential outcomes [26]. In this manuscript, we define and derive the controlled direct and the indirect effects along the distribution of the outcome with two quantile regression models, one for the mediator and one for the outcome. We formalize our estimands using the potential outcome framework and allow for an exposure-mediator interaction in the model for the outcome. Because many observational studies collect longitudinal data, we also allow the mediator and outcome variables to be repeated measurements. This work generalizes previous work on mediation models now allowing for quantile estimation and longitudinal data [14,26–28].

Using a causal framework, we apply the quantile mediation model to an environmental health example in which we examine the effects of air pollution and methylation on the entire distribution of fibrinogen, a known coagulation marker. We hypothesize that individuals with higher fibrinogen levels may be more susceptible to air pollution and changes in methylation. In this manuscript, we estimate the indirect effect of particle number exposure on the fibrinogen distribution via a distributional change in interferon-gamma (IFN-γ) methylation and its direct effect not through IFN-γ methylation. While particle number is a marker for traffic-related air pollution, fibrinogen and IFN-γ are known to be cardiovascular markers.

2. Methods

2.1. Notations

This paper aims to define and derive the direct exposure effect on the distribution of an outcome and its indirect effect via a change in a given percentile of a mediator. We allow exposure-mediator interaction and repeated mediator and outcome measurements from a longitudinal cohort. Let A_ij, M_ij, and Y_ij represent the observed exposure, mediator, and outcome of interest for an individual i at a visit j, respectively. Let ψ_p (M_ij) be the p^th percentile of the observed M_ij distribution and let ζ_q (Y_ij) be the q^th percentile of the observed Y_ij distribution. Let ${\mathrm{M}}_{ij}^a$ denote the potential mediator that would have been observed if A were set to a and let ${\mathrm{Y}}_{i,j}^{a,m}$ represent the potential outcome that would have been observed if A were set to a and M were set to the value m. Let ${\mathrm{\Psi }}_p(M_{ij}^a)$ be the p^th percentile of the distribution of the potential outcome M_ij distribution when A_ij is set to a and let ${\xi }_q(Y_{ij}^{a,m})$ denote the q^th percentile of the distribution of the potential outcome Y_ij distribution when A_ij is set to a and M_ij is set to m. Thus, ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}\right)}\right)$ corresponds to the q^th percentile of the potential outcome distribution that would have been observed if A_ij were set to a and if M_ij were set to the value of the p^th percentile of the distribution of the potential outcome M_ij if A_ij were set to a*. Contrasts of these percentiles will be used to define direct and indirect effects of exposure along the outcome distribution. Because the exposure and mediator are generally not randomized in observational studies, we define the distributions in terms of quantiles conditional on covariates, and conditional on random intercepts to allow longitudinal mediator and outcome.

2.2. Quantile regression models with random intercepts

We consider two quantile regression models that include covariates, random intercepts b_0i and g_0i (not necessarily independent of each other), and an exposure-mediator interaction for the outcome model. C_ij corresponds to the sets of covariates included in the mediator and outcome models:

$${\psi }_p(M_{ij}|Cij=c,A_{ij}=a,b_{0i})=({\beta }_0+b_{0i})+{\beta }_{1}a+{\beta }_c^{T}c$$

$${\zeta }_q(Y_{ij}|C_{ij}=c,A_{ij}=a,M_{ij}=m,g_{0i})=({\gamma }_0+g_{0i})+{\gamma }_{1}a+{\gamma }_{2}m+{\gamma }_{3}am+{\gamma }_c^{T}c.$$

We note that the parameters depend on the chosen quantiles p and q. For simplicity in the proof (i.e., derivation of the estimands), the coefficients β’s and γ’s introduced above will not carry the quantile-specific indices p and q, respectively. Later on, when presenting the motivating example, the coefficients of interest β₁, γ₁, γ₂, will be denoted with their associated quantile-specific indices, that is, β_1,p, γ_1,q, γ_2,q.

2.3. Identification assumptions

Four assumptions will suffice to identify the direct and indirect effects on the outcome distribution that we will present later:

1. $Y_{ij}^{a,m}{\displaystyle \coprod A_{ij}|C_{ij}=c,b_{0i},g_{0i}}$

2. $Y_{ij}^{a,m}{\displaystyle \coprod M_{ij}|A_{ij}=a,C_{ij}=c,b_{0i},g_{0i}}$

3. $M_{ij}^a{\displaystyle \coprod A_{ij}|C_{ij}=c,b_{0i},g_{0i}}$

4. $Y_{ij}^{a,m}{\displaystyle \coprod M_{ij}^{a\ast }|C_{ij}=c,b_{0i},g_{0i}},$

where the symbol ∐ conveys the independence between two random variables.

Conditional on the measured covariates C_ij and the random intercepts, the first assumption is met if there is no unmeasured exposure-outcome confounding. The second is met if there is no unmeasured mediator-outcome confounding. The third holds if there is no unmeasured exposure-mediator confounding, and the fourth holds if there is no mediator-outcome confounder affected by the exposure. Similar assumptions have been presented in a recent paper presenting identification assumptions that hold conditionally on random effects, but not unconditionally [28].

Although assumption 2 requires that we control for all mediator-outcome confounders, assumption 4 requires that the exposure does not affect any of these confounders that we adjusted for in assumption 2. In principle, we could have a set of mediator-outcome confounders that included variables affected by the exposure in which case assumption 4 would not hold and thus, it is essential to check whether the exposure affects the confounders of the mediator-outcome relationship.

Because unmeasured confounding is difficult to rule out, complementary analyses can be performed. Researchers can: 1) consider subsets of potential confounding variables and assess whether the resulting conclusions change when controlling for them, 2) perform some sensitivity analyses that estimate “how much” confounding is required to reverse the results, or 3) add a design stage involving matching strategies in order to create balance in covariates in the exposed vs. unexposed groups.

2.4. Assumptions of no time-varying confounding and no interference

We assume exogeneity with respect to the exposure and the mediator. Time-varying confounding in this setting has already been described [28]. Briefly, time-varying confounding would occur if there were an effect of M_ij or Y_ij on a subsequent measurement of A_ij′ or an effect of A_ij or Y_ij on a subsequent measurement of M_ij′ (j’ > j). This would likely be plausible in environmental health context with exogenous exposure (e.g., air pollution), as shown in a recent mediation analysis investigating the effects of air pollution on inflammation via changes in DNA methylation [28]. In addition, we assume no interference between units i.

2.5. Estimands

In the Appendix, we show that, under the mixed-effects models we have considered, ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)$, the q^th percentile of the potential outcome Y_ij distribution setting A_ij to a and M^ij to ${\mathrm{\Psi }}_p(M_{ij}^{a^{\ast }})$ conditioning on the covariates and random intercepts, is equal to ${\gamma }_0+g_{0i}+{\gamma }_{1}a+({\gamma }_2+{\gamma }_{3}a)({\beta }_0+b_{0i}+{\beta }_1{a}^{\ast }+{\beta }_c^{T}c)+{\gamma }_c^{T}c.$

2.5.1. Controlled direct effect

Recall that the controlled direct effect (CDE) of exposure A on outcome Y comparing A = a with A = a* and setting M to m can be obtained by comparing Y ^a,m to $Y^{a^{\ast },m}$. We define and derive the controlled direct effect of the exposure on the q^th percentile of the outcome Y_ij distribution by contrasting two percentiles of the potential outcome distributions ${\xi }_q(Y_{ij}^{a,m})$, one setting A_ij to a and the other one setting A_ij to a*; while holding M_ij to the same value ${\mathrm{\Psi }}_p(M_{ij}^{a^{\ast }})$: ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)-{\xi }_q\left(Y_{ij}^{a^{\ast },{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)$.

This direct effect captures the effect on the q^th quantile of the distribution of Y when changing the exposure from a* to a, but in both cases fixing the mediator to the p^th quantile of the distribution of the mediator when exposure is set to a*. Under the quantile regression models we have considered and in the absence of exposure-mediator interaction, this is: γ₁ (a − a*). In the absence of exposure-mediator interaction, the direct effect does not depend on the quantile p, that is, this is the same for all mediator quantiles. In the presence of exposure-mediator interaction, the contrast between ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)-{\xi }_q\left(Y_{ij}^{a^{\ast },{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)$ depends on the individual random effects: ${\gamma }_1(a-a^{\ast })+{\gamma }_3(a-a^{\ast })({\beta }_0+b_{0i}+{\beta }_{1}a+{\beta }_c^{T}c)$. To obtain an estimate of the population controlled direct effects, the random effects “b_0i” can be integrated out. If researchers are interested in individual-level controlled direct effects, quantile mixed-effects models can be considered to estimate the random effects b_0i (code not shown). The natural direct effect (NDE) of exposure A on outcome Y comparing A = a with A = a* intervening to set M to what it would have been if exposure had been A = a* is generally obtained by comparing $Y^{a,M^{a^{\ast }}}-Y^{a^{\ast },M^{a^{\ast }}}$. Because of the focus on specific mediator and outcome quantiles, the natural direct effect (in its usual definition) cannot be defined.

2.5.2. Indirect effect

We now define the indirect effect on the q^th percentile of the potential outcome Y_ij distribution through the p^th percentile of the M_ij distribution as the contrast between the percentiles of the potential outcome distribution ${\xi }_q(Y_{ij}^{a,m})$, one setting M_ij to ${\mathrm{\Psi }}_p\left(M_{ij}^a\right)$ and the other setting M_ij to ${\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}\right)$; while holding A_ij to a: ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^a|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)-{\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)$.

This indirect effect captures the effect on the q^th quantile of the potential outcome Y_ij distribution, when the exposure is fixed to a, but the mediator is changed from the p^th quantile of mediator when the exposure is a* to the p^th quantile of the mediator distribution when the exposure is a. Under the mixed-effects effects model we have considered, this is: (γ₂ + γ₃ a) β₁ (a − a*). If there is no exposure-mediator interaction, this is equal to the standard “mediation formula”, γ₂ β₁ (a − a*). Note that these indirect effects depend on both quantiles p and q. Similarly as before, the natural indirect effect (NIE) comparing A = a with A = a* and intervening to set exposure A to a is generally defined by comparing $Y^{a,M^a}$ to $Y^{a,M^{a^{\ast }}}$. Note that, because of our focus on specific quantiles, the natural indirect effect (in its usual definition) cannot be defined here.

2.5.3. Additional remarks

We note that the controlled direct and indirect effects we have defined above do not add up to the (usual) total effect (of the exposure on the q^th percentile of the outcome distribution) resulting from the difference between ${\xi }_q(Y_{ij}^a)$ and ${\xi }_q(Y_{ij}^{a^{\ast }})$. Instead, the sum of the two effects is equal to the contrast: ${\xi }_q\left(Y_{ij}^{a,{\mathrm{\Psi }}_p\left(M_{ij}^a|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)-{\xi }_q\left(Y_{ij}^{a^{\ast },{\mathrm{\Psi }}_p\left(M_{ij}^{a^{\ast }}|C_{ij}=c,b_{0i},g_{0i}\right)}|C_{ij}=c,b_{0i},g_{0i}\right)$. This contrast can be decomposed into sum of the controlled direct and indirect effects we have defined, which is not a quantity that has been of interest in causal inference, but could be defined as a new type of “total effect”.

The framework described in this manuscript is not restricted to models with random intercepts only. It can be extended to models including random intercepts and slopes. For example, one can add two random slopes b_1i and g_1i that allow for heterogeneous exposure and mediator effects across subjects, respectively. In this case, the direct and indirect effects (conditional on covariates and random effects) can be obtained by replacing β₁ and γ₁ by β₁ + b_1i and γ₁ + g_1i, respectively.

The method developed here applies to cross-sectional data as well by setting the variance of the random intercept b_0i and g_0i to zero. In such a setting, the controlled direct effect and and the indirect effect still equals γ₁ (a − a*) and γ₂ β₁ (a − a*), respectively. In situations with missing covariates, we recommend to multiply-impute them before conducting the quantile mediation analysis. If variables are measured with differential error, we recommend a recent developed method relying on sensitivity parameters [29].

2.6. Variance of the control direct and indirect effects

If there is no exposure-mediator interaction in the outcome model, the variance of the direct effect (γ₁) can be easily obtained from the software output. The indirect effect formula in the absence of exposure-mediator interaction consists of a product term γ₂β₁. The bivariate delta method can be used to derive Var(γ₂β₁) which is approximately equal to ${\sigma }_{{\beta }_1}^2{\gamma }_2^2+2{\sigma }_{{\beta }_1,{\gamma }_2}{\gamma }_2{\beta }_1+{\sigma }_{{\gamma }_2}^2{\beta }_1^2$. The Bootstrap procedure can also be used to estimate the variances of the indirect effects in complex settings. The Bootstrap technique is useful to estimate variances non-parametrically, especially with quantile regression models allowing for longitudinal data [30], with mediation models with exposure-mediator interactions [28], or in more complex situations in which asymptotic theory does not apply. In longitudinal settings, the observations should be sampled with replacement by subject in order to preserve the correlation structure of the dataset [31].

2.7. Estimation

We used the R package rqpd to estimate the coefficients of the quantile regressions for longitudinal data [30]. We used the Bootstrap procedure to estimate the variance of the direct and indirect effects on the outcome distribution. We provide software in the form of R code in the Appendix.

Similarly as in mean mediation analysis for longitudinal data [28], the random effects could be dependent with each other. For example, in a situation in which random slopes for the mediator and outcome models are correlated, these two models (i.e., mediator and outcome models) should be estimated jointly. Sophisticated software should be considered.

3. Motivating example: Air pollution, DNA methylation, and fibrinogen

3.1. Scientific question

The role of DNA methylation, although very complex, has been summarized as a “switch” that can control gene expression. Recent results have suggested that air pollution distorts the distribution of epigenetic outcomes (e.g., IFN-γ methylation), and that larger impacts are observed among individuals whose epigenetic outcomes’ levels are low [12]. These results suggest that participants who already have higher risk of coagulation may also be the ones primarily affected by air pollution. With our developed method, we conduct a quantile mediation analysis to examine this hypothesis, but in a mediation analysis context with a cardiovascular marker as the outcome. Our approach modeling percentiles of mediator and outcomes can detect whether larger effects are observed at the adverse end(s) of health outcomes’ distributions.

Using the quantile causal mediation model described in the previous sections, we investigate whether there is a direct air pollution (i.e., particle number) effect on different quantiles of the outcome distribution of a coagulation marker (i.e., fibrinogen) and whether there is an indirect air pollution effect on this outcome distribution through different quantiles of the epigenetic mediator (i.e., IFN-γ methylation).

3.2. Data description

We analyze data from a longitudinal cohort study including participants from the Normative Aging Study. This investigation, described in a previous paper [32], was established in Boston in 1963 by the U.S. Veterans Administration. Between 1999 and 2009, a total of 777 participants had their levels of DNA methylation and fibrinogen measured one to five times with intervals of three to five years. Participants blood was collected at every medical visit after an overnight fast and smoking abstinence.

The exposure of interest is particle number, which is commonly used as a surrogate of ultrafine particles from traffic. Hourly particle number concentrations were measured with a Condensation Particle Counter (TSI Inc, Model 3022A, Shoreview, MN) 1 km away from the medical center. The intermediary mechanism of interest is DNA methylation on the IFN-γ gene. IFN-γ is an important cytokine that plays a role in innate and adaptive immunity against foreign compounds. IFN-γ methylation was assessed with highly quantitative methods based on bisulfite polymerase chain reaction (PCR) pyrosequencing. The outcome of interest is fibrinogen, which is a precursor of fibrin involved in blood clotting. Plasma fibrinogen concentration was measured using MDA Fibriquick (Trinity Biotech, Bray, Ireland), a bovine thrombin reagent.

The relevant exposure windows for the air pollution effects on DNA methylation and fibrinogen are not clearly determined. We consider the intermediate-term exposure window of 28-day moving average preceding each individual medical examination. This time window could serve as a median choice between short- and long-term exposures to air pollution. The medians of the mean distances of the participant homes from the monitor were about 20 km.

3.3. Methods

We standardize the exposure (i.e., particle number), the mediator (i.e., IFN-γ methylation), and the outcome (i.e., fibrinogen) of interest and present the controlled direct and the indirect effects as the result of a one-unit increase of the standardized exposure. We fit two separate quantile regressions, one to model the exposure-mediator relationship and another one to model the effects of the exposure and the mediator on the outcome:

$${\psi }_p(M_{ij}|C_{ij}=c,A_{ij}=a,b_{0i})=({\beta }_0+b_{0i})+{\beta }_{1}a+{\beta }_c^{T}c$$

$${\zeta }_q(Y_{ij}|C_{ij}=c,A_{ij}=a,M_{ij}=m,g_{0i})=({\gamma }_0+g_{0i})+{\gamma }_{1}a+{\gamma }_{2}m+{\gamma }_c^{T}c.$$

Using the same method described in a previous paper [12], we construct an alternative way of presenting the estimated coefficients from the quantile regressions by illustrating the distributional shift associated with a two-unit increase in standardized exposure or mediator. The predicted curve, constructed using the quantile regression coefficients, assumes a constant trend within decile intervals.

We compare our quantile mediation analysis results to what we would have found using a standard mediation analysis modeling the means of the mediator and outcome:

$$E(M_{ij}|C_{ij}=c,A_{ij}=a,b_{0i})=({\beta }_0+b_{0i})+{\beta }_{1}a+{\beta }_c^{T}c$$

$$E(Y_{ij}|C_{ij}=c,A_{ij}=a,M_{ij}=m,g_{0i})=({\gamma }_0+g_{0i})+{\gamma }_{2}m+{\gamma }_c^{T}c.$$

Note that in the regressions modeling the outcome mean, the exposure-mediator interaction was not significant (p-value_interaction=0.88) and its addition did not change the effect estimates. We therefore fit all mediation models with no exposure-mediator interaction.

Our four assumptions about confounding in Section 2.3 need to hold for the controlled direct and indirect effects to be identified from the data. Therefore, we included “a priori” the following covariates C_ij in the regression models: temperature, relative humidity, seasonal sine and cosine (to allow the regression analysis to estimate both the amplitude and the phase of the seasonal cycle), batch of DNA methylation measurement, age, body mass index (BMI), smoking, diabetes, statin use, percentage of neutrophils in blood count, percentage of lymphocytes in blood count, percentage of monocytes in blood count, and percentage of basophils in blood count.

As in a recent mean mediation analysis [28], we assume no endogeneity. For instance, we assume that the mediator (i.e., IFN-γ methylation) and outcome (i.e., fibrinogen) measured at previous visits do not affect the concentrations of particle number at any subsequent visit; and that particle number and fibrinogen measured at previous visits do not affect IFN-γ methylation at any subsequent visit. This is plausible because air pollution is an exogenous variable and medical visits occur far apart, i.e., three to five years.

3.4. Results

3.4.1. Direct effect

We found evidence of heterogeneity in the direct effect of particle number on fibrinogen across the outcome distribution (Figures 1.1 and 1.2). Figure 1.1 represents the effect of (standardized) particle number on each decile of the fibrinogen distribution. Figure 1.2 reports the predicted distributional change on fibrinogen per two-unit increase in the standardized exposure. Only participants with higher fibrinogen levels were significantly affected by particle number exposure, which tends to increase their fibrinogen levels even further. For instance, for a one-unit increase in standardized particle number concentrations, there is a 0.29 [95%CI_Bootstrap: 0.08; 0.44] increase in fibrinogen levels among participants belonging to the 90^th percentile, although we observed null associations among participants belonging to the lower half of the distribution (see coefficients γ_1,q in Table 1).

FIGURE 1.1.

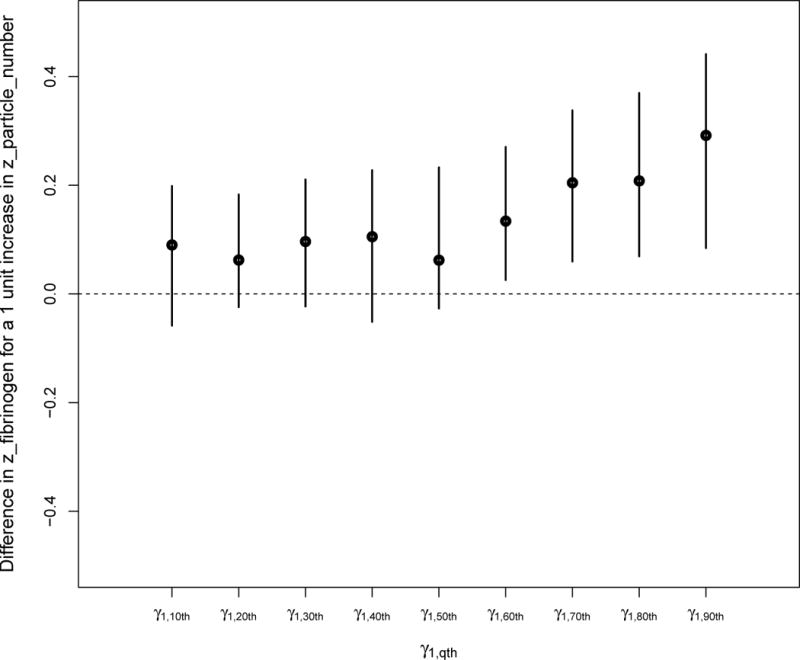
Quantile regression coefficients of the associations between particle number exposure and the deciles of the fibrinogen distribution.

FIGURE 1.2.

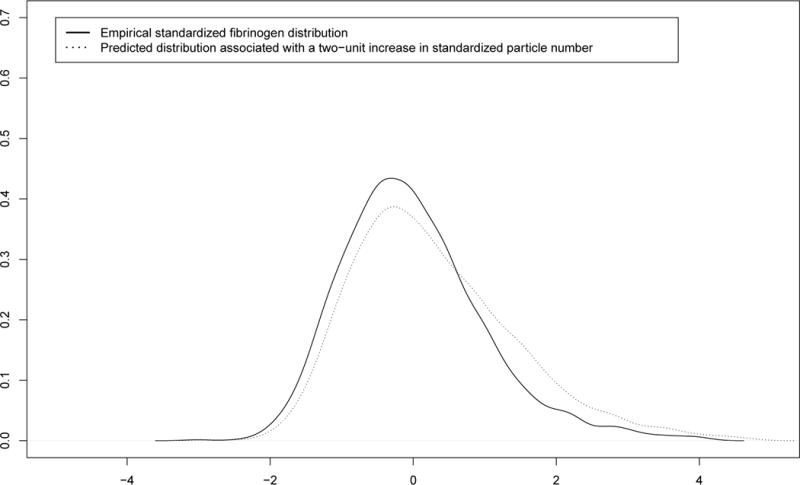
Distributional change of the standardized IFN-γ methylation distribution due an increase in particle number exposure

Table 1.

Quantile and mean regressions results

Coefficient γ1,q	Quantile estimate	95% CIBootstrap
γ1,10	0.0903	[−0.0583 to 0.1986]
γ1,20	0.0625	[−0.0242 to 0.1830]
γ1,30	0.0966	[−0.0230 to 0.2106]
γ1,40	0.1055	[−0.0514 to 0.2277]
γ1,50	0.0623	[−0.0268 to 0.2329]
γ1,60	0.1342	[0.0256 to 0.2705]
γ1,70	0.2047	[0.0597 to 0.3378]
γ1,80	0.2083	[0.0693 to 0.3698]
γ1,90	0.2920	[0.0844 to 0.4413]
Coefficient β1,p	Quantile estimate	95% CIBootstrap
β1,10	−0.1942	[−0.3346 to 0.0347]
β1,20	−0.1833	[−0.2865 to −0.0621]
β1,30	−0.1591	[−0.2714 to −0.0641]
β1,40	−0.1507	[−0.2716 to 0.0495]
β1,50	−0.1546	[−0.2348 to −0.0500]
β1,60	−0.0967	[−0.1628 to −0.0066]
β1,70	−0.0442	[−0.1121 to 0.0206]
β1,80	−0.0220	[−0.0730 to 0.0824]
β1,90	−0.0633	[−0.0460 to 0.1548]
Coefficient γ2,q	Quantile estimate	95% CIBootstrap
γ2,10	−0.0100	[−0.1191 to 0.0794]
γ2,20	−0.0287	[−0.1124 to 0.0485]
γ2,30	−0.0366	[−0.1347 to 0.0378]
γ2,40	−0.0571	[−0.1385 to 0.0357]
γ2,50	−0.0540	[−0.1246 to 0.0404]
γ2,60	−0.0601	[−0.1029 to 0.0360]
γ2,70	−0.0350	[−0.1131 to 0.0602]
γ2,80	−0.0243	[−0.1481 to 0.0537]
γ2,90	−0.1774	[−0.2595 to 0.0323]
Mean coefficient	Quantile estimate	95% CIAsymptotic
β1,mean	−0.2453	[−0.3572 to −0.1334]
γ1,mean	0.1586	[0.0508 to 0.2665]
γ2,mean	−0.0027	[−0.0629 to 0.0574]

3.4.2. Indirect effect

We followed our investigation by decomposing the mediated effect in two parts: we first examined the effect of the exposure on the mediator distribution (see coefficients β_1,p in Table 1) and then investigated the effect of the mediator on the outcome distribution (see coefficients γ_2,q in Table 1).

Exposure-mediator relationship

We observed heterogenous effects of particle number exposure on the IFN-γ methylation mediator distribution across deciles (Figures 2.1 and 2.2). Only participants with low methylation levels seem to be affected by ultrafine particles. For instance, a one-unit increase in standardized particle number was associated with a 0.19 decrease in the 10^th decile of the standardized IFN-γ methylation and was not significantly associated with the upper deciles (i.e., 70^th to 90^th) of standardized IFN-γ methylation.

FIGURE 2.1.

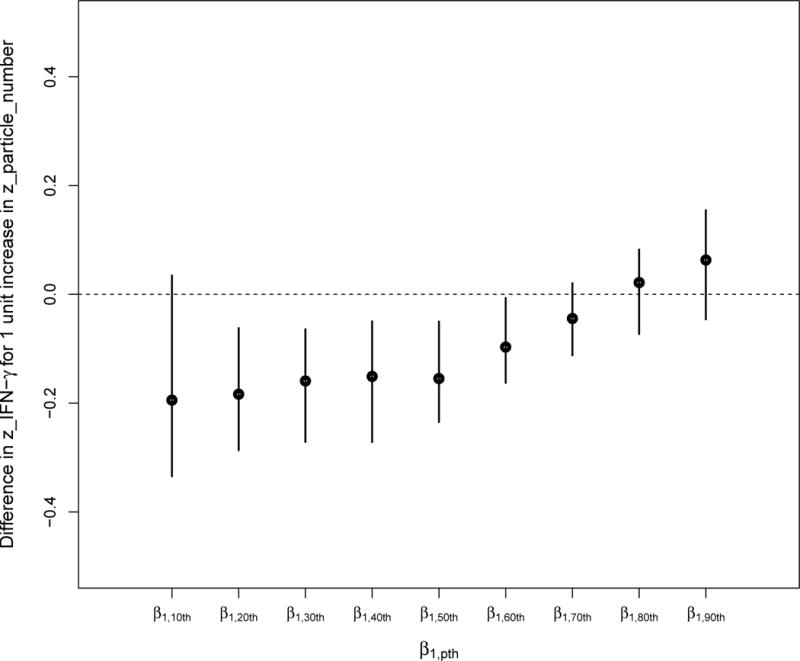
Quantile regression coefficients of the associations between particle number exposure and the deciles of the IFN-γ methylation distribution.

FIGURE 2.2.

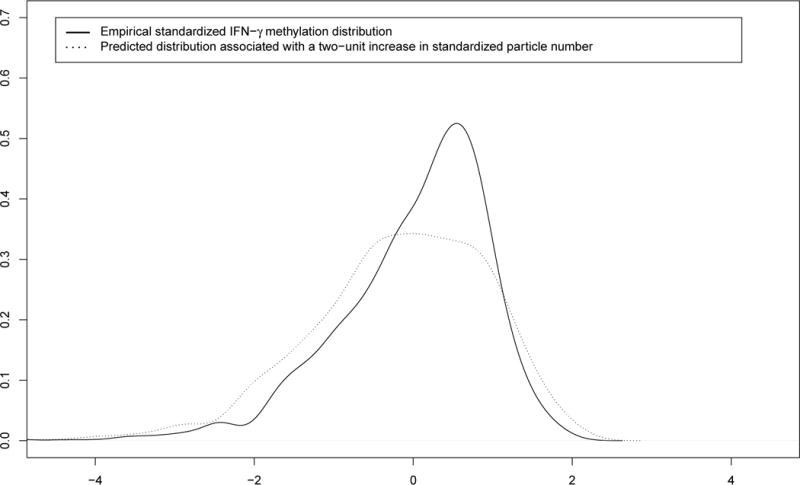
Distributional change of the standardized IFN-γ methylation distribution due to standardized particle number exposure.

Mediator-outcome relationship

The effect of the IFN-γ methylation mediator on the fibrinogen outcome was less clear (Figures 3.1 and 3.2), but Figure 3.1 suggests a negative impact of IFN-γ hypomethylation among participants belonging to the 90^th percentile of the fibrinogen distribution. A decrease in IFN-γ methylation among these participants was marginally associated with an increase in fibrinogen. Therefore, for those with lower levels of IFN-γ methylation and higher levels of fibrinogen, an increase in particle number will generally further decrease their IFN-γ methylation levels, resulting in an increase in fibrinogen.

FIGURE 3.1.

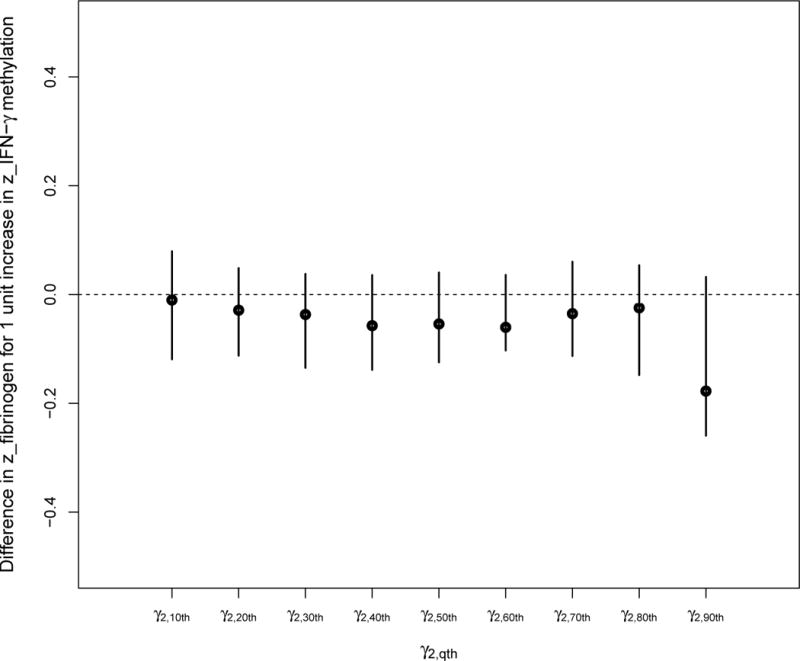
Quantile regression coefficients of the associations between IFN-γ methylation and the deciles of the fibrinogen distribution.

FIGURE 3.2.

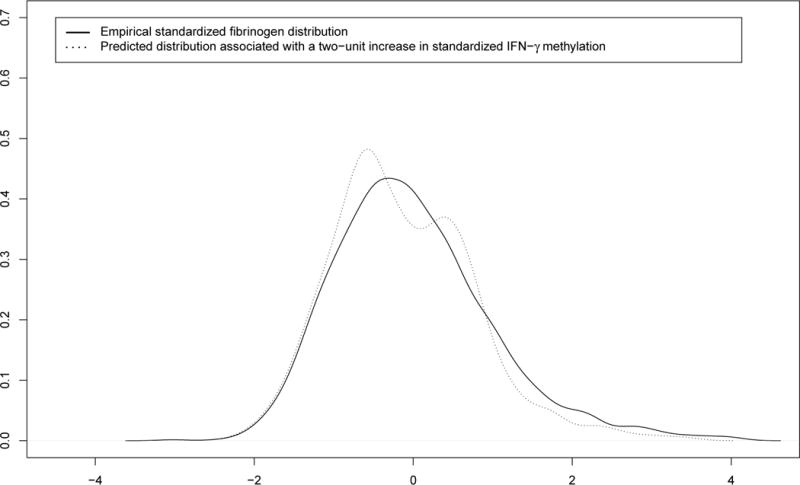
Distributional change of the standardized fibrinogen distribution due to a change in standardized IFN-γ methylation.

This sequence of effects among participants with lower IFN-γ methylation and higher fibrinogen is consistent with the positive association between exposure to particle number and fibrinogen at the higher quantiles of the fibrinogen distribution (as seen in Figure 1.1).

Quantile mediated effects

We then calculated the indirect effects of particle number on the fibrinogen distribution through three percentiles (20^th, 50^th, and 80^th) of the IFN-γ DNA methylation distribution (Figures 4.1 to 4.3). We calculated 95% confidence intervals via the Bootstrap procedure we described in section 2.6. Although the quantile-specific indirect effects were not strictly significant, Figures 4.1 and 4.2 suggest some indirect effect among participants in the 90^th percentile of fibrinogen having also low IFN-γ methylation. We observed no indirect effect of particle number on fibrinogen via IFN-γ methylation among participants in the upper percentile of IFN-γ methylation (Figure 4.3).

FIGURE 4.1.

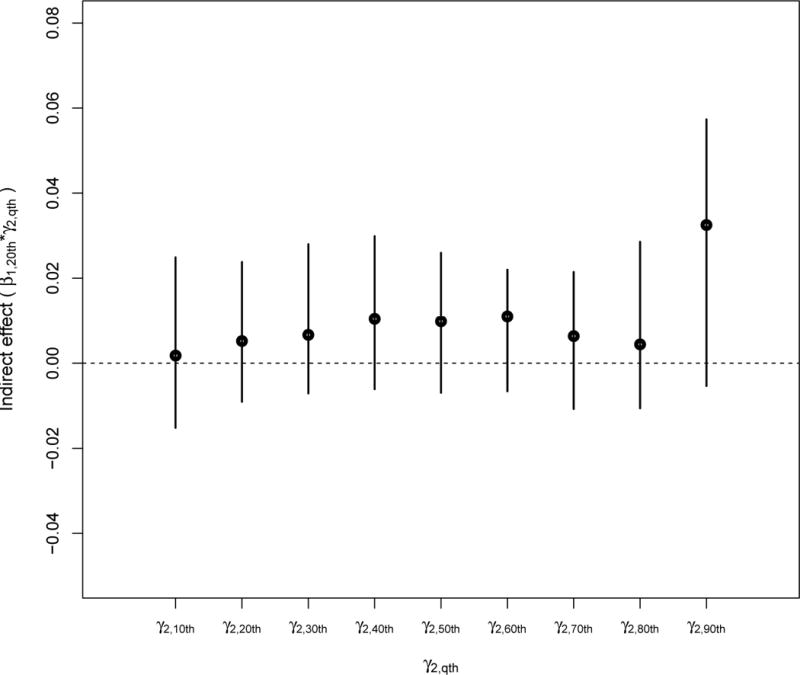
Indirect effects of standardized particle number on standardized fibrinogen through a change in the 20th percentile of the standardized IFN-γ methylation distribution.

FIGURE 4.3.

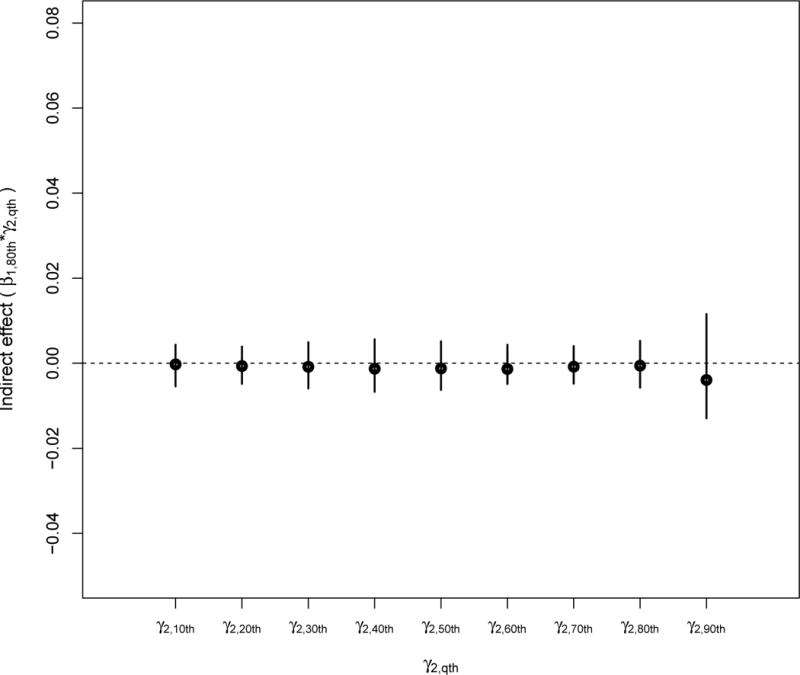
Indirect effects of standardized particle number on standardized fibrinogen through a change in the 80th percentile of the standardized IFN-γ methylation distribution

FIGURE 4.2.

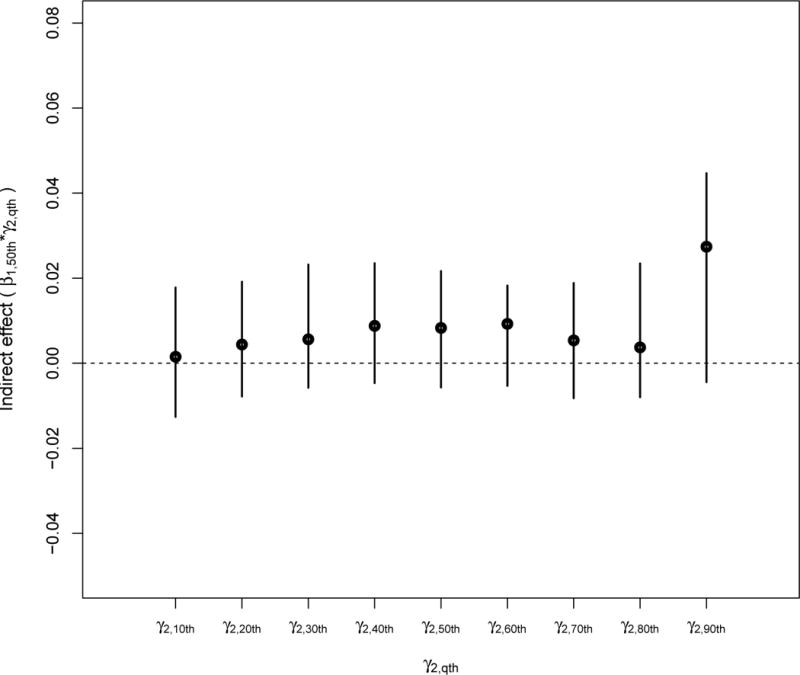
Indirect effects of standardized particle number on standardized fibrinogen through a change in the 50th percentile of the standardized IFN-γ methylation distribution

We also present the indirect effects of particle number on the q^th percentile of the fibrinogen distribution through the p^th percentile of the IFN-γ DNA methylation distribution on a heat map (Figure 5.1) and a 3D-plot (Figure 5.2). We observe that participants with low levels of IFN-γ methylation and high levels of fibrinogen have the largest indirect effects of particle number on fibrinogen via a decrease in IFN-γ methylation.

FIGURE 5.1.

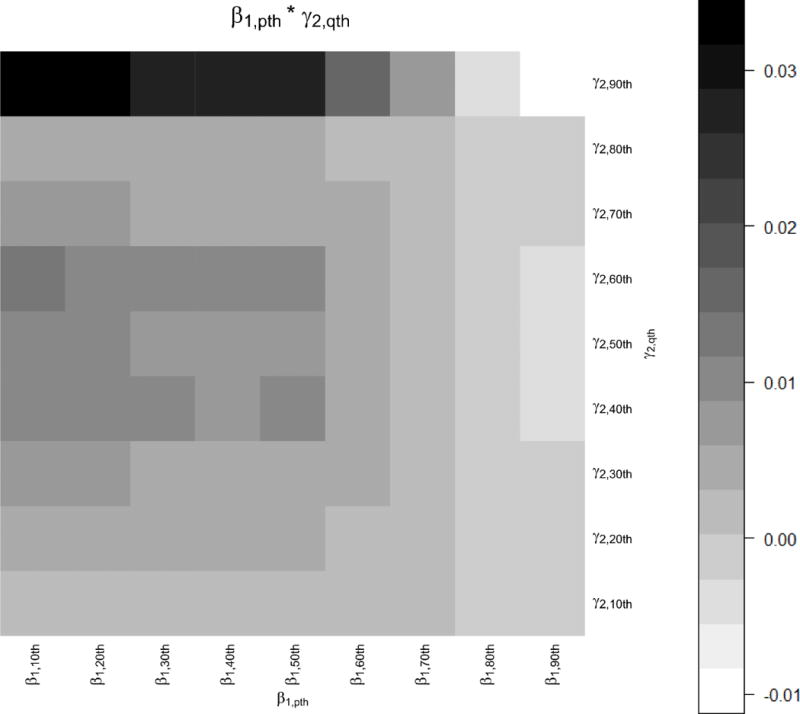
Heatmap representing the indirect effects of standardized particle number on the qth percentiles of the standardized fibrinogen distribution through a change in the pth percentiles of the standardized IFN-γ methylation distribution

FIGURE 5.2.

3-D plot representing the indirect effects of standardized particle number on the qth percentiles of the standardized fibrinogen distribution through a change in the pth percentiles of the standardized IFN-y methylation distribution

Mean mediated effects vs. quantile mediated effects

We contrasted our findings using quantile regression to what one would obtain if a standard mean regression analysis was conducted (see coefficient estimates from the mean models in Table 1). We used a mean mediation model for longitudinal data [28]. We fit two mixed-effects, one modeling the mediator mean, the second modeling the outcome mean. We control for the same covariates we adjusted for in the quantile mediation analysis. The direct effect of particle number (standardized) on the mean of fibrinogen (standardized) was equal to 0.16 [95%CI: 0.05 to 0.26]. The indirect effect of a one unit increase in standardized particle number on the mean of standardized fibrinogen via a change in the mean standardized IFN-γ DNA methylation was equal to 0.00 [95%CI: −0.01 to 0.02], while the estimated indirect effect is equal to 0.03 [95%CI: −0.01 to 0.06] at the 20^th quantile of IFN-γ methylation and the 90^th quantile of fibrinogen.

4. Simulation study

We present a simulation study contrasting: 1) two scenarios for which the effects are only present at the extreme quantiles of the simulated study population, vs. 2) a scenario for which the effects are present for a larger portion of the population (See supplementary materials).

5. Discussion

This approach extends previous work that defined direct and indirect effects using quantile regressions [4, 26]. Using a causal framework, we considered two quantile regression models and formally derived the controlled direct exposure effect along the outcome distribution and its indirect effect via a given percentile of the mediator using potential outcomes. Our approach allows for exposure-mediator interaction in the outcome model and allows for longitudinal setting with repeated measurements of mediator and outcome. With this methodology, we present an alternative method (vs. the standard mean mediation analysis) that investigates shifts in the distributions of the mediator and outcome, rather than just shifts in the means of these distributions. We are able to detect interesting patterns of particle number health effects that would be missed using ordinary mean mediation analysis. This research tool is valuable for many disciplines, especially in epidemiological studies that aim to investigate pathways and determine susceptibility.

The direct and indirect effects we derived based on specific quantiles of the mediator and outcome distributions may be more difficult to interpret as compared to those estimated in a mean mediation analysis are conducted. The controlled direct effect on the q^th percentile of the outcome Y_ij distribution, defined by contrasting ${\xi }_q(Y_{ij}^{a,m})$, one setting A_ij to a and the other one setting A_ij to a*; while holding M_ij to the same value ${\mathrm{\Psi }}_p(M_{ij}^{a^{\ast }})$ may not generally be of interest if the p represents a quantile at the tail of the distribution, unless the direct effect occurs for participants belonging to the tail of the mediator. Other quantities of interest could be considered. For example, one could consider a mean regression model for the mediator and a quantile regression model for the outcome. If the median and mean of the mediator are close to each other, this analysis should provide similar estimates to what one would obtain by fitting a median regression for the mediator and the same quantile regression model for the outcome.

Many disciplines have shown interest in quantile regression [12, 16, 17] and mediation analysis to investigate existant or new biological mechanisms, as well as their relative importance [4–6, 8–11]. These biological findings are relevant to the understanding of air pollution adverse effects. They provide evidence of an impact of ultrafine particles on IFN-γ methylation followed by a potential increase in coagulation. Such findings are relevant to several fields, such as molecular biology, environmental epidemiology, and risk assessment. These results also add evidence towards the intermediate role that DNA methylation may play in air pollution effects on cardiovascular disease and provide evidence towards susceptibility to air pollution (i.e., ultrafine particles) based on levels of mediator (i.e., DNA methylation) and outcome (i.e., fibrinogen).

We applied the method to an interesting environmental health example and identified cardiovascular-related responses with different individual susceptibility. This method can be applied in many environmental studies with exogenous exposure to examine whether the exposure-outcome, exposure-mediator, and mediator-outcome effects are heterogeneous within the study population, and whether certain tails of the distributions of the mediator and outcome are more affected by the exposure and/or the mediator. We highlight a way to examine heterogeneity in responses without making assumptions about the mediator and outcome distributions or their residuals. It was interesting that, under high particle number exposure, the right-tail of the fibrinogen distribution and the left-tail of the IFN-γ DNA methylation distribution become longer than would be expected under low exposure conditions. Participants with elevated fibrinogen, often due to clotting dysfunction, were more likely to be affected by particle number exposure and a change in IFN-γ methylation. Participants with low IFN-γ methylation were also more susceptible to particle number exposure. The key result is that stronger effects were found among participants in the lower tail of the IFN-γ methylation distribution and in the higher tail of the fibrinogen distribution. These larger effects were therefore seen in people at the adverse end of the mediator and outcome distributions, which have important public health implications and need to be considered by air pollution health impact assessments.