Testing the validity of conflict drift-diffusion models for use in estimating cognitive processes: A parameter-recovery study

Abstract

Researchers and clinicians are interested in estimating individual differences in the ability to process conflicting information. Conflict processing is typically assessed by comparing behavioral measures like RTs or error rates from conflict tasks. However these measures are hard to interpret because they can be influenced by additional processes like response caution or bias. This limitation can be circumvented by employing cognitive models to decompose behavioral data into components of underlying decision processes, providing better specificity for investigating individual differences. A new class of drift-diffusion models has been developed for conflict tasks, presenting a potential tool to improve analysis of individual differences in conflict processing. However, measures from these models have not been validated for use in experiments with limited data collection. The present study assessed the validity of these models with a parameter-recovery study to determine whether and under what circumstances the models provide valid measures of cognitive processing. Three models were tested: the Dual-Stage Two Phase model (Hübner, Steinhauser, & Lehle, 2010), the Shrinking Spotlight model (White, Ratcliff, & Starns, 2011), and the Diffusion Model for Conflict Tasks (Ulrich, Schröter, Leuthold, & Birngruber, 2015). The validity of the model parameters was assessed using different methods of fitting the data and different numbers of trials. The results show that each model has limitations in recovering valid parameters, but they can be mitigated by adding constraints to the model. Practical recommendations are provided for when and how each model can be used to analyze data and provide measures of processing in conflict tasks.

Introduction

There is strong interest in identifying differences in cognitive processes across individuals. Myriad studies have been conducted to assess how cognitive processing varies as a function of different factors like psychopathology, development and aging, experimental manipulations, pharmacological intervention, and personality traits (e.g., Logan, Yamaguchi, Schall, & Palmeri, 2015; Ratcliff, Thapar, & McKoon, 2001; Ratcliff & Van Dongen, 2009; van Wouwe et al., 2016; Verbruggen, Chambers, & Logan, 2013; White & Poldrack, 2014; White, Ratcliff, Vasey, & McKoon, 2010; Wylie et al., 2012). Likewise, individual differences in cognitive function have been used to probe neural activation in studies using methodologies like electroencephalography (Kelly & O’Connell, 2013; Philiastides, Heekeren, & Sajda, 2014; Servant, White, Montagnini, & Burle, 2016), electromyography (Servant, White, Montagnini, & Burle, 2015) and functional magnetic resonance imaging(Forstmann, van den Wildenberg, & Ridderinkhof, 2008; White et al., 2014). The traditional approach is to compare behavioral measures like RTs or accuracy rates to infer differences in processing.

More recently, choice RT models like the drift-diffusion model (DDM; Ratcliff & McKoon, 2008; described below) have been employed with great success to decompose behavioral data into measures of different cognitive components, providing deeper insight into the hypothesized mechanisms underlying differences in task performance. However, standard DDMs are generally not applicable to tasks where there is conflicting evidence for a response. To address this, newer variants of the DDM have been developed to account for decision behavior in such conflict tasks. The present study investigates the validity and practical usage of these conflict DDMs with a simulation-recovery study. The goal was to identify whether and in what circumstances such models can be used to recover valid parameters for measuring individual differences in processing for conflict tasks. This work will provide validation for the use of these models as well as practical guidelines for employing them on behavioral data. Before the recovery study is presented, we describe the limitations of using RTs and/or accuracy rates to infer differences in cognitive processing. Then we discuss how models like the DDM can circumvent these limitations, and describe a new class of conflict DDMs that can broaden the scope of DDM-based analysis. Finally, we present the results of the recovery study with practical guidelines for how and when the conflict DDMs can be used for measuring individual differences in processing.

Conflict tasks are those in which multiple aspects of the stimulus can provide conflicting evidence for the correct response. These tasks include the Stroop task (Stroop, 1935), where the written word can conflict with the color in which it is rendered, the Flanker task (Eriksen & Eriksen, 1974), where the flanking items can conflict with the target item, the Simon task (Simon & Small, 1969), where the location of the stimulus can conflict with the response. These tasks are of particular interest for comparisons of group or individual differences, as they can provide measures of cognitive control, which for these tasks reflects the ability to reduce/suppress conflicting information when making a decision (Kornblum, Hasbroucq, & Osman, 1990; Ridderinkhof, 2002).

Cognitive control is typically measured by taking the difference in RTs (or error rates) between compatible and incompatible trials, with larger differences indicating greater interference and thus weaker/slower cognitive control. However, behavioral measures like RTs are determined by various factors like stimulus processing, how cautiously participants respond, and whether they have a bias for one response over another. This results in a reverse inference problem: an RT difference between individuals in a conflict task is inferred to reflect differences in conflict processing, but it might instead reflect differences in some other factor like response caution.

This reverse inference problem can be circumvented by using choice RT models to analyze the data. RT models can decompose the behavioral data into measures of underlying cognitive processes for stimulus discriminability, response caution, response bias, and encoding and motor time. This decomposition separates the effects of these processes that are conflated in RT measures and provides greater specificity for identifying the locus of differences between individuals. The most commonly employed RT model is the drift-diffusion model (DDM; Ratcliff, 1978; Ratcliff & McKoon, 2008), which belongs to a broader class of stochastic accumulator or sequential sampling models that assume noisy evidence is accumulated over time until a threshold level is reached, at which point the decision is committed (Forstmann, Ratcliff, & Wagenmakers, 2016). Recent variants of the DDM have been developed to account for behavior in conflict tasks. These models, described below, specify how the decision evidence varies over time as a function of the compatible and incompatible information. They all share the general assumption that early conflicting decision evidence decays or can be suppressed by controlled processing, resulting in decision evidence that changes over time to improve behavior. While these models can successfully account for data from conflict tasks, it has yet to be established that they can be used to analyze individual differences in the manner of the standard DDM described above. For the models to be employed in this manner, it is crucial that the model parameters estimated from the data are valid estimates of the underlying parameters for an individual. The present study seeks to assess the validity of conflict DDMs using a parameter recovery study.

Conflict Diffusion Models

Early stochastic accumulator models of conflict tasks assumed that decision evidence was the sum of automatic and controlled processes, with only the former being subject to interference from irrelevant stimulus attributes (Cohen, Dunbar, & McClelland, 1990; Logan, 1980; Logan, 1996). These models assumed that the effect of automatic processing was constant over time, but empirical evidence arose that showed the automatic interference varied over time (e.g., Dyer, 1971; Glaser & Glaser, 1982; Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988). Consequently, newer models were proposed in which the automatic activation decreased over time due to spontaneous decay (Hommel, 1993, 1994) or active suppression (Ridderinkhof, 2002). The models tested in this study are grounded in this concept of automatic and controlled processing, the former of which varies over time as a function of cognitive control.

Different assumptions about how automatic and conflict processing combine to drive the decision process have been incorporated into the DDM framework, resulting in conflict DDMs that account for RT and accuracy data from conflict tasks. Three conflict DDMs are considered in this study: the Dual Stage Two Phase model (DSTP; Hübner et al., 2010), the Shrinking Spotlight model (SSP; White, Ratcliff, et al., 2011), and the Diffusion Model for Conflict Tasks (DMC; Ulrich et al., 2015). At a broad level, each conflict DDM assumes there is automatic processing that is typically fast and nonselective, and controlled processing that is more selective to the relevant aspect of the stimulus. The decision is thus driven by a combination of automatic and controlled processing, with the former being subject to interference from the conflicting stimulus attribute and the latter being free from such interference. The differences among the models lie in how conflicting information is processed to drive the drift rate, or average decision evidence per unit time, that is accumulated during the decision. The models can be differentiated by their conceptual generality and the tasks to which they can be applied, the type of processes that are assumed, their theoretical foundation, and the manner in which decision evidence changes over the course of the decision (Table 1).

Table 1.

Overview of drift diffusion models of conflict processing.

Model	Theoretical Foundation	Relevant Tasks	Nature of processes	Change in drift rate over time
SSP	visual attention	Flanker	continuous	gradual
DSTP	visual attention	Flanker, Stroop	sequential	discrete
DMC	automaticity	Flanker, Simon, Stroop	parallel	gradual

Each of the models shares the general DDM framework in which noisy evidence is accumulated over time until a boundary is reached. Accordingly, all three models include the following parameters (Figure 1). Boundary separation (a) reflects differences in caution or speed/accuracy settings. A wide boundary separation indicates a cautious response style, which leads to slower but more accurate responses. Nondecision time (Ter) reflects the duration of stimulus encoding and motor execution, both of which are assumed to be outside of the decision process itself. Longer nondecision time indicates slower encoding and/or execution of the motor response. Finally, starting point of evidence accumulation (z) reflects a priori preference for one response over the other. If the decision process starts closer to one boundary, those responses will be faster and more probable than responses at the other boundary.

Figure 1.

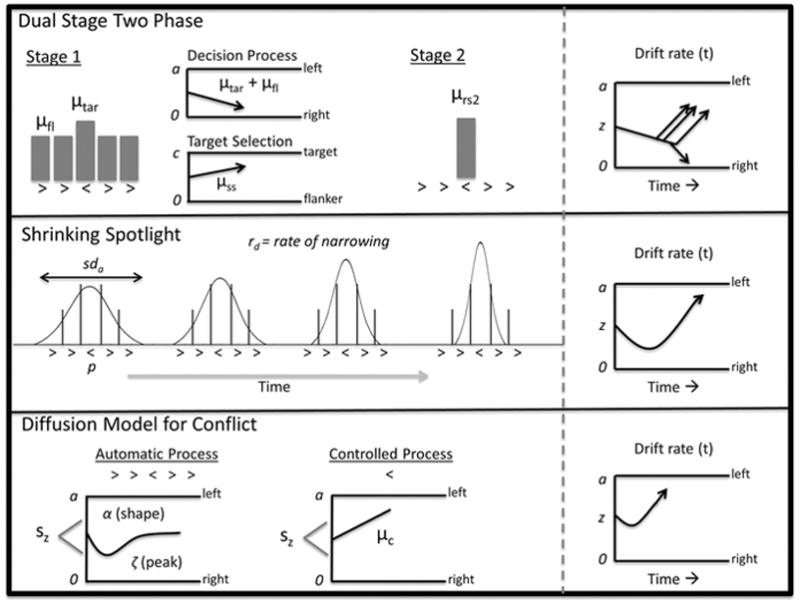
Schematic of conflict DDMs. Left panels shows the processes by which the time-varying drift rate is determined. Right panel shows the time-varying drift rate for an incompatible trial in the DDM framework. See text for description of parameters.

For coherence, each of the models shown in Figure 1 is described in terms of processing the interfering information, which is automatic and early, and the target (relevant) information, which is controlled and has stronger influence later in the decision process. For further simplicity, the models are described for a Flanker task in which the flanking stimuli are incompatible with the target stimulus (e.g., ≪>≪), and a situation with no response bias so that the starting point of evidence accumulation will be halfway between the two boundaries (though this assumption can be relaxed if needed). The general framework of each model is described below, but readers are directed to the referenced papers for more detail.

Dual Stage Two Phase Model

The DSTP is based on theories of visual attention and assumes that there is a late selection phase of processing that selects the relevant target information and effectively suppresses early interference (Hübner et al., 2010). The model was developed to provide a general account of conflict processing and thus can theoretically account for data from various tasks like the Flanker and Stroop tasks (but not the Simon, see Servant et al., 2014). The model posits two simultaneous diffusion processes, one for the decision itself and the other for target selection/categorization. During the first stage of processing attention is diffuse and distributed to both the target and the flankers, resulting in a drift rate that is determined by a weighted average of target and flanker information. While evidence is accumulated in the first stage, a second diffusion process occurs that selects the target information from the stimulus. If the target selection process reaches a boundary before the first stage selects a response, the model transitions into the second stage where the decision process is driven by a new drift rate based on the selected target. Thus the DSTP assumes dual-processes, one automatic and one controlled, that occur sequentially to drive the decision evidence over time. As shown in the right panel of Figure 1, the drift rate for incompatible trials favors the right (incorrect) response early in the trial, but switches to favor the left (correct) response after target identification occurs.

The DSTP includes the following parameters to govern the time-varying drift rate: early drift rate for the target (μ_tar), early drift rate for the interference (μ_fl), boundary separation(c) and drift rate (μ_ss) for the target selection process, and drift rate for the selected target in the second stage (μ_rs2). The piecewise drift rate for the decision is given as:

$$v(t)={\mu }_{\mathit{tar}}+{\mu }_{fl}(\mathit{Stage}\mathit{1});v(t)={\mu }_{rs\mathit{2}}(\mathit{Stage}\mathit{2})$$ (1)

With the evidence coming from Stage 1 if the stimulus selection process has not yet finished, or from Stage 2 thereafter. The values of μ_fl can be positive or negative depending on whether the flankers are compatible or incompatible with the target.

Shrinking Spotlight Model

The SSP is based on theories of visual attention (Eriksen & Schultz, 1979; Logan, 1996; 2002) and was developed for tasks like the Flanker task where attention is narrowed on the target to overcome interference from flanking stimuli. Accordingly the model is less general than DSTP or DMC (see below) in that it is specified for the Flanker task (and not Stroop or Simon). The model assumes that attention is like a spotlight centered on the stimulus, which can be narrowed/focused over time on the target. In this model, early processing is influenced by both the target and the flanking items, but the interference is reduced as the spotlight shrinks to the target. Thus the model assumes gradual reduction of interference over time and a continuous improvement in the drift rate. The drift rate is the sum of perceptual evidence from each item in the display weighted by the amount of attentional spotlight dedicated to that item. The SSP includes the following parameters to determine the time-varying drift rate: perceptual strength for the contribution of each item in the display (p_fl for flankers, p_tar for the target), spotlight width at stimulus onset (sd_a), and shrinking rate (r_d). With these parameters, the drift rate is given as:

$$v(t)=a_{fl}(t)\times p_{fl}+a_{\mathit{tar}}(t)\times p_{\mathit{tar}}$$ (2)

Where a is the amount of attentional spotlight covering the item governed by the spotlight width (sd_a) and shrinking rate (r_d), and p is the perceptual strength of each item that can be either positive (compatible) or negative (incompatible). The attention allocated to each item in a display that is (arbitrarily) centered at 0 and 5 units wide (one for each arrow) is given as:

$$a_{fl}(t)={\int }_{0.5}^{\infty }\phi (x\mid 0,{[\mathit{sda}(t)]}^2)dx{a}_{\mathit{tar}}(t)={\int }_{-0.5}^{0.5}\phi (x\mid 0,{[\mathit{sda}(t)]}^2)dx$$ (3)

Where φ(x| 0, [sd_a(t)²] is the probability density function of a normal distribution with mean 0 and standard deviation sd_a(t) = sd_a − r_d(t). It is typically assumed that the value of p is numerically the same for targets and flankers but differs in sign (positive/negative) based on the direction that the arrows are facing (White, Ratcliff, Starns, 2011). With the SSP, on incompatible trials the drift rate favors the incorrect response early in the trial, but gradually changes to favor the correct response as the attentional spotlight narrows.

Diffusion Model for Conflict Tasks

The DMC is based on theories of automaticity and incorporates the standard assumptions of the DDM, but adds a component to account for early, automatic activation that operates on task-irrelevant sensory information. The DMC was explicitly developed for all cognitive conflict tasks (Simon, Stroop, and Flanker). In the example Flanker task, the model posits evidence accumulation that is the combination of early automatic processing, driven by the flanking arrows, and controlled processing driven by the target arrow only. The early activation process is modeled as a scaled gamma function which captures the assumption that early activation is short-lived and only affects the early portion of the decision process (Figure 1).

The controlled activation is modeled with a constant drift rate akin to the assumption of the standard DDM. In the DMC, the time-varying drift rate is equal to the superimposed automatic and controlled activations, resulting in a gradual change in evidence as the automatic activation diminishes over time. The original implementation of the DMC also includes parameters to account for across-trial variability in the starting point of evidence accumulation (variability in response bias) and in the nondecision time (variability in encoding/motor time), which have likewise been incorporated to standard DDMs (see Ratcliff & McKoon, 2008). Note that these variability parameters could be added to the DSTP and SSP, but were left out of each model for sake of parsimony. The DMC has the following parameters to govern the time-varying drift rate: the shape (α), peak amplitude (ζ), and characteristic time (τ) for the automatic activation gamma function, and the drift rate for the controlled process (μ_c). The peak latency of the automatic activation is located at τ(α−1). In the DMC the time-varying drift rate is calculated as the sum of the automatic process, v_a(t) and the controlled process, μ_c:

$$v(t)=v_a(t)+{\mu }_c$$ (3)

The DMC is more general and flexible than the DSTP or SSP because the automatic activation can occur early or later in the process. Although DMC does not have more free parameters than DSTP or SSP, the parameters of DMC can produce a wider range of behavior and thus more flexibility than the other models (Pitt & Myung, 2002). Specifically, a small (large) value of the peak latency τ(α−1) of the gamma function generates an automatic activation that develops early (late) and a decrease (increase) in the magnitude of the interference effect (as assessed by RT differences) as decision time increases. The decrease of the interference effect is a crucial pattern of data seen in the Simon task (Schwarz & Miller, 2012). Because the SSP and DSTP can only produce an increase of the interference effect on RTs as decision time increases (Servant, Montagnini, & Burle, 2014), they do not account for data from the Simon task.

The DSTP and SSP models have proven to account for Flanker task data under a wide variety of experimental manipulations (Dambacher & Hübner, 2015; Hübner, 2014; Hübner et al., 2010; Hübner & Töbel, 2012; Servant et al., 2014; White, Brown, & Ratcliff, 2011; White, Ratcliff, et al., 2011). The DMC has been successfully applied to both Flanker and Simon task data (Servant et al., 2016; Ulrich et al., 2015). While the models generally provide accurate quantitative accounts of RT distributions and accuracy data from these tasks, it has yet to be established whether they are appropriate to use for analyzing individual subject data under practical experimental constraints.

Estimating Parameters from Conflict Models

The models are only useful as measurement tools to the extent that when fitted to data the recovered parameters are accurately estimated. A pressing concern for practical implementation of these models is that they can require a significant number of RTs to accurately estimate the underlying model parameters. This could restrict the application of the models because often researchers are limited in the amount of data they can collect from participants. For instance, certain patient populations might be restricted to only 15 minutes of data collection, which might not be sufficient for using the conflict DDMs. To address the practical utility of these models, we performed a simulation-recovery study to investigate 1) whether the models can accurately estimate the different components of the decision process, and 2) the necessary number of observations to provide accurate parameter estimates. The end goal of the simulation-recovery study is to determine whether and under what circumstances these conflict models can be used by researchers who want a model-based analysis of data from conflict tasks. We then perform a cross-fitting study to assess model mimicry and help determine how to select among the models when choosing one to interpret the data.

Methods

The general approach in the recovery study was to 1) simulate data from each of the models across a range of parameter values, 2) fit the models to the simulated data using different data-fitting approaches, and 3) assess the reliability of the recovered parameters as a function of the fitting procedure and the number of simulated trials. Thus the independent variables in this exercise are the randomly selected parameter values for simulation, and the dependent variables are the recovered parameters and subsequent predictions for RTs and accuracy. This exercise will reveal whether the model parameters provide reliable estimates of the underlying cognitive mechanisms, and establish practical guidelines for the amount of data (i.e., number of trials) needed to use the models to analyze individual differences. All of the codes for simulating and fitting the models are available in the supplementary material and on the Open Science Framework website (osf.io).

Model simulations

Because the SSP and DMC are mathematically intractable (Ulrich et al., 2015; White, Ratcliff, et al., 2011), predictions from the 3 models were approximated using the Euler-Maruyama method (e.g., Kloeden & Platen, 1992) and an integration constant dt = 1 ms¹. The diffusion coefficient of SSP and DSTP models was fixed at σ = 0.1, similar to White et al. (2011) and Hübner et al. (2010).

The diffusion coefficient of the DMC was fixed at σ = 4, similar to Ulrich et al. (2015) and Servant, White, Montagnini, and Burle (2016). Models were coded in Python 2.7 using the Numpy and Scipy packages for scientific computing.

For each model, we sampled 100 different parameter sets from uniform distributions, with the mean and range taken from previous studies using the models, specifically the Flanker task for the SSP and DMC, and the Simon and Flanker tasks for the DMC (Table 2). These realistic parameters were used to simulate 100 datasets in each of 6 conditions, defined by the number of trials N per compatibility condition. We chose N = 50, 100, 200, 500, 1000, and 5000 to examine the performance of the models in real-world experimental situations (N = 50–500) and characterize the improvement in recovery as N increases (N = 1000–5000). Data were simulated for a simple conflict task in which there was one compatible and one incompatible condition.

Table 2.

Ranges of parameter values used to simulate data.

DSTP	a	Ter	c	μta	μfl	μss	μrs2
Hübner et al, 2010; Hübner, 2014; Dambacher & Hübner, 2015	.14–.38	.15–.45	.14–.38	.05–.15	.05–.25	.25–.55	.4–1.2
SSP	a	Ter	P	sda	rd
White et al. (2011)	.07–.19	.15–.45	.2–.55	1–2.6	0.01–0.026
DMC	a	Ter	μc	ζ	α	τ
Ulrich et al. (2015); Servant et al., (2016)	90–160	270–400	.2–.8	15–40	1.5–4.5	20–120

Note. The nondecision time parameter is expressed in units of the integration constant dt (seconds for SSP and DSTP, milliseconds for DMC). The diffusion coefficient σ was set at 0.1 for SSP and DSTP and 4 for DMC. These arbitrary conventions were used in previous applications of the models.

Fitting procedure

Two approaches to fitting conflict-based DDMs have been employed in the literature, and both were tested in this study. Both approaches involve a comparison between observed versus predicted data through a chi-square statistic, and a minimization of this statistic with a Simplex downhill algorithm (Nelder & Mead, 1965). The data considered in the chi-square formula differs between the two procedures.

The first procedure has been developed by Ratcliff and Tuerlinckx (2002), and is commonly used to fit sequential sampling models to behavioral data (e.g., Ratcliff & Smith, 2004; White & Poldrack, 2014). Models are simultaneously fit to correct and error RT distributions (.1, .3, .5, .7, .9 quantiles) and to accuracy data. Because the number of errors, Ne, is generally low, particularly in the compatible condition, we used an adaptive procedure that only considered the median RT if 0 <Ne≤ 5, three RT quantiles (.3, .5, .9) if 5 <Ne≤ 10, and five RT quantiles (.1, .3, .5, .7, .9) if Ne> 10. If there are no errors, the error RT distribution does not contribute to the chi-square calculation. The chi-square statistic has the form:

$${\chi }^2=\sum _{i=1}^2{N}_i\sum _{j=1}^X\frac{{(p_{ij}-{\pi }_{ij})}^2}{{\pi }_{ij}}$$ (4)

Where N_i is the number of observations per compatibility condition i. p_ij and π_ij are, respectively, the observed and predicted proportions of trials in bin j of condition i, and sum to 1 across each pair of correct and error distributions. The variable X represents the number of bins bounded by RT quantiles across each pair of correct and error distributions. Consequently, we have X = 8 if 0 <Ne≤ 5, X = 10 if 5 <Ne ≤ 10, and X = 12 if Ne> 10.

The second procedure is similar to the first one, with the exception of error data provided by conditional accuracy functions (CAFs; Hübner, 2014; Hübner et al., 2010; Servant et al., 2016; Ulrich et al., 2015). CAFs represent accuracy as a function of decision time (Gratton, et al., 1988). They are constructed by sorting correct and error trials into 5 bins, each containing 20% of the data. The proportion of errors in each bin constitutes the error data considered in the fitting procedure. Consequently, the variable X in the above formula equals 11 (6 bins bounded by RT quantiles for correct trials and 5 CAF bins). The difference between procedures 1 and 2 is subtle. Procedure 1 fits full error RT distributions. By contrast, procedure 2 fits relative densities of correct and RT distributions (i.e., CAF data). Chi-square statistics computed from procedures 1 and 2 were minimized using the same methodology. Because Simplex is sensitive to initial parameter values, we used 20 different starting points, each one being a random draw from the uniform distributions defined in Table 2. For each model, 10,000 trials per compatibility condition and fit cycle were simulated. To polish our results, we submitted the two best parameter sets (obtained from different starting points) to additional Simplex runs, and simulated 50,000 trials per condition and fit cycle. On average, fitting one dataset on Vanderbilt’s advanced computing center for education and research took approximately 15 hours for the SSP, 25–30 hours for the DMC, and 35–40 hours for the DSTP.

Assessment of goodness of fit and parameter recovery

Parameter recovery was assessed using two approaches. The first was to compare the simulated versus recovered parameter values to establish correspondence between the two. For each model, condition, and fitting procedure, we computed correlation coefficients between simulated and recovered parameters. We also computed the goodness-of-recovery statistic η defined as follows:

$$\eta =\frac{{\displaystyle \sum _{i=1}^{100}}(\mid \mathit{simulated}\theta -\mathit{recovered}\theta \mid )}{\mathit{range}\theta }$$ (5)

Where θ is a given parameter of a given model. The summation over i extends over the 100 simulated datasets, and is normalized by the uniform range for θ defined in Table 2. The statistic η allowed us to further quantify the discrepancy between simulated and recovered parameters, and determine the superiority of one fitting procedure over another.

Results

Table 3 shows the goodness-of-recovery statistic η for each model parameter, condition, and fitting procedure. The first fitting procedure generally provides a better recovery performance than the second one, reflected by smaller η values. The superiority of the first procedure also tends to increase as the number of simulated trials N decreases. This is explained by the nature of the error data considered in the chi-square computation. As detailed in the Methods section, procedure 2 takes into account relative densities of correct and error RT distributions (i.e. CAF data), while procedure 1 embraces full error RT distributions. Full error distributions provide more constraints on parameter estimates, particularly when the precision of the estimation increases (as N increases). Consequently, the remaining of the section focuses on results from fitting procedure 1.

Table 3.

Goodness-of-recovery η statistic for each model parameter, condition, and fitting procedure (η values for fitting procedure 2 are provided in parentheses).

	DSTP
	a	Ter	c	μta	μfl	μss	μrs2	Σ(η)
N= 50	16.5(16.2)	14.2(14.7)	25.8(27.5)	32(27.1)	16.2(20.2)	27.3(23.5)	30.7(30.5)	163(160)
N= 100	14.2(15.3)	12.3(14)	24.8(28.1)	31.4(26)	15.2(14.5)	22.1(21.2)	30.2(27.9)	150(147)
N = 200	16.7(16.9)	12.2(13)	22.4(23.7)	24.6(30.1)	12.5(13.4)	15.8(17.1)	26(27.5)	130(142)
N = 500	14.6(16.1)	12(14.8)	24.2(22.3)	27.8(27.5)	10.5(11.4)	17.5(16.6)	30.5(29.8)	137(139)
N = 1000	12.6(12.9)	10.9(11.6)	21.5(23)	26.1(29.2)	10.5(12.2)	17.4(16.4)	27.5(26.1)	127(131)
N = 5000	12.5(13.9)	11.8(11.9)	21.4(20.6)	24.5(27.5)	10.3(11.6)	15.4(14.9)	24.9(27)	121(127)
	SSP
	a	Ter	P	sda	rd			Σ(η)
N= 50	9.9(9.6)	3.6(4.2)	9.4(10.9)	22.6(25.9)	32.3(38.4)			78(89)
N= 100	6.9(8.5)	2.8(3.3)	6.8(7.2)	21.3(21.7)	33(30)			71(71)
N = 200	5.9(6.4)	2.1(2.5)	5.9(5.2)	18.9(20.3)	31.2(32.7)			64(67)
N = 500	3.7(4.5)	1.5(1.8)	3.3(3.4)	18.1(19)	29(30.1)			56(58)
N = 1000	3.2(3.3)	1.(1.3)	3.1(2.9)	17.2(19.5)	28.4(30.6)			53(58)
N = 5000	2.2 (1.8)	0.7(0.7)	1.8(1.3)	17(20.8)	28.1(34.1)			50(59)
	DMC
	a	Ter	μc	ζ	α	τ		Σ(η)
N= 50	16.3(17.1)	6(6.8)	10.3(9.3)	22(22.9)	22(24)	22.7(27.2)		99(107)
N= 100	12.5(14.2)	4.1(4.9)	8.3(7.1)	22.9(21.6)	23.3(22.5)	26.2(27.3)		97(98)
N = 200	12.1(10.5)	4.5(3.4)	6.5(5.2)	19.5(14.9)	20.2(16.4)	23(17.8)		86(68)
N = 500	7.7(8.1)	2.6(2.9)	4.3(4.3)	13.2(14.7)	16.2(16.8)	21.8(22.6)		66(69)
N = 1000	7.6(7)	2.6(2.6)	3.8(3.4)	12.7(17.2)	15.6(19.6)	20.5(22.9)		63(73)
N = 5000	6.4(6.7)	2.4(2.5)	2.6(3.2)	12.3(12.5)	15.8(17.2)	19.2(19.9)		59(62)

Note. Σ(η) represents the sum of η values over all parameters of a model.

Goodness-of-fit

The goodness-of-fit of each model to its own simulated data can be qualitatively appreciated in Figure 2. The first, second, and third columns respectively show predicted (y-axis) versus simulated (x-axis) RT quantiles for correct responses, accuracy data, and RT quantiles for errors. Each row represents a number of simulated trials N per compatibility condition. The goodness-of-fit of each model is very good: datapoints are gathered around the ideal predicted = simulated line, with no systematic deviation. Because the precision of RT quantiles and accuracy data estimation monotonically increases as N increases, the fit quality increases as a function of N, reflected by a smaller dispersion of scatterplots. As expected from our adaptive procedure (see Methods), the number of RT quantiles for errors increases as N increases, providing more constraints on parameter estimates. Optimized chi-square statistics averaged over the 100 datasets for each condition and each model are shown in Table 4. Remember that the chi-square statistic is weighted by the number of observations (see Equation 4), which explains why it increases as N increases. For realistic experimental settings (N = 50–500), chi-square values appear relatively similar across models, enabling a fair parameter recovery comparison.

Figure 2.

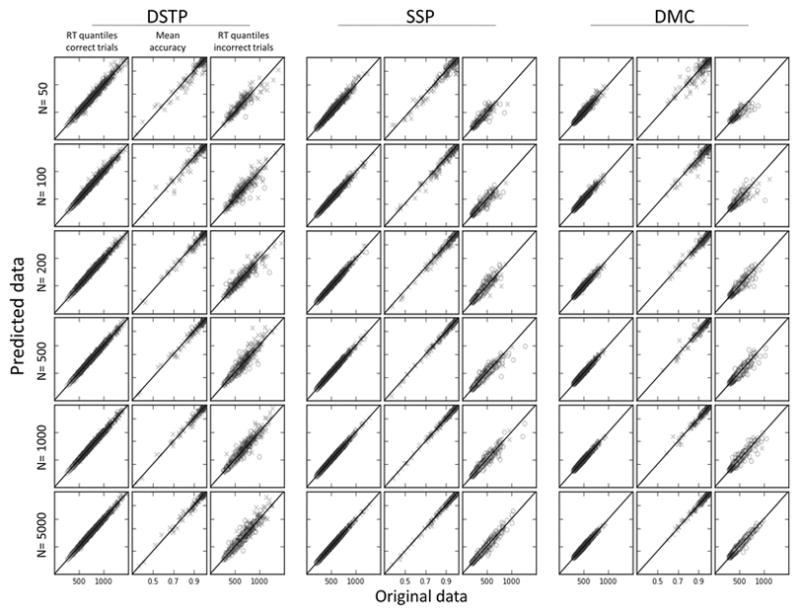
Predicted versus simulated data for each model and condition (N trials). Values along the identity line indicated correspondence between predicted and simulated RTs and error rates.

Table 4.

Chi-square goodness-of-fit statistic averaged over the 100 datasets.

	$\overline{{\chi }^2}$
	DSTP	SSP	DMC
N= 50	10.4	11.6	12.5
N= 100	15.2	12.1	14
N = 200	16.7	15.6	20
N = 500	25.1	16.6	24.5
N = 1000	39.0	19.7	29.8
N = 5000	117.8	31.2	76.9

Parameter recovery

Figures 3, 4 and 5 respectively show correlations between simulated versus recovered parameters as a function of N for the DSTP, SSP, and DMC models. A rapid look at the figures shows that the general recovery performance decreases when the number of free parameters of the model increases, SSP (5 parameters) > DMC( 6 parameters) > DSTP (7 parameters). The general recovery performance of a model is quantified by the sum of the goodness-of-recovery η statistic over all parameters of a given model (Table 3, rightmost column). This statistic reveals a clear SSP>DMC>DSTP performance pattern, whatever the condition N. In addition, the general recovery performance monotonically increases as N increases, due to stronger model constraints provided by more precise RT quantiles and accuracy data estimates.

Figure 3.

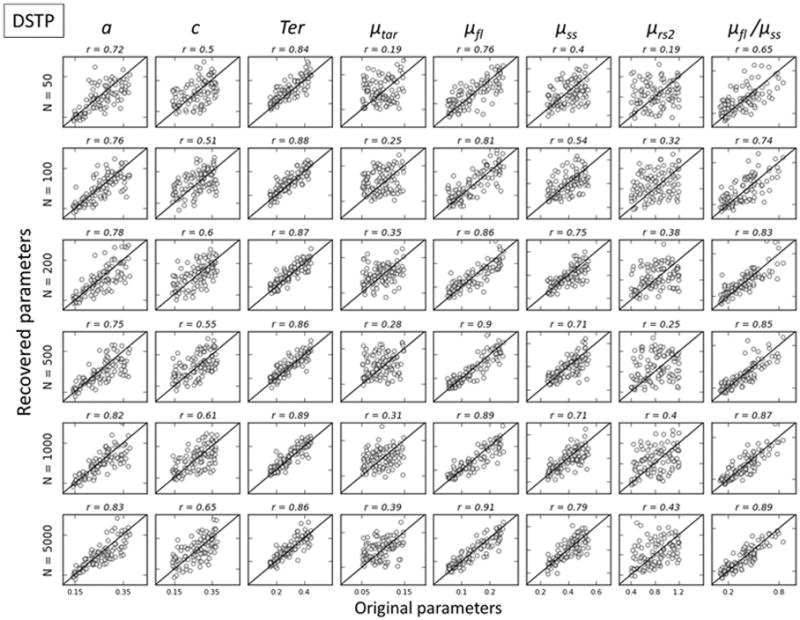
Parameter recovery for DSTP. Simulated values are plotted against recovered values for each parameter. Values along the identity line indicate good recovery, which is quantified by the correlation between simulated and recovered (r).

Figure 4.

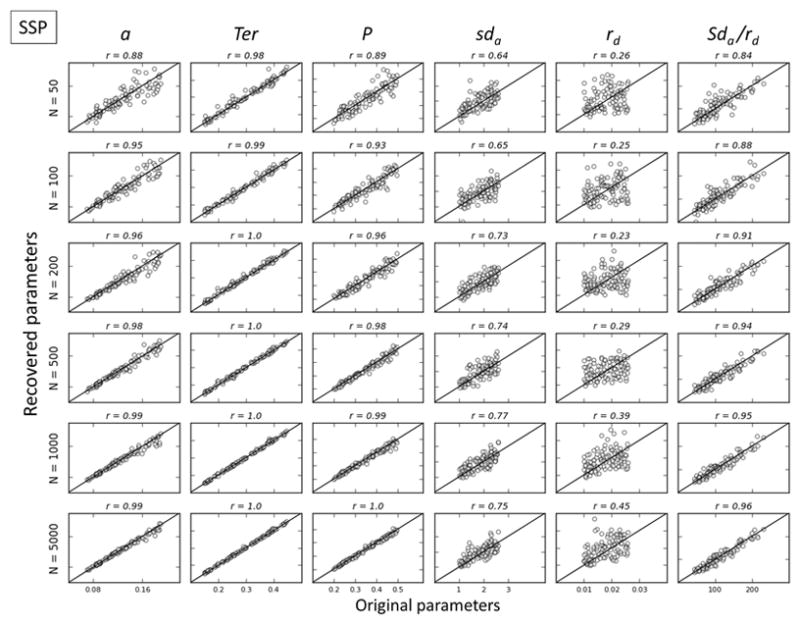
Parameter recovery for SSP. Simulated values are plotted against recovered values for each parameter. Values along the identity line indicate good recovery, which is quantified by the correlation between simulated and recovered (r).

Figure 5.

Parameter recovery for DMC. Simulated values are plotted against recovered values for each parameter. Values along the identity line indicate good recovery, which is quantified by the correlation between simulated and recovered (r).

Standard diffusion parameters (boundary separation for the decision process, a, and nondecision time, Ter) are generally well recovered, particularly for SSP and DMC models, with correlations ranging from .81 to .1 provided N ≥ 100. To facilitate the interpretation of other (model-specific) parameters, we adopted the following criterion. The quality of the recovery was considered poor if correlation coefficients between original and recovered parameters were below .5, fair if .5<r<.75, good if .75<r<.9 and excellent if r> .9. DSTP parameters were poorly/fairly recovered, except for the early drift rate for the interference μ_fl. The recovery of parameters related to the processing of the relevant stimulus attribute in SSP (perceptual input of the target p) and DMC (drift rate for the controlled process μ_c) models was excellent, with correlations ranging from .89 to 1. However, the recovery of conflict-related parameters (SSP: initial spotlight width sd_a and shrinking rate r_d; DMC: peak amplitude ζ, shape α, and characteristic time τ parameters of the gamma function) was poor/fair for realistic experimental settings (N = 50–500).

Quantification of cognitive control

Experimental findings in conflict tasks suggest that the automatic activation is short-living (reviewed by Ulrich et al., 2015). It is unclear, however, whether the automatic activation triggered by the irrelevant stimulus attribute passively decays (e.g., Hommel, 1993, 1994) or is actively suppressed (e.g., Ridderinkhof, 2002). As detailed in the introduction section, SSP and DSTP models assume that early interference is actively suppressed. The automatic activation in SSP is reflected by the initial width of the spotlight sd_a, and suppression is quantified by the spotlight shrinking rate r_d. Our recovery results show that activation and suppression components cannot be quantified separately within SSP. This is because a wide initial spotlight width combined with a high shrinking rate mimics a narrow spotlight width combined with a weak shrinking rate. We therefore examined whether the ratio sd_a/r_d, termed interference time, was better recovered. This ratio quantifies the time it takes for the spotlight to narrow on the target, or equivalently, the time it takes to suppress interference from the flankers. Figure 4 (column 6) shows that the recovery of the interference time is good for small values of N (50 and 100), and excellent for N ≥ 200. Notice that the interference time is a composite measure: a short interference time can either reflect a weak automatic activation or a strong suppression (or both).

Within the DSTP model framework, automatic activation is quantified by the early drift rate for the interference μ_fl, a parameter that is well recovered. However, the recovery of parameters that drive suppression (drift rate for stimulus selection/categorization μ_ss and drift rate for response selection in phase 2 μ_rs2) ranges from poor to fair. Figure 3 (column 8) shows that the ratio μ_fl/μ_ss was well recovered, provided N ≥ 200. This ratio can be interpreted in a similar way as the interference time for the SSP. However, it does not specify the theoretical latency necessary to overcome interference. Interference suppression also depends on the drift rate for response selection in phase 2, μ_rs2, which complicates the analysis.

Contrary to SSP and DSTP models, the DMC is agnostic regarding whether the automatic activation passively decays or is actively suppressed (Ulrich et al., 2015). The time-course of the automatic activation is modeled by a gamma function, and the gamma decay can be driven by spontaneous decay, active suppression or both. Also, parameters of the gamma function do not directly map onto automatic activation and decay components. We therefore examined the quality of the recovery for different statistics computed from the gamma function parameters. These statistics offer a more direct window into activation and decay/suppression components. We first computed the peak latency of the gamma function t_max = τ(α−1), corresponding to the onset latency of decay/suppression. The recovery for t_max was good even for the lowest N values (Figure 5, column 7). We then computed the interference time statistic t_90th, defined as the 90^th percentile of the gamma percent point function. This statistic corresponds to the latency at which 90% of the gamma impulse has been emitted, and quantifies the time it takes for the interference to disappear, akin to the ratio sd_a/r_d for the SSP. Figure 5 (column 8) shows that the recovery of t_90th is good provided N≥ 200. The good recovery of t_90th and t_max statistics has an implicit advantage allowing the estimation of the decay/suppression strength, defined as t_90th − t_max.

Ulrich et al. (2015) fixed the shape parameter α of the gamma at 2. This constraint simplifies parameter estimation, and might improve the quality of the recovery for the other model parameters. To test this hypothesis, we simulated data from the 100 DMC parameter sets previously used, but fixed α = 2. Correlations between simulated versus recovered parameters for this constrained DMC model are shown in the online appendix. Fixing the shape parameter substantially improved the recovery for the peak amplitude (ζ) and characteristic time parameter τ of the gamma function. Notice, however, that τ now corresponds to the peak latency of the gamma (peak latency = τ(2−1)=τ). For each number of simulated trials N, the quality of the recovery for the peak latency of the gamma for the constrained DMC model (r = .71–.93) was worse than the unconstrained model (r = 86–.97; see Figure 5, column 7)². The recovery for the other model parameters (decision separation a, drift rate for the controlled process μ_c and nondecision time Ter), was virtually similar between the two models. Consequently, researchers should fix the shape parameter α of the gamma at 2 when they are mainly interested in quantifying the peak amplitude of the automatic activation.

Assessing mimicry among models

The above analysis focused on determining the amount of confidence we can have for recovered parameters for each of the models. However this does not address the issue of how to select which model to use in the first place. Standard model selection tools can be used theoretically, but there is still concern about model mimicry in which two or more of the models fit the data equally well. In the case of the Flanker task, White et al., (2010) and Hübner et al. (2014) found substantial mimicry between the 2 models, though their fits suggest some differences between model predictions (see also Servant et al., 2014). Thus it is unclear the extent to which model mimicry is a problem for these conflict DDMs. To evaluate model mimicry, we fit the SSP to data simulated from the DSTP (referred to as SSP_DSTP) for the N = 5000 trials condition and vice-versa (DSTP_SSP). These cross-fits produced chi-squares considerably higher than those obtained when fitting the models to their own data (see supplementary Table S1). This result shows that the SSP and DMC can be distinguished, because they produce distinct behavioral patterns. Predictions of each model are plotted in supplementary Figure S2 (columns 1 and 2). SSP predicts slower (faster) errors than DSTP for the compatible (incompatible) condition. DSTP predicts faster .9 RT quantiles than SSP, due to its second phase of response selection (typically associated with a very high drift rate; see μ_rs2 values in Table 1). For thoroughness, we examined the correlation between interference measures of the SSP (s_da/r_d) and DSTP (μ_ss/μ_rs2). This correlation was positive and high for SSP_DSTP(r = .63, p< .001) and DSTP_SSP (r = .57, p< .001), showing that the models agree to a large extent on the amount of interference in the data.

The DMC was explicitly developed as a general model for all conflict tasks (Simon, Flanker, and Stroop). In particular, the DMC is the only model able to produce a decrease of interference on RTs as RT increases, as commonly observed in the Simon task (but not in Flanker and Stroop tasks; see Introduction). To evaluate whether the DMC produces behavioral signatures and estimates of interference different than SSP and DSTP models in the Flanker task, we fit the DMC to data generated by SSP (DMC_SSP) and DSTP (DMC_DSTP). Once more, chi-squares from cross-fits were substantially larger than chi-squares obtained when fitting the models to their own data (supplementary Table S1). The DMC predicts slower errors than SSP and DSTP models, particularly for the compatible condition. The automatic activation favors the correct response in compatible trials, reducing the probability of errors in the early period of the decision process. The shape of RT distributions for correct responses predicted by DMC and DSTP models are also different. In particular, the DMC predicts slower .9 RT quantiles for correct responses than the DSTP. Interestingly, the estimated amount of interference predicted by the DMC (t_90th) diverged from estimates of the other models, particularly SSP (DMC_SSP: r = .16, p = .11; DMC_DSTP: r = .38, p< .001).

To summarize, SSP and DSTP models appear to converge on the estimated amount of interference conveyed by Flanker task behavioral data, despite distinct behavioral predictions. The DMC model is conceptually more general, and is able to capture data from different conflict tasks. The DMC generates measures of interference that diverge from SSP and DSTP models in the Flanker task. These findings motivate a model comparison experiment, beyond the scope of the present work. Our parameter recovery study tells us how much faith we can put in particular parameter values, which in cases of poor recovery is not much. Model comparison tells us how much faith we can put in one model vs. another, and appears as a complementary step in exploring and evaluating the models.

Discussion

There is great interest in comparing performance in conflict tasks across individuals or groups. The common approach of using RT or accuracy values is limited by problems of reverse inference, whereby multiple decision components can lead to differences in performance. This reverse inference problem can be circumvented, in theory, by using conflict DDMs to decompose behavioral data into distinct decision processes and make inferences on the resulting estimated parameters. However, a DDM-based analysis is only meaningful if the estimated parameters reflect true differences in decision processing. Consequently, the present study assessed the ability of conflict DDMs to accurately recover parameters reflecting processing in conflict tasks. Using a parameter-recovery analysis, we assessed model performance for the Shrinking Spotlight Model, the Dual-Stage Two Phase Model, and the Diffusion Model for Conflict Tasks for standard compatible/incompatible conditions across a broad and plausible range of parameter values. The models generally showed accurate recovery of the basic components of a standard DDM (boundary separation and nondecision time), but the results for the conflict-specific parameters of the models were more nuanced. Overall, each model showed limitations in recovering the conflict parameters that drive the time-varying decision evidence in conflict tasks, but parameter recovery could be improved by calculating derived measures to quantify interference and cognitive control.

There are two primary questions for selecting which model to use to make inferences from data: Is this model appropriate for the task (i.e., does the model fit the data) and can we trust the recovered parameter values? Task appropriateness is based by the scopes of the models and extant empirical validation: the SSP is specific to spatial attention and should be used only for the Flanker task, the DSTP more broadly accounts for selective attention and can be used for Flanker or Stroop task, and the DMC provides the most general account of conflict processing and can be used for Flanker, Stroop, or Simon tasks. In the cases of Flanker and Stroop data, where more than one model accounts for the data,, the standard recommendation would be to use model selection techniques to select the most appropriate model based on data fit (and model flexibility). However, model selection tools that account for both fit and flexibility, like the Bayesian Information Criterion (BIC), do not account for the validity of parameter recovery, which is particularly important for studying individual differences. The simulation-recovery study showed that although each of the models provided good fits to their own data, they differed significantly in the quality of parameter recovery. Whereas SSP and DMC showed strong parameter recovery when the derived measures were used, DSTP did not. Thus even if DSTP provided a better fit than DMC or SSP to a data set, the latter models should be preferred for studying individual differences so long as they show good fits to the data. Accordingly, we recommend using model selection for choosing between SSP and DMC for Flanker data, and using DMC for Stroop or Simon data. Still, the issue of model selection with these models deserves in depth consideration and remains an important future direction.

The present work focuses on determining the validity of recovered parameters when a model is chosen to estimate parameter values for the decision process and conflict resolution. Although the focus was not on model selection per se, the results demonstrate an important consideration for model selection: model performance must be assessed by more than just a good fit to the data (Roberts & Pashler, 2000). In many cases the models provided good fits to the simulated data (Figure 2) even though the recovered parameters were not accurate. Thus it is critical to demonstrate not only that a model can account for the behavioral data, but that the estimated parameters provide accurate measures of the underlying processes. Doing so for the conflict DDMs in this study revealed the necessity of calculating derived measures of interference and cognitive control and establishes practical guidelines for employing these models to analyze behavioral data. Below we summarize the primary findings and recommendations for employing these models to draw inferences from conflict data.

DSTP

The Dual-Stage Two Phase model showed limitations in recovery for the parameters governing the time-varying drift rate in conflict tasks. The raw values of these parameters were not recovered well from the simulated data, limiting the inferences that can be obtained from fitting the DSTP to data. To overcome this limitation, we calculated a parameter ratio (μ_fl/μ_ss) to index the amount of flanker interference relative to the speed of stimulus selection. This ratio can be interpreted as the amount of interference from incompatible stimuli. While the new ratio was better recovered than the raw parameter values, the correlations between simulated and recovered parameters were still low compared to the SSP and DMC. These results have consequences for null hypothesis testing. The DSTP - should generally only be used in cases of high statistical power to detect differences among conditions or groups of participants, and thus one should be prudent when drawing inferences from DSTP fits.

The performance of the DSTP could be improved by using more complex factorial designs, in which variables that should affect one property of the model are manipulated independently of variables that should affect another property of the model (Hübner et al., 2010; Servant et al., 2014; White et al., 2011). Another approach to improve parameter estimation for the DSTP is to use a jackknife procedure (Dambacher & Hübner, 2013; Ulrich et al., 2015) when comparing group performance. However this approach sacrifices the estimation of individual participant parameters and thus forgoes fine-grained analysis of individual differences.

SSP

The Shrinking Spotlight Model includes two parameters to govern interference in conflict tasks, the width of the attentional spotlight (sd_a) and the shrinking rate (r_d). These parameters were not accurately recovered in their raw form because they can tradeoff with each other. That is, a wide spotlight with a fast shrinking rate can produce similar interference as a narrow spotlight with a slow shrinking rate. Fortunately, this tradeoff can be accounted for by taking the ratio of these two parameters (sd_a/r_d), which conceptually provides an index of the duration of interference that occurs on incompatible trials. This interference ratio was accurately recovered in the simulation study, suggesting it can be used as a valid measure of interference. It is important to note that this interference ratio is a composite measure: short interference can either reflect weak automatic activation, strong suppression, or both. Thus the SSP cannot differentiate the separate contribution of activation and suppression, but rather their relative values³. Overall, the parameters of the SSP showed strong recovery from the simulations, suggesting that the model can be used to analyze data with as few as 50 observations per condition per subject. Thus researchers can confidently employ the SSP to analyze data, but they should use the interference ratio (sda/rd) rather than the raw parameters for spotlight width and shrinking rate. This ratio can be calculated post hoc after fitting the model, making analysis with the SSP fairly straightforward. Because the model was designed to account for the Flanker task, we recommend that it only be used for that task until/unless it is shown to adequately account for data from other conflict tasks.

DMC

The Diffusion Model for Conflict Tasks showed strong recovery for the standard parameters of the DDM framework for boundary separation (a), nondecision time (Ter), and drift rate for controlled processing (μ_c), but not for the parameters governing the gamma distribution for automatic activation (ζ, α, and τ). However, the derived measures of interference/suppression, t_max and t_90th, showed good recovery so long as the number of trials per subject was 200 or larger. These derived measures allow to selectively quantify the onset latency (t_max) and strength (t_90th − t_max) of suppression/decay of the automatic activation. This is a major advantage over SSP and DSTP models, as suppression efficiency has been the focus of many theoretical (Burle, Possamai, Vidal, Bonnet, & Hasbroucq, 2002; Forstmann et al., 2008; Ridderinkhof, 2002) and clinical studies (Ridderinkhof, Scheres, Oosterlaan, & Sergeant, 2005; van Wouwe et al., 2016; Wylie et al., 2012; Wylie, Ridderinkhof, Bashore, & van den Wildenberg, 2010; Wylie et al., 2009).

Overall, for DMC these results suggest that although the specific parameters for the gamma distribution of automatic activation are not well-recovered, the model can be applied to estimate the derived measures of interference/suppression for designs with a larger number of observations. The DMC has been shown to account for data from a wider range of conflict tasks including the Simon and the Flanker, (Ulrich et al., 2015), and thus can be more broadly applied than the SSP or DSTP.

Future Directions

While the parameter recovery analysis in this study was comprehensive, there remain potential avenues to improve parameter estimation for future use of conflict DDMs. One would be to implement hierarchical Bayesian versions of the models, which in theory can improve parameter estimation (especially with low numbers of trials). However there are three potential limitations to this approach. First, improvements in parameter estimation will be dependent on the use of prior information to restrict the parameter space, and there is currently no empirical information to support the selection of such these priors. Second, Bayesian hierarchical models require a likelihood function for RT and accuracy data. However, the likelihood function for models with time-varying drift rates, like the SSP and DMC, is mathematically intractable (Ratcliff, 1980; Ulrich et al., 2015; White et al., 2011). One way to circumvent this problem is to use likelihood-free methods such as approximate Bayesian computation (Turner & Van Zandt, 2014) or probability density approximation (Turner & Sederberg, 2014). Third, these methods are complex and computationally intensive, which can restrict practical usage. Although the use of cluster computing can mitigate this problem, such resources are not available for many researchers who wish to use these models to analyze their data.

It is also the case that parameter recovery can be improved with more complex factorial experimental design. The present study focused on parameter validity in the most basic case for conflict tasks: one compatible condition and one incompatible condition. However the addition of other conditions that only affect certain parameters can improve parameter estimation. For example, multiple stimulus conditions that are intermixed are generally assumed to affect drift rate but not boundary separation or response bias, based on the idea that the latter components are not adjusted on a trialwise basis dependent on the type of stimulus being shown (see Ratcliff & McKoon, 2008). In such cases the models can be constrained to fit all of the conditions simultaneously with only the parameters governing the drift rate varying across condition while the other parameters are held constant (for a recent example with the DMC, see Servant et al., 2016). This places stronger constraints on the parameter estimation and can improve model performance.

Conclusion

The results of the simulation-recovery analysis in the present study suggest that among the newly-developed diffusion models for conflict tasks, the Shrinking Spotlight model and Diffusion Model for Conflict Tasks can be used confidently to estimate parameters from behavioral data, but only if derived measures are used to quantify interference/suppression. Fortunately, these derived measures provide conceptually useful indices of the amount of interference (and conversely suppression or cognitive control) for participants in conflict tasks. Overall, this study demonstrates the importance of thoroughly evaluating models like the conflict DDMs to ensure they provide valid and meaningful parameter estimates when fitted to data.

Supplementary Material

1. Table S1.

Optimized chi-square goodness-of-fit statistic for cross-fits averaged over the 100 simulated datasets.