Posterior cingulate neurons dynamically signal decisions to disengage during foraging

Abstract

Foraging for resources is a fundamental behavior balancing systematic search and strategic disengagement. The foraging behavior of primates is especially complex and requires long-term memory, value comparison, strategic planning, and decision making. Here we provide evidence from two different foraging tasks that neurons in primate posterior cingulate cortex (PCC) signal decision salience during foraging to motivate disengagement from the current strategy. In our foraging tasks, salience refers to the difference between decision thresholds and the net harvested reward. Salience signals were stronger in poor foraging contexts than rich ones, suggesting low harvest rates recruit mechanisms in PCC that regulate strategic disengagement and exploration during foraging.

Introduction

Animals forage for a wide range of resources (Stephens and Krebs 1986), making a series of sequential, non-exclusive, accept-or-reject decisions (Stephens 2008; Calhoun and Hayden 2015). Hypothesized as a major selective pressure driving the expansion of neocortex in primates (Milton 1988; Genovesio et al. 2014; DeCasien et al. 2017), foraging is a fundamental cognitive skill (Newell 1994; Hills et al. 2010) applicable in a variety of domains including search (Cain et al. 2012; Wolfe 2013), memory (Hills et al. 2015), and social (Hills and Pachur 2012; Turrin et al. 2017) and executive processing (Payne et al. 2007; Wilke et al. 2009; Metcalfe and Jacobs 2010; Payne and Duggan 2011). Despite widespread relevance, the neural circuits mediating foraging have only recently begun to be described (Hayden et al. 2011; Kolling et al. 2012; Shenhav et al. 2014).

The anterior and posterior cingulate cortices, strongly and reciprocally connected (Heilbronner and Haber 2014), are both implicated in control (Botvinick et al. 2004; Pearson et al. 2011). During foraging, dorsal anterior cingulate cortex (dACC) carries signatures of reward-based computations (Hayden et al. 2011; Kolling et al. 2012; Shenhav et al. 2014) but the role of the posterior cingulate cortex (PCC) remains unknown. Neuroimaging studies link PCC activity with value (Kable and Glimcher 2007; Knutson and Bossaerts 2007), strategy (Wan et al. 2015), and change detection (Summerfield et al. 2011; McGuire et al. 2014). PCC neurons signal rewards (McCoy et al. 2003), risk (McCoy and Platt 2005), task switches (Hayden and Platt 2010), and exploratory decisions (Pearson et al. 2009). In addition, microstimulation of PCC provokes preference reversals (Hayden et al. 2008) and inactivation impairs learning (Heilbronner and Platt 2013). This diverse array of observations may reflect computations that regulate foraging behavior.

Here we show PCC neurons signal salience in motivating decisions to disengage during foraging. Salience refers to attentional capture by environmental events (Treisman and Gelade 1980; Gottlieb et al. 1998) or decision outcomes (Pearce and Hall 1980; Esber and Haselgrove 2011; Kahnt et al. 2014), and regulates stimulus processing (Corbetta and Shulman 2002), learning (Yu and Dayan 2005) and motivation (Bromberg-Martin et al. 2010; Kahnt and Tobler 2013). PCC neurons are known to signal outcome salience, including reward size (McCoy et al. 2003), omission (McCoy et al. 2003), and variance (McCoy and Platt 2005), as well as offer salience, the absolute difference of option values from a standard (Heilbronner et al. 2011).

Here we report that foraging salience, defined as the absolute difference between experienced and threshold cumulative reward, regulated strategy in two separate foraging tasks involving distinct decisions to disengage. In the patch foraging task, monkeys chose between harvesting reward from a diminishing source and disengaging to forage in a new one. In the traveling salesman task, a circular array of targets was baited unpredictably with large and small rewards. Monkeys developed routine circular patterns of target exploitation, known as a trapline in behavioral ecology (Berger-Tal and Bar-David 2015; cf. Freeman 1968 after Darwin). In both tasks, PCC neurons forecast decisions to disengage and signaled foraging salience, with stronger signals in poor environments than rich ones. Our results suggest PCC neurons signal foraging salience to promote strategic disengagement and exploration.

Results

Travel times and decision salience drive patch leaving decisions

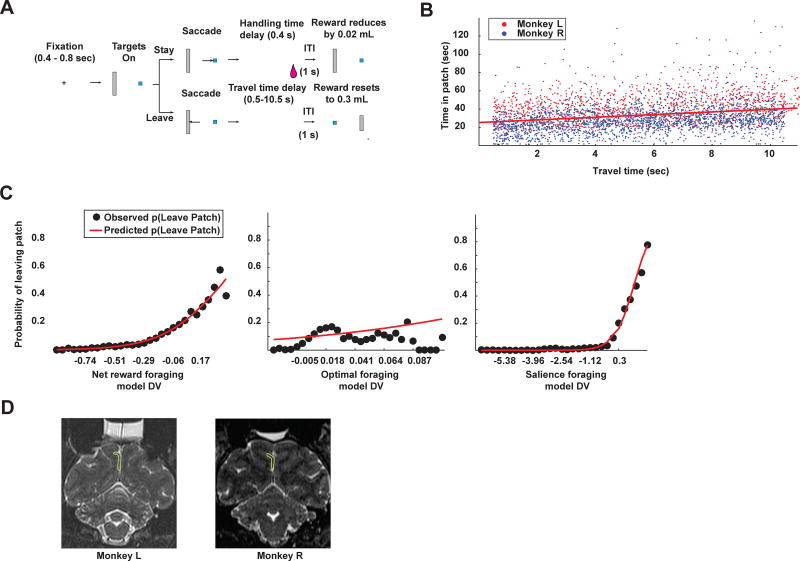
In the patch leaving task, monkeys (M. mulatta) decided to harvest reward from a depleting patch or to disengage and replenish it (Figure 1A). They made a series of decisions to harvest a juice reward that decreased over time as it was repeatedly chosen (initially 0.3 mL, decreasing in ~0.02 mL steps) or to reset the value of the patch, incurring a “travel time” that varied from patch to patch. Patch residence time increased as travel times increased (Figure 1B), corroborating prior observations (Hayden et al. 2011) (linear regression, p < 0.00001, β = 1.40; Monkey L (ML): p < 0.00001, β = 1.11; Monkey R (MR): p < 0.00001, β = 1.50).

Figure 1.

Patch foraging task reveals sensitivity of monkeys to salience during foraging. A. The patch leaving task. Monkeys fixate on the central cross for 400 – 800 ms. Fixation then extinguishes and targets appear. If monkeys choose the small blue rectangle (stay in patch option), then a small reward is delivered after a brief delay (handling time; 400 ms) followed by one second intertrial interval (ITI) and beginning of a new trial. Reward associated with the stay in patch option also decreases by a small amount. If monkeys choose the large gray rectangle (leave patch option), they must wait through a time-out period corresponding to the height of the gray bar, and do not receive reward. This is followed by one second ITI and beginning of a new trial in a new patch. At onset of a new patch, reward associated with the blue rectangle resets to a constant initial amount, locations of the blue and gray rectangles are swapped, and a new height for the gray bar, signaling the travel timeout to replenish the patch, is selected from a uniform distribution, which correlates with a delay ranging from 0.5 to 10.5 seconds. B. Time in patch plotted as a function of travel time. As travel times grew, monkeys stayed longer in a patch. 3511 patches in 43 electrophysiology sessions across both monkeys. C. Probability of leaving a patch vs. the decision variable for three different behavioral models. Black circles: mean observed probability of leaving a patch for the corresponding value of the decision variable. Red lines: predicted leave probability. All three plots display a logistic regression of leave or stay decisions against the decision variable. Left panel: net reward foraging model; middle panel: optimal foraging model; right panel: salience foraging model. D. Recording locations for both monkeys.

We considered three models of patch-leaving decisions: an optimal foraging model based on the Marginal Value Theorem (MVT; Charnov 1976), a net foraging model based on survival analysis (Fox 2001), and a salience model inspired by attentional learning theory (Pearce and Hall 1980). The optimal foraging model set the decision variable to the difference between the current reward rate and the MVT-calculated optimal reward rate for departing a patch. The net foraging model captured the central tendencies of the decision to leave a patch by setting the leave threshold to the mean of the exponential reward intake function and setting the decision variable to the reward differential, the difference between the current net harvested reward computed over the whole patch and threshold net harvested reward computed from the mean of the intake function. The salience foraging model set the decision variable to the product of the reward differential and weighted salience, the absolute value of the reward differential.

The salience foraging model provided the best fit to patch leaving decisions (Figure 1C; mean AIC score ± s.e.m.: net foraging model: 509.87 ± 28.88; ML: 400.50 ± 31.45; MR: 604.97 ± 36.73; optimal foraging model: 488.65 ± 28.50; ML: 373.23 ± 29.57; MR: 589.02 ± 35.46; salience foraging model: 398.75 ± 26.60; ML: 272.80 ± 21.27; MR: 508.27 ± 31.84; see methods). Corroborating these fits, response times were faster for more salient choices (linear regression by day of response times vs. salience; ML: mean β = −0.022 ± 0.025, Student’s t-test, p > 0.39, t(19) = −0.88; MR: mean β = −0.13 ± 0.0089, Student’s t-test, p < 1×10⁻¹², t(22) = −14.94).

PCC neurons forecast leave decisions and dynamically signal salience during patch foraging

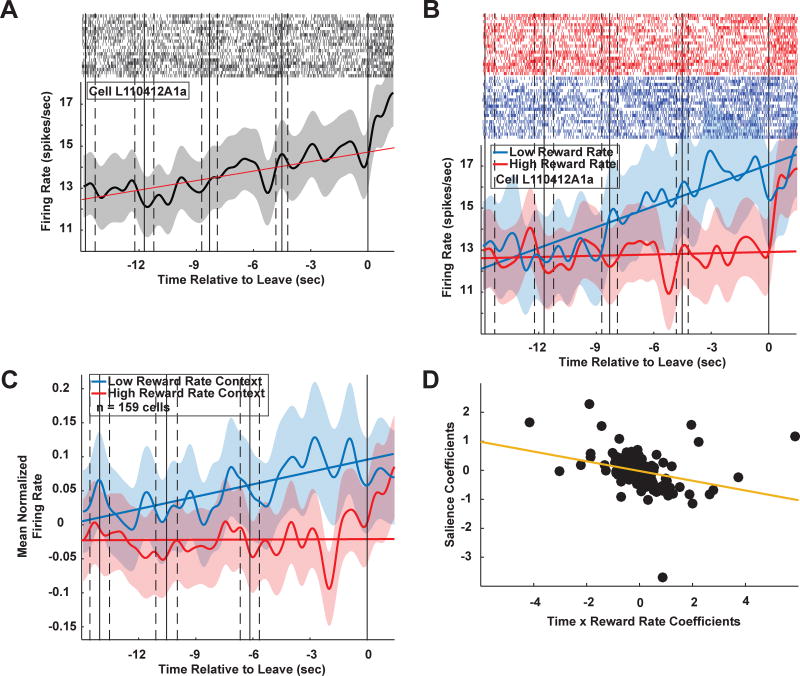
We recorded activity of 159 PCC neurons (Figure 1D; 96 in ML, 63 in MR; individual monkey results in Supplement). Firing rates predicted patch leaving decisions many seconds in advance by ramping up or down in the last 15 s in patch (example cell, Figure 2A; patch exit epoch; linear regression during patch exit epoch, p < 1×10⁻²⁰, β = 0.20 ± 0.020, Figure 2A). Eighty-six (54%) of 159 cells showed a significant increase or decrease in activity approaching patch exit (linear regression during patch exit; p < 0.05). This pattern is reminiscent of ramping of neuronal activity to a threshold observed for perceptual and foraging decisions (Gold and Shadlen 2007; Hayden et al. 2011) but extended continuously across multiple actions. We focused the remaining analyses on this patch exit epoch.

Figure 2.

PCC neurons predict patch departures several seconds in advance. A. Sample cell PSTH starting 15 seconds before patch departure. This cell shows a marked increase in firing (thick black line) during the 15 second patch exit window. Red line: linear fit to firing rate within the patch exit window. Gray shading: ± 1 s.e.m. Light gray tickmarks: Sample raster plots from 20 patches. B. Same cell as in (A), showing differences in firing dynamics depending on environmental richness preceding decisions to leave a patch. Rich contexts (red trace): reward rate z-score ≥ 0; poor contexts (blue trace): reward rate z-score < 0. C. Population plot for rich and poor environments, matching the pattern observed in the sample cell in (B). n = 159 cells (96 from ML, 63 from MR). D. Salience coefficients plotted against the interaction of time and reward rate coefficients. Later and lower reward rates resulted in stronger salience signaling. See also Figure S3. See Figure S1 for individual monkey results.

Because PCC neurons signal and causally facilitate learning in low value contexts but not high ones (Heilbronner and Platt 2013), we next queried whether PCC neurons signal patch departures differently in distinct reward rate contexts. Reward rate was defined as the net reward harvested in a patch divided by time spent harvesting. Poor environments presented low (z-score ≤ 0) reward rate decision contexts and rich environments presented high (z-score > 0) ones. An example neuron showed a significant increase in firing rate preceding the decision to leave the patch in poor environments (Figure 2B; linear regression, p < 1×10⁻²³) but not rich ones (p > 0.4). The slopes of these regressions differed significantly (ANCOVA, p < 1×10⁻¹³, F(1,596) = 62.57). Environmental richness modulated this neuron’s ramping activity across patches (linear regression of patch-by-patch slopes vs. z-scored reward rate, p < 0.001), a pattern seen in the slopes of 20 (13%) of 159 cells (linear regression, p < 0.05). This pattern was also evident in the average population activity (Figure 2C; linear regression, poor: p < 1×10⁻⁹, rich: p > 0.35; ANCOVA, p < 0.00005, F(1,596) = 17.21).

The observation that firing rates of PCC neurons predict impending patch departures prompts the question of whether PCC neurons also signal salience, and if so, whether salience signals vary with environmental richness. Rich environments may attenuate salience signaling because the current strategy remains profitable. Combined with differences in ramping across contexts, the dependency of salience signaling on environmental richness predicts a three-way interaction during the patch exit epoch between time, reward rate, and salience. Spike counts in 50 ms bins were regressed against all three covariates and all interactions using a generalized linear model (GLM) with a log-linear link function and Poisson distributed noise. Of 159 neurons, 25 (16%) showed significant interactions of all three covariates (ML: 17 (18%) of 96 neurons; MR: 8 (13%) of 63 neurons; see methods). To examine temporal dynamics, all spikes in a sliding boxcar (3 s width, 50 ms steps) were regressed against reward rate, salience, and their interaction (Figure S3A, cells sorted from negative (top) to positive (bottom) by the sum of the beta coefficients). This analysis revealed a pattern of positive and negative salience coefficients over time, with some cells positively signaling foraging salience and others negatively, indicating PCC neurons do not store salience information between patch leaving decisions.

Context dependent salience signaling also predicts stronger salience signals in poor environments. Coefficients for salience were negatively correlated with coefficients for the interaction of reward rate and time in patch (Figure 2D; linear regression, β = −0.17 ± 0.042, p < 0.0005), confirming this prediction.

Finally, this context dependency predicts the influence of salience on firing rates in poor patches should be larger than in rich ones. We regressed spike counts during the whole trial epoch (1 s before choice to 1 s after) against salience for poor and rich patches separately. In rich environments there was no population-level effect of salience (linear regression, mean β = 0.098 ± 0.090, Student’s t-test, p > 0.27, t(158) = 1.10). By contrast, in poor environments, greater salience was accompanied by increased average firing rates in the whole population (mean β = 0.48 ± 0.18, p < 0.01, t(158) = 2.67). The influence of salience was also larger in poor environments than in rich ones (Student’s t-test, mean Δβ = 0.38 ± 0.18, p < 0.05, t(158) = 2.16).

Monkeys trapline forage to solve a traveling salesman problem

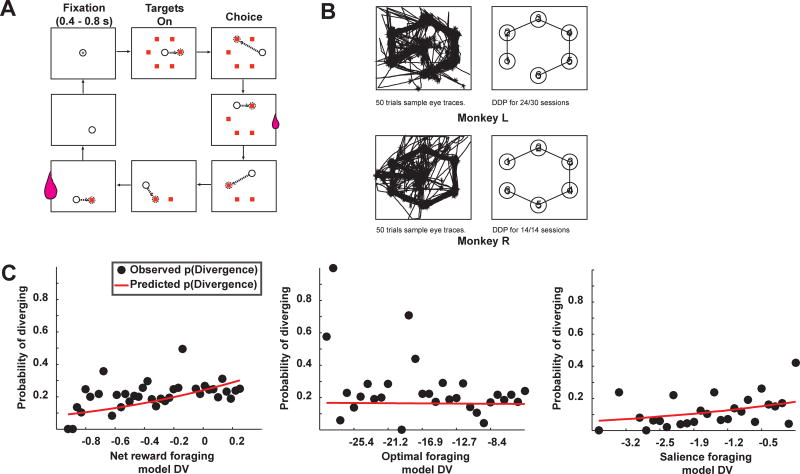
In our traveling salesman task, monkeys visually navigated through a circular array of six targets (Figure 3A). Two targets were randomly baited on each trial, one with large and one with small reward. Monkeys spontaneously developed traplines, defined as a set sequence of choices. They typically chose targets in the same sequence across days, tracing a circle, the most efficient route (the daily dominant pattern, DDP; ML: same DDP across 24 of 30 sessions; MR: same DDP across all 14 sessions; Figure 3B; see methods).

Figure 3.

Monkeys spontaneously diverged from traplines in a traveling salesman task. A. Traveling salesman task. Monkeys fixate on the central cross for 400–800 ms. Fixation extinguishes and targets appear. Monkeys are free to select targets in any pattern, but must select all six targets to advance to the next trial. Two targets were baited, one with a small reward and one with a large reward (small and large juice drops respectively). B. Sample eye traces from 50 trials each for monkey L (top) and monkey R (bottom). Left panel shows eye traces; right panel lists the typical order in which targets were selected (daily dominant pattern; DDP) for each monkey. C. Probability of diverging from trapline vs. the decision variable for three different behavioral models, the same models as fit to the patch leaving task choices. Same conventions as Figure 1C.

Though monkeys usually chose targets in the same order, they occasionally diverged from this routine, providing an opportunity to investigate changes in foraging strategy in a second task. Across all recording days, mean proportion of diverge trials was high, 0.21 ± 0.017 of all trials (ML: 0.22 ± 0.025; MR: 0.18 ± 0.0078). To capture these divergences, the three foraging models used in the patch foraging task were fit to monkeys’ choices on the traveling salesman task (see methods). Choices were coded as decisions to stay on the trapline or diverge from it, excluding trials where monkeys started with an off-trapline choice. Again, the salience foraging model provided the best fit to decisions to diverge (Figure 3C; mean AIC score ± s.e.m.: net foraging model (×10³): 1.80 ± 0.21; ML: 1.86 ± 0.29; MR: 1.66 ± 0.26; optimal foraging model (×10⁴): 3.12 ± 0.22; ML: 3.01 ± 0.26; MR: 3.34 ± 0.44; salience foraging model (×10³): 1.73 ± 0.21; ML: 1.80 ± 0.29; MR: 1.58 ± 0.26; see methods). Corroborating these fits, response times were faster for more salient choices (linear regression by day of response times vs. salience; ML, mean β = −0.058 ± 0.013, Student’s t-test, p < 0.0005, t(29) = −4.49; MR, mean β = −0.039 ± 0.0090 (Student’s t-test, p < 0.001, t(13) = −4.28).

PCC neurons predict path divergences and dynamically signal salience during traplining

We predicted that the patterns of neural activity observed in PCC during patch foraging also would be evident during traplining. To test this hypothesis, we recorded spiking activity of 124 new neurons in the same two monkeys (Figure 1D; 84 in ML; 40 in MR). Firing rates predicted when monkeys would diverge from traplines. In our population, 59 (48%) of 124 neurons signaled choices on which monkeys diverged from traplines (linear regression on spike counts during anticipation epoch from 250 ms before choice saccade to 250 ms hold fixation after, p < 0.05; see methods), and 54 (44%) of 124 neurons predicted decisions to diverge from traplines one choice in advance (linear regression on average firing rates during anticipation epoch, p < 0.05). Forty-four (35%) of 124 neurons signaled diverge decisions in both conditions.

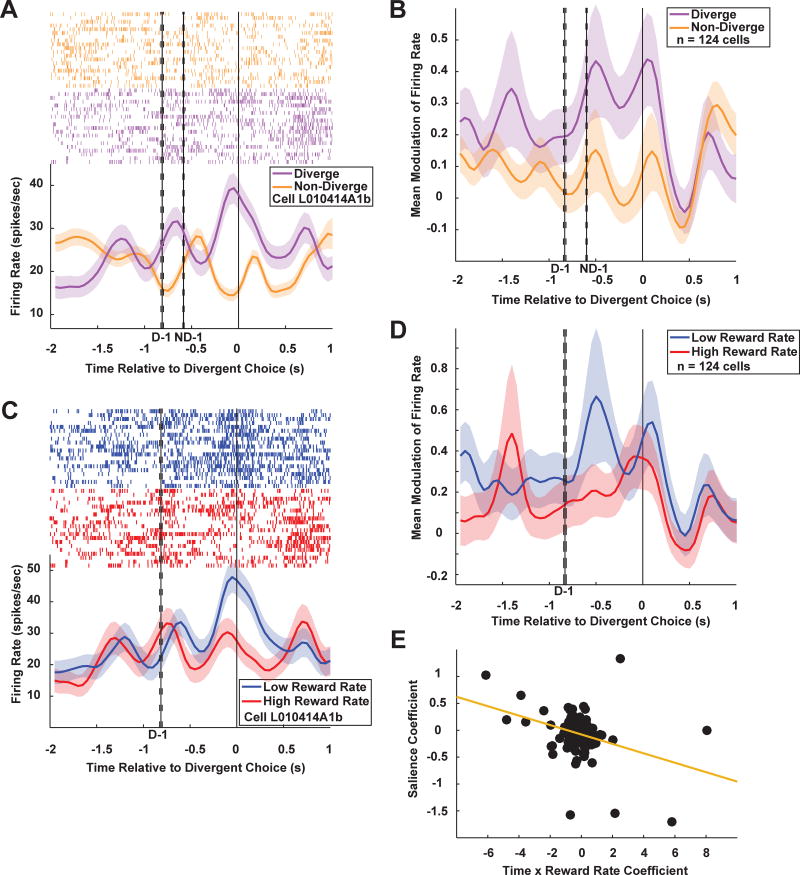
PCC neurons forecast divergences from traplines with phasic responses, as illustrated by the example cell (Figure 4A) and population response (Figure 4B). To quantify this difference, mean firing rate in a 1 s epoch before divergence was compared to the mean firing rate before the last non-diverge choice. Of 124 neurons, 59 (48%) fired more preceding diverge choices than preceding non-diverge choices (Student’s t-test, p < 0.05). An example neuron (Figure 4A) showed higher firing rates on choices immediately prior to diverging (Student’s t-test, p < 1×10⁻⁹, t(288) = 6.58). This same pattern characterized the population response (Figure 4B), with higher firing rates prior to decisions to diverge compared to non-diverge (Student’s t-test, p < 1×10⁻⁸, t(38) = 8.01).

Figure 4.

PCC neurons predict trapline divergences in advance. A. Sample cell PSTH showing elevated activity during the inter-choice interval of diverge trials (purple trace) compared to non-diverge trials (orange trace). B. Population plot for diverge (purple trace) and non-diverge (orange trace) trials. C. Same cell as in (A), showing differences in firing dynamics depending on environmental richness preceding divergences. Rich contexts (red trace): reward rate z-score > 0; poor contexts (blue trace): reward rate z-score ≤ 0. Activity was elevated prior to diverge decisions in poor environments only. D. Population plot for rich and poor environments. E. Salience coefficients plotted against time X reward rate coefficients. Later and lower reward rates resulted in stronger salience signaling, matching observations prior to leaving a patch (Figure 2D). See also Figure S3. B, D: n = 124 cells (84 from ML, 40 from MR). See Figure S2 for individual monkey results.

Akin to the differences in patch leave signaling in PCC neurons, this predictive signaling for path divergences differed in rich environments compared to poor. After sorting rich (reward rate z-score > 0) and poor (reward rate z-score ≤ 0) environments, the same sample neuron showed differences in predictive signaling across contexts (Figure 4C), with higher firing rates in poor environments (linear regression of mean firing rates by trial vs. z-scored reward rate, p < 0.005). The activity of 19 of 124 cells (15%) was correlated with reward rate (linear regression, p < 0.05). Elevated activity in poor compared to rich environments was also observed in the population preceding decisions to diverge (Figure 4D; linear regression, p < 0.05).

We next explored whether PCC neurons signal foraging salience during trapline foraging and if such signals depend on environmental richness. The dependency of salience signaling on environmental richness predicts a three-way interaction preceding a diverge decision between time, reward rate, and salience. PCC neurons signaled the interaction between all three covariates, albeit more weakly than during patch foraging: of 124 PCC neurons, 13 (10%) signaled the interaction of all three covariates (GLM, spikes sorted in 50 ms bins from first choice in trial to diverge choice and regressed against time before diverge, reward rate, salience and all interactions, Bonferroni corrected; ML: 9 (11%) of 84 neurons; MR: 4 (10%) of 40 neurons; see methods). A sliding boxcar plot (Figure S3B) revealed a much noisier but similar pattern of positive and negative salience coefficients as observed in the patch-leaving task (Figure S3A).

Such context dependent signaling also predicts a negative correlation between beta weights for salience and for the interaction of reward rate and time. Regression of the salience coefficients against coefficients for the interaction of reward rate with time revealed a significant negative correlation (Figure 4E; linear regression, β = −0.078 ± 0.021, p < 0.0005; ML: β = −0.12 ± 0.030, p < 0.0005; MR: β = −0.012 ± 0.023, p > 0.5 but with one outlier removed, β = −0.087 ± 0.045, p = 0.0612).

Finally, this context dependency predicts the strength of salience coding in poor environments should be larger than in rich ones. After sorting decisions by rich and poor contexts, we regressed spike counts during the whole choice epoch (250 ms before choice to 500 ms after choice) against salience. Just as in the patch foraging task, in rich environments there was no population-level effect of salience (linear regression, mean β = 0.12 ± 0.075, Student’s t-t-test, p > 0.1, t(121) = 1.57) while one was observed in poor environments (mean β = 0.23 ± 0.084, p < 0.01, t(122) = 2.77). While the influence of salience was greater in poor than rich contexts, this difference was not statistically significant (Student’s t-test, mean Δβ = 0.12 ± 0.098, p > 0.2, t(121) = 1.18).

Discussion

In both tasks, the salience foraging model best described behavior. Conceptually, salience reflects the occurrence of statistically improbable environmental events that are relevant to an animal. Foraging requires tracking the environment in order to detect and adapt to changes in the quality, spatial location, and abundance of resources. Foraging salience provides an efficient way to track the need to change behavior. We hypothesize that the salience model best described behavior because, unlike the optimal or net foraging models, it captures factors that influence orienting (Simion and Shimojo 2007) and attention (Orquin and Loose 2013). Salience generally plays an important role in allocating attention (Gottlieb et al. 1998) to motivate behavior (Bromberg-Martin et al. 2010) or to learn (Pearce and Hall 1980), and can be thought of as an increase in signal gain (Reynolds and Heeger 2009) to enable faster and more accurate stimulus processing. In the best-fit model, foraging salience similarly serves as a multiplicative gain on cumulative harvest.

Possible cognitive roles for foraging salience signals in PCC include motivating disengagement, computing the value of alternative options, and tracking choice difficulty. First, salience signals may reflect integration of environmental information with the goal of optimizing rewards by motivating disengagement. Several neuroimaging studies of environmental change detection have reported activity in PCC reflecting integration of environmental signals (Summerfield et al. 2011; McGuire et al. 2014), and PCC neurons signal behavioral goals (Dean et al. 2004), option values (McCoy et al. 2003), reward uncertainty (McCoy and Platt 2005), decision strategies (Pearson et al. 2009), and decision salience (Heilbronner et al. 2011). In our study, PCC neurons signaled foraging salience and the interaction of salience with elapsed time and reward rate, a synthesis of multiple sources of evidence that can be used to adapt behavior to the environment. Salience signals in PCC were also stronger in poor foraging contexts, suggesting control signals are amplified when strategic changes in behavior are favored. Second, the observed signals may reflect the value of searching for alternatives, similar to activity in dACC (Kolling et al. 2012). In support of this, as the cumulative reward approaches the threshold for leaving, salience decreases and the value of disengaging increases in both tasks. Third, signals observed in PCC may reflect choice difficulty. Recent debate regarding dACC activity during foraging has explicitly contrasted the value of search with choice difficulty (Shenhav et al. 2014). As the agent approaches the threshold net reward for disengaging, salience decreases, making the decision more difficult. Given our experimental design, we are unable to distinguish between these possibilities.

Foraging salience signals may be computed locally within PCC, though imaging studies have failed to identify other types of salience signals (Litt et al. 2010; Kahnt and Tobler 2013; Kahnt et al. 2014). Failure to find salience signals in PCC in fMRI studies may reflect variation in the sign of salience signals across the population and across time within the same neuron (Figure S1). Salience signals may also be sent to PCC from other areas. PCC is preferentially innervated by projections from locus coeruleus (LC) and expresses a greater proportion of noradrenergic receptors than other cingulate regions (Bozkurt et al. 2005). LC contributes to change detection (Nassar et al. 2012), exploration (Jepma and Nieuwenhuis 2011), and outcome salience (Aston-Jones and Cohen 2005) for orienting attention (Corbetta et al. 2008) and learning (Sara and Bouret 2012), potentially a source of salience signals in PCC. Alternatively, salience signals have been observed in cortical areas connected with PCC, including lateral prefrontal cortex (Kobayashi et al. 2006), posterior parietal cortex (Kahnt et al. 2014), anterior cingulate cortex (Litt et al. 2010; Kahnt et al. 2014), orbitofrontal cortex (Ogawa et al. 2013) and temporoparietal junction (Kahnt et al. 2014). PCC may integrate information from some or all of these areas to compute foraging salience to adapt behavior to the current environment (Pearson et al. 2011).

The framework of disengagement decisions covers many cognitive behaviors that evolve over multiple actions and involve many types of resources, both external and internal (Hills et al. 2008). Foraging presents a powerful approach for studying how decisions unfold over multiple actions, and may be the foundation upon which more complex strategic decisions are built (Pearson et al. 2014), a view supported by finding a common set of neural computations regulating disengagement decisions in patch leaving and traplining.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, David L. Barack (dbarack@gmail.com).

Experimental Model and Subject Details

Two mature (aged ~6–9 years) male rhesus macaques (M. mulatta) participated. Monkeys were single housed in cages in a colony room with other monkeys, allowing auditory and visual contact. Monkeys received daily enrichment and biannual health check-ups. As of the beginning of the first task, one of the monkeys had been used on two previous experiments for both recording and inactivation in PCC (ML) and one was naïve (MR).

After initial behavioral training, a head-restraint prosthesis (titanium; Crist Instruments) and recording chamber (acrylic; Crist Instruments) permitting access to PCC were implanted using standard aseptic surgical techniques. All surgeries were performed in accordance with protocols approved by the Duke University institutional animal care and use committee and were in accord with the Public Health Service Guide to the Care and Use of Laboratory Animals. Monkeys were anesthetized using isoflourane, received analgesics and antibiotics after surgery, and permitted a month to heal before any recordings were performed.

Method Details

Two monkeys were trained on both tasks, first the patch leaving task, followed by neural recordings, and then the traveling salesman task, followed by neural recordings. Neural recordings began once a stable pattern of behavior emerged, within two weeks of onset of training for both tasks. For the patch leaving task, we regarded behavior as stabilized when a significant influence of travel time on total time in patch emerged (cf. (Houston and McNamara 1999). For the traveling salesman task, we regarded behavior as stable when monkeys exhibited the same pattern of choices (a trapline) over the course of five behavioral sessions.

During training and recording, monkeys’ access to fluid was controlled outside of experimental sessions. Custom software written in MATLAB (Mathworks, Natick, MA, USA) using Psychtoolbox (Brainard 1997) controlled stimulus presentation, reward delivery, and recorded all task and behavioral events. Horizontal and vertical eye traces were sampled at 1000 Hz by an infrared eye-monitoring camera system (SR Research, Osgoode, ON) and recorded using the Eyelink toolbox (Cornelissen et al. 2002). Solenoid valves controlled juice delivery. All data were analyzed using custom software written in MATLAB.

Patch Leaving Task Behavioral Modeling

This task simulates a patch-leaving problem by presenting the animal with a two-alternative forced choice decision between continuing to forage at a depleting resource and waiting to replenish the resource (Hayden et al. 2011); Figure 1A). To begin the trial, the animal fixated (± 0.5°) on a centrally presented cross for a random fixation time drawn from a uniform distribution (400 – 800 ms). If the animal prematurely shifted his gaze from the fixation cross before exhausting this time, the fixation clock resets to zero. If the animal exhausted the fixation time, the fixation cross was extinguished and the targets, a small blue rectangle and a large gray rectangle, one each on the left and right side of the screen, were presented. The animal could make a choice by aligning gaze with a target and holding it there for 250 ms. The animal was free to peruse the options, glancing back and forth without penalty or registration of choice, so long as the choice fixation period was not exhausted.

If the monkey selected the blue rectangle, he was permitted to freely look about while the rectangle shrank at 65 pixels/s until it disappeared. This shrink time simulated the ‘handling time’ for the food item, and was constant across all trials and reward sizes. At the end of this handling time period, the animal received a squirt of juice, followed by a 1 second intertrial interval (ITI) and the reappearance of the fixation cross. The reward size for the first trial in patch was always ~0.30 mL of juice. As the animal continued to select the blue rectangle (‘stay in patch’ decision), the amount of juice associated with that choice dropped each trial by ~0.02 ± ε mL of juice (where ε is a random term with mean = 0.002 mL and sd = 0.0001 mL). After a series of stay in patch decisions, the animal typically decided to select the gray rectangle (‘leave patch’ decision). After selecting that option, the monkey was free to look about while the gray rectangle shrank also at 65 pixels/s. The height of the gray rectangle signaled the time-out penalty for leaving the patch (the ‘travel time’), and did not vary so long as the animal continued to stay in the patch. Once the monkey chose to leave, the gray bar shrank, which was followed by a 1 second ITI and the reappearance of the fixation cross; no juice was delivered for this choice. On the first trial in the ‘new patch’, three changes occurred. First, the juice reward associated with the blue rectangle was reset to its full amount, 0.30 mL. Second, the height of the gray bar was selected randomly from the distribution of 0.5 – 10.5 s. Third, the locations of the targets were switched. To avoid changes in behavior due to satiety, each session was limited to one hour.

Behavioral data were analyzed with three foraging models using custom software in MATLAB. The three foraging models were constructed on the basis of the best-fit distribution for cumulative reward intake. The foraging threshold was computed from the mean of the exponential gain function for foraging in a patch, which reflected the reward encounter rate. This exponential gain function was computed from the experiment-defined sequence of rewards and the experiment-defined trial event times (inter-trial interval = 1 s; handling time = 0.4 s; target acquisition fixation time = 0.25 ms; mean fixation time = 0.6 s; and time for reward delivery for each trial in patch) and empirically measured response time means, which varied daily. We then modeled the reward gain function g(t) over all reward harvesting choices in a patch as an exponential survival curve

$$g(t)=1-e^{-\lambda \prime T}$$

for fit reward encounter rate λ′ and cumulative time in patch T using maximum likelihood estimation. In order to fit this exponential, all rewards were normalized by the maximum possible net reward.

Like other value-based decisions (Busemeyer and Townsend 1993; Krajbich and Rangel 2011), foraging decisions can be modeled as the integration of a decision variable to a threshold (Kacelnik et al. 2011; Calhoun and Hayden 2015). In our task, we considered two different approaches to model the decision threshold, one based on foraging theory (Stephens and Krebs 1986) and the other based on survival analysis (Fox 2001) using the mean of the maximum entropy distribution for encountered rewards, the exponential gain function.

First we developed a foraging theory model inspired by the marginal value theorem (MVT; (Charnov 1976). We computed the average reward rate from the Gamma-distributed patch residence times and exponential gain function (Stephens and Krebs 1986):

$$R(\hat{t})=\frac{\lambda g(\hat{t})}{1+\lambda \hat{t}}$$

for average reward rate R(t̂), patch encounter rate λ, estimated patch residence time t̂, and reward gain function g(t̂). Rate-maximizing patch residence times t̂ were found using maximum likelihood estimation and the fmincon function in MATLAB. The MVT predicts that advanced knowledge of a longer travel time to the next patch will increase the time spent foraging in the current patch, whereas knowledge of a shorter travel time will decrease foraging time (Stephens and Krebs 1986; Houston and McNamara 1999), as we confirm in Figure 1. We incorporated this influence of travel time by computing the threshold for each i^th patch separately as though drawn from a set of patches with mean travel time t_i = (1/λ) (Stephens and Krebs 1986). The decision variable for this model was the difference between net received reward and the MVT-computed optimal foraging threshold. For the optimal foraging model, the decision variable ΔV was equal to the reward rate computed from the rate maximizing foraging time t̂ minus the current within patch reward rate

$$\Delta V=R(\hat{t})-R(t)$$

for optimal reward rate R(t̂) and actual current reward rate R(t).

Second, we developed a net foraging model based on the cyclical nature of patch-based foraging and the mean net reward harvested from a patch. Patch foraging is characterized by a renewal cycle (Houston and McNamara 1999): the animal makes an iterated series of decisions (begin foraging in patch – stay in patch – stay in patch – stay in patch – leave patch – begin foraging in patch etc.). Each such cycle can be modeled as lasting a certain amount of time. These patch residence times are modeled as a survival process (Fox 2001) using the net reward harvested so far in a patch, computed with the exponential gain function above (Houston and McNamara 1999). A leave threshold was calculated from the mean of the exponential gain function g(t) for rewards harvested from a patch. To capture the influence of travel time on time in patch, this threshold was modulated by an additive gain term computed from the z-scored travel time for each patch. For the net foraging model, the decision variable ΔV on trial t was the reward differential, defined as the difference between net received reward and threshold net reward for leaving

$$\mathrm{\Delta }{V}_t=\left(\sum _{i=1}^{t-1}{R}_i\right)-T_j$$

for trials in patch 1 through t − 1, rewards R, and threshold T for patch with travel time j.

Third, we developed a salience foraging model also based on the mean net reward harvested in a patch but that included a salience term. Salience plays a key role in attentional learning models (Esber and Haselgrove 2011). In these models, the associability of a conditioned stimulus (CS) is the degree to which the CS can be associated with an unconditioned stimulus (US) (Mackintosh 1975; Pearce and Hall 1980; Esber and Haselgrove 2011). This associability can be defined in terms of its salience, the absolute value of the difference on the previous trial of the intensity of the US and the CS predicted strength (Mackintosh 1975; Pearce and Hall 1980). A similar sort of rule can be adopted for decision-making. The value of the current offer can be compared to a standard, and the absolute value of the difference of the offer value from the standard represents the salience of the offer (Heilbronner et al. 2011).

The salience model computes the same decision variable as the net foraging model, but then multiplicatively scales this decision variable based on salience. Salience was defined as the absolute value of the difference between net received reward and the mean net reward computed from the exponential distribution. Salience was multiplied by the value of the net offered reward minus the decision threshold and weighted by a coefficient fit to the choice data (MLE). The decision variable ΔV for this model was the reward differential times the weighted salience

$$\mathrm{\Delta }{V}_t={\beta }_s\left|\right(\sum _{i=1}^{t-1}{R}_i)-T_j|\left(\right(\sum _{i=1}^{t-1}{R}_i)-T_j)$$

for salience coefficient β_s and other variables as above. Despite containing more parameters, the salience foraging model was the best fit model even after correcting for the number of parameters (as reported in the results).

In Figures 1C and 5C, we computed the probability of choosing to leave a patch for these foraging models using a sigmoidal choice function with a single decision variable. The observed choice behavior was fit with the net foraging model, optimal foraging model, and the salience foraging model using the respective decision variables. For all three models, a standard sigmoidal choice function was used to calculate the probability of choosing the leave option:

$$p_L=\frac{e^{\mathrm{\Delta }V/\sigma }}{1+e^{\mathrm{\Delta }V/\sigma }}$$

for the probability of choosing the leave option p_L, value difference ΔV as defined for each model above, and constant σ fit using MLE. Both σ and β_s were simultaneously fit using MLE for the salience foraging model.

Traveling Salesman Task Behavioral Modeling

In our traveling salesman task, monkeys foraged through a visual array of six targets by sequentially aligning gaze with them (Figure 5A). On every trial, one of six targets delivered a large reward (~0.2 mL), one delivered a small reward half the size of the large one (~0.1 mL), and the remaining four delivered no rewards. After aligning gaze (± 0.5°) with a fixation cross for 500 – 1000 ms, the target array was presented. Monkeys selected a target by directing their gaze on to it and holding fixation for 250 ms (± 0.5° from edge of target; targets were 60 pixels in width). While the locations of the targets were always the same, the identities of the rewarded targets varied pseudo-randomly from trial to trial. Monkeys were free to choose the targets in any order, but they had to select every target before being allowed to advance to the next trial, mimicking traplining problems in natural foraging. After completing the array, a 1000 ms inter-trial interval was imposed, and then a new fixation cross appeared on the screen.

Our model-based analysis of behavior in the traveling salesman task computed cumulative rewards and reward rates. Cumulative rewards were equal to the total reward harvested during a trial, and cumulative reward rates divided that net reward by the cumulative elapsed time between choices. The total reward harvested at choice n within a trial was the sum of the rewards received from the previous choices 1:n-1 in that trial. The elapsed time at choice n was the sum of the choice fixation times (250 ms) for previous choices 1:n-1 and the variable response times of the monkey for all choices 1:n. Response times were calculated from the end of saccade for the last decision to end of saccade for the current decision.

For each day’s run, we determined the daily dominant pattern by assessing the similarity between every possible pair of trials on a given day by computing the pair’s Hamming score (Hamming 1950). To compute the similarity between two trials, each trial’s pattern of choices by target number was first coded as a digit string (e.g., 1, 2, 4, 5, 6, 3). The Hamming distance D_i,i′ between two strings i, i′ of equal length is equal to the sum of the number of differences d between each entry in the string,

$$D_{i,i\prime }=\sum _{n}d(x_n,y_n)$$

for strings x, y of length n. We computed D_i,i’ for every pair of trials, and then, for each unique pattern of choices, computed the average Hamming distance D̄_i,i′. Larger D_i,i’ correspond to strings with more differences. The daily dominant pattern corresponded to the pattern with the minimum D̄_i,i′.

We analyzed the choices made in the traveling salesman task as decisions to continue on the trapline, as defined by the daily dominant pattern, or to diverge from it. We made two adjustments to accommodate this analysis. First, we excluded trials where the monkeys diverged at the very beginning of foraging, that is, trials where the first choice diverged from the DDP, because this behavior was not influenced by the reward harvested over the course of the trial. Second, we fit 30 different exponential gain functions, one for each possible sequence of experienced rewards during a trial (not counting zeros as unique). To compute the different foraging thresholds for each choice in a trial, we used the mean lambda from the set of gain functions that were consistent with the sequence of rewards the monkey had experienced leading up to that choice number in the trial. We fit the same set of models from the patch-leaving task analysis to the behavioral data from the traveling salesman task, and models were compared using the same method as well.

Quantification and Statistical Analysis

The outcomes of statistical tests are detailed in the Results, and included the use of Student’s t-test, linear regression, ANCOVA to compare ramp-ups during the patch leaving task, and a generalized linear model (GLM). Significance was set at α = 0.05, and multiple comparisons were always Bonferroni corrected. Results reported are mean ± standard error of the mean. For individual cell results, n was set to the number of patches (patch leaving tasks) or number of diverge and non-diverge trials (traveling salesman task). For population results, n was the number of recorded cells.

Behavioral models were compared using log-likelihoods. All zero probabilities were rectified to very small probabilities (1×10⁻¹⁵). We then took the sum of the logs of these probabilities for model comparison. Models were compared using the Akaike Information Criterion (AIC) (Akaike 1974), a measure of goodness-of-fit that penalizes models possessing more parameters. AIC is defined as

$$\mathit{\text{AIC}}=-\mathit{2}\mathit{\text{LL}}+\mathit{2}k$$

for the log-likelihood of the data given the model, LL, and the number of free parameters in the model, k.

Neuronal firing rates often show non-linearities (Dayan and Abbott 2001), which can be captured using a GLM (Aljadeff et al. 2016). All regressions on neuronal firing rates were performed using a GLM with a log-linear link function, Poisson distributed noise, and dispersion estimated from the data, and all reported results utilized Bonferroni corrected p-values. The use of this GLM effectively models neuronal responses as an exponential function of a linear combination of the input variables. GLMs were run using the glmfit function in MATLAB.

Patch Leaving Task Neural Analysis

Analysis of neural recordings focused on the whole trial epoch, a two-second-wide window ranging from one second before choice to one second after, and a patch exit epoch, from 15 seconds before the acquisition of the leave target to that acquisition time. Peri-stimulus time histograms (PSTHs) were computed to depict neuronal activity at the patch-level, corresponding to analyses time-locked to patch exits. For these patch-level PSTHs, data were aggregated into 50 ms bins and convolved with a Gaussian of mean 0 and standard deviation 125 ms.

Neuronal firing rates were also modeled during the patch exit window, the last 15 seconds in a patch. The activity of each cell for each patch was retained, and the firing rates were treated as a time series of binned spike counts in 50 ms bins. We first regressed the mean firing rate in each bin against time before patch exit. Next, we ran the same regression for each patch separately, regressing the binned firing rates against time. We then correlated those regression slopes with the z-scored reward rates from the leave trials. A similar regression was performed for the population after normalizing the activity of each cell by subtracting the mean activity and then dividing by that mean. To investigate the dynamics of neuronal activity around the time of patch exit, these spike counts were regressed against reward rate, time before exiting the patch, salience, and all 2-way and the 3-way interactions. Due to variability in the timing of task events and response times (both fixation acquisition and choice), all three covariates were decorrelated (time X reward rate: mean R² = 0.14 ± 0.0079; time X salience: mean R² = 0.14 ± 0.011; reward rate X salience: mean R² = 0.30 ± 0.013).

To compare neural coding of salience in rich and poor foraging environments, whole trial epoch spike counts for those trials in the patch exit window were regressed against salience. Patches were first sorted into poor (reward rate z-score < 0) and rich (z-score ≥ 0) ones, and spike counts regressed separately for each. Patch reward rates were computed by summing the reward received in a patch and divided by the elapsed time in patch, though choosing an instantaneous reward rate, equal to the most recent reward before the current choice divided by the elapsed time since that reward, yielded similar findings.

Traveling Salesman Task Neural Analysis

We analyzed neuronal firing rates during the traveling salesman task for two different epochs: first, a 1000 ms epoch in 50 ms bins preceding either diverge or non-diverge decisions, to compare the two types of decision; second, a time series of spike counts in 50 ms bins from the start of a trial up to the choice to diverge. For PSTHs, data were binned in 50 ms bins and convolved with a Gaussian of mean 0 and standard deviation of 75 ms.

Divergent and non-divergent choices were analyzed as follows. Only choices corresponding to the first divergent choice in a trial were counted as divergent. Furthermore, because we were interested in exploring the processes that resulted in diverging from a trapline while the trapline was being executed, divergent choices that occurred on the first choice in a trial were excluded. Such trials begin with a divergence before reward rates or other returns were possible during a trial and hence cannot reflect the influence of those variables. Non-divergent choice neural activity was drawn from the fifth choice on trials that matched the daily dominant pattern. The fifth choice corresponds to the point in the trial where there are two targets left, as well as to the last point in the trial at which the monkey could still diverge.

To compare diverge decisions to non-diverge decisions, the mean firing rate in a 1 s epoch on every non-excluded trial preceding the decision was analyzed. The two groups were compared using a Student’s t-test. We then split the diverge group into poor (reward rate z-score < 0) and rich (reward rate z-score ≥ 0) environments, and compared the firing rates during choices of each type to the firing rate on non-diverge choices. To assess neural coding of diverge decisions across reward rates, we linearly regressed the mean firing rate on diverge trials during this 1 s epoch against z-scored reward rate. A similar regression was performed for the population after normalizing the activity of each cell by subtracting the mean activity and then dividing by that mean.

A GLM was used to determine the influence of salience on decisions to diverge. All the spikes from the onset of the trial up to the decision to diverge were sorted into 50 ms bins and then regressed against reward rate, time before divergence, salience, and all 2-way and the 3-way interactions. As with the patch leaving task, time, reward rate, and salience were decorrelated (time X reward rate: R² = 0.063 ± 0.0048; time X salience: R² = 0.020 ± 0.0057; reward rate X salience: R² = 0.15 ± 0.0050). Computed coefficients from this regression for salience and for the interaction of reward rate and time were subsequently regressed against each other. 9 neurons for which fewer than 5% of trials were diverge trials (all from monkey L) were excluded from this analysis.

To examine differences in the strength of salience signaling for diverge trials in high and low reward rate contexts, spike counts from the whole choice epoch, from 250 ms before the end of a choice saccade to 500 ms after (covering a 250 ms hold fixation period to register a choice and a 250 ms post-choice period), were regressed against salience. Diverge trials were sorted into poor (reward rate z-score < 0) and rich (reward rate z-score ≥ 0) environments, and spike counts regressed separately for each. The reward rate was calculated by summing the rewards over the whole trial and dividing by the elapsed trial time, though choosing an instantaneous reward rate, equal to the most recent reward divided by the elapsed time from receipt of that reward to the current choice, yielded similar findings. Two cells were excluded from this analysis because there were too few spikes on diverge choices yielding coefficients in excess of 100, both from monkey L.

Highlights.

• ·Offer salience drives monkeys’ choices to switch strategies in two foraging tasks
• ·PCC neurons signaled salience in both tasks more strongly in poor than rich contexts
• ·More PCC neurons predicted strategy switches in both tasks in poor than rich contexts