Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Oct 19;11(11):11661–11668. doi: 10.1021/acsnano.7b06765

Width-Dependent Band Gap in Armchair Graphene Nanoribbons Reveals Fermi Level Pinning on Au(111)

Néstor Merino-Díez †,‡, Aran Garcia-Lekue †,§, Eduard Carbonell-Sanromà ‡, Jingcheng Li ‡,⊥, Martina Corso ‡,§,⊥, Luciano Colazzo ∥, Francesco Sedona ∥, Daniel Sánchez-Portal †,⊥, Jose I Pascual ‡,§, Dimas G de Oteyza †,‡,§,⊥,*
PMCID: PMC5789393  PMID: 29049879

Abstract

graphic file with name nn-2017-067654_0006.jpg

We report the energy level alignment evolution of valence and conduction bands of armchair-oriented graphene nanoribbons (aGNR) as their band gap shrinks with increasing width. We use 4,4″-dibromo-para-terphenyl as the molecular precursor on Au(111) to form extended poly-para-phenylene nanowires, which can subsequently be fused sideways to form atomically precise aGNRs of varying widths. We measure the frontier bands by means of scanning tunneling spectroscopy, corroborating that the nanoribbon’s band gap is inversely proportional to their width. Interestingly, valence bands are found to show Fermi level pinning as the band gap decreases below a threshold value around 1.7 eV. Such behavior is of critical importance to understand the properties of potential contacts in GNR-based devices. Our measurements further reveal a particularly interesting system for studying Fermi level pinning by modifying an adsorbate’s band gap while maintaining an almost unchanged interface chemistry defined by substrate and adsorbate.

Keywords: graphene nanoribbon, on-surface synthesis, Fermi level pinning, Ullmann coupling, dehydrogenation, scanning, tunneling microscopy and spectroscopy, density functional theory

Graphene nanoribbons (GNRs) have long been proposed as extremely interesting materials for a variety of applications, ranging from their key role in composites with mechanically robust films and high gas barrier efficiencies1 to thermoelectric devices,2,3 capacitors,4,5 batteries,6 photodetectors,7 transistors,8 or directly integrated circuits.9 Among the most appealing attributes that make GNRs so interesting, we find the greatly tunable properties they display as a function of their precise atomic structure. While this holds enormous interest for many of the applications mentioned above, it also underlines the need for atomic precision in their synthesis if the full potential of GNRs is to be exploited. That was achieved for the first time in 2010 with the bottom-up synthesis of armchair-oriented nanoribbons (aGNRs) with 7 dimer lines across their width (7-aGNR).10 Ever since, following a similar “on-surface synthesis” approach, great efforts are being devoted to the synthesis of GNRs with different widths,11−13 edge orientations,14,15 dopants,16−20 as well as heterostructures thereof.21−24

The increasing pool of available GNRs with well-defined structures has allowed the subsequent characterization of their fundamental electronic properties, as well as the correlation with their performance when integrated into devices like field effect transistors.25,26 Interestingly, it has been found that the device performance is strongly dominated by contact effects, in particular, by the Schottky barrier at the GNR–contact interface. As opposed to studies of other GNR properties like their band gaps, systematic studies of the energy level alignment between GNRs and common contact materials are still missing in spite of their determining role in the ultimate response of GNR-based devices. In this work, we amend our understanding of such interface energetics between GNRs and gold, in particular, Au(111) surfaces.

Armchair-oriented nanoribbons are known to display a width-dependent band gap. Calculations reveal that they can be classified into three different subfamilies depending on the number of dimer lines p across their width (3p, 3p+1, or 3p + 2), their band gaps being inversely proportional to the width within each of those families.27−29 The reported band gap values of the various aGNRs synthesized to date confirm this picture with scattered points along the predictions for each of the GNR families.29,30 In this work, we provide a systematic study of the band gap and energy level alignment of GNRs focused on the 3p family, addressing from the smallest possible GNR (3-aGNR) to its four immediately following sister structures (6-, 9-, 12-, and 15-aGNRs). Starting from the synthesis of poly-para-phenylene wires (PPP or 3-aGNR) on Au(111), subsequent annealing drives their lateral fusion and results in the required atomically precise GNRs of varying width.31 The following characterization by scanning tunneling spectroscopy (STS) and density functional theory (DFT) calculations reveals, in addition to the width-dependent band gap, the onset of Fermi level pinning for widths ≥6 dimer lines.

Results and Discussion

We use 4,4″-dibromo-p-terphenyl (DBTP) as a molecular precursor to synthesize the structures described in this work. Figure 1 summarizes the stepwise synthesis of aGNRs starting from the precursor. A submonolayer of DBTP is initially deposited on a Au(111) single crystal held at room temperature. After postdeposition annealing above 250 °C, the precursor undergoes Ullmann-like coupling,31,32 yielding poly-para-phenylene (PPP) nanowires. Figure 1b shows a scanning tunneling microscopy (STM) image of a representative sample. As previously reported,31 these nanowires are highly aligned, separated by arrays of bromine atoms between them (see Figure S1a), and present impressive lengths of up to 200 nm. PPP has been occasionally termed as a 3-aGNR and would thus fit into a family of 3p-aGNRs. However, as previously concluded from near-edge X-ray absorption fine structure (NEXAFS) measurements, it displays a nonplanar structure on Au.20 While not recognizable in constant current (“topographic”) STM imaging (Figure 1b), mapping of the density of states (DOS) at the onset of valence band (VB) and conduction band (CB) clearly reveals a modulated intensity that mirrors an alternating tilt of subsequent phenyl rings (Figure S1). The nonplanarity of gold-supported PPP is also confirmed by DFT calculations even when using functionals that incorporate the vdW interaction, although reduced with respect to that in gas-phase PPP. As discussed later, this nonplanar structure leads to a substantial difference in the electronic properties of the polymer with respect to the rest of the wider (and planar) 3p-aGNRs.

Figure 1.

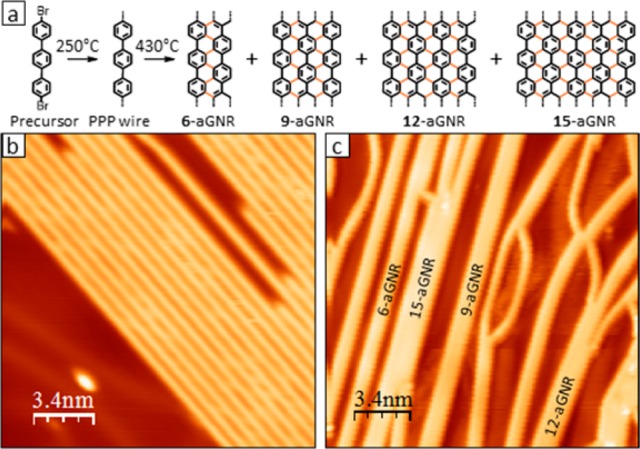
Figure 1

Open in a new tab

(a) Schematic synthesis from DBTP molecular precursor on Au(111). STM topography images of (b) PPP nanowires (24.6 nm × 24,6 nm, It = 0.22 nA, Vs = 1.0 V) and (c) a-GNRs (24.6 nm × 24,6 nm, It = 0.22 nA, Vs = −1.7 V), where text inlets indicate the different widths of aGNRs.

Above 430 °C, PPP nanowires merge sideways through dehydrogenation,31 forming aGNRs of different width, as shown in Figure 1c. This synthetic step relies on random diffusion effects imposed by the high temperature and results in an interconnected network of nanoribbons of different widths. There is a significant number of curved aGNRs, but most of them preserve the preceding nanowire’s straight orientation. The final nanoribbon width depends on the number of nanowires getting fused. Discretized by the intrinsic width of PPP nanowires (3-aGNR), we find 6-, 9-, 12-, and 15-aGNRs are formed from the fusion of two, three, four, and five nanowires, respectively. Having them all next to each other on the same Au(111) surface reveals itself as an excellent testbed to measure and compare their respective electronic properties.

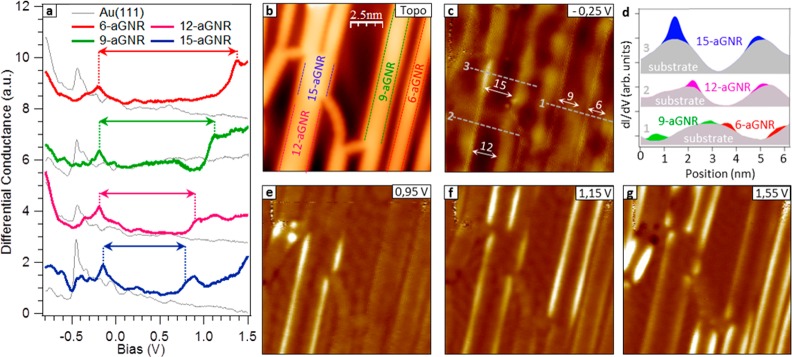
The aGNR’s electronic properties have been characterized by STS, measuring both differential conductance (dI/dV) point spectra and dI/dV maps at various sample bias voltages (Figure 2). The point spectra were taken over the sides (where the measured GNR signal is highest22,33,34) of straight GNR segments, featuring a well-defined width and defect-free structure over substantial lengths. While segments of 6- and 9-aGNRs easily exceed tens of nanometers, the wider the ribbons, the shorter the average segments are. To avoid notable band gap variations from finite length effects, spectra are only taken into account from segments longer than 4 nm (i.e. ∼9 unit cells). While the convergence behavior of the GNR band gap with its length depends on a series of aspects such as the ribbon’s own polarizability and thus on its particular structure, for the GNRs studied here, the probed electronic properties at these lengths can be considered to be close to those of an infinite ribbon.35,36Figure 2a displays representative STS spectra for ribbons with different widths, together with background spectra of the bare Au(111) surface nearby, as a reference.

Figure 2.

Figure 2

Open in a new tab

(a) Spectra recorded on 6-aGNR (red), 9-aGNR (green), 12-aGNR (pink), and 15-aGNR (blue), where the Au(111) signal (black) is added to every spectrum as background reference (open-feedback parameters: Vs = 1.55 V, It = 1.4–10 nA; modulation voltage Vrms = 10 mV). (b) STM topography image (12.4 nm × 12.4 nm; Vs = −1.1 V; It = 0.61 nA). (c) Conductance map near the valence band onset (Vs = −0.25 V), with white arrows as a guide for the eye to the intensity along each aGNR edge. (d) Profiles across the conductance map in (c), highlighting the contribution from the VB of differently wide GNRs on top of the dominating Au(111) surface state contribution. Conductance maps near the conduction band onsets for (e) 15-aGNRs and 12-aGNRs (Vs = 0.95 V), (f) 9-aGNR (Vs = 1.15 V), and (g) 6-aGNR (Vs = 1.55 V). The displayed spectra have been taken from ribbons on different sample locations (not necessarily on those of panels b–g). Differences in the reference spectra relate to different tips and positions. The comparable intensity in 12- and 15-aGNRs’ edges in image (d) probably relates to the limited length of the 15-aGNR segment. Its reduced length causes an increased band gap and thus leads to an upshift in the energy of the conduction band onset, making it overlap with that of the longer 12-aGNR. Size and set point for all conductance images were 12.4 nm × 12.4 nm and It = 0.61 nA, respectively.

All STS spectra show a clear conductance rise at positive bias, which is attributed to the onset of the conduction band. The position of these bands is observed at different energies as a function of the ribbons’ width: the wider the ribbon, the closer to EF its conduction band is. In this way, the onsets range from 0.86 eV, for the wider 15-aGNR, to 1.47 eV for the narrower 6-aGNR. Regarding the filled states (Vs < 0), the first nanoribbon-related feature in the spectra is detected at bias values close to −0.2 eV for all measured widths. We associate it with the corresponding onset of the aGNR valence band. A more detailed analysis reveals that the valence band onset follows a similar, although less pronounced, width-related trend as the one observed in the conduction band case. The valence bands are slightly closer to EF as the GNRs become wider, ranging from −0.17 to −0.23 eV. It is worth noting that the detection of the VB onset is particularly difficult on Au(111) since the surface state signal overlaps with the 3p-AGNRs spectroscopic features. Additionally, the density of states of the valence band of 3p-AGNRs decays particularly fast along the direction perpendicular to the GNR plane.12,34 Both of these reasons severely complicate its detection by STS. Nevertheless, our analysis of both valence and conduction bands is in excellent agreement with the recently reported electronic structure and energy level alignment of 9-aGNRs synthesized selectively on Au(111) from appropriate precursors.12

The conclusions derived above from our dI/dV point spectra are supported by dI/dV maps obtained at different biases (Figure 2c–g). When probing the empty states (Vs > 0), as one increases the energy, only the oscillations associated with scattered surface state electrons are initially visible (Figure S2). However, there is an energy threshold at which an increased conductance starts becoming visible along the sides of the ribbons, first for the wider ribbons (Figure 2e) and as the energy increases also for 9-aGNRs (Figure 2f) and 6-aGNRs (Figure 2g). Such intensity in conductance maps is related to the local density of states (LDOS) of aGNR bands,11,34 and the threshold energies at which the increased conductance sets in are in agreement with the width-dependent band onsets determined from the point spectra. In the case of the filled states (Vs < 0), conductance maps at −0.25 V reveal the strong intensity of the scattered surface state. Superimposed to it, we observe a weak but recognizable intensity distributed along the edges of every nanoribbon (Figure 2c) further highlighted in the profiles displayed in Figure 2d and Figure S2. This agrees with the VB onsets being at similar energies for all GNRs, as observed in the spectra (Figure 2a). Besides the frontier bands, our spectroscopy measurements reveal an additional nanoribbon-related signal at higher negative bias (Figure S3). We associate it with the second valence band (VB-1), which is easier to be probed by the tip of the STM than is the VB. Its slower decay away from the nanoribbon plane explains,12,34 together with the absence of the Au(111) surface state at these energies, its stronger and more easily measurable signal (Figure S3). For a clear visualization of the overall data, Table 1 summarizes the energies of all band onsets averaged over several measurements on different aGNRs, as well as the associated band gaps.

Table 1. Average Spectroscopic Results on VB-1, VB, CB, and Resulting Band Gaps.

structure VB-1 (eV) VB (eV) CB (eV) band gap (eV)
PPP wire   –1.09 ± 0.05 2.14 ± 0.06 3.23 ± 0.08
6-aGNR –1.73 ± 0.04 –0.23 ± 0.08 1.47 ± 0.05 1.69 ± 0.10
9-aGNR –1.17 ± 0.06 –0.20 ± 0.05 1.14 ± 0.05 1.35 ± 0.07
12-aGNR –0.84 ± 0.04 –0.18 ± 0.04 0.96 ± 0.04 1.13 ± 0.05
15-aGNR –0.66 ± 0.09 –0.17 ± 0.03 0.86 ± 0.03 1.03 ± 0.04
Open in a new tab

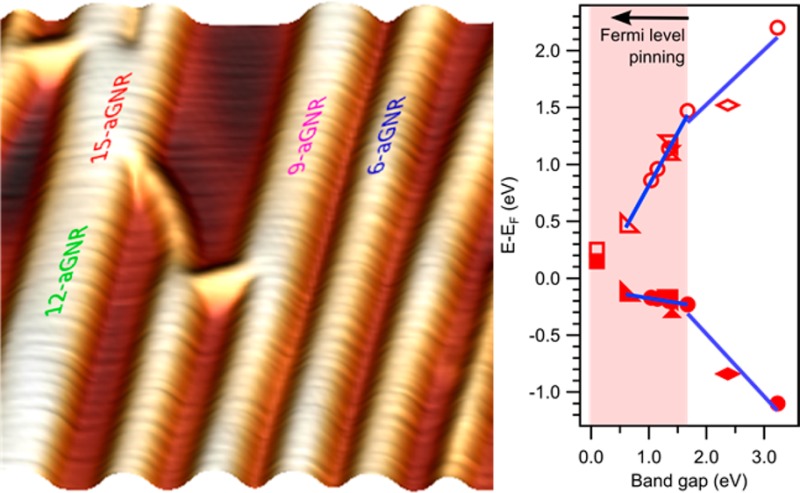
The average band gaps obtained for the differently wide aGNRs are displayed in Figure 3, where PPP nanowires (analyzed in Figure S1) are included for comparison as 3-aGNRs. The values fit into the predicted range for gold-supported nanoribbons of similar widths,29 and their smooth evolution is also in line with predictions.27,29 However, 3-aGNRs clearly stick out of the smoothly varying trend of a monotonously decreasing band gap with incremental width within the 3p-aGNR family. The reason behind this is that, in addition to the larger band gap associated with its narrower width, it is the only nonplanar structure. As a result, the degree of conjugation is reduced,37 causing an anomalous band gap increase for this particular structure different from the wider graphene nanoribbons. Figure 3 also displays the average onset energies of valence and conduction band for the differently wide aGNRs. It becomes immediately clear that GNRs display an overall p-type alignment on Au(111) and that for 6- and wider aGNRs, as the band gap decreases, the conductance band onset approaches the Fermi level much faster than the valence band.

Figure 3.

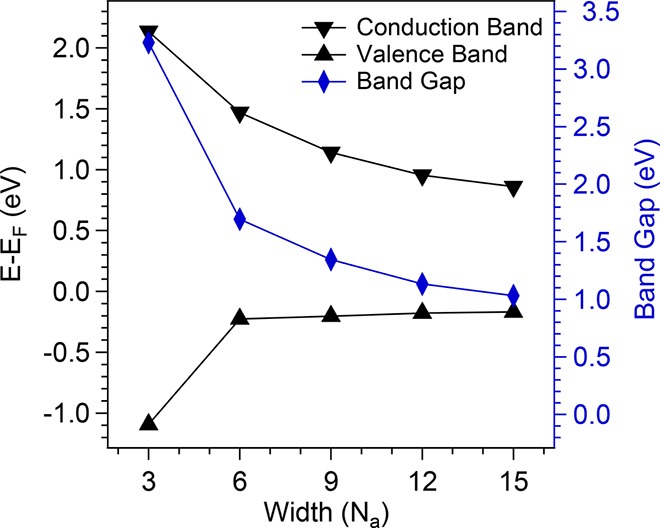
Figure 3

Open in a new tab

Average spectroscopic results for valence and conduction bands (black lines, left scale) and the resulting band gaps (blue line, right scale).

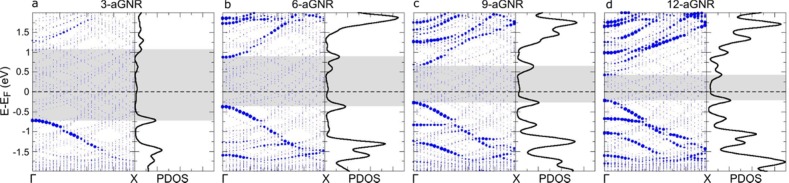
Both of these effects are indeed reproduced by DFT calculations of Au(111)-supported graphene nanoribbons from 3 (PPP wires) to 12 dimer lines. Figure 4 displays the band structure of the various systems, where the diameter of blue symbols is proportional to the weight of each state on the carbon atoms and thus on the GNRs. Next to the band structures, the figure displays the density of states projected onto C. The ribbons show a clear p-type alignment with the Au(111) substrate. In line with our experiment-based observations, after a notable upshift of the valence band from 3-aGNR to 6-aGNR, for wider ribbons, the band onset appears close to the Fermi energy at a position fairly independent of the ribbon width. It shifts by only ∼0.16 eV when going from 6-aGNRs to 12-aGNRs, to be compared with an about 3 times larger shift of the conduction band for the same widths.

Figure 4.

Figure 4

Open in a new tab

Calculated band structure (left) and PDOS (right) for (a) 3-aGNRs, (b) 6-aGNRs, (c) 9-aGNRs, and (d) 12-aGNRs. The diameter of the blue circles denotes the density of states projected onto the GNR’s carbon atoms. The shadowed areas indicate the respective band gaps.

Experimentally, the p-type alignment of GNRs seems reasonable due to the p-type doping observed for gold-supported graphene,38−42 which stems from the much larger work function of gold as compared to that of graphene. However, calculations have shown the understanding of this alignment not to be trivial as it depends on the dipole layer formed at the metal–graphene interface and displays a marked dependence on the details of the graphene–substrate interaction and the associated adsorption distance.43−45 GNRs have a weak interaction with the Au(111) surface, dominated by van der Waals forces. As a weakly interacting semiconducting adsorbate approaches a metal surface, the substrate’s intrinsic surface dipole is modified by an amount Δ as a result of a variety of processes that include, among others, the surface’s electron cloud redistribution arising from Pauli repulsion with the adsorbate (commonly termed as “pillow effect”) or intrinsic adsorbate’s dipole moments.46 In the case of aGNRs on Au(111), only the former process is relevant, giving rise to an effective reduction of the substrate work function. Indeed, for extended graphene on Au(111), the effect is such that, although at the equilibrium adsorption height (∼3.3 Å) p-doping is predicted by first-principles calculations, for only slightly smaller distances (<3.2 Å), n-doping is obtained instead.43,44 Therefore, the strong p-type alignment observed here for the aGNRs is not necessarily obvious. Particularly intriguing is the observation, in agreement with experiment, of very asymmetric shifts of the VB and CB onsets in the DFT calculations. Although the VB approaches the Fermi level as the GNRs become wider, in our calculations, it remains below the Fermi level without indications of a partial charge transfer to the substrate. In the absence of charge transfer, one would expect a rather symmetric closing of the gap. Thus, the observed behavior requires a width-dependent alignment of the aGNR levels with respect to those of Au(111). At this point, it is worth noting that the dependence of the ribbon’s polarizability on its width has been recently proposed as instrumental to understand the width dependence of the band gap of adsorbed GNRs.29 However, in contrast to our experimental observations, this effect should affect both the VB and CB in a comparable way.

Figures S4 and S5 show the relaxed geometry and the distribution of the induced charge upon adsorption of the 6-aGNR on Au(111), respectively. The computed equilibrium adsorption height of the central portion of the ribbon is in the range of 3.23–3.34 Å (larger for wider ribbons). The limit for extended graphene is 3.34 Å, in good agreement with previous calculations.43Figure S4 shows how the electron charge accumulated in the surface as a result of the “pillow effect” extends beyond the region covered by carbon, piling up along the edges. This is most probably favored by the positive partial charge on the hydrogen atoms along the GNR edges. Thus, we find that the charge distribution is noticeably affected by the finite width of the ribbons. This characteristic distribution of the induced charge produces a width-dependent decrease of the interface dipole Δ, favoring a stronger p-type alignment the narrower is the GNR. This effect partially compensates the downshift of the VB as the GNRs become narrower while increases the upshift of the CB. Therefore, it can explain the asymmetric level movement observed in the DFT calculations and, as a consequence, be a key ingredient to understand also our experimental results. However, this effect smoothly scales inversely proportional to the GNR width, while the experiment evidences a relatively sharp transition from a rapidly varying valence band alignment at widths below 6-aGNRs to an almost unchanged valence band as the width increases (see Figure 3). In fact, as will be shown below, the transition seems to relate directly to the GNR’s band gap, which is no longer inversely proportional to the width if different families of armchair GNRs or even differently oriented GNRs are considered. Thus, in addition to the width-dependent interface dipole, additional band-gap-dependent effects must be responsible for our observations.

A sharp transition from having a varying onset energy in frontier band’s to having them quasi-unchanged (close to the Fermi energy) is typically termed as Fermi level pinning. It is a well-known phenomenon observed at metal–semiconductor interfaces when one of the semiconductor’s bands gets close in energy to the substrate’s Fermi level, typically due to particularly high or low work functions (Figure S6a). Observing a transition from a non-Fermi level pinning behavior to the pinning usually requires the work function to be changed and thereby the interface chemistry. Instead, in this particular study on Fermi level pinning, the same phenomenology is observed while keeping the interface chemistry almost unchanged, the only varying parameter being the GNR’s width and thus its associated band gap (Figure S6b).

The typically proposed explanation for Fermi level pinning is as follows. In the current case of an unchanged substrate and a decreasing adsorbate’s band gap, valence and conduction band onsets plotted vs the band gap would be expected to symmetrically approach the midgap value with a slope S = 0.5 (Figure 5a). However, as one of the bands (e.g., valence band in Figure 5a) gets close to the Fermi level, further band gap reductions create a compensating dipole moment σ to refrain the band from crossing the Fermi level. Although not confirmed by our calculations, whether due to the inability of current semilocal functionals to describe the energies of the electronic levels with sufficient accuracy for the free-standing ribbons and adequately incorporate correlation effects upon adsorption, or to slight deviations in the calculated adsorption distances that can substantially alter the interface energetics,43 this is typically assumed to occur through partial charge transfer into metal-induced gap states.47−49 As a result, the nonpinned band (conduction band in Figure 5a) now supports a shift equal to the full band gap decrease (S = 1), while the alignment of the pinned band remains unchanged (S = 0). To prevent the semiconductors’ bands from crossing the Fermi level, the interfacial charge transfer is reduced. It is therefore commonly observed with physisorbed materials because its absence would imply substantial charge transfers and consequently a chemisorption scenario.50 This is exactly what we could expect from the interaction of graphene nanoribbons with an inert surface like Au(111).

Figure 5.

Figure 5

Open in a new tab

(a) Schematic evolution of the energy level alignment of valence and conduction band for varying adsorbate band gap. The energy level diagrams depict the interface dipole Δ from the molecular adsorption, as well as the additional dipole σ responsible for Fermi level pinning as the band gap gets narrower and one of the bands approaches the Fermi level (the valence band in this figure). It also displays the changing slopes of valence and conduction band onset vs band gap as Fermi level pinning sets in. (b) Valence and conduction band onsets of GNRs studied in this work and in other reports of Au(111)-supported ribbons vs their respective band gap (width given by numbers next to the CB symbols). Linear fits in selected regions display the changes in slope, evidencing notable similarity with the model scenario of panel (a).

Indeed, we observe a striking agreement between the model Fermi level pinning behavior of band onset vs band gap (Figure 5a) and the experimentally observed values from this work, together with results from other Au(111)-supported GNRs reported elsewhere, like 13-aGNR,11 9-aGNRS,12 7-aGNR,33,34 5-aGNRs,51 and even (3,1) chiral GNRs52 (Figure 5b). As displayed in Figure 4b, for band gaps above the critical value of ∼1.7 eV, valence and conduction bands shift symmetrically around their midgap value with a slope close to S = 0.5. However, as the band gap gets below that threshold value, the valence band remains almost constant (S = −0.08 ± 0.05) while the conduction band supports almost the full band decrease by shifting with a slope of S = 0.92 ± 0.05. Several GNRs have been characterized previously on an even less interacting substrate, namely, on Au(111) with an intercalated Si layer. On that substrate the GNRs display a slightly larger band gap due to the reduced substrate screening. However, not only does the band alignment similarly fit into our proposed Fermi level pinning picture, as expected from such weakly interacting surface, but it actually displays strikingly similar energies30 (Figure S7). Fermi level pinning energies of molecular adsorbates’ orbitals may vary substantially from system to system, which is normally associated with the different density of states hosted by the frontier orbitals and how far in energy the tails of the frontier bands’ density of states extend into the gap. In general, typical values remain below 0.4 eV away from the Fermi level,53,54 which coincides with our observations.

Although still maintaining the same trend of a reduced slope of the valence band shift and an increased slope for the conduction band shift, 5-aGNRs deviate somewhat from the tendency observed for the rest of GNRs and even show a valence band onset slightly above the Fermi level. This is presumably due to the small band gap of GNRs belonging to the 3p + 2 family.51 They have correspondingly minute effective masses on their frontier bands55 and thus a very low density of states around the gap. As a consequence, in a similar way as observed for graphene on a variety of substrates due to its associated low density of states around the Dirac point,38,43 the bands of 5-aGNRs can cross the Fermi level with very little associated charge transfer and thus without creating substantial interface dipoles. Instead, the case of nanoribbons with sizable band gaps is utterly different in that it exhibits a large density of states at the van Hove singularity of the valence band onset, causing a clearer Fermi level pinning.

Conclusions

In conclusion, we report spectroscopic evidence of the width-dependent band gap predicted for armchair graphene nanoribbons a decade ago and the associated energy level alignment. Starting with the synthesis of PPP wires (3-aGNRs), subsequent annealing drives their lateral fusion into 6-, 9-, 12-, or 15-aGNRs depending on the number of involved PPP chains. That is, the first 5 members of 3p-aGNR family are obtained on the same surface, on which both valence and conduction bands are probed by means of STS. We observe a continuously decreasing band gap as the GNRs structures get wider. Most importantly, Fermi level pinning of the valence band is found on Au(111) for 6 or more dimer lines wide aGNRs, in qualitative agreement with DFT calculations. Results known from other GNRs equally fit the pinning phenomenon proposed here, whenever their bandgap is below ∼1.7 eV. This has important implications on the energy level alignment across GNR/metal interfaces, which may in turn be crucial for future GNR-based devices displaying similar interfaces at charge collection electrodes.

Methods

Experimental Procedures

Samples were prepared by deposition of precursor molecules from a Dodecon molecular evaporator containing a Knudsen cell where the molecular precursors are placed and heated up to a sublimation temperature of 400 K. We used a single monocrystalline Au(111) surface as substrate. Standard sputtering/annealing cycles (1.5 kV Ne, 730 K) were performed to obtain an atomically clean Au(111) surface. We grew PPP nanowires and aGNRs by initial DBTP deposition and subsequent annealing at 250 and 430 °C, respectively, in the 10–10 mbar range. The annealing processes were performed in such a way that the maximum temperature of 250 or 430 °C was maintained for 30 min, respectively. STM measurements were performed using a home-built STM with the samples held at 4.2 K in UHV conditions. A tungsten tip was used for topography and spectroscopic measurements. Topography was obtained in constant current mode of the STM. For spectroscopic measurements, the tunneling differential conductance was measured by a lock-in amplifier, while the sample bias was modulated by a 767 Hz, 12–18 mV (rms) sinusoidal voltage under open-feedback conditions.

All STM images were processed by WSxM.56

Computational Procedures

The electronic structure and geometries were calculated using density functional theory, as implemented in the SIESTA code.57 We use a supercell description of the system, made up of a slab containing 4 layers of Au(111), with a graphene nanoribbon of 3, 6, 9, or 12 dimer lines on the top Au surface. We employed the stacking geometry suggested in ref (43), where 2 × 2 graphene and Au(111) √3 × √3 unit cells are directly matched (more details of the setup in the Supporting Information). The bottom Au surface was passivated with hydrogen atoms to quench one of the Au(111)’s Shockley surface states close to the Fermi level.58 In order to properly capture the “pillow effect”, it is instrumental to describe adequately the decay of the metal electron density into vacuum and the subsequent modifications of the surface dipole layer upon adsorption of the ribbon. The use of a basis set of extended, optimized atomic orbitals to describe the Au surface atoms is thus crucial to capture the correct level alignment. To avoid interactions between periodic surfaces, we considered a vacuum region of more than 10 Å. The GNRs and the top two Au layers were fully relaxed until forces were <0.01 eV/Å, and the dispersion interactions were taken into account by the nonlocal optB88-vdW functional.59 The basis set consisted of double-ζ plus polarization (DZP) orbitals for C, H, and bulk Au atoms. Au atoms on the topmost layer were treated with a DZP basis set optimized for the description of the (111) surface of Au.60 A 9 × 1 × 1 Monkhorst–Pack mesh was used for the k-point sampling of the three-dimensional Brillouin zone, where the 9 k-points are taken along the direction of the ribbon. A cutoff of 300 Ry was used for the real-space grid integrations.

Acknowledgments

The project leading to this publication has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 635919), from the European Union FP7 FET-ICT “Planar Atomic and Molecular Scale devices” (PAMS) project (Contract No. 610446), from the Spanish Ministry of Economy, Industry and Competitiveness (MINECO, Grant No. MAT2016-78293-C6), from the Basque Department of Education (PI-2016-1-0027), and from the University of Padova (Grant CPDA154322, Project AMNES).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b06765.

  • dI/dV point spectra on PPP nanowires and conductance maps at onset energies of valence and conduction band; conductance maps and associated profiles revealing the valence band of GNRs; point spectra and conductance maps in a wider energy range on aGNRs of varying width, displaying the onset of the second valence band (VB-1); example of Au(111)-GNR unit cell used for DFT calculations; isosurface of the computed induced charge upon adsorption of a 6-aGNR on Au(111); schematic model of the changing energy level alignment of weakly interacting adsorbate’s valence and conduction bands with varying work function of the substrate for fixed adsorbate’s band gap, compared to the alignment with a fixed work function and a varying adsorbate’s band gap; experimental data of valence and conduction band onset of GNRs studied in this work, as well as for works reported elsewhere on other Au(111)-supported ribbons and ribbons on Au(111) with an intercalated Si layer (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn7b06765_si_001.pdf (1.7MB, pdf)

References

  1. Xiang C.; Cox P. J.; Kukovecz A.; Genorio B.; Hashim D. P.; Yan Z.; Peng Z.; Hwang C.-C.; Ruan G.; Samuel E. L. G.; Sudeep P.; Konya Z.; Vajtai R.; Ajayan P. M.; Tour J. M. Functionalized Low Defect Graphene Nanoribbons and Polyurethane Composite Film for Improved Gas Barrier and Mechanical Performances. ACS Nano 2013, 7, 10380–10386. 10.1021/nn404843n. [DOI] [PubMed] [Google Scholar]
  2. Mazzamuto F.; Hung Nguyen V.; Apertet Y.; Caër C.; Chassat C.; Saint-Martin J.; Dollfus P. Enhanced Thermoelectric Properties in Graphene Nanoribbons by Resonant Tunneling of Electrons. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 235426. 10.1103/PhysRevB.83.235426. [DOI] [Google Scholar]
  3. Sevinçli H.; Sevik C.; Çağın T.; Cuniberti G. A Bottom-up Route to Enhance Thermoelectric Figures of Merit in Graphene Nanoribbons. Sci. Rep. 2013, 3, 1228. 10.1038/srep01228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Liu M.; Tjiu W. W.; Pan J.; Zhang C.; Gao W.; Liu T. One-Step Synthesis of Graphene Nanoribbon–MnO2 Hybrids and Their All-Solid-State Asymmetric Supercapacitors. Nanoscale 2014, 6, 4233. 10.1039/c3nr06650a. [DOI] [PubMed] [Google Scholar]
  5. Li L.; Raji A.-R. O.; Fei H.; Yang Y.; Samuel E. L. G.; Tour J. M. Nanocomposite of Polyaniline Nanorods Grown on Graphene Nanoribbons for Highly Capacitive Pseudocapacitors. ACS Appl. Mater. Interfaces 2013, 5, 6622–6627. 10.1021/am4013165. [DOI] [PubMed] [Google Scholar]
  6. Li L.; Raji A.-R. O.; Tour J. M. Graphene-Wrapped MnO 2 -Graphene Nanoribbons as Anode Materials for High-Performance Lithium Ion Batteries. Adv. Mater. 2013, 25, 6298–6302. 10.1002/adma.201302915. [DOI] [PubMed] [Google Scholar]
  7. Freitag M.; Low T.; Zhu W.; Yan H.; Xia F.; Avouris P. Photocurrent in Graphene Harnessed by Tunable Intrinsic Plasmons. Nat. Commun. 2013, 4, 1951. 10.1038/ncomms2951. [DOI] [PubMed] [Google Scholar]
  8. Schwierz F. Graphene Transistors. Nat. Nanotechnol. 2010, 5, 487–496. 10.1038/nnano.2010.89. [DOI] [PubMed] [Google Scholar]
  9. Kang J.; Sarkar D.; Khatami Y.; Banerjee K. Proposal for All-Graphene Monolithic Logic Circuits. Appl. Phys. Lett. 2013, 103, 083113. 10.1063/1.4818462. [DOI] [Google Scholar]
  10. Cai J.; Ruffieux P.; Jaafar R.; Bieri M.; Braun T.; Blankenburg S.; Muoth M.; Seitsonen A. P.; Saleh M.; Feng X.; Muellen K.; Fasel R. Atomically Precise Bottom-up Fabrication of Graphene Nanoribbons. Nature 2010, 466, 470–473. 10.1038/nature09211. [DOI] [PubMed] [Google Scholar]
  11. Chen Y.-C.; de Oteyza D. G.; Pedramrazi Z.; Chen C.; Fischer F. R.; Crommie M. F. Tuning the Band Gap of Graphene Nanoribbons Synthesized from Molecular Precursors. ACS Nano 2013, 7, 6123–6128. 10.1021/nn401948e. [DOI] [PubMed] [Google Scholar]
  12. Talirz L.; Söde H.; Dumslaff T.; Wang S.; Sanchez-Valencia J. R.; Liu J.; Shinde P.; Pignedoli C. A.; Liang L.; Meunier V.; Plumb N. C.; Shi M.; Feng X.; Narita A.; Müllen K.; Fasel R.; Ruffieux P. On-Surface Synthesis and Characterization of 9-Atom Wide Armchair Graphene Nanoribbons. ACS Nano 2017, 11, 1380–1388. 10.1021/acsnano.6b06405. [DOI] [PubMed] [Google Scholar]
  13. Zhang H.; Lin H.; Sun K.; Chen L.; Zagranyarski Y.; Aghdassi N.; Duhm S.; Li Q.; Zhong D.; Li Y.; et al. On-Surface Synthesis of Rylene-Type Graphene Nanoribbons. J. Am. Chem. Soc. 2015, 137, 4022–4025. 10.1021/ja511995r. [DOI] [PubMed] [Google Scholar]
  14. de Oteyza D. G.; García-Lekue A.; Vilas-Varela M.; Merino-Díez N.; Carbonell-Sanromà E.; Corso M.; Vasseur G.; Rogero C.; Guitián E.; Pascual J. I.; Ortega J. E.; Wakayama Y.; Peña D. Substrate-Independent Growth of Atomically Precise Chiral Graphene Nanoribbons. ACS Nano 2016, 10, 9000–9008. 10.1021/acsnano.6b05269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ruffieux P.; Wang S.; Yang B.; Sánchez-Sánchez C.; Liu J.; Dienel T.; Talirz L.; Shinde P.; Pignedoli C. A.; Passerone D.; Dumslaff T.; Feng X.; Müllen K.; Fasel R. On-Surface Synthesis of Graphene Nanoribbons with Zigzag Edge Topology. Nature 2016, 531, 489–492. 10.1038/nature17151. [DOI] [PubMed] [Google Scholar]
  16. Bronner C.; Stremlau S.; Gille M.; Brauße F.; Haase A.; Hecht S.; Tegeder P. Aligning the Band Gap of Graphene Nanoribbons by Monomer Doping. Angew. Chem., Int. Ed. 2013, 52, 4422–4425. 10.1002/anie.201209735. [DOI] [PubMed] [Google Scholar]
  17. Nguyen G. D.; Toma F. M.; Cao T.; Pedramrazi Z.; Chen C.; Rizzo D. J.; Joshi T.; Bronner C.; Chen Y.-C.; Favaro M.; Louie S. G.; Fischer F.; Crommie M. Bottom-Up Synthesis of N = 13 Sulfur-Doped Graphene Nanoribbons. J. Phys. Chem. C 2016, 120, 2684–2687. 10.1021/acs.jpcc.5b09986. [DOI] [Google Scholar]
  18. Kawai S.; Saito S.; Osumi S.; Yamaguchi S.; Foster A. S.; Spijker P.; Meyer E. Atomically Controlled Substitutional Boron-Doping of Graphene Nanoribbons. Nat. Commun. 2015, 6, 8098. 10.1038/ncomms9098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cloke R. R.; Marangoni T.; Nguyen G. D.; Joshi T.; Rizzo D. J.; Bronner C.; Cao T.; Louie S. G.; Crommie M. F.; Fischer F. R. Site-Specific Substitutional Boron Doping of Semiconducting Armchair Graphene Nanoribbons. J. Am. Chem. Soc. 2015, 137, 8872–8875. 10.1021/jacs.5b02523. [DOI] [PubMed] [Google Scholar]
  20. Basagni A.; Vasseur G.; Pignedoli C. A.; Vilas-Varela M.; Peña D.; Nicolas L.; Vitali L.; Lobo-Checa J.; de Oteyza D. G.; Sedona F.; Casarin M.; Ortega J. E.; Sambi M. Tunable Band Alignment with Unperturbed Carrier Mobility of On-Surface Synthesized Organic Semiconducting Wires. ACS Nano 2016, 10, 2644–2651. 10.1021/acsnano.5b07683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Cai J.; Pignedoli C. A.; Talirz L.; Ruffieux P.; Söde H.; Liang L.; Meunier V.; Berger R.; Li R.; Feng X.; Müllen K.; Fasel R. Graphene Nanoribbon Heterojunctions. Nat. Nanotechnol. 2014, 9, 896–900. 10.1038/nnano.2014.184. [DOI] [PubMed] [Google Scholar]
  22. Chen Y.-C.; Cao T.; Chen C.; Pedramrazi Z.; Haberer D.; de Oteyza D. G.; Fischer F. R.; Louie S. G.; Crommie M. F. Molecular Bandgap Engineering of Bottom-up Synthesized Graphene Nanoribbon Heterojunctions. Nat. Nanotechnol. 2015, 10, 156–160. 10.1038/nnano.2014.307. [DOI] [PubMed] [Google Scholar]
  23. Carbonell-Sanromà E.; Brandimarte P.; Balog R.; Corso M.; Kawai S.; Garcia-Lekue A.; Saito S.; Yamaguchi S.; Meyer E.; Sánchez-Portal D.; Pascual J. I. Quantum Dots Embedded in Graphene Nanoribbons by Chemical Substitution. Nano Lett. 2017, 17, 50–56. 10.1021/acs.nanolett.6b03148. [DOI] [PubMed] [Google Scholar]
  24. Jacobse P. H.; Kimouche A.; Gebraad T.; Ervasti M. M.; Thijssen J. M.; Liljeroth P.; Swart I. Electronic Components Embedded in a Single Graphene Nanoribbon. Nat. Commun. 2017, 8, 119. 10.1038/s41467-017-00195-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bennett P. B.; Pedramrazi Z.; Madani A.; Chen Y.-C.; de Oteyza D. G.; Chen C.; Fischer F. R.; Crommie M. F.; Bokor J. Bottom-up Graphene Nanoribbon Field-Effect Transistors. Appl. Phys. Lett. 2013, 103, 253114. 10.1063/1.4855116. [DOI] [Google Scholar]
  26. Llinas J. P.; Fairbrother A.; Borin Barin G.; Shi W.; Lee K.; Wu S.; Yong Choi B.; Braganza R.; Lear J.; Kau N.; Choi W.; Chen C.; Pedramrazi Z.; Dumslaff T.; Narita A.; Feng X.; Müllen K.; Fischer F.; Zettl A.; Ruffieux P.; et al. Short-Channel Field-Effect Transistors with 9-Atom and 13-Atom Wide Graphene Nanoribbons. Nat. Commun. 2017, 8, 633. 10.1038/s41467-017-00734-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Son Y.-W.; Cohen M. L.; Louie S. G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. 10.1103/PhysRevLett.97.216803. [DOI] [PubMed] [Google Scholar]
  28. Yang L.; Park C.-H.; Son Y.-W.; Cohen M. L.; Louie S. G. Quasiparticle Energies and Band Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2007, 99, 186801. 10.1103/PhysRevLett.99.186801. [DOI] [PubMed] [Google Scholar]
  29. Kharche N.; Meunier V. Width and Crystal Orientation Dependent Band Gap Renormalization in Substrate-Supported Graphene Nanoribbons. J. Phys. Chem. Lett. 2016, 7, 1526–1533. 10.1021/acs.jpclett.6b00422. [DOI] [PubMed] [Google Scholar]
  30. Deniz O.; Sánchez-Sánchez C.; Dumslaff T.; Feng X.; Narita A.; Müllen K.; Kharche N.; Meunier V.; Fasel R.; Ruffieux P. Revealing the Electronic Structure of Silicon Intercalated Armchair Graphene Nanoribbons by Scanning Tunneling Spectroscopy. Nano Lett. 2017, 17, 2197–2203. 10.1021/acs.nanolett.6b04727. [DOI] [PubMed] [Google Scholar]
  31. Basagni A.; Sedona F.; Pignedoli C. A.; Cattelan M.; Nicolas L.; Casarin M.; Sambi M. Molecules–Oligomers–Nanowires–Graphene Nanoribbons: A Bottom-Up Stepwise On-Surface Covalent Synthesis Preserving Long-Range Order. J. Am. Chem. Soc. 2015, 137, 1802–1808. 10.1021/ja510292b. [DOI] [PubMed] [Google Scholar]
  32. Ullmann F.; Bielecki J. Ueber Synthesen in der Biphenylreihe. Ber. Dtsch. Chem. Ges. 1901, 34, 2174–2185. 10.1002/cber.190103402141. [DOI] [Google Scholar]
  33. Ruffieux P.; Cai J.; Plumb N. C.; Patthey L.; Prezzi D.; Ferretti A.; Molinari E.; Feng X.; Müllen K.; Pignedoli C. A.; Fasel R. Electronic Structure of Atomically Precise Graphene Nanoribbons. ACS Nano 2012, 6, 6930–6935. 10.1021/nn3021376. [DOI] [PubMed] [Google Scholar]
  34. Söde H.; Talirz L.; Gröning O.; Pignedoli C. A.; Berger R.; Feng X.; Müllen K.; Fasel R.; Ruffieux P. Electronic Band Dispersion of Graphene Nanoribbons via Fourier-Transformed Scanning Tunneling Spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 045429. 10.1103/PhysRevB.91.045429. [DOI] [Google Scholar]
  35. Wang S.; Talirz L.; Pignedoli C. A.; Feng X.; Müllen K.; Fasel R.; Ruffieux P. Giant Edge State Splitting at Atomically Precise Graphene Zigzag Edges. Nat. Commun. 2016, 7, 11507. 10.1038/ncomms11507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zdetsis A. D.; Economou E. N. Rationalizing and Reconciling Energy Gaps and Quantum Confinement in Narrow Atomically Precise Armchair Graphene Nanoribbons. Carbon 2017, 116, 422–434. 10.1016/j.carbon.2017.02.006. [DOI] [Google Scholar]
  37. Kertesz M.; Choi C. H.; Yang S. Conjugated Polymers and Aromaticity. Chem. Rev. 2005, 105, 3448–3481. 10.1021/cr990357p. [DOI] [PubMed] [Google Scholar]
  38. Tesch J.; Leicht P.; Blumenschein F.; Gragnaniello L.; Fonin M.; Marsoner Steinkasserer L. E.; Paulus B.; Voloshina E.; Dedkov Y. Structural and Electronic Properties of Graphene Nanoflakes on Au(111) and Ag(111). Sci. Rep. 2016, 6, 23439. 10.1038/srep23439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wofford J. M.; Starodub E.; Walter A. L.; Nie S.; Bostwick A.; Bartelt N. C.; Thürmer K.; Rotenberg E.; McCarty K. F.; Dubon O. D. Extraordinary Epitaxial Alignment of Graphene Islands on Au(111). New J. Phys. 2012, 14, 053008. 10.1088/1367-2630/14/5/053008. [DOI] [Google Scholar]
  40. Enderlein C.; Kim Y. S.; Bostwick A.; Rotenberg E.; Horn K. The Formation of an Energy Gap in Graphene on Ruthenium by Controlling the Interface. New J. Phys. 2010, 12, 033014. 10.1088/1367-2630/12/3/033014. [DOI] [Google Scholar]
  41. Leicht P.; Zielke L.; Bouvron S.; Moroni R.; Voloshina E.; Hammerschmidt L.; Dedkov Y. S.; Fonin M. In Situ Fabrication Of Quasi-Free-Standing Epitaxial Graphene Nanoflakes On Gold. ACS Nano 2014, 8, 3735–3742. 10.1021/nn500396c. [DOI] [PubMed] [Google Scholar]
  42. Wu Y.; Jiang W.; Ren Y.; Cai W.; Lee W. H.; Li H.; Piner R. D.; Pope C. W.; Hao Y.; Ji H.; Kang J.; Ruoff R. S. Tuning the Doping Type and Level of Graphene with Different Gold Configurations. Small 2012, 8, 3129–3136. 10.1002/smll.201200520. [DOI] [PubMed] [Google Scholar]
  43. Giovannetti G.; Khomyakov P. A.; Brocks G.; Karpan V. M.; van den Brink J.; Kelly P. J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 2008, 101, 026803. 10.1103/PhysRevLett.101.026803. [DOI] [PubMed] [Google Scholar]
  44. Khomyakov P. A.; Giovannetti G.; Rusu P. C.; Brocks G.; van den Brink J.; Kelly P. J. First-Principles Study of the Interaction and Charge Transfer between Graphene and Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 195425. 10.1103/PhysRevB.79.195425. [DOI] [Google Scholar]
  45. Gebhardt J.; Viñes F.; Görling A. Influence of the Surface Dipole Layer and Pauli Repulsion on Band Energies and Doping in Graphene Adsorbed on Metal Surfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 195431. 10.1103/PhysRevB.86.195431. [DOI] [Google Scholar]
  46. Kahn A.; Koch N.; Gao W. Electronic Structure and Electrical Properties of Interfaces between Metals and ?-Conjugated Molecular Films. J. Polym. Sci., Part B: Polym. Phys. 2003, 41, 2529–2548. 10.1002/polb.10642. [DOI] [Google Scholar]
  47. Mead C. A.; Spitzer W. G. Fermi Level Position at Metal-Semiconductor Interfaces. Phys. Rev. 1964, 134, A713–A716. 10.1103/PhysRev.134.A713. [DOI] [Google Scholar]
  48. Tung R. T. Formation of an Electric Dipole at Metal-Semiconductor Interfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 64, 205310. 10.1103/PhysRevB.64.205310. [DOI] [Google Scholar]
  49. Goiri E.; Borghetti P.; El-Sayed A.; Ortega J. E.; de Oteyza D. G. Multi-Component Organic Layers on Metal Substrates. Adv. Mater. 2016, 28, 1340–1368. 10.1002/adma.201503570. [DOI] [PubMed] [Google Scholar]
  50. Heimel G.; Duhm S.; Salzmann I.; Gerlach A.; Strozecka A.; Niederhausen J.; Bürker C.; Hosokai T.; Fernandez-Torrente I.; Schulze G.; Winkler S.; Wilke A.; Schlesinger R.; Frisch J.; Bröker B.; Vollmer A.; Detlefs B.; Pflaum J.; Kera S.; Franke K. J.; et al. Charged and Metallic Molecular Monolayers through Surface-Induced Aromatic Stabilization. Nat. Chem. 2013, 5, 187–194. 10.1038/nchem.1572. [DOI] [PubMed] [Google Scholar]
  51. Kimouche A.; Ervasti M. M.; Drost R.; Halonen S.; Harju A.; Joensuu P. M.; Sainio J.; Liljeroth P. Ultra-Narrow Metallic Armchair Graphene Nanoribbons. Nat. Commun. 2015, 6, 10177. 10.1038/ncomms10177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Merino-Díez N.; Li J.; Garcia-Lekue A.; Vasseur G.; Vilas-Varela M.; Carbonell-Sanromà E.; Corso M.; Ortega J. E.; Peña D.; Pascual J. I.; de Oteyza D. G.. Unraveling the Electronic Structure of Narrow Atomically-Precise Chiral Graphene Nanoribbons. arXiv:1710.05813 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Braun S.; Salaneck W. R.; Fahlman M. Energy-Level Alignment at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 2009, 21, 1450–1472. 10.1002/adma.200802893. [DOI] [Google Scholar]
  54. Hwang J.; Wan A.; Kahn A. Energetics of Metal–organic Interfaces: New Experiments and Assessment of the Field. Mater. Sci. Eng., R 2009, 64, 1–31. 10.1016/j.mser.2008.12.001. [DOI] [Google Scholar]
  55. Raza H.; Kan E. C. Armchair Graphene Nanoribbons: Electronic Structure and Electric-Field Modulation. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 245434. 10.1103/PhysRevB.77.245434. [DOI] [Google Scholar]
  56. Horcas I.; Fernández R.; Gómez-Rodríguez J. M.; Colchero J.; Gómez-Herrero J.; Baro A. M. WSXM: A Software for Scanning Probe Microscopy and a Tool for Nanotechnology. Rev. Sci. Instrum. 2007, 78, 013705. 10.1063/1.2432410. [DOI] [PubMed] [Google Scholar]
  57. Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. The SIESTA Method for Ab Initio Order- N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. 10.1088/0953-8984/14/11/302. [DOI] [Google Scholar]
  58. Gonzalez-Lakunza N.; Fernández-Torrente I.; Franke K. J.; Lorente N.; Arnau A.; Pascual J. I. Formation of Dispersive Hybrid Bands at an Organic-Metal Interface. Phys. Rev. Lett. 2008, 100, 156805. 10.1103/PhysRevLett.100.156805. [DOI] [PubMed] [Google Scholar]
  59. Klimeš J.; Bowler D. R.; Michaelides A. Chemical Accuracy for the van Der Waals Density Functional. J. Phys.: Condens. Matter 2010, 22, 022201. 10.1088/0953-8984/22/2/022201. [DOI] [PubMed] [Google Scholar]
  60. García-Gil S.; García A.; Lorente N.; Ordejón P. Optimal Strictly Localized Basis Sets for Noble Metal Surfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 075441. 10.1103/PhysRevB.79.075441. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn7b06765_si_001.pdf (1.7MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES