Lumpy species coexistence arises robustly in fluctuating resource environments

Significance

Explaining why there are more species than limiting resources in natural systems constitutes a long-standing challenge among ecologists. Recently, this apparent paradox was resolved theoretically by showing that species can coexist in clumps along niche gradients. However, models demonstrating this effect have failed to account for a ubiquitous feature of nature, namely variability in environmental conditions. This leaves open the question of whether the proposed mechanisms underpinning “lumpy coexistence” apply in nature or arise as a coincidence of modeling frameworks. Here, we demonstrate the emergence of lumpy coexistence in assemblages self-organizing under fluctuating resource supplies. We show that clumps form predictably as the result of the dynamic pattern in ambient resources driven by the most competitive species in the assemblage.

Abstract

The effect of life-history traits on resource competition outcomes is well understood in the context of a constant resource supply. However, almost all natural systems are subject to fluctuations of resources driven by cyclical processes such as seasonality and tidal hydrology. To understand community composition, it is therefore imperative to study the impact of resource fluctuations on interspecies competition. We adapted a well-established resource-competition model to show that fluctuations in inflow concentrations of two limiting resources lead to the survival of species in clumps along the trait axis, consistent with observations of “lumpy coexistence” [Scheffer M, van Nes EH (2006) Proc Natl Acad Sci USA 103:6230–6235]. A complex dynamic pattern in the available ambient resources arose very early in the self-organization process and dictated the locations of clumps along the trait axis by creating niches that promoted the growth of species with specific traits. This dynamic pattern emerged as the combined result of fluctuations in the inflow of resources and their consumption by the most competitive species that accumulated the bulk of biomass early in assemblage organization. Clumps emerged robustly across a range of periodicities, phase differences, and amplitudes. Given the ubiquity in the real world of asynchronous fluctuations of limiting resources, our findings imply that assemblage organization in clumps should be a common feature in nature.

Predicting assemblage composition is a long-standing goal in community ecology. The study of phytoplankton has been key in developing our understanding because it forms a species-rich group (1) for which the observed number of species at any given moment far exceeds the number of potentially growth-limiting resources. This violation of the competitive exclusion principle, known as the “Paradox of Plankton” (2), has generally been attributed to environmental variability. Explanations relying on environmental variability have typically focused on competition for resources in fluctuating environments. When resources fluctuate, niche theory (3) suggests that multiple species can coexist if the resources they require for growth differ sufficiently (4–10). Later theories have deviated from these niche-based explanations by suggesting that high diversity can be maintained even when life-history traits are very similar (i.e., neutral coexistence) (11). A reconciliation of niche and neutral theory, termed “lumpy coexistence,” describes the self-organization of assemblages into competing clumps, in which species within clumps have very similar traits and are thus considered nearly neutral (12). However, the role of fluctuating resources in shaping the composition of assemblages in which species are distinguished by their life-history traits remains unexplored.

When resource supply is constant, the competitive exclusion principle states that the number of coexisting species cannot exceed the number of limiting resources (13). Specifically, for a system with two species, in which two resources are growth-limiting and the species show a tradeoff in their competitive abilities (species A is a superior competitor for resource 2 and species B for resource 1; Fig. 1A), coexistence is stable when the resources are supplied within the region of coexistence (dark shading, Fig. 1A) (5). However, when resources fluctuate, the resource ratio may fall outside the region of coexistence, at least for some portion of the time. In such scenarios, predicting which species will persist in the long term becomes more challenging. Indeed, Sommer (14) has noted that a key unresolved point of interest is whether species interactions under a fluctuating resource supply could lead to an assemblage structure that is different from that predicted under a constant resource supply.

Fig. 1.

Conceptual framework for species coexistence in a stable environment and model configuration. (A) A two-species, two-resource system, for which resource ratio theory (5) predicts the coexistence of species A and B at steady state when available ambient resources fall within the dark shaded region and the persistence of a single species in the light-shaded regions. The two species present a tradeoff in their competitive abilities: Species A requires more of resource 1 to maintain a stable population (R*_1A > R*_1B), whereas species B requires more of resource 2 (R*_2B > R*_2A). Each species consumes resources 1 and 2 according to a fixed ratio. Points in the resource space corresponding to this ratio fall on the consumption vectors Q_A and Q_B, which delimit the region of species coexistence. Note that lower R* values indicate greater competitive ability—that is, minimum required resource to maintain a stable population. (B) The R* values for the 300 species present in the initial species pool follow a downward tradeoff curve, driven by the species-specific K values. (Inset) Fluctuation of resource inflow.

Understanding whether fluctuating resources lead to different assemblage structures is fundamental for understanding real-world systems that are typically subject to resource variability. Here we focus on recurrent resource fluctuations that might arise due to regular cyclical processes such as those driven by planetary and lunar cycles, and the resulting seasonal and tidal cycles. These cycles can lead to variation in the supply of growth-limiting nutrients such as nitrogen and phosphorus. For example, short-term fluctuations can arise from tidal movements that cause resuspension of nutrients from sedimentary matter (15–17). Over longer time scales, seasonal climatic forcing and upwelling events may also lead to alternating periods of limitation of major nutrients through the winter dominance of nitrogen-rich freshwater inflows and summer dominance of nitrogen-limiting oceanic upwelling (18, 19). Although environmental fluctuations are a well-documented mechanism for sustaining phytoplankton diversity (e.g., refs. 20–23), they have been studied primarily in the context of emergent resource fluctuations (despite constant supply) or exogenous variability in a single resource. However, the role of fluctuations in the inflow of multiple resources has not been explored with respect to its potential to drive lumpy coexistence.

Here, our aim was to identify the distribution of traits of coexisting species in self-organized assemblages subjected to recurrent fluctuations in the supply of two growth-limiting resources and to understand the underpinning mechanisms of coexistence. We used computational experiments to simulate self-organization from an initial species-rich pool with traits drawn from a wide range observed in the field (Fig. 1B) and investigated how the dynamic pattern of available resources (Fig. 1B, Inset) gave rise to the distribution of traits of surviving species. We explored how the trait distribution along the niche axis varied as a function of the resource supply periodicity, phase difference, and amplitude. The high density of species along the trait axis in the initial species pool implied strong trait similarity between neighboring species (Fig. 1B), enabling us to investigate the effects of trait redundancy in the final assemblage composition. By extending the reasoning of Tilman (5), we hypothesized that under fluctuating resources, species persistence—and thus coexistence—would depend on the proportion of time that the resource concentrations were favorable for the growth of each species. In turn, we expected that the available resources would be shaped by the distribution of traits of surviving species and the biomass each developed during the self-organization process.

Results

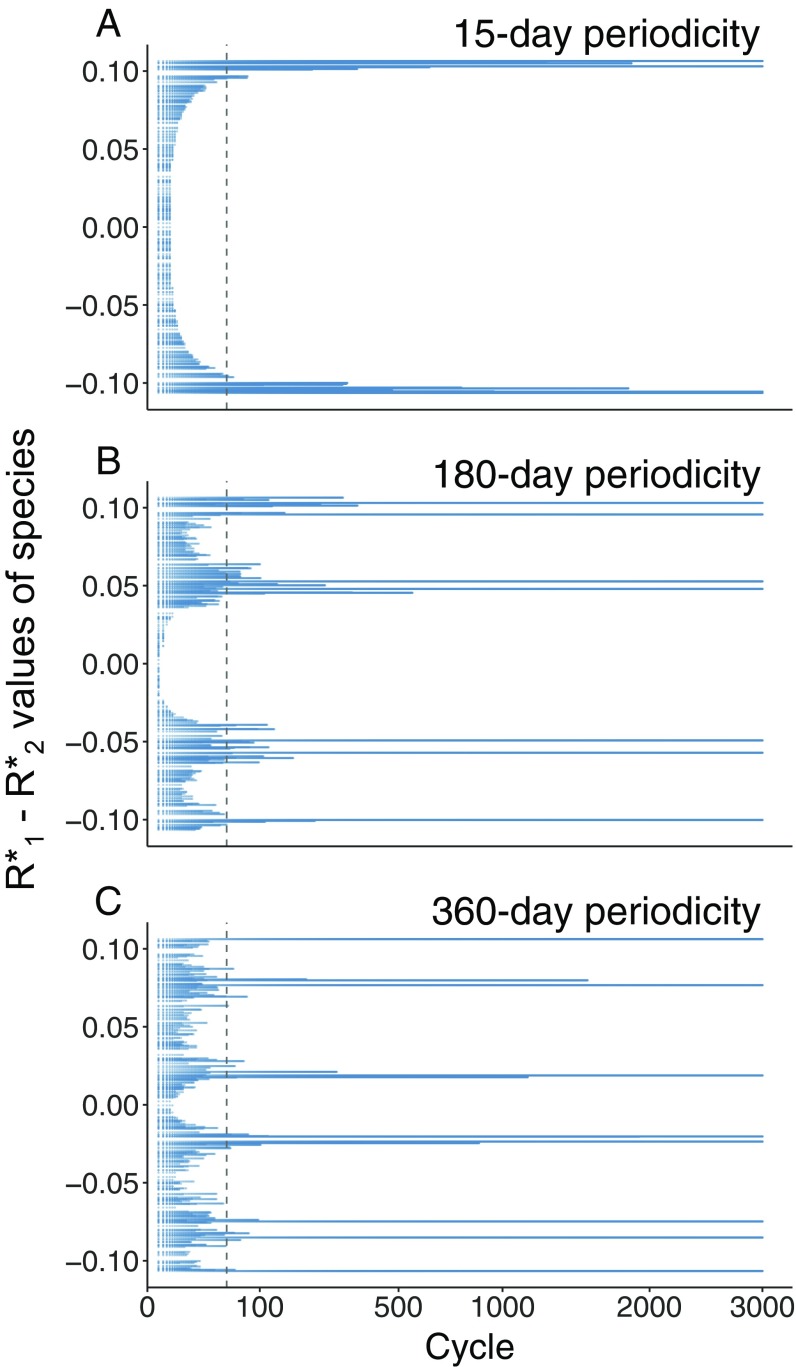
Assemblages demonstrating lumpy coexistence emerged through self-organization for the three resource fluctuation periodicities of 15, 180, and 360 d, as indicated by clustering in the R* values of surviving species (see Fig. 2 for representative assemblages). Because the maximum growth and flushing rates were constant and equal among our species and R* was directly proportional to competitive ability K, the R* continuum also represents the competitive ability trait axis. In the range from shorter to intermediate resource fluctuation periodicities, species with intermediate competitive abilities (i.e., difference between R*₁ and R*₂ values is close to zero) were excluded earlier than species that were more competitive for either resource (i.e., difference between R*₁ and R*₂ values close to −0.10 or 0.10, respectively), leading to the formation of two to four clumps (Fig. 2 A and B). For longer periodicities, species with intermediate competitive abilities were not competitively excluded (Fig. 2C). Irrespective of resource periodicity, species clumps had formed by the 50th resource fluctuation cycle. Thereafter, competitive exclusion was slower, eventually leading to either one or two species surviving per clump as defined at the 50th cycle (e.g., see 3,000th resource fluctuation cycle relative to 50th cycle in Fig. 2). Clumps formed predictably in similar positions along the trait axis when the model was initialized with random replicates of initial species-rich assemblages (Fig. S1).

Fig. 2.

Clump formation over resource fluctuation cycles for our focal periodicities. Blue shading indicates the persistence of each of the initial 300 species over cycles (square root scale), positioned along the axis indicated by the difference in R* values for the two resources. The vertical dashed line indicates the emergence of clumps due to competitive exclusion at around the 50th resource fluctuation cycle. By the 3,000th resource fluctuation cycle, species richness is stable, with four species in the 15-d cycle (A), seven species in the 180-d cycle (B), and eight species in the 360-d cycle (C).

The number of cycles required for the assemblage to stabilize depended on the periodicity of the resource fluctuation cycle. Species richness stabilized after the fewest cycles for the 180-d periodicity (558 cycles), whereas 1,918 cycles were required in the 360-d periodicity, and 2,466 were required in the 15-d periodicity. For the 15-d periodicity, all species had reached the biomass attained at cycle 3,000 by cycle 1,718 (Fig. S2A and Table S1), whereas in the 360-d periodicity, this required 2,885 cycles (Fig. S2C and Table S1). In contrast, a periodic pattern in the concentration of ambient resources and total assemblage biomass had emerged a lot earlier in the self-organization process, showing limited variation after cycle 2 (Fig. S3).

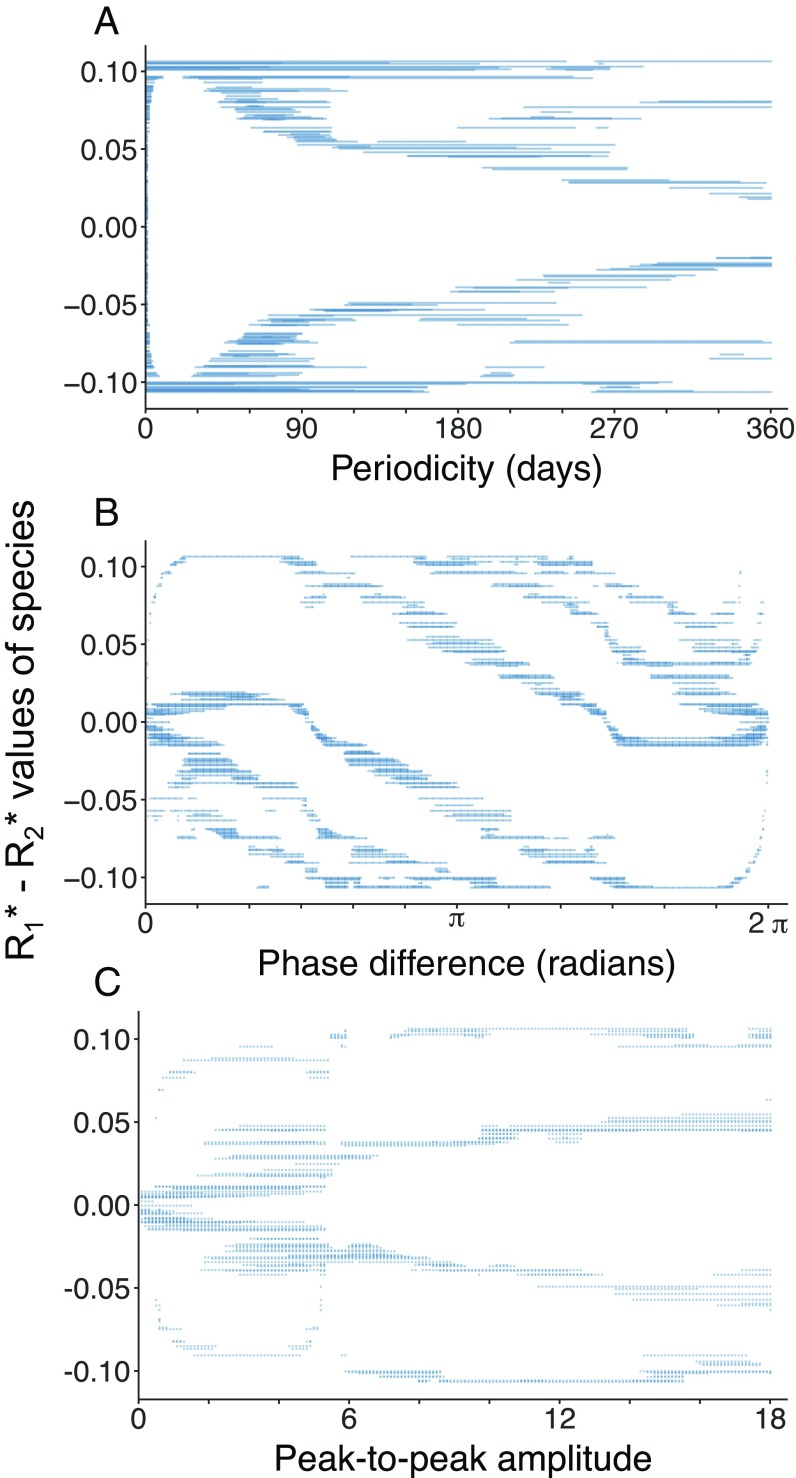
Species clump formation was robust across a continuum of fluctuation periodicities, phase differences between the two resources, and amplitudes of the resource inflow concentrations. However, the number of clumps and their positions in trait space varied. Regarding fluctuation periodicities, we found that rapid fluctuations with a period of 1 d did not lead to clump formation (Fig. 3A), with surviving species distributed along the full resource axis, as indicated by the near-continuous location of R* values of species along the axis. A progressive increase in fluctuation periodicity, corresponding to slower resource fluctuations from 15 to 360 d, led to an increase in the number of clumps from 2 to 6.

Fig. 3.

Bifurcation diagrams showing the difference in R* values for the two resources of surviving species at resource fluctuation cycle 100, across three continuously varying parameters characterizing resource fluctuations: (A) periodicity of fluctuation in the resource supply concentrations, (B) phase difference in the supply, and (C) peak-to-peak amplitude of nutrient concentration. All other parameters and initial conditions are as in the baseline scenario (i.e., Fig. 2B).

We examined the effect of phase difference, focusing on scenarios in which the fluctuation periodicity was 180 d, and found that when the two resources varied in a perfectly synchronous manner (phase difference 0 or 2π), only one clump emerged in the middle of the resource axis (Fig. 3B). When resource 1 led by π/2 (and resource 2 lagged correspondingly), four clumps formed. Three of these clumps were characterized by R*₁−R*₂ values below zero, indicating that resource fluctuations favored species that were more competitive for resource 1. This pattern was reversed when resource 2 led and resource 1 lagged by 3π/2. When the two resources varied in opposite phase (our baseline π difference, depicted in Fig. 2B and center of Fig. 3A), four clumps formed symmetrically across the resource axis.

We investigated the role of peak-to-peak amplitude, still focusing on scenarios with a periodicity of 180 d, and observed that when the two resources were supplied at a constant inflow concentration of 11 μM (i.e., zero amplitude), only two species survived in the center of the trait axis (Fig. 3C). When the peak-to-peak amplitude for a resource was increased slightly to 2 μM (i.e., resources fluctuated within a range from 9.5 to 11.5 μM), then four species clumps formed. Although the number of clumps was constant throughout most of the tested amplitude range (i.e., near-zero to 18 μM), the position of clumps varied. Specifically, for small amplitudes, the position of clumps was more concentrated toward the center of the trait axis, whereas clumps were more evenly spaced when resources varied from 2 to 20 (our baseline scenario, also depicted in Fig. 2B).

The presence of clumps and their locations along the resource tradeoff were also robust to additional testing for unequal initial population densities, a phase shift of π/2 in the initial resource supply concentrations, increased noise in species traits, and noise in the resource inflow concentrations (Fig. S4).

Insights into the mechanism for the formation of clumps were obtained by extending the reasoning of resource ratio theory to account for fluctuating resources (see Fig. 1A for an illustration of two species competing for two resources under stable supply). Fig. 4 shows the dynamic pattern of available ambient resources (after consumption) during a fluctuation cycle using a simplified version of our model with fewer species. When resources fluctuated with a 15-d periodicity, only species 1 and 300 ultimately persisted. Solving the model with only these two species showed that the remaining ambient resources, after consumption by the two species, followed a figure-of-eight pattern (Fig. 4A). The highest frequency of resource combinations fell at the extremities of the persistence regions of these two species, as shown by the higher density of arrowheads at the extremities of the light shaded regions. This pattern of variability in the ambient resources offered no opportunity for species with intermediate traits to exploit the remaining resource because the intermediate resource regions favoring their growth occurred at low concentration and frequency.

Fig. 4.

2D resource space showing the positions of species as defined by their R* values for resources 1 and 2 and their respective regions promoting coexistence of adjacent species (dark shading) or single species persistence (light shading). Black arrows show the trajectory of the available ambient resources at 90 time points within resource fluctuation cycle 4, by which time nutrient dynamics over the period of resource supply fluctuation had stabilized. (A) Figure-of-eight trajectory for the model solved for species 1 and 300 under the 15-d resource fluctuation periodicity. (B) Butterfly-shaped trajectory under the model solved for the 180-d fluctuation periodicity with only species 12 and 295, with Inset showing the persistence and coexistence regions of two potential intermediate species. (C) More accentuated butterfly-shape trajectory for the model solved for species 12, 40, 68, 80, 147, 221, 229, 286, and 295.

In contrast, when we solved the model for the 180-d periodicity with only the two most competitive surviving species from the full model (species 12 and 295), the concentration of remaining ambient resources followed a butterfly-shape trajectory (Fig. 4B). The most frequent resource combinations, after consumption by the two most competitive species, now fell in regions of resource space that were no longer at the extremities of the persistence regions for these two species. As a result, the persistence regions of potential intermediate species could therefore align with these resource combinations. For example, the persistence regions (light shading) and coexistence regions (dark shading) of two hypothetical intermediate species in Fig. 4B, Inset fulfill this criterion.

This mechanism was validated by solving the model for nine species: seven that persisted in the long term (species 12, 68, 80, 221, 229, 286, and 295) and two nonsurvivors (species 40 and 147). Species in four clumps (consisting of species 12, 68 and 80, 221 and 229, and 286 and 295) survived because resources occurred at both high concentration and frequency (on average, 27 out of 180 time points per cycle) within their regions of persistence (light shading) and coexistence (dark shading) (Fig. 4C). Species 40 and 147 were eventually outcompeted because resources were available at low concentration and frequency within their respective regions (on average, 13 out of 180 time points per cycle). Nonetheless, the trajectory of remaining ambient resources continued to follow a butterfly-shape trajectory (Fig. 4C) with the same intersection point as in the case of only two species (Fig. 4B). Even with larger numbers of species, those at the extremes of the trait axis continued to generate a butterfly-shaped trajectory. As typically observed, the strong competitive abilities of these species allowed them to draw down resources and develop biomass very early in the self-organization process (see the first resource fluctuation cycle for the full model in Fig. S5).

Discussion

Findings from this computational experiment indicate that recurrently fluctuating resources can lead to the survival of species whose traits are organized in clumps, in line with lumpy coexistence (1). Our self-organized clumps emerged by the 50th resource fluctuation cycle and the system thereafter followed a long transient phase during which competitive exclusion occurred at a much slower rate. Interestingly, more than one species per clump continued to persist despite having very similar R* values for resources 1 and 2. This finding shows that assemblage organization toward a state of lumpy coexistence is relevant not only over ecological timescales but also over much longer periods.

From a theoretical perspective, this mechanism for the formation of clumps under dynamic resource conditions is important because it extends classic theory on resource competition to more realistic ecological conditions (24). Further realism in our approach was achieved by parameterizing our model with empirically established life-history traits and relationships governing their competitiveness. Our work demonstrates that the emergence of species clumps is robust under different fluctuation periodicities, phase differences, and amplitudes. A single clump emerged only when the two resources were perfectly in phase or when the resource fluctuation amplitude was zero (representing a constant supply of both resources). On the other hand, survival of species across the trait range emerged only in the case when fluctuation periodicity was 1 d. For this periodicity, fluctuations occurred on the same timescale as the maximum growth rates, implying that favorable resource concentration ratios occurred at a higher rate than flushing, even for less competitive species.

Given the ubiquity in the real world of resource fluctuations and nonzero phase differences between them, our findings imply that assemblage organization in multiple species clumps ought to be common in nature. These findings also show that the number of clumps and their positioning along the niche axis depend on the characteristics of resource fluctuations such as the periodicity, amplitude, and phase difference. Recent findings from estuarine phytoplankton assemblages provide support for clumpy species organization in a symmetrical and regular pattern along the niche axis (25). Our work suggests that a plausible explanation for this pattern is that resources fluctuate in the opposite phase. Indeed, in estuarine systems characterized by wet and dry seasons, we observe seasonal switching in dominance between land-based resource inflows and ocean mixing (18, 19). Nevertheless, phytoplankton traits in other systems might be distributed asymmetrically due to other phase differences in resource fluctuations, potentially meriting further investigation as an explanation for the high phytoplankton diversity observed globally.

For rapid resource fluctuations (periodicities 1 < days < 15), the system only supported the coexistence of two very competitive species clumps at either extreme of the trait axis. This was because the rapid fluctuation forced the assemblage to exploit two niches: high resource 1 in conjunction with low resource 2, and vice versa (Fig. 4A), resource concentration ratios that occurred at higher frequencies than intermediate values. This finding is consistent with previous work on the effect of sinusoidal environmental variation, which favored species adapted to the extremities of this variation (23). However, for longer resource fluctuation periodicities (e.g., >100 d), a butterfly trajectory emerged in the variability of ambient resources. This was driven by the slowly changing resource concentrations in the inflow, in conjunction with resource consumption by the species at the extremes of the trait axis. In turn, this trajectory created additional niches consisting of regions in resource space that occurred at high concentrations and frequency and that enabled the survival of species in clumps at specific intermediate positions along the trait axis. It was striking to uncover that the available ambient resources settled into a repeating pattern (Fig. S3) much sooner than the assemblage structure emerged and that the life-history traits of the surviving species at intermediate positions did not change the overall butterfly shape and intersection point. Alongside findings in Fig. 4, these arguments show that assemblage organization in our system was driven by the fluctuation of resource concentrations in the supply. This is in contrast to previously suggested diversity-sustaining mechanisms that rely on nutrient fluctuations generated by oscillatory population dynamics in systems without exogenous resource fluctuations (26).

In summary, our computational experiments show that surviving species, in assemblages self-organized under fluctuating resource supply concentrations, can be expected to form clumps robustly in areas of trait space favored by niche availability, with niche construction driven primarily by the species at the extremes of the trait axis. Specifically, species for which the required resources were available at higher frequency and concentration during each resource fluctuation cycle survived in clumps. Further investigation could help quantify the relative importance of the regions of single species persistence and coexistence and of the absolute concentration levels required for species survival. Our findings are in line with growing evidence on lumpy coexistence from field communities (see ref. 25 and meta-analysis in ref. 27). Furthermore, coexistence in clumps is consistent with findings from functional ecology showing that important ecosystem functions are carried out by different functional groups, each of which consists of multiple species with mutually redundant traits. This trait redundancy results in greater ecological stability because remaining species can compensate following an extinction event (28–31). The consistency with which certain combinations of traits failed to favor the survival of species has important practical implications for invasion ecology, potentially enabling the prediction of invasion outcomes based on trait analysis.

Methods

We conducted computational experiments to examine the self-organization of assemblages initiated with a species-rich pool. We analyzed the distribution of surviving species along the trait axis in relation to three continuous variables characterizing the fluctuation of two resources—namely, the period, phase difference, and amplitude. Specifically, two resources fluctuated in a recurrent manner, both following a sinusoidal function (Fig. 1B, Inset). Our baseline models were solved for three periodicities of 15, 180, and 360 d; a phase difference of π between the fluctuation cycles of the two resources; and a resource amplitude of 18 μM (see also Supporting Information). In three additional experiments, we varied the periodicity from 1 to 360 d, the phase difference between the two resources from 0 (perfect synchronicity) to 2π, and the peak-to-peak amplitude (i.e., distance between peak and trough) from 0 (both resources had a constant inflow concentration of 11) to 18 (both resources fluctuated between 2 and 20 μM). The range of resource periodicities in the baseline models was chosen to capture the effect of resource fluctuation periodicities corresponding to natural mechanisms. For example, the 15-d periodicity roughly corresponds to resource fluctuations and associated phytoplankton abundance driven by tidal movements (16, 17). Six-monthly and yearly periodicities in phytoplankton abundance have also been observed (e.g., ref. 32). Mechanisms driving six-monthly cycles include light availability (e.g., influenced by a combination of photoperiod and turbidity) (32) and coastal upwelling driven by monsoon winds (ref. 33; see, e.g., refs. 34 and 35, for phytoplankton blooms associated with Northeast and Southwest monsoons around Sri Lanka). Yearly cycles are explained by seasonal inflow, as might be seen in systems affected by nitrogen-rich terrestrial runoff leading to alternating periods of nitrogen and phosphate limitation (36–40).

Mathematical Model.

To simulate the population dynamics of the species growing under these conditions, we adapted a well-known mathematical model previously used for modeling population dynamics and assemblage composition of plants and algae (5, 41, 42) growing on multiple growth-limiting resources. The model describes a system in which the average rate of inflow of resources is equal to the (constant) flushing rate, which in our approach also represents mortality. The model used is described in detail in refs. 21 and 22.

The population dynamics, in days (d), for each of the 300 competing species were modeled using the equation

$$\frac{d{N}_i}{dt}={\mu }_i{N}_i-\nu N_i\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i=1\dots 300,$$ [1]

in which N_i is the population density (10⁶ cells per liter) of species i, µ is the specific growth rate (per day) of species i, and ν is the hydraulic flushing rate (per day).

The growth rate of each species was calculated based on the widely used Monod relationship (43). Because growth depends on two resources, we used Liebig’s Law of the Minimum (44) to determine which inorganic nutrient was limiting the growth of each species at any resource combination (Eq. 2).

The specific growth rate for each species i was given by

$${\mu }_i={\mu }_{\max }\left(\min \left[\frac{R_j}{R_j+K_{ji}}\right]\right)\hspace{1em}\hspace{1em}\hspace{1em}j=1,2\hspace{0.17em}\text{and}\hspace{0.17em}i=1\dots 300,$$ [2]

where µ_max is the maximum specific growth rate for species i (per day), R_j is the concentration of each growth-limiting resource j (in units of micromolar), and K_ji is the half-saturation coefficient of species i for limiting resource j (also in units of micromolar).

The dynamics of each of the two limiting resources were modeled according to the equation

$$\frac{d{R}_j}{dt}=\nu \left(R_{\text{inflow}j}-R_j\right)-{\displaystyle \sum _{i=1}^{300}}{Q}_{ji}{\mu }_{\iota }{N}_i\hspace{1em}\hspace{1em}\hspace{1em}j=1,2\hspace{0.17em}\text{and}\hspace{0.17em}i=1\dots 300,$$ [3]

in which R_{inflow j} is the varying concentration in the supply of resource j (in units of micromolar), Q_ji is the cellular content of resource j for each species i (in micromoles per 10⁶ cells), and other parameters are the same as previously described.

Differential Eqs. 1 and 3 were solved numerically with a fourth-order Runge–Kutta method using a constant time step of 0.002 d. To reduce computation time, this was selected over an adaptive step size control algorithm (fifth-order Runge–Kutta with local error tolerance of 10⁻⁹) since the model behavior was similar (the rms error was lower than 2 × 10⁻⁴ throughout the simulation and the same surviving species were observed). The solutions were computed in Fortran 95, and the results were analyzed using R version 3.4.1 (45).

Model Parameterization.

Our simulated assemblages were self-organized from an initial species pool consisting of 300 species. This number was selected to represent species-rich plankton systems commonly encountered in the field (e.g., refs. 46–48). The traits of the 300 species in the initial species pool were assigned according to established relationships (21, 22). Specifically, for a given species, there was a tradeoff between the half-saturation coefficients K_ji for the two resources, meaning that as the competitive ability increased for one resource, it decreased for the other (5). The half-saturation coefficients K_ji were assigned randomly from a uniform distribution with range 0.04–1 and uniform noise in the range 0–0.008. Consistent with experimental evidence (49) and the argument that a species with a high cellular content of a resource requires high ambient availability of this resource (49), we assumed a proportional relationship between half-saturation coefficient K_ji and consumption rate Q_ji, a proxy for cellular content, with proportionality constant 1. The selected ranges of 0.04–1 for the half saturation coefficient and the cellular resource content, in units of micromolar and micromoles per 10⁶ cells, respectively, represent typical values measured in phytoplankton (2, 50).

To generate the initial species-rich pool, we further defined the relationship between the 300 interacting species that compete for the two resources. To do this, we used the parameter R*_ji, which is directly related to the ability of species i to exploit resource j and is defined as

$$R_{ji}^{\ast }=\frac{\nu K_{ji}}{{\mu }_{\max }-\nu }\hspace{1em}\hspace{1em}\hspace{1em}\text{for}\hspace{0.17em}j=1,2\hspace{0.17em}\text{and}\hspace{0.17em}i=1\dots 300$$. [4]

As the maximum growth rate μ_max and the flushing rate v are the same for all species, R*_ji is directly proportional to K_ji with proportionality constant 1/9. Thus, knowledge of the latter enabled determination of R*_ji values for each species i (5, 14). The relationship between the competitive ability of the 300 species for the two resources was defined within a 2D resource tradeoff space by following a downward-curved distribution along the resource plane (Fig. 1B). This relationship was established based on experimental data on phosphorus–silicate and nitrate–silicate tradeoffs (51). The procedure is detailed in Supporting Information and in refs. 21 and 22.

Initial population densities were identical for all species and were set at N_{i,t = 0} = 0.1 × 10⁶ cells per liter. In the baseline models, resource concentrations varied between 2 and 20 µM. The total flushing rate (ν = 0.1 per day) and maximum specific growth rate (µ_max = 1 per day) were constant. All parameterizations were within the range typically observed for phytoplankton assemblages and pelagic environments (2, 50, 52). For resource 1 (R₁), we used the 2–20 μM range, as this is observed for nitrogen concentrations over the course of a year for many rivers flowing into mesotrophic bays, such as the ones along the Gulf of Mexico. For resource 2 (R₂), we also used a 2–20 μM range, so the units of R₂ should be interpreted as “nitrogen equivalents.” The K and Q parameters for R₁ are in units of nitrogen, micromolar and micromoles per 10⁶ cells, respectively, and should also be interpreted as nitrogen equivalents.

To evaluate when the assemblage had stabilized, we established when species richness ceased to vary and the number of cycles required for maximum biomass per cycle of each species to reach the biomass attained at cycle 3,000, to the chosen precision of the numerical output of the solver (three decimal places, selected to permit manageable file sizes). Once the assemblage had reached oscillatory steady state, species with biomass lower than 0.01 × 10⁶ cells per liter across all time points of the resource fluctuation cycle were considered to have been competitively excluded from the assemblage.

We conducted robustness checks for sensitivity to initial conditions. Firstly, instead of equal initial population densities, we simulated the initial population density for each species by drawing from a uniform distribution over the interval 0.02–0.18 × 10⁶ cells per liter. Second, compared with our baseline scenario shown in Fig. 2B, resource supply was initialized with a phase shift for both resources of π/2. Third, we increased stochasticity in species traits by adding uniform random noise in the range 0–0.016 for the half-saturation coefficients K for each resource independently. Finally, stochasticity was added to the resource supply concentrations by adding uniform random noise in the range 0–0.6 μΜ to the baseline values.