Unified description of H-atom–induced chemicurrents and inelastic scattering

Significance

Catalytic reactions at surfaces are exceptionally complex, as they require a multitude of elementary steps. It is therefore very difficult to predict which chemical compounds are catalytically effective. In inelastic scattering experiments in ultrahigh vacuum, the first step of most surface reactions, which is the adsorption, can be studied on model systems in great detail. Based on such experiments new theoretical models can be developed that accurately describe the delicate interplay between electronic and nuclear motion in prototypical chemical reactions, a capability that is needed to make accurate predictions of reaction rates in heterogeneous catalysis, to design useful energy-conversion devices based on chemicurrents, and to understand photocatalysis.

Abstract

The Born–Oppenheimer approximation (BOA) provides the foundation for virtually all computational studies of chemical binding and reactivity, and it is the justification for the widely used “balls and springs” picture of molecules. The BOA assumes that nuclei effectively stand still on the timescale of electronic motion, due to their large masses relative to electrons. This implies electrons never change their energy quantum state. When molecules react, atoms must move, meaning that electrons may become excited in violation of the BOA. Such electronic excitation is clearly seen for: (i) Schottky diodes where H adsorption at Ag surfaces produces electrical “chemicurrent;” (ii) Au-based metal–insulator–metal (MIM) devices, where chemicurrents arise from H–H surface recombination; and (iii) Inelastic energy transfer, where H collisions with Au surfaces show H-atom translation excites the metal’s electrons. As part of this work, we report isotopically selective hydrogen/deuterium (H/D) translational inelasticity measurements in collisions with Ag and Au. Together, these experiments provide an opportunity to test new theories that simultaneously describe both nuclear and electronic motion, a standing challenge to the field. Here, we show results of a recently developed first-principles theory that quantitatively explains both inelastic scattering experiments that probe nuclear motion and chemicurrent experiments that probe electronic excitation. The theory explains the magnitude of chemicurrents on Ag Schottky diodes and resolves an apparent paradox––chemicurrents exhibit a much larger isotope effect than does H/D inelastic scattering. It also explains why, unlike Ag-based Schottky diodes, Au-based MIM devices are insensitive to H adsorption.

Most theoretical studies of atoms and molecules interacting with metal surfaces are based on the Born–Oppenheimer approximation (BOA) (1). However, a growing number of examples have been found where electronic and nuclear degrees of freedom are strongly coupled in violation of the BOA (2–6). H-atom interactions at metals offer a remarkable opportunity to test non-BOA theories against experiment, since H-adsorption–induced chemicurrent experiments (7–14) offer a direct measure of electronic excitation and H-atom inelastic scattering experiments (15) directly probe nuclear motion. In chemicurrent experiments, exothermic H interactions like adsorption and recombination produce hot electrons that pass over a potential barrier to be collected. Hence, the magnitude of the chemicurrent is dependent on both the reaction-induced production of hot electrons and the likelihood of transmission over the barrier. To reduce uncertainties associated with barrier transmission, the ratio of hydrogen- and deuterium-induced chemicurrent is often measured––H-induced chemicurrents are typically two to five times larger than those from D atoms (7, 11–13). H-atom surface scattering experiments yield H-atom translational energy loss distributions. The importance of H-atom translation to electronic excitation could be inferred by comparing energy loss for H-atom collisions with metals and insulators and by comparing experiment to theory (15, 16). As we will show below, D-atom energy loss on Au and Ag is nearly identical to that of H, introducing an apparent paradox between chemicurrent and inelastic scattering observations. Clearly, a simultaneous theoretical description of these two very different experiments would represent a significant advance in our ability to describe non-Born–Oppenheimer dynamics.

In this work, we report experimental results that show the isotope effect in H and D scattering from Au(111) and Ag(111), which complement the chemicurrent experiments mentioned above. Beyond this, we show results of a first-principles theory without adjustable parameters that simultaneously explains these diverse experiments. The theory uses global full-dimensional potential energy surfaces (PES) fitted to ab initio electronic energies. It employs Langevin molecular dynamics (MD) to obtain H/D-atom translational energy loss distributions including the effect of electron–hole pair (EHP) excitation; this part of the theory builds on previous work employing a local density friction approximation (LDFA) (17). LDFA combined with ab initio molecular dynamics (AIMD) has also been previously applied to study the associative desorption of diatomics at metal surfaces (18–20). Here, we extend the LDFA theory to describe the energy spectrum of the excited EHPs produced by the MD trajectories by implementing a forced oscillator model (FOM) (21–23). From reported barrier heights and barrier transmission probabilities of chemicurrent devices, we then determine what fraction of the excited electrons is detected as a chemicurrent.

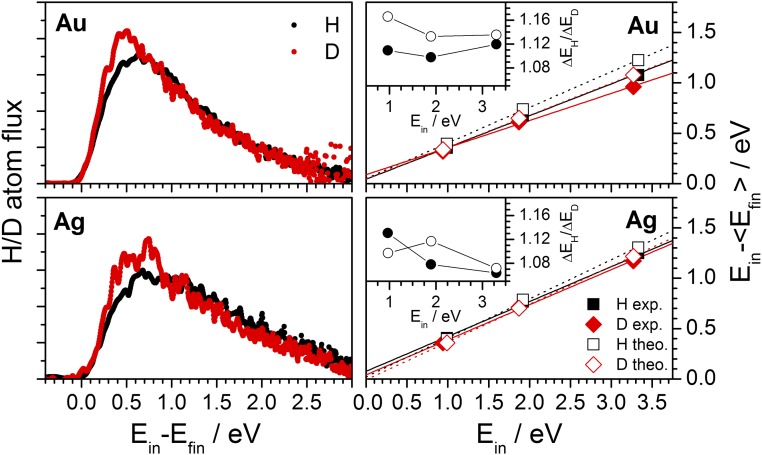
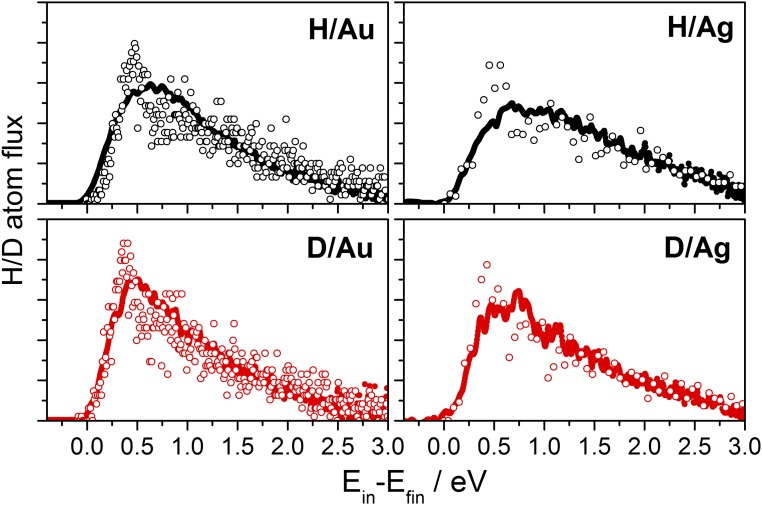
Fig. 1 (Left) shows typical translational energy loss distributions derived from the scattering experiments. For both metals, only an ∼10% isotope effect is observed––slightly more energy is lost for H than D. Average translational energy losses $\langle \mathrm{\Delta }{E}_{\text{H}}\rangle$ and $\langle \mathrm{\Delta }{E}_{\text{D}}\rangle$ are shown in Fig. 1 (Right) at several incidence energies for both Au(111) and Ag(111). The average energy loss is a constant fraction of the H(D) incidence energy and the isotope effect is uniformly small (Fig. 1, Insets). The values of $\langle \mathrm{\Delta }{E}_{\text{H}}\rangle$ and $\langle \mathrm{\Delta }{E}_{\text{D}}\rangle$ predicted from our MD simulations are also shown in Fig. 1 and the results are in excellent agreement with experiment. Fig. 2 shows representative comparisons of the full translational energy loss distributions obtained from experiment (black) and theory (red) for H/D on Au(111) and Ag(111) at 3.3-eV incidence energy. Even at this more detailed level of comparison, agreement between experiment and theory is excellent and both reveal only a small isotope effect.

Fig. 1.

Experimentally observed isotope effect in H/D scattering from Au(111) and Ag(111) is small as predicted by theory. (Left) Exemplary energy loss distributions for the incidence conditions: $E_{\text{H},in}$ = 3.33 eV, $E_{\text{D},in}$ = 3.27 eV, ${\vartheta }_i=45°,{\phi }_i=0°,{\vartheta }_s=45°$, $T_S=300$ K. (Right) Average translational energy loss, $\langle \mathrm{\Delta }{E}_{\text{H}}\rangle$ and $\langle \mathrm{\Delta }{E}_{\text{D}}\rangle$, plotted versus incidence translational energy $E_{in}$ for H and D atoms scattered from Au(111) and Ag(111). Black symbols correspond to H and red to D. Filled symbols are experimental results; open symbols are the results of the MD calculations. The distributions are normalized to the area. Angular distributions for H and D atoms scattered from metal surfaces are broad and without structure; translational energy loss spectra depend only weakly on incidence and scattering angles. (Insets) Isotopic ratios.

Fig. 2.

MD calculations describe the small isotope effect in scattering experiments accurately. Energy loss distributions for H (black) and D (red) scattering from Au(111) and Ag(111) obtained with MD calculations (open circles) with experiment (closed circles). The incidence conditions are the same as in Fig. 1.

This strongly contrasts with the isotope effects seen in chemicurrent experiments.

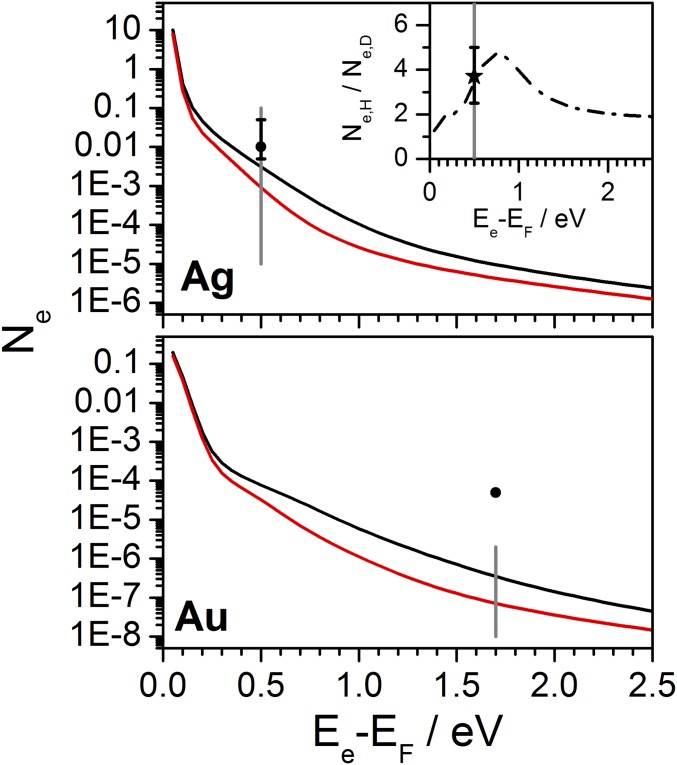
Fig. 3 shows the theoretically predicted electronic excitation resulting from H and D atoms interacting with Ag(111) and Au(111) surfaces under conditions close to those used in refs. 7, 11, and 13, respectively. The theoretically predicted chemicurrent for H (black curve) and D (red curve) are shown as a function of the device’s barrier height, $E_e$. Fig. 3 (Inset) shows the predicted chemicurrent isotope effect versus barrier height. In Fig. 3 (Upper), the gray vertical line at 0.5 eV marks the Schottky barrier for Ag on n-doped silicon––the theoretically predicted isotope effect (3.7) is in excellent agreement with experiment (black star in the figure). Remarkably, the theoretically predicted absolute magnitude of the chemicurrent (0.0036 e/H) is in good agreement with experiment (∼0.01 e/H) (9–11). This suggests that barrier crossing losses in these devices are small, in good agreement with conclusions from ref. 10, where the transmission probability at the device interface was estimated to be ∼1 based on the theory of ballistic electron emission microscopy.

Fig. 3.

MD calculations describe the large isotope effect in chemicurrent experiments accurately. The figure shows atomic-scale simulations of electronic excitation in H- (black) and D (red) collisions with Ag(111) and Au(111). N_e is the theoretically predicted number of electrons per MD trajectory with energy more than E_e above the Fermi energy E_F averaged over all trajectories. The gray lines mark the barriers of the experimentally employed chemicurrent devices (Au = 1.7 eV, Ag = 0.5 eV). In accordance with experimental reports, internal losses of the device are negligible and discounted in the calculations for Ag and taken as 10⁻² for Au. (Inset) Isotopic chemicurrent ratio as a function of the cutoff energy for the case of Ag. (Inset) Black star with error bar shows the isotope effect on Ag measured in ref. 11. The solid circles in both panels show the experimentally reported chemicurrent on the silver Schottky diode and gold MIM device. The predicted H-adsorption–induced chemicurrent is far smaller than observed. Conditions for Au(111) are $E_{in}=0.2$ eV, ${\vartheta }_{in}=0°$, $T_S=300$ K, and for Ag(111) $E_{in}=0.1$ eV, ${\vartheta }_{in}=0°$, $T_S=135$ K.

The good agreement with two very different kinds of experiments gives us confidence to use the theoretical simulations to gain insights into the dynamics of both processes. First, we can understand the apparent paradox in the isotope effect: a weak isotope effect in the inelastic scattering experiments versus a large isotope effect for chemicurrent experiments. Fig. 4 presents results of analysis of MD trajectories detailing how much of the H/D-atom translational energy loss appears as excitation of nuclear degrees of freedom and how much appears as electronic excitation. The solid black line represents the Au-atom mechanical excitation probability––the gray shaded area is the electronic excitation. The areas under each distribution are normalized to unity. For the electronic excitation distribution, we have also divided the trajectories into classes defined by the number of collisions the H or D atom has had with a Au atom. We see here that the percentage of translational energy loss appearing as Au-atom mechanical excitation is larger for D than for H (10% for H, 21% for D), while that appearing as electronic excitation is larger for H than for D (90% for H, 79% for D). Simply put, the small isotopic influence on translational inelasticity arises from the compensation of two mass-dependent effects: the efficiency of phonon excitation is higher for D due to its higher mass, while the efficiency of translational damping by electronic excitations is lower due to the D atom’s lower speed. This compensation effect, together with the fact that multiple H/D–Au collisions dominate the scattering, tends to blur the differences in the translational energy loss distributions. In contrast to this, chemicurrents arise only from the electronic excitation resulting from the H/D interaction at the surface; hence, the isotope effect is not compensated. Additionally, H interactions induce more highly excited electrons compared with D; this amplifies the isotope effect further.

Fig. 4.

Analysis of MD trajectories for H/D scattering from Au(111). A balancing phenomenon explains the small isotope effect in scattering experiments. The solid black line shows the probability distribution for Au-atom translational energy resulting from H/D collisions. The gray shaded area shows the probability distribution for electronic excitation, subdivided into three classes of trajectories: single-bounce (magenta), double-bounce (blue), and more than two-bounce (yellow) collisions between H/D and a Au atom. Incidence conditions are the same as in Fig. 1.

The MD simulations also reveal the dynamics of chemicurrent production. The chemicurrent depends approximately linearly on incidence energy, $E_{in}$: $P\left(e^{-}/H\right)=0.00153E_{in}\left(\text{eV}\right)+0.00288$ and $P\left(e^{-}/D\right)=0.000626E_{in}\left(\text{eV}\right)+0.00061$. At high $E_{in}$, chemicurrent is produced primarily by trajectories that penetrate below the surface of the metal; however, even at low $E_{in}$ penetration is the most important mechanism of chemicurrent production. In all cases chemicurrent is dominated by trajectories that lead to adsorption; scattering contributed negligibly to chemicurrents.

Finally, we turn to the curious question of why Schottky diodes based on silver show sensitivity to H adsorption, whereas MIM devices based on Au show sensitivity to H–H recombination (13). Fig. 3 (Lower) shows results of our H and D adsorption calculations for conditions relevant to the experiments of ref. 13. The gray vertical line marks the barrier height of the MIM device (1.7 eV). Experiment suggests that the internal losses associated with electrons transiting the barrier in these Au-based MIM devices are on the order of 10⁻². Using this loss factor, the theory predicts that H-adsorption–induced chemicurrent ($={10}^{-2}\times 3.5\times {10}^{-5}$ e/H) is much smaller than that seen in experiment ($5\times {10}^{-5}$ e/H). This analysis is consistent with previous work suggesting that only the H–H recombination reaction on Au produces hot electrons (24) and chemicurrent (13). We also note that the H-adsorption–induced chemicurrents seen by Schottky diode experiments on Ag surfaces (7, 11) were performed at a surface temperature (100–135 K) far lower than the H₂ recombinative desorption temperature (∼170 K) (25). Thus, there was no chance that this source of hot electrons could have been seen in those experiments. Contrasting this, the MIM chemicurrent measurements of Schindler et al. (26) were performed at 300 K. All of these considerations taken together suggest that the H–H recombination reaction on Au, which releases ∼1.3-eV reaction barrier energy (27), is intrinsically more efficient at producing EHPs with energies exceeding 1.7 eV than is the H-adsorption reaction on Ag, which releases ∼2 eV. It appears therefore likely that more than one mechanism for producing chemicurrents is active when H atoms interact with metal surfaces.

In this work, we have presented experiments on the translational inelasticity for H and D in scattering from Ag(111) and Au(111) and results of a first-principles theory without adjustable parameters that quantitatively and comprehensively describes nonadiabatic effects present in H/D adsorption at metal surfaces, one of the simplest and most fundamental chemical reactions. The theory captures both the damping of nuclear motion induced by electronic excitation seen in the scattering experiments as well as nuclear-motion–induced electronic excitation seen in chemicurrent devices.

Successful theories of chemical reactivity are fundamentally important as they may be used to make predictions about the transformation of matter and conversion of energy between various forms. There is, furthermore, a host of interesting phenomena that require a deeper understanding of how nuclear and electronic motions interact with one another during chemical events. In photocatalysis, hot electrons may interact with surface adsorbates to make and break bonds (28). The rate of a reaction on a metal surface is governed by the rate of passage through the transition state of the reaction, which may be influenced by energy dissipation to electronic degrees of freedom (24, 29). If the coupling is too strong, transition-state theory may even break down. Chemicurrents also provide a simple means for direct conversion of chemical energy to electrical current (30); with this theory, we have a tool for the design of practical chemicurrent devices.

Methods

MD simulations of atomic scattering from surfaces demand a large number of trajectories to collect enough statistics for comparison with the experimental results. We fulfill this need by propagating nuclei classically on a precalculated ground-state PES while accounting for nonadiabatic effects in the framework of the electronic friction model. Elements of the molecular dynamics simulations used in this work have been previously described (31, 32). The Fortran source code of the MD simulation program implementing the applied method is available online (33). In short, full-dimensional PES for H/D on Au(111) and Ag(111) were constructed by optimizing the parameters of the effective medium theory (EMT) to fit ab initio electronic structure data derived from density-functional theory (DFT) calculations at the generalized gradient approximation level. The electronic structure data included geometries with metal atoms fixed at their relaxed fcc lattice sites as well as geometries from a single AIMD trajectory representing a hydrogen atom scattering event. The resulting PES reproduces the energy values, obtained from many other AIMD trajectories not included in the training set, with an rms error less than 0.2 eV. The PES describes H-atom binding at the surface as well as subsurface H-atom interactions. The DFT-based EMT function also yields atomic configuration-dependent background electron density, which was used to calculate electronically nonadiabatic H- and D-atom translational energy loss at the level of the LDFA (17, 20).

Attempts to theoretically describe chemicurrents have been previously reported (21–23, 34–37). In this work, we employed an FOM to obtain the energy spectrum of excited electrons that result from H/D atom collisions at the metal (21–23). Here, the EHP excitation spectrum is related within the perturbation theory to the rate of the nonadiabatic energy transfer by the following equation (23):

$$n_{el}\left(E,t\right)=\frac{1}{\pi \hslash }\text{PV}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{d\left(\hslash \omega \right)}{{\left(\hslash \omega \right)}^2}{\left|\underset{t_0}{\overset{t}{{\displaystyle \int }}}d\tau \sqrt{\eta \left(r\right)}\dot{r}{e}^{i\omega \tau }\right|}^2\left[f\left(E-\hslash \omega \right)-f\left(E\right)\right],}$$

where $\eta \left(r\right)$ is the electronic friction coefficient along trajectory $r\left(t\right)$, $f\left(E\right)$ is the Fermi function, and “PV” refers to the Cauchy principal value (PV) of the integral. In contrast to refs. 21–23 and 34, where taking the PV integral was avoided by imposing a zero temperature limit, we calculate the EHP excitation spectrum $n_{el}\left(E,t\right)$ using the PV definition:

$$\text{PV}\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}dx\hspace{0.17em}g\left(x\right)=\underset{\mathit{ϵ}\to 0}{\lim }\left[{\displaystyle \underset{-\infty }{\overset{-\mathit{ϵ}}{\int }}dx\hspace{0.17em}g\left(x\right)}+{\displaystyle \underset{\mathit{ϵ}}{\overset{\infty }{\int }}dx\hspace{0.17em}g\left(x\right)}\right],$$

and find that the integrals converge at $\mathit{ϵ}={10}^{-7}{\text{eV}}^{-1}$. The trajectories allow us to calculate the instantaneous rate of electronically nonadiabatic energy transfer at each time step, and this serves as input to obtain the electronic excitation spectrum. In this way, we predict the probability to produce an excited EHP induced by a H or D collision with the metal surface. By defining a cutoff value E_e-E_F, which is taken from the barrier heights of Schottky and MIM devices reported in refs. 8 and 13, we calculate an upper limit for the chemicurrent neglecting losses after creation of the initial EHP. In Fig. 3, we have included the experimentally determined electron transmission losses to be able to compare with experiment. For chemicurrents, we calculated 100 trajectories in this way at each incidence condition. One million trajectories were calculated for comparison with scattering experiments. We emphasize that the theory includes no adjustable parameters.

For experimental isotope studies on Au and Ag, we employed a setup that is described in detail in ref. 15. In short, a monoenergetic H/D atom beam is formed by photolysis of a supersonic jet of H/D–halide (Br or I) molecules using an excimer laser operated with ArF or KrF. A small fraction of the H/D photoproduct passes a skimmer and two differential pumping apertures to enter an ultrahigh-vacuum scattering chamber. Here, the atomic beam hits a clean single-crystalline Au(111) or Ag(111) surface held on a six-axis manipulator, with which both polar and azimuthal incidences angles, ${\vartheta }_{in}$ and ${\phi }_{in}$ (with respect to the [10-1] direction) can be varied. The translational energy and angular distributions of the scattered H atoms are detected by Rydberg-atom tagging time-of-flight (TOF) (38), where two laser pulses excite the atoms to the long-lived (n = 34) Rydberg state. The neutral Rydberg atoms travel 250 mm, pass a grounded mesh, and are field-ionized. The ions are detected using a multichannel plate detector. A multichannel scalar records the TOF distributions. The detector is rotatable making it possible to measure TOF spectra for various scattering angles, ${\vartheta }_s$. The Au and Ag samples were cleaned using argon ion sputtering and annealing. The cleanliness and structure of the surfaces is monitored by Auger electron spectroscopy and low-energy electron diffraction.