Reliability of a Feedback-Controlled Treadmill Algorithm Dependent on the User’s Behavior

Abstract

The reliability of the treadmill belt speed using a feedback-controlled treadmill algorithm was analyzed in this study. Using biomechanical factors of the participant’s walking behavior, an estimated walking speed was calculated and used to adjust the speed of the treadmill. Our proposed algorithm expands on the current hypotheses of feedback-controlled treadmill algorithms and is presented below. Nine healthy, young adults walked on a treadmill controlled by the algorithm for three trials over two days. Each participant walked on the feedback-controlled treadmill for one 16-minute and one five-minute trial during day one and one 16-minute trial during day two. Mean, standard deviation, interclass correlation coefficient (ICC), and standard error of measurement (SEM) were analyzed on the treadmill belt speed mean, standard deviation, and coefficient of variation. There were significantly high ICC for mean treadmill speed within- and between-days. Treadmill speed standard deviation and coefficient of variation were significantly reliable within-day. These results suggest the algorithm will reliably produce the same treadmill belt speed mean, but may only produce a similar treadmill belt speed standard deviation and coefficient of variation if the trials are performed in the same day. A feedback-controlled treadmill algorithm that accounts for the user’s behavior provides a greater level of control and minimizes any possible constraints of walking on a conventional treadmill.

I. Introduction

The idea of a feedback-controlled treadmill algorithm is not new, as many have been previously developed [1] [14]. Such algorithms record one or more parameters, submit it through the algorithm, and update the treadmill in real-time. A continuous process, it allows the treadmill belt speed to adjust to the user, rather than constraining the user to a constant speed. Various user-based parameters have been used to control the speed of the treadmill: ground reaction forces [3] [5], [14]; distance from predetermined location on treadmill using forces [2], [6] or position data [1], [7] [12], [15]; and swing foot velocity [13]. Although these algorithms remove the invariant speed constraint, they may present disadvantages regarding mimicking the behavior of the user. Any algorithm recording and utilizing ground reaction forces in the speed estimation has required an instrumented treadmill. Algorithms that are primarily, or solely, dependent on a referenced position of the user on the treadmill do not fully acknowledge the behavior of the walker and may constrain the individual to fluctuate around a set location when walking at a steady speed. The swing foot velocity algorithm [13] requires specific interpolation parameters per user, which may improve the individual use of feedback-controlled treadmills and is a step in the right direction, but is not applicable to a broad setting.

We propose a new algorithm that allows the treadmill belt speed to simulate the walking speed of the user dependent on biomechanical factors using kinematic and position variables. The proposed algorithm acknowledges and expands on the benefits of the previous [2], [11], [13]. Rather than strictly using the position of the individual on the treadmill, our algorithm is primarily dependent on biomechanical factors (i.e. center of mass velocity, leg swing velocity) and secondarily influenced by the position on the treadmill. The current algorithm creates an enhanced representation of walking behavior and allows the user to comfortably walk at various locations on the treadmill without being continuously forced to a predefined position. The algorithm is presented below, as well as the reliability of the average, standard deviation, and coefficient of variation of the treadmill belt speed.

II. Methods

1. Demographics

Nine healthy, young adults (21.22 ± 1.56 years; 173.06 ± 11.67 cm; 71.65 ± 10.56 kg) participated in the study. All participants were free from any musculoskeletal and neuromuscular disorders. The experimental protocol was approved by the university’s Institutional Review Board. Prior to beginning the study, informed consent was obtained.

2. Equipment

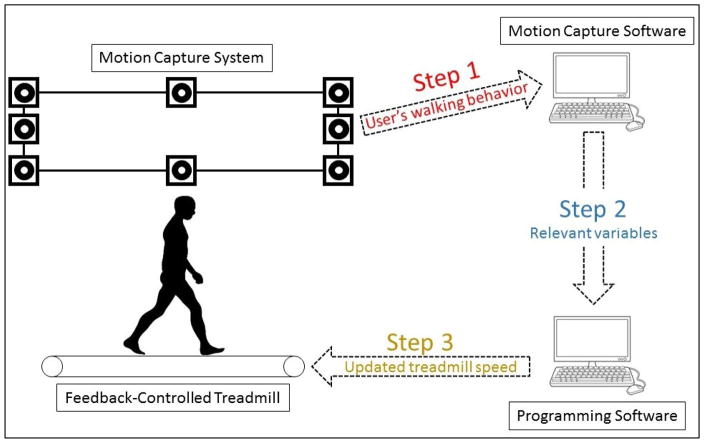
A treadmill (Bertec; Columbus, OH) was governed by the algorithm under investigation. Motion capture technology (eight cameras; 100 Hz; Vicon; Oxford, UK) provided detail of the individual’s walking behavior from anatomically placed, reflective markers using a lower-body, bi-lateral 27-marker set. The motion capture data were integrated into a programming software application (300 Hz; D-Flow; Motekforce Link, Netherlands) and the position data of interest were recorded in real-time. The algorithm’s calculations were executed in the programming software application – which had the ability to externally control the treadmill – allowing the final output of the algorithm to set the speed of the treadmill. An illustrated example of the experimental setup is displayed in Figure 3.

Fig. 3.

Diagram of the experimental setup and how the treadmill speed is updated. Step 1: Marker position data captured by the cameras is recorded into the software. Step 2: Specific marker positions are transferred to the computer program. Step 3: The algorithm calculates an estimated treadmill speed and updates the treadmill.

3. Procedure

Each participant walked on the feedback-controlled treadmill for one 16-minute and one 5-minute trial during day one and one 16-minute trial during day two. (The 16-minute trials were completed in order to perform further analyses that require longer trials.) Day one and day two were separated by a minimum of one week. The trials in day one provided the intra-session reliability, and the trial in day two provided inter-session reliability. The participants were instructed to begin walking on the treadmill, find a comfortable pace, and continue walking at their preferred speed for the duration of the trial. With the proposed algorithm, the participants were able to start the treadmill from zero speed. Treadmill belt speed was recorded.

4. Analyses

Mean, standard deviation (SD), and coefficient of variation (CV) were quantified from downsampled treadmill speed data (300 to 3 Hz). The first minute of data were excluded in all analyses, as the participants were able to start the treadmill from zero speed (as stated above) and time was needed to find a comfortable walking speed.

To assess reliability of the treadmill belt speed within-day and between-days, interclass correlation coefficient (ICC) of type (3, 1) and standard error of measurement ( $SD\ast \sqrt{1-\mathit{ICC}}$) were used.

Instantaneous accelerations of the treadmill belt speed were recorded and separated into positive, negative, and no accelerations within ten sections of the treadmill (each 0.13 meters in length). The location of the sacrum (representing the center of mass) determined the current section of treadmill. At each time frame, the belt accelerations were marked as either greater than, equal to, or less than zero. Within each section of the treadmill, the percentage of time that the belt acceleration was greater than, equal to, or less than zero were analyzed.

5. Algorithm

Although other algorithms have been developed to regulate the treadmill speed to adjust based on the user, this algorithm is novel. The proposed algorithm incorporates parameters that directly measure the walking behavior of the individual, encompassing biomechanical factors that affect walking speed.

If one were walking on a treadmill at a constant speed, the change in center of mass velocity – relative to a global system – from step to step is negligible. The effect on the change in leg swing velocity is similar. Yet, when changing speed, the center of mass and/or leg swing velocity differs from the previous step. This algorithm combines the two said parameters to adjust the speed of the treadmill.

Change in center of mass velocity is measured on a step to step basis, as the position of the center of mass at toe off (CoM_Pos,TO) is subtracted from the position at heel strike (CoM_Pos,HS) and then divided by step time (t_Step) (Equation 1).

$${\mathit{CoM}}_{\mathit{Vel}}=({\mathit{CoM}}_{\mathit{Pos},HS}-{\mathit{CoM}}_{\mathit{Pos},TO})/t_{\mathit{Step}}$$ (1)

Change in leg swing velocity is also measured at each step (Equation 2).

$$\mathit{\Delta }{\mathit{LegSwing}}_{\mathit{Vel}}={\mathit{LegSwing}}_{\mathit{Vel}}(i)-{\mathit{LegSwing}}_{\mathit{Vel}}(i-1)$$ (2)

LegSwing_Vel(i) is the most recent step’s leg swing velocity, and LegSwing_Vel(i-1) is the previous ipsilateral step’s leg swing velocity.

From the previous two equations, the estimated change in the user’s walking velocity (ΔUser_EstVel) is then calculated, as summation of the change in center of mass velocity and leg swing velocity (Equation 3).

$$\mathit{\Delta }{\mathit{User}}_{\mathit{EstVel}}={\mathit{CoM}}_{\mathit{Vel}}+\mathit{\Delta }{\mathit{LegSwing}}_{\mathit{Vel}}$$ (3)

The combination of these two variables creates a unique, robust method of estimating the user’s walking velocity, truly based on the walking behavior of the individual. With this method, the treadmill speed will not arbitrarily increase – or decrease – if the individual is not at a predefined location on the treadmill, as adjustments to the treadmill speed are due to adjustments in biomechanical measures. This method provides the walker with the ability to walk at a variety of locations on the treadmill without being forced to a certain location.

Walking on a treadmill imposes a variety of constraints, namely the length of the treadmill. Contrary to conventional algorithms based solely on position, our proposed algorithm does not automatically increase belt speed when the user is in the front or back of the treadmill. However, under these conditions, it is more difficult to significantly change the center of mass or leg swing velocity to adjust belt speed to match the intended walking speed. Therefore, a nonlinear gain is introduced to scale the estimated speed change. Either Equation 4 or Equation 5 will be implemented depending on if the ΔUser_EstVel is positive or negative, respectively. The gains are depicted in Figure 1.

Fig. 1.

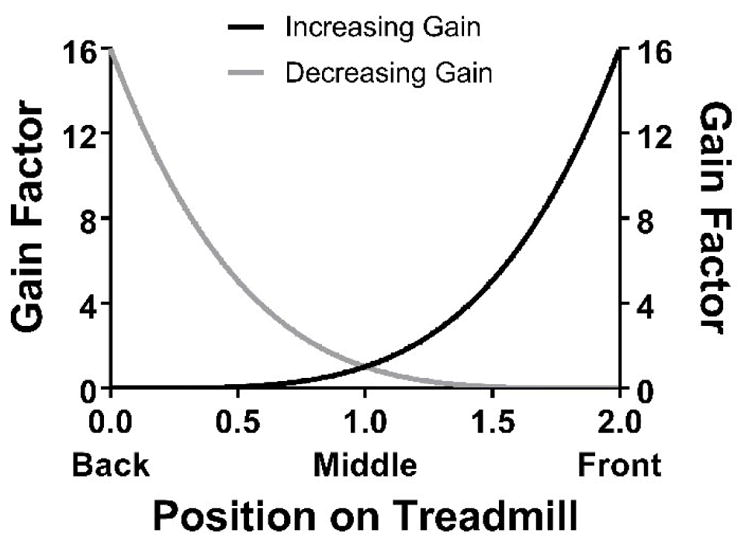
Nonlinear gain when estimated walking speed (blue) increases or (red) decreases. X-axis is user’s position: 0 = back of treadmill, 1 = center of treadmill, 2 = front of treadmill. Equations 4 & 5 have 2 divided by the treadmill length to set the gains on a scale from 0 to 2 (as depicted in the figure).

$${\mathit{Gain}}_{\mathit{Increase}}={({\mathit{CoM}}_{\mathit{Pos}}·(2/{TM}_{\mathit{Length}}))}^4$$ (4)

$${\mathit{Gain}}_{\mathit{Decrease}}={(({\mathit{CoM}}_{\mathit{Pos}}-2)·(2/{TM}_{\mathit{Length}})))}^4$$ (5)

If one were to walk at the center of the treadmill, the gain would have minimal, if any effect on the change in belt speed; consequently, the only factor would be from the biomechanical parameters of the walker. If the user were at the front of the treadmill, the increasing gain (Gain_Increase) would have an amplifying effect on the belt speed change when the estimated speed is increasing; however, the decreasing gain would have a damping effect – yet it would still decrease – if the estimated speed were decreasing. The effect is opposite at the back of the treadmill. Figure 2 illustrates the effect of the gain.

Fig. 2.

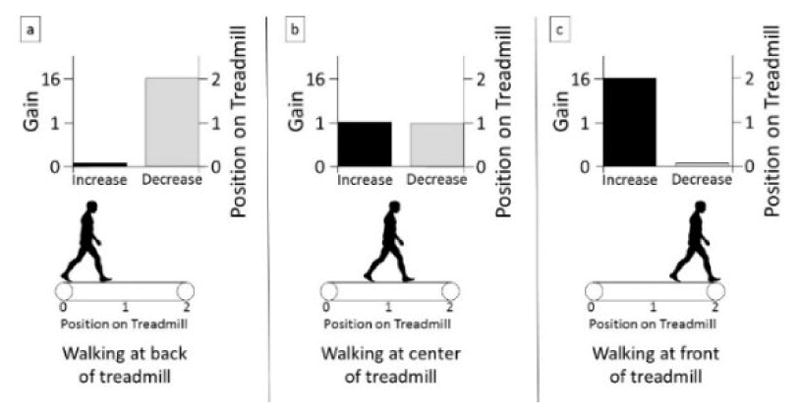
The increasing gain (left column on x-axis) is (a) below, (b) at, and (c) above 1 when walking at the (a) back, (b) center, and (c) front of the treadmill, respectively. The decreasing gain (right column on x-axis) is (a) above, (b) at, and (c) below 1 when walking at the (a) back, (b) center, and (c) front of the treadmill, respectively.

The gain is also intended to keep the individual on the treadmill. The gain is a factor of position on the treadmill – similar to the previously developed algorithm’s sole method [1], [7] [12]. The novelty and benefit of this gain method allows the treadmill speed to increase or decrease, regardless of the location on the treadmill, yet still addresses the safety issue and keeps the walker on the treadmill.

The change in treadmill speed from Equation 3 is multiplied by the gain, which is then divided by the sampling rate of the software program (Hz). Dividing the change in treadmill speed by the computer software program’s sampling rate creates a gradual adjustment to the belt speed. The benefit of continuously updating the treadmill speed is twofold: 1) provides a greater control of the treadmill and 2) does not create additional acceleration to the individual when the belt speed adjusts. It is then added to the previous treadmill speed (TM_Vel(i-1)), providing the treadmill with the new speed (Equation 6).

$${TM}_{\mathit{Vel}}(i)={TM}_{\mathit{Vel}}(i-1)+((\mathit{\Delta }{\mathit{User}}_{\mathit{EstVel}}·\mathit{Gain})/Hz)$$ (6)

The treadmill speed is then set to the variable TM_Vel(i) from Equation 6, and is updated after each iteration of the algorithm. An illustrated example of the algorithm is displayed in Figure 4.

Fig. 4.

Illustrated equations of the algorithm. Top row: Estimation of the user’s velocity change from previous stride to the current. Bottom row: The estimated user’s velocity change is added to the previous speed of the treadmill in increments (determined by sampling rate).

III. Results

Interclass correlation coefficient and standard error of measurement of treadmill speed mean, standard deviation, and coefficient of variation within- and between-day are presented in Table 1. All variables were reliable within-day, while only the mean treadmill speed was significantly reliable between days. Additionally, there were no within-subject differences for any variables for within- and between-day comparisons (p > 0.05).

Table 1.

Means and standard deviations of treadmill speed mean, standard deviation and coefficient of variation. Within-day and between-day reliability of treadmill speed mean, standard deviation and coefficient of variation.

	Day 1		Day 2
Treadmill Speed	Trial 1	Trial 2	Trial 1
Mean (m/s)	1.22	1.22	1.20
SD	0.25	0.25	0.17
SD (m/s)	0.07	0.09	0.07
SD	0.04	0.04	0.03
CV (%)	6.49	7.41	5.77
SD	4.34	3.78	2.13
	Within-Day
Treadmill Speed	ICC (3,1)	p-Value	SEM
Mean	0.915	< 0.001	0.065
SD	0.755	0.006	0.017
CV	0.718	0.010	2.083
	Between-Day
Treadmill Speed	ICC (3,1)	p-Value	SEM
Mean	0.842	0.001	0.089
SD	0.227	0.264	0.030
CV	0.328	0.178	3.429

Treadmill speed mean was significantly reliable within-day (ICC = 0.915, F(8) = 22.538, p < 0.001) and between-day (ICC = 0.842, F(8) = 11.633, p = 0.001). Treadmill speed standard deviation was significantly reliable within-day (ICC = 0.755, F(8) = 7.162, p = 0.006) but not significantly reliable between-day (ICC = 0.227, F(8) = 1.589, p = 0.264). Treadmill speed coefficient of variation was significantly reliable within-day (ICC = 0.718, F(8) = 6.103, p = 0.010) but was not significantly reliable between-day (ICC = 0.328, F(8) = 1.974, p = 0.178).

IV. Discussion

A treadmill that adjusts speed due to the behavior of the user provides a greater interaction between the user and treadmill and may alleviate the constraints that arise from a fixed-speed treadmill. Although other algorithms have been developed, the proposed algorithm expands on the ability to control the treadmill speed.

This algorithm provides a higher level of adjustment of the treadmill – allowing a more natural walking behavior – than position-alone algorithms (as seen in Figure 5) due to the reliance on biomechanical factors. Multiple adjustments (i.e. increase, maintain, or decrease speed) can occur at any section of the treadmill with the proposed algorithm (Figure 5b); however, only one type of adjustment can exist within a section (i.e. increase speed at front, decrease speed at back) with a position-dependent algorithm (Figure 5c). Using biomechanical factors as the main support in our algorithm, it is possible to walk at the front of the treadmill without any adjustment in the treadmill speed, thus improving both safety and control (Figure 5b).

Fig. 5.

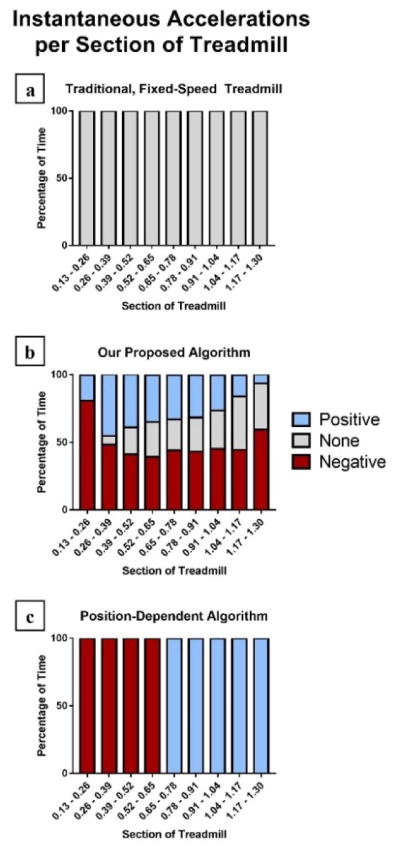
Averaged data across subject, condition, and day for (a) theoretical data from a fixed-speed treadmill condition, (b) experimental data from our proposed algorithm conditions and (c) theoretical data from position-dependent algorithms assuming the reference position is the middle of the treadmill (at 0.65 meters). The x-axis is the treadmill separated into 9 sections of 0.13 meters each. The section 0–0.13 is excluded because the participants never walked in that section during the analyzed timeframe. The y-axis is a percentage of time. These data provide proof that the treadmill belt speed is able to accelerate positively, negatively, and maintain constant speed at all sections of the treadmill – except for the second furthest posterior section in which only positive and negative acceleration were observed.

The position-alone algorithms make sense at a basic level, derived from the hypothesis that a subject walking faster will be at the front of the treadmill, while a subject walking slower will be at the back. However, this assumption does not take into account the user’s preference, as some users may only feel comfortable walking at the front of the treadmill for safety purposes. Position-dependent algorithms take no account for this fact and will continuously increase the speed of the treadmill until the individual is eventually forced back to the reference point. Theoretically, the treadmill belt speed would only be able to negatively accelerate in the back half of the treadmill, while positive acceleration is only observed when the user is at the front half of the treadmill (Figure 5c). As the position dependent data are theoretical, a future direction would be to compare the algorithms.

A possible reason for the relative high percentage of negative accelerations, particularly at the front sections of the treadmill, could be due to the negative accelerations occurring more gradually than the positive accelerations (Figure 5). Especially at the front, if the belt speed were to increase, it would occur more rapidly than a decrease in belt speed due to the non-linear gains (Figure 1). As the graph only represents the amount of time the acceleration was greater than, equal to, or less than zero, it does not represent the amount of acceleration.

The average treadmill speed was statistically reliable within and between days. However, although standard deviation and coefficient of variation were statistically reliable within days, they were not reliable between days. Figure 6 is a representation of two participants’ conditions from both days.

Fig. 6.

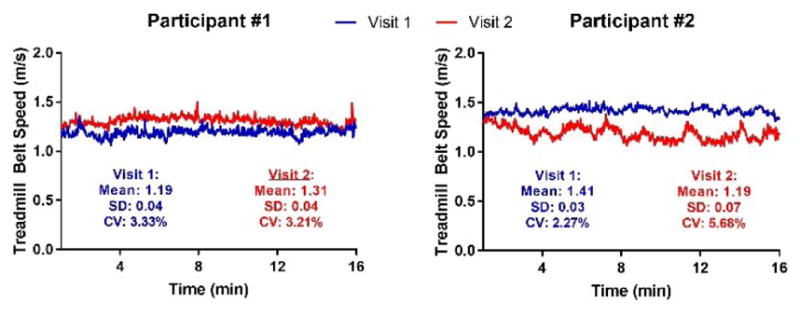
Exemplar data of treadmill speed vs. time graphs for two participants from each day. (First minute excluded.)

High reliability has been observed in another feedback-controlled treadmill algorithm [2] in treadmill speed mean and coefficient of variation, yet our proposed algorithm had lower ICC values in both within- and between-day. Possible explanations are: 1) people walk differently from day to day, and the algorithm is flexible enough to allow the user’s true behavior to emerge; 2) there is a learning effect, and the users adjusted to the algorithm after repeated use; or 3) the users were not able to naturally walk on the treadmill due to a negative relationship between the user and algorithm. We believe it is a combination of explanations 1 and 2, as the intention of the algorithm is to adjust the treadmill belt speed to the behavior of the user, rather than the user adjust his/her behavior to the treadmill belt speed. However, comparing our ICC values to Reference [2] is not an exact assessment. We used an ICC type (3,1) due to the variables being a single measure; however, to use an ICC type (3,k) – used in Reference [2] – the variables were average measures, which would require multiple trials to produce the reliable values.

It should be noted that treadmill speed is not a direct measure of a user’s walking behavior. It is the final output from the algorithm – an algorithm which measures biomechanical factors – providing an estimated walking speed while keeping the user on the treadmill. Thus, it is assumed the treadmill speed is strongly, positively correlated with the walking speed of the user. The data and results we show offer insight into the proposed algorithm and the reliability of it from trial to trial, day to day. Future work will be done to analyze the behavior of the user while using the algorithm.

Limitations did exist in this study and with the algorithm. The results are a representation of the algorithm when used by young, healthy individuals. This population has a normal and adaptive walking behavior. If the algorithm does force or constrain the user in any way, the young, healthy individuals may have been able to adapt and still complete the task, negating any imposing effect of the algorithm. The effectiveness of the algorithm on an older population and/or a population with a walking disorder is currently unknown. These results cannot be generalized to all individuals; further work must be done.

Future directions in this project are to analyze the dynamics of the individual, investigate the effectiveness of the algorithm in other populations (e.g. elderly, walking disorder), and comparison to overground. Also, the algorithm is still being adapted and modified. Due to research results, user’s opinions, or another form of feedback, modifications to the algorithm may be done. However, the core calculations and methodology, presented above, are believed to be of supreme value and will not likely be altered.