EMR-Radiological Phenotypes in Diseases of the Optic Nerve and their Association with Visual Function

Abstract

Multi-modal analyses of diseases of the optic nerve, that combine radiological imaging with other electronic medical records (EMR), improve understanding of visual function. We conducted a study of 55 patients with glaucoma and 32 patients with thyroid eye disease (TED). We collected their visual assessments, orbital CT imaging, and EMR data. We developed an image-processing pipeline that segmented and extracted structural metrics from CT images. We derive EMR phenotype vectors with the help of PheWAS (from diagnostic codes) and ProWAS (from treatment codes). Next, we performed a principal component analysis and multiple-correspondence analysis to identify their association with visual function scores. We find that structural metrics derived from CT imaging are significantly associated with functional visual score for both glaucoma (R²=0.32) and TED (R²=0.4). Addition of EMR phenotype vectors to the model significantly improved (p<1E-04) the R² to 0.4 for glaucoma and 0.54 for TED.

1 Introduction

Pathologies of the optic nerve affect millions of Americans each year and cancan severely affect an individual’s quality of life due to loss of visual function [1]. Accurate characterization of these diseases and timely intervention can preserve visual function. 3D computed tomography (CT) imaging of the eye orbit can capture structural changes in the eye orbit, which indicate the extent of disease progression and characterize pathology. In prior studies [2, 3], a quantitative relationship between 3D structural metrics of the eye orbit was shown to be associated with visual outcomes such as visual acuity and field vision in patients with optic nerve disorders. However, the percentage of explained variance due to structural data was low (R2 ~ 0.1–0.2). Several factors influence a model’s ability to explain outcomes, particularly the selection of predictive features. Also, while information is available in radiological imaging, evaluation of radiology within the context of an individual’s health history is important in determining functional changes, progression of disease, and prognosis. With the rise in adoption of digital electronic medical record (EMR) systems in the US health care system[4, 5], these records are available to medical research scientists with increasing ease.

In this study we develop an automated pipeline for segmentation and metric calculation of CT eye orbits for glaucoma and thyroid eye disease (TED). Further, we show that integrating EMR data, such as ICD-9 (International Classificaion of Diseases – 9) codes, and CPT (Current Procedural Terminology) codes, with imaging biomarkers improves the explained variance of disease outcomes.

2 Methods

2.1 Data

The study was conducted on a retrospective cohort of patients at Vanderbilt University Medical Center. Subjects were retrieved under Institutional Review Board (IRB) approval based on both having met clinical criteria for eye disease and undergoing CT imaging as part of their regular clinical care. The data collected include imaging records, visual testing, demographic data, complete ICD-9 codes and CPT codes. The disease groups included in this study are glaucoma (n=55) and TED (n=32).

2.2 Outcomes: Visual function scores

The outcomes in this study were calculated based on clinical visual acuity and visual field testing. Nine different outcome measures are calculated for a complete visual function evaluation as defined by the American Medical Association [6]. Right and left visual acuity scores are calculated as VAS_od and VAS_os respectively. The visual acuity for both eyes, VAS_ou is calculated as the best of VAS_od and VAS_os. The functional acuity score, FAS is a weighted score of VAS_od, VAS_os, and VAS_ou with weights 1:1:3. The scores from visual field testing, VFS_od, VFS_os, VFS_ou, and FFS are calculated similarly. A final score of visual function called functional visual score (FVS), is calculated as the average of FAS and FFS.

2.3 Image processing

Figure 1 shows the image segmentation pipeline. First, multi-atlas segmentation was employed to identify four labels: the globe, the optic nerve, the extraocular muscles and the periorbital fat. A set of twenty-five expertly labeled example 3D CT atlases is used as training examples to obtain the segmentation from a new input 3D CT scan. Each of the example atlases is non-rigidly registered to the cropped input image space [7]. The corresponding labels of the example atlases are propagated to the input image space using the non-rigid deformations. Next, non-local statistical label fusion is used to obtain a segmented result with the four labels[8]. Segmenting the individual extra-ocular rectus muscles is challenging in diseased eyes, since obtaining true labels is difficult at the back of the orbit due to inflammation. So, we employ Kalman filters to segment muscle labels obtained from the multi-atlas algorithm[3] to identify the superior rectus muscle, the inferior rectus muscle, the lateral rectus muscle, the medial rectus muscle. Once the final segmentation is obtained twenty-five structural metrics are computed bilaterally [2]. For each structure, the volume, cross-sectional area, and diameter/length are measured. Indices of orbital crowding, i.e., Barrett’s muscle index and volumetric crowding index are computed. In addition, degree of proptosis and orbital angle are computed. For each patient, i, a vector with 50 elements is constructed for 25 structural metrics computed bilaterally,

Fig. 1.

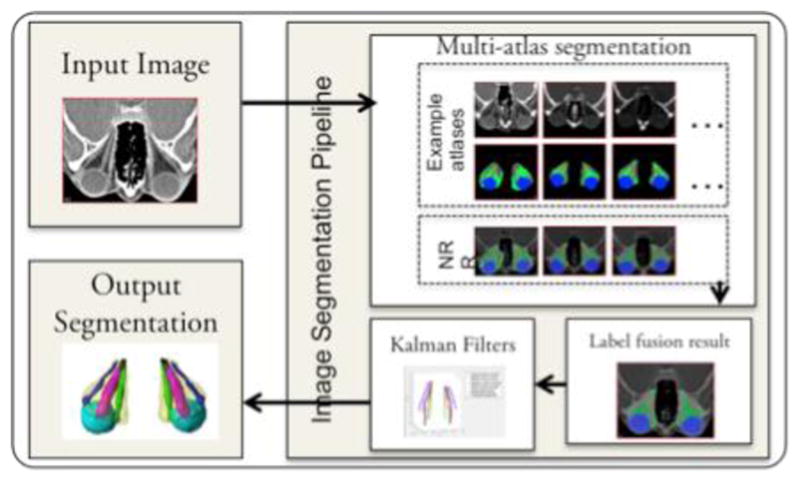
Overview of image segmentation. Multi-atlas label fusion is used to segment the optic nerve, globe, muscle, and orbital fat. Kalman filters are used to segment the four individual extraocular muscles based on the result to achieve the final 3D segmentation result.

$${\mathit{x}}_{CT}^{\{i\}}=[s{m}_{1\_os}s{m}_{2\_\text{os}}\dots s{m}_{25\_\text{os}}s{m}_{1\_\text{od}}s{m}_{2\_\text{od}}\dots s{m}_{25\_\text{od}}]$$

where, sm_{k_os} indicates k^th structural metric of the left eye and sm_{k_od} indicates k^th structural metric of the left eye.

2.4 EMR Features

From the EMR, complete ICD-9 codes and CPT codes were extracted for diagnostic and treatment information for each patient. However, only the ICD-9 and CPT codes available one month or more before the diagnosis are considered, since we are interested in understanding how a patient’s history provides a context for imaging information.

PheWAS codes

There are over 14,000 ICD-9 codes defined. A hierarchical system was defined that maps each ICD-9 code to a smaller group of 1865 phenotype codes originally used in phenome-wide association studies (PheWAS)[9]. Each phenotype, called a PheWAS code, indicates a related group of medical diagnoses and conditions.

ProWAS codes

We introduce a similar hierarchical grouping to map each CPT code to a group of related procedures, which we indicate by a procedure wide association study (ProWAS) code. We define 1682 ProWAS codes, which are finer granularity subgroups of the Clinical Classification Systems coding provided by the Healthcare Cost and Utilization Project (HCUP) Agency for Healthcare Research and Quality [10].

For each patient, i, a binary vector with 1865 elements, ${\mathit{x}}_{\mathit{PheWAS}}^{\{i\}}$ is defined,

$${\mathit{x}}_{\mathit{PheWAS}}^{\{\mathit{i}\}}=[\begin{array}{cccc}{d}_1& d_2& \dots & d_{1865}\end{array}]$$

where, d_k is 1 if the patient i has had the diagnosis phenotype d_k in the past and 0 otherwise. Similarly, a binary vector, ${\mathit{x}}_{\mathit{ProWAS}}^{\{i\}}$ is defined with 1682 elements,

$${\mathit{x}}_{\mathit{ProWAS}}^{\{\mathit{i}\}}=[\begin{array}{cccc}{t}_1& t_2& \dots & t_{1682}\end{array}]$$

where, t_k is 1 if the patient i has had the treatment phenotype t_k in the past and 0 otherwise.

2.5 Dimensionality reduction: PCA and MCA

A large amount of data is available for each patient; the final data vector for a patient i has 3597 elements in it. However, the data are correlated with each other, and it is possible to find underlying principal variables in the data. For the structural metrics, a principal component analysis (PCA)[11] is performed to reduce the dimensionality of the dataset. The first five principal components explaining about three fourths of the variance are extracted to give, for subject i,

$${\mathit{x}}_{CT\_\mathit{pca}}^{\{i\}}=[\begin{array}{cccc}s{m}_1^{\prime }& s{m}_2^{\prime }& \dots & s{m}_5^{\prime }\end{array}]$$ (1)

For the PheWAS and ProWAS binary vectors, multiple correspondence analysis (MCA) [12] is used to extract orthogonal components that are decomposed using the χ²-statistic. The first five components are considered for both PheWAS and ProWAS vectors. As a result of MCA, we get two vectors of smaller dimensionality for each patient,

$${\mathit{x}}_{\mathit{PheWAS}\_\mathit{mca}}^{\{i\}}=[\begin{array}{cccc}{d}_1^{\prime }& d_2^{\prime }& \dots & {\mathrm{d}}_5^{\prime }\end{array}]$$ (2)

$${\mathit{x}}_{\mathit{ProWAS}\_\mathit{mca}}^{\{i\}}=[\begin{array}{cccc}{t}_1^{\prime }& t_2^{\prime }& \dots & {\mathrm{t}}_5^{\prime }\end{array}]$$ (3)

2.6 Stepwise generalized linear model

The visual acuity scores are between 0 and 100 with most patients having scores close to 100 and values closer to 0 being extremely rare. This makes the distribution of the visual outcomes left skewed. Therefore, a generalized regression model (GLM) with a Poisson distribution [13] is used to find the explanatory value of each set of datasets, given by equations (1), (2) and (3), and all the data together. These datasets are regressed over the visual outcome scores s_v, where v ∈ {VAS_ou, VAS_od, VAS_os, VAS, FAS, VFS_ou, VFS_od, VFS_os, FFS, FVS}. Four models are defined for each v,

$$\begin{gathered} M1:s_v={\beta }_0+{\beta }_{1}s{m}_1^{\prime }+\cdots +{\beta }_{k}s{m}_k^{\prime }+{\beta }_{k+1}{d}_k^{\prime }+\cdots +{\beta }_{k+1}{d}_1^{\prime }+{\beta }_{k+l+1}{t}_1^{\prime }+\cdots \\ +{\beta }_{k+l+m}{t}_m^{\prime }+{\mathrm{\beta }}_{\mathrm{k}+\mathrm{l}+\mathrm{m}+1}\mathit{age}+{\beta }_{k+l+m+2}\mathit{sex}+\epsilon \\ M2:s_v={\beta }_0+{\beta }_{1}s{m}_1^{\prime }+\cdots +{\beta }_{k}s{m}_k^{\prime }+{\mathrm{\beta }}_{\mathrm{k}+1}\mathit{age}+{\beta }_{k+2}\mathit{sex}+\epsilon \\ M3:s_v={\beta }_0+{\beta }_1{d}_1^{\prime }+\cdots +{\beta }_l{d}_l^{\prime }+{\mathrm{\beta }}_{\mathrm{l}+1}\mathit{age}+{\beta }_{l+2}\mathit{sex}+\epsilon \\ M4:s_v={\beta }_0+{\beta }_1{t}_1^{\prime }+\cdots +{\beta }_m{t}_m^{\prime }+{\mathrm{\beta }}_{\mathrm{m}+1}\mathit{age}+{\beta }_{m+2}\mathit{sex}+\epsilon \end{gathered}$$

The four models are built using stepwise regression[14], with forward selection of variables. At each step, the variable that most significantly improves the model deviance is added until there is no more improvement. The explained variance of each model, R² is noted.

2.7 Test of deviance

The deviance of a model M, with fitted parameters θ̂ is given by,

$$D(M)=-2\left(log\left(p\left(y\mid \widehat{\theta }\right)\right)-log(p(y\mid {\theta }_s))\right)$$

where, θ_s are the parameters of the saturated model, i.e., a model with parameters for each data point such that it is fitted exactly. The deviance can be used to test significance between two nested models M_p(θ̂_p|X) and M_q (θ̂_q|X), where θ̂_p ⊂ θ̂_q and the difference in the parameters between the two models is given by δ. The difference of the deviance between the two models follows a χ² –squared distribution with degree of freedom δ. The null hypothesis, H₀ for the test of deviance is that adding δ parameters to model M_p to get M_q does not improve the model. This test is used to compare models M2–4 with M1.

3 Results

The average age group for glaucoma cohort 65.4±19.5 years and 72% of the subjects were female. 91% of TED subjects were female, and the average age for this group is 57.8±16.2 years. On an average, each patient had 410 ICD-9 codes, and 660 CPT codes recorded. Figure 2 shows the individual distribution by sex along the first two components of the three datasets in models M2, M3, and M4. For glaucoma, the first component of the PCA on structural metrics corresponded to muscle and optic nerve measurements, and the second component corresponded to orbital and globe measurements. For TED, the first component corresponded to mostly muscle measurements, and the second component corresponded to measurements of the optic nerve. Some of the conditions associated with the first MCA component of the ICD-9 vector for Glaucoma are malaise, osteoarthrosis, and hypovolemia, and conditions associated with the second component included female genitourinary symptoms and symptoms associated with the eye such as pain and swelling. The first MCA component for TED’s ICD-9 vector was associated with conditions including hyperlipidemia, diabetes, and circulatory problems, and some of the conditions most associated with the second MCA component were myalgia and abnormal blood chemistry. For the CPT vector for glaucoma, the first dimension was associated with a wide range of procedures such as CT scans, and pathology labs, and the second component was associated with cardiac testing. For TED, the first component was associated with procedures such as urinalysis and blood work, the second component was associated with physical therapy related procedures.

Fig. 2.

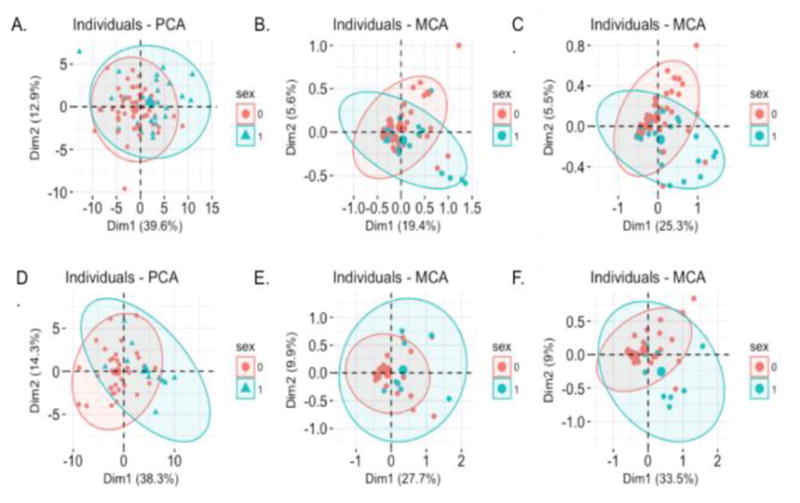
Distribution of individuals by sex along the first two components from equations (1), (2), and (3). Red and blue indicate 95% confidence ellipses for females and males respectively. (A) x_{CT_pca} for glaucoma. (B) x_{PheWAS_mca} for glaucoma. (C) x_{ProWAS_mca} for glaucoma. (D) x_{CT_pca} for TED. (E) x_{PheWAS_mca} for TED. (F) x_{ProWAS_mca} for TED.

Tables 1 and 3 show the R² values of models M1, M2, M3, and M4 regressed over functional visual scores for glaucoma and TED respectively. The behavior of the models is the same for both the diseases. Addition of treatment and diagnostic phenotypes to model M2 to get model M1 results in significant improvement of explained variance in most of the visual outcomes: FVS, FFS, VFS_ou, VFS_od, VFS_os, VAS_od and VAS_os. The R² values that improve between model M2 to M1 are indicated by ** in Tables 1 and 3. The statistical significance of this improvement is tested using the test of deviance as described in section 2.7. Tables 2 and 4 show the p-values of the tests of deviance performed between M1 and its nested models M2, M3, and M4.

Table 1.

Explained variance in Glaucoma.

R2	VASod	VASos	VFSod	VFSod	VASou	VFSou	FFS	FVS	FAS
M1	0.48**	0.33**	0.47**	0.39**	0.24	0.27**	0.33**	0.40**	0.35
M2	0.45	0.13	0.37	0.16	0.24	0.18	0.23	0.33	0.35
M3	0.07	0.07	0.16	0.08	0.08	0.05	0.08	0.07	0.00
M4	0.04	0.00	0.20	0.06	0.00	0.05	0.09	0.06	0.00

^**indicates that model M1 is significantly better than model M2, i.e. using structural metrics alone, based on the p-values in Table 2.

Table 3.

Explained variance in TED.

R2	VAS od	VAS os	VFS od	VFS od	VAS ou	VFS ou	FFS	FVS	FAS
M1	0.61**	0.30**	0.59**	0.37**	0.28	0.36**	0.42**	0.54**	0.44
M2	0.49	0.23	0.45	0.26	0.28	0.23	0.28	0.40	0.44
M3	0.30	0.22	0.33	0.24	0.16	0.20	0.24	0.28	0.20
M4	0.28	0.18	0.29	0.18	0.16	0.17	0.19	0.29	0.20

^**indicates that model M1 is significantly better than model M2, i.e. using structural metrics alone, based on the p-values in Table 4.

Table 2.

Test of deviance.

p-value	VASod	VASos	VFSod	VFSod	VASou	VFSou	FFS	FVS	FAS
M1 vs M2	4.30E-05	5.89E-09	2.92E-26	3.31E-38	na	5.38E-07	1.34E-07	1.18E-07	na
M1 vs M3	1.66E-28	1.55E-10	3.17E-62	9.70E-46	0.001	2.65E-11	8.46E-15	2.39E-26	2.40E-06
M1 vs M4	1.42E-29	3.59E-12	3.22E-58	8.32E-47	0.0005	8.48E-12	2.35E-14	3.15E-26	2.40E-06

Na indicates that the model ist he same in both M1 and M2, as the same features were selected.

Table 4.

Test of deviance.

p-value	VASod	VASos	VFSod	VFSod	VASou	VFSou	FFS	FVS	FAS
M1 vs M2	4.56E-06	0.00027	5.15E-24	6.75E-07	na	4.38E-08	7.50E-09	9.70E-10	na
M1 vs M3	1.09E-17	0.00049	7.27E-45	1.23E-08	na	7.02E-10	1.88E-12	3.53E-18	1.12E-05
M1 vs M4	1.60E-18	6.84E-05	4.61E-52	1.30E-10	na	9.51E-12	6.77E-15	2.36E-19	1.12E-05

Na indicates that the model ist he same in both M1 and M2, as the same features were selected.

However, it is interesting to note that composite visual acuity scores VAS_ou and FAS do not show an improvement between models M2 and M1, even though the right and left acuity scores VAS_od and VAS_os do. Note from the definition of these scores that they weight the best performing eye higher. This might indicate that changes in visual acuity might not be bilateral in these conditions. Whereas, for visual field scores the behaviour of the individual eye scores is reflected in the composite scores, indicating that visual field changes might be bilateral in glaucoma and TED.

4 Discussion

To identify imaging biomarkers associated with diseases of the optic nerve such as glaucoma and thyroid eye disease, their relationship with visual function scores must be established. This study shows that addition of treatment and diagnostic phenotypes derived through MCA on ProWAS and PheWAS data can improve traditional imaging biomarker studies by providing the context of an individual’s health history from clinical data. This is the first known study with the application of ProWAS mapping to identify treatment phenotypes for eye disease. We show that structural metrics of the eye orbit derived from CT imaging, treatment, and diagnostic phenotypes show a significant association with visual function scores and explain about 40% – 60% of the variance for visual outcomes in glaucoma and thyroid eye disease.