Complementarity and competitiveness of the intrinsic and extrinsic components of the total ventricular load: Demonstration after valve replacement in aortic stenosis

In this issue of the Journal, Nemes et al¹ consider alterations in aortic stiffness during a 1-year follow-up after aortic valve replacement (AVR). Twelve patients with severe aortic stenosis (AS) who underwent AVR were prospectively investigated. As expected, stenosis severity and left ventricular (LV) mass decreased significantly after AVR. Moreover, aortic luminal diameter changes (systolic minus diastolic dimensions) progressively increased and aortic stiffness decreased to levels comparable to those of age-, gender-, and risk factor–matched controls at 1 year.

Some readers might find it counterintuitive that the pulse pressure in uncorrected severe AS tended to be greater than at 12 months after AVR. Rethinking the apparently simple but actually complex is central to understanding the interacting hemodynamic changes beneath this seemingly paradoxical finding. We start with an integrative overview of ventricular loading.

The ventricular systolic ejection load represents pressure against which the walls contract and is to be distinguished from myocardial loading or wall stress, to which it is related by complex cardiomorphometric and histoarchitectonic factors. The total ventricular systolic load, or afterload, determines the manner by which the mechanical energy generated by the actin-myosin interactions in the ventricular walls is converted to the work that pumps blood through the circulation. Under any given contractile state, increased afterload reduces ejection rate and stroke volume. Conversely, when afterload decreases, a larger volume is ejected at higher ejection velocities.^2–5 These changes result from the inverse force–velocity relation of the working myocardium.^3,4

Extrinsic component of the total ventricular systolic load

It is the interaction of the ejection flow patterns generated by the left (right) ventricle at the aortic (pulmonic) root with the systemic (pulmonary) input impedance^6,7 that gives rise to the extrinsic component of the total ventricular systolic load. This view differs from the widely quoted formulation, by Milnor,⁸ of the arterial impedance as the complete representation of the ventricular afterload. First, Milnor’s formulation neglects entirely the intrinsic component of systolic ventricular loading (ie, the intraventricular flow–associated pressure gradient). Second, Milnor arrived at his conception that arterial impedance per se represents the systolic load because he felt that it would be wrong to conclude that the ventricle plays a part in determining its own afterload. However, invoking such a need is somewhat arbitrary. It is tantamount to accepting that the load imposed on, eg, the muscular system of a cross-country runner, is embodied solely in the terrain and not in the way (speed and acceleration patterns) in which he interacts with it.

An elevated aortic stiffness raises the systemic input impedance because it augments the aortic characteristic impedance, which increases the amplitude of the primary (outgoing) pressure pulse and the pulse wave velocity, causing reflected primary pressure wave components to return early to the aortic root; there, they boost pressure levels in late systole while ejection is still unfolding, rather than in early diastole. Thus, aortic stiffness is a major determinant of central pulse pressure. By augmenting the outgoing pressure wave, it enhances the extrinsic component of the total ventricular load and the systemic impedance to LV ejection over the frequency band (1–4 Hz) that normally contains the greatest energy of the LV ejection (flow) wave.⁹

Aortic stiffness is largely determined by wall structure and function and luminal diameter and by the distending arterial pressure levels. Complex reciprocal influences exist between aortic stiffness and pressure¹⁰ that affect LV systolic loading and ventriculoarterial coupling¹¹ after AVR. Key load-bearing components of the aortic wall are elastin, stiffer collagen, and smooth muscle. Smooth muscle contraction raises stiffness because of a decrease in luminal diameter and shifting of load onto the stiffer collagen fibers. Increasing mean distending aortic root pressure causes a small increase in diameter, which would tend to lower stiffness, but the ensuing transfer of wall stress from elastin to collagen overshadows this effect, leading to a rise in stiffness.

Intrinsic component of the total ventricular load

In the 1980s and early 1990s, intensive catheterization and computer simulation studies of ejection were undertaken in patients evaluated for all kinds of heart disease and others found to have normal ventricular function.³ These studies demonstrated the presence of intraventricular ejection gradients of substantial magnitude in the human left ventricle in the absence of any organic or dynamic outflow obstruction,^3,12 and delineated characteristics distinguishing them from obstructive gradients and transvalvular pressure drops.^3,13–16 Larger intraventricular gradients can be demonstrated when blood is ejected rapidly from an enlarged chamber through a normal-sized aortic anulus^3,4 as in aortic regurgitation, an instance of systolic ventriculoannular disproportion.³

Analogous concepts were more recently put forward,^17–19 that govern previously unrecognized important aspects of the diastolic ventricular filling load. A new mechanism, the convective deceleration load,^18,19 was formulated as an important determinant of diastolic inflow during the upstroke of the E wave. The larger the chamber, the larger becomes the convective deceleration load. This underlies the concept of a diastolic ventriculoannular disproportion.^17–19

In the presence of left (right) ventricular outflow tract obstruction, including aortic (pulmonic) valvular stenosis, intraventricular ejection gradients of large magnitude are typical.^2,3,20

The total systolic ejection load

Through the above-mentioned endeavors, the view was developed^3,13 that total ventricular systolic load comprises both extrinsic (the aortic root ejection pressure waveform) and intrinsic (flow-associated intraventricular pressure gradients) components. Figure 1 provides a framework for understanding systolic loading dynamics. A new concept was advanced of complementarity and competitiveness^3,13 in the dynamic interaction between the extrinsic and intrinsic components of the total systolic load under any given preload and contractility levels.

Figure 1.

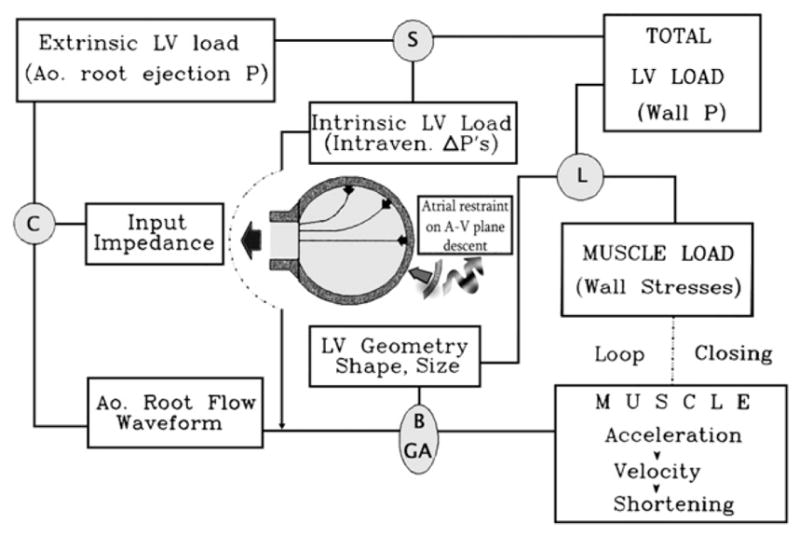
Framework for envisaging systolic loading and complementarity and competitiveness in the dynamic interactions between the intrinsic and extrinsic total systolic LV load components. Ao., Aortic; Intraven., intraventricular; A-V, atrio-ventricular; P, pressure; C, mathematical operation of convolution; S, summation; L, operation of the Laplace law; B, Bernoulli effects; GA, geometric actions; ΔP’s, pressure gradients. Modified from Pasipoularides³ by permission of the American College of Cardiology.

A striking example of complementarity and competitiveness is provided in Figure 2. Immediately after aortic valvuloplasty to relieve AS, the great reduction of the ventricular ejection gradient (intrinsic component) is seen to be counterbalanced by a complementary increase of the aortic root systolic pressure (competing extrinsic component). Consequently, instead of decreasing acutely—as might be expected in the absence of complementarity and competitiveness—the LV systolic pressure (total systolic load) remains essentially unchanged.^15,21 This could explain why changes in aortic valve area after balloon valvuloplasty have not correlated with short-term clinical outcome.

Figure 2.

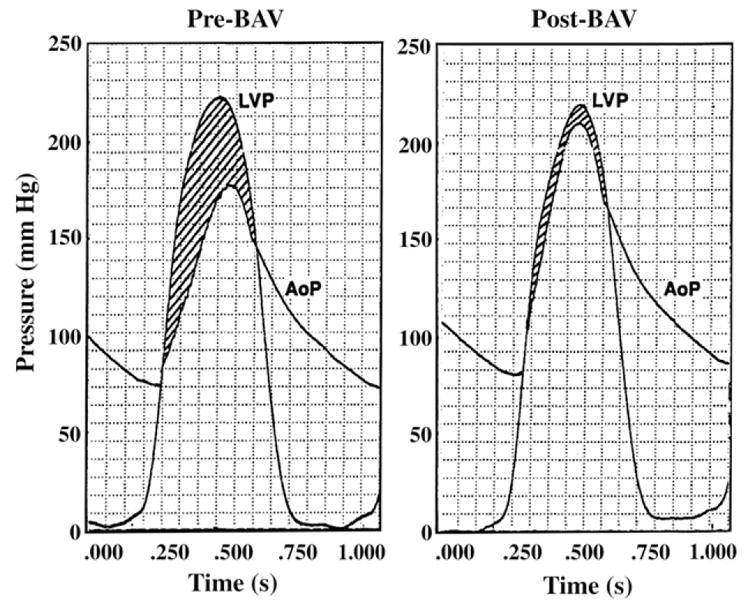
Complementarity and competitiveness between intrinsic and extrinsic components of the total LV systolic load. Immediately after aortic valvuloplasty, the great reduction of the ventricular ejection gradient (intrinsic component) is counterbalanced by a complementary increase of the aortic root systolic pressure (competing extrinsic component). LV systolic pressure (total systolic load) remains essentially unchanged. AoP, Aortic root pressure; BAV, balloon aortic valvuloplasty; LVP, left ventricular (deep chamber) pressure. Modified from Shim et al¹⁵ by permission of the American Heart Association.

A related intriguing phenomenon in AS is “pressure loss recovery,”^3,22 in which some of the intrinsic LV load going into convective acceleration of the flow upstream of the stenosed orifice²⁰ is regained as the flow reexpands in the aortic root. Aortic stiffness may be an unrecognized determinant of this recovery.

LV systolic load changes after AVR

Within the scope of this integrative framework, we interpret the findings of Nemes et al¹ as follows: Before AVR, aortic stiffness was greatly elevated from control in severe AS. The authors suggest that endothelial dysfunction, ischemia, and other factors²³ might bring about the increased stiffness. In any case, this stiffening augments the aortic input impedance, so that not only the intrinsic but also the extrinsic component of the total systolic LV load is elevated. Although measurements are not available immediately post-AVR, Figure 2 and findings after balloon valvuloplasty^15,21 suggest that the great reduction of the systolic ejection gradient (intrinsic component) can be transitorily counterbalanced by a complementary increase of the aortic root systolic pressure (the extrinsic component). The measurements 3 weeks, 6 months, and 12 months after AVR show the ensuing gradual decrease in aortic stiffness and the extrinsic component of the systolic LV load. This decrease abets the immediate sharp drops in the peak and the mean aortic pressure gradients, which reflect the intrinsic component of the systolic load. Pari passu with these changes in systolic LV load, LV mass and geometry tend to revert to normal.

Clearly, the pulse pressure before AVR is greater than at 12 months post-AVR because of the gradually ensuing substantial decrease in aortic stiffness, which was demonstrated for the first time by this seminal study! Its remarkable findings¹ underscore the need for serial studies to detail mechanisms underlying the evolution of the interplay between the intrinsic and extrinsic components of LV load in the setting of interventions aimed at relief of AS.