Gravity orientation tuning in macaque anterior thalamus

Abstract

Gravity may provide a ubiquitous allocentric reference to the brain’s spatial orientation circuits. Here we describe neurons in the macaque anterior thalamus tuned to pitch and roll orientation relative to gravity, independent of visual landmarks. We show that individual cells exhibit two-dimensional tuning curves, with peak firing rates at a preferred vertical orientation. These results identify a thalamic pathway for gravity cues to influence perception, action and spatial cognition.

Introduction

Our brain has adapted to living on earth and gravity likely sculptures how we interact with the world. Gravity is sensed by the otolith organs of the inner ear, but gravity and inertial accelerations must be differentiated, and this is achieved by a distributed brainstem/cerebellar circuit^1–4 using an internal model of the physical laws of nature^5–7. We⁷ have hypothesized that gravity provides a global allocentric reference for spatial orientation. Head direction (HD) cells form a “neuronal compass”, encoding head orientation in the horizontal plane⁸ as well as head orientation relative to vertical, as shown recently in the dorsal presubiculum of bats⁹. Here we searched for gravity-tuned cells in the macaque anterior thalamus, where HD cells are found in rodents⁸.

Results

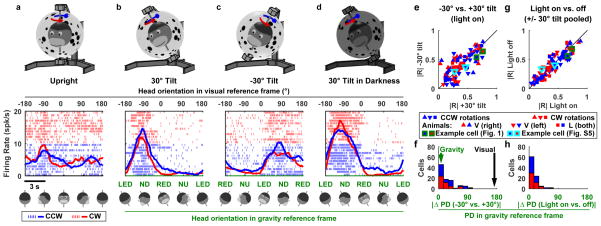
We recorded from 95 neurons (Supplementary Fig. 1a,b) while head-fixed macaques were passively rotated inside an independently movable spherical enclosure (Supplementary Fig. 1c; Supplementary Video 1). First, we rotated animals in a horizontal plane while oriented upright relative to gravity. Most neurons were unmodulated in this condition (Fig. 1a, Supplementary Fig. 2). Next, the rotation axis and the visual environment were tilted together 30° away from vertical (right-ear down; Fig. 1b). Despite identical visual surround, the cell now exhibited strong directional tuning peaking at −90° orientation in the visual reference frame (upper black scale), corresponding to nose-down (ND) orientation in the gravity reference frame (lower green scale). Note that clockwise (CW, blue) and counter-clockwise (CCW, red) responses were similar for this neuron.

Figure 1. Neuronal responses during yaw rotations around upright and tilted axes.

(a–d) Example neuron responses during (a) yaw rotation around an earth-vertical axis, with the animal upright (in light), yaw rotations around axes tilted ±30° in light (b,c) and darkness (d). Abbreviations: NU: nose-up, ND: nose down, LED: left ear down, RED: right ear down. Upper row: illustration of the stimuli. Middle row: neuronal responses as a function of head orientation relative to the visual environment (a–d, top axis) or relative to gravity (b–d, lower axis). The drawings below the plots illustrate head position in space. Red/Blue raster plots and lines: individual spikes and average response during multiple cycles of counterclockwise (CCW) and clockwise (CW) rotation respectively. Neuron recorded in Animal L, right hemisphere. A total of 48 neurons were recorded. (e–h) Population responses (n=48). (e,g) Resultant (R) vector length. (e) Comparison between +30° and −30° tilt. (g) Comparison between rotations in light and darkness. (f,h) Distributions of the absolute difference in Preferred Direction (PD) relative to gravity between (f) +30° and −30° tilt, and (h) rotations in light and darkness. Each cell appears twice in red/blue plots (for CCW and CW rotations, respectively).

We tested whether the tuning in Fig. 1b is anchored to gravity. First, we tilted the setup to the opposite direction (left-ear down) by −30° (Fig. 1c). This reversed head orientation relative to gravity (Fig. 1c, green scale) while the visual surround remained unchanged. The cell’s tuning shifted relative to the visual reference frame by 180° (now peaking at 90°), but maintained the ND tuning in the gravity reference frame. Next, we found that the cell’s tuning was maintained during rotation in complete darkness (Fig. 1d), further demonstrating that it was independent of visual cues. Third, we tested the cell during ±30° pitch and roll rotations (Supplementary Fig. 3a,b). The firing rate increased in ND (forward pitch), consistent with the tilted yaw protocols. Thus, the cell exhibited a consistent tuning to orientation relative to gravity, regardless of visual cues and of the particular rotation plane being used to bring the animal in that orientation.

We analyzed 48 cells that exhibited significant tuning during tilted rotations. The population exhibited similar tuning strength during +30° and −30° tilted yaw rotations (paired Wilcoxon rank test, p = 0.2; Fig. 1e) and aligned preferred direction (|ΔPD|<45° in 83% of the cells, Fig. 1f). Both tuning strength and PD were identical when measured in darkness and light (Fig. 1g,h, p = 0.5). Furthermore, tuning strength and PD during vertical (pitch/roll) plane rotations were similar to those during tilted yaw rotation (Supplementary Fig. 3c–f). Neuronal responses were also identical when only the rotation axis, but not the visual environment, was tilted (Supplementary Fig. 4). Collectively, these results demonstrate that neuronal responses were anchored to gravity and persist in complete darkness.

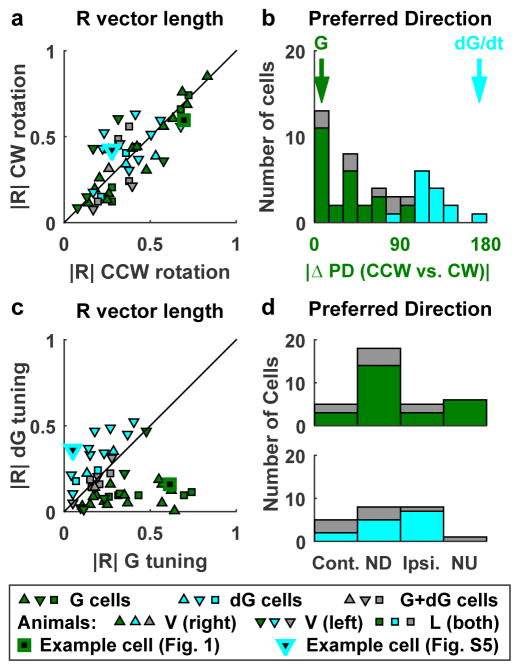
Fig. 1 demonstrates a prominent cell type that was tuned to gravity, where CCW and CW responses were similar. Other cells exhibited comparable modulation but distinct preferred directions for CCW and CW rotations (Fig. 2a,b; Supplementary Fig. 5), indicating that they also encode gravity velocity (see on-line Methods). We separated gravity (G) and gravity velocity (dG) responses (Supplementary Fig. 6) and classified cells into G-tuned (n=26, Fig. 2, green), dG-tuned (n=14, cyan) and intermediate (G+dG cells, n = 8, gray) cells. The G tuning preferred mostly the pitch plane (i.e. NU and ND; Fig. 2d; 24/34 cells; X²=14.2, dof = 3, p = 0.003), whereas the dG components appeared uniformly distributed (Fig. 2d, X²=6, dof = 3, p = 0.1).

Figure 2. Gravity (G) and Gravity-derivative (velocity, dG) responses.

Cells are classified as G-tuned (green), dG-tuned (cyan) and G+dG-tuned (gray) (see Suppl. Fig. 6 for details). (a,b) Comparison of resultant vector length, |R|, and PD between CW and CCW rotations. Cells showed similar modulation strength during CW (|R| = 0.36 ± 0.2 SD) and CCW (|R| = 0.35± 0.2 SD) rotation (paired Wilcoxon rank test, p=0.93), but often differed in PD. Identical PDs are characteristic of G-tuned whereas opposite PDs are characteristic of dG-tuned cells. (c) Resultant vector length, |R|, of the G and dG components. G-tuned cells: |R(G)| = 0.37 ± 0.2 SD, |R(dG)| = 0.11 ± 0.1 SD; dG-tuned cells: |R(G)| = 0.18 ± 0.1 SD, |R(dG)| = 0.33 ± 0.1 SD. (d) Distribution of the preferred direction of the G component (upper panel, G-tuned and G+dG-tuned cells) and dG component (lower panel, dG-tuned and G+dG-tuned cells). ND, Contralateral (Cont.), NU and Ipsilateral (Ipsi.) refer to the direction of tilt (G component) or tilt velocity (dG component).

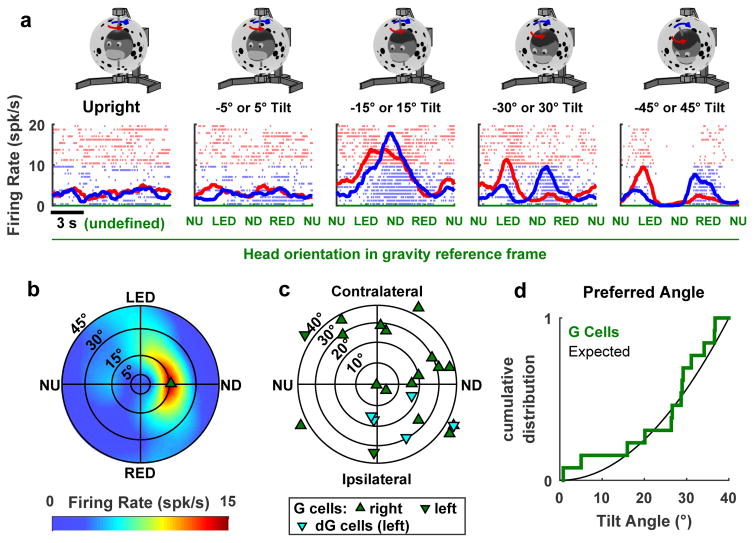
In a subset of cells (n=31), neuronal responses were measured at tilt angles ranging from 5° to 45°. In many neurons, tuning strength peaked at an intermediate tilt angle (e.g. ±15° in Fig. 3a). In contrast, the tuning strength of afferent signals from the otolith gravity sensors would increase with tilt (Supplementary Fig. 7). The reconstructed two-dimensional tuning curve of this example cell (Fig. 3b, see also Supplementary Fig. 8) formed a hill of activity, with the firing rate peaking at a preferred orientation and tilt angle. The direction (i.e. NU, ND, Ipsilateral or contraleral tilt) of peak firing for G-tuned (Fig. 3c, green) were distributed broadly (circular R test, n = 18, p = 0.14) and G-tuned cells had preferred tilt angles uniformly distributed in this plane (Kolmogorov-Smirnov test, p>0.2; Fig. 3d). That is, a larger fraction of neurons preferred 30°–40° tilt, compared to 0°–10° tilt, since the area of the former sector is larger than that of the later. Too few dG-tuned neurons were included in this sample (Fig 3c, cyan) to justify firm conclusions.

Figure 3. Example cell exhibiting hill-shaped tuning to Gravity and population summary.

(a) Responses during rotation in upright orientation ±5° to ±45° tilt (positive and negative tilt are averaged). 31 cells were recorded with this protocol. (b) Two-dimensional gravity (G) tuning curve of this example cell, extracted from the data. In this polar plot, the distance from the center represents the tilt angle and the 360° circular angle represents the direction of the tilt (Suppl. Fig. 1d). Note that, because of the elongated shape of the hill of activity, the cell fires at 5–10 spk/s in LED and RED at 45° tilt, and is silent in NU and ND, leading to the double-peaked response during yaw rotation with ±45° tilt. (c) Location of the peak response for G-tuned cells (n=18) and dG-tuned cells (n=5). ND, Contralateral, NU and Ipsilateral refer to the direction of tilt for G-tuned cells and the direction of tilt velocity for dG-tuned cells. (d) Cumulative distribution of preferred tilt angles for G-tuned cells (n=13). Black curve: expected cumulative distribution assuming that the cells are distributed uniformly. Cells with preferred angle > 40° (n=5) are excluded from the cumulative distribution.

In summary, we have shown that neurons in the macaque anterior thalamus carry a gravity-anchored orientation signal that is independent of visual landmarks. These neurons fire maximally at a particular head orientation relative to gravity, in a way analogous to rodent azimuth-tuned HD cells, whose preferred direction is anchored to visual landmarks^8,9. The gravity-tuned cells didn’t appear to be tuned to head azimuth; however the tuning of HD cells is frequently suppressed during head-fixed rotation in rodents¹⁰. It is therefore unknown, but possible, that some of these gravity-tuned cells are traditional azimuth-tuned HD cells.

We found that gravity orientation tuning is two-dimensional, and accordingly individual gravity-tuned neurons exhibit 2D hill-shaped tuning curves. A quarter of spatially modulated cells also exhibited gravity-derivative (velocity) tuning, implying a distributed representation of the integration process. The most remarkable property of gravity tuning is that it is independent of the rotation plane (in egocentric coordinates) that changes head orientation - we found similar tuning relative to gravity for yaw rotations on one hand, and pitch and roll rotations on the other hand. Thus, the underlying neuronal circuits should integrate rotation velocity signals around all three egocentric (yaw, pitch, roll) axes simultaneously. Indeed, the circuitry that produces an internal model of gravity in the cerebellum has this exact property^2–3.

Discussion

Based on these findings, we propose that gravity-tuned cells may comprise the two vertical degrees of freedom of a 3D orientation compass in the macaque thalamus. This hypothesis could also be consistent with the finding of vertically-tuned HD cells in bats¹¹. Both species show a small dominance of pitch-tuned over roll-tuned cells. Since roll does not change the direction the head is facing, and neither macaques nor bats perform frequent roll head movements, it is possible that there is a selective adaptation for spatial orientation to be tuned mostly in the direction the head faces. Yet, although less frequent, roll-tuned cells are found in both species. The gravity signals identified here may also govern the updating of the reference frame of azimuth-tuned HD cells during 3D movements¹². Future experiments should investigate whether gravity-tuning is found in physiologically-identified azimuth-tuned HD cells.

Online Methods

Animals

We recorded from the anterior thalamus of two naïve male rhesus macaques (V and L, both 5 years old, pair-housed with normal light/dark cycle) implanted with a circular delrin ring to immobilize the head, scleral search coils to measure eye movements, and a delrin platform for neural recordings^13,14. Neuronal recordings in the Anterior Thalamus were performed in animal V prior to this study. Experimental procedures were conducted in accordance with US National Institutes of Health guidelines and approved by the Animal Studies and Use Committee at Baylor College of Medicine.

Electrodes were positioned daily using a delrin platform that was implanted stereotaxically. The anterior thalamus was localized by matching stereotaxic MRI scans (Supplementary Fig. 1a, b) onto a vectorized brain atlas¹⁵. Stereotaxic MRI scans were performed using MRI-compatible ear bars and additional MRI-compatible markers placed stereotaxically on the recording platform, allowing reconstruction of stereotaxic coordinates directly from MRI images. Recording locations were reconstructed by superimposing MRI and recording platform coordinates. Positioning accuracy was verified in initial experiments, where two landmark regions¹⁴ (the oculomotor nuclei and midbrain burst neurons, identified physiologically based on their characteristic firing patterns during vertical pursuit and saccadic eye movements) were recorded using the same positioning system. During experiments, the anterior thalamus was reached by lowering the electrode until it entered the lateral ventricle, which could be clearly recognized by the absence of neural activity. The electrode was lowered further and we searched for rotation-tuned cells as soon as neural activity resumed.

Experimental apparatus

During experiments the animal was comfortably seated in a primate chair secured inside a vestibular stimulator composed of a motorized three-axis rotator surrounded by a light tight sphere (1.8m diameter) (Acutronics Inc., Switzerland). A fourth rotation axis allowed tilting of the rotator and the sphere together as a single unit (Supplementary Fig. 1c). The inside of the sphere was painted in white and black dots of different sizes. Animals were positioned such that all four rotation axes were aligned with the center of the head and the stereotaxic-horizontal plane was earth-horizontal when the animal was at rest.

Experimental protocols

As illustrated by the Supplementary Video 1, all yaw rotation protocols were delivered using the rotator’s innermost axis (Axis I, Supplementary Fig 1c). Animals were passively rotated alternatively in counterclockwise (CCW) and clockwise (CW) directions, at a constant velocity of 28.6°/s (i.e. 0.5 rad/s). Each movement lasted 12.6s, covering the full 360° rotation, and a total of 24 movements (12 in each direction) were performed. Stimulus protocols were delivered as follows:

1. Yaw rotation with the animal upright (no change in head orientation relative to gravity).

2. Yaw rotation around a head and visual tilted axis (gravity/vision conflict). This was achieved using Axis IV to tilt the whole system (3D rotator and spherical enclosure) either +30° or −30°. This condition generated a sensory conflict with visual cues identical to those observed during upright yaw rotation (condition 1), but with gravity cues signaling a different orientation relative to gravity.

3. Yaw rotation around a head tilted axis only (non-conflict condition). In this case, the ±30° tilt was introduced using Axis II (head/body), whereas Axis IV (spherical enclosure) remained upright. In this condition, vestibular/somatosensory cues were congruent with visual cues (that indicated a tilted orientation within the upright visual surround).

4. In addition, neurons were also tested with pitch rotations, where Axis I was positioned such that Axis II was aligned with the animal’s inter-aural axis. Axis II was then rotated back and forth to ±30°, at a constant velocity of 28.6°/s, thus pitching the animal alternatively forward and backward. A total of 24 movements (12 in each direction) were performed. We also performed roll rotations, where Axis I was positioned such that Axis II was behind the animal and aligned with the naso-occipital axis. Axis II was then rotated back and forth to ±30°, at a constant velocity of 28.6°/s, thus rolling the animal alternatively rightward and leftward.

5. If cell isolation was maintained, the tilted yaw rotation protocol 3 was also delivered for tilt angles other than ±30°: ±5°, ±15°, and ±45°.

All isolated neurons were first recorded during protocols (1) and (3), and the rest of the stimuli were only used for responsive neurons. Protocols were performed in the following order: (1), (3), (2), (4) and (5). Protocols (1) to (4) were performed first in light and then repeated in complete darkness.

Neural recordings

Extracellular recordings from isolated single neurons were obtained with epoxy-coated tungsten microelectrodes (1–2 MΩ impedance; FHC, Bowdoinham, ME). Each electrode reached the midbrain and thalamus through a 26 gauge cannula, and was manipulated with a remote-controlled microdrive (FHC, Bowdoinham, ME). Neural activity was amplified and filtered (300 Hz – 6 kHz). Neuronal data was also acquired at 33 kHz using an analog channel of a Power-1401 data acquisition interface (Cambridge Electronic Design Ltd) and analyzed offline using custom Matlab (Mathworks) scripts to extract spike timing from the raw neuronal data based on spike statistics (amplitude, peak latency) and principal component analysis.

Statistics

No statistical methods were used to pre-determine sample size, but our sample sizes are typical of those used in the field. Depth of modulation was compared across tasks using Wilcoxon rank sum tests. All statistical tests were two-sided. Data collection and analysis were not performed blind to the conditions of the experiments.

Modulation during yaw rotation

We used Rayleigh’s mean vector R as a measure of modulation depth during yaw rotations around upright or tilted axes. Head orientation α, in the plane of rotation (i.e. the position of the yaw rotation axis), which ranged from 0° to 360°, was divided in 100 bins of width δα = 3.6°. We computed the mean firing rate, FR(α), within each bin. The mean vector R (as defined in¹⁶) is the complex number:

$$\mathrm{R}=\text{c.}{\sum }_{\mathrm{\alpha }}\text{FR}(\mathrm{\alpha }).{\mathrm{e}}^{\mathrm{i}.\mathrm{\alpha }.\mathrm{\pi }/180}{\sum }_{\mathrm{\alpha }}\text{FR}(\mathrm{\alpha }),\text{with}\mathrm{c}=(\mathrm{\delta }\mathrm{\alpha }/2)\ast (180/\mathrm{\pi })/sin(\mathrm{\delta }\mathrm{\alpha }/2).$$

The length of the mean vector, |R|, represents the strength of the neuron’s modulation and ranges from 0 (when spikes are distributed uniformly) to 1 (when all spikes occur at the same head orientation α). The phase of R represents the preferred direction of the neuron. Note that R was always computed independently for CCW and CW rotations since some neurons (dG-tuned, see below) exhibited out of phase responses during CCW and CW rotations.

The significance of |R| was assessed by bootstrap analysis. Each bootstrap sample was constructed by splitting the dataset into individual rotation cycles. Within each cycle, the head orientation variable (α) was shifted circularly by a random number ranging from 0° to 360°. A value of |R| was computed based on this shuffled dataset; and the procedure was repeated 1000 times. Cells were considered significantly modulated when |R| was higher than in 99% of the bootstrap samples (i.e. |R| was significant at p=1%) in both CCW and CW directions.

Reconstructing Gravity and Gravity-Derivative tuning curves

We separated Gravity (G) and Gravity-derivative (dG) responses based on the difference between the experimentally measured response curves (FR^CCW(α) and FR^CW(α)) during CCW and CW rotations. Parameter α is expressed in a gravity reference frame, and data from protocols (2) and (3) in both light and in darkness have been pooled for this analysis. Mathematically, FR^CCW(α) and FR^CW(α) would be expected to be identical for a cell that responds to orientation (position) relative to gravity (as in Fig. 1; see also Supplementary Fig. 6). In contrast, FR^CCW(α) and FR^CW(α) would be expected to be 180° out of phase for a cell that responds to dG (as in Supplementary Fig. 5 and Supplementary Fig. 6). Based on these properties, we extracted a G tuning curve, T_G(α), and a dG tuning curve, T_dG(α), from the response curves FR^CCW(α) and FR^CW(α). This was performed by building a system of equations, as follows. During CCW rotation, we assumed that the firing rate was the sum of the G and dG tuning curves with an average firing rate, FR₀., i.e.:

$${\text{FR}}^{\text{CCW}}(\mathrm{\alpha })={\text{FR}}_0+{\mathrm{T}}_{\mathrm{G}}(\mathrm{\alpha })+{\mathrm{T}}_{\text{dG}}(\mathrm{\alpha })$$ (eq. 1)

During CW rotation, we assumed that the response to G remained identical, but that the dG response would shift by 180°, i.e.:

$${\text{FR}}^{\text{CW}}(\mathrm{\alpha })={\text{FR}}_0+{\mathrm{T}}_{\mathrm{G}}(\mathrm{\alpha })+{\mathrm{T}}_{\text{dG}}(\mathrm{\alpha }+180°)$$ (eq. 2)

Next, we replaced α by α+180° in eq. 1 and 2 and created two new equations:

$${\text{FR}}^{\text{CCW}}(\mathrm{\alpha }+180°)={\text{FR}}_0+{\mathrm{T}}_{\mathrm{G}}(\mathrm{\alpha }+180°)+{\mathrm{T}}_{\text{dG}}(\mathrm{\alpha }+180°)$$ (eq. 3)

$${\text{FR}}^{\text{CW}}(\mathrm{\alpha }+180°)={\text{FR}}_0+{\mathrm{T}}_{\mathrm{G}}(\mathrm{\alpha }+180°)+{\mathrm{T}}_{\text{dG}}(\mathrm{\alpha })$$ (eq. 4)

Note that T_dG(α+360°) is replaced by T_dG(α) in eq. 4 since α+360° and α are the same point. It can also be shown that the system has a rank of 3 and is therefore overdetermined. The unknown variables T_G(α) and T_dG(α), which represent the variations of the cell’s firing rate around the average rate FR₀, can be reconstructed from these equations at each point α.

Cell classification

We assessed how much G and dG contribute to a cell’s firing rate by computing partial correlation coefficients¹. Cells were classified as either G-tuned or dG-tuned based upon whether R²_G|dG or R²_dG|G was significantly higher than the other using a bootstrap analysis^2,3, or as G+dG cells if neither was significantly higher. Each bootstrap sample was produced by drawing n cycles with replacement from the cell’s dataset (consisting of n rotation cycles and including CW and CCW rotations) and re-computing T_G(α), T_dG(α), R²_G|dG and R²_dG|G. We generated 1000 bootstrap samples and classified the cell as either G or dG tuned depending upon whether R²_G|dG or R²_dG|G was higher in 95% of the samples. The proof of concept analysis is shown in Supplementary Fig. 6f).

2D tuning curves

Two-dimensional tuning curves, U_G and U_dG, were reconstructed based on neuronal responses during yaw rotation at θ = 0°, 5°, 15°, 30° and 45° tilt angles (Protocol 5). Because data were collected in this restricted range of tilt angle, we didn’t attempt to fit Gaussian curves to the cell’s firing. Instead, we extracted the G and dG curves, as in the previous section, as well as the average firing rate FR₀(θ) at each tilt angle θ. Note that, in the 2D analysis, tuning curves T_G(θ,α) and T_dG(θ,α) were a function of both α and θ. Values at intermediate tilt angles of θ, were linearly interpolated. Both T_G(θ,α) and T_dG(θ,α) were set to zero at 0° tilt. Cells were classified as G-tuned or dG-tuned by computing R²_G|dG and R²_dG|G as described above, then summing them across each tilt angle. The 2D tuning function was expressed in polar coordinates (as a function of θ and α) or in Cartesian coordinates, G_X/dG_X and G_Y/dG_Y, and smoothed using a 1 m/s² (for G tuning) or 0.5 m/s³ (for dG tuning) width 2D window filter. The maximum value of the tuning curves defined the cell’s two-dimensional preferred direction (PD), which was capped at θ_o = 40° (i.e. 5° lower than the largest sampled tilt angle, after which we considered that the preferred angle could not be determined accurately).

Note that our approach allows separation of the G- and dG-tuning curves, T_G(θ,α) and T_dG(θ,α), for each tilt angle θ. These curves represent variations of the firing around the average value FR₀(θ), which varies as a function of θ. We assumed that the variations of FR₀(θ) are attributable to G and dG tuning in G- and dG-tuned cells respectively. Based on this assumption, the reconstructed 2D tuning curves of G- and dG-tuned cells were T_G(θ,α)+FR₀(θ) and T_dG(θ,α)+FR₀(θ), respectively. However, we could not make a similar assumption for G+dG cells, and therefore we didn’t reconstruct the 2D tuning of G+dG cells (Fig. 3c).

Comparison of the responses to yaw and pitch/roll rotations

In order to compare responses to yaw rotations around a tilted axis (protocols 2–3) and to pitch/roll tilt (protocol 4), a linear model (FR = k_x.G_x + k_y.G_y + k₀) was fitted to neuronal firing rate. Based on this model, the gravity gain and PD are (k_x² + k_y²)^1/2 and atan(k_y, k_x). The model was fitted independently to neuronal responses during yaw and pitch/roll, and the resulting response gains and PD were compared (Supplementary Fig. 3c,d). The same approach, where G_x and G_y were replaced by dG_x and dG_y, was used to compare the dG tuning during yaw and pitch/roll rotations (Supplementary Fig. 3e,f).

Although neuronal responses generally formed a hill of activity in the G_X/G_Y or dG_X/dG_Y plane, the linear model was used only as an approximation of the response at a given tilt angle. Because the same tilt angle (30°) was used in protocols (2–3) and (4), the projection of the gravity vector in the X–Y plane peaked at the same value of 0.5 G. This made the linear model well suited to compare G tuning in both protocols (Supplementary Fig. 3c,d). In contrast, the derivative of gravity had a magnitude of 0.25 G/s during protocol (2–3) and 0.5 G/s during protocol (4). Therefore, the comparison of the dG tuning was less accurate (Supplementary Fig. 3e,f).

Topology of tilt orientation

Whereas for small tilt angles, we have approximated the 2D space of tilts using a polar plot (Fig. 3b,c and Supplementary Fig. 1d, 8), in general it adopts a spherical geometry. Intuitively, it is so because 180° tilt in any direction (NU, ND, etc) brings the head in the same orientation (upside-down). In other words, all points at 180° tilt have to be the same, and this is archived by folding the plot into a sphere.