Abstract
Kohn–Sham density functional theory has been tremendously successful in chemistry and physics. Yet, it is unable to describe the energy degeneracy of spin-multiplet components with any approximate functional. This work features two contributions. (1) We present a multistate density functional theory (MSDFT) to represent spinmultiplet components and to determine multiplet energies. MSDFT is a hybrid approach, taking advantage of both wave function theory and density functional theory. Thus, the wave functions, electron densities and energy density-functionals for ground and excited states and for different components are treated on the same footing. The method is illustrated on valence excitations of atoms and molecules. (2) Importantly, a key result is that for cases in which the high-spin components can be determined separately by Kohn–Sham density functional theory, the transition density functional in MSDFT (which describes electronic coupling) can be defined rigorously. The numerical results may be explored to design and optimize transition density functionals for configuration coupling in multiconfigurational DFT.
Graphical abstract
Kohn–Sham density functional theory (KS-DFT) and time-dependent density functional theory (TDDFT) are widely used to study the structures and properties of ground and excited states of atoms, molecules and condensed-phase systems.1 In principle, in the absence of an external magnetic field, the ground-state energy of a many-electron system, irrespective of its degeneracy, is solely determined by its exact charge density, ρ.2 However, KS-DFT,3 on the basis of a single Slater determinant, is incapable of describing the zero-field degeneracy of spin-multiplet components, ultimately limiting its application to modeling low-spin states in transition metal chemistry, bond dissociation and photochemistry.4 For example, whereas the high-spin components of a triplet diradical can be adequately modeled by KS-DFT, the Ms = 0 component is of two-configurational character, which needs to be treated by multiconfigurational approaches beyond the Kohn–Sham density functional approximation.5 For the open-shell singlet state, spin-polarized DFT is typically used,6 in which the approximate exchange-correlation functional is dependent on both the spin-up (ρα ) and spin-down (ρβ) densities. In this case, the single determinant representation of the singlet state is spin-contaminated, and a weighted broken-symmetry scheme is often used to estimate the singlet–triplet energy splitting.7 The latter approach only works well for simple situations.8 Analogously, excited states of open-shell systems from unrestricted TDDFT can be heavily spin-contaminated, and spin-adapted (SA) TDDFT approaches9–11 should be used to correctly yield excitation energies.12,13 Therefore, there is urgency and it is significant to develop DFT-based methods to overcome these difficulties.
In this Letter, we first describe a multistate density functional theory (MSDFT)14–16 for representing spin-multiplet components and for determining high and low-spin energy gaps of open-shell systems. Then, we show that, for spin-multiplet systems examined in this work, the transition density functional in MSDFT, characterizing the electronic coupling of spin-localized configurations, can be rigorously defined for a given density functional approximation.
In wave function theory (WFT), there is a well-established, systematic route to treat the electronic structure of open-shell systems with inclusion of both static and dynamic correlations. In DFT, multiconfigurational approaches have been explored,5,14–23 but they have yet gained widespread applications. A most effective method for predicting singlet–triplet splitting, both in WFT and DFT, is the spin-flip (SF) method,24–27 which describes both closed and open-shell singlet states by electronic excitation with an α → β spin inversion, starting from a high-spin reference state (e.g., the triplet state). However, the SF approach does not deal with the general question of multiplet degeneracy. For a given spin-multiplet component Ms, the density variables ρα and ρβ are dependent on the projection of the total spin S with a spin density of QMS = {MS/S}QS, where QS is that of the highest component. Although the ground-state energy depends only on the total density that is identical for all components, an Ms-dependent functional is currently not available in the framework of KS-DFT. The general approach to this problem is to transform the spin-dependent densities into spin-independent variables. This was first described by using the Ms independent on-top pair density (along with ρ) as the DFT input instead of the spin polarization,5 and an alternative transformation of the total density and the density of effectively unpaired electrons has been made to replace ρα and ρβ.28 It is important to note that the first method employs a multiconfiguration self-consistent field (MCSCF) reference wave function, such as the complete-active-space self-consistent field (CASSCF), to yield the on-top pair density, whereas single determinants that differ only in spin orientations of unpaired electrons are used in the latter case to model their energy degeneracy. As in standard KS-DFT, the determinant to yield the transformed densities does not model the correct symmetry and corresponds to mixed pure spin states.28
Multistate density functional theory (MSDFT)14,16 is a hybrid approach that combines advantages of both WFT and DFT, and it belongs to the “dynamic-then-static” (DTS) ansatz for treating electron correlation.29,30 There are two computational steps: (1) the construction of an active space consisting of Np states {ΨA; A = 1, …, Np}, in which dynamic correlation is first modeled into each constituent configuration, and (2) diagonalization of the configuration interaction (CI) Hamiltonian or MCSCF optimization of the wave function to include static correlation. In other words, DFT is used as an effective Hamiltonian to define the Np electronic configurations in the active (primary) space, which, by construction, includes dynamic correlation in the first place. Then, WFT is employed to yield the wave functions and energies of the adiabatic states, especially for systems with strong static correlation caused by near degeneracies of the ground and low-lying excited states. Other approaches with similar spirit include multireference CI based on Kohn–Sham orbitals (DFT/MRCI)19 and spin-restricted ensemble DFT.18,31
In MSDFT,16 the wave function ΦI, electron density ρI, and energy density-functional for the adiabatic ground state (I = 0) and excited states (I < Np) are given as follows
| (1) |
| (2) |
| (3) |
where aAI is a configuration coefficient for state I, satisfying the normalization condition with SAB being the overlap between determinants ΨA and ΨB. The electron density of configuration A (A = B), and the transition density ρAB(x) between basis configurations A and B are expanded over a set of m atomic orbital basis functions {χμ(x), μ = 1, …, m}:
| (4) |
where x specifies the spatial (r) and spin (σ) coordinates, and DAB is the density matrix defined by two (in general) nonorthogonal determinants ΨA and ΨB.14,32–34 , which is the diagonal matrix element of the Hamiltonian, is the KS-DFT energy for state ΨA, and ETDF[ρAB(r)] is the transition density functional that defines the electronic coupling between ΨA and ΨB.
The superscript KS in eq 3 emphasizes that MSDFT is built up on KS-DFT and makes use of the wide range of exchange-correlation functionals that have been developed, such as local density approximation (LDA), generalized gradient approximation (GGA) and hybrid functionals. The superscript TDF specifies a new class of correlation functionals with the transition density from multiconfigurational methods as input. We note that ρAB satisfies the symmetry, rank, and generalized idempotency conditions,14 though it can be nonpositive or even complex (for further details, see ref 16).
First, eqs 1 through 3 represent a departure from conventional KS-DFT, in that there is a multiconfigurational wave function for each adiabatic state in MSDFT, which defines the corresponding total electron density as a sum of the weighted KS densities and transition densities. The latter emphasizes the importance of configuration coupling, which is lacking in ensemble density functional theory.35 Furthermore, the electronic coupling can be used to estimate the transfer integral needed to compute the rate of electron transfer and excited energy transfer processes.15 Note that the energy density-functional in MSDFT does not explicitly use the total electron density as an input for an exchange-correlation functional, a fundamental difference from other multiconfigurational density functional approaches.23 As discussed in ref 16., when Np = 1, MSDFT reduces to the conventional KS-DFT, and when Np = Nf, the full configurational space, MSDFT is equivalent to full CI. In approaching the latter limit, a second-order perturbation-based scaling can be made to convert the diagonal DFT energies into pure determinant energies.16 Thus, MSDFT is a hybrid WFT and DFT, bridging the two branches of electronic structure theory for molecular systems.
Second, the wave function (eq 1) and energy density-functional (eq 3) can be obtained either with the orbitals held fixed for each configuration, involving only one diagonalization of the Hamiltonian (which is used in this study), or by variational optimization of both the configurational and orbital coefficients of all states as in an MCSCF calculation, such as CASSCF. As shown previously, MSDFT provides a natural approach to define electronic diabatic states directly, called diabatic at construction (DAC),36 for nonadiabatic processes. In this regard, the basis configurations, {ΨA; A = 1, …, Np}, used in the former approach are called the variational diabatic configurations (VDC), and in the latter, the consistent diabatic configurations (CDC).37
Third, the introduction of transition densities, which is natural in a multiconfigurational approach, and of transition density functional ETDF[ρAB (r)], which is beyond the Kohn–Sham approximation, represent the key concept of MSDFT. A rigorous definition of ETDF can be made for certain special situations that are examined here in association with a given, approximate exchange-correlation functional developed in KS-DFT. This is the key result of this work (below).
The transition density functional (TDF), representing the electronic coupling between configurations ΨA and ΨB, includes two components, the contribution identical to that in standard WFT, 〈ΨA|H|ΨB〉, and a dynamic correlation functional, , involving the external space:16
| (5) |
where H is the electronic Hamiltonian. The first term in eq 5 is the electronic coupling between, in general, two nonorthogonal determinant configurations,32 including correlation within the active space, which has been used in the MOVB (mixed molecular orbital and valence bond) approach.33,34 An approximation to resolve double counting of electron correlation in the active space was given in ref 16, and an alternative approach has been suggested by Savin and co-workers.38 Since the number of configurations in this study is small, and mostly degenerate, such a static correlation is not included in KS-DFT, which captures dynamic effects of the external space in the present systems. The second term in eq 5 is a transition density contribution, representing dynamic correlation not included in the first term.16
As noted above, there is no correspondence in KS-DFT for , and approximations such as overlap or 〈ΨA|H|ΨB〉 weighted correlation energies have been used previously with encouraging results.14,15,39,40 Grimme proposed to scale 〈ΨA|H|ΨB〉 by an exponential function to approximate HAB.19 Importantly, the multistate density functional (eq 3) needed for determining the energy of a low-spin component can be obtained rigorously by making use of the energy degeneracy condition of a given (high) spin multiplet, an idea that has been explored.41,42 This is straightforwardly illustrated by considering the Ms = 0 component of the ground state of carbon, which is a triplet 3P state.
Here, both the Ms = 0 component of the 3P ground state (denoting the pure spin state that is both eigenfunction of Ŝ2 and of Ŝ z by |S,Ms〉, i.e., |1,0〉) and the first, singlet 1D excited state (|0,0〉) of carbon result from spin-coupling interactions of the determinants and , where the superscript C indicates carbon atom, c specifies all doubly occupied core orbitals (which will be omitted below throughout for simplicity) and the bar denotes an electron withβ spin in a valence orbital. These two determinant configurations fully define the active space (Np = 2 in eq 1) for the spin-multiplet states |1,0〉 and |0,0〉. In general, the dimension of eq 1 is the number of spin components in consideration. For C, as well as for O, there are three spin-coupled pairs, whose combinations yield three low-spin components of the 3P term, and three of the five components of the 1D state (the other two come from coupling among the three doubly occupied, closed-shell p-orbitals). Diagonalization of the 2 × 2 Hamiltonian matrix yields their wave functions with in-phase (positive) and out-phase (negative) combinations, respectively, and their energies.
| (6a) |
| (6b) |
For a given exchange-correlation functional used to compute the diagonal matrix terms, and , where and are used as Kohn–Sham determinants for the respective configurations, we make use of the condition that the energies of the high spin component from a single-determinant restricted open-shell KS-DFT calculation, , and of the low spin component from MSDFT using are identical in the absence of an external magnetic field:41–43
| (7) |
Then, the correlation energy of the TDF can be uniquely determined by
| (8) |
where is the energy difference between KS-DFT and Hartree–Fock theory using the Kohn– Sham determinant ΨA. Note that for the two single-determinants of mixed states. The correlation energy defined in eq 8 for the transition density functional also leads to the energy for the 1D singlet state (eq 6b). Together, they yield the singlet–triplet (S-T) energy splitting ΔEST = ES (|0,0〉)−ET (|1,0〉) (of course, we have ET (|1,1〉) = ET (|1,0〉)).
Equation 8 is generally applicable to molecular diradicals for determining ΔEST. One simply replaces the atomic orbitals by the corresponding MOs, and this is used in the AH2 isovalent electron cases and ortho, meta, and para-didehydrotoluene (DHT), two systems that have been extensively used for validation of theory.25,27,44
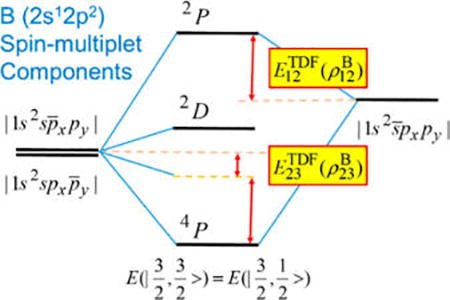
For interactions involving nondegenerate orbitals, the TDFs can be similarly determined. This is illustrated by the low-energy states of boron (Figure 1). In this case, transition from the doublet ground-state (2P) to the 2s12p2 configuration yields its lowest excited state, a quartet (4P) state, and three doublets, 2D, 2S, and 2P, in order of increasing energy (2P is above the ionization limit). The component of the 4P state, , of single-determinant character, can be conveniently approximated by RO-KS-DFT, whereas the active space that defines the component and the 2D and 2P multiplets consists of three low-spin determinant configurations: , , and . The wave function for the MS = 1/2 component of the quartet state from MSDFT is given by
| (9) |
Then, the condition
after solving the secular equation leads to the TDF correlation energies as follows:
| (10) |
| (11) |
where the numbers in the subscript specify the determinant configurations of the basis states that have been defined above. Notice that for B, .
Figure 1.
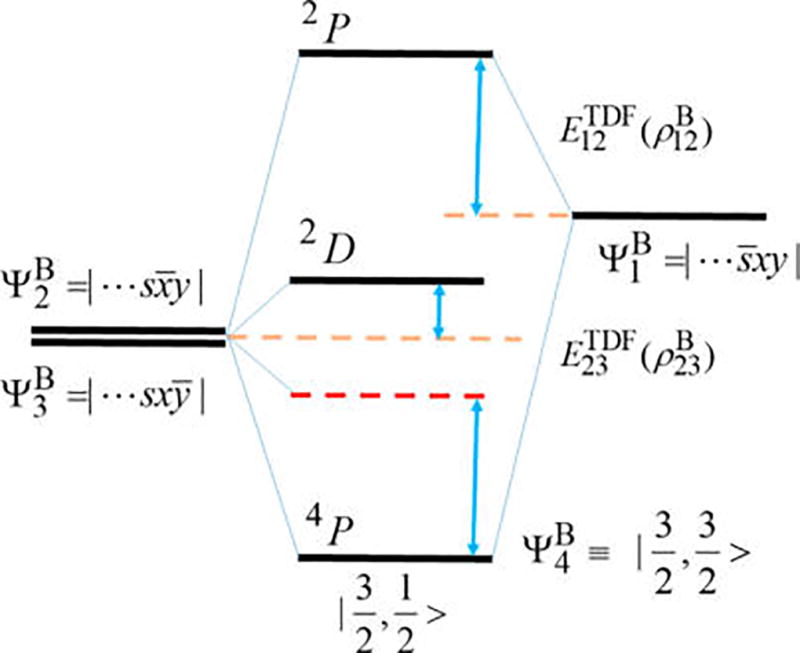
Interaction diagram illustrating electronic coupling among the three determinant configurations for the excited 2s12p2 configuration of boron atom.
In addition to the low-spin component of the 4P state, the TDF couplings given in eqs 10 and 11 also determines the energies of the 2D and 2P states:
| (12a) |
| (12b) |
It is interesting to note that the configuration in fact involves a two-electron transition of the ground state , 2px → 2py and 2s̅ → 2p̅x, not included in conventional TD-DFT. Of course, they are treated properly in SF-TDDFT by double SF45 and SA-TD-DFT approaches.9,12,13
Illustrative examples are presented to show the ability of MSDFT for representing spin multiplet components and for determining energy gaps of high and low spin multiplets. We have selected a series of atomic energy levels of first-row elements. These systems are chosen because there is no ambiguity for comparison with experimental data associated with the geometries and zero-point energies of different adiabatic states of molecules. To further demonstrate its applicability to molecular systems, the energies of low-lying states in the isovalent electron system of CH2, NH2+, SiH2, and PH2+, and of three isomers of didehydrotuluene (DHT) are computed. These compounds exhibit different degrees of diradical character. The hybrid PBE0 and M06-HF functionals are used in the present work, along with the PBEC functional, which, as M06-HF, uses 100% Hartree–Fock exchange. The aug-cc-pVQZ basis set is used for the atoms and AH2 hydrides, and cc-pVTZ for the DHT isomers; these basis functions are sufficiently large, as shown in previous studies for these systems.25,27 The MSDFT calculations are performed using a modified version of GAMESS.46 We have used restricted open-shell (RO) KS-DFT to model the high-spin components, which are adequately represented by single determinant, and their orbitals are used in the low-spin multiconfigurational calculations.
For atomic systems, the orbital basis functions are partitioned into four blocks: three of px, py, and pz symmetry, and the fourth including the rest of the core and valence s electrons. Without sacrificing generality here, we use the real atomic orbitals instead of spherical harmonics with specific magnetic quantum numbers. For the diradical series AH2 (A = C, N, Si, and P), the molecular orbitals (MO) are divided into three blocks, corresponding to pz (perpendicular to the molecular plane), nx (an sp2-type hybrid orbital in the orientation (x) bisecting the two chemical bonds), and the remainder of orbitals (which are doubly occupied MOs). This may be generalized to other open-shell diradical cases such as DHT, of three orbital blocks consisting of two singly occupied MOs and the rest of doubly occupied orbitals. In each case, the orbitals for the Ms = S state are optimized using RO-KS-DFT, and its energy is denoted by E(|S,MS = S〉). These orbitals are then used to construct configurations in the active space for the lower spin components of S, and its lower spin multiplets. However, for the AH2 series, the two closed shell determinants for the ã1A1 and c̃1A1 states, corresponding to the configuration |cnxn̅x| and its double excitation to |cpzp̅z|, are optimized separately—a situation that is different from the SF approaches.
The computed atomic valence-excitation energies for Be through O are listed in Table 1 along with the specific pure spin states indicated by |S,Ms〉 (negative Ms components are omitted). The corresponding linear combinations of determinant configurations are given in the Supporting Information along with energies from unrestricted calculations for open-shell systems. Note that each |S,MS〉 state in Table 1 has been explicitly constructed, and they are shown to emphasize that the energies of multiplet components are exactly degenerate. For each configuration, only the highest spin component is of single-determinant character, while all other states are multiconfigurational. States that are of single-determinant character are determined by RO-KS-DFT. Thus, the results for the high-spin states reflect the accuracy of the exchange-correlation functional used for these cases, i.e., excitation energies. The computed energies for all valence excited states in Table 1 are reasonable in comparison with experiments, with the mean-unsigned-deviations (MUD) being 0.42, 0.48, and 0.53 eV for PBE0, PBEC, and M06-HF density functionals, respectively, without inclusion of the two highly excited states (1S of C and O, 3P of Be, and 2P of B). If one only considers the spin-multiplet energy splittings for C, N, and O, the MUD errors are 0.33, 0.04, and 0.30 eV using PBE0, PBEC, and M06-HF. Not surprisingly, Table 1 shows that the MUD errors are noticeably larger for results with the MOVB method, which does not include dynamic correlation. Nevertheless, the main purpose of this study is to show that MSDFT can be used to treat both high and low-spin states as well as their individual components with the correct symmetry and energy degeneracy exactly.
Table 1.
Experimental and Computed Atomic Excitation Energies (eV) of Beryllium, Boron, Carbon, Nitrogen, and Oxygen Using Multistate Density Functional Theory (MSDFT) and Mixed Molecular Orbital-Valence Bond Theory (MOVB)a
| configuration | term | |S,Ms) | expb | MOVB | PBE0 | PBEC | M06HF |
|---|---|---|---|---|---|---|---|
| Be (2s22p0) | 1S | |0,0〉 | 0 | 0 | 0 | 0 | 0 |
| 2s12p1 | 3P | |1,1〉, |1,0〉 | 2.72 | 1.62 | 2.29 | 2.21 | 3.06 |
| 1P | |0,0〉 | 5.28 | 5.90 | 4.59 | 6.07 | 4.54 | |
| 2s02p2 | 1D | |0,0〉 | 7.05 | 6.44 | 6.22 | 7.08 | 7.12 |
| 3P | |1,1〉, 1,0〉 | 7.40 | 7.38 | 6.41 | 7.54 | 7.36 | |
| B (2s22p1) | 2P | |1/2,1/2〉 | 0 | 0 | 0 | 0 | 0 |
| 2s12p2 | 4P | |3/2,3/2〉, 3/2,1/2〉 | 3.55 | 2.08 | 3.18 | 2.96 | 4.27 |
| 2D | |1/2,1/2〉 | 5.93 | 6.08 | 5.59 | 6.14 | 6.43 | |
| 2S | |1/2,1/2〉 | 7.88 | 7.39 | 7.00 | 7.62 | 6.95 | |
| 2P | |1/2,1/2〉 | 8.99 | 10.14 | 7.75 | 9.83 | 7.43 | |
| C (2s22p2) | 3P | |1,1〉, 1,0〉 | 0 | 0 | 0 | 0 | 0 |
| 1D | |0,0〉 | 1.26 | 1.58 | 1.01 | 1.31 | 1.65 | |
| 1S | |0,0〉 | 2.68 | 3.18 | 3.69 | 3.60 | 1.21 | |
| 2s12p3 | 5S | |2,2〉, 2,1〉 | 4.19 | 2.43 | 3.96 | 3.60 | 5.34 |
| 3D | |1,1〉 | 7.95 | 8.13 | 7.68 | 8.27 | 8.38 | |
| 3P | |1,1〉 | 9.33 | 9.76 | 9.30 | 10.12 | 9.95 | |
| N (2s22p3) | 4S | |3/2,3/2〉, 3/2,1/2〉 | 0 | 0 | 0 | 0 | 0 |
| 2D | |1/2,1/2〉 | 2.38 | 2.89 | 1.96 | 2.45 | 2.75 | |
| 2P | |1/2,1/2〉 | 3.58 | 4.82 | 4.35 | 4.60 | 3.36 | |
| 2s12p4 | 4P | |3/2,3/2〉, 3/2,1/2〉 | 10.33 | 10.78 | 10.58 | 11.27 | NCc |
| O (2s22p4) | 3P | |1,1〉, 1,0〉 | 0 | 0 | 0 | 0 | 0 |
| 1D | |0,0〉 | 1.97 | 2.21 | 1.92 | 2.51 | 2.41 | |
| 1S | |0,0〉 | 4.19 | 5.56 | 5.00 | 4.63 | 2.36 | |
| MUD | 0.64 | 0.42 | 0.48 | 0.53 |
The pure spin state is indicated by |S,MS) (the combination of determinant configurations is given in the Supporting information). The hybrid functional PBE0 and PBEC with 25% and 100% Hartree-Fock exchange as well as M06-HF, also containing 100% Hartree-Fock exchange, are used. The aug-cc-pVQZ basis is used in all computations. MUD: mean unsigned deviations from experiment.
Reference 47.
NC: RO-SCF not converged.
The isovalent series of CH2, NH2+, SiH2, and PH2+ molecules have been extensively studied experimentally and computationally, and they are popular choices for testing theory. The qualitative picture of their electronic structures has been lucidly summarized by Slipchenko and Krylov.44 In addition to the open-shell triplet and singlet states, resulting from configuration interactions of two singly occupied 3a1 and 1b1 (5a1 and 2b1 for the heavier hydrides) orbitals (simply denoted by pz and nx, where the latter is an spn hybrid orbital), there are two closed-shell singlet states. All three singlet states as well as the MS = 0 component of the triplet state are muticonfigurational.
The configuration space for the hydride species in MSDFT calculations includes four determinant configurations, , and (as usual, we have omitted core orbitals in the notation), and their linear combinations yield the four low-spin adiabatic states that are eigenfunctions of Ŝ2 and Ŝz. The TDF for the coupling between the two open-shell determinants was determined exactly for a given exchange-correlation functional. However, an exact expression for the coupling between two doubly occupied configurations ( and ) is not available. Here, we have used a weighted correlation energy to approximate the TDF dynamic correlation:
| (13) |
Computed excitation energies for the hydride series are given in Table 2 along with results from the SF approaches.27 The MSDFT results are compared with SF-CCSD(T) energies, which has a mean error of about 0.036 eV relative to the 7 available experimental data that have been corrected for zero-point vibrational energies.27 An MUD error of 0.136 eV was found for MSDFT over all 12 excitation energies, which is just slightly greater than that from noncollinear (NC) SF-TDDFT, both using the PBE0 functional. Of the four S-T energy splittings, the relative errors are 0.045 and 0.057 eV for MSDFT and SF-TDDFT, respectively, with respect to CCSD(T) values. The PBE0 functional performs exceptionally well for S-T splitting in the NC-SF-TDDFT calculations, but other functionals show large fluctuations and even the opposite sign.27 This behavior was attributed to using the MS = 0 component for the triplet-state, rather than the high-spin reference itself, which has a small amount of spin contamination. In MSDFT, however, we use restricted open-shell orbitals, which raises the energy for the triplet state by 0.07 eV (1.65 kcal/mol), which contributes to errors in the calculated S-T energies. For the two closed-shell singlet states (1A1), the resonance stabilization energy (their coupling) due to dynamic correlation (eq 13) is relatively small (0.02 eV) compared to that of the determinant contribution (0.23 eV) in eq 5.
Table 2.
Computed Adiabatic Excitation Energies (eV) of CH2, NH2+, SiH2, and PH2+ Moleculesa
| hydride | state | SF-CCSD(T)b | NC-SF-DFTb | MSDFT | expt.c |
|---|---|---|---|---|---|
| CH2 (X̃3B1) | ã1A1 | 0.420 | 0.507 | 0.431 | 0.39 |
| b̃1B1 | 1.410 | 1.410 | 1.285 | 1.425 | |
| c̃1A1 | 2.530 | 2.820 | 2.749 | ||
| NH2+ (X̃3B1) | ã1A1 | 1.253 | 1.336 | 1.206 | 1.306 |
| b̃1B1 | 1.865 | 1.856 | 1.609 | ||
| c̃1A1 (c̃1 ) | 3.318 | 3.701 | 3.576 | ||
| SiH2 (X̃1A1) | ã3B1 | 0.892 | 0.944 | 0.854 | 0.91 |
| Ã1B1 | 1.937 | 1.918 | 2.033 | 1.928 | |
| B̃1A1 | 3.365 | 3.507 | 3.633 | ||
| PH2+ (X̃1A1) | ã3B1 | 0.794 | 0.800 | 0.712 | 0.75 |
| Ã1B1 | 1.993 | 1.943 | 2.008 | 1.92 | |
| B̃1A1 | 3.640 | 3.784 | 3.853 | ||
| MUD (ΔEST) | (0.036) | 0.057 | 0.045 | ||
| MUD (total) | (0.034) | 0.105 | 0.136 |
Spin-flip (SF) results are taken from Ref. 27 for comparison. The PBE0 exchange-correlation functional is used both in SF and in multistate (MS) DFT, and the aug-cc-pVQZ basis set is used in all calculations. Total energies are −39.11577, −55.42594, −290.50214, and −342.03056, for CH2, NH2+, SiH2, and PH2+, respectively, using MSDFT(4)/aug-cc-pVQZ, using geometries optimized by FCI/TZ3P for CH2,48 and CISD/TZ3P(2d,2f) in other cases. 49−51
Reference 27.
Values are taken from ref 27.
Figure 2 shows the adiabatic and “vertical” excitation energies of CH2 at the optimal geometries of the four states. Clearly seen is that the energy from MSDFT for each state is in its minimum at the optimal geometry. The trends can be rationalized by considering the Walsh diagrams.44 As the bending angle between the AH bonds reaches 180°, the closed-shell (ã1A1) and the open-shell (b̃1B1) singlet states become degenerate, denoted by 1Δg. At 170°, the optimal geometry of the c̃1A1 state, the energy difference between ã1A1 and b̃1B1 states is 0.05 eV from MSDFT (Figure 2).
Figure 2.
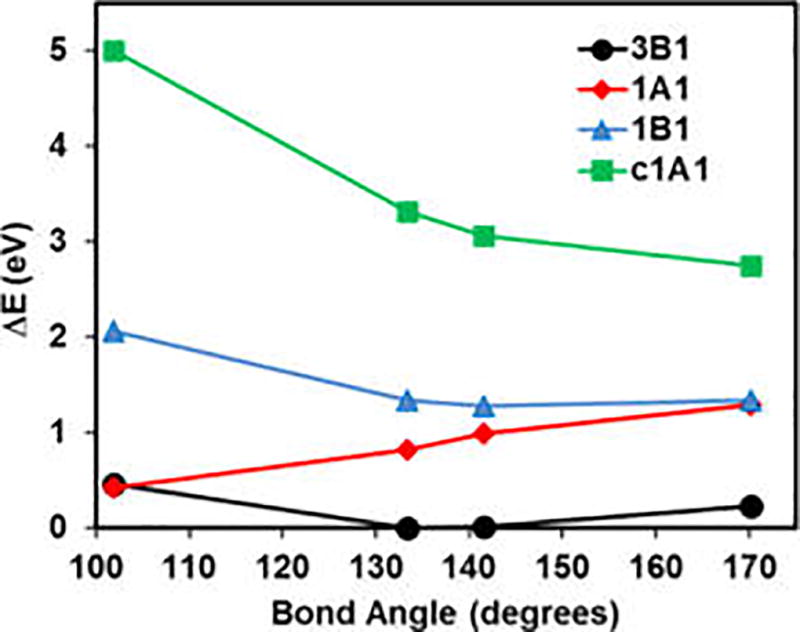
Computed adiabatic and vertical excitation energies of CH2 at the four adiabatic geometries. The PBE0 exchange-correlation functional is used in multistate density functional theory along with the aug-cc-pVQZ basis set. Geometries were optimized using FCI/TZ2P from ref 47.
Didehydrotoluene (Scheme 1) has three isomeric structures (α-2, α-3, and α-4-DHT), which are examples of σ−π diradicals. Unlike the AH2 dihydride systems above, the closed-shell configurations correspond to π and σ localized zwitterions that do not have significant interactions and are much higher in energy (ca. 1.5 and 3.0 eV above the ground state, respectively). Therefore, the S-T energy gap is determined by spin coupling between the αβ and βα localized configurations, whose TDF is fully determined by the Mz = 0 degeneracy with the |1,1〉 component. MSDFT results are listed in Table 3 along with the SF benchmarks reported by Krylov and co-workers.27 The ground state of ortho- and para-DHT are triplet, whereas the singlet state was predicted to be slightly lower in energy than the triplet state in the meta-DHT isomer from the SF approaches.27 Overall, the S-T gaps are well described by MSDFT; however, the small stabilization of the singlet of α-3-DHT was not reproduced. Nevertheless, the trend of relatively smaller energy gap than the other two isomers is obtained. As noted by Bernard et al.,27 the seemingly good agreement between SF-TDDFT/PBE0 with the CCSD-(T) results was in fact an artifact of spin contamination, which is not so lucky with other functionals. Of course, the results from MSDFT are pure spin states. Table 3 also lists the results from MOVB, which follows an identical procedure as MSDFT except that dynamic correlation is not included. Even for small S-T energy gaps of these σ−π diradicals, dynamic correlation still makes noticeable contributions.
Scheme 1.
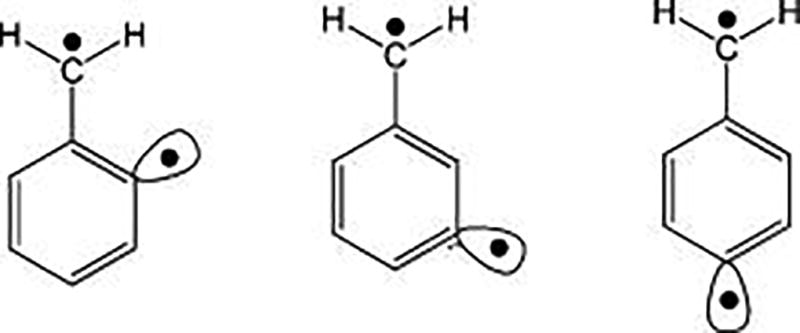
Structures of α-2, α-3, and α-4-Didehydrotuluene (DHT)
Table 3.
Computed Singlet-Triplet Energy Gaps (eV) for α-2, α-3, and α-2-Didehydrotoluene (DHT) Using Multistate Density Functional Theory (MSDFT) and Mixed Molecular Orbital and Valence Bond (MOVB) Method along with Results from Spin Flip (SF) Approachesa
| ground state | singlet | MSDFT | MOVB | NC-SF- TDAb |
SF- CCSD(T)b |
|---|---|---|---|---|---|
| α-2-DHT (3B2) | 1A1 | 0.172 | 0.144 | 0.230 | 0.247 |
| α-3-DHT (3B2) | 1A1 | 0.024 | 0.031 | −0.025 | −0.066 |
| α-4-DHT (3B2) | 1A1 | 0.175 | 0.098 | 0.248 | 0.250 |
PBE0 is used in DFT methods, and cc-pVTZ basis is used in all calculations. The total energies for the 2, 3, and 4 diradical isomers are, respectively, −269.98684, −269.98639, −269.98630 au from MSDFT/PBE0/cc-pVTZ, and −268.55012, −268.54904, and −268.54927 au from MOVB/cc-pVTZ.
Reference 27.
Note that the computational accuracy of MSDFT on multiplet splitting is dictated by the specific functional used since the spin-coupling given by the transition density functional is uniquely determined for a given KS functional used to characterize the determinant states. In comparison with SF-TDDFT, the states from MSDFT are pure spin states, whereas the SF approach does not guarantee energy degeneracy of spin-multiplet components. This difference contributes to the difference in computational results in comparison with experiments or high-level reference data. Another difference is the treatment of configuration coupling in that the TDF correlation energy in MSDFT is different from that in the NC-SF-TDDFT, whereas it is not present is conventional SF-TDDFT.
In summary, the multistate density functional theory (MSDFT) is extended to describe spin multiplets and excitation energies of atoms and molecules. In MSDFT, spin multiplet components are expressed as eigenfunctions of both Ŝ2 and Ŝz operators, and their energy degeneracy in the absence of an external magnetic field is exactly reproduced. MSDFT is a hybrid approach, taking advantage of both wave function theory and density functional theory. Consequently, the wave functions, electron densities and energy functionals for ground and excited states and for different spin multiplet components are treated on the same footing. Valence excitation energies of first row atoms, Be through O, and the isovalent hydrides, including CH2, NH2+, SiH2, and PH2+ molecules, have been evaluated using MSDFT along with the PBE0, PBEC and M06-HF density functionals. Energetic results are found to be in accord with experiments, and of comparable or better accuracy in comparison with SF-TDDFT for singlet–triplet energy splittings. Of the atomic states considered, the mean average deviation is about 0.4 eV from experiments, whereas it is 0.1 eV for the hydride states relative to the SF-CCSD(T) results. Importantly, a key result of this study is that for cases in which the high-spin component can be determined separately by KS-DFT, with a given exchange-correlation functional (LDA, GGA or hybrid), the associated transition density functional in the multistate approach, representing configuration coupling of spin-localized states, can be rigorously determined. This is possible by enforcing the energy degeneracy condition of spin multiplet components. Therefore, even though the exact functional dependency (ETDF[ρAB]) on the transition density ρAB is not fully known, its value that defines the energy of the low-spin components can be evaluated exactly based on the exchange-correlation energies of the relevant KS determinants. Therefore, the numerical results may be explored to design and optimize transition density functionals for configuration coupling in multiconfigurational DFT.
Supplementary Material
Acknowledgments
This work has been generously supported by the Ministry of Science and Technology of China (Grant number 2017YFB0203400), and the National Institutes of Health (GM46736).
Footnotes
ASSOCIATED CONTENT
- Summary of the relationships between the transition density functional and Kohn–Sham density functional correlation energies for spin multiplet components (PDF)
The authors declare no competing financial interest.
References
- 1.Becke AD. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014;140:18A301. doi: 10.1063/1.4869598. [DOI] [PubMed] [Google Scholar]
- 2.Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964;136:B864. [Google Scholar]
- 3.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:A1133. [Google Scholar]
- 4.Cohen AJ, Mori-Sanchez P, Yang W. Insights into Current Limitations of Density Functional Theory. Science. 2008;321:792–794. doi: 10.1126/science.1158722. [DOI] [PubMed] [Google Scholar]
- 5.Becke AD, Savin A, Stoll H. Extension of the Local-Spin-Density Exchange-Correlation Approximation to Multiplet States. Theor. Chim. Acta. 1995;91:147–156. [Google Scholar]
- 6.von Barth U, Hedin L. A local exchange-correlation potential or the spin polarized case: I. J. Phys. C: Solid State Phys. 1972;5:1629–1642. [Google Scholar]
- 7.Noodleman L. Valence Bond Description of Anti-Ferromagnetic Coupling in Transition-Metal Dimers. J. Chem. Phys. 1981;74:5737–5743. [Google Scholar]
- 8.Luo SJ, Averkiev B, Yang KR, Xu XF, Truhlar DG. Density Functional Theory of Open-Shell Systems. The 3d-Series Transition-Metal Atoms and Their Cations. J. Chem. Theory Comput. 2014;10:102–121. doi: 10.1021/ct400712k. [DOI] [PubMed] [Google Scholar]
- 9.Li ZD, Liu WJ. Spin-adapted open-shell random phase approximation and time-dependent density functional theory. I. Theory. J. Chem. Phys. 2010;133:064106. doi: 10.1063/1.3463799. [DOI] [PubMed] [Google Scholar]
- 10.Li ZD, Liu WJ, Zhang Y, Suo BB. Spin-adapted open-shell time-dependent density functional theory. II. Theory and pilot application. J. Chem. Phys. 2011;134:134101. doi: 10.1063/1.3573374. [DOI] [PubMed] [Google Scholar]
- 11.Li Z, Liu W. Spin-adapted open-shell time-dependent density functional theory: III. An even better and simpler formulation. J. Chem. Phys. 2011;135:194106. doi: 10.1063/1.3660688. [DOI] [PubMed] [Google Scholar]
- 12.Li ZD, Liu WJ. Critical Assessment of Time-Dependent Density Functional Theory for Excited States of Open-Shell Systems: II. Doublet-Quartet Transitions. J. Chem. Theory Comput. 2016;12:2517–2527. doi: 10.1021/acs.jctc.5b01219. [DOI] [PubMed] [Google Scholar]
- 13.Li ZD, Liu WJ. Critical Assessment of TD-DFT for Excited States of Open-Shell Systems: I. Doublet-Doublet Transitions. J. Chem. Theory Comput. 2016;12:238–260. doi: 10.1021/acs.jctc.5b01158. [DOI] [PubMed] [Google Scholar]
- 14.Cembran A, Song L, Mo Y, Gao J. Block-localized density functional theory (BLDFT), diabatic coupling, and its use in valence bond theory for representing reactive potential energy surfaces. J. Chem. Theory Comput. 2009;5:2702–2716. doi: 10.1021/ct9002898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ren HS, Provorse MR, Bao P, Qu ZX, Gao JL. Multistate Density Functional Theory for Effective Diabatic Electronic Coupling. J. Phys. Chem. Lett. 2016;7:2286–2293. doi: 10.1021/acs.jpclett.6b00915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gao J, Grofe A, Ren H, Bao P. Beyond Kohn-Sham approximation: Hybrid multistate wave function and density functional theory. J. Phys. Chem. Lett. 2016;7:5143–5149. doi: 10.1021/acs.jpclett.6b02455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nagy A. Exact Ensemble Exchange Potentials for Multiplets. Int. J. Quantum Chem. 1995;56:297–301. [Google Scholar]
- 18.Filatov M, Shaik S. Spin-restricted density functional approach to the open-shell problem. Chem. Phys. Lett. 1998;288:689–697. [Google Scholar]
- 19.Grimme S, Waletzke M. A combination of Kohn-Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 1999;111:5645–5655. [Google Scholar]
- 20.Huix-Rotllant M, Nikiforov A, Thiel W, Filatov M. Description of Conical Intersections with Density Functional Methods. Top. Curr. Chem. 2015;368:445–476. doi: 10.1007/128_2015_631. [DOI] [PubMed] [Google Scholar]
- 21.Grafenstein J, Cremer D. Development of a CAS-DFT method covering non-dynamical and dynamical electron correlation in a balanced way. Mol. Phys. 2005;103:279–308. [Google Scholar]
- 22.Kurzweil Y, Lawler KV, Head-Gordon M. Analysis of multi-configuration density functional theory methods: theory and model application to bond-breaking. Mol. Phys. 2009;107:2103–2110. [Google Scholar]
- 23.Bao JL, Sand A, Gagliardi L, Truhlar DG. Correlated-Participating-Orbitals Pair-Density Functional Method and Application to Multiplet Energy Splittings of Main-Group Divalent Radicals. J. Chem. Theory Comput. 2016;12:4274–4283. doi: 10.1021/acs.jctc.6b00569. [DOI] [PubMed] [Google Scholar]
- 24.Krylov AI. Spin-flip configuration interaction: an electronic structure model that is both variational and size-consistent. Chem. Phys. Lett. 2001;350:522–530. [Google Scholar]
- 25.Shao YH, Head-Gordon M, Krylov AI. The spin-flip approach within time-dependent density functional theory: Theory and applications to diradicals. J. Chem. Phys. 2003;118:4807–4818. [Google Scholar]
- 26.Li ZD, Liu WJ. Theoretical and numerical assessments of spin-flip time-dependent density functional theory. J. Chem. Phys. 2012;136:024107. doi: 10.1063/1.3676736. [DOI] [PubMed] [Google Scholar]
- 27.Bernard YA, Shao YH, Krylov AI. General formulation of spin-flip time-dependent density functional theory using non-collinear kernels: Theory, implementation, and benchmarks. J. Chem. Phys. 2012;136:204103. doi: 10.1063/1.4714499. [DOI] [PubMed] [Google Scholar]
- 28.Staroverov VN, Davidson ER. A density functional method for degenerate spin-multiplet components. Chem. Phys. Lett. 2001;340:142–150. [Google Scholar]
- 29.Liu WJ. Ideas of relativistic quantum chemistry. Mol. Phys. 2010;108:1679–1706. [Google Scholar]
- 30.Liu WJ, Hoffmann MR. iCI: Iterative CI toward Full CI. J. Chem. Theory Comput. 2016;12:1169–1178. doi: 10.1021/acs.jctc.5b01099. [DOI] [PubMed] [Google Scholar]
- 31.Filatov M. Ensemble DFT Approach to Excited States of Strongly Correlated Molecular Systems. Top. Curr. Chem. 2015;368:97–124. doi: 10.1007/128_2015_630. [DOI] [PubMed] [Google Scholar]
- 32.King HF, Stanton RE, Kim H, Wyatt RE, Parr RG. Corresponding orbitals and the nonorthogonality problems in molecular quantum mechanics. J. Chem. Phys. 1967;47:1936. [Google Scholar]
- 33.Mo Y, Gao J. Ab initio QM/MM simulations with a molecular orbital-valence bond (MOVB) method: application to an SN2 reaction in water. J. Comput. Chem. 2000;21:1458–1469. [Google Scholar]
- 34.Mo Y, Gao J. An Ab Initio Molecular Orbital-Valence Bond (MOVB) Method for Simulating Chemical Reactions in Solution. J. Phys. Chem. A. 2000;104:3012–3020. [Google Scholar]
- 35.Mermin ND. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 1965;137:A1441–A1443. [Google Scholar]
- 36.Grofe A, Qu Z, Truhlar DG, Li H, Gao J. Diabatic-At-Construction Method for Diabatic and Adiabatic Ground and Excited States Based on Multistate Density Functional Theory. J. Chem. Theory Comput. 2017;13:1176–1187. doi: 10.1021/acs.jctc.6b01176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Song L, Gao J. On the Construction of Diabatic and Adiabatic Potential Energy Surfaces Based on Ab Initio Valence Bond Theory. J. Phys. Chem. A. 2008;112:1292–12935. doi: 10.1021/jp803050e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Miehlich B, Stoll H, Savin A. A correlation-energy density functional for multideterminantal wavefunctions. Mol. Phys. 1997;91:527–536. [Google Scholar]
- 39.Mo YR, Bao P, Gao JL. Energy decomposition analysis based on a block-localized wavefunction and multistate density functional theory. Phys. Chem. Chem. Phys. 2011;13:6760–6775. doi: 10.1039/c0cp02206c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chan W-L, Berkelbach TC, Provorse MR, Monahan NR, Tritsch JR, Hybertsen MS, Reichman DR, Gao J, Zhu X-Y. The quantum coherent mechanism for singlet fission: Experiment and theory. Acc. Chem. Res. 2013;46:1321–1329. doi: 10.1021/ar300286s. [DOI] [PubMed] [Google Scholar]
- 41.Ziegler T, Rauk A, Baerends EJ. Calculation of Multiplet Energies by Hartree-Fock-Slater Method. Theoretica Chimica Acta. 1977;43:261–271. [Google Scholar]
- 42.Mineva T, Goursot A, Daul C. Atomic multiplet energies from density functional calculations. Chem. Phys. Lett. 2001;350:147–154. [Google Scholar]
- 43.Slater JC. Quantum Theory of Atomic Structure. I McGraw-Hill Book Co., Inc.; New York: 1960. [Google Scholar]
- 44.Slipchenko LV, Krylov AI. Singlet-triplet gaps in diradicals by the spin-flip approach: A benchmark study. J. Chem. Phys. 2002;117:4694–4708. [Google Scholar]
- 45.Casanova D, Slipchenko LV, Krylov AI, Head-Gordon M. Double spin-flip approach within equation-of-motion coupled cluster and configuration interaction formalisms: Theory, implementation, and examples. J. Chem. Phys. 2009;130:044103. doi: 10.1063/1.3066652. [DOI] [PubMed] [Google Scholar]
- 46.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Matsunaga N, Nguyen KA, Su SJ, Windus TL, Dupuis M, Montgomery JS. GAMESS. (11) 1993 [Google Scholar]
- 47.Moore CE. Atomic Energy Levels. National Bureau of Standards; Washington, DC: 1971. NBS Circ. No. 467. [Google Scholar]
- 48.Sherrill CD, Leininger ML, van Huis TJ, Schaefer HF. III Structures and vibrational frequencies in the full configuration interaction limit: Predictions for four electronic states of methylene using a triple-zeta plus double polarization (TZ2P) basis. J. Chem. Phys. 1998;108:1040. [Google Scholar]
- 49.Yamaguchi Y, Van Huis TJ, Sherrill CD, Schaefer HF. III The X̃1A1, ã3B1, ã1B̃1, and B̃1A1 electronic states of SiH2. Theor. Chem. Acc. 1997;97:341–349. [Google Scholar]
- 50.Stephens JC, Yamaguchi Y, Sherrill CD, Schaefer HF. III ~ 3B1, ã 1A1, b̃ 1B1, and c̃ 1 Electronic States of NH2+ J. Phys. Chem. A. 1998;102:3999–4006. [Google Scholar]
- 51.Van Huis TJ, Yamaguchi Y, Sherrill CD, Schaefer HF. III X̃ 1A1, ã 3B1, Ã 1B1, and B̃ 1A1 Electronic States of PH2+ J. Phys. Chem. A. 1997;101:6955–6963. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



