Right ventricular diastolic relaxation in conscious dog models of pressure overload, volume overload, and ischemia

Abstract

Objective

Limitations in clinical understanding of right ventricular relaxation can be attributed to the paucity of information from basic studies in animal models of right ventricular disease. This study examined, in the conscious state, right ventricular relaxation dynamics under normal conditions (n = 15) and in subacute (2–5 weeks) canine models of right ventricular pressure overload (n = 6), volume overload (n = 7), and free wall ischemia (n = 7).

Methods

Right-heart micromanometric measurements were obtained by using multisensor catheters. A new algorithm was developed to obtain representative ensemble averages of hemodynamic waveform data sets. Right ventricular relaxation was analyzed by using an exponential model with 3 parameters: P₀, τ, and P_b. Significant changes versus control values were determined by means of analysis of variance and the Student unpaired t test with Bonferroni’s adjustment.

Results

In the state of pressure overload, right ventricular pressure decay exhibits an increased P₀ (56.2 ± 19.1 vs 13.1 ± 5.1 mm Hg [mean ± SD]) and prolonged τ (57.1 ± 2.8 vs 27.8 ± 3.9 ms); there is also a decreased P_b (− 7.9 ± 1.5 vs 0.28 ± 1.8 mm Hg). The only significant change in volume overload is an increased asymptote, P_b (5.3 ± 2.9 mm Hg). In right ventricular ischemia, prolongation of τ (41.4 ± 13.0 ms) and decreased P_b (− 1.95 ± 1.1 mm Hg) attain high significance.

Conclusions

Distinctive abnormalities in right ventricular relaxation dynamics accompany pressure overload, volume overload, and ischemia and may contribute to clinical right ventricular dysfunction.

Right ventricular (RV) dysfunction is implicated in nearly 20% of all deaths associated with congestive heart failure,^1–4 and the right ventricle plays a crucial role in the cardiopulmonary interactions of many disease states.^1,2 Moreover, RV dysfunction is often the limiting factor for the success of coronary bypass surgery, heart transplantation, or heart-lung transplantation.^5,6

Despite its physiologic and clinical importance, however, little attention has been paid to relaxation abnormalities, specifically those of the right ventricle.^1–4,6 Limitations of our understanding can be attributed to the paucity of information from basic studies of RV relaxation in appropriate animal disease models. The aim of the present study was to study RV relaxation dynamics in subacute animal models of RV pressure overload, RV volume overload, and RV free wall ischemia.

Methods

All animals received humane care in compliance with the “Guide for the Care and Use of Laboratory Animals” prepared by the Institute of Laboratory Animal Resources, National Research Council, and published by the National Academy Press, revised 1996.

Acquisition of Control Data

Lying on its right side, each dog (20–30 kg) was sedated with morphine (0.7 mg/kg); dosage was adjusted so as to sedate the animal while keeping it awake.

A 30-cm, 8F sheath introduced through a jugular cutdown allowed passage of a custom RV catheter (Millar Instruments, Inc, Houston, Tex). Mounted on the catheter were 2 micromanometers, 5 cm apart, with the distal one at the tip. The micromanometers were soaked in saline solution at 36°C to 38°C for a minimum of 3 hours; they were simultaneously balanced and calibrated immediately before each study.

Once proper functioning of micromanometers had been verified, the RV catheter was advanced during fluoroscopy until the proximal and distal micromanometers were located inside the right atrium and ventricle, respectively. When a steady-state physiologic condition was reached, pressure data were obtained and digitized at 400 Hz.

Multiple data sets were recorded under control conditions and under each disease state. Each set was between 20 and 30 seconds to ensure sufficient numbers of beats for analysis.

Induction of RV Pressure Overload

Dogs (20–30 kg) were premedicated with cefazolin (500 mg) and iron dextran (100 mg) and anesthetized with intravenous pentobarbital (20 mg/kg) and succinylcholine (1 mg/kg). They were intubated and ventilated with a Bennett MA 1 respirator (Puritan-Bennett, Los Angeles, Calif). Thoracotomy was performed under sterile conditions through the left fifth intercostal space, exposing the heart and major vessels. RV pressure overload was induced through pulmonary artery (PA) occlusion by using a silicone rubber pneumatic occluder around the main PA. The trunk beneath the occluder was wrapped with polytetrafluoroethylene to prevent PA rupture. Pressure overload was induced by inflating the PA occluder until peak RV systolic pressure reached at least 60 mm Hg or approximately twice its control level. The occluder remained inflated throughout the study period. The occluders were filled with hypertonic glycerin solution. This kept balloon volumes very stable; few leaked, and a few even swelled by drawing in fluid. We recorded the inflation volume and checked the balloon volume weekly to maintain inflation. If any leak was detected, the degree of occlusion was readjusted by either echocardiography or catheterization. An additional check was on the volume of glycerin in the balloon, which could be briefly deflated and then reinflated with the original volume found to provide the desired gradient. At the time of the study, echocardiography and right-heart catheterization confirmed stable PA stenosis. Pressure overload data were collected between the third and fifth weeks after its induction.

Induction of RV Volume Overload

Tricuspid regurgitation (TR) was used for volume overload. The right external jugular vein was exposed after achievement of local anesthesia with 1% lidocaine, and an 8F, 25-cm introducer sheath was positioned into the right ventricle under fluoroscopy. A 6F urologic biopsy forceps (Circon Instruments, Santa Barbara, Calif) was inserted into the right ventricle through the sheath, and multiple passes were taken to sever chordae until 3 to 4+ regurgitation developed. Regurgitation severity was confirmed by means of contrast fluoroscopy and central venous pressure. TR was achieved such as to yield both complete filling of the atrium with contrast medium within several cycles and an increase of peak right atrial pressures (V wave) to greater than 15 mm Hg with obliteration of the X–Y descent. This model produced consistent RV dysfunction, with dilatation at 1 week and ensuing reproducible failure. Hemodynamic data were collected between the second and third week after TR.

Induction of RV Free Wall Ischemia

A left lateral thoracotomy was performed after achievement of general anesthesia, as described earlier. An open chest greatly enhanced the surgeon’s ability to produce controllable ischemia associated with only the RV free wall, without affecting the LV. A 50-mg dose of intravenous lidocaine was administered, and the right coronary artery was ligated. After stabilization, multiple RV branches off the left anterior descending and posterior descending coronary arteries were also ligated to limit collateral flow. Hemodynamic data were collected in the second week after the procedure. At the time of autopsy, the condition of ischemia was assessed by means of visual inspection of the infarcted myocardium. Ischemia was confirmed by means of histopathologic staining (hematoxylin and eosin), showing a 30% or greater infarcted cross-sectional myocardial region of the RV free wall.

Analysis of Cardiodynamic Data

Data processing involved determination of steady-state beats and ensemble averaging to obtain a waveform representative of any given measurement set. Because RV pressure in conscious animals is strongly influenced by respiration,⁷ data were averaged over several respiratory cycles. Furthermore, compared with each of its constituent waveforms, the ensemble average has a higher signal/noise ratio proportional to the square root of the number of pulses used. Hemodynamic signal processing was performed with custom software developed in our laboratory. It included the following steps: conversion of any given data file into standard format; separation of individual beats; selection of steady-state beats; length adjustment of individual beats; ensemble average calculation; and modeling of RV relaxation dynamics.

Conversion of data into standard format

Each standard data file contained values for right atrial pressure and RV pressure and its change with respect to time $\left(RV\frac{dp}{dt}\right).RV\frac{dp}{dt}$ was computed digitally from the micromanometric pressure data.

Separation of beats

The beginning of a beat was defined at the onset of RV relaxation, occurring at the nadir of RV pressure change with respect to time.^8,9 The software needed to detect a period of continuous pressure decline of at least 150 ms before locating maximum value of $\left(-\frac{dp}{dt}\right)$ to reduce the effect of confounding transients associated with outflow deceleration and aortic valve closure.¹⁰ The end point of one beat coincides with the start of the next. After an entire train had been processed, the beginning and length of each beat were recorded.

Selection of steady-state RV pulses

A subset of the individual beats from the previous step was selected for ensemble averaging. Whether the individual waveforms used are truly representative of the physiologic steady state is the factor determining the quality of the resulting average. It was therefore required that the SD of the length of selected steady-state beats be within less than 5% of the average length. Table 1 shows that the beat ensembles used contain beats that are very similar in length. The SDs of these ensembles are between 2% and 5% of the mean length.

TABLE 1.

Statistics on length variation of hemodynamic waveforms

	Control	PO	VO	Ischemia
Mean length (ms)	550	480	530	435
Maximum length (ms)	700	595	640	520
Mean SD (ms)	12	17	14	16
Maximum SD (ms)	18	24	22	25
Mean SD/length (%)	2.4	3.3	2.8	3.6
Maximum SD/length (%)	3.1	4.2	3.9	4.7

SD, Standard deviation; PO, pressure overload; VO, volume overload.

Standardization of beat length and ensemble averaging

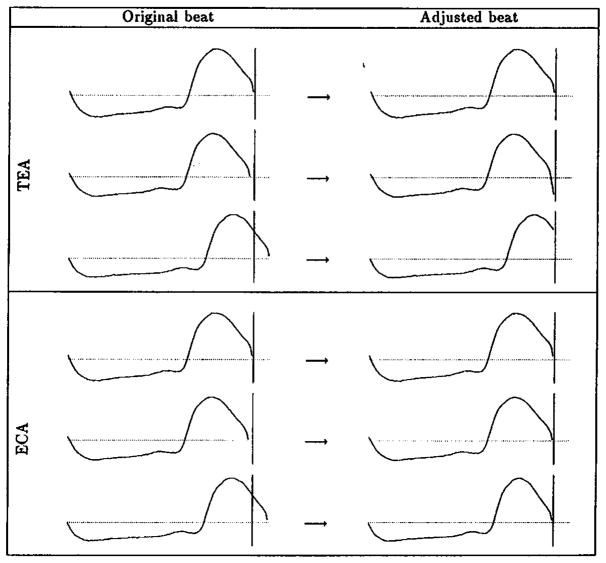
Ensemble averaging requires each individual beat to have the same length. A new expansion-contraction (EC) algorithm adjusted all selected waveforms to the mean length of their ensemble while maintaining all the shape characteristics of the constituent waveforms. The EC algorithm normalizes all constituent beats to a standard length before averaging, as opposed to another algorithm that truncates or extrapolates (TE) to offset individual beat-length differences.

The EC algorithm is based on recreating each beat in an ensemble by using an adjustable sampling frequency. The number (N_av) of data points in a pulse of the average length, t_av, is given by the following formula:

$${\mathrm{N}}_{\text{av}}={\mathrm{t}}_{\text{av}}\mathrm{f}+1$$ (1)

where f is the actual sampling frequency. Beats whose length (t_i) differed from t_av were recreated by using an adjustable sampling frequency (f_i), such that the number (N_i) of points in the resampled beat was exactly the same as N_av as follows:

$$fi=\frac{N_{av}-1}{t_i}$$

where an additive factor of 1 is again included to account for both end points of the beat. Values at each time step in the resampled beat were calculated by linearly interpolating between the 2 immediately surrounding points of the original beat.

With the length of all constituent beats correctly adjusted, an ensemble-averaging subroutine was used to calculate the algebraic mean of all pressure pulse signals point by point. The EC algorithm possesses a significant advantage over the traditional TE algorithm in that it preserves the overall periodicity and the details of the individual beats in the ensemble. Figure 1 shows a graphic comparison of the EC versus TE algorithms.

Figure 1.

Comparison of TE and EC algorithms. The top panels show application of the TE algorithm to 3 waveforms: the second and third were extrapolated and truncated, respectively. The bottom panels show application of the EC algorithm to the same waveforms: all 3 beats preserve their original shapes.

Mathematic modeling of RV Relaxation

The exponential^8,9,11–13 model (equation 2) represented well the time course of RV pressure decay. The RV pressure decay period was fixed as the interval from the beat beginning (defined above) up to the last point satisfying the following criteria: (1) it preceded the point of minimum RV diastolic pressure, and (2) its pressure level was at least 3 mm Hg higher than the subsequent end-diastolic pressure^8,9,12,14 for the case of RV pressure overload and 1 mm Hg for control conditions, volume overload, and ischemia. Further analysis was restricted to this interval:

$${\mathrm{P}}_{\mathrm{R}}={\mathrm{P}}_0·exp(-\mathrm{t}/\tau )+{\mathrm{P}}_{\mathrm{b}}$$ (2)

The exponential model characterizes the decay of RV pressure (P_R) with 3 parameters: P₀, τ, and P_b. Among them, τ, the time constant of relaxation, is the most important because it quantifies the rate of relaxation.¹⁵ P_b is also important because it represents the asymptotic level to which the pressure would tend if the decaying process was allowed to proceed indefinitely. Previous studies have shown that the value of P_b should not differ greatly from zero. If found to do so, it is a hallmark of the inapplicability of the monoexponential model as an accurate descriptor of relaxation dynamics.^8,12,15 Finally, when the mean pleural pressure does not deviate significantly from zero, the parameter P₀ is indicative of the beginning level of the exponential RV pressure decay. With the use of the nonlinear regression routine from the statistical software SPLUS,¹⁶ the experimental data were fitted to the exponential model, and least-squares parameter estimators were obtained.

Statistics

The exponential model parameters were used to assess the effect of each mode of RV failure on RV relaxation dynamics. For each parameter, a set of data was recorded under each condition (ie, control, pressure overload, volume overload, and ischemia). All data sets are presented as means ± SD. An analysis of variance for each variable was performed, with the 4 data groups being control (n = 15), pressure overload (n = 6), volume overload (n = 7), and ischemia (n = 7). Because the mean of each data set did not differ significantly from the median, the Student unpaired t test was performed to assess statistical significance between the control and each of the RV disease models.

The α level for the Student t test was adjusted with the Bonferronian inequality, thus using a more conservative critical value for the t statistics to accommodate the fact that 3 comparisons were made against the control set for each variable.

The paired Student t test was applied to determine whether values of the asymptote P_b in the conditions investigated were statistically different from zero.

Results

Representative RV Hemodynamics

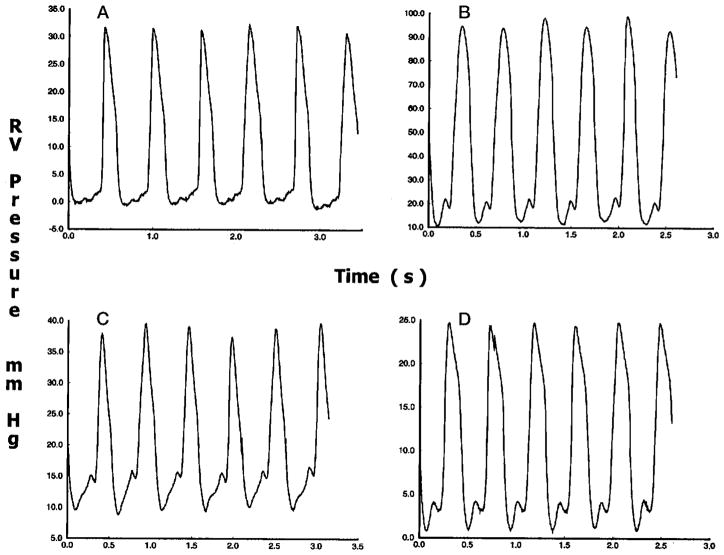
Figure 2 contains 4 panels, each showing a train of representative steady-state RV pressure pulses. The most distinctive difference between the tracings from pressure overload and control is in pressure level. Although under control conditions the measured RV pressure decreased to around 0 mm Hg, the lowest pressure under pressure overload remained greater than 10 mm Hg. In addition, peak systolic pressure was greater than 90 mm Hg compared with less than 35 mm Hg under control conditions.

Figure 2.

Steady-state RV pressure pulses under control conditions (A), pressure overload (B), volume overload (C), and ischemia (D). Peak systolic pressure is greatly increased under pressure overload, slightly increased under volume overload, and slightly decreased under ischemia.

Although the peak systolic pressure for volume overload was not significantly higher than that under control conditions, the minimum pressure was increased to about 10 mm Hg. There was also a more pronounced pressure increase during filling: the difference between the nadir of the diastolic pressure and the peak of the atrial wave was about 5 mm Hg, approximately twice as much as that under control conditions.

The peak RV systolic pressure reached in ischemia was significantly depressed compared with that under control conditions. The magnitude of the pressure increase during filling, however, was similar to that under control conditions.

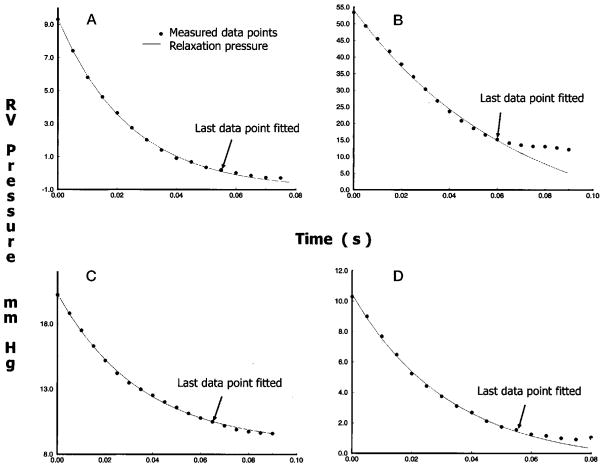
Figure 3 shows the mathematic modeling of RV relaxation dynamics. Data labeled as measured pressure in each of the 4 panels show the relaxation portion of the ensemble-averaged waveform. Data labeled as relaxation pressure show the tracing of the exponential model that best fits the measured pressure within the defined RV pressure decay period.

Figure 3.

Tracings of RV isovolumic pressure decay under control conditions (A), pressure overload (B), volume overload (C), and ischemia (D). Dots denote every other point in the digital ensemble average of the measured waveforms. The line shows the exponential fit. Arrows indicate the last points used in regression.

Control Conditions

The exponential model was applied to the RV relaxation process. Table 2 shows each parameter of the exponential model under control conditions. The paired Student t test showed that P_b values (0.28 ± 1.8 mm Hg [mean ± SD]) did not differ from zero (P > .54).

TABLE 2.

Isovolumic relaxation dynamics

		Po (mm Hg)	Pb (mm Hg)	τ (ms)
Condition (mean ± SD)	Control	13.1 ± 5.1	0.28 ± 1.8	27.8 ± 3.9
	PO	56.2 ± 19.1	−7.9 ± 1.5	57.1 ± 2.8
	VO	11.3 ± 5.1	5.3 ± 2.9	26.8 ± 6.1
	Ischemia	9.0 ± 3.5	−1.95 ± 1.1	41.4 ± 13.0
Analysis of variance	F statistic	43.33	51.62	31.81
	P value	.0001	.0001	.0001
PBONF* = .0167	PO vs control	.0001	.0001	.0001
	VO vs control	.2295	.0001	.3140
	Ischemia vs control	.0355	.0038	.0004

SD, Standard deviation; PO, pressure overload; VO, volume overload. Values significantly different from control are presented in boldface.

^*ANOVA with Bonferroni’s inequality. For the 3 comparisons, a conservative critical value for the modified t statistics is given by using a significance level, P_BONF, of (P/3) = (.05/3) = .0167.

Pressure Overload

Dramatic increases in peak systolic pressure were observed (Figures 2 and 3). Table 2 shows the values of the exponential parameters for subacute (3–5 weeks) pressure overload. The increase in systolic pressure resulted in an increased P_0. In addition, τ increased to 57 ± 2.8 ms from27.8 ± 3.9 ms under control conditions (P < .0001). This was accompanied by a general decrease in the value of P_b. However, P_b remained well above − 10 mm Hg. Therefore, the exponential model remained applicable to pressure overload.^8,12,15 However, P_b was statistically less than 0 mm Hg (P < .0001). The SD values show that data for all 3 parameters fall into relatively narrow ranges.

Volume Overload

Table 2 summarizes the exponential parameters for subacute (2–4 weeks) volume overload. P₀ does not show significant change from that under control conditions, which is consistent with no change in RV pressure at the onset of the relaxation period. The values of τ are likewise similar to those under control conditions. The level of P_b (5.3 ± 2.9 mm Hg [mean ± SD]) is statistically greater than 0 mm Hg (P < .001) and shows a significant increase from that under control conditions.

Ischemia

Table 2 summarizes the values of each parameter for subacute (1–2 weeks) ischemia. Unlike the 2 interventions already discussed, a significant reduction in peak RV systolic pressure was observed. The mean P₀ was reduced to less than 10 mm Hg, which is consistent with the general depression of RV pressure. The τ value, however, was increased significantly (P < .0004). For ischemia, the mean τ (41.4 ± 13.0 ms) falls in between the means under control conditions and pressure overload. P_b (− 1.95 ± 1.11 mm Hg [mean ± SD]) is decreased from that at the control condition and is now less than 0 mm Hg (P < .001). P_b values during ischemia were uniformly negative. Similar to τ, the level of P_b under ischemia was between those under control conditions and under pressure overload.

Statistical Analysis of the Effect of RV Disease Models on Relaxation

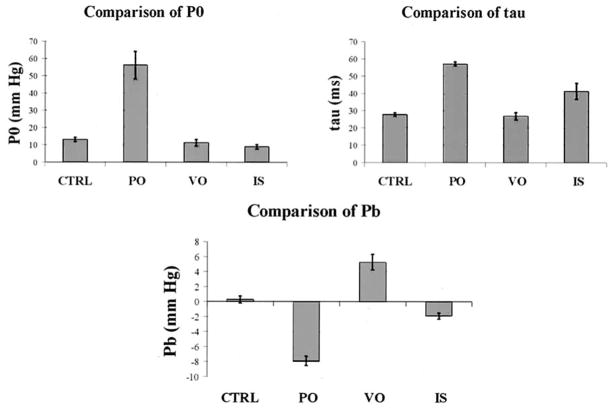
The bar charts in Figure 4 show descriptive statistics for the exponential model coefficients under control conditions, pressure overload, volume overload, and ischemia. Bar height and error brackets indicate means and SE, respectively. Table 2 displays analysis of variance F statistics and associated P values. Also included are results of Student t tests comparing the mean of each exponential coefficient in each disease state with that under control conditions. Results of the Student t tests that are significant under the Bonferronian inequality are presented in boldface.

Figure 4.

Descriptive statistics of the exponential model coefficients. CTRL, Control condition; PO, pressure overload; VO, volume overload; IS, ischemia.

Pressure overload differs significantly from control conditions in all 3 parameters: there are increases in both P₀ and τ and a decrease in P_b. Volume overload, on the other hand, displays only a significant increase in P_b. This is consistent with the observations made above on the relatively high pressure at the nadir of the RV diastolic pressure and the lack of significant changes from control conditions in P₀ and τ. RV ischemia is associated with a significant increase in τ and a decrease in P_b. The directions of change for τ and P_b are identical to those under pressure overload. However, the magnitudes of the changes are greater for pressure overload. There is also evidence (P = .035) of a significant decrease in P₀ under RV ischemia, which is consistent with the reduced peak systolic pressure (Figures 2 and 3).

Discussion

Using a combination of newly developed surgical chronic animal models and mathematic analyses, the present study compared, for the first time, relaxation dynamics in the normal and chronically diseased right ventricles of awake dogs to characterize important abnormalities resulting from both pressure and volume overload and from RV free wall ischemia.

RV Applicability of the Exponential Model With Asymptote

In the analysis of RV relaxation mechanics, we demonstrated the general applicability of the monoexponential model with asymptote^8,15 in describing the characteristics of RV pressure decay. In the case of the left ventricle, it was previously recommended that the lower cutoff pressure used in the regression should exceed the subsequently attained end-diastolic pressure by 3 mm Hg.^8,9,12,14 This recommendation was followed in the analysis of RV pressure overload, when the range of operating pressure is similar to that in the left ventricle. For the analysis of control, volume overload, and ischemia, we adjusted the cutoff level to at least 1.0 mm Hg greater than the subsequent end-diastolic pressure level. Because the RV operating pressure range is significantly lower, this adjustment from earlier LV applications was needed to have sufficient data points for the regression. In no case were there fewer than 23 points available for curve-fit parameter estimation; there were at least 7 points per estimated model coefficient.

We validated the suitability of the 3-parameter exponential model for RV use by applying it successfully to normal and subacute animal models simulating RV dysfunction states with distinct causes. Craig and colleagues¹⁵ introduced the nonzero pressure asymptote and showed that forcing a zero asymptote can yield spurious changes in τ. Care should be taken in determining circumstances when the monoexponential model is actually inadmissible.^8,12,15 Most notably, caution must be exercised when P_b is found to deviate greatly from zero because this is a hallmark of the nonapplicability of the monoexponential model as an accurate descriptor of relaxation dynamics.

RV Relaxation Abnormalities in Pressure Overload, Volume Overload, and Ischemia

For control, P_b in the right ventricle was not found to be significantly different from zero (P > .54). This result is in agreement with studies on the left ventricle.^9,11–13 Considering the 3 RV disease states, however, we found that P_b increased significantly in RV volume overload (P < .0001) and decreased in pressure overload and ischemia (P < .001). These findings indicate that for the right ventricle, as for the left, the exponential model is well suited to describing RV pressure decay under normal (control) conditions, regardless of whether it allows for a nonzero asymptote or not. However, to describe the decay under subacute pressure overload, volume overload, and ischemia, the exponential with nonzero asymptote is appropriate.

Previous studies on LV ischemia^8,13 have shown that impairment of relaxation is often associated with a lengthening of τ. The same pattern was observed in our RV study for both pressure overload and ischemia. The prolongation of τ in ischemia might reflect the decreased rate of Ca⁺⁺ reuptake by the sarcoplasmic reticulum, which is an active process.^{8,12,13,15,17} Because during RV pressure overload the hypertrophied right ventricle has to overcome an increased systolic load during ejection, RV myocardial perfusion might fail to increase sufficiently to satisfy the increased RV myocardial mass and metabolic demand. This might result in regional subendocardial ischemia of the RV free wall.¹⁸ Our results on the right ventricle agree with those of previous studies on the left ventricle.⁸ The decrease in P_b in ischemia might result from increased sympathetic tone.^8,11

In contrast to the results obtained for RV pressure overload and ischemia, no significant lengthening of τ was found for volume overload. This result suggests that the relaxation mechanism is unimpaired in subacute volume overload. It correlates with previous empiric observations¹ that the right ventricle, as a thin-walled, low-pressure system, tolerates an increase in the preload significantly better than it tolerates increases in the afterload. The only significant change detected by the model in RV volume overload is the increase of the asymptote, P_b. This reflects increased diastolic constraint because of the elevated right-heart volumes.^7,8,14

Clinical Significance

This study is clinically important because it is the first to demonstrate several abnormalities of RV relaxation, which might have clinical significance and implications for patient management.¹⁹ A previous acute surgical experimental study²⁰ on open-chest anesthetized dogs had reported absence of isovolumic relaxation, which appears to be referable to the applying highly unphysiologic state and methods. Ihara and coworkers¹¹ have shown, in elegant experiments, that in the anesthetized state immediately after the chest was closed after instrumentation procedures, ejection time was greatly prolonged compared with that during control awake conditions, whereas left ventricular end-systolic stress and mean systolic arterial pressure were reduced substantially. Together, these factors act to factitiously encroach on the isovolumic relaxation period. This effect should be similar on the right side and enhanced in the open-chest state because of a lack of the RV afterload component represented in the intact awake state by the action of pleuropericardial adhesive forces and lung elasticity, creating negative intrathoracic pressure. In a human multisensor catheterization study, Condos and coworkers⁷ showed that under awake conditions, conventional RV systolic ejection period was 371 ± 17 ms (mean ± SD), whereas RV flow time (catheter-mounted electromagnetic flow sensor) was only 298 ± 19 ms. Considering that their onset is simultaneous, there is substantial underestimation (by 73 ms on average) of the true extent of the isovolumic relaxation period if its onset is incorrectly assumed to be the end of the conventional systolic ejection period (incisural nadir).

The impairment of RV relaxation (increased τ) demonstrated in pressure overload and ischemia suggests that the pressure-overloaded or ischemic right ventricle might be less tolerant of tachycardia than the normal or volume-overloaded right ventricle. In pressure overload or ischemia, tachycardia would cause disproportionately large increases in RV diastolic pressure, which in turn would accentuate wall stress and central venous pressures. By reducing the heart rate, myocardial oxygen consumption would decrease, resulting in a better relationship between supply and demand; this is true regardless of whether there is epicardial coronary disease (ischemia) or whether there is just hypertrophy and subendocardial ischemia (pressure overload). In pressure overload, treatment should be aimed at normalizing load and preventing or regressing (or both) RV hypertrophy. In ischemia it should be aimed at decreasing myocardial oxygen consumption (demand) and increasing myocardial blood flow (supply). Both catheter-based and surgery-based methods of revascularization have been shown to improve left-sided diastolic dysfunction.¹⁹

On the other hand, in volume overload, RV pressures during relaxation are disproportionately augmented by an increased pressure asymptote (P_b). This suggests that the volume-overloaded right ventricle experiences a more constant elevation of diastolic pressure that would be independent of heart rate and that might result from or be accentuated by pericardial constraint. Increase of P_b might therefore contribute to less tolerance of pericardial constraint or scarring in RV volume overload than in pressure overload or ischemia. Increased RV diastolic pressure during exercise might also limit subendocardial blood flow during increased myocardial oxygen demand, worsening diastolic dysfunction. As indicated in the setting of LV diastolic failure,¹⁹ treatment should be aimed at normalizing RV volume by increasing venous capacitance with nitrates, nitroprusside, or morphine; fluid and sodium restriction; or surgical intervention.

Conclusions

We conclude that significant abnormalities in the dynamics of RV relaxation result from both pressure and volume overload and from RV free wall ischemia. These changes, demonstrated in animal models of RV dysfunction of distinct causes, and their interactions with associated alterations in RV passive diastolic properties²¹ should influence^8,21 filling dynamics in RV dysfunction and are in need of further investigation.