In vivo bone strain and finite element modeling of a rhesus macaque mandible during mastication

Abstract

Finite element analysis (FEA) is a commonly used tool in musculoskeletal biomechanics and vertebrate paleontology. The accuracy and precision of finite element models (FEMs) are reliant on accurate data on bone geometry, muscle forces, boundary conditions and tissue material properties. Simplified modeling assumptions, due to lack of in vivo experimental data on material properties and muscle activation patterns, may introduce analytical errors in analyses where quantitative accuracy is critical for obtaining rigorous results. A subject-specific FEM of a rhesus macaque mandible was constructed, loaded and validated using in vivo data from the same animal. In developing the model, we assessed the impact on model behavior of variation in (i) material properties of the mandibular trabecular bone tissue and teeth; (ii) constraints at the temporomandibular joint and bite point; and (iii) the timing of the muscle activity used to estimate the external forces acting on the model. The best match between the FEA simulation and the in vivo experimental data resulted from modeling the trabecular tissue with an isotropic and homogeneous Young’s modulus and Poisson’s value of 10 GPa and 0.3, respectively; constraining translations along X,Y, Z axes in the chewing (left) side temporomandibular joint, the premolars and the m₁; constraining the balancing (right) side temporomandibular joint in the anterior-posterior and superior-inferior axes, and using the muscle force estimated at time of maximum strain magnitude in the lower lateral gauge. The relative strain magnitudes in this model were similar to those recorded in vivo for all strain locations. More detailed analyses of mandibular strain patterns during the power stroke at different times in the chewing cycle are needed.

1. Introduction

Hypothesized associations between loading regimes, internal stress regimes, and shapes of biological structures are commonly evaluated using either simple beam models (e.g., Preuschoft et al., 1983; Hylander, 1984, 1985; Daegling, 1993, 2001; Hylander and Johnson, 1994; Ravosa, 1996, 2000; Ross and Hylander, 1996; Hylander et al., 1998, 2000; Daegling and Hylander, 2000; Ravosa et al., 2000; Ross, 2001; Metzger et al., 2005; Daegling and McGraw, 2009) or, more recently, complex finite element models (FEMs) (e.g., Ross et al., 2005; Strait et al., 2005; Kupczik et al., 2009; Panagiotopoulou and Cobb, 2011; Porro et al., 2013; Prado et al., 2016; Janovic et al., 2014, 2015; Cox et al., 2011; Smith et al., 2015; Benazzi et al., 2016; Ledogar et al., 2016a; McIntosh and Cox, 2016; Panagiotopoulou et al., 2016a, b; Smith and Grosse, 2016). These modeling methods are especially important for testing hypotheses regarding form–function relationships (design) in skeletons of fossil animals for which in vivo data are not available (e.g., Rayfield et al., 2001; Strait et al., 2009; Berthaume et al., 2010; Grine et al., 2010; Falkingham et al., 2011a,b; Dzialo et al., 2014; Smith et al., 2015; Ledogar et al., 2016b). The validity and power of the conclusions drawn from these models depend on the appropriateness of the modeling methods for the questions being addressed.

Although simple beam models have advanced our understanding of the mechanics of the primate jaw during feeding (e.g., Beecher, 1977, 1979; Hylander, 1979a, b, 1984, 1985, 1988; Bouvier, 1986a,b; Ravosa, 1991, 1992, 2000, 2007; Hylander et al., 2011), the use of mandibular cross-sectional geometry in dietary inference is problematic (Daegling, 1989; Daegling and Hylander, 1998). As reviewed elsewhere (Ross and Iriarte-Diaz, 2014; Ross et al., 2016), the most controlled studies of closely related and sympatric primates do not reveal strong relationships between mandibular cross-sectional geometry and diet (Daegling and McGraw, 2001, 2007). While beam models give accurate estimates of the distribution of dorsoventral bending and transverse and sagittal shear stresses in the mandible, they are not as accurate in predicting reaction force magnitudes and orientations, nor torsional and mediolateral bending stress within the mandible (Porro et al., 2011). Beam models perform even more poorly when used to estimate patterns of stress in primate crania (e.g., Endo, 1966, 1973; Roberts and Tattersall, 1974; Greaves, 1985; Preuschoft et al., 1983). Predictions of the facial stress and strain regimes from simple beam models are compatible with in vivo bone strain data from the plate- and beam-like postorbital septum and zygomatic arch (Ross and Hylander, 1996; Hylander and Johnson, 1997), but they perform less well in predicting loading scenarios in whole facial skeletons, which are characterized by complex geometry and material properties (Ross, 2001; Metzger et al., 2005; Chalk et al., 2011).

Many of the limitations of beam models of biological structures are overcome by FEMs, which minimize assumptions about geometry and make explicit the assumptions regarding material properties and constraints. As with any model, simplification and assumptions are inevitable in finite element analysis (FEA), in particular when data on bone material properties and muscle activation patterns are not known. While some workers highlight the limitations of FE modeling to question its utility (Grine et al., 2010), FEMs are clearly superior to simple beam models in minimizing and precisely articulating assumptions regarding geometry, material properties, constraining conditions, and loading regimes of biological structures. For us the question is not whether FEMs will replace beam models in biology—they clearly will—but how to build the best models for addressing the questions of interest. In a comparative context, it is unlikely that simplified FEMs can affect model comparisons considering that modeling assumptions and potential errors are constant amongst models. Nevertheless, in such cases the user needs to be aware of any model simplifications, control them when possible via sensitivity and convergence analyses and thoroughly consider them during data analysis. FEMs aimed at clinical studies such as surgical implantations or for studying the functional adaptations of anatomical tissues need to be more rigorous.

As with any rigorous model, validation and sensitivity analyses are essential prerequisites to evaluate the accuracy of the FEM’s predictions and to test how variations in input parameters will affect the model’s mechanical behavior. In both biology and engineering one important way to assess the validity of FEMs is to compare strain data extracted from part of the FE model with strains measured from the same locations in vitro or in vivo. The importance of strain data for validation inheres in part in their hypothesized relevance for the design of biological structures. For example, control of strain magnitude is hypothesized to be an important design criterion for biological structures because strain magnitudes are related to fracture probability (Burstein et al., 1972; Reilly and Burstein, 1975) and because strains activate adaptive bone remodeling, repair and modeling in response to load (Frost, 1987; Forwood and Turner, 1995; Turner, 1998). The importance of strain data for FEM validation also derives from the fact that, in contrast to external (joint and substrate) reaction forces generated by FEMs, strain regimes are sensitive to a wide range of modeling parameters, including model geometry, material properties, loading conditions, and constraining conditions. Thus, strain data provide a biologically relevant and sensitive test of the validity of FEM behavior.

To date, in vivo bone strain data have been used to validate only a handful of FEMs, including the cranium of Macaca (Metzger et al., 2005; Strait et al., 2005; Porro et al., 2011; Ross et al., 2011). Ross et al.’s (2011) validation study involved comparison of in vivo or in vitro strain data recorded from several Macaca mulatta individuals with in silico strain data extracted from a FEM of a cranium of Macaca fascicularis. This potentially introduces a wide range of confounding factors related to inter-individual and/or interspecific variation in structure and/or function, making it difficult to explain similarities and differences between models and in vivo data. For example, there is good correspondence between the FEM and in vivo data in gradients of relative strain magnitudes across the cranium, as well as in strain orientation data from the zygomatic arch and anterior zygoma root. In contrast, there is poor correspondence between strain orientations recorded from areas of the cranium experiencing low strain magnitudes in vivo and in silico. Is this due to the fact that strain orientations show a lot of variation across small areas both in vivo and in silico, or is it due to inter-specific differences between M. fascicularis and M. mulatta (Ross et al., 2011)?

With these questions in mind, we designed the present study with the goals of evaluating not only our ability to build a FEM of the in vivo behavior of a primate mandible during chewing, but also the sensitivity of the model’s strain regimes to variation in input variables for which the most assumptions need to be made – i.e., material properties, external forces, and constraining conditions. To this end, we collected in vivo data on mandibular corpus bone strain, jaw elevator muscle activity, and jaw kinematics from a single adult female rhesus macaque (M. mulatta), then collected ex vivo data on mandible geometry, cortical bone material properties, and architectural properties of the jaw-elevator muscles from the same individual post mortem. We used these data to build and load a subject-specific FEM of the mandible in that animal chewing on grapes. We performed sensitivity analyses to address the impacts on mandibular corpus strain regimes of variation in assumptions regarding (i) the elastic modulus of the trabecular bone and dental tissues; (ii) the nature of the constraints at the temporomandibular joints and teeth; and (iii) the relative timing of electromyography (EMG) data and muscle force used in calculating the external muscle forces acting on the mandible.

2. Materials and methods

2.1. Subject

One adult captive-bred female rhesus macaque (M. mulatta) with no known pathologies of its masticatory apparatus or dentition was used in the study. As part of prior research, the animal had been implanted with microelectrode arrays in the orofacial sensorimotor cortex and head posts in the calvaria for attachment of a halo (Arce-McShane et al., 2014, 2016). Seven 2.7 mm × 10 mm Vitallium cortical bone screws (OFSQ13; 3I Implant Company, West Palm Beach, FL, USA) had been implanted, four in the cranium (two in each zygomatic arch) and three in the mandible (symphysis and anterior corpora) to measure mandible kinematics (Reed and Ross, 2010; Iriarte-Diaz et al., 2011; Ross et al., 2012).

All in vivo primate work was done at the University of Chicago under Animal Care and Use Protocol 72154.

2.2. Experimental procedures

2.2.1. Electromyography electrode and strain gauge placement

The subject was deprived of food 24 h prior to surgery, sedated using dexmedetomidine (150–200 μg/kg) and ketamine (4 mg/kg), then anesthetized via inhalation of isoflurane in O₂ (Theriault et al., 2008). Fine-wire bipolar electrodes were inserted into the superficial and deep masseter, anterior and posterior temporalis, and medial pterygoid muscles of both the right and left side of the head using methods described previously (Hylander and Johnson, 1985, 1994; Hylander et al., 2005; Ross et al., 2005). The bared ends of each electrode pair were fed into the distal end of a 22-gauge needle, the wires were bent back to make a hook, then the needle was inserted into the muscles through the skin and gently removed leaving the tips of the electrode wires embedded in the muscles. Electrode placements were as follows: superficial masseter, electrode inserted midway between its posterior and anterior borders, ca. 10 mm above the inferior border of the mandible; deep masseter, electrode inserted at a 45° angle relative to the transverse and coronal planes, ca. 5 mm below the zygomatic arch and 10 mm anterior to the jaw joint; anterior temporalis, electrode inserted ca. 10 mm posterior to the orbital margin, ca. 10 mm inferior to the temporal line in a coronal plane and 45° to the sagittal plane; posterior temporalis electrode inserted 5–10 mm above the external auditory meatus; medial pterygoid muscle electrode inserted along the medial aspect of the mandibular angle in a coronal plane similar to the superficial masseter (Hylander and Johnson, 1985, 1994; Hylander et al., 2000, 2005; Ross et al., 2005).

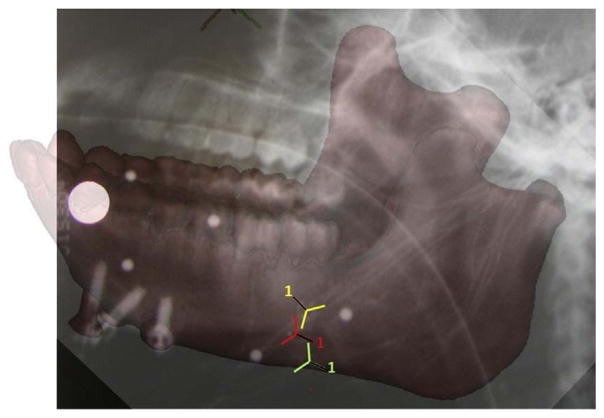
To place the strain gauges a small skin incision was opened at the inferior border of the left mandibular corpus, inferior to the left third molar. The cortical bone was exposed by reflecting the periosteum, the bone was degreased with chloroform, and three strain gauge rosettes were bonded to the bone using a cyanoacrylate adhesive. All three strain gauges were delta rosettes (SA-06-030WY-120; Micro-Measurements, Raleigh, NC, USA) wired in a three-wire quarter bridge configuration. One gauge was bonded to the medial/lingual surface of the left mandibular corpus, below the insertion of the mylohyoid muscle; and two were bonded to the lateral/buccal surface of the left corpus, close to the most anterior attachment of the superficial masseter muscle (Fig. 1). The incision was sutured closed with 4-0 Vicryl with the wires exiting the wound; the wires were secured to the skin overlying the superficial masseter (near the axis of rotation of the mandible; Ross et al., 2016), and radiographs were taken to document the precise position and orientation of the gauges (Fig. 1). While the animal was anesthetized, reflective markers were attached to the mandibular and cranial bone screws (Reed and Ross, 2010).

Fig. 1.

Radiograph of the mandible of the experimental subject showing the location of the medial [MED] (in yellow); the upper lateral [ULAT] (in red) and the lower lateral [LLAT] (in green) gauge locations. The reference axes for each gauge (numbered 1) are indicated with a black line.

2.2.2. Recording procedure

The animal was placed in a primate chair (514-AG; Plas-Labs, Lansing, MI, USA) with its head restrained and recovered from anesthesia for approximately 3 h. Each element of the rosette gauges was connected to form one arm of a Wheatstone bridge, supplied excitation voltage of 2 V, and their output conditioned and amplified using a Vishay 2100 system (Vishay Precision Group, Malvern, PA, USA). The EMG electrodes were connected to Grass 15A54 Quad amplifiers (Grass Instrument Co., West Warwick, RI, USA). Then, while the animal fed, we recorded marker kinematics (250 Hz), and bone strain and EMGs (5 kHz) onto a PC running Vicon Motion capture software (Vicon Motion Systems Ltd., Oxford, UK). At the end of the recordings, the animal was anesthetized, the EMG electrodes, optical markers and strain gauges removed, the gauge incisions sutured closed, analgesics and antibiotics were administered, and the animal recovered. All EMG and strain data were exported from Vicon as C3D files, imported into MatLab (Mathworks, Natick, MA, USA) using the Biomechanical ToolKit (BTK) (Barre and Armand, 2014) and analyzed by J.I.-D. using custom scripts in Matlab.

2.2.3. Electromyography analysis

All raw EMG signals were filtered using a digital Butterworth, high-pass filter (30 Hz cut-off frequency), then rectified and quantified by calculating the root-mean-square (rms) values using a 42 ms time constant following Hylander et al. (2000).

2.2.4. Strain analysis

Strain (ε) is a dimensionless variable that equals the change in length of an object divided by its original length. Strain is traditionally reported in microstrain (με) units, which are equal to 1 ×10⁻⁶ mm/mm. The maximum principal strain (ε₁) represents a positive value and indicates the maximum tensile value. The minimum principal strain (ε₂) represents a negative value and indicates the maximum compressive value. The bone strain data from the medial (MED), lower lateral (LLAT), and upper lateral (ULAT) gauge locations were down-sampled to a rate of 1000 Hz and converted to microstrain using calibration files created during data collection.

The magnitude and timing of peak maximum (ε₁) and minimum (ε₂) principal strains were calculated for each strain gauge and each power stroke using custom written software in IGOR Pro (versions 4.0 and 6.43a) (WaveMetrics, Lake Oswego, OR, USA). The ratio of the principal strains was calculated using the equation (ε₁/|ε₂|). The orientations of the vectors in relation to the mandible were estimated using radiographs and notes taken following the surgery.

2.2.5. Three-dimensional kinematics of the cranium and mandible

Kinematic data were processed in Matlab using customized scripts based on the KineMat toolbox kit (http://isbweb.org/software/movanal/kinemat/) and the BTK toolbox. At each time step the marker positions were rotated so that a new coordinate system was created, fixed to the cranium with the origin midway between the mandibular condyles. The horizontal plane (X–Y plane) was parallel to the occlusal plane of the maxillary teeth, so that the X-axis was positive forward, the Y-axis was positive towards the subject’s left, and the Z-axis was positive upward. The 3D displacement of the mandibular markers was used to calculate the rigid body kinematics of the mandible using the helical axes of the moving mandible with respect to the mandible in occlusion (Iriarte-Diaz et al., 2011). A simplified description of the mandibular movement was obtained by using helical angles, i.e., the projection of the helical axes onto the axes of the Cartesian coordinate system fixed to the cranium (Woltring, 1994). During chewing, most of the mandible movement consists of rotations around the X-axis (jaw depression and elevation) and around the vertical Z-axis (medial and lateral displacement of the teeth). We used the helical angles around the X-axis to define the chewing cycles and the helical angles around the Z-axis to define the chew side for each chewing cycle.

In the present work, we focused on modeling the mandible during rhythmic chewing cycles, defined between two consecutive maximum gape events. Maximum gape events were automatically identified using a custom Matlab script, but we manually selected only those events that represented rhythmic chewing. For each of these selected cycles, we found the time of minimum gape, when the helical angle around the X-axis was at a local minimum. We then defined the cycle as either a left or a right chew depending on the direction of the lateral displacement of the mandible prior to the minimum gape based on the change in the helical angle around the Z-axis.

2.2.6. Post-processing of analog signals

The kinematic, EMG, and strain data in each cycle were divided into 100 time steps using interpolation and the mean values calculated for each time step across all left chews on grapes. To calculate the external muscle forces to apply to the model, two specific time points were chosen: the time in the mean cycle at which maximum mean bone strain was recorded in the LLAT gauge, and the time in the mean cycle at which the maximum total muscle activation was measured; i.e., the maximum of the summed mean EMG values for all muscles (see supplementary Fig. S1).

2.3. Finite element analysis

2.3.1. Model creation: model geometry, 3D models and mesh files

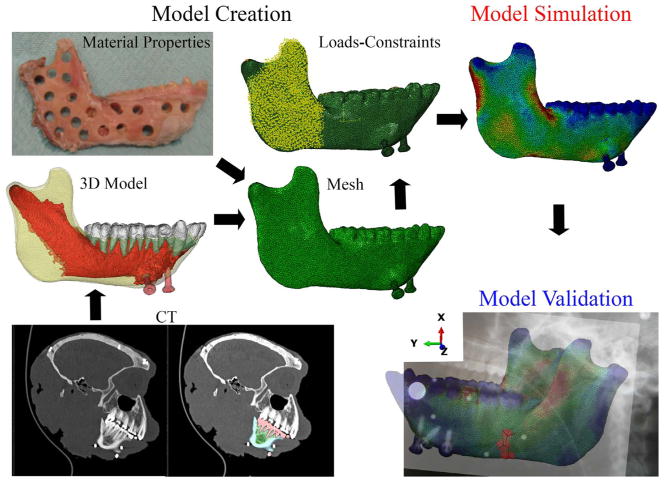
The skeletal geometry of the macaque skull was captured with computed tomography (CT) scan data collected on a Philips Brilliance Big Bore scanner at the University of Chicago (isometric slice thickness 0.8 mm, 768 × 768 pixel images and 0.2 mm pixel size). The skull was scanned along with calibration phantoms (Gammex 465; Sun Nuclear Corp., Melbourne, CA, USA) of known radiodensity (ρ) and apparent density (Dapp). Using Mimics Materialise software (v.17) (Materialise, Leuven, Belgium), the mandible was isolated from the cranium and the three-dimensional (3D) surfaces of the cortical bone, trabecular bone, teeth, periodontal ligament (PDL) and mandibular bone screws were extracted (Fig. 2). Automatic thresholding was used when possible; then, manual segmentation was used to remove artefactual connections between opposing or adjacent tooth crowns and to segment the PDL as a continuous structure between the alveoli and the tooth roots.

Fig. 2.

Steps involved in FEA: model creation, model simulation and model validation. Model creation phase involves assignment of the model’s 3D geometry using CT scans (bottom left and middle left); the transformation of the geometric model into a set of discrete finite elements, the mesh; and the assignment of tissue material properties and boundary conditions (loads and constraints). Model simulation refers to the solution process of the FEM using default functions of the FEA software (Erdemir et al., 2012). Model validation involves comparison of the strains extracted from the FEM with experimental data from the same locations. Note the axes indicating the local coordinate system: X-axis in the supero-inferior direction, Y-axis in the anterior-posterior direction, Z-axis in the mediolateral direction.

In 3-matic software v.10 (Materialise, Leuven, Belgium) the 3D surface datasets of the cortical bone, trabecular tissue, teeth, PDL, and bone screws were then assembled to create a 3D non-manifold file (Fig. 2 and supplementary Fig. S2). All assembly parts were converted into volumetric .inp mesh files of solid continuum linear tetrahedral elements (type C3D4) and imported into Abaqus CAE Simulia software v. 6.13 (Dassault Systèmes, Vélizy-Villacoublay, France) for modeling. The whole assembly had 622,134 elements in total and the maximum nominal element size was 0.7 mm. The number of elements for each part is listed in Table 1. The local coordinate system of the model has the X-axis in the supero-inferior direction, the Y-axis in the anterior–posterior direction, and the Z-axis oriented mediolaterally (Fig. 2, Model validation local coordinate axis).

Table 1.

Finite element model specifications.

Constants across all models	Cortical bone				PDL		Screws	Teeth	Trabecular tissue
# elements	313 939				74 999		10 963	68 349	153 884
Young’s modulus (E)	Heterogeneous				0.00068		105	17 or 24.5	1,2,3, or 10
Poisson’s ratio (υ)	Heterogeneous				0.49		0.36	0.3	0.3
Variables across models	Model A	Model B	Model C	Model D	Model E	Model F	Model G	Model H	Model I
Material properties (E)
Trabecular Tissue	1 GPa	2 GPa	3 GPa	10 GPa
Teeth	17 GPa				24.5 GPa
Constraints
Balancing (Right) Side TMJ	Translation along X, Y, Z axes constrained					Translation along X, Y axes constrained
Working (Left) Side TMJ	Translation along X, Y axes constrained					Translation along X, Y, Z axes constrained
Left P3 and P4	Translation along X axis constrained					Translation along X,Y,Z axes constrained			none
Left M1	Translation along X axis constrained					Translation along X,Y,Z axes constrained
Left M2 and M3	Translation along X axis constrained					Translation along X,Y,Z axes constrained	none		Translation along X,Y,Z axes constrained
Time of muscle force modeling	Time of Max Muscle Force							Time of Max strain in LLAT gage

Axes: X =supero-inferior; Y =anteroposterior; Z =mediolateral

2.3.2. Model creation: material properties assignment

In all models the periodontal ligament (PDL) and titanium screws were assigned isotropic, homogeneous and linear elastic material properties, the PDL with a Young’s modulus (E) = 6.80E–04 GPa and a Poisson’s ratio (v) = 0.49 (Provatidis, 2000; Wood et al., 2011) and the titanium screws an E = 105 GPa and v = 0.36 (Kraaij et al., 2014) (Table 1).

In all models the cortical bone was assigned 80 heterogeneous and orthotropic E and v values based on measurements on the mandible of the experimental subject, performed as follows and described in detail by Dechow et al. (2017, this issue). Following acquisition of the CT scan data, the mandible was detached from the cranium, cleaned and stored in a freezer at −20 °F. Later, the mandible was thawed and 30 cortical bone sample sites on the labial and lingual aspects of the mandibular symphysis and right ramus and corpus (Fig. 2, top left) were marked with a pencil line, with an arrow oriented towards the rostral end of the jaw. At each site a low-speed, cylindrical, 4 mm diameter, water-cooled dental drill was used to remove a cortical bone cylinder (stored in a solution of 250 ml deionized water and 250 ml ethanol to sterilize them without altering their elastic properties) (Ashman et al., 1984). The thickness of the cortical bone samples was measured using a digital caliper (accurate to the nearest 0.001 mm) and the density of each sample was measured using a Metler Toledo X5105 balance equipped with a densitometry kit (Fisher Scientific LLC, Pittsburgh) following Archimedes’ principle of buoyancy (Ashman, 1989).

The ultrasonic velocities of each sample were measured using previously published protocols (Ashman et al., 1984; Dechow et al., 1993; Dechow and Hylander, 2000; Schwartz-Dabney and Dechow, 2002, 2003). Velocities coupled with the density of each sample were used to create a matrix of elastic coefficients according to Hooke’s law and the elastic constants (Young’s modulus, shear modulus and Poisson’s ratio) for each sample were calculated as described in detail elsewhere (Ashman, 1982; Ashman et al., 1984; Ashman and Van Buskirk, 1987; Carter, 1989). In brief, at each sample location Young’s moduli and Poisson’s ratios were calculated from the compliance (C) and stiffness (S) tensors (C_ij, with i and j in the range 1…6, matrix inverse S_ik) and densities ρ of the experimental samples via:

$$E=\frac{1}{3}\left(\frac{1}{S_{11}}+\frac{1}{S_{22}}+\frac{1}{S_{33}}\right)$$ (1)

$$v=\frac{1}{3}(S_{21}{E}_2+S_{31}{E}_3+S_{12}{E}_1)$$ (2)

To apply these material property data to the cortical bone parts of the FEM, Poisson’s ratio and Young’s modulus were assumed to be linear functions of bone density obtained from the CT scans. The mandible CT scan electron densities were converted to physical densities using a piecewise linear model relating the electron and physical densities in the CT scan phantoms (supplementary Fig. S3). A linear model relating the bone density to Young’s moduli and Poisson ratios across the sample locations was then constructed as:

$$E(\mathrm{\rho })=\mathrm{a}\mathrm{\rho }+b$$ (3)

$$v(\mathrm{\rho })=c\mathrm{\rho }+d$$ (4)

with a, b, c and d constants, and ρ the density. Fits of the form:

$$E(\mathrm{\rho })={\mathrm{a}}_1{\mathrm{\rho }}^r+a_2{\mathrm{\rho }}^s+b$$ (3b)

$$v(\mathrm{\rho })=c_1{\mathrm{\rho }}^p+c_2{\mathrm{\rho }}^q+d$$ (4b)

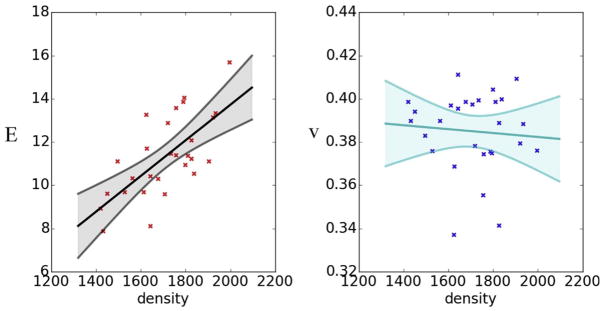
were considered, but exhibited poorer performance (measured by an AIC), and were rejected in favor of the simpler models. Using ordinary least squares regression, the model with the best fit to the sample data had a= −2.75, b= 0.00824, c= 0.401, and d = 0.00000913 (Fig. 3). Following the interpolation of the experimental measurements and the model, 80 heterogeneous and orthotropic material properties were assigned to the cortical bone.

Fig. 3.

Linear models of the relationships between Young’s modulus (E) and Poisson’s ratio (v) against material density estimated from calibrated CT scans. Each data point represents the data from a sampled location (see Fig. 2, top left); lines represent best fit linear models.

The mandibular bone composition for FEA is usually captured using computed tomography (CT) and/or micro computed tomography (μCT). However, constraints on image resolution mean that defining the geometry of the individual trabeculae in the subcortex can be problematic, as CT/μCT cannot accurately capture the fine details of the trabeculae within the subcortex (Rho et al., 1993; Dechow and Hylander, 2000; Rapoff et al., 2008). An alternative approach, and the one adopted here, models subcortical bone as a single solid (called ‘trabecular tissue’) and assigns it an E-value lower than that of cortical bone in accordance with the principle that, due to its increased porosity, subcortical tissue has an E-value 20–30% lower than that of cortical bone (Cowin, 2001; Currey, 2002). The trabecular bone and the teeth were assigned isotropic and homogenous material properties with a Poisson’s ratio of 0.3 and values of E that were varied as part of the sensitivity analyses. In Models A to D, the E of the teeth was 17 GPa and the E of the trabecular tissue was 1, 2, 3 or 10 GPa (Table 1), corresponding to the range of properties assigned to trabecular tissue in FEA studies of human bone (e.g., Meijer et al., 1993; Patra et al., 1998; Menicucci et al., 2002; Pierrisnard et al., 2002; Zarone et al., 2003; Van Staden et al., 2006). In Models E to I, the trabecular tissue was assigned E = 10 GPa, and the teeth were assigned E =24.5 GPa (Table 1).

2.3.3. Model creation: boundary conditions

Tie constraints were used to bind together all intersecting surfaces within the model and prevent any friction that would influence the FEA solution. One node on the top and the approximate center of each mandibular condyle was selected to apply constraints and a sensitivity analysis was performed to assess whether constraining results closer to the in vivo data were obtained by fixing (constraining all displacements) of the working (chewing) or balancing (non-chewing) side condyle. In Model E the balancing-side (right) temporomandibular joint (RTMJ) was fixed against translation in the X, Y, and Z directions and the working-side (left) temporomandibular joint (LTMJ) was fixed against translation only in the superior–inferior (X) and anterior–posterior (Y) directions (Table 1). The LTMJ was not constrained in the mediolateral (Z) direction to allow mediolateral movement for the lateral transverse bending of the mandible (Hylander, 1984). In contrast to Model E, in Model F the LTMJ was fixed against translation in the X, Y, and Z directions, and the RTMJ was constrained only against displacement along the X and Y axes (Table 1).

To simulate bite forces generated during chewing, the models were constrained at nodes on the occlusal surfaces of the teeth against displacement in the X direction (see supplementary Fig. S4 for an image of the nodes fixed on each tooth). In Models A–E all the working-side (left) post-canine teeth were constrained in the X direction (Table 1). In Model F, all postcanine teeth were constrained against displacement in the X, Y, and Z directions. In Model G, only the working-side premolars and m₁ were constrained in the X, Y, and Z directions (Table 1).

2.3.4. Model creation: external muscle forces

Total maximum force-generating capacity for each jaw elevator muscle was estimated from the muscle’s physiological cross-sectional area (PCSA) using previously published fiber architecture protocols (Taylor and Vinyard, 2004, 2009, 2013; Taylor et al., 2009, 2015; Terhune et al., 2015). The right and left masseter, temporalis and medial pterygoid muscles were harvested en masse from the skull, and the deep and superficial masseters were separated. All muscles were blotted dry, trimmed of fat and fascia, and weighed to the nearest 0.0001 g. The superficial masseter and medial pterygoid muscles were sectioned along their supero-inferior lengths into approximately 1.5 cm thick segments; the temporalis muscles were sectioned into anterior, middle and posterior segments. A maximum of six adjacent fibers was measured at the superior and inferior ends of the masseter and medial pterygoid segments and at the proximal and distal ends of the anterior, middle and posterior temporalis segments. For each fiber, fiber length (L_f) was measured as the distance between the proximal and distal myotendinous junctions (MTJ) and the perpendicular distance (a) from the distal MTJ to the central tendon was estimated for use in estimates of the pinnation angle. The parallel-fibered deep masseter was chemically digested in 30% nitric acid in saline (Loeb and Gans, 1986; Antón, 1999, 2000) for approximately 90 min, until such time as individual fibers could be manually separated without tearing (the deep masseter is parallel-fibered, so no measurement of pinnation angle was needed). Small fiber bundles were then dissected from the whole muscle in 1 X PBS under a dissecting microscope. A minimum of three fiber bundles was isolated from different regions of the deep masseter, mounted on slides, and L_f was measured under a microscope using a reticle to the nearest 0.1 mm. For all muscles/muscle regions, L_f was normalized to a standard sarcomere length following Felder et al. (2005). In situ sarcomere length (L_s, ± 0.01 μm) was measured from all fibers using laser diffraction (Lieber et al., 1984) and used to calculate normalized fiber lengths (NL_f), i.e., L_f was normalized to an optimal L_s of 2.41 μm (Walker and Schrodt, 1974) as NL_f=L_f (2.41 μm/L_s).

Using these normalized fiber length data, average NL_f was calculated for the right and left superficial masseter, deep masseter, medial pterygoid and anterior and posterior regions of the temporalis. Pinnation angle for each muscle/muscle region was then computed as the arcsine of a/NL_f and PCSA was estimated as PCSA =M x cos θ/ρ x L_f, where θ is pinnation angle and ρ is the specific density of muscle (1.0564 g cm⁻³) (Murphy and Beardsley, 1974).

To apply muscle forces to the model, surface nodes representing the insertion of the jaw muscles (anterior and posterior temporalis; deep and superficial masseters; and medial pterygoids) were selected using images of the dissection of the experimental subject. To assign a directional vector component to the muscles, the centroid node on the attachment of each muscle to the mandible (Point Mandible) and the cranium (Point Cranium) was selected, their x, y and z coordinates and the x, y, z components of the muscle vector calculated by subtracting Point Cranium from Point Mandible (supplementary Table S1 and Fig. S5). For each muscle the instantaneous force magnitude applied to the mandible at the time being modelled was calculated as the mean normalized EMG amplitude × estimated PCSA× specific tension of muscle (30 N/cm²) (Sinclair and Alexander, 1987) (supplementary Table S1 and Fig. S1). The estimated muscle forces (N) at time of maximum total muscle force were calculated and applied to Models A–G and the estimated muscles forces (N) at time of maximum strain magnitude in the lower lateral gauge were calculated and applied to Models H and I (Table 1).

2.3.5. Model simulation

All nine FEMs were solved using the Abaqus default implicit direct static solver. Solution time, using 4 processors and 8 tokens, was approximately 10 min per model.

2.4. Model validation

Model validation entailed comparison of surface strains from the gauge sites on the model with in vivo strain data recorded from the strain gauges. To locate the gauge sites in the FEMs a figure of the model mesh file was overlaid on the radiograph of the macaque head and aligned manually to achieve best fit (supplementary Fig. S6). The surface elements of the FEM that matched the location of each strain gauge were then manually selected, expanded by two elements diametrically, the XYZ positions of the centroids of these three node sets were calculated, and the six unique components of their strain tensors (i.e., ε_xx, ε_yy, ε_zz, ε_xy, ε_xz, and ε_yz) were obtained at the three locations. The orientation of the plane formed by all elements in each node set was calculated using a single-value decomposition method and this orientation, in the form of a direction cosine matrix, was used to rotate the strain tensor of each element from the coordinate system of the FEM to the coordinate system of the strain gauge. The reference axis of the plane was oriented to the reference element of the rosette strain gauge, obtained from the radiographs made during the experiment. To compare FEM data to the strain gauge data, all the out-of-plane components of the strain tensor (i.e., ε_zz, ε_xz, ε_yz) were set to zero and principal strains—the eigenvalues and eigenvectors of the rotated strain tensors— at the gauge sites were calculated using a custom-written Matlab script (see Ross et al., 2011 for details). The orientation of the principal strains was analyzed using the circular statistics toolbox, CirscStat for Matlab (Berens, 2009).

Raw in vivo strain data are provided in supplementary Table S2. Descriptive statistics for in vivo strain data are presented in Table 2. FEM strain data (converted to microstrain) are provided in supplementary Table S3; principal strain magnitudes are illustrated in Figs. 4 and 5, compared between models in Fig. 6, and descriptive statistics are plotted in Fig. 7. Strain orientations are compared in Figs. 8–10. Note that there are only two principal strains recorded by the strain gauges (ε₁ and ε₂) but three (ε_1, ε_2, ε₃) in FEA. In this study, ε₁ and ε₂ refer to the maximum (i.e., tension) and minimum (i.e., compression) principal strains respectively for both the in vivo experiment and FEA.

Table 2.

Descriptive statistics for mean, maximum (Max) and minimum (Min) strain (ε₁ and ε₂) and |(ε₁/ε₂)| magnitude for the in vivo experiment while the M. mulatta was chewing grapes. Gauge location: ULAT, LLAT and MED are abbreviations for upper lateral, lower lateral and medial (Fig. 1). SD represents standard deviations.

Gauge location	n	ε1				ε2				ε1 Orientations				ε1/ε2 ratio
		Mean	SD	Min	Max	Mean	SD	Min	Max	Mean	SD	Min	Max	Mean	SD
ULAT	163	81	44	10	206	−90	55	−196	−9	78	17	0	179	1.07	0.39
LLAT	163	56	37	5	133	−48	29	−109	−4	110	18	85	174	1.15	0.18
MED	163	50	21	12	107	−69	29	−145	−10	16	35	0	179	0.80	0.42

Fig. 4.

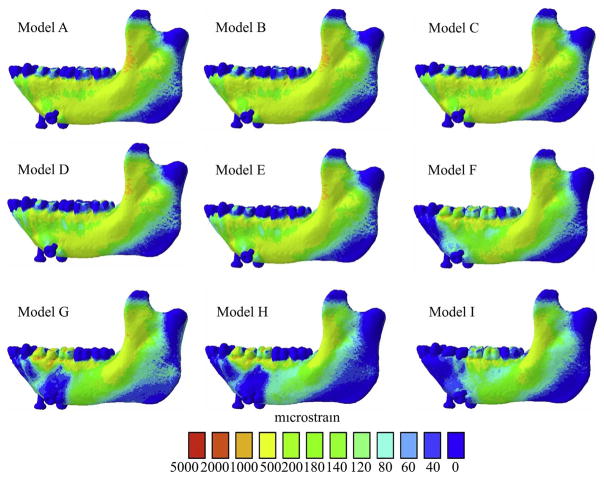
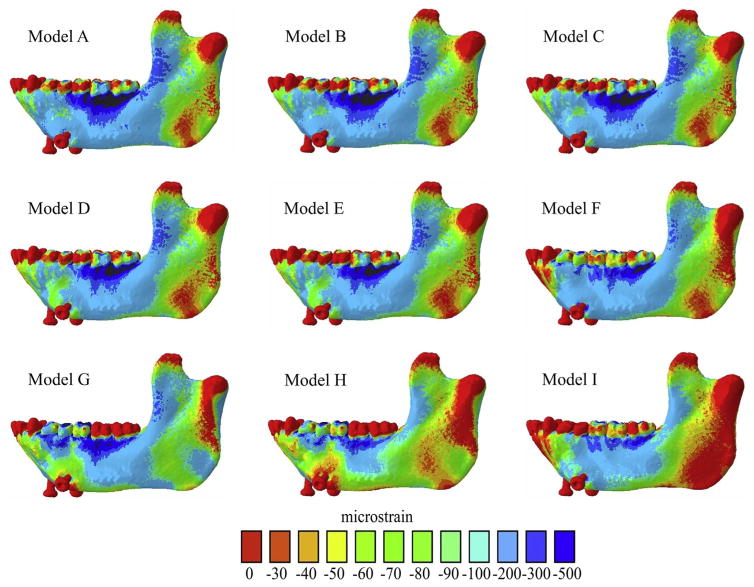
Maps of distribution of maximum principal strains (ε₁) of all FEMs of the macaque mandible. Warmer and cooler colors represent higher and lower ε₁ concentrations, respectively.

Fig. 5.

Maps of distribution of minimum principal strains (ε₂) of all FEMs of the macaque mandible.

Fig. 6.

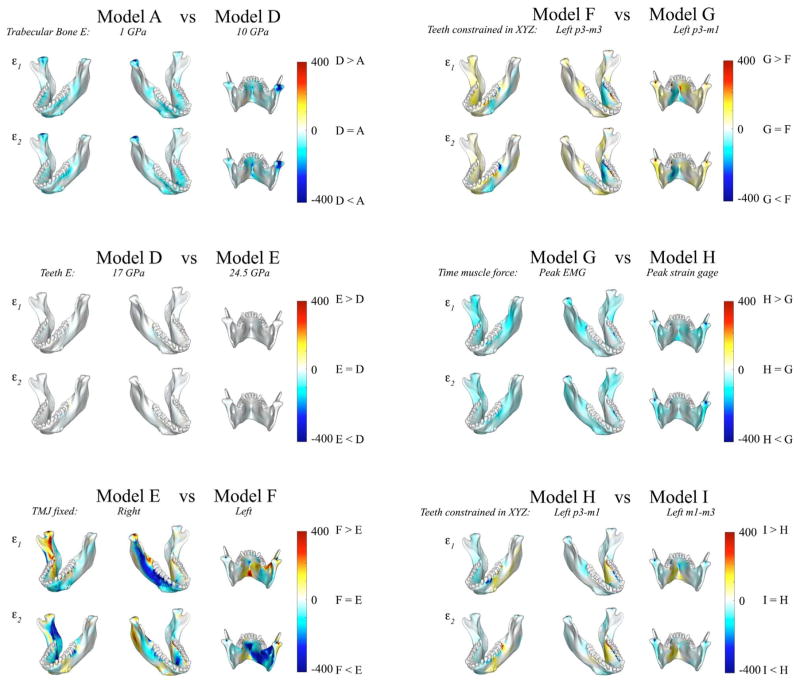
Comparisons of principal strain magnitudes in FEM model pairs. Six pairs of FEM models are compared by mapping the surface distribution of differences in principal strains between the two models on the surfaces of the model. Each panel compares ε₁ and ε₂ magnitudes between the model pairs in three views. Scale bars to the right of each panel indicate the difference in principal strains (in microstrains) between models.

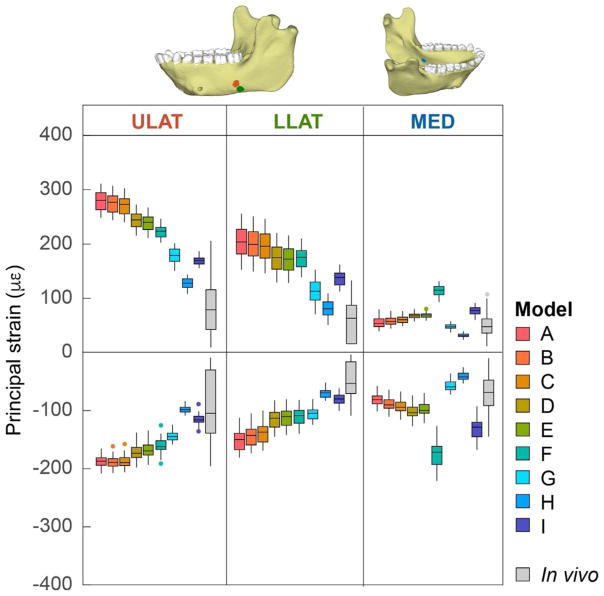
Fig. 7.

Box plots of ε₁ (positive) and ε₂ (negative) principal strain magnitudes at the ULAT, LLAT and MED gauge sites for all FEMs and the in vivo experiment. Center lines represent the median, upper and lower box boundaries represent 25th and 75th percentiles, respectively; upper and lower whiskers represent 1.5 × inter-quartile range; points are outliers.

Fig. 8.

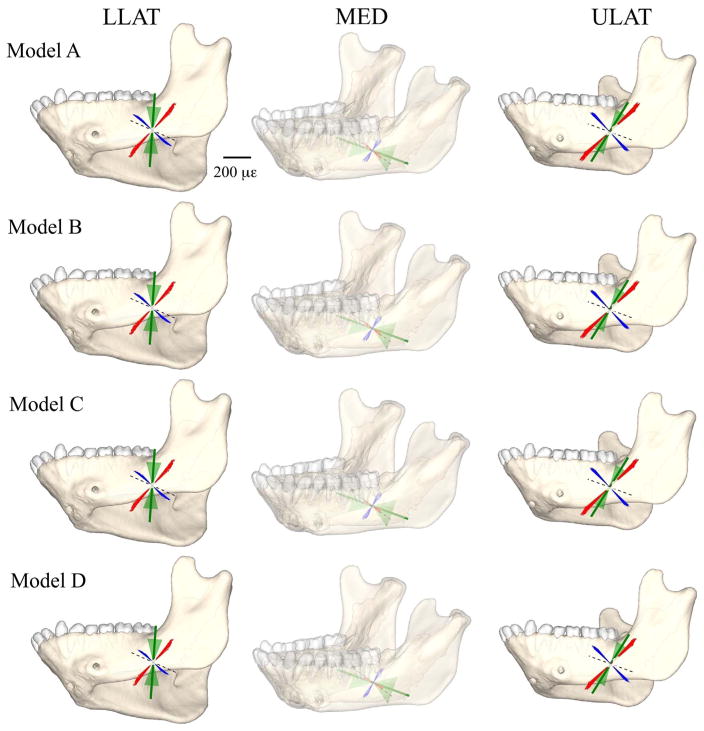
Polar histogram of the distribution of ε₁ orientations (in degrees) at the LLAT, ULAT, and MED gauge sites of the FEMs compared to the in vivo experiment. Grey histogram illustrates the orientation distribution of the in vivo data, and the colored histogram illustrates the orientation distribution of the specific FEM (models are color-coded as in Fig. 7). Red and black solid lines indicate the mean orientation of the in vivo and the FEM data, respectively. Orientations are relative to the reference axes of the gauges (illustrated by dashed lines in Fig. 9).

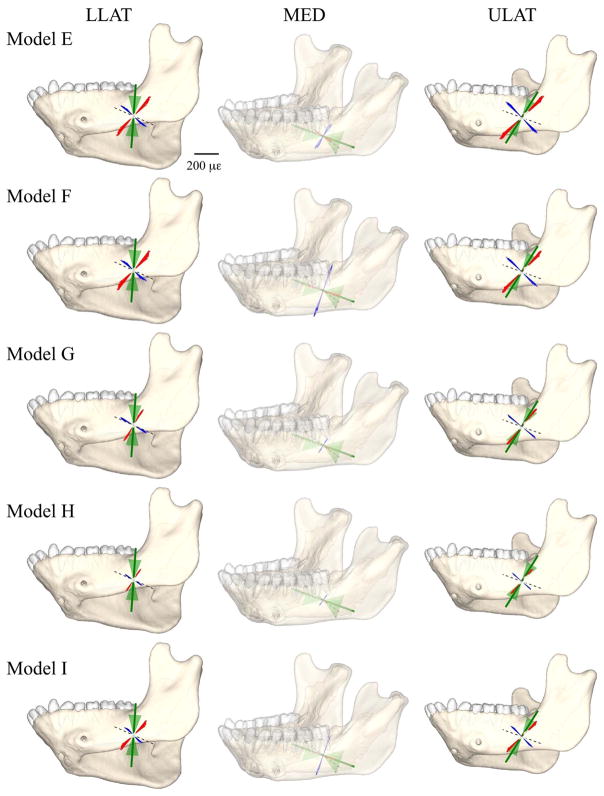
Fig. 10.

Comparison of principal strain vector plots from FEMs E through I with those from the in vivo data. The left, middle, and right panels show the principal strains at the location of the lower lateral (LLAT), medial (MED), and upper lateral (ULAT) strain gauges, respectively. The figures in the middle panel are transparent because the medial gauge is located on the lingual side of the mandible. Red lines, orientation and magnitude of the FEM maximum principal strain (ε₁); blue lines, orientation and magnitude of FEM minimum principal strains (ε₂); dashed lines, orientation of the reference axis of the strain gauge (strain orientations positive in the counter-clockwise direction); the green solid line represents the mean orientation of in vivo ε₁, and the green shaded are corresponds to the mean orientation ± 1 SD.

3. Results

3.1. In vivo strain magnitudes, ratios and orientations

The upper lateral (ULAT) strain gauge recorded higher magnitudes of mean ε₁ and ε₂ strains (81 με, −90 με) and maximum ε₁ and ε₂ strains (206 με, −196 με) than the medial (MED) (means: 50 με, −69 με; maxima: 107 με, −145 με) and lower lateral (LLAT) gauges (means: 56 με, −48 με; maxima: 133 με, −109 με) (Table 2). Mean ε₁ orientations were 78°, 110° and 16°, respectively for the ULAT, LLAT and MED gauge sites (Table 2). Maximum ε₁ orientations at the ULAT, LLAT and MED gauge sites were 179°, 174° and 179°, respectively. Minimum ε₁ orientations were 0° at the ULAT, 85° at the LLAT and 0° at the MED gauge locations (Table 2).

3.2. Sensitivity analysis

3.2.1. Effect of varying Young’s modulus of the trabecular tissue

Comparisons between FEMs A–D – with E values for the trabecular tissue of 1 GPa, 2 GPa, 3 GPa and 10 GPa, respectively – reveal that at the lateral gauge sites, as expected, the highest mean ε₁ values were found in the least stiff Model, A (279 με and 204 με for the ULAT and LLAT gauge sites) (Table 3, Figs. 4 and 7) and the lowest mean ε₁ values were found in the stiffest Model, D (244 με and 174 με for the ULAT and LLAT gauge sites). In contrast, at the MED gauge site, the highest mean ε₁ value (68 με) was found in the stiffest Model (D) and the lowest mean ε₁ values (55 με) were measured in the least stiff Model (A). Model D also had the smallest mean ε₂ values at the ULAT and LLAT gauge locations (−172 με and −115 με), when compared to Models A–C (Table 3 and Fig. 7). At the MED gauge site Model A showed smaller mean ε₂ values (−80 με) than Models A–C.

Table 3.

Descriptive statistics for maximum (Max), minimum (Min) and mean principal (ε₁ and ε₂) and |(ε₁/ε₂)| strain magnitude (με) for all FEMs. Gauge location: ULAT, LLAT and MED are abbreviations for upper lateral, lower lateral and medial (cf. Fig. 1). SD represents standard deviation.

Gauge location	FEM ID	n elements	ε1				ε2				ε1/ε2 ratio
			Mean	SD	Min	Max	Mean	SD	Min	Max	Mean	SD	Min	Max
ULAT	A	56	279	18	249	311	−188	9	−208	−166	1.49	0.05	1.35	1.59
	B	56	275	17	244	307	−189	10	−208	−162	1.45	0.05	1.32	1.56
	C	56	271	17	240	302	−188	10	−206	−158	1.44	0.05	1.30	1.57
	D	56	244	15	216	273	−172	13	−198	−138	1.42	0.07	1.28	1.64
	E	56	239	14	211	267	−168	13	−194	−135	1.42	0.07	1.28	1.64
	F	56	223	12	202	247	−160	12	−190	−124	1.40	0.08	1.21	1.68
	G	56	178	13	151	201	−144	8	−158	−124	1.23	0.06	1.11	1.36
	H	56	127	9	108	144	−98	6	−109	−84	1.29	0.06	1.16	1.41
	I	56	169	8	156	187	−115	8	−137	−90	1.47	0.09	1.26	1.79
LLAT	A	54	204	27	153	256	−151	18	−181	−113	1.36	0.13	1.04	1.62
	B	54	200	26	149	251	−143	18	−174	−105	1.40	0.12	1.10	1.68
	C	54	196	26	146	246	−138	18	−169	−100	1.43	0.11	1.15	1.72
	D	54	174	23	129	220	−115	15	−145	−83	1.53	0.11	1.26	1.85
	E	54	172	22	129	216	−112	15	−142	−81	1.54	0.11	1.27	1.87
	F	54	175	19	139	210	−110	14	−140	−82	1.59	0.10	1.36	1.94
	G	54	113	21	71	153	−105	12	−125	−81	1.06	0.12	0.83	1.26
	H	54	80	15	51	109	−70	8	−83	−52	1.15	0.12	0.90	1.35
	I	54	137	13	113	162	−80	9	−101	−62	1.72	0.11	1.49	2.07
MED	A	48	55	10	39	80	−80	11	−102	−58	0.69	0.11	0.47	0.92
	B	48	58	8	45	77	−88	11	−111	−65	0.67	0.09	0.49	0.92
	C	48	61	6	49	77	−92	12	−116	−68	0.67	0.10	0.52	0.93
	D	48	68	6	57	81	−101	13	−127	−74	0.69	0.11	0.54	0.97
	E	48	69	5	59	81	−97	12	−122	−70	0.73	0.12	0.57	1.02
	F	48	114	10	93	132	−176	22	−221	−127	0.66	0.10	0.52	0.90
	G	48	48	5	37	58	−58	9	−73	−37	0.85	0.10	0.70	1.08
	H	48	32	4	24	39	−41	7	−54	−26	0.78	0.10	0.64	1.01
	I	48	77	8	60	91	−132	18	−167	−93	0.60	0.10	0.45	0.83

Principal strain distributions in Models A and D are compared in Fig. 6 (top left). This comparison yields information on the effects of uniform increases in the stiffness of the internal trabecular tissue in the FEM (illustrated in the interactive pdf file, supplementary Fig. S2). As expected, the majority of the sites across the mandible reveal negative values (illustrated by blue shading in Fig. 6), indicating that the stiffer Model D experiences lower principal strain magnitudes than Model A. However, the decreases in strain magnitudes are not uniform in space or in magnitude. It is noteworthy that in small and limited areas at the inferior buccal left corpus and the most inferior border of the lingual symphysis Model A experiences slightly lower principal strain magnitudes than Model D. Some areas of the mandible – alveolar bone, the basal symphysis, the right retromolar trigon and the right condyle – display comparatively large decreases in principal strains (Fig. 6). These differences in strain magnitudes across Models A through D are accompanied by only slight variation in ε₁ orientations at the ULAT and LLAT gauge sites and higher variation at the MED gauge site: mean ε₁ orientations at the ULAT, LLAT and MED gauge sites were 63°, 72° and 0° in Model A and 64°, 72° and 5° in Model D (Table 4 and Fig. 8). Most of the variation in both principal strain magnitudes and ε₁ orientations between Models A and D are found at the MED gauge site.

Table 4.

Descriptive statistics for maximum (Max), minimum (Min) and mean ε₁ orientation for all FEMs. Gauge location: ULAT, LLAT and MED are abbreviations for upper lateral, lower lateral and medial (Fig. 1). SD represents standard deviation.

Gauge location	Model ID	n elements	ε1 Orientation (degrees)
			Mean	SD	Min	Max
ULAT	A	56	63	2	59	66
	B	56	63	2	60	67
	C	56	64	2	60	67
	D	56	64	2	60	68
	E	56	64	2	60	67
	F	56	66	2	62	69
	G	56	70	1	68	73
	H	56	69	1	66	72
	I	56	65	2	60	68
LLAT	A	54	72	2	67	75
	B	54	72	2	67	75
	C	54	72	3	66	76
	D	54	72	3	66	76
	E	54	72	3	65	76
	F	54	71	3	64	76
	G	54	84	2	80	88
	H	54	81	2	78	85
	I	54	69	3	62	74
MED	A	48	0	6	−10	13
	B	48	3	6	−7	14
	C	48	4	5	−5	14
	D	48	5	4	−2	13
	E	48	5	4	−3	13
	F	48	17	1	14	20
	G	48	4	3	−1	11
	H	48	1	3	−5	8
	I	48	17	1	14	20

Comparison of the in vivo and FEM strain data reveals that Model D (with E = 10 GPa for trabecular tissue) had the mean ε₁ and ε₂ magnitudes closest to the in vivo experiment at the ULAT and LLAT gauge locations, and Model A was closer to the in vivo experiment at the MED site (Table 5), but all Models showed higher strains and were overall less stiff than the mandible in vivo.

Table 5.

Absolute difference between the FEMS (A–H) and the in vivo experiment, where n elements is 54, 48, 56 for the upper lateral (ULAT), lower lateral (LLAT), and medial (MED) locations, respectively.

Gauge location	Comparison		ε1 magnitude (με)			ε2 magnitude (με)			Mean ε1 orientation (degrees)
			Mean	Min	Max	Mean	Min	Max
ULAT	In vivo	A	198	239	105	98	12	157	−15
	In vivo	B	194	234	101	99	12	153	−15
	In vivo	C	190	230	96	98	10	149	−14
	In vivo	D	163	206	67	82	2	129	−14
	In vivo	E	158	201	61	78	−2	126	−14
	In vivo	F	142	192	41	70	−6	115	−12
	In vivo	G	97	141	−5	54	−38	115	−8
	In vivo	H	46	98	−62	8	−87	75	−9
	In vivo	I	88	146	−19	25	−59	81	−13
LLAT	In vivo	A	148	148	123	103	72	109	−38
	In vivo	B	144	144	118	95	65	101	−38
	In vivo	C	140	141	113	90	60	96	−38
	In vivo	D	118	124	87	67	36	79	−38
	In vivo	E	116	124	83	64	33	77	−38
	In vivo	F	119	134	77	62	31	78	−39
	In vivo	G	57	66	20	57	16	77	−26
	In vivo	H	24	46	−24	22	−26	48	−29
	In vivo	I	81	108	29	32	−8	58	−41
MED	In vivo	A	5	27	−27	11	−43	48	−16
	In vivo	B	8	33	−30	19	−34	55	−13
	In vivo	C	11	37	−30	23	−29	58	−12
	In vivo	D	18	45	−26	32	−18	64	−11
	In vivo	E	19	47	−26	28	−23	60	−11
	In vivo	F	64	81	25	107	76	117	1
	In vivo	G	−2	25	−49	−11	−72	27	−12
	In vivo	H	−18	12	−68	−28	−91	16	−15
	In vivo	I	27	48	−16	63	22	83	1

3.2.2. Effect of varying Young’s modulus in the teeth

FEMs D (with E= 17 GPa for the teeth) and E (with E= 24.5 GPa for the teeth) yield similar ε₁ and ε₂ strain patterns and magnitudes (Figs. 4, 5 and 6). However, Model E had the lowest mean ε₁ (239 με ULAT and 172 με LLAT) and ε₂ (−168 με ULAT, −112 με LLAT, and −97 με MED) magnitudes. At the MED gauge site Models D (68 με) and E (69 με) gave similar mean ε₁ magnitudes (Table 3 and Fig. 7). Mean ε₁ orientations in FEMs D (Table 4 and Fig. 8) and E (Table 4, Figs. 8 and 9) were similar. As expected, comparisons of Models D and E reveal only very minor differences in principal strain distributions associated with changing the material properties of the teeth (Fig. 6, left middle). These will not be discussed further. The strains were higher in FEMs D and E than in vivo, with Model E being the closest to the in vivo mean ε₁ (158 με ULAT and 116 με LLAT) and ε₂ (78 με ULAT,64 με LLAT, 28 με MED) magnitudes (Table 5). At the MED gauge Models D and E were similar, yet Model D was closer to the in vivo mean ε₁.

Fig. 9.

Comparison of principal strain vector plots from FEMs A through D with those from the in vivo data. The left, middle, and right panels show the principal strains at the location of the lower lateral (LLAT), medial (MED), and upper lateral (ULAT) strain gauges, respectively. The figures in the middle panel are transparent because the medial gauge is located on the lingual side of the mandible. Red lines, orientation and magnitude of the FEM maximum principal strain (ε₁); blue lines, orientation and magnitude of FEM minimum principal strains (ε₂); dashed lines, orientation of the reference axis of the strain gauge (strain orientations positive in the counter-clockwise direction); the green solid line represents the mean orientation of in vivo ε₁, and the green shaded are corresponds to the mean orientation ± 1 SD.

3.2.3. Effects of varying TMJ constraints

Comparisons of ε₁ (Fig. 4) and ε₂ (Fig. 5) magnitudes (Table 3) and orientations (Table 4, Figs. 8 and 9) reveal that at the MED gauge site both ε₁ and ε₂ magnitudes were higher in Model F (in which the left TMJ was fixed and all left postcanine teeth were constrained along the X, Y and Z axes) than Model E (in which the right TMJ was fixed and the left postcanine teeth were constrained along the X axis), whereas at the ULAT gauge site mean ε₁ and ε₂ magnitudes were lower in Model F than in Model E (Table 3). At the LLAT gauge site Model F gave higher mean ε₁ but lower mean ε₂ magnitudes than Model E (Table 3). Moreover, absolute differences in mean ε₁ and ε₂ magnitude between the in vivo experiment and Models E and F showed that Model F was closer to the in vivo experiment at the ULAT gauge site but Model E gave mean ε₁ and ε₂ magnitudes closer to the in vivo data at the MED gauge location. At the LLAT location, Model E gave closer mean ε₁ magnitudes to the in vivo data, yet Model F gave mean ε₂ magnitudes closer to the in vivo strains (Table 5). Interestingly, comparison of the strain distributions between Models E and F (Fig. 6, bottom left) reveal large effects of changing the fixed condyle from the right TMJ (Model E) to the left TMJ (Model F) and changing constraints of the postcanine teeth from the superior-inferior axis only (Model E) to constraint against translations along all axes (Model F) (Fig. 6). Fixing the left condyle instead of the right results in increases in tensile (ca. 200 με–700 με) strains on the lingual face of the symphysis, the anterior region of the lingual aspect of both balancing and working side corpora, and entocondylar crests on the rami (ridge from lingual surface of condylar neck angling down towards the toothrow), and in compressive strains on the labial face of the symphysis. These changes are indicative of a change from medial to lateral “wishboning” of the mandible.

3.2.4. Effects of varying bite point constraints

Changing the bite point constraints between Model F (all working-side [left] post-canine teeth constrained) and G (working-side premolars and m₁ constrained) had the largest effect on strain magnitudes at the MED gauge site of any of the modeling changes, bringing principal strain magnitudes into the range of the in vivo results. Model G had lower mean ε¹ magnitudes at all gauge sites (178 με, 113 με and 48 με for the ULAT, LLAT and MED) (Table 3, Figs. 4 and 7) than Models A through F.

Direct comparisons of Models G and F reveal that concentrating the bite point at p₃-m₁ (Model G) results in increases in ε₁ magnitudes in the lingual symphysis, decreases in ε₁ magnitudes around the anterior face of the working side corpus lingually and buccally, and a decrease in compressive strains in the labial symphysis. The largest differences in mean ε₁ orientations between Models F and G were in the ULAT and LLAT gauge sites, where mean ε₁ orientations were respectively 66° and 71° for Model F and 70° and 84° for Model G (Tables 4 and 5, Figs. 8 and 10).

Both FEMs G and F yield strain magnitudes higher than the in vivo experiment at the ULAT and LLAT gauge locations. When compared against the in vivo experiment absolute differences in the mean ε₁ magnitudes from Model G were closer to the in vivo data than Model F at all strain locations (Table 5).

3.2.5. Effects of varying the time of muscle force estimation

Variation in the time of muscle force estimation between Models G (muscle force estimated at time of maximum overall muscle force) and Model H (muscle force estimated at the time of maximum strain magnitude in lower lateral gauge) resulted in Model H yielding mean ε₁ and ε₂ strain magnitudes closer than Model G to the magnitudes recorded in vivo for ULAT and LLAT gauge sites (Table 5 and Fig. 7). However, Model G gave mean ε₁ and ε₂ strain magnitudes closer to the in vivo experiments than Model H at the MED location (Table 5). Specifically, Model H displayed mean ε₁ magnitudes of 127 με, 80 με and 32 με at the ULAT, LLAT and MED locations, respectively (Table 3). Mean ε₂ magnitudes in Model H were −98 με, −70 με and −41 με for ULAT, LLAT and MED gauge sites (Table 3). Model G gave mean ε₁ magnitudes of 178 με ULAT, 113 με LLAT and 48 με MED and mean ε₂ magnitudes of −144 με, −105 με and −58 με respectively for the ULAT, LLAT and MED sites (Table 3).

As shown in Fig. 6, there were subtle differences in both ε₁ and ε₂ magnitudes between Models G and H. This change is associated with decreases in principal strains almost everywhere in Model H.

Mean ε₁ orientations in Models G and H were similar at all gauge sites, with Models G and H yielding 70° and 69°, respectively, at ULAT, 84° and 81° at LLAT, and 4° and 1° at MED gauge site (Tables 4 and 5, Figs. 8 and 10).

3.2.6. Effects of moving bite point from anterior to posterior tooth row

In most cases shifting the bite point from the anterior tooth row (p₃-m₁) (Model H) to the posterior tooth row (m₁-m₃) (Model I) resulted in higher strain magnitudes at the in silico gauge sites, and strain magnitudes further from the mean in vivo values (Fig. 7).

Principal strain magnitudes in Models H and Model I are compared in the bottom right of Fig. 6. Both are loaded using muscle forces calculated at the time of peak strain in the LLAT gauge but they differ in the bite point. Model H is constrained along the anterior postcanine tooth row (p₃-m₁) and Model I is constrained along the molar tooth row (m₁-m₃). There are predictable local effects in the alveolar bone, with Model I showing lower strains around the anterior teeth and higher strains around the posterior teeth. The changes in strain magnitudes associated with restricting the bite point to the posterior tooth row are the reverse of those associated with restricting the bite point to the anterior tooth row (Model F vs. Model G): i.e., higher strains in the lingual and buccal aspects of the posterior half of the working side corpus, decreases in the superior transverse torus strains, and increases in the inferior transverse torus strains. Mean ε₁ orientations in Model H are also closer to the in vivo data than Model I at the lateral gauge locations, but Model I gives mean ε₁ orientations closer to the in vivo experiment (and to Model F) at the MED gauge site.

4. Discussion

4.1. General aspects

The present study presents a subject-specific FEM of a rhesus macaque mandible during left chews on grapes and evaluates the effects on the FEM of variation in trabecular and dental tissue material properties, bite point locations, TMJ constraints, and muscle force modeling.

Our in vivo strain magnitudes (Table 2) are lower than those reported by Hylander and colleagues (Hylander, 1979b; Hylander and Crompton, 1986; Dechow and Hylander, 2000) and summarized by Lad et al. (2016). Our mean ε₁ in vivo strain magnitudes from the labial and lingual corpus ranged between 50 με and 81 με whereas the mean ε₁ data recorded by Hylander and colleagues from the corpus ranged from 116 με to 388 με. Further, the mean ε₂ in vivo strains recorded from the left corpus in our experiment ranged from −48 με to −90 με, whereas the mean ε₂ data recorded by Hylander and colleagues ranged from −100 με to −423 με. Many factors can influence strain comparisons between in vivo strain gauge studies, such as species variance, bite location, muscle activations, the location of the gauge site, and bone stiffness. However, the differences in strain magnitudes between our study and those summarized by Lad et al. (2016) are likely due to variations in the hardness/toughness of the food the monkeys chewed. While the monkey in our study fed on grapes, in the studies by Hylander and colleagues the animals chewed apples (Hylander, 1979b), apple skin (Hylander and Crompton, 1986), biscuits (Hylander and Crompton, 1986) and popcorn kernels (Dechow and Hylander, 2000). We speculate that grape skin is similar to apple skin and grape pulp similar to apple flesh in material properties (Williams et al., 2005). Comparison of our in vivo ε₁ strain orientations from the lateral (buccal) corpus with those from the work of Hylander (summarized in Fig. 1 of Ross et al., 2016) reveals close similarity between the orientations recorded at our upper lateral gauge site during grape chewing and those reported by Hylander and colleagues during chewing on a wide range of foods. We therefore conclude that our in vivo strain data are similar to those reported elsewhere in independent studies. Contrary to the lateral gauge site, the medial gauge location in our in vivo experiment gave more variable mean ε₁ orientations but orientations similar to those of Dechow and Hylander (2000) (i.e., upwards and forwards on the working side). The variability may be due to the fact that the working side corpus is a low strained area lingually and posteriorly during unilateral postcanine chewing on grapes. Future research when the animal is chewing on tougher and harder food particles will allow us to readdress this issue. As expected, variation in the material properties of the teeth (Models D and E), had negligible effect on strain magnitudes (Fig. 6 and Table 5), regimes (Figs. 4 and 5) or orientations (Figs. 8 and 9, Table 5). As hypothesized, bone strain regimes in the corpus away from the alveolar bone are relatively insensitive to variations in modeled teeth material properties.

To assess the effects of variation in the material properties of the trabecular tissue when assigning it an isotropic and homogeneous value for E, we varied the magnitude of E across a range of 1–10 GPa. Our results show that the stiffest model, with an E value of 10 GPa for the trabecular tissue, yielded strain magnitude data closer to the experimental values for the buccal gauge sites than the less stiff models but still larger than those recorded in vivo (Fig. 7 and Table 5). In contrast, the medial gauge site recorded principal strain magnitudes closer to the in vivo experiment in the least stiff model, Model A, with strains increasing away from this value in the order Model A, B, C, D, although these increases are slight.

While in silico strain regimes at the medial gage site were slightly affected by variation in the material properties of the trabecular tissue, strains at this location were more significantly impacted by changes in constraints at the TMJs and teeth between Models E and F. In Model F the working side (left) TMJ is fixed and the balancing (right) is allowed to displace laterally (the opposite of Model E) and all the postcanine teeth are fixed in all directions, rather than just in X. The effect of this was to alter the deformation regime from medial transverse bending (medial wishboning) to lateral transverse bending (lateral wishboning) of the mandible. This change in deformation regime is accompanied by only minor changes in strain orientations (0–2°) and strain magnitudes at the lateral gage sites, but larger changes in strain orientations (7°) and very large increases in strain magnitudes at the medial gauge site (MED) (Table 4, Fig. 7). Changes from a medial to a lateral deformation regime are associated with even larger changes in strain regimes elsewhere in the mandible, especially in the lingual symphysis and the lingual aspect of the corpora and entocondylar crests, where in vivo strain data are difficult/impossible to obtain (Fig. 6).

Under this more realistic lateral wishboning deformation regime, variation in the location of bite point constraints—the entire post-canine tooth row (Model F), the premolars and m₁ (Models G and H), or all the molars (Model I)—had large effects on principal strain distributions (Figs. 4, 5 and 6), magnitudes (Fig. 7 and Table 5), and orientations (Figs. 8, 9, and 10, Table 5). At medial and lateral gauge sites large changes in ε₁ and ε₂ magnitudes (decreases) and ε₁ orientations resulted from switching the tooth row constraints from the entire post-canine tooth row (Model F) to only the premolars and m₁ (Model G). These changes were largely or completely reversed by again constraining m_2–3 in Model I. Importantly however, switching to Model I saw larger increases in tensile strains in the lateral corpus and larger increases in compressive strains in the medial corpus, suggesting that constraining m_2–3 causes the corpus to be subjected to greater amounts of transverse bending. Accompanying the increases in strain magnitudes in the working-side corpus with constraints at m_2–3 there was increase in ε₁ (tensile) and ε₂ (compressive) magnitudes in the labial symphysis and the balancing side corpus buccally and lingually, resulting from the larger bending moment arm of the bite reaction force about the symphysis.

Our sensitivity analysis showed that the FEM strain data most closely resembled the in vivo data when only the premolars and the first molar of the chewing side were constrained against all translations, suggesting that the animal chewed grapes on the anterior region of the tooth row. Future experimental studies using bi-planar videofluoroscopy will test this hypothesis in other animals.

It is noteworthy that the effects of bite point variation on strain orientations were greatest at the medial and lower lateral gauge site: strains at the in silico upper lateral gauge site were less affected by variation in modelled bite point. This upper lateral gauge site is the most common (and most easily accessed) location of strain gauge placement for in vivo feeding studies (Hylander, 1979a,b; Ross et al., 2016) and food-type-associated variation in strain orientation at this site in vivo is minimal (Ross et al., 2016). The modeling results presented here suggest that this site might not be the best place to detect variation in in vivo strain regimes associated with variation in food type, especially if food type variation elicits variation in bite point during chewing.

Amongst all sensitivity variables evaluated here (material properties of trabecular tissue and teeth, constraints of teeth and TMJ, time of muscle force estimation), constraints of teeth and TMJ had the strongest effect on strain magnitudes, patterns and orientations. The FEM results most closely resembled the in vivo experiment in Model H, which had the left TMJ and the left premolars and m₁ constrained in all translations and modelled muscle forces at the time of peak strain in the lower lateral strain gauge (Figs. 7 and 10), which occurs after peak EMG in the muscles (supplementary Fig. S1). Modeling the mandible at the time of peak LLAT strain rather than peak EMG results in widespread decreases in tensile and compressive strains (Fig. 6) accompanied by changes in strain orientations (Fig. 8). These changes suggest that detailed modeling of the relative timing of external forces and kinematics throughout the power stroke is needed to understand the full range of deformation, stress, and strain regimes in the primate mandible during chewing.

4.2. Limitations and future work

In the individual macaque studied here remodeling of the bone around the bone screws in the lateral symphysis created lateral bulging of the cortical and trabecular bone (supplementary Fig. S2). Although this reflects the effects of experimental interventions aimed at capturing high resolution jaw kinematics, it was important to accurately model this geometry in order to validate the model. Whether this bone modeling significantly alters the strain, stress and deformation regimes of the mandible remains to be evaluated. Comparisons of our in vivo corpus strain data with those reported elsewhere suggest this bone modeling response had little effect. Future studies employing bi-planar videofluoroscopy will circumvent the need for percutaneous bone screws.

The study reported here only validated the FEM of left chews on grapes. Given the importance of variation in feeding behavior and diet in hypotheses of the evolution of mandible form (Hylander, 1985, 1988; Ravosa, 1996, 2000), future work will address the validity of modeling of chewing on other foods and other feeding behaviors.

4.3. Conclusions

Finite element modeling is superior to beam models for the analysis of stress, strain and deformation regimes in primate mandibles, but it is important to understand which modeling parameters need particular attention in order to construct FEMs that accurately represent reality. The present study is the first to combine in vivo experimental data on jaw kinematics, muscle activity and bone strain with ex vivo data on cortical bone material properties to create a FEM simulation of a single rhesus mandible during feeding. The similarities between the strain regimes recorded in vivo and those generated by the model are marked. Our sensitivity analyses suggest that modeling mandibular trabecular tissue as an isotropic, homogeneous tissue of high stiffness (10 GPa) is suitable for reconstructing strain regimes in the mandibular corpus during ipsilateral chewing. Variation in the bite point and TMJ constraints is associated with significant variation in strain regimes in the mandible, which future experimental and modeling work should address. Our results also suggest that it is important to carefully document the relative timing of bite reaction and muscle forces during the chewing cycle to understand the full range of stress, strain and deformation regimes of the mandible during chewing, let alone other feeding behaviors.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.zool.2017.08.010.