Underactuated Potential Energy Shaping with Contact Constraints: Application to a Powered Knee-Ankle Orthosis

Abstract

Body-weight support (i.e., gravity compensation) is an effective clinical tool for gait rehabilitation after neurological impairment. Body-weight supported training systems have been developed to help patients regain mobility and confidence during walking, but conventional systems constrain the patient's treatment in clinical environments. We propose that this challenge could be addressed by virtually providing patients with bodyweight support through the actuators of a powered orthosis (or exoskeleton) utilizing potential energy shaping control. However, the changing contact conditions and degrees of underactuation encountered during human walking present significant challenges to consistently matching a desired potential energy for the human in closed loop. We therefore derive a generalized matching condition for shaping Lagrangian systems with holonomic contact constraints. By satisfying this matching condition for four phases of gait, we derive passivity-based control laws to achieve virtual body-weight support through a powered knee-ankle orthosis. We demonstrate beneficial effects of virtual body-weight support in simulations of a human-like biped model, indicating the potential clinical value of this proposed control approach.

I. Introduction

Individuals who have sustained a stroke, spinal cord injury, or other neurological condition often struggle to ambulate. Gait training is needed to help these patients regain mobility and independence. Patients are often provided with body-weight support (BWS), i.e., gravity compensation for the body's center of mass, to help them practice and relearn the coordinated muscle activities needed for walking. This locomotor retraining technique provides weight support for patients through a torso or hip harnesses attached to an overhead lift [1]. The percentage of BWS is often adjusted progressively as the patient's gait improves through the training process. Over the past two decades, the use of BWS training systems to enhance ambulation and motor function in individuals has received considerable attention [1]–[5].

Current body-weight supported training systems can be classified into two categories: treadmill/stationary training systems and ceiling-mounted overground training systems. The former one involves stepping on a motorized treadmill while a percentage of the patient's body weight is unloaded by a counterweight-harness system [5], whereas the latter one is mounted to a ceiling track so that the therapist can work hand in hand with the patient to allow personalized assistance [6]. Conventional static and passive training systems usually consist of winches, counterweights, and elastic springs [7], while recently, several robotic BWS devices have been developed to automate the assistance during gait training. For example, the Lokomat exoskeleton system uses motors to drive the patient's lower limbs based on a reference trajectory over a treadmill [8]. The LOPES treadmill system provides BWS via cable-driven series elastic actuators with an impedance controller [9]. The ceiling-mounted ZeroG system allows patients with severe gait impairment to practice gait and balance activities in a controlled manner inside a gait laboratory [6]. By unloading a certain percentage of body weight utilizing the aforementioned rehabilitation systems, patients can practice walking without the full strength or control of their muscles.

Despite the fact that robot-assisted rehabilitation systems have shown promise in improving patients' gaits, significant challenges still remain in aspects of control and mobility. The Lokomat system uses an impedance controller combined with supportive torques estimated through an adaptive algorithm, which makes the patient follow a specific joint position trajectory [8]. However, studies have shown that for subacute stroke patients, conventional labor-intensive interventions are more effective than Lokomat-assisted gait training [10]. Although new control strategies based on potential force fields have improved the mechanical transparency of the Lokomat to encourage patient participation during training [11], these control strategies still depend on predefined reference trajectories that may not generalize well across patients or tasks. In contrast, the ceiling-mounted ZeroG system allows freedom of motion while providing constant BWS with minimum horizontal dragging force as the patient walks [6]. However, patients can only receive therapy in clinical environments with treadmill or ceiling-mounted training devices, which greatly reduces the flexibility, convenience, and frequency of the therapy.

Many recent powered orthoses and exoskeletons address the issue of mobility, but the vast majority of these devices compensate for chronic deficits rather than provide therapeutic assistance for gait retraining [12], [13]. In one of the closest approaches to mobile BWS [14], the Vanderbilt exoskeleton provides a combination of feedforward movement assistance and gravity compensation for the swing leg to allow user adaptation of joint patterns with minimal interference from the exoskeleton. Although not designed for physical rehabilitation, the BLEEX enhances the ability of an able-bodied user to carry extra heavy loads, using force control to minimize the user's interaction forces with the exoskeleton so the user does not feel the weight of the backpack [15]. However, minimizing interaction forces with the exoskeleton does not offload the body weight of the human user. The passive gravity-balancing orthosis in [16] can provide variable gravity compensation to the patient's swing leg by adjusting the geometry of the links and the spring locations of the device. However, the use of physical springs could make the device too cumbersome to adjust for the progressive levels of support needed in a clinical setting. Powered orthoses/exoskeletons that provide easily adjustable BWS during both stance and swing might enable greater flexibility during gait rehabilitation, motivating the development of novel control strategies for this purpose.

Energy shaping, a control method that alters the dynamical characteristics of a mechanical system [17]–[21], could possibly be used to augment the gravitational forces perceived by the human body. Energy shaping approaches have already seen success in applications to bipedal walking robots [22]–[24]. Because weight is equal to mass times gravity, virtual BWS could be achieved by shaping the gravitational constant or the mass terms in the potential energy of the human body. This idea was attempted in simulations of a simple compass-gait biped model in [25], ignoring the different contact conditions and unactuated degrees of freedom (DOFs) encountered during human walking. This simplification prevented translation to a real orthosis that can be used by patients. More realistic models are needed to design orthotic control strategies that are appropriate for the underactuated phases of the human gait cycle. However, shaping the potential energy is difficult for underactuated dynamical systems since the Matching Condition, whose solutions dictate the achievable forms of a system's closed-loop energy, can be quite challenging to satisfy [22]. The changing contact conditions from heel strike to toe off also result in different unactuated DOFs throughout the gait cycle, making it difficult to consistently match a desired potential energy for the human in closed loop.

This paper develops a generalized methodology for underactuated potential energy shaping that leverages the contact constraints encountered during human walking. As an extension of the initial results presented in [26], we generalize the classical potential energy matching condition for constraint-free Lagrangian dynamics (used in [25]) to the case of Lagrangian dynamics with holonomic contact constraints. By modeling generalized dynamics instead of lower-dimensional contact-specific dynamics, a single position-feedback control law with passivity properties can be derived for all stance contact conditions. In addition to virtual BWS in [26], the proposed framework is used to examine another therapeutic control strategy, where weight is virtually added (i.e., negative BWS) for challenge-based training as defined in [27]. Because the potential shaping control approach does not prescribe reference joint trajectories, it is fundamentally task-invariant.

We begin in Section II by modeling the contact constraints for four phases of gait: heel contact, flat foot, toe contact, and no contact (i.e., swing). In Section III the generalized matching condition is derived and satisfied to obtain BWS control laws for stance and swing. Then, passivity and stability of the shaped human system are shown in Section IV. Finally, simulations of an 8-DOF biped in Section V demonstrate that the positive BWS controller results in shorter and slower steps accompanied by higher swing foot clearance, whereas the negative BWS controller results in longer and faster steps without sacrificing swing heel clearance. These results suggest that orthotic potential energy shaping could provide variable weight augmentation for mobile gait training, ranging from assistive to resistive therapies.

II. Dynamics of the Biped

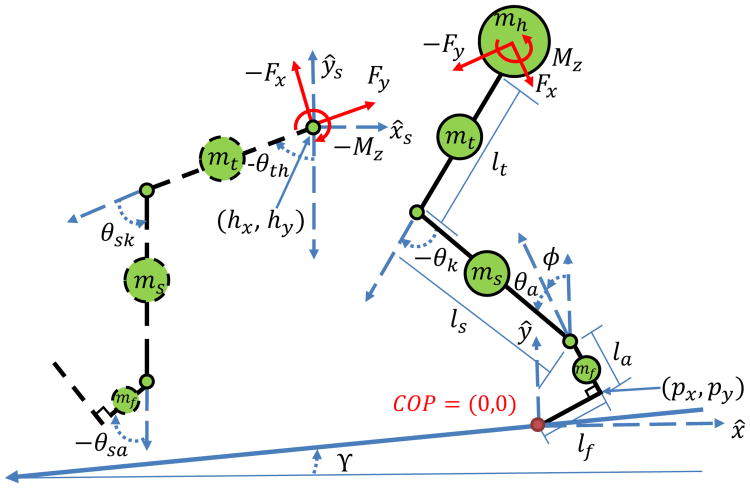
In this section, we are interested in controlling a powered knee-ankle orthosis using only feedback local to its leg. For the purpose of control derivation, we separate the dynamical models of the stance and swing legs, which are coupled through interaction forces (Fig. 1). We also assume the masses m_i, i ∈ {f, s, t, h}, shown in Fig. 1 are the combined masses of the human limb and its orthosis.

Fig. 1.

Kinematic model of the biped. The stance leg is shown in solid black and the swing leg in dashed black. For the simulation study we assume the biped is walking on a slope with angle γ.

A. Stance Leg

The stance leg is modeled as a kinematic chain with respect to an inertial reference frame (IRF) defined at either the heel or toe, depending on the phase of the stance period (to be discussed later). The generalized coordinates of this leg are given by q_st = (p_x, p_y, ϕ, θ_a, θ_k)^T, where p_x and p_y are the Cartesian coordinates of the heel, ϕ is the angle of the heel defined with respect to the vertical axis, and θ_a and θ_k are the ankle and knee angles, respectively. Following [28], [29] the generalized Lagrangian dynamics can be expressed as

$$M_{\text{st}}(q_{\text{st}}){\ddot{q}}_{\text{st}}+C_{\text{st}}(q_{\text{st}},{\dot{q}}_{\text{st}}){\dot{q}}_{\text{st}}+N_{\text{st}}(q_{\text{st}})+A_{\ell }{(q_{\text{st}})}^T\lambda =B_{\text{st}}{u}_{\text{st}}+B_{\text{st}}{v}_{\text{st}}+J_{\text{st}}{(q_{\text{st}})}^{T}F,$$ (1)

where M_st is the inertia/mass matrix, C_st is the Coriolis/centrifugal matrix, N_st is the potential forces vector with gravity constant g = 9.81, A_ℓ ∈ ℝ^c×5 is the constraint matrix defined as the gradient of the constraint functions, c is the number of contact constraints that may change during different contact conditions, and ℓ ∈ {heel, flat, toe} indicates different contact configurations. The Lagrange multiplier λ is calculated using the method in [29]. Assuming the orthosis has actuation at the ankle and knee joints, i.e., u_st = (u_a, u_k)^T ∈ ℝ^2×1, where u_a and u_k are the torques at the ankle and knee joints, the matrix B_st = (0_2×3, I_2×2)^T maps joint torques into the coordinate system. The interaction forces F = (F_x, F_y, M_z)^T ∈ ℝ^3×1 between the hip of the stance model and the swing thigh are composed of 3 parts: two linear forces and a moment in the sagittal plane [29]. Force vector F is mapped into the system's dynamics by the body Jacobian matrix J_st(q_st) ∈ ℝ^3×5. The human input term v_st = (v_a, v_k)^T ∈ ℝ^2×1 provides additional torques at the ankle and knee joints, i.e., v_a and v_k. While designing the energy shaping controller, we make no assumptions about the human inputs or interaction forces.

The stance period can be divided into three phases: heel contact, flat foot, and toe contact (Fig. 2), for which holonomic contact constraints can be appropriately defined.

Fig. 2.

Heel contact configuration (left), flat foot configuration (center), and toe contact configuration (right) during stance on a slope with angle γ.

1) Heel Contact: During this period the heel is fixed to the ground as the only contact point, about which the stance leg rotates. The IRF is defined at the heel, yielding the constraint a_heel(q_st) = 0 and matrix A_heel = ∇_qst a_heel where

$$\begin{array}{l}{a}_{\text{heel}}(q_{\text{st}})≔{(p_{\mathrm{x}},p_{\mathrm{y}})}^T,\hfill \\ A_{\text{heel}}=[I_{2\times 2},0_{2\times 3}].\hfill \end{array}$$ (2)

2) Flat Foot: At this configuration the foot is flat on the ground slope, where ϕ is equal to the slope angle. The IRF is still defined at the heel, which yields the constraint a_flat(q_st) = 0 and the constraint matrix A_flat = ∇_qst a_flat where

$$\begin{array}{c}{a}_{\text{flat}}(q_{\text{st}})≔{(p_{\mathrm{x}},p_{\mathrm{y}},\varphi -\gamma )}^T,\\ A_{\text{flat}}=[I_{3\times 3},0_{3\times 2}].\end{array}$$ (3)

3) Toe Contact: The toe contact condition begins when the center of pressure (COP), the point along the foot where the ground reaction force (GRF) is imparted, reaches the toe (detecting this event will be discussed later). When switching to this configuration, the IRF shifts instantly from the heel to the toe, where the COP is currently located. During this phase the toe is the only contact point, about which the stance leg rotates. We define the IRF at this contact point to simplify the contact constraints. The coordinates of the heel are then defined with respect to the toe, which gives us the constraint a_toe(q_st) = 0 and the constraint matrix A_toe = ∇_qst a_toe where

$$\begin{array}{c}{a}_{\text{toe}}(q_{\text{st}})≔{(p_{\mathrm{x}}-l_{\mathrm{f}}cos(\varphi ),p_{\mathrm{y}}-l_{\mathrm{f}}sin(\varphi ))}^T,\\ A_{\text{toe}}(q_{\text{st}})=\left[\begin{array}{ccccc}1& 0& l_{\mathrm{f}}sin(\varphi )& 0& 0\\ 0& 1& -l_{\mathrm{f}}cos(\varphi )& 0& 0\end{array}\right].\end{array}$$ (4)

B. Swing Leg

We choose the hip as a floating base for the swing leg's kinematic chain in Fig. 1. The full configuration of this leg is given as q_sw = (h_x, h_y, θ_th, θ_sk, θ_sa)^T, where h_x and h_y are the positions of the hip, θ_th is the angle defined between the vertical axis and the swing thigh, and θ_sk and θ_sa are the angles of the swing knee and ankle, respectively. By deriving the equations of motion [28], we obtain

$$M_{\text{sw}}(q_{\text{sw}}){\ddot{q}}_{\text{sw}}+C_{\text{sw}}(q_{\text{sw}},{\dot{q}}_{\text{sw}}){\dot{q}}_{\text{sw}}+N_{\text{sw}}(q_{\text{sw}})=B_{\text{sw}}{u}_{\text{sw}}+B_{\text{sw}}{v}_{\text{sw}}-J_{\text{sw}}{(q_{\text{sw}})}^{T}F,$$ (5)

where M_sw is the inertia/mass matrix, C_sw is the Coriolis/centrifugal matrix, and N_sw is the potential forces vector. The matrix B_sw = (0_2×3, I_2×2)^T maps the orthosis torque vector u_sw = (u_sk, u_sa)^T ∈ ℝ^2×1 into the system, where u_sk and u_sa are the torques at the swing knee and swing ankle, respectively. The vector F = (F_x, F_y, M_z)^T ∈ ℝ^3×1 contains the interaction forces between the swing leg and hip (including human hip torques), and J_sw(q_sw) ∈ ℝ^3×5 is the body Jocabian matrix that maps F into the dynamics. The input vector v_sw = (v_sk, v_sa)^T ∈ ℝ^2×1 contains human knee and ankle torques v_sk and v_sa, respectively. As in the case of the stance leg, we design the energy shaping controller without assumptions on the human inputs or interaction forces. There are no contact constraints during swing, i.e., A_sw = 0.

III. Energy Shaping Control

A. Strategies for Rehabilitation

According to the literature review in [27], assistive control strategies and challenged-based control strategies are two of the main categories of robotic movement training. These two categories can be treated as part of a continuum along which task difficulty can be modulated from easier-than-normal to harder-than-normal [30]. In the assistive category, studies have demonstrated the clinical efficacy of BWS methods that unload a certain percentage of a patient's body-weight using different types of devices [2]–[4]. However, evidence in [31] suggests that adding resistance to a patient's lower limbs can enhance flexor muscle activity during treadmill locomotion in incomplete spinal cord injury. Therefore, in this section, we will derive a general potential energy shaping framework that is capable of the following two control strategies:

$$\begin{array}{llll}1.\hfill & \text{Positive Virtual BWS}(\text{assist})\hfill & \text{where}\hfill & \stackrel{\sim }{g}<g,\hfill \\ 2.\hfill & \text{Negative Virtual BWS}(\text{challenge})\hfill & \text{where}\hfill & \stackrel{\sim }{g}>g.\hfill \end{array}$$

We will see that the gravity constant g can only be shaped in certain rows of N_sw and, depending on the contact condition, N_st. Because weight is equal to mass times gravity, shaping the gravity constant in these rows is equivalent to shaping the masses of the shank, thigh, and hip during stance or the foot and shank during swing.

B. Definition of Matching Condition

Although we modeled the biped with contact constraints explicitly appearing in the generalized dynamics (1), this section will review the concept of potential energy shaping for a Lagrangian system without explicit constraints [17]–[21], though contact constraints could be implicit if only a subset of the generalized coordinates are modeled. We will later prove that potential energy shaping can be equivalently achieved in a generalized Lagrangian system with explicit constraints.

Consider a forced Euler-Lagrange system with configuration space ℚ, taken for simplicity to be equal to ℝⁿ, and described by a Lagrangian L : T ℚ → ℝ:

$$L(q,\dot{q})=\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}-P(q),$$ (6)

where $\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}$ is the kinetic energy and P (q) is the potential energy. The Lagrangian dynamics are given by

$$\frac{d}{dt}{\partial }_{\dot{q}}L(q,\dot{q})-{\partial }_{q}L(q,\dot{q})=B(q)u+F_{\text{nc}},$$ (7)

where B(q) : ℝ^m → T_q*ℚ≃ℝⁿ with rank m maps the torque vector u ∈ ℝ^m into the dynamical system. We consider the underactuated case, hence m < n. The vector F_nc ∈ ℝⁿ contains the external (non-conservative) forces. We can express (7) in the following form for a mechanical system:

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+N(q)=B(q)u+F_{\text{nc}},$$ (8)

where terms on the left-hand side are defined similarly to (1) with N (q) = ∇_q P (q).

Now consider an unforced Euler-Lagrange system defined by another Lagrangian L̃ : T ℚ → ℝ:

$$\stackrel{\sim }{L}(q,\dot{q})=\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}-\stackrel{\sim }{P}(q)$$ (9)

for a new potential energy P̃(q), resulting in the dynamics

$$\frac{d}{dt}{\partial }_{\dot{q}}\stackrel{\sim }{L}(q,\dot{q})-{\partial }_q\stackrel{\sim }{L}(q,\dot{q})=F_{\text{nc}}.$$ (10)

These Lagrangian dynamics can be expressed in the form

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+\stackrel{\sim }{N}(q)=F_{\text{nc}}$$ (11)

with Ñ (q) = ∇_q P̃(q).

Definition 1: The systems (8) and (11) match if (11) is a possible closed-loop system of (8), i.e., there exists a control law u such that (8) becomes (11).

Standard results in [19] show that systems (8) and (11) match if and only if there exists a full-rank left annihilator B(q)^⊥ ∈ ℝ^(n−m)×n of B(q), i.e., B(q)^⊥B(q) = 0 and rank(B(q)^⊥) = (n − m), ∀q ∈ ℚ, such that

$$B^{\perp }(N-\stackrel{\sim }{N})=0.$$ (12)

Equation (12) is the so-called matching condition. From now on, we will omit q in the dynamical terms to abbreviate notations. Assuming (12) is satisfied, the control law that achieves the closed-loop dynamics (11) is given as

$$u={(B^{T}B)}^{-1}{B}^T(N-\stackrel{\sim }{N}),$$ (13)

where Ñ is the desired potential forces vector, which can be chosen with properties such as weight augmentation.

C. Equivalent Constrained Dynamics

The classical matching condition and control law in the previous section cannot be directly applied to the generalized dynamics (1). Although a dynamical system in the form of (8) could be separately modeled for each phase by dropping constrained coordinates from the generalized coordinate vector, this would require a clever change of coordinates for some constraints (e.g., rolling contact [32]). The dimension and degree of underactuation of the resulting hybrid system would also change between phases, requiring different models of potential energy for control law (13). Switching between control models in real time would require precise estimates of gait cycle phase and knowledge of the contact constraints, which can be difficult to achieve in practice. Moreover, the full generalized coordinates are required to derive impact maps [33], [34], so a system of the form (1) would still be needed.

Instead of modeling a different dynamical system for each phase, we will extend the results of the previous section to a single generalized Lagrangian system (1) to obtain a shaping framework which can accommodate any holonomic contact constraints (and the resulting unactuated DOFs) that could occur during various locomotor tasks. This generalized framework will show exactly what terms can and cannot be shaped with each contact constraint. Although the generalized matching condition will depend on the contact constraints, we will see that the resulting control laws are identical and thus can accommodate uncertainty in the contact constraints that the non-generalized approach cannot.

We start by plugging expressions for A_ℓ and λ into (1) to obtain the form of (8), which is denoted as the equivalent constrained dynamics. We will derive the energy shaping control laws in the next section based on these constrained dynamics, which have fewer (possible zero) unactuated DOFs compared to the generalized dynamics (1) without constraints. The constraint matrices for each contact condition are already defined in Section II-A, and we follow the method in [28], [29] to determine the GRF vector as

$$\begin{array}{l}\lambda =\widehat{\lambda }+\stackrel{⌣}{\lambda }{u}_{\text{st}}+\overline{\lambda }F,\text{where}\hfill \\ \widehat{\lambda }=W({\dot{A}}_{\ell }{\dot{q}}_{\text{st}}-A_{\ell }{M}_{\text{st}}^{-1}(C_{\text{st}}{\dot{q}}_{\text{st}}+N_{\text{st}}-B_{\text{st}}{v}_{\text{st}})),\hfill \end{array}$$ (14)

$$\begin{array}{l}\stackrel{⌣}{\lambda }=W{A}_{\ell }{M}_{\text{st}}^{-1}{B}_{\text{st}},\hfill \\ \overline{\lambda }=W{A}_{\ell }{M}_{\text{st}}^{-1}{J}_{\text{st}}^T,\text{where}W={(A_{\ell }{M}_{\text{st}}^{-1}{A}_{\ell }^T)}^{-1}.\hfill \end{array}$$ (15)

Note that N_st appears in λ̂, so this term must also be shaped by control. Plugging in A_ℓ and λ, dynamics (1) become:

$$M_{\lambda }{\ddot{q}}_{\text{st}}+C_{\lambda }{\dot{q}}_{\text{st}}+N_{\lambda }=B_{\lambda }{u}_{\text{st}}+B_{\lambda }{v}_{\text{st}}+J_{\lambda }^{T}F,$$ (16)

where

$$\begin{array}{l}{M}_{\lambda }=M_{\text{st}},\hfill \\ C_{\lambda }=[I-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}]C_{\text{st}}+A_{\ell }^{T}W{\dot{A}}_{\ell },\hfill \\ B_{\lambda }=[I-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}]B_{\text{st}},\hfill \\ N_{\lambda }=[I-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}]N_{\text{st}},\hfill \\ J_{\lambda }=J_{\text{st}}{[I-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}]}^T.\hfill \end{array}$$ (17)

We wish to achieve in closed-loop the constrained dynamics

$$M_{\lambda }{\ddot{q}}_{\text{st}}+C_{\lambda }{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\lambda }=B_{\lambda }{v}_{\text{st}}+J_{\lambda }^{T}F,$$ (18)

where we choose

$${\stackrel{\sim }{N}}_{\lambda }=[I-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}]{\stackrel{\sim }{N}}_{\text{st}},$$ (19)

given the desired potential forces vector Ñ_st, which will be introduced in Section III-D.

Given that (16) and (18) have the form of (8) and (11), respectively, the equivalent constrained matching condition has the same form as (12):

$$B_{\lambda }^{\perp }(N_{\lambda }-{\stackrel{\sim }{N}}_{\lambda })=0,$$ (20)

and the control law that achieves (18) is similarly given as

$$u_{\text{st}}={(B_{\lambda }^T{B}_{\lambda })}^{-1}{B}_{\lambda }^T(N_{\lambda }-{\stackrel{\sim }{N}}_{\lambda }).$$ (21)

Remark 1: This control methodology has the beneficial property of requiring only local position feedback q_st based on the definitions of B_λ and N_λ in (17). Explicitly modeling the inertial DOFs allows the generalized approach to accommodate uncertainty in the contact conditions that the classical approach cannot, as we will see in Section V-C3.

We now wish to prove that the control law (21) actually brings (1) into the desired dynamics

$$M_{\text{st}}{\ddot{q}}_{\text{st}}+C_{\text{st}}{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\text{st}}+A_{\ell }^T\stackrel{\sim }{\lambda }=B_{\text{st}}{v}_{\text{st}}+J_{\text{st}}^{T}F,$$ (22)

where Ñ_st is the desired potential forces vector, and

$$\stackrel{\sim }{\lambda }=\mathrm{W}({\dot{A}}_{\ell }{\dot{q}}_{\text{st}}-A_{\ell }{M}_{\text{st}}^{-1}(C_{\text{st}}{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\text{st}}-B_{\text{st}}{v}_{\text{st}}))+\overline{\lambda }F$$ (23)

is the GRF vector associated with the new potential energy.

Lemma 1: If matching condition (20) is satisfied, the control law (21) with Ñ_λ defined as (19) brings the generalized Lagrangian system (1) into the form of (22) with the desired potential forces vector Ñ_st and associated GRF vector (23). Therefore, system (1) matches system (22).

Proof: By construction we can equate (1) and (16):

$$\begin{array}{ll}0\hfill & =M_{\text{st}}{\ddot{q}}_{\text{st}}+C_{\text{st}}{\dot{q}}_{\text{st}}+N_{\text{st}}+A_{\ell }^T\lambda -B_{\text{st}}{u}_{\text{st}}-B_{\text{st}}{v}_{\text{st}}-J_{\text{st}}^{T}F\\ & =M_{\lambda }{\ddot{q}}_{\text{st}}+C_{\lambda }{\dot{q}}_{\text{st}}+N_{\lambda }-B_{\lambda }{u}_{\text{st}}-B_{\lambda }{v}_{\text{st}}-J_{\lambda }^{T}F.\hfill \end{array}$$

Given satisfaction of (20), control law (21) provides the closed-loop dynamics (18), so the previous equality becomes

$$0=M_{\lambda }{\ddot{q}}_{\text{st}}+C_{\lambda }{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\lambda }-B_{\lambda }{v}_{\text{st}}-J_{\lambda }^{T}F.$$

Expanding expressions from (17), we can then obtain

$$0=M_{\text{st}}{\ddot{q}}_{\text{st}}+C_{\text{st}}{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\text{st}}-B_{\text{st}}{v}_{\text{st}}-J_{\text{st}}^{\mathrm{T}}F+A_{\ell }^{\mathrm{T}}\mathrm{W}{\dot{A}}_{\ell }{\dot{q}}_{\text{st}}-A_{\ell }^{\mathrm{T}}W{A}_{\ell }{M}_{\text{st}}^{-1}(C_{\text{st}}{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\text{st}}-B_{\text{st}}{v}_{\text{st}})-A_{\ell }^{T}W{A}_{\ell }{M}_{\text{st}}^{-1}{J}_{\text{st}}^{T}F.$$

Leveraging the definitions (23) and (14), we finally have

$$0=M_{\text{st}}{\ddot{q}}_{\text{st}}+C_{\text{st}}{\dot{q}}_{\text{st}}+{\stackrel{\sim }{N}}_{\text{st}}-B_{\text{st}}{v}_{\text{st}}-J_{\text{st}}^{T}F+A_{\ell }^T\stackrel{\sim }{\lambda },$$

which is equivalent to (22) and matches (1). ■

Remark 2: Although N_λ contains the inertia matrix in (17), Lemma 1 shows that components of this matrix should not be changed in Ñ_λ even if common parameters (like masses) are changed in Ñ_st. We will later see that the inertia matrix terms may disappear from control law (21) after simplification.

We can now establish the usefulness of the equivalent constrained form and the associated matching condition (20).

Theorem 1: The generalized systems (1) and (22) match if the equivalent constrained systems (16) and (18) match.

Proof: By construction, control law (21) brings (16) into (18) if and only if matching condition (20) is satisfied. By Lemma 1, control law (21) then brings (1) into (22). ■

In the next section, we will plug A_ℓ into (17) to obtain B_λ for each stance contact condition. We will choose the annihilators for each B_λ to satisfy the matching condition (20) and derive the corresponding control law based on (21).

D. Matching Conditions for Stance

Before evaluating the matching condition (20) for each contact constraint, the desired potential forces vector Ñ_st in (19) must be specified. To provide BWS we wish to replace the gravity constant g in N_st with g̃ = μg, where μ < 1 for positive BWS and μ > 1 for negative BWS. However, orthosis actuators located at the stance ankle and knee will only be able to shape the gravity constant applied to the masses of the stance shank, thigh, and hip (i.e., body center of mass). The gravity shaping strategy is equivalent to replacing the masses of the shank, thigh, and hip in the shapeable rows of N_st.

To help evaluate the matching condition (20), $M_{\text{st}}^{-1}$ is decomposed using the blockwise inversion method [35]. To begin M_st is decomposed into four submatrices:

$$M_{\text{st}}=\left[\begin{array}{ll}{M}_1\hfill & M_2\hfill \\ M_3\hfill & M_4\hfill \end{array}\right],$$ (24)

where M₁ and M₄ are square and $M_3=M_2^T$. Given that well-defined inertia matrices are nonsingular [28], the inverse of M_st can be obtained as

$$\left[\begin{array}{cc}{\mathrm{\Delta }}^{-1}& -{\mathrm{\Delta }}^{-1}{M}_2{M}_4^{-1}\\ -M_4^{-1}{M}_3{\mathrm{\Delta }}^{-1}& M_4^{-1}+M_4^{-1}{M}_3{\mathrm{\Delta }}^{-1}{M}_2{M}_4^{-1}\end{array}\right],$$ (25)

where $\mathrm{\Delta }=(M_1-M_2{M}_4^{-1}{M}_3)$.

This inversion method can only be used if M₄ and Δ are nonsingular. Submatrix M₄ corresponds to an inertia matrix of a lower-DOF kinematic chain based on the results in [24], which implies that M₄ is nonsingular [28]. Using the formulae of Schur in [36] to calculate the determinant of M_st, we have

$$det(M_{\text{st}})=det(M_4)det(\mathrm{\Delta }).$$

Since det(M_st) ≠ 0 and det(M₄) ≠ 0, we have det(Δ) ≠ 0 by [36], which proves that Δ is nonsingular. We will now utilize (25) to evaluate the matching condition (20) and obtain a control law (21) for each phase of stance. For brevity we will denote phase-specific matrices with subscripts 1, 2, or 3 instead of heel, flat, or toe, respectively.

1) Heel Contact: Let M₁ ∈ ℝ^2×2, M₂ ∈ ℝ^2×3, M₃ ∈ ℝ^3×2, M₄ ∈ ℝ^3×3 so that the multiplication of A_heel and $M_{\text{st}}^{-1}$ can be greatly simplified. We plug A_heel into (17) using the decomposition of $M_{\text{st}}^{-1}$ from (25) to obtain

$$[I-A_{\text{heel}}^{T}W{A}_{\text{heel}}{M}_{\text{st}}^{-1}]=\left[\begin{array}{cc}{0}_{2\times 2}& M_2{M}_4^{-1}\\ 0_{3\times 2}& I_{3\times 3}\end{array}\right].$$ (26)

Let $Y_1=[Y_{11},Y_{12}]=M_2{M}_4^{-1}$, where Y₁₁ ∈ ℝ^2×1 and Y₁₂ ∈ ℝ^2×2. Plugging B_st and (26) into (17), we have

$$\begin{array}{l}\hfill B_{\lambda 1}=\left[\begin{array}{l}\hfill Y_1{B}_{\text{st}(3,5)}\hfill \\ \hfill B_{\text{st}(3,5)}\hfill \end{array}\right]=\left[\begin{array}{l}\hfill Y_{12}\hfill \\ \hfill 0_{1\times 2}\hfill \\ \hfill I_{2\times 2}\hfill \end{array}\right],\hfill \\ \hfill N_{\lambda 1}=\left[\begin{array}{l}\hfill Y_1{N}_{\text{st}(3,5)}\hfill \\ \hfill N_{\text{st}(3,5)}\hfill \end{array}\right]=\left[\begin{array}{l}\hfill Y_{11}{N}_{\text{st}(3,3)}+Y_{12}{N}_{\text{st}(4,5)}\hfill \\ \hfill N_{\text{st}(3,3)}\hfill \\ \hfill N_{\text{st}(4,5)}\hfill \end{array}\right],\hfill \end{array}$$ (27)

where subscript (i, j) indicates rows i through j of a matrix. Because we constrained the first two DOFs to zero in (2), the first two rows of B_st and N_st disappear in B_λ1 and N_λ1, respectively. Hence, only the terms relevant to this contact condition will be considered in the matching condition (20).

We choose the annihilator of B_λ1 as

$$B_{\lambda 1}^{\perp }=\left[\begin{array}{ccc}{I}_{2\times 2}& 0_{2\times 1}& -Y_{12}\\ 0_{1\times 2}& 1& 0_{1\times 2}\end{array}\right].$$ (28)

It is obvious that $B_{\lambda 1}^{\perp }{B}_{\lambda 1}=0$ and $\text{rank}(B_{\lambda 1}^{\perp })=3$. Plugging terms into (20), the matching condition holds if Ñ_st(3,3) =N_st(3,3), i.e., not shaping the heel orientation DOF. Assuming this case in (19), we can achieve Ñ_λ1 in the closed-loop constrained dynamics with control law u_heel defined by (21).

2) Flat Foot: At this configuration let M₁ ∈ ℝ^3×3, M₂ ∈ ℝ^3×2, M₃ ∈ ℝ^2×3, M₄ ∈ ℝ^2×2, which have different dimensions than the previous case in order to handle three contact constraints instead of two. Plugging A_flat into (17) with the decomposition of $M_{\text{st}}^{-1}$ from (25), we obtain

$$B_{\lambda 2}=\left[\begin{array}{c}{Y}_2\\ I_{2\times 2}\end{array}\right],N_{\lambda 2}=\left[\begin{array}{c}{Y}_2{N}_{\text{st}(4,5)}\\ N_{\text{st}(4,5)}\end{array}\right],$$ (29)

where $Y_2=M_2{M}_4^{-1}\in {\mathbb{R}}^{3\times 2}$. Choosing the annihilator

$$B_{\lambda 2}^{\perp }=[\begin{array}{ll}{I}_{3\times 3},\hfill & -Y_2\hfill \end{array}],$$ (30)

where $\text{rank}(B_{\lambda 2}^{\perp })=3$ and $B_{\lambda 2}^{\perp }{B}_{\lambda 2}=0$, we immediately see that matching condition (20) holds. The corresponding energy shaping control law u_flat is given by (21).

3) Toe Contact: Although toe contact provides the same number of constraints as in Heel Contact, we decompose M_st as in Flat Foot to simplify the matching proof. Plugging A_toe into (17) with the decomposition of $M_{\text{st}}^{-1}$ from (25), we obtain

$$B_{\lambda 3}=\left[\begin{array}{c}{Y}_3\\ I_{2\times 2}\end{array}\right],N_{\lambda 3}=\left[\begin{array}{c}{Y}_4{N}_{\text{st}(1,3)}+Y_3{N}_{\text{st}(4,5)}\\ N_{\text{st}(4,5)}\end{array}\right],$$ (31)

where $Y_3=U{M}_2{M}_4^{-1}$ and Y₄ = I_3×3 − U with

$$\begin{array}{ll}\hfill U\hfill & \hfill =R^T{(R{\mathrm{\Delta }}^{-1}{R}^T)}^{-1}R{\mathrm{\Delta }}^{-1},\hfill \\ \hfill R\hfill & \hfill =\left[\begin{array}{lll}\hfill 1\hfill & \hfill 0\hfill & \hfill l_{\mathrm{f}}sin\left(\varphi \right)\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -l_{\mathrm{f}}cos\left(\varphi \right)\hfill \end{array}\right].\hfill \end{array}$$ (32)

We split up N_st in this way because the upper-left part of the matrix in (26) is no longer zero.

The annihilator of B_λ3 is chosen as

$$B_{\lambda 3}^{\perp }=[\begin{array}{ll}{I}_{3\times 3},\hfill & -Y_3\hfill \end{array}],$$ (33)

where $B_{\lambda 3}^{\perp }{B}_{\lambda 3}=0$ and $\text{rank}(B_{\lambda 3}^{\perp })=3$. Plugging in (31) and (33), the left-hand side of the matching condition (20) is

$$B_{\lambda 3}^{\perp }(N_{\lambda 3}-{\stackrel{\sim }{N}}_{\lambda 3})=Y_4(N_{\text{st}(1,3)}-{\stackrel{\sim }{N}}_{\text{st}(1,3)}).$$ (34)

The matching condition is not immediately satisfied unless we assume N_st(1,3) = Ñ_st(1,3), which means that the unactuated DOF corresponding to ϕ is unshaped (recall that the rows for p_x and p_y get constrained). This results in the toe-contact control law u_toe of the form (21) with

$${\stackrel{\sim }{N}}_{\lambda 3}=\left[\begin{array}{c}{Y}_4{N}_{\text{st}(1,3)}+Y_3{\stackrel{\sim }{N}}_{\text{st}(4,5)}\\ {\stackrel{\sim }{N}}_{\text{st}(4,5)}\end{array}\right].$$

It is worth noting that all three stance control laws are slope-invariant because γ does not appear in any A_ℓ matrix. We can also show that the three stance control laws are identical.

4) Unified Control Law for Stance: A unified controller for stance would avoid the practical difficulties in distinguishing between contact phases and thus would be beneficial for future experimental implementations. Now that we have shown that only N_st(4,5) can be shaped for each stance phase, we can show that control law (21) is the same between phases.

Proposition 1: Equation (21) yields the same control law for all three stance contact conditions:

$$u_{\text{st}}=N_{\text{st}(4,5)}-{\stackrel{\sim }{N}}_{\text{st}(4,5)}=(1-\mu )N_{\text{st}(4,5)}.$$ (35)

Proof: Starting with the heel contact condition, we obtained B_λ1 and N_λ1 in (27) and know the shapeable form of Ñ_λ1. Control law (21) becomes (35) by taking the product of

$$B_1^{+}={(Y_{12}^T{Y}_{12}+I_{2\times 2})}^{-1}[\begin{array}{lll}{Y}_{12}^T\hfill & 0_{2\times 1}\hfill & I_{2\times 2}\hfill \end{array}]$$ (36)

and

$$N_{\lambda 1}-{\stackrel{\sim }{N}}_{\lambda 1}=\left[\begin{array}{c}{Y}_{12}(N_{\text{st}(4,5)}-{\stackrel{\sim }{N}}_{\text{st}(4,5)})\\ 0\\ N_{\text{st}(4,5)}-{\stackrel{\sim }{N}}_{\text{st}(4,5)}\end{array}\right],$$ (37)

where $B_1^{+}$ is the left-pseudo inverse of B_λ1. For the other conditions we have

$$B_k^{+}={(Y_k^T{Y}_k+I_{2\times 2})}^{-1}[Y_k^T,I_{2\times 2}],$$ (38)

$$N_{\lambda k}-{\stackrel{\sim }{N}}_{\lambda k}=\left[\begin{array}{c}{Y}_k(N_{\text{st}(4,5)}-{\stackrel{\sim }{N}}_{\text{st}(4,5)})\\ N_{\text{st}(4,5)}-{\stackrel{\sim }{N}}_{\text{st}(4,5)}\end{array}\right],$$ (39)

where k ∈ {2, 3} indicates flat foot or toe contact. Multiplying (38) with (39), we obtain (35). ■

It is clear from the proof that the unified control law requires only angular position feedback and does not depend on inertia matrix terms. The generalized framework determined which terms of the potential forces vector were relevant to the matching condition in the presence of specific contact constraints. The same terms could be shaped across contact conditions, resulting in a unified, simple control law. We now turn our attention to the swing period of the orthosis.

E. Matching Condition for Swing

For the swing leg there are no contact constraints defined in the dynamics (5). With A_ℓ = 0 equation (20) reduces to the classical matching condition (12). Orthosis actuators at the swing ankle and knee will only be able to shape the weights of the swing shank and foot in their respective rows of N_sw.

Letting $B_{\text{sw}}^{\perp }=[I_{3\times 3,}{0}_{3\times 2}]$, we know that $B_{\text{sw}}^{\perp }{B}_{\text{sw}}=0$ and $\text{rank}(B_{\text{sw}}^{\perp })=3.$. The left-hand side of condition (12) is

$$B_{\text{sw}}^{\perp }(N_{\text{sw}}-{\stackrel{\sim }{N}}_{\text{sw}})=(N_{\text{sw}(1,3)}-{\stackrel{\sim }{N}}_{\text{sw}(1,3)}),$$

where Ñ_sw is the desired potential forces vector, and N_sw(1,3) and Ñ_sw(1,3) contain the first three rows of N_sw and Ñ_sw, respectively. Therefore the matching condition can only be satisfied if the first three rows of N_sw (corresponding to unactuated inertial DOFs) are unshaped, i.e., Ñ_sw(1,3) = N_sw(1,3). The swing controller for the orthosis is then

$$u_{\text{sw}}={(B_{\text{sw}}^T{B}_{\text{sw}})}^{-1}{B}_{\text{sw}}^T(N_{\text{sw}}-{\stackrel{\sim }{N}}_{\text{sw}}),$$ (40)

where ${\stackrel{\sim }{N}}_{\text{sw}}={[N_{\text{sw}(1,3)}^T,{\stackrel{\sim }{N}}_{\text{sw}(4,5)}^T]}^T$. This controller can make the swing knee and ankle to move as though the shank and foot are lighter, but because the first three rows of N_sw are unshaped, the weight of the swing leg (and orthosis) cannot be offloaded from the hip of the human user. Nevertheless we will see in the next section that control law (40) still has beneficial properties such as improved foot clearance above ground.

IV. Passivity and Stability

Energy shaping is intimately related to the notion of passivity [17]–[20], through which safe interactions between the orthosis control strategy and the human user can be guaranteed. Input-output passivity implies that the change in some storage quantity (often energy) is bounded by the “energy” injected through the input, i.e., the system cannot generate “energy” on its own. We will show that the shaped human system is passive from the human inputs to joint velocity, implying that energy growth is controlled by the human and thus interaction with the orthosis should be safe. Given this property, we will highlight stability results for certain human control policies.

A. Passivity of the Control System

Consider the equivalent constrained dynamics (16) of the human leg wearing the orthosis in stance, where we treat the external forces of the right-hand side as an input $\tau =B_{\lambda }{u}_{\text{st}}+B_{\lambda }{v}_{\text{st}}+J_{\lambda }^{T}F\in {\mathbb{R}}^5$. The state vector of this system is given by $x={(q_{\text{st}}^T,{\dot{q}}_{\text{st}}^T)}^T\in {\mathbb{R}}^{10}$. Now consider an output y = h(x) ∈ ℝ⁵, to be specified later. The definition of input/output passivity for this system is given as follows [37]:

Definition 2: Let S(x) : ℝ¹⁰ → ℝ be a continuously differentiable non-negative scalar function, then the system (16) is said to be passive from input τ to output y with storage function S(x) if Ṡ (x) ≤ y^T τ.

A kinematic chain with dynamics of the form (8) is passive from joint torque input to joint velocity output with total energy as the storage function, where the proof is based on the skew-symmetry property (Ṁ − 2C)^T = −(Ṁ − 2C) [38]. The Appendix shows that a similar property also holds for constrained matrices M_λ and C_λ, implying that the constrained system (16) is passive from input τ to output y = q̇_st with storage function $E_{\lambda }(q_{\text{st}},{\dot{q}}_{\text{st}})=\frac{1}{2}{\dot{q}}_{\text{st}}^T{M}_{\lambda }(q_{\text{st}}){\dot{q}}_{\text{st}}+P_{\lambda }(q)$:

$$\begin{array}{ll}{\dot{E}}_{\lambda }\hfill & ={\dot{q}}_{\text{st}}^T{M}_{\lambda }{\ddot{q}}_{\text{st}}+\frac{1}{2}{\dot{q}}_{\text{st}}^T{\dot{M}}_{\lambda }{\dot{q}}_{\text{st}}+{\dot{q}}_{\text{st}}^T{N}_{\lambda }\hfill \\ & ={\dot{q}}_{\text{st}}^T(\tau -C_{\lambda }{\dot{q}}_{\text{st}}-N_{\lambda })+\frac{1}{2}{\dot{q}}_{\text{st}}^T{\dot{M}}_{\lambda }{\dot{q}}_{\text{st}}+{\dot{q}}_{\text{st}}^T{N}_{\lambda }\hfill \\ & ={\dot{q}}_{\text{st}}^T\tau +\cancel{\frac{1}{2}{\dot{q}}_{\text{st}}^T({\dot{M}}_{\lambda }-2C_{\lambda }){\dot{q}}_{\text{st}}}\hfill \end{array}$$ (41)

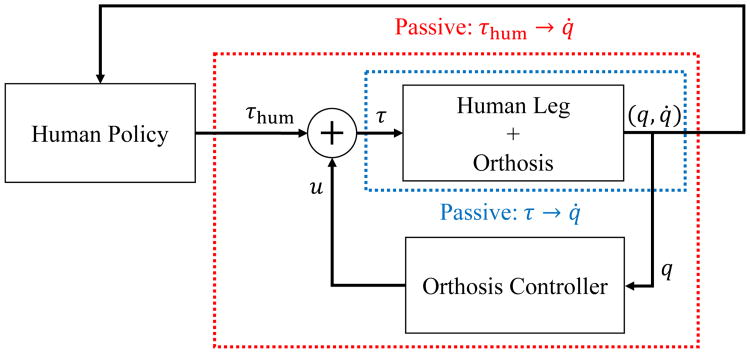
For a human leg without an orthosis (u_st = 0), muscular input v_st and hip force F provide the torque input in the passive mapping to leg joint velocity (note that studies of passivity in human joint control date back to [39]). If an energy-shaping orthosis preserves this human passivity property in closed loop (Fig. 3), then energy growth of the coupled human-machine system is controlled by the human.

Fig. 3.

Feedback loops and passive mappings of a human leg wearing an energy-shaping orthosis, where τ_hum is the total human input, u is the orthosis input, τ is the combined human-orthosis input, and (q, q̇) contain the joint angles and velocities of the leg. Subscripts associated with stance vs. swing have been dropped for simplicity.

Lemma 2: The shaped energy function ${\stackrel{\sim }{E}}_{\lambda }(q_{\text{st}},{\dot{q}}_{\text{st}})=\frac{1}{2}{\dot{q}}_{\text{st}}^T{M}_{\lambda }(q_{\text{st}}){\dot{q}}_{\text{st}}+{\stackrel{\sim }{P}}_{\lambda }(q_{\text{st}})$ is positive-definite.

Proof: The constrained potential energy can be defined in terms of the shapeable and unshapeable rows of N_λ using the variable gradient method [40]:

$$\begin{array}{ll}{P}_{\lambda }(q_{\text{st}})\hfill & ={\int }_0^{q_{\text{st}}}\sum _{n=1}^5{N}_{\lambda \left(n\right)}(s)\mathrm{d}s\hfill \\ & ={\int }_0^{q_{\text{st}}}\sum _{n=1}^3{N}_{\lambda (n)}(s)\mathrm{d}s+{\int }_0^{q_{\text{st}}}\sum _{n=4}^5{N}_{\lambda (n)}(s)\mathrm{d}s\hfill \\ & ={\int }_0^{q_{\text{st}}}{\psi }_1(s)N_{\text{st}(1,3)}(s)\mathrm{d}s+{\int }_0^{q_{\text{st}}}{\psi }_2(s)N_{\text{st}(4,5)}(s)\mathrm{d}s\hfill \\ & ≔P_{\lambda 1}(q_{\text{st}})+P_{\lambda 2}(q_{\text{st}}),\hfill \end{array}$$ (42)

where the subscript (n) indicates the n-th row of N_λ, and the integration variable is denoted as s. The matrices ψ₁(q_st) ∈ ℝ^1×3 and ψ₂(q_st) ∈ ℝ^1×2 are defined for heel contact as

$$\begin{array}{l}{\psi }_1(q_{\text{st}})=[0_{1\times 2},\sum _{j=1}^2{Y}_{11}(j,1)+1],\hfill \\ {\psi }_2(q_{\text{st}})=[\sum _{j=1}^2{Y}_{12}(j,1)+1,\sum _{j=1}^2{Y}_{12}(j,2)+1],\hfill \end{array}$$

for flat foot as

$${\psi }_1(q_{\text{st}})=0,{\psi }_2(q_{\text{st}})=[\sum _{j=1}^3{Y}_2(j,1)+1,\sum _{j=1}^3{Y}_2(j,2)+1],$$

and for toe contact as

$$\begin{array}{l}{\psi }_1(q_{\text{st}})=[\sum _{j=1}^3{Y}_4(j,1),\sum _{j=1}^3{Y}_4(j,2),\sum _{j=1}^3{Y}_4(j,3)],\hfill \\ {\psi }_2(q_{\text{st}})=[\sum _{j=1}^3{Y}_3(j,1)+1,\sum _{j=1}^3{Y}_3(j,2)+1],\hfill \end{array}$$

where the argument (l, k) indicates the element located at the l-th row and the k-th column of the matrix. Due to the way we defined Ñ_st in Section III, the following properties hold:

$$\begin{array}{ll}{\stackrel{\sim }{N}}_{\text{st}(1,3)}=N_{\text{st}(1,3)},\hfill & {\stackrel{\sim }{N}}_{\text{st}(4,5)}=\mu N_{\text{st}(4,5)}\hfill \end{array},$$ (43)

where $\mu ≔\frac{\stackrel{\sim }{g}}{g}=\frac{{\stackrel{\sim }{m}}_i}{m_i}$ is a strictly positive number defined as the ratio between the shaped and the original parameters. Given (42) and (43), we can obtain the shaped potential energy

$$\begin{array}{ll}{\stackrel{\sim }{P}}_{\lambda }(q_{\text{st}})\hfill & ={\int }_0^{q_{\text{st}}}{\psi }_1(s)N_{\text{st}(1,3)}(s)\mathrm{d}s+{\int }_0^{q_{\text{st}}}{\psi }_2(s){\stackrel{\sim }{N}}_{\text{st}(4,5)}(s)\mathrm{d}s\hfill \\ & ={\int }_0^{q_{\text{st}}}{\psi }_1(s)N_{\text{st}(1,3)}(s)\mathrm{d}s+\mu {\int }_0^{q_{\text{st}}}{\psi }_2(s)N_{\text{st}(4,5)}(s)\mathrm{d}s\hfill \\ & =P_{\lambda 1}(q_{\text{st}})+\mu P_{\lambda 2}(q_{\text{st}}).\hfill \end{array}$$ (44)

Given (44), the shaped total energy takes the following form:

$$\begin{array}{ll}{\stackrel{\sim }{E}}_{\lambda }(q_{\text{st}},{\dot{q}}_{\text{st}})\hfill & =\frac{1}{2}{\dot{q}}_{\text{st}}^T{M}_{\lambda }(q_{\text{st}}){\dot{q}}_{\text{st}}+{\stackrel{\sim }{P}}_{\lambda }(q_{\text{st}})\hfill \\ & =\frac{1}{2}{\dot{q}}_{\text{st}}^T{M}_{\lambda }(q_{\text{st}}){\dot{q}}_{\text{st}}+P_{\lambda 1}+\mu P_{\lambda 2}.\hfill \end{array}$$

Assuming the biped has an upright posture, the center of mass of every link is above that link's reference frame. Hence, every link's potential energy is positive, implying that P_λ1 > 0 and P_λ2 > 0. Given that the kinetic energy $\frac{1}{2}{\dot{q}}_{\text{st}}^T{M}_{\lambda }(q_{\text{st}}){\dot{q}}_{\text{st}}$ is positive-definite and μ is strictly positive, the overall shaped energy is positive-definite. ■

Theorem 2: The closed-loop system (18) is passive from human input ${\tau }_{\text{hum}}=B_{\lambda }{v}_{\text{st}}+J_{\lambda }^{T}F$ to joint velocity output y = q̇_st with storage function Ẽ_λ(q_st, q̇_st), i.e., $\frac{d}{dt}{\stackrel{\sim }{E}}_{\lambda }={\dot{q}}_{\text{st}}^T{\tau }_{\text{hum}}$.

Proof: The non-negativity requirement of a storage function is satisfied by Lemma 2. The same procedure as (41) with closed-loop dynamics (18) yields $\frac{d}{dt}{\stackrel{\sim }{E}}_{\lambda }={\dot{q}}_{\text{st}}^T{\tau }_{\text{hum}}$. ■

The same result applies for the swing period by setting A = 0 in the definition (17) for the terms in (18).

B. Stability of the Control System

Input-output passivity enables several stability results through passivity-based control. For example, negative feedback of the output through the input guarantees asymptotic convergence of the output to zero [38]. Feedback and parallel interconnections of passive systems are also passive [37], through which interconnected systems can be stabilized.

Here we highlight two possible results for the human control policy in Fig. 3. It is well established that human motor control effectively modulates joint impedance, i.e., the stiffness and viscosity of a joint [39], [41]. Joint impedance control involves feedback of joint angle and velocity, where the latter is the output of a passive mapping. We first consider feedback control with only the passive output and then consider the more general case with joint stiffness.

We leverage a standard result for passive systems to state the following [37]:

Proposition 2: Consider the passive system (18) with input τ_hum and output y = q̇_st. Given output feedback control τ_hum = σ(y), where σ is any continuous function satisfying y^T σ(y) ≤ 0, then lim_t→∞y(t) → 0 and the origin (q_st, q̇_st) = (0, 0) is stable in the sense of Lyapunov.

Therefore, if we assume the human is controlling the viscosity part of joint impedance, i.e., τ_hum = −K_dy = −K_dq̇_st, where K_d is a positive-definite diagonal matrix, we will have

$${\dot{\stackrel{\sim }{E}}}_{\lambda }=y^T{\tau }_{\text{hum}}=-K_d{y}^2\le 0$$ (45)

and thus convergence of the joints and Lyapunov stability of the upright posture (the origin).

Consider now the impedance controller with stiffness, which we will ultimately use in our simulations based on previous human modeling studies [42]. This control law is given by τ_hum = −K_pe−K_dė, where K_p is a positive-definite diagonal matrix, e ≔ q_st−q̄_st is the difference between q_st and the fixed equilibria vector q̄_st, and ė = q̇_st = y. To utilize Lyapunov stability analysis [28], we define a Lyapunov function

$$V(q_{\text{st}},{\dot{q}}_{\text{st}})={\stackrel{\sim }{E}}_{\lambda }(q_{\text{st}},{\dot{q}}_{\text{st}})+\frac{1}{2}{e}^T{K}_{\mathrm{p}}e.$$ (46)

It is clear that adding a quadratic term to the positive-definite shaped energy (Lemma 2) produces a positive-definite function. Using Theorem 2, the time derivative of V (q_st, q̇_st) with closed-loop dynamics (18) yields

$$\begin{array}{ll}\dot{V}(q_{\text{st}},{\dot{q}}_{\text{st}})\hfill & =y^T{\tau }_{\text{hum}}+{\dot{e}}^T{K}_{\mathrm{p}}e\hfill \\ & =y^T(-K_{\mathrm{p}}e-K_{\mathrm{d}}\dot{e}+K_{\mathrm{p}}e)\hfill \\ & =-y^T{K}_{\mathrm{d}}y\le 0,\hfill \end{array}$$ (47)

implying that the shaped human leg is Lyapunov stable [28].

V. Simulations and Results

Now that we have designed controllers for the orthosis and proven passivity for the closed-loop system, we wish to study it during simulated walking with the full biped model, i.e, combining the stance and swing legs together in Fig. 1. This requires us to consider the coupled dynamics of the two legs [29]. The full biped model's configuration space is given as $q_{\mathrm{e}}={(q_{\text{st}}^T,{\theta }_{\mathrm{h}},\theta {}_{\text{sk}},{\theta }_{\text{sa}})}^T$, where θ_h is defined as the hip angle between the stance and swing thigh. The extended coordinates are related to the swing leg model in Section II-B through a change of coordinates, i.e., θ_h is a relative angle whereas θ_th is an absolute angle. For simplicity we assume symmetry in the full biped, i.e., identical orthoses on both human legs [29].

A. Human Inputs

In order to predict the effects of virtual BWS on human locomotion, we must first construct a human-like, stable walking gait in simulation. According to the results in [43], a simulated 7-link biped can converge to a stable, natural-looking gait using joint impedance control. The control torque of each joint can be constructed from an energetically passive spring-damper coupled with phase-dependent equilibrium points [42]. We adopt this control paradigm to generate dynamic walking gaits that preserve the ballistic swing motion [44] and the energetic efficiency down slopes [45] that are characteristic of human locomotion. We assume that the human has input torques at the ankle, knee and hip joints of both legs. We keep the human impedance parameters constant instead of having a different set of parameters with respect to each phase of stance as in [42]. The total input torque vector, i.e., orthotic inputs plus human inputs, for the full biped model is given as

$$\begin{array}{ll}\tau \hfill & ={(B_{st}^T,0_{2\times 3})}^T{u}_{\text{st}}+{(0_{2\times 3},B_{\text{sw}}^T)}^T{u}_{\text{sw}}+\upsilon ,\hfill \\ \upsilon \hfill & ={[0_{1\times 3},{\upsilon }_{\mathrm{a}},{\upsilon }_{\mathrm{k}},{\upsilon }_{\mathrm{h}},{\upsilon }_{\text{sk}},{\upsilon }_{\text{sa}}]}^T\in {\mathbb{R}}^{8\times 1},\hfill \end{array}$$ (48)

where u_st is the stance controller given by (21), and υ is the vector of human inputs including the hip input υ_h. The human torque for a single joint in υ is given by

$${\upsilon }_j=-K_{\mathrm{p}j}({\theta }_j-{\overline{\theta }}_j)-K_{\mathrm{d}j}{\dot{\theta }}_j,$$ (49)

where K_pj, K_dj, θ̄_j respectively correspond to the stiffness, viscosity, and equilibrium angle of joint j ∈ {a, k, h, sk, sa}.

B. Hybrid Dynamics and Stability

Biped locomotion is modeled as a hybrid dynamical system which includes continuous and discrete dynamics. Impacts happen when the swing heel contacts the ground and subsequently when the flat foot slaps the ground. The corresponding impact equations map the state of the biped at the instant before impact to the state at the instant after impact. Note that no impact occurs when switching between the flat foot and toe contact configurations, but the location of the IRF does change from heel to toe. Based on the method in [29], the hybrid dynamics and impact maps during one step are computed in the following sequence:

$$\begin{array}{llll}1.\hfill & M_{\mathrm{e}}{\ddot{q}}_{\mathrm{e}}+T_{\mathrm{e}}+A_{{\mathrm{e}}_{\text{heel}}}^T{\lambda }_{\mathrm{e}}=\tau \hfill & \text{if}\hfill & a_{{\mathrm{e}}_{\text{flat}}}\ne 0,\hfill \\ 2.\hfill & {\dot{q}}_{\mathrm{e}}^{+}=(I-X{(A_{{\mathrm{e}}_{\text{flat}}}X)}^{-1}{A}_{{\mathrm{e}}_{\text{flat}}}){\dot{q}}_{\mathrm{e}}^{-}\hfill & \text{if}\hfill & a_{{\mathrm{e}}_{\text{flat}}}=0,\hfill \\ 3.\hfill & M_{\mathrm{e}}{\ddot{q}}_{\mathrm{e}}+T_{\mathrm{e}}+A_{{\mathrm{e}}_{\text{flat}}}^T{\lambda }_{\mathrm{e}}=\tau \hfill & \text{if}\hfill & \left|c_{\mathrm{p}}(q,\dot{q})\right|<l_{\mathrm{f}},\hfill \\ 4.\hfill & {\dot{q}}_{\mathrm{e}}^{+}={\dot{q}}_{\mathrm{e}}^{-},{(q_{\mathrm{e}}{\left(1\right)}^{+},q_{\mathrm{e}}{\left(2\right)}^{+})}^T=\mathcal{G}\hfill & \text{if}\hfill & \left|c_{\mathrm{p}}(q,\dot{q})\right|=l_{\mathrm{f}},\hfill \\ 5.\hfill & M_{\mathrm{e}}{\ddot{q}}_{\mathrm{e}}+T_{\mathrm{e}}+A_{{\mathrm{e}}_{\text{toe}}}^T{\lambda }_{\mathrm{e}}=\tau \hfill & \text{if}\hfill & h(q_e)\ne 0,\hfill \\ 6.\hfill & (q_{\mathrm{e}}^{+},{\dot{q}}_{\mathrm{e}}^{+})=\mathrm{\Theta }(q_{\mathrm{e}}^{-},{\dot{q}}_{\mathrm{e}}^{-})\hfill & \text{if}\hfill & h(q_{\mathrm{e}})=0,\hfill \end{array}$$

where the subscript e indicates the dynamics of the full biped model, $X=M_{\mathrm{e}}^{-1}{A}_{{\mathrm{e}}_{\text{flat}}}^T$, and 𝒢 = (l_f cos(γ), l_f sin(γ))^T models the change in IRF. The vector c_p(q, q̇) is the COP defined with respect to the heel IRF calculated using the conservation law of momentum. The vector T_e groups the Coriolis/centrifugal terms and potential forces for brevity. The ground clearance of the swing heel is denoted by h(q_e), and Θ denotes the swing heel ground-strike impact map derived based on [33]. The aforementioned sequence of continuous and discrete dynamics repeats after a complete step, i.e., phase 6 switches back to phase 1 for the next step.

The combination of nonlinear differential equations and discontinuous events makes stability difficult to prove analytically for hybrid systems in general. Fortunately, the method of Poincaré sections [46] provides analytical conditions for local stability that can be checked numerically by simulation. Letting $x_{\mathrm{e}}={(q_{\mathrm{e}}^T,{\dot{q}}_{\mathrm{e}}^T)}^T$ be the state vector of the full biped, a walking gait corresponds to a periodic solution curve x̄_e(t) of the hybrid system such that x̄_e(t) = x̄_e(t + T), for all t ≥ 0 and some minimal T > 0. The set of states occupied by the periodic solution defines a periodic orbit 𝒪 ≔ {x_e|x_e = x̄_e(t) for some t} in the state space. The step-to-step evolution of a solution curve can be modeled with the Poincaré map 𝒫 : G → G, where G = {x_e|h(q_e) = 0} is the switching surface indicating initial heel contact [29]. The intersection of a periodic orbit with the switching surface is a fixed point $x_{\mathrm{e}}^{\ast }=\mathcal{P}(x_{\mathrm{e}}^{\ast })=\mathcal{O}\cap G$ with standard assumptions in [46]. If $x_{\mathrm{e}}^{\ast }$ is a locally exponentially stable fixed point of the discrete system x_e(k + 1) = 𝒫(x_e(k)), then 𝒪 is a locally exponentially stable periodic orbit of the hybrid system defining the Poincaré map 𝒫 : G → G. Therefore, the periodic orbit 𝒪 is locally exponentially stable if the eigenvalues of the Jacobian ${\nabla }_{x_{\mathrm{e}}}\mathcal{P}(x_{\mathrm{e}}^{\ast })$ are within the unit circle.

The Jacobian eigenvalues can be numerically calculated through a perturbation analysis as described in [47], [48]. In fact, a similar analysis using normal kinematic variability instead of explicit perturbations has shown that human walking is orbitally stable [49]. The simulations of the next section will show that the energy-shaping controller maintains the orbital stability of a nominal walking gait, which suggests that human walking will remain orbitally stable with an orthosis utilizing this control strategy (see preliminary experiments in [50]).

C. Results and Discussion

We chose the model parameters of Table I to consist of average values from adult males reported in [51], with the trunk masses grouped at the hip as in [29]. The BWS controllers can compensate for the weight of the orthoses (at least during stance), so we neglected the orthosis masses in the parameters of Table I to simplify the analysis and find generic properties independent of any one exoskeleton design. The foot length was set to 0.2 m to provide reasonable amounts of time in both the flat foot and toe contact conditions.

Table I. Model and Simulation Parameters.

Parameter	Variable	Value
Hip mass	mh	31.73 [kg]
Thigh mass	mt	9.457 [kg]
Shank mass	ms	4.053 [kg]
Foot mass	mf	1 [kg]
Thigh moment of inertia	It	0.1995 [kg·m2]
Shank moment of inertia	Is	0.0369 [kg·m2]
Full biped shank length	ls	0.428 [m]
Full biped thigh length	lt	0.428 [m]
Full biped heel length	la	0.07 [m]
Full biped foot length	lf	0.2 [m]
Slope angle	γ	0.095 [rad]
Hip equilibrium angle	θh	0.2 [rad]
Hip proportional gain	Kph	182.258 [N·m/rad]
Hip derivative gain	Kdh	18.908 [N·m·s/rad]
Swing knee equilibrium angle	θ̄sk	0.2 [rad]
Swing knee proportional gain	Kpsk	182.258 [N·m/rad]
Swing knee derivative gain	Kdsk	18.908 [N·m·s/rad]
Swing ankle equilibrium angle	θ̄sa	−0.25 [rad]
Swing ankle proportional gain	Kpsa	182.258 [N·m/rad]
Swing ankle derivative gain	Kdsa	0.802 [N·m·s/rad]
Stance ankle equilibrium angle	θ̄a	0.01/rad]
Stance ankle proportional gain	Kpa	546.774 [N·m/rad]
Stance ankle derivative gain	Kda	21.257 [N·m·s/rad]
Stance knee equilibrium angle	θ̄k	−0.05 [rad]
Stance knee proportional gain	Kpk	546.774 [N·m/rad]
Stance knee derivative gain	Kdk	21.257 [N·m·s/rad]

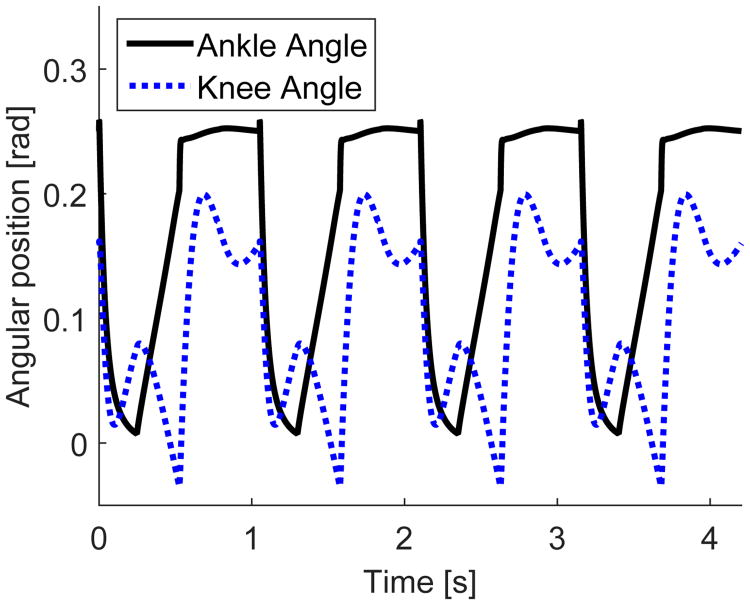
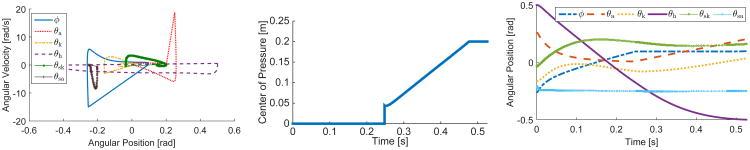
We first tuned the human joint impedance gains to find a stable nominal gait, where the gains are given in Table I. The knee and ankle trajectories over four steady-state strides are shown in Fig. 4, and the biped's complete angular kinematics are shown for one step in Fig. 5 (right). This walking gait is perfectly periodic, leading to the periodic orbit shown in the phase portrait of Fig. 5 (left). The COP moves monotonically from the heel to the toe (Fig. 5, center), providing a flag to detect the transition between flat foot and toe contact. The nominal gait spent 248 ms in heel contact, 228 ms in flat foot, and 49 ms in toe contact.

Fig. 4.

Knee and ankle trajectories of one leg over four steady-state strides (stance and swing) of the nominal “human” gait.

Fig. 5.

Phase portrait (left), center of pressure (center), and angular positions (right) over one steady-state step of the nominal “human” gait.

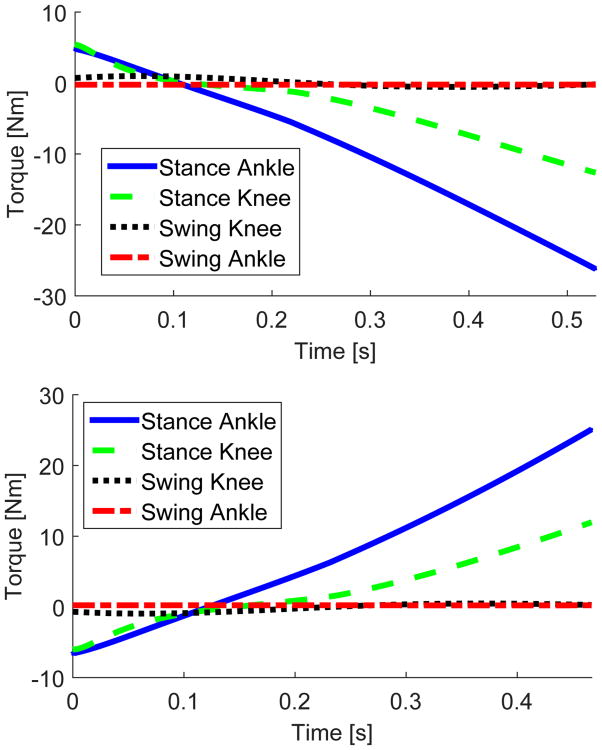
We then added the virtual BWS controller and progressively increased or decreased the BWS percentage to study its effect on the nominal gait. For notational purposes, X% BWS corresponds to Ñ_st(4,5) = (1 − 0.01X)N_st(4,5) and Ñ_sw(4,5) = (1 − 0.01X)N_sw(4,5). For each sampled BWS percentage, the biped was simulated to obtain a steady-state gait and record its features. The human impedance parameters were kept constant in order to isolate the effects of energy shaping. The torque profiles for ±24.5% BWS are given in Fig. 6. Positive BWS performs negative net work by removing potential energy, whereas negative BWS does the opposite by injecting potential energy. The work done has an approximately linear trend from 2.0 J/kg at -30% BWS to -1.3 J/kg at 24.5% BWS (with 0 J/kg at 0% BWS). Other gait features are shown over BWS percentage in Figs. 7 and 8. Animations of the walking gaits are available for download as supplemental multimedia.

Fig. 6.

The virtual BWS control torque with 24.5% BWS (top) and −24.5% BWS (bottom) over one steady-state step.

Fig. 7.

Step linear velocity (left), step length (center), step time period (right) from −30% to 25% virtual BWS, real gravity support (GS), and real mass support (MS). Divided by a red dotted line, the sign of the x-axis denotes negative or positive BWS.

Fig. 8.

Minimum heel clearance (left), minimum toe clearance (center), maximum absolute eigenvalue (right) from −30% to 25% virtual BWS, real gravity support (GS), and real mass support (MS). Divided by a red dotted line, the sign of the x-axis denotes negative or positive BWS.

For comparison with virtual BWS, we repeated this procedure while scaling 1) the true gravity constant g in all rows of N_st and N_sw, or 2) the true masses in both the potential and kinetic energies. The former is referred to as real gravity support (“real GS”), and the latter is referred to as real mass support (“real MS”). Even though virtual BWS does not shape all weights in the potential forces vector, it closely approximates the real GS case (Figs. 7 and 8). Virtual BWS also approximates the real MS case without attempting to shape kinetic energy, likely because potential energy is more influential at these walking speeds.

1) Positive BWS: The walking gait tends to have a smaller step length and velocity with higher BWS percentages (Fig. 7) due to the decreasing potential energy. Patients may benefit from starting with slower, shorter steps at the beginning of therapy, after which the BWS percentage could be lowered to encourage faster and longer steps. Fig. 8 (left, center) shows that the swing clearances of both toe and heel increase with BWS percentage. This implies that trips commonly associated with stroke gait [52] could potentially be avoided with virtual BWS. Fig. 7 (right) shows that the time spent on each step tends to increase with the percentage of virtual BWS and real GS but not with real MS due to the effect of smaller masses in the inertia matrix (i.e., kinetic energy).

Fig. 8 (right) shows that the maximum absolute eigenvalues tend to increase with BWS percentage, suggesting slower local convergence rates to the associated periodic orbit. Because walking gaits of passive bipeds are sensitive to model parameters [47], we could only examine up to 24.5% virtual BWS, 18% real GS, or 25% real MS before there was insufficient potential energy to maintain a stable gait. However, a patient or therapist could likely compensate for gait stability better than the passive biped model, which would expand the range of virtual BWS percentages to the limits of the orthosis actuators.

2) Negative BWS: Once patients have regained some functionality of their lower limbs, therapists could prescribe the negative BWS controller to challenge the patients by virtually adding weight to their body. Athletes might also benefit from negative BWS in their daily training to improve muscle strength and endurance. Fig. 7 (left, center) shows that more negative BWS percentages cause longer and faster steps. If this effect holds true for real human subjects, it might be beneficial for patients when they have finished training with assistive strategies and want to further enhance their gaits by challenging their muscles. The time spent during each step period decreases with negative percentages of virtual BWS and real GS (Fig. 7, right), implying that patients can spend less time per step without sacrificing step length and velocity. For negative percentages of real MS, the step time period slowly increases due to the larger masses in the inertia matrix.

Fig. 8 (left, center) shows that negative BWS increases minimum heel clearance but decreases minimum toe clearance. Fig. 8 (right) demonstrates that the eigenvalues tend to decrease with negative BWS. As was the case with positive BWS, the passive biped loses stability beyond a certain percentage of negative BWS (−30% virtual BWS, −20% real GS, and −30% real MS) due to an excess of potential energy.

3) Comparison to Classical Approach: We now wish to demonstrate the benefit of the generalized shaping approach in terms of contact invariance. The classical (non-generalized) framework of Section III-B is based on contact-specific dynamics and thus would require contact phase detection to switch between contact-specific control laws. Assuming no knowledge of the contact condition, we implemented the classical control law associated with the flat foot configuration during all three phases of stance:

$$u_{\text{ng}}={(B_{\text{ng}}^T{B}_{\text{ng}})}^{-1}{B}_{\text{ng}}^T(N_{\text{ng}}-{\stackrel{\sim }{N}}_{\text{ng}})$$ (50)

with model terms N_ng(θ_a, θ_k) = N_st(4,5)(0, 0, 0, θ_a, θ_k) ∈ ℝ², Ñ_ng(θ_a, θ_k) = Ñ_st(4,5)(0, 0, 0, θ_a, θ_k) ∈ ℝ², and B_ng = I_{2 × 2}. The appropriate control law (40) was utilized during swing.

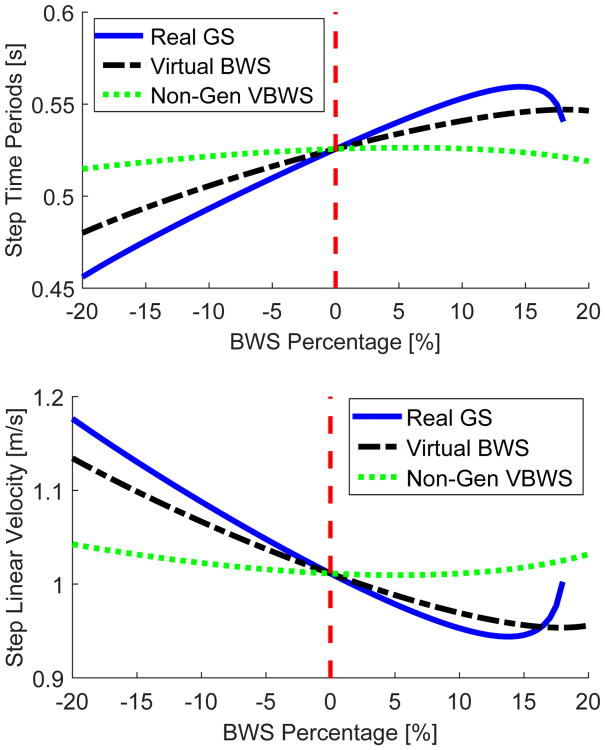
Fig. 9 compares the effects of real GS with the generalized and non-generalized cases of virtual BWS. The non-generalized case immediately diverges from the desired characteristics of real GS, which are closely approximated by the generalized case. These differences were likely the effect of the inertial DOFs during heel and toe contact, which are not explicitly modeled in the non-generalized controller (50).

Fig. 9.

Step time period (top) and step linear velocity (bottom) from −20% to 20% BWS with real GS, virtual BWS, and non-generalized virtual BWS (Non-Gen VBWS). The non-generalized case corresponds to flat-foot control (50), which does not measure inertial coordinates, during all phases of stance.

The contact invariance of the generalized approach should justify the implementation challenge of measuring the necessary coordinates for the control law. Fortunately, the cartesian coordinates p_x and p_y do not need to be measured because they do not appear in the potential forces vector, which is defined as the gradient of the potential energy. The global orientation of the foot ϕ can be measured using an inertial measurement unit (IMU) as demonstrated by preliminary experiments with a powered ankle orthosis in [50]. The only parameters that must be specified in control law (35) are the leg segment lengths and the relative changes in weight (not necessarily the absolute mass values), which are easily determined.

VI. Conclusion

This paper derived an orthotic control strategy for augmenting the perceived weight of a patient through underactuated potential energy shaping. The closed-loop energy that can be altered via control was determined by a generalized matching condition defined from Lagrangian dynamics with holonomic contact constraints. The proposed framework can be applied to different contact conditions with a unified control law. Simulation results suggest that walking gaits can be augmented in beneficial ways for rehabilitation. At the initial stage of gait training, patients can start with easier gaits having higher toe and heel clearances to avoid tripping. Clinicians can easily adjust the BWS percentage, where positive values would assist and negative values would challenge the patient. Because this control strategy does not prescribe joint kinematics, it is task-invariant and would allow training on slopes and stairs. Created as a rehabilitation tool, virtual BWS could potentially reduce physical labor from clinicians and enable training outside the clinic. Future work will include experimental implementations of this control method on powered orthoses.

Biographies

Ge Lv (S'15) received the B.S. degree (2011) and the M.S. (2013) degree in information science and engineering from Northeastern University, Shenyang, China.

He joined the Department of Electrical Engineering at the University of Texas at Dallas as a Ph.D. student in 2013. His research is in the control of bipedal locomotion with applications to orthoses and exoskeletons. He received the Best Student Paper Award of the 2015 IEEE Conference on Decision and Control.

Robert D. Gregg (S'08-M'10-SM'16) received the B.S. degree (2006) in electrical engineering and computer sciences from the University of California, Berkeley and the M.S. (2007) and Ph.D. (2010) degrees in electrical and computer engineering from the University of Illinois at Urbana-Champaign.

He joined the Departments of Bioengineering and Mechanical Engineering at the University of Texas at Dallas (UTD) as an Assistant Professor in 2013. Prior to joining UTD, he was a Research Scientist at the Rehabilitation Institute of Chicago and a Postdoctoral Fellow at Northwestern University. His research is in the control of bipedal locomotion with applications to autonomous and wearable robots.

Appendix

We now show that ${\dot{q}}_{\text{st}}^T({\dot{M}}_{\lambda }-2C_{\lambda }){\dot{q}}_{\text{st}}=0$ for the proof of passivity. Plugging in M_λ = M and C_λ from (17) we obtain

$$\begin{array}{l}{\dot{q}}_{\text{st}}^T({\dot{M}}_{\lambda }-2C_{\lambda }){\dot{q}}_{\text{st}}\hfill \\ =\cancel{{\dot{q}}_{\text{st}}^T({\dot{M}}_{\lambda }-2C){\dot{q}}_{\text{st}}}+2{\dot{q}}_{\text{st}}^T(A_{\ell }^{T}W{A}_{\ell }{M}^{-1}C-A_{\ell }^{T}W{\dot{A}}_{\ell }){\dot{q}}_{\text{st}}\hfill \\ =2{\dot{q}}_{\text{st}}^T{A}_{\ell }^{T}W{A}_{\ell }{M}^{-1}C{\dot{q}}_{\text{st}}-2{\dot{q}}_{\text{st}}^T{A}_{\ell }^{T}W{\dot{A}}_{\ell }{\dot{q}}_{\text{st}},\hfill \end{array}$$ (51)

where the standard skew-symmetry property of Ṁ − 2C was applied. By definition of a contact constraint a_ℓ (q_st) = 0,

$$\begin{array}{lll}\frac{\mathrm{d}}{\text{dt}}{a}_{\ell }(q_{\text{st}})=A_{\ell }(q_{\text{st}}){\dot{q}}_{\text{st}}=0\hfill & \Rightarrow \hfill & {\dot{q}}_{\text{st}}^T{A}_{\ell }^T(q_{\text{st}})=0\hfill \end{array}.$$

Hence, the remaining terms on the right side of (51) are zero. Note that ${\dot{q}}_{\text{st}}^T({\dot{M}}_{\lambda }-2C_{\lambda }){\dot{q}}_{\text{st}}=0$ does not necessarily imply skew-symmetry of Ṁ_λ − 2C_λ, but it does suffice for passivity in Section IV.