Knowledge-Based Biomedical Word Sense Disambiguation with Neural Concept Embeddings

Abstract

Biomedical word sense disambiguation (WSD) is an important intermediate task in many natural language processing applications such as named entity recognition, syntactic parsing, and relation extraction. In this paper, we employ knowledge-based approaches that also exploit recent advances in neural word/concept embeddings to improve over the state-of-the-art in biomedical WSD using the public MSH WSD dataset [1] as the test set. Our methods involve weak supervision – we do not use any hand-labeled examples for WSD to build our prediction models; however, we employ an existing concept mapping program, MetaMap, to obtain our concept vectors. Over the MSH WSD dataset, our linear time (in terms of numbers of senses and words in the test instance) method achieves an accuracy of 92.24% which is a 3% improvement over the best known results [2] obtained via unsupervised means. A more expensive approach that we developed relies on a nearest neighbor framework and achieves accuracy of 94.34%, essentially cutting the error rate in half. Employing dense vector representations learned from unlabeled free text has been shown to benefit many language processing tasks recently and our efforts show that biomedical WSD is no exception to this trend. For a complex and rapidly evolving domain such as biomedicine, building labeled datasets for larger sets of ambiguous terms may be impractical. Here, we show that weak supervision that leverages recent advances in representation learning can rival supervised approaches in biomedical WSD. However, external knowledge bases (here sense inventories) play a key role in the improvements achieved.

I. Introduction

Biomedical natural language processing (NLP) that goes beyond simple text processing is increasingly becoming indispensable to derive value and insights from vast amounts of unstructured data generated in the form of scientific articles [3]–[5], clinical narratives [6]–[8] and health related social media posts [9]–[11]. Specialized components including named entity recognition (NER) programs, syntactic parsers, and relation extractors form the backbone of many high level information extraction and knowledge discovery applications. For most components in an NLP application pipeline, there is a clear snowball effect of errors in a component in the beginning of the pipeline leading to more errors in other subsequent components and the final results of the full application.

Resolving lexical mentions in text to correct named entities from a fixed terminology is essential in building an effective NER program, which is typically the next step after sentence segmentation and part-of-speech tagging in most NLP pipelines. All other downstream components and the full application suffer if lexical ambiguities are not correctly resolved. Recent research also shows that resolving ambiguities provides performance gains in information retrieval and search system design [12]. In this effort, we employ knowledge-based methods, neural concept and word vectors learned through unsupervised deep learning approaches, and a straightforward nearest neighbor approach to achieve new state-of-the-art results over a public gold standard dataset [1] in biomedical word sense disambiguation (WSD).

For this effort, WSD specifically deals with identifying the correct sense of a term, among a set of given candidate senses for that term, when it is presented in a brief narrative along with its context (surrounding text). For example, consider the ambiguous term ‘discharge’. It has two unique senses in biomedicine – (S1). The first is the administrative process of releasing a patient from a healthcare facility following an in-patient stay for some treatment or procedure. (S2). The second sense pertains to bodily secretions of certain fluids from an orifice or wound. In our task the ambiguous term ‘discharge’ is specified along with the sense set {S1, S2} and an example context – “Low risk patients identified using CADILLAC risk score with STEMI treated successfully with primary PCI have a low adverse event rate on the third day or later of hospitalization suggesting that an earlier discharge is safe in properly selected patients.” Our goal is to identify the correct sense S1 for this specific occurrence of ‘discharge’.

Next, we outline the organization of the rest of the paper. In Section II, we discuss earlier efforts in biomedical WSD and recent approaches that incorporate word embeddings. Our main methods that employ concept/word embeddings including the nearest neighbor approach are detailed in Section III. We then present our main results and takeaways in Section IV. Finally, in Section V, we conclude with some future research directions involving recurrent neural architectures for biomedical WSD.

II. Background and Related Work

For a thorough overview of approaches to WSD, we direct the readers to the survey by Navigli [13], which suggests mainly three categories – supervised, knowledge-based, and unsupervised approaches. Supervised approaches for WSD [14], [15] use a labeled dataset along with interesting lexical/syntactic features derived from the context around the term to build machine learned models that predict the correct sense in unseen test contexts. Knowledge-based approaches [1], [16] do not use any corpus but solely rely on thesauri or sense inventories such as WordNet and the Unified Medical Language System (UMLS) that contain brief definitions of different senses and corresponding synonyms. Unsupervised approaches may employ topic modeling [17] based methods to disambiguate when the senses are known ahead of time. Some unsupervised approaches [18] are often referred to as performing word sense discrimination or induction as opposed to disambiguation because they employ clustering approaches where different clusters are expected to represent the different senses, which are not known a priori.

A. WSD in Biomedicine

In biomedicine, knowledge-based word sense disambiguation efforts mostly relied on the UMLS knowledge base [19], which contains over 3.4 million unique concepts expertly sourced from ≈ 200 different terminologies in biomedicine and allied fields. The UMLS is maintained by the US National Library of Medicine (NLM) and is updated every year to reflect new concepts and other changes. For each concept in the UMLS, there is usually a brief definition and sometimes additional relations (both hierarchical and associative) connecting it with other concepts. Each concept has a unique ID called the concept unique identifier (CUI), an alphanumeric string that starts with a ‘C’. For example, the sense S1 (administrative process) for ‘discharge’ in Section I is represented by CUI C0030685 and sense S2 (body substance) is represented by the CUI C0012621. S1 has a short definition “The administrative process of discharging the patient, alive or dead, from hospitals or other health facilities”. For S2 we notice the definition – “In medicine, a fluid that comes out of the body. Discharge can be normal or a sign of disease.” In the MSH WSD dataset that we use in this effort, the candidate senses for each ambitious word are represented in the form of these unique CUIs. The task is to identify the correct CUI given a particular context (few sentences) containing an ambiguous term. For the rest of the manuscript, we use the three terms CUI, concept, and sense synonymously as they refer to the same notion.

Schuemie et al. [20] present a nice survey of approaches and efforts in biomedical WSD until 2005 including the well-known NLM WSD dataset [21], which has 50 ambiguous terms with 5000 test instances. Disambiguation efforts were also focused on a small set of 10–15 ambiguous abbreviations [22], [23] using combinations of supervised and unsupervised approaches. More recent approaches [24], [25] used supervised models including Naive Bayes, SVMs, logistic regressors, decision lists with a variety of features using both subsets of the NLM WSD dataset and other smaller datasets. Berster et al. [26] encoded senses, contexts, and ambiguous terms using random indexing and conducted supervised ten-fold cross validation experiments on the NLM WSD dataset using the binary splatter code method. McInnes and Pedersen [16] used the network structure of the UMLS (specifically the hypernymic trees) and concept definitions to devise concept relatedness measures which are in turn used for WSD for the MSH WSD dataset. Chasin et al. [27] demonstrated the application of topic modeling for a clinical WSD dataset of 50 ambiguous terms curated from the Mayo Clinic [25]. Recently, Wang et al. [28] used an active learning strategy to involve domain experts in an interactive supervised machine learning framework for biomedical WSD. Among all the datasets available, the MSH WSD that we use in our current effort is the largest publicly available dataset [1] for biomedical WSD (more in Section III) and also has the least skewed distribution (the average percentage of majority sense is 54% [28]).

In a recent approach Jimeno-Yepes and Berlanga [2] used a hybrid approach that combined a knowledge-based component that exploits the UMLS definitions and synonyms for different concepts with unlabeled biomedical narratives (from Medline/PubMed) to derive word-concept probability estimates P (w|c) for any word w and UMLS concept c. They exploited the Naive Bayes formulation and selected the correct sense as the CUI c that maximizes P(T|c) = ∏_i P(w_i|c), where w_i is the i-th word in the test context T that contains the ambiguous term. With this approach they achieved an accuracy of 89.1% on the MSH WSD dataset [1]. This result corresponds to the best performance thus far on the MSH WSD dataset without using supervised models. Given we employ this method as a component of our best model, for completeness, we provide its high level summary in the Appendix.

In this effort, we use recent advances in neural word embeddings to generate new state-of-the-art results on the MSH WSD dataset achieved without supervised cross validation experiments. Our methods can be classified as weakly supervised given we employ the well-known biomedical concept mapping tool MetaMap [29] to generate concept vectors and employ them in combination with the knowledge-based method from Jimeno-Yepes and Berlanga [2].

B. Neural Embeddings for WSD

Neural word representations have been shown to capture both semantic and syntactic information and a few recent approaches learn word vectors [30]–[32] (as elements of ℝ^d, where d is the dimension) in an unsupervised fashion from textual corpora. These dense word vectors obviate the sparsity issues inherent to the so called one-hot representations of words¹. Chen et al. [34] adapted neural word embeddings to compute different sense embeddings (of the same word) and showed competitive performance on the SemEval 2007 WSD dataset [35]. Disambiguation is achieved by picking the sense that maximizes the cosine similarity of the corresponding sense vector with the context vector for an ambiguous term. Recently, Iacobacci et al. [36] evaluated and demonstrated the superiority of neural word embeddings as features in supervised WSD models on the same SemEval dataset.

In a very recent effort Pakhomov et al. [37] use word embeddings (without corpus enhanced concept embeddings) for the MSH WSD dataset but only report 77% accuracy although the central aim of their paper is not limited to WSD. Their approach relies on vectors of words that co-occur with words in the definitions of different senses (CUIs) in the UMLS. In our effort, we use a similar framework as Chen et al. [34] to directly learn sense vectors using a pure distributional semantics framework that does not rely on word vectors. Additionally, we employ complementary evidences beyond cosine similarity to achieve further improvements that rival performances typically reported using supervised approaches.

III. Our Approach

There are 203 ambiguous terms in the MSH WSD dataset [1] with a total of 424 unique CUIs (from the UMLS), each of which is a unique sense. Thus, on average, the dataset has 424/203 = 2.08 senses. There are a total of 38,495 test instances of contexts (a few sentences) each with one of the 203 ambiguous terms along with the correct sense (CUI). Besides being the largest biomedical WSD dataset, it also includes a richer set of ambiguities including 106 ambiguous abbreviations, 88 ambiguous noun phrases, and 9 that are combinations of both. Due to these features, the NLM encourages researchers to use this dataset over their older dataset (please see https://wsd.nlm.nih.gov). Our goal is to directly test on this dataset by employing weakly supervised approaches. For this, we learn vector representations of words and CUIs using well-known approaches that apply deep neural networks to NLP tasks.

A. Neural Word and Concept Embeddings

We ran the well-known word2vec [32] word embedding program (the skip-gram model) from Google on over 20 million biomedical citations (titles and abstracts) from PubMed to obtain word vector representations with a word window size of ten words and dimensionality d = 300 with all other parameters set to the default settings. To learn concept or CUI vectors of the same dimensionality, we curated a dataset of five million randomly chosen citations (published between 1998 and 2014). For this subset of PubMed, we ran MetaMap [29] with its WSD option turned on so we obtain unique CUIs for potential ambiguous terms². The text was passed through MetaMap two adjacent non-stop words at a time, to capture as many CUIs as possible. Next, we treated these sequences of CUIs in each citation thus obtained through NER as a semantic version of the free text corpus. We ran word2vec on this corpus of CUI texts, just like how we ran it on free text articles with the same parameters. As a result we obtained 300 dimensional dense vectors for each CUI, including all 424 CUIs corresponding to the 203 ambiguous terms in our test set. This component of our methodology to derive dense concept vectors involves weak supervision because although MetaMap with its WSD option is in and of itself not a powerful solution (see Section IV), it nevertheless was useful to learn concept vectors that in turn helped us achieve state-of-the-art results. This deep neural network based distributional semantics approach to learning CUI vectors aids in modeling complementary aspects of similarity. This is because we use, as a component, the CUI definition based information via the word-probability estimate based approach [2] outlined earlier.

B. WSD with Word/Concept Embeddings and Knowledge-Based Approaches

Our main idea is that besides comparing pairs of word vectors and concept vectors, we can also compare a word vector with a concept vector given at a high level there is a direct connection between words and concepts – words are often lexical manifestations of high level concepts. The fact that we simply replaced word sequences in free text with the corresponding concept sequences to generate CUI vectors of the same dimensionality as the word vectors also makes it feasible to compare word vectors and their compositions to concept vectors. As will see in Section IV, this intuition appears to work as well as other state-of-the-art approaches [2].

We establish some notation for the rest of the paper. In any WSD problem, a test instance corresponds to a three tuple (T, w, C(w)) where T is a context, typically a few sentences, that contains the ambiguous term w and C(w) is the set of different senses that w can assume depending upon the context T³. Specifically, C(w) in this effort is the set of different CUIs that capture the different senses for w. Our WSD goal is to construct a function f(T, w, C(w)) that maps T to the CUI c ∈ C(w) that corresponds to the correct sense in which w was used in T. We have four approaches that apply the embeddings from Section III-A to our test set. We specify them in terms of functions f^?(T, w, C(w)) where ? indicates symbols that identify the underlying method(s) used, made clear as follows.

1. Our first approach uses vector cosine similarity with

   $$f^c(T,w,C(w))=\underset{c\in C(w)}{\arg max}\cos ({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c}),$$

   where ${\overrightarrow{T}}_{\mathit{avg}}$ is the average of non-stop words’ vectors in the context T and $\overrightarrow{c}$ is the context vector for c. This formulation is well-known given cosine similarity is a popular approach to measure semantic similarity of entities (words, concepts,…) represented by the corresponding vectors.
2. Our second approach is based on vector projections with

   $$f^p=\underset{c\in C(w)}{\arg max}\left[\rho [\cos ({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})]\cdot \frac{\Vert \mathcal{P}({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})\Vert }{\Vert \overrightarrow{c}\Vert }\right],$$

   where $\mathcal{P}(\overrightarrow{r},\overrightarrow{s})$ refers to the projection of $\overrightarrow{r}$ on to $\overrightarrow{s}$, is the Euclidean norm, and ρ is the sign function. Using straightforward manipulation based on vector projections in Euclidean spaces [39, Chapter 5], we have

   $$\Vert \mathcal{P}({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})\Vert =\frac{|{\overrightarrow{T}}_{\mathit{avg}}•\overrightarrow{c}|}{\Vert \overrightarrow{c}\Vert },$$

   which is what we used in our implementation (with ● denoting vector dot product). Although f^c (approach one) accounts for the overall directional similarity (thematic orientation) of the vectors, it does not account for the strength or magnitude of association, an aspect that seems ignored in others’ efforts we reviewed for this paper. By considering the vector projection of the context vector onto the CUI vector $\overrightarrow{c}$, in f^p we also account for the magnitude of the context vector’s projection in relation to that of the CUI vector. The sign function ρ is essentially to account for situations when 90 < θ ≤ 180, the angle between ${\overrightarrow{T}}_{\mathit{avg}}$ and $\overrightarrow{c}$.
3. Our third approach is based on the first two approaches where we set

   $$f^{c,p}=\underset{c\in C(w)}{\arg max}\left[\cos ({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})\cdot \frac{\Vert \mathcal{P}({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c}\Vert }{\Vert \overrightarrow{c}\Vert }\right].$$

   We simply incorporate both evidences (magnitude and orientation of association) to compare different CUIs.

4. Our final approach uses a probabilistic model developed in an earlier effort by Jimeno-Yepes and Berlanga [2] (as outlined in Section II-A and elaborated in the Appendix) that selects the c that maximizes P (T|c). We involve this knowledge-based approach as a third scoring component and set

   $$f^{c,p,k}=\underset{c\in C(w)}{\arg max}\left[\cos ({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})\cdot \frac{\Vert \mathcal{P}({\overrightarrow{T}}_{\mathit{avg}},\overrightarrow{c})\Vert }{\Vert \overrightarrow{c}\Vert }+P(T|C)\right].$$

   Although there are different ways of combining evidences from multiple sources of predictive information, we rely on this straightforward combination as a form of unsupervised rank aggregation from two different sources.

The methods discussed thus far can be summarized using the schematic in Figure 1.

Fig. 1.

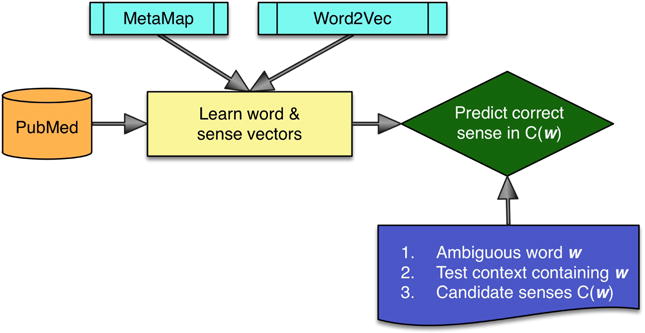
Architecture for WSD approaches from Sections III-A and III-B

C. WSD with Weak Supervision

From methods in Section III-B, we have multiple ways of disambiguating CUIs for any ambiguous term given a sample context. We exploit them to build a weakly supervised dataset for the 203 ambiguous terms in our test dataset. For each sentence in an independent corpus of biomedical citations that contains any ambiguous term from our dataset, we employ methods in Section III-B to assign the predicted CUI. Thus we can create a weakly supervised dataset for each ambiguous term with thousands of examples if we choose a large corpus. These examples can then be used to train traditional discriminative models or nearest neighbor models. We emphasize here that we are proposing to label arbitrary sentences (not our test sentences) in an external corpus based on our methods in Section III-B. Hence we still have our full MSH WSD dataset to finally test the approach we propose here with other models in a fair way.

For the k nearest neighbor (k-NN) model, let ${\mathcal{D}}^w\subseteq \mathcal{D}$ be the set of instances for the ambiguous term w in the weakly supervised dataset $\mathcal{D}$. We rank instances $(D,w,c)\in {\mathcal{D}}^w$ for a given test instance T based on $\cos ({\overrightarrow{T}}_{\mathit{avg}},{\overrightarrow{D}}_{\mathit{avg}})$, where c is the sense assigned to D from C(w) based on methods in Section III-B. Let $R_k({\mathcal{D}}_w)$ be the set of top k instances in ${\mathcal{D}}^w$ when ranked in descending order based on $\cos ({\overrightarrow{T}}_{\mathit{avg}},{\overrightarrow{D}}_{\mathit{avg}})$. Now the predicted sense for T is chosen based on

$$f^{k-NN}=\underset{c\in C(w)}{\arg max}\left[{\displaystyle \sum _{(D,w,c)\in R_k({\mathcal{D}}^w)}\cos ({\overrightarrow{T}}_{\mathit{avg}},{\overrightarrow{D}}_{\mathit{avg}})}\right].$$

The expression in the arg max boils down to summing up the similarities of the test context with those contexts in the training dataset that have the same assigned CUI c. We subsequently pick the particular c that maximizes that summation. Intuitively, our approach aggregates evidence from training instances that are semantically most similar to our test instance. The choice of k also plays an important role in the performance of k-NN approaches as we observe in the next section.

IV. Results and Discussion

Our results are shown in Table I based on methods introduced in the previous section. MetaMap does not perform as well on this dataset (row 1) even with the WSD option achieving an accuracy⁴ of 81.77%. However, it may not be fair to compare MetaMap with our methods given it does not try to particularly disambiguate our specific 203 terms, for each of which we are already given candidate concepts that contain the correct sense. In row 2 of the table, we show the performance achieved by Jimeno-Yepes and Berlanga using word-concept probability estimates P(w|c) derived from synonymous names of concepts in the UMLS Metathesaurus.

TABLE I.

Performance on MSH WSD Dataset

Method	Accuracy
MetaMap with WSD	81.77%
Jimeno-Yepes and Berlanga [2]	89.10%
Cosine similarity (fc)	85.54%
Projection length proportion (fp)	88.68%
Combining fc and fp (fc,p)	89.26%
Combining fc, fp, and [2] (fc,p,k)	92.24%
Convolutional neural networks	87.78%
k-NN with k = 3500 (fk−NN)	94.34%

Rows 3–6 show performances of our methods that leverage neural word/concept embeddings from Section III-B. The cosine similarity and projection approaches both score above 85% but when used together, they achieve an accuracy of 89.26% which is slightly better than the current best result [2] achieved through unsupervised and knowledge-based approaches. Row 6 shows an accuracy of 92.24% achieved by our ensemble method that combines our word/concept vector approach with the knowledge-based method by Jimeno-Yepes and Berlanga [2]. The time complexity of these methods is linear in terms of the number of words in the test context T and the number of candidate senses |C(w)|, considering the computation of ${\overrightarrow{T}}_{\mathit{avg}}$ and evaluation of the arg max expressions for each c ∈ C(w).

We created a weakly supervised dataset as outlined in Section III-C with the same corpus of five million biomedical citations used for training word and concept vectors (Section III-A). From this corpus, we considered the so called utterances that represent clauses (from the input text) that MetaMap outputs as distinct fragments with the corresponding CUIs. For each utterance that contains an ambiguous term in our test set, we apply our best linear method f^c,p,k (corresponding to row 6 of Table I) to assign one specific CUI from all possible candidates. There were seven million such utterances, with an average length of 18 words, that contained an ambiguous term out of a total of 78 million utterances from the corpus. Given our prior experiences in convolutional neural networks (CNNs) in biomedical text classification [40] that proved superior over traditional linear classifiers such as support vector machines and logistic regression models, we built 203 multiclass CNN models, one for each ambiguous term based on this weakly supervised dataset. The configuration of the CNN and its various hyper parameters were determined as per our prior effort [40, Sections 3.2 and 4.2]. This setup however resulted in accuracy of 87.78% which does not match the performance of simpler approaches (rows 4–6 of Table I).

We finally applied the k-NN approach outlined in Section III-C with the weakly supervised dataset with the number of nearest neighbors k ∈ {20, 50, 100, 200, 300, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000}. The corresponding accuracies are plotted as shown in Figure 2. We obtained the best accuracy of 94.34% when k = 3500 as shown in the last row of Table I. Overall, the accuracy rapidly increases as the numbers of neighbors used increase. The gains become smaller as more neighbors are added, reaching the top score at k = 3500 after which the accuracy descends abruptly. At k = 5000, the accuracy is same as that achieved with k = 300. This phenomenon is not surprising – at first more neighbors contribute to additional evidence, consistency, and robustness against noise in comparing the candidate concepts. However, considering an increasing number of neighbors at some point also leads to the semantic drift of their content from that of the test context. So neighbors ranked further down the list negatively affect the prediction given they are not as related to the test context, thus lowering overall accuracy. We realize that the value of k = 3500 is specific to this biomedical dataset and that there could be a value 3000 < k < 4000 that achieves a slightly higher accuracy. Our analysis is essentially a proof of concept for the high-level nearly monotonous nature of performance of k-NN based approaches. Given that there are over 38,000 test instances in our dataset, we believe k ≈ 3500 is appropriate in domains with similar characteristics (e.g., average number of senses per word, distributions of senses, and average length of test contexts). However, researchers may be able to derive more appropriate k values for their domains if they have access to relevant datasets.

Fig. 2.

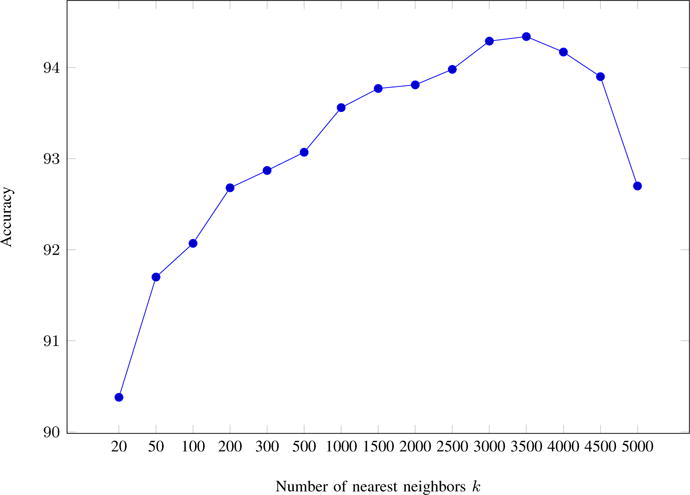
Accuracy of the k-NN approach with varying k

Finally, it is well known that k-NN approaches are infamous for high test time complexity because of the nearest neighbor search in high dimensional space. Our implementation involves cosine similarity computation with all training instances for the corresponding ambiguous term. In this effort, on average there are nearly 40,000 training instances created through weak supervision per ambiguous term. So given a new test instance (T, w, C(w)), cosine similarity (of 300 dimensional vectors) needs to be computed for the test instance T with about 40,000 contexts to impose the ranking on these potential neighbors. The threshold of a chosen k (say, 3500) can only be applied after this ranking is created. However, this similarity computation can be parallelized in a straightforward manner by distributing the similarity computations across multiple processors and pooling the results to incrementally build the ranked neighbor list. Although real time disambiguation may not be feasible, having the k-NN models run overnight every day to address disambiguation in new articles may be practical. Alternative approaches such as locality sensitive hashing [41] that address the dimensionality problems without having to compute cosine similarities may be helpful to alleviate the situation. Overall, however, it is clear that k-NN based approaches with weakly supervised datasets offer an interesting alternative to purely supervised approaches in biomedical WSD.

V. Conclusion

Biomedical WSD is an important task with implications for downstream components in NLP applications. In this effort, we applied recent approaches in neural word embeddings to construct concept embeddings. Our linear time method uses these embeddings to combine cosine similarity, projection magnitude proportion, and a prior knowledge-based approach to produce an accuracy of 92.24%. This is an absolute 3% improvement over just using the knowledge-based approach, which generated the previous best result obtained without supervised learning. Based on predictions from our best linear method, we created a new weakly supervised dataset and built a k-NN model that achieves an accuracy of 94.34%.

Our results rival performances achieved by supervised approaches – the best published supervised result achieves 93% macro accuracy over ten fold cross validation experiments on the MSH WSD dataset with the Naive Bayes model [1]. Based on additional ten fold cross validation experiments with support vector machines that use neural word vector features, Jimeno-Yepes [42] was able to achieve close to 96% macro accuracy. However, we cannot directly compare these cross validation results (from the supervised experiments) to the 94.34% accuracy we obtained without supervision in this paper. Specifically, in each iteration, the cross validation framework tests only on one-tenth of MSH WSD dataset by training on the remaining nine folds of the dataset. In our method, we test on the full MSH WSD dataset without using any of it for training.

Overall, our results in this paper contribute new evidence that dense neural embeddings function as useful representations of textual data for biomedical NLP applications. Furthermore, they also showcase the potential of knowledge-based approaches in learning better dense vector representations (via MetaMap that uses UMLS) and their complementary contributions to WSD tasks. We conclude with some limitations and future research directions.

• Although linear method’s accuracy is above 92.24%, there is still room for improvement in terms of incorporating modifications that account for sense level errors. That is, in addition to accuracy, for each ambiguous term, if we study the errors (false positives, false negatives) associated with each of its senses, we might be able to modify our approaches to account for any common patterns in which errors manifest. This task involves manual qualitative analysis with over 400 unique senses in the MSH WSD dataset and is a important future research direction.

• In Section III-B, the test context ${\overrightarrow{T}}_{\mathit{avg}}$ is the vector formed by element-wise averaging of the word vectors of the corresponding words in the test context T. Although averaging is simple and intuitive, it may not be the best representation of the semantic content of the narrative in the test context. As such, more powerful alternatives that can better represent information in the context sentences might be helpful. To this end, one option is to directly model paragraphs as fixed size vectors using a word2vec style unsupervised learning architecture as demonstrated by Le and Mikolov [43] where paragraph vectors are learned along with word vectors.

• A second approach is to consider a weighted average of the word vectors corresponding to tokens in the context vector where the weight selected for a word is inversely proportional to its distance from the ambiguous term w in the test context. Besides word vectors, we can also compute the weighted average of concept vectors associated with the CUIs (other than those associated with w) in the test context. The weighted averages of the words and contextual CUIs can then be compared separately with the candidate concept vectors from C(w) to generate two different scores ∈ [0, 1] whose sum can form the final score to select the correct sense.

• Both the paragraph vector approach [43] and the weighted averaging approach discussed earlier do not explicitly model word order when composing test context words to form fixed size vectors that better capture the semantics of the full context. Recurrent neural networks (RNNs [44, Chapter 3]), especially with long short-term memory units [45], are a more suitable alternative for such scenarios but would need training data to set the parameters of the recurrent layer. The dataset created using weak supervision in Section III-C can be used here to estimate RNN parameters corresponding to the model for each ambiguous term.

Appendix

As a component of main methods in Section III-B, we use the knowledge-based approach developed by Jimeno-Yepes and Berlanga [2] which we briefly discussed in Section II-A. Here we give some additional details. The main idea is to model P(c|T), probability of CUI c given a context T. If this is estimated accurately, our WSD solution is to simply pick the candidate sense c that maximizes P(c|T). Using Bayes theorem, we have

$$P(c|T)=\frac{P(T|c)P(c)}{P(T)}\propto P(T|c)={\displaystyle \prod _{w_j\in T}P(w_j|c)},$$

with the naive assumption of independence of tokens w_j that constitute the context T given the sense c. So our solution now depends on estimating the word-concept probabilities P(w|c) for any word w and CUI c. The rest of this appendix outlines how Jimeno-Yepes and Berlanga accomplish that.

A straightforward first cut to obtain P(w|c) is to simply model it as the maximum likelihood estimate

$$P(w|c)=\frac{\mathit{count}(w,c)}{{\displaystyle {\sum }_{w\prime \in \mathit{lex}(c)}\mathit{count}(w\prime ,c)}},$$

where lex(c) is the synonymous name set of c in the UMLS. Instead of limiting the search of w to the lexical space of c, they propose to extend it to lexical spaces of concepts that are related to c based on the UMLS relations available as part of the MRREL file in the Metathesaurus [19]. That is, we now have P_k(w|c₀), which denotes the probability of w being selected for the set of concepts R_k(c₀) that are k hops away from the original concept c₀ = c. Specifically, they estimate

$$P_k(w|c_0)={\displaystyle \sum _{c_k\in R_k(c_0)}{P}_k(w,c_k,c_{k-1},\dots |c_0)}=\frac{{\displaystyle {\sum }_{c_k\in R_k(c_0)}{P}_k(w,c_k,c_{k-1},\dots ,c_0)}}{P(c_0)}=\frac{{\displaystyle {\sum }_{c_k\in R_k(c_0)}{P}_0(w|c_k){\displaystyle {\prod }_{l=0,\dots ,k-1}P(c_{l+1}|c_l)P(c_0)}}}{P(c_0)}={\displaystyle \sum _{c_k\in R_k(c_0)}{P}_o(w|c_k)}{\displaystyle \prod _{l=0,\dots ,k-1}P(c_{l+1}|c_l)},$$

where Markov assumption is used for estimating P_k(w, c_k,…, c₀) in terms of traversal probabilities, P(c_l+1|c_l), of hopping from concept c_l to c_l+1 in the UMLS relation graph. This is mathematically estimated as

$$P(c_{l+1}|c_l)=\frac{|r(c_{l+1},c_l)|}{|r(\ast ,c_l)|},$$

with r(c₁, c₂) denoting the number of UMLS relations connecting c₁ and c₂ and the denominator indicating the number of relations where c_l participates.

The word concept probabilities P_j(w|c) obtained at different values of j = 0,…, l are finally combined using a linear combination to estimate

$$P(w|c)={\displaystyle \sum _{j=0,\dots ,l}{\alpha }_j{P}_j(w|c)}\text{where}{\alpha }_0,\dots ,{\alpha }_l>0\text{and}{\displaystyle \sum _{j=0,\dots ,l}{\alpha }_j=1.}$$

They start with each α_j = 1/l with l being the number of hops considered and update them using expectation-maximization, details of which are presented in their paper [2, Section 3.3].