Mechanically Loading Cell/Hydrogel Constructs with Low-Intensity Pulsed Ultrasound for Bone Repair

Abstract

Low-intensity pulsed ultrasound (LIPUS) has been shown to be effective for orthopedic fracture repair and nonunion defects, but the specific mechanism behind its efficacy is still unknown. Previously, we have shown a measurable acoustic radiation force at LIPUS intensities traditionally used for clinical treatment and have applied this force to osteoblastic cells encapsulated in type I collagen hydrogels. Our goal in this study is to provide insight and inform the appropriate design of a cell therapy approach to bone repair in which osteoblasts are embedded in collagen hydrogels, implanted into a bony defect, and then transdermally stimulated using LIPUS-derived acoustic radiation force to enhance bone formation at the earliest time points after bone defect repair. To this end, in this study, we demonstrate the ability to measure local hydrogel deformations in response to LIPUS-induced acoustic radiation force and reveal that hydrogel deformation varies with both LIPUS intensity and hydrogel stiffness. Specifically, hydrogel deformation is positively correlated with LIPUS intensity and this deformation is further increased by reducing the stiffness of the hydrogel. We have also shown that encapsulated osteoblastic cells respond to increases in LIPUS intensity by upregulating both cyclooxygenase 2 and prostaglandin E₂ (PGE₂), both implicated in new bone formation and well-established responses to the application of fluid forces on osteoblast cells. Finally, we demonstrate that combining an increase in LIPUS with a three-dimensional culture environment upregulates both markers beyond their expression noted from either experimental condition alone, suggesting that both LIPUS and hydrogel encapsulation, when combined and modulated appropriately, can enhance osteoblastic response considerably. These studies provide important information toward a clinically relevant cell therapy treatment for bone defects that allows the transdermal application of mechanical loading to bone defects without physically destabilizing the defect site.

Introduction

Cell therapy for bone repair has been used clinically in the form of autogenous bone marrow aspirate that is collected and reinjected into a bony defect¹ or as a constituent part of a bone autograft that is harvested from a patient in need of bony reconstruction and reimplanted within that same patient. Cells have also been aspirated from bone marrow and added to an allograft (that has been devitalized as part of the processing protocol) to try to restore some of its lost functionality, and then implanted into a bony defect.^1,2

Despite their successes, these approaches face certain challenges to more widespread clinical utility, including (1) concerns about cell persistence after delivery in the absence of a carrier and/or (2) an invasive surgical procedure required for implantation.

To overcome these limitations, clinicians and researchers alike have evaluated the utility of loading cells into hydrogels to form a minimally invasive, injectable cell/hydrogel construct that can deliver cells and retain them at the defect site.³ While efficient at cell retention, there is a clear mechanical mismatch between a nonload-bearing cell/hydrogel construct and the surrounding bone; so rigid fixation would often be mandated to stabilize the defect during the initial healing phase. Doing so, however, insulates the implanted cells from the well-documented benefits of physical loading.⁴ Finding a way to add localized and controllable physical loading while the bone defect is immobilized may result in enhanced healing over a mechanically isolated defect.

Toward this end, we have developed a methodology that can mechanically stimulate hydrogel-encapsulated cells using low-intensity pulsed ultrasound (LIPUS)-derived acoustic radiation force (ARF).⁵ ARF is the force that is introduced when an area is irradiated with a sound field⁶ and manifests itself by driving particles within the sound field to drift and cluster. Traditionally, ARF is used at very high intensities, as high as 1 MW/cm², for techniques such as tissue imaging and elastography to evaluate the mechanical properties of intact human tissue,^7–9 but resulting thermal effects from the required high intensities limit its clinical utility.

We have demonstrated a measurable acoustic radiation force at far lower intensities, within the range used for LIPUS-based treatment of fractures and nonunions, which avoids local heating altogether and permits longer exposure times without damage to local tissue.⁵ We have shown that this force is capable of loading and physically deflecting type-I collagen hydrogels, the same material found in unmineralized osteoid in healing bone defects, and through this deflection can induce enhanced phenotypic expression of osteoblasts that have been encapsulated within the gel.⁵

We have also shown that we can modulate the effect of the ARF on hydrogels and cells encapsulated within them by changing either the stiffness of the hydrogel or the intensity of the acoustic radiation force. Our ultimate goal is to be able to apply this force transdermally to cell–hydrogel constructs that have been delivered to large bony defects, which would permit the physical stimulation of the encapsulated cells during the repair process, despite the fact that these defects will have been mechanically stabilized. We feel this may induce more rapid and robust defect healing, despite the mechanical stabilization.

Building on our previous work on the impact of hydrogel stiffness and ARF intensity on both cells and hydrogels,⁵ in this study, we have pursued an in-depth understanding of how the hydrogel is affected regionally when physically stimulated, how the magnitude of hydrogel deformation is influenced by ARF intensity and can vary in the x, y, and z plane, and how encapsulated cells respond to this stimulation. The goals of this work were as follows: (1) to evaluate the nature of the hydrogel deformation under ARF to better understand the physical forces experienced by encapsulated cells, (2) to compare the short-term response of osteoblasts seeded on a two-dimensional (2D) rigid substrate (tissue culture polystyrene [TCP]) to osteoblasts encapsulated within the three-dimensional (3D) flexible hydrogels, and (3) to evaluate the effect of adding ARF at two different intensities to these same cells.

Materials and Methods

Finite element analysis model of hydrogel deformation

To predict hydrogel deformation from ARF, we modeled our in vitro hydrogel testing conditions using the Acoustics-Structure Interaction Module of COMSOL Multiphysics^® software (Version 4.4) in the frequency domain. Two geometries were constructed: one for the hydrogel and the other for the cell culture media in which the hydrogel would be tested. The media volume was defined as a cylinder with radius of 1.1 cm and height of 0.8 cm to match the TCP well used in our in vitro setup. The shape of the hydrogel was approximated to be a cylinder with a radius of 1 cm and height to 0.6 cm, slightly smaller than the TCP well used in our in vitro setup.

The Young's modulus of a hydrogel was input as 1.5 kPa (based on mechanical tests of actual type I collagen hydrogels), the density of the hydrogel was calculated to be 1200 kg/m³, and the Poison's ratio was input as 0.499, and the speed of sound in a hydrogel was set to 1480 m/s, which are reasonable approximations given the high water content of the hydrogels. Frequency inputs of 1 MHz, 1 kHz, and 1 Hz were computed to analyze the different ways in which the hydrogel responded. Finally, a fixed constraint condition was applied to the bottom of the hydrogel and a free tetrahedral mesh was constructed with a custom mesh size over the hydrogel geometry. Resulting deformations were imaged using pseudocolor heat maps to display regional differences in hydrogel deformation.

Acoustic radiation force generation

For in vitro testing, LIPUS was used to generate ARF and applied to type I collagen hydrogels in six-well tissue culture plates using a 1.2 MHz unfocused immersion transducer (Olympus NDT, Inc., Waltham, MA), a waveform generator (Agilent Technologies, Santa Clara, CA), and an ENI RF amplifier (Bell Electronics, Renton, WA). Acoustic force was generated using a 1 MHz carrier frequency pulsed at 1 kHz and delivered with a duty cycle (the portion of a 1 ms time span in which the pulsed carrier frequency is on) of 20%, which corresponds to clinical treatment for bone defects, 50%, or 100%. Input amplitude was adjusted to generate two distinct spatial intensities, 30 mW/cm², which is the clinically prescribed intensity for bone fracture and nonunion repair, and a 5 × higher intensity of 150 mW/cm². All analyses were carried out at these two intensities to evaluate the impact of its modulation on hydrogel displacement and cellular response.

Hydrogel synthesis and displacement

Synthesis of collagen hydrogels and quantification of ARF-driven deformation have been described previously.⁵ Briefly, five different concentrations of Type I rat tail collagen (BD Biosciences, Franklin Lakes, NJ) were formulated (0.05%, 0.075%, 0.1%, 0.2% and 0.3%) to test the impact of collagen concentration on mechanical displacement (0.05–0.2%) and cellular response (0.3%).

For gel displacement studies, polystyrene beads embedded with a green fluorescent dye measuring 1 μm in diameter (Fisher Scientific, Pittsburgh, PA) were encapsulated (3 × 10⁸ beads/hydrogel) within the hydrogels and their position under ARF was tracked in three dimensions using epifluorescence microscopy (magnification = 60 × ) (Hamamatsu Corp., Bridgewater, NJ), with automated z-stack acquisition. Volocity™ acquisition and quantification software (Improvision, Inc., Coventry United Kingdom) was used to capture the movement of fluorescent beads in each of the hydrogels during three distinct phases of testing: (1) before ARF application to establish a baseline, (2) during ARF application, and (3) after ARF application ended to quantify postacoustic gel response.

Each concentration of hydrogel was subject to a 20%, 50%, and 100% duty cycle. The position of several beads (n > 100 bead paths/hydrogel) from each hydrogel was tracked for each experimental condition following deconvolution of a time series of z-stacks of images. All images were acquired with sub-Rayleigh pixel resolution of 266 nm and subdepth of field resolution of 250 nm. The datasets included 61 time points, acquired continuously at 20 frames per second, over a span of 90 s. The z-stacks for each time point spanned a full range of 7.5 um, based on 31 focal planes. An estimate of the deconvolved error would be the mean change in measured bead position between every image frame before acoustic exposure, yielding an extremely conservative error estimate of 230 nm for bead positions, including microscope and camera error, bead homogeneity, the deconvolution routine, and Brownian motion.

Notably, although, this displacement error is angle independent, as opposed to the vectored response of each bead track upon acoustic excitation. From these tracking data, vector maps were generated using Matlab Graphical Software (Mathworks, Inc.). The vector maps illustrate the x–y movement, with a vector associated with each tracked bead that reveals that bead's x–y plane displacement magnitude and direction and interpolates displacement vectors in between. Furthermore, these x–y maps were superimposed on a heat map that revealed the z-plane displacement of the bead before, during, and after ARF irradiation at two different duty cycles (50% and 100%).

To quantify the overall path length of the beads, and therefore the displacement of the hydrogel, in each of the x-, y-, and z-directions, 10 beads from each hydrogel were selected and each bead's displacement was summed in each coordinate for 90 s (30 s each before, during, and after ARF application). From each of the ten beads tracked, a mean path length was calculated (±standard deviation) and interpreted as a measure of the hydrogel displacement around that bead as a result of ARF.

Cell culture

MC3T3-E1 mouse preosteoblast cells were obtained from ATCC (Manassas, VA) and used for ARF studies. Cells were initially cultured on TCP for expansion in α-minimum essential media (α-MEM) media supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin. Cells were maintained in 37°C and 5% CO₂ and the medium was changed every two days. For all assays, cells were seeded on TCP at a density of 5 × 10⁴ cells per well (six-well plate) or were encapsulated in 3 mL of 0.3% type 1 collagen hydrogel at a density of 2.5 × 10⁵ cells/hydrogel (6-well plate) in α-MEM media as described above. Variations in seeding density were to accommodate the larger volume available to the cells in the 3D hydrogels compared to the available area on the 2D TCP.

Cyclooxygenase-2 expression quantification

Real-time quantitative reverse transcription polymerase chain reaction (RT-PCR) was performed for cyclooxygenase 2 (COX-2) by TaqMan gene expression assays (Thermo Fisher Scientific, Waltham, MA). Cells were seeded on TCP (as the 2D rigid substrate) and within hydrogels as described above and cultured for 24 h, after which ARF was applied for 20 min at either 30 or 150 mW/cm² intensity. Cell cultures were then incubated for 30 min and cells isolated from hydrogels by digesting the collagen with enzyme collagenase (Thermo Fisher Scientific, Waltham, MA), and total RNA was extracted from cells on TCP and within gels with RNeasy Mini (Qiagen, Valencia, CA). cDNA was then synthesized using the Clontech EcoDry Premix (Double Primed) reverse transcription kit (Clontech, Mountain View, CA).

Amplification curves for the experimental and the control genes were recorded over the iQ5 RT-PCR machine (BioRad, Valencia, CA) and the relative gene levels between samples were quantified. Data were calculated by the delta–delta Ct method and normalized to housekeeping gene GAPDH, and relative to the day 1 control sample.

Prostaglandin E₂ expression quantification

To measure prostaglandin E₂ (PGE₂) expression, cells were seeded on TCP and within hydrogels as described above and cultured for 72 h, after which ARF was applied for 20 min at either 30 mw/cm² or 150 mw/cm² intensity. Cell cultures were then incubated for 1 h and media collected from cells seeded on both TCP (as the 2D rigid substrate) and encapsulated in hydrogels. PGE₂ release into the media was determined using a competitive enzyme immunoassay kit (R&D Systems, Minneapolis, MN) following the manufacturer's protocol. Briefly, 150 μL of the cell medium aspirate was allowed to bind to the PGE₂ antibody for 1 h at room temperature on a horizontal orbital shaker.

During the second incubation (2 h, at room temperature on the horizontal orbital shaker), horseradish peroxidase-labeled PGE₂ bound to the remaining antibody sites. After the wells were aspirated and washed thoroughly to remove the unbound material, an enzyme substrate solution was added to determine the bound enzyme activity. Subsequently, the color development was stopped and the absorbance was read at 450 nm using a spectrophotometer. The intensity of the color was inversely proportional to the concentration of PGE₂ in the sample. Each group contained n = 4 samples. All PGE₂ concentration was normalized by the total number of cells and the graph represents PGE₂ concentration per 100,000 cells.

Statistical evaluation

The numerical data from COX-2 and PGE₂ assays were expressed as mean values ± standard deviation. Each experiment was performed in triplicate per group. To determine the effect of ultrasound intensity or substrate stiffness on COX-2 and PGE₂ expression statistical differences between groups was evaluated using a two-way analysis of variance (p < 0.05). When significance was noted, further analysis between specific groups was conducted using Tukey post-hoc testing.

Results

Hydrogel deformation testing in silico and in vitro under acoustic radiation force

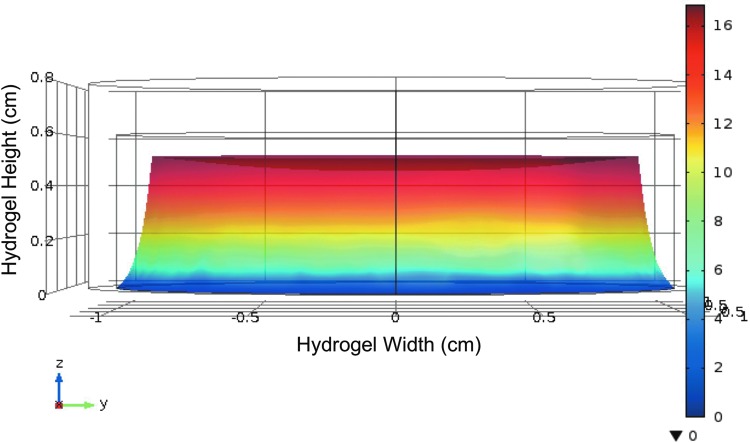
Finite element analysis was used to develop a predictive model of how a flexible hydrogel mechanically similar to those tested in this study would respond to ultrasound, as a mimic of ARF, while fixed to a solid substrate such as TCP. Results showed that hydrogel deformation in response to ultrasound that was directed to the top of the gel was most dramatic closest to the ultrasound source (Fig. 1) and decreased as the distance from the source increased. This was expected given that the bottom of the gel was modeled to be attached to a rigid substrate, as in our in vitro experimental studies, and acoustic intensity decreases with distance from the transducer, and therefore attenuation increases. This model may allow us to predict hydrogel deformation in silico and may be useful as a tool in subsequent experiments for modeling cell loading by deflected hydrogels by adding the acoustic impedance of cells¹⁰ to our model.

FIG. 1.

Heat maps demonstrate hydrogel deformation in a simulated application of acoustic radiation force to a flexible hydrogel. Finite element analysis of a hydrogel under acoustic radiation force, simulated to be applied to the top of the gel, indicates the greatest deformation occurred closest to the application of radiation force, with diminishing deformation further from the force application.

Real-time in vitro measures of hydrogel deformation under ARF were taken by tracking the deflection of embedded fluorescent μbeacons and revealed more detailed information about hydrogel deformation. Figure 2 showed vector maps of beads embedded in hydrogels before, during, and after acoustic radiation force. These Figures indicated that bead deflection, and correspondingly hydrogel deformation, was not confined to the z-plane, but rather was distributed across the x, y, and z planes. Pseudocolor heat maps indicated the degree of deformation by mapping the z-plane location of individual beads before (A, D), during (B, E), and after (C, F) ARF was applied. Maps indicated a greater deflection downward with the 100% duty cycle (Fig. 2D–F) than with the 50% duty cycle (Fig. 2A–C).

FIG. 2.

Vector maps of individual μbeacons (white X) and displacements (arrows) embedded in 0.1% type I collagen hydrogels before (A), during (B), and after (C) acoustic radiation force with 50% duty cycle. Vectors indicate interpolated direction and magnitude of displacement in the x–y plane, while heat maps indicate displacement in the z-plane. Results demonstrate that bead, and therefore hydrogel, displacement is not dominated by z-plane deflections, but rather is shared across all three axes of movement. Vector maps of individual μbeacons (white X) and displacements (arrows) embedded in 0.1% type I collagen hydrogels before (D), during (E), and after (F) acoustic radiation force with 100% duty cycle demonstrate that bead, and therefore hydrogel, displacement is greater in the z-direction with the higher duty cycle, indicating that increasing duty cycle increases hydrogel deformation.

They also indicated partial recovery to the starting point after ARF was turned off, which was expected given the viscoelasticity of the hydrogels. While not immediately apparent from the qualitative representation of the vector maps, the average cumulative μbeacon path length recorded during the application of acoustic force showed a dependence of path length on both hydrogel stiffness and radiation force duty cycle (Table 1). The path length of the μbeacons, which is a measure of the deformation of the hydrogel at the point of the measured beacon, was seen to increase as hydrogel concentration (and therefore stiffness) decreased.

Table 1.

Mean Path Length of μbeacons Encapsulated Within Hydrogels of Differing Stiffness (± Standard Deviation; n = 10) with Different Duty Cycles Shows Increasing Path Length as Duty Cycle Increases (Top to Bottom) and Hydrogel Concentration, and Therefore Stiffness, Decreases (Right to Left)

	0.05% Collagen		0.075% Collagen		0.2% Collagen
Duty cycle, %	Mean path length (μm)	Standard deviation	Mean path length (μm)	Standard deviation	Mean path length (μm)	Standard deviation
20	22.74	9.97	9.90	3.15	4.16	3.72
50	31.71	6.68	13.94	1.27	6.02	6.47
100	55.40	18.36	23.85	0.53	5.80	2.14

Path length is a representation of the deformation of the hydrogel around the μbeacon and therefore a suggestion of the forces that an embedded cell may experience under acoustic radiation force.

Of course, the path length also increased as duty cycle (and therefore applied force) increased. Considering the motion of the beads in the xy-and z-planes independently reveals that, despite the application of the ARF normal to the surface of the hydrogel, motion of the gel was not limited to that plane. Indeed for the less stiff gels, the majority of bead, and therefore hydrogel, motion during ARF was in the xy-plane (Table 2). As the hydrogel stiffened, the distribution of displacement was more evenly distributed. This provides important insight into the nature of the forces that would be applied to an encapsulated cell by the surrounding deflected hydrogel.

Table 2.

Mean (n = 10) Path Length of μbeacons in the X–Y Plane and the Z-Plane Indicates That the Less Stiff Hydrogels Show More Displacement Orthogonal to the Direction of the Ultrasound than Stiffer Hydrogels, but more Importantly that the Displacement is not Confined to One Direction, but Rather Distributed Across Multiple Directions

Path length (μm)
	0.05% Hydrogel	0.075% Hydrogel	0.2% Hydrogel
20% duty cycle
XY-direction	16.47	6.37	0.85
Z-direction	7.82	1.12	1.06
50% Duty cycle
XY-direction	34.01	12.76	1.64
Z-direction	4.98	1.08	1.50
100% Duty cycle
XY-direction	54.20	24.82	1.68
Z-direction	10.93	0.93	1.34

COX-2 expression quantification

COX-2 expression was upregulated in cells encapsulated within hydrogels over cells on rigid 2D TCP (see Fig. 3, TCP control vs. 0.3% Type I collagen hydrogel control), although not with statistical significance. The addition of ARF to encapsulated cells further increased cellular COX-2 expression over encapsulated cells without ARF with statistical significance (control 0.3% type I collagen hydrogel vs. 30 and 150 mW/cm²) (Fig. 3) and over cells seeded on TCP with ARF (TCP vs. 0.3% type I collagen hydrogel for both 30 and 150 mW/cm²).

FIG. 3.

COX-2 gene expression was quantified and upregulations noted when acoustic force was applied to cells on TCP (30 and 150 mW/cm², not significant) and cells encapsulated in type I collagen hydrogels (both 30 and 150 mW/cm², statistically significant). Interestingly, cells encapsulated within hydrogels also expressed an upregulation of COX-2 gene expression, although not significant, with no acoustic force (Control) when compared to cells seeded on TCP with no acoustic radiation force (Control). There was, however, a statistically significant upregulation of COX-2 expression when comparing acoustic radiation force applied to encapsulated cells versus cells on TCP. Statistical significance noted (*p < 0.05). COX-2, cyclooxygenase 2; TCP, tissue culture polystyrene.

These data show that simply encapsulating cells within a hydrogel can induce an upward trend in COX-2 expression over cells seeded on a rigid 2D surface like TCP, and adding ARF to those encapsulated cells further increases COX-2 expression over both encapsulated cells with no ARF and cells seeded on 2D rigid substrates with ARF, suggesting an additive effect of both 3D tissue culture in hydrogels and the application of ARF.

PGE₂ expression

PGE₂ expression of MC3T3-E1 cells varied depending on the substrate and the presence of ARF (Fig. 4), but followed very similar trends to those seen with COX-2 expression. Specifically, applying ARF to cells seeded on rigid TCP induced an upregulation of PGE₂ expression. Simply encapsulating cells within the hydrogel (with no ARF applied) also induced an upregulation of PGE₂ expression. Finally, applying ARF to cells encapsulated within hydrogels further increased PGE₂ expression over encapsulated cells with no ARF applied, suggesting an additive effect of both tissue culture substrate and ARF, similar to what was observed with COX-2 expression.

FIG. 4.

Response of cellular PGE₂ expression to acoustic radiation force. Applying either 30 or 150 mW/cm² of acoustic intensity shows increasing PGE₂ expression over the control (0 mW/cm²). Seeding cells in hydrogels also upregulates PGE₂ expression over cells on TCP in the absence of acoustic intensity, while applying either 30 or 150 mW/cm² increases PGE₂ expression even further. Statistical significance noted (*p < 0.05). PGE₂, prostaglandin E_2.

Discussion

LIPUS, independent of cell/hydrogel constructs, has been used for some time as a noninvasive treatment for both fracture and nonunion repair, and has been shown to be clinically effective.^11,12 One theory behind its efficacy suggests that LIPUS induces greater blood flow at the defect site and thus promotes better in vivo healing,¹³ but in vitro studies have shown that it is more complex than that. LIPUS also increases osteoblast production of vascular endothelial growth factor and fibroblast growth factor,¹⁴ promotes chondrocyte aggrecan and type II procollagen synthesis,¹⁵ inhibits osteoclastogenesis,¹⁶ stimulates PGE₂ and COX-2 expression,¹⁷ and elevates intracellular calcium,¹⁵ osteocalcin, and gene expression for alkaline phosphatase, transforming growth factor-beta (TGF-β), osteopontin, and BMP-7, to name a few.¹⁸

Despite what has been learned, no definitive mechanism behind LIPUS' clinical efficacy has been identified, but a comparison between in vitro cellular response to LIPUS and in vitro cellular response to externally applied physical forces like shear forces from fluid flow shows numerous similarities,^19–26 suggesting a possible link between the two.

Given this potential link, we have built upon our previous analysis of LIPUS-derived ARF and its effect on cell/hydrogel constructs⁵ to examine its impact on hydrogel deformation in three dimensions and evaluate the acute response of encapsulated cells. Previously, we have reported that the magnitude of hydrogel deformation was proportional to ARF intensity and inversely proportional to hydrogel stiffness.⁵ In this study, we have developed a finite element analysis model to predict the response of a hydrogel to an ultrasonic force using COMSOL Multiphysics Modeling software.

The model predicted regional variations of deformation within the hydrogel with greater amounts proximal to the transducer and lesser amounts more distal as the ultrasound attenuates (Fig. 1), but measurable deformation throughout the thickness of the hydrogel, where not affixed to the immovable substrate. This model may prove as a useful tool to predict cellular deflections within the hydrogel when determining forces applied to cells as the gels are loaded.

Our vector maps of in vitro hydrogel displacement studies tracked individual bead displacements in the x, y, and z directions (Fig. 2) and revealed that displacement of beads within the hydrogel was not confined to the z-direction, but rather expressed in all three directions before, during, and after ARF. Quantifying these displacements revealed varied bead path lengths depending on testing parameters (Table 1), but also varied deflection magnitudes in all three directions (Table 2), which was counter to what was expected given the orientation of the acoustic transducer in the z-direction. This suggests that the forces experienced by encapsulated cells in our system are not purely uniaxial and not confined to the z-direction, but rather experienced in three dimensions. This may more accurately replicate the forces experienced by a cell in situ within an actual extracellular matrix under an externally applied physical force.

Equally important, however, are the forces imparted by that cell on the surrounding extracellular matrix. The constitutive cells of the musculoskeletal system interact with their surroundings passively and actively, by not only responding to externally generated forces but also imparting their own forces on their immediate surroundings. External forces can vary from shear forces applied directly to the cell, as in the case of endothelial cells within a blood vessel or osteocytes within the lacunae of cortical bone, to compressive and tensile forces that are translated to a cell through a displaced extracellular matrix, as with chondrocytes under load within the gelatinous cartilage matrix or osteoblasts and stem cells within a soft callus during bone repair.⁴

Cell-generated forces, which serve to pull and tug on the extracellular space during cell locomotion or migration,²⁷ can vary in magnitude depending on the stiffness of that extracellular space.²⁸ These forces can be observed and measured in vitro using techniques like traction force microscopy,²⁷ and exploited to manipulate cell behavior by controlling and adjusting the stiffness of the extracellular space. For example Engler et al. examined the impact of substrate stiffness on mesenchymal stem cells and reported that MSCs seeded on flexible 2D substrates underwent osteogenic differentiation when the substrate mechanical properties roughly approximated that of newly formed, unmineralized osteoid,²⁹ by observing an upregulation of core binding factor alpha 1,²⁹ a key early marker of osteogenesis.³⁰

This observation that substrate stiffness alone can influence osteoblastic and mesenchymal stem cell response³¹ suggests that the stiffness of the 3D environment encapsulating cells can be a tool if that stiffness is predictable and controllable. We have previously reported that matrix stiffness did influence the behavior of osteoblasts encapsulated in type I collagen hydrogels over 7 days of culture.⁵ Those studies also determined that applying LIPUS-derived ARF to cell/hydrogel constructs elicited an upregulation of osteoblastic markers implicated in new bone formation, alkaline phosphatase and osteocalcin expression, from encapsulated osteoblasts.⁵

Understanding the different contribution of externally applied and internally generated forces is critical to fully characterizing our system, especially given the work of Orr et al. and You et al.^32,33 in which mathematical simulations were run to model bone cells under fluid flow-derived forces within the canaliculi of bone and suggested that the forces derived from the extracellular space may have as much or more to do with cellular response than the fluid forces applied directly to the cell. Estimates were made of the flow-induced shear forces experienced by a cell that arise when a bone is mechanically loaded and were compared to the drag forces that applied to the pericellular space by the same fluid flow.^32,33 Their conclusions suggested that the pericellular drag forces, the forces that preferentially load the pericellular space, are an order of magnitude stronger than the fluid shear forces, the forces experienced directly by cells due to flow, and therefore mechanically dominate the cellular response.^32,33

This is important for our system since the goal of our design has been to have the encapsulated cells be physically stimulated in two ways: directly through the LIPUS-derived ARF and indirectly through ARF-induced hydrogel deformation around the encapsulated cells, the latter of which may mimic the pericellular drag forces seen in vivo. By studying the effect of ARF intensity and hydrogel stiffness on hydrogel deformation, we intend to use these parameters as tools in future studies to manipulate the hydrogel deformation such that it maximally loads encapsulated cells, perhaps by exploiting any differences in hydrogel and encapsulated cell displacement under ARF.

This specific point is the subject of ongoing and future studies. In this study, we have shown that cell behavior can indeed be impacted mechanically in two ways: either by applying ARF to cells encapsulated within a hydrogel or by modifying the mechanical stiffness and subsequent deformation of the hydrogel itself, and when these two loading strategies are combined, the result is a cumulative effect on cell behavior that exceeds either one applied separately.

To determine this, we cultured MC3T3-E1 osteoblasts either on rigid TCP, as is commonly reported in the literature, or within highly flexible type I collagen hydrogels and compared the resulting COX-2 and PGE₂ expression. We then applied ARF to each culture condition and again compared the COX-2 and PGE₂ expression. We hypothesized that adding ARF to cells on a rigid substrate would elicit an upregulation of both COX-2 and PGE₂ expression, similar to reports of osteoblasts under fluid-derived mechanical loading,^34,35 and simply placing the cells within the flexible hydrogel would also stimulate a response similar to those reported in the literature.^28,29

We then hypothesized that combining the 3D hydrogel culture with ARF application would produce a cumulative effect, upregulating COX-2 and PGE₂ to a greater extent than either condition independently, because the effects of the more flexible hydrogel on cell behavior would manifest during non-ARF culture periods and would be supplemented by the 20-min daily physical loading provided by the ARF. Results confirmed that (1) cells exposed to acoustic radiation force did express higher COX-2 and PGE₂ expression than those not exposed, (2) cells seeded within the flexible hydrogel did express higher COX-2 and PGE₂ expression than those seeded on rigid TCP, and (3) the combination of both conditions increased both COX-2 and PGE₂ expression over either one independently (Figs. 3 and 4), suggesting that combining the two distinct conditions is cumulative.

While our previous work showed how osteoblasts respond to ARF after several days of daily exposure,⁵ in this study, we were interested in the immediate effects of stimulation as it related to early markers known to play important roles in subsequent bone formation. The literature reveals almost immediate, but transient expression of both COX-2 and PGE₂ in response to mechanical stimulation;^36,37 so we chose to examine the immediate response to ensure capturing what may be a short lived, but physiologically relevant, upregulation of expression. Future studies will examine whether altering experimental parameters such as hydrogel stiffness or ultrasound intensity impact the short- and long-term expression of these, and other, markers.

Studies have been done that examine the relationship between imparted mechanical loading (using fluid flow) and actin polymerization^34,38 and have revealed a correlation between steady fluid flow and reorganization of the actin filaments, suggesting that actin polymerization responds to fluid-induced mechanical forces. This response was noted in studies we performed on actin polymerization after ultrasound exposure (data not shown), but only on 2D rigid substrates. When cells were seeded on 2D hydrogels, the actin appeared far more punctate and diffuse, much like that reported in the literature of similar studies on soft surfaces.^28,29,39

Interestingly, when ARF was applied to the cells in our study, the directional orientation of polymerization was not observed, suggesting that the forces experienced by the cells on hydrogels was different than that experienced by cells on TCP. What was perhaps more notable, however, was the evidence of actin polymerization within cells on rigid TCP in the absence of any applied acoustic force, suggesting that the adhesion to a rigid substrate alone was inducing a less intense, but noticeable, response within the cell similar to that experienced with the application of force. It is reasonable to expect that a cell encapsulated within a hydrogel may respond differently to ARF than one seeded on top of one,⁴⁰ and it is also reasonable that 3D hydrogels may more closely mimic the natural environment as cell substrates, a thought that has been echoed by others⁴¹ and is the subject of considerable ongoing work. Nonetheless, this may provide some insight into why simply seeding cells within a flexible hydrogel induces a different response from that of TCP alone.

In summary, in this study, we describe how collagen hydrogels respond to LIPUS-derived acoustic radiation force and how this response can be tracked in three dimensions with regional specificity. We also demonstrate how controlling these parameters can influence cellular response very soon after stimulation. These techniques will be valuable tools in future studies that parse the impact of specific parameters on cell response. The work described herein adds to the knowledge base of how cells respond to ultrasound and how a change in the substrate environment can further influence that cellular response.

It also contributes to the informed design of a cell therapy approach for bone repair that would allow the implantation of cells within a carrier to a bony defect. Those cells could then be subsequently physically loaded after implantation with precise control over the impact of that loading through acoustic force intensity and hydrogel stiffness modulation, and a combination of both. We therefore suggest that delivering cells within a flexible hydrogel and adding ARF-induced loading may, by virtue of the upregulated response of key bone formation markers noted herein, lead to an uptick in bone formation during the earliest stages of fracture repair. This is particularly relevant given the recognized clinical benefit of micromotion within the callus during fracture repair at the earlier points of healing when marrow-derived stem cells and osteoblasts are found within the soft forming callus vs. later time points when the callus has mineralized and is less susceptible to micromotion.⁴

Acknowledgments

Research reported in this publication was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under Award Number R21AR064432. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Disclosure Statement

No competing financial interests exist.