Machine Learning for Fetal Growth Prediction

Abstract

Birthweight is often used as a proxy for fetal weight. Problems with this practice have recently been brought to light. We explore whether data available at birth can be used to predict estimated fetal weight using linear and quantile regression, random forests, Bayesian additive regression trees, and generalized boosted models. We train and validate each approach using 18,517 pregnancies (31,948 ultrasound visits) from the Magee-Womens Obstetric Maternal and Infant data, and 240 pregnancies in a separate dataset of high-risk pregnancies. We also quantify the relation between smoking and small-for-gestational-age birth, defined as a birthweight in the lower 10th percentile of a population birthweight standard, and estimated and predicted fetal weight standard. Using mean squared error and median absolute deviation criteria, quantile regression performed best among the regression-based approaches, but generalized boosted models performed best overall. Using the birthweight standard, smoking during pregnancy increased the risk of small-for-gestational-age 3.84-fold (95% CI: 2.70, 5.47). This ratio dropped to 1.65 (95% CI: 1.50, 1.81) when using the correct fetal weight standard, which was no different from the machine learning-based predicted standards, but higher than the regression-based predicted standards. Machine learning algorithms show promise in recovering missing fetal weight information.

Introduction

Adequate growth from conception into early childhood is central to optimal health and survival. ¹ Because of its predominant role in shaping the risk of adverse perinatal outcomes, fetal or intrauterine growth restriction is often itself considered to be an outcome of epidemiologic interest, usually quantified as small versus appropriate for gestational age. Additionally, there is a growing interest in quantifying the precise relation between the continuum of fetal growth and the occurrence of adverse perinatal and childhood outcomes. Because fetal (intrauterine) weight is typically not measured in populo, birthweight is often used as a proxy for fetal weight in population health studies. However, recent work shows that this practice can lead to potentially serious missing data or selection bias problems, particularly at early gestational ages.²

Attempts have been made to resolve the problems posed by missing fetal growth curves in clinical and population-level data. These include the use of population referents based solely on (i) birthweight,³ (ii) fetal weight estimates,^4,5 and (iii) hybrid references that average growth curves generated from livebirth and intrauterine weights,⁶ or switch from intrauterine to birth weight distributions at 37 weeks.⁷ While these proposals partially overcome the missing data problem, they are based on the presupposition that fetal growth characteristics in a given sample of pregnancies can adequately serve as a referent for populations potentially far removed from the sample in which the referent curves were generated. Additionally, while fetal growth standards play an important clinical role in identifying high-risk patients, they cannot be used as a replacement for measured fetal weight data, particularly when interest lies in confounding adjustment or effect measure modification of an exposure-response relation by fetal weight history, or evaluating the gestational age specific relation between the fetal weight continuum and the risk of adverse outcomes.

Here, we take a different approach to overcoming the problem of missing fetal weights in population data. We focus on generating algorithms that take as input maternal and infant birth characteristics, and output predicted fetal weights. We then evaluate how predicted fetal weights compare to actual fetal weights using several different approaches: 1) by estimating the correlation between predicted and actual fetal weights; 2) by comparing the gestational week specific quantiles of actual and predicted fetal weights; and 3) by examining the relation between smoking status and small-for-gestational-age birth, with the latter defined using actual and predicted data. In principle, correctly capturing features of birth data that accurately predict fetal weight across gestation would enable researchers to generate such predictions in a wide range of empirical settings.⁸ We evaluate this principle in practice.

Specifically, we explore the potential of combining data available at birth with regression-based and machine learning algorithms to generate population-specific fetal weight curves for a given application. In particular, we: (1) assess whether machine learning algorithms can accurately predict estimated fetal weight over the course of gestation using readily available ex utero information (e.g., birthweight, race, gestational age at birth); and (2) assess the relationship between smoking and fetal/birthweight weight across gestation when the latter is quantified with: a) clinically estimated and predicted fetal weight distributions, and b) actual birthweight distributions.

Methods

Data

Data were obtained from the Magee Obstetric Medical and Infant (MOMI) database, which includes maternal, fetal and neonatal demographic and clinical data from all deliveries at Magee-Womens Hospital, University of Pittsburgh Medical Center, Pittsburgh, PA. MOMI data were used with the approval of the Institutional Review Board of the University of Pittsburgh (IRB# PRO15020176, approved Feb 16 2015). Patients provided informed consent upon admission. The database is updated to incorporate new data every 3–6 months. With each update, data points included in the MOMI database are selected randomly and compared against prenatal records and delivery documentation to assure accuracy of variables including, gestational age at delivery, neonatal sex, parity, Apgar scores. We considered all singleton pregnancies that resulted in live births between 1999–2013, our main cohort consisted of 18,517 live-born singleton pregnancies, with data on 31,948 clinical ultrasound visits from 20 weeks of gestation onwards.

Because ultrasound is collected more regularly from high-risk women, our sample may be subject to selection bias. To evaluate the impact of the potentially higher proportion of high-risk women in our sample, we repeated all analyses in three subsets of the original MOMI sample: 1) pregnancies with five minute Apgar scores ≥ 8; 2) pregnancies with fewer than four ultrasounds; and 3) pregnancies with five minute Apgar scores ≥ 8 and fewer than four ultrasounds. Additional details are provided in eAppendix 1.

We also used data from 240 pregnancies from the Obstetrical Determinants of Neonatal Survival (ODNSR).⁹ The study population consists of infants born in the NICHD Maternal Fetal Medicine Units Network in 1992. The study sought to evaluate factors that facilitate predicting survival in extremely low birth weight infants. Eligible infants weighed less than 1,000 grams, and were followed until death, discharge from the hospital, or 120 days of survival.

For both cohorts, ultrasound estimates of fetal weight (in grams) were our outcome, computed using the equation derived by Hadlock et al.¹⁰ We also abstracted medical chart information on the gestational week at which the ultrasound was obtained, gestational age at birth, birthweight, race, maternal age at birth, one and five minute Apgar scores, infant gender, maternal smoking status, and the year of birth. Additional details are provided in the eAppendix.

Analytic Strategy

Fetal Growth Prediction

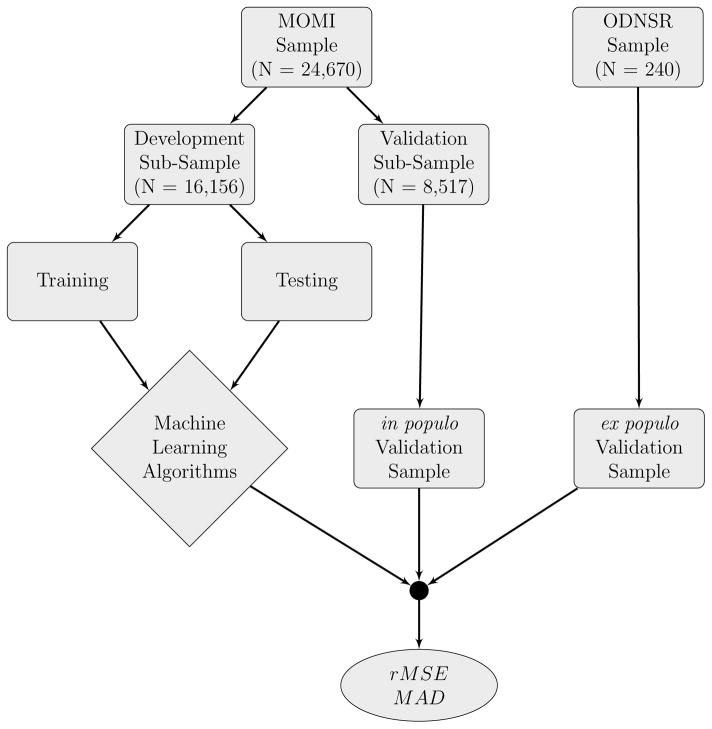
We examined the performance of regression-based and data mining techniques to predict fetal growth trajectories using routine information collected at delivery. Our analytic strategy, outlined in Figure 1, was to first split the MOMI data into algorithm development and algorithm validation subsamples. The validation subsample consisted of all pregnancies that occurred in 2010–2013 (inclusive, N = 8, 517 pregnancies, M = 13, 354 ultrasound visits). This allowed us to evaluate the performance of our prediction algorithms in a validation sub-sample temporally separated from our development sub-sample. Such temporal separation creates more difficult circumstances under which the predictions are made. The development subsample consisted of all available pregnancies prior to 2010 (N = 16, 156 pregnancies, M = 24, 852 ultrasound visits). The development subsample was then further split as required into training and testing datasets to optimize the selection of tuning parameters using K-fold cross validation.

Figure 1.

Analytic strategy used to train, test, and validate regression-based and machine learning algorithms to predict fetal growth. rMSE = root Mean Squared Error; MAD = median absolute deviation. MOMI: Magee Obstetrics Maternal and Infant Database; ODNSR: Obstetrical Determinants of Neonatal Survival Study Data.

Once generated, we input maternal and birth characteristics extracted from the MOMI validation subsample into our prediction algorithms to output fetal weight predictions for each pregnancy. Predictions were generated for each gestational week with an available fetal weight measurement. These predictions were then compared to actual fetal weight measurements obtained using standard ultrasound protocols. These comparisons were used to assess how well our algorithms performed at predicting fetal weight in populo.

We also carried out an ex populo assessment by inputting maternal and birth characteristics extracted from the ODNSR sample into our machine learning algorithms. Fetal weight predictions were obtained and compared to actual fetal weight estimates available in the ODNSR sample. This ex populo validation enabled us to assess how well our algorithms performed at predicting fetal weight for pregnancies in a population distinct from the one in which the algorithms were developed.

Regression-Based and Machine Learning Algorithms for Fetal Weight Prediction

We assessed how well two regression-based methods and three data adaptive ensemble learning algorithms predicted fetal weight. Regression-based methods consisted of standard linear regression¹¹ and quantile regression.¹² Machine learning algorithms consisted of random forests,¹³ Bayesian additive regression trees,¹⁴ and generalized boosted models.^15,16 Each approach (regression-based and machine learning) maps some component of the outcome’s distribution (e.g., mean, median) to a function of the covariates X, such as:

$$\gamma (Y\mid \mathbf{X}=\mathbf{x})=h(\mathbf{x}).$$ (1)

Specific details on the variables in X for our analyses are included in the eAppendix. Here, we focus on a general overview of each approach. Standard linear regression takes γ() as the expected value function, and h(x) = h(x; β) the linear predictor function in which categorical covariates were entered as disjoint indicator variables and continuous covariates were entered using restricted cubic splines. The parameters of this model were estimated by minimizing a quadratic loss function via ordinary least squares.

Quantile regression sets γ() as the conditional quantile function Q_y(τ | X = x), and h() is the modified linear predictor in which parameters are made functionals of τ, where τ ∈ [0, 1] indexes the τth quantile of the outcome’s distribution. Again, categorical predictors were entered as disjoint indicator variables and continuous predictors were entered using restricted cubic splines. The parameters of this model were estimated for τ = 0.5 by minimizing an absolute loss function via least absolute deviations.¹²

Random forests, Bayesian additive regression trees, and generalized boosted models are based on classification and regression trees. For a continuous outcome, regression tree algorithms take γ() to be the conditional expectation, and h() a tree-based algorithm in which the sample of observations is recursively split into subsets defined by predictor values. Once sample-splitting is complete, the average outcome in each terminal node is estimated.

For random forests, many regression trees are fit to bootstrap resamples of the data and then their results are aggregated (averaged) into one tree, a process known as bagging.¹³ Furthermore, the trees are built by choosing the best split in each bootstrap sample using a randomly selected subset of the predictors. Best splits that define each tree are determined by minimizing a residual sum of squares criterion.^17(p233) In our analysis, we fit 5,000 trees with a random selection of 8 out of 12 predictors.

For Bayesian additive regression trees, h() is taken to be a sum of regression trees model, with the error assumed normally distributed with mean zero and variance σ². The parameters in each tree are solved by minimizing an expected loss function (−log Likelihood). The Bayesian additive regression tree also consists of a regularization prior on the joint distribution of the sum of trees model and the residual error variance. The posterior distribution of the sum of trees model is computed via the Markov Chain Monte Carlo algorithm, from which the averages over all trees are obtained. Tuning parameters for our Bayesian additive regression tree were chosen as the set of values that minimized cross-validation error in a preliminary run.

Finally, generalized boosted models treat h() as a sequence of regression trees, iteratively combined to create an overall function for predicting average fetal weights. The trees in each iteration are fit to a randomly selected (but not bootstrapped) subsample of the data. Each subsequent tree is fit to the residuals of the model from the previous iteration, which results in “boosting” the performance of each subsequent fitting procedure. Predictions from each regression tree are combined using a shrinkage parameter that improves the overall fit of the sequence of models. A generalized cross validation criterion is used to avoid overfitting.^16,17(p269) We fit 5,000 trees with a shrinkage rate of 0.005, a subsampling rate of 50%, and 5-fold cross-validation using a quadratic loss function.

Performance Measures

From each of these five approaches, we generated individual-level predictions for estimated fetal weight. The performance of each approach was then evaluated using the root mean squared error and median absolute deviation, defined as:

$$\mathit{rMSE}=\sqrt{\frac{1}{N}{\sum }_{ij}{(y_{ij}-{\widehat{y}}_{ij})}^2},$$ (2)

$$\mathit{MAD}=m(\mid y_{ij}-{\widehat{y}}_{ij}\mid ),$$ (3)

where y_ij and ŷ_ij denote the actual and predicted fetal weight estimates for pregnancy i at visit j, and where m() denotes the median function. These functions quantify the squared and absolute distance between the actual and predicted fetal weights on the original scale of interest (grams), and thus provide a summary measure of how well each method performs at predicting fetal weight. Variability estimates for root mean squared error and median absolute deviation were obtained using the nonparametric percentile bootstrap with 2,000 resamples.

Small for Gestational Age Analysis

We examined the impact of using different criteria to define small-for-gestational-age birth in the MOMI data. Small-for-gestational-age was defined as a birthweight in: (i) the lower 10th percentile of a gestational age specific population referent birthweight standard (SGA_B);¹⁸ (ii) the lower 10th percentile of the gestational age specific distribution of actual fetal weight + birthweight in the MOMI data (SGA_FB); or (iii) the lower 10th percentile of the gestational age specific distribution of predicted fetal weight + birthweight in the MOMI data (SGA_PB). Hereafter, we refer to these as the birthweight standard, the actual fetal weight standard, and the predicted fetal weight standard, respectively. For each approach, we quantified the proportion of babies classified as small-for-gestational-age, and estimated risk differences and ratios for the association between maternal smoking status (1 = any smoking during pregnancy, 0 otherwise) and small-for-gestatational-age birth under each definition using a generalized linear regression model.¹⁹ These models were adjusted for maternal race, infant gender, maternal age, and their 2- and 3-way interactions.

We also evaluated how smoking status related to the entire distribution of fetal/birthweight, rather than just the proportion of births classified as small-for-gestational-age. This step was important to evaluate whether our algorithms were able to accurately predict the entire conditional distribution of fetal weight, rather than just the first moment of the conditional distribution. To do this, we fit regression quantiles at the 25th, 50th, and 75th percentiles of the actual and predicted fetal weight + birthweight distribution, smoothed across gestation, among smokers and non-smokers. We then took the differences in these actual and predicted fetal weight + birthweight percentiles at each gestational week, and used a locally weighted scatterplot smoother (loess) to evaluate the quantile differences in weight between smokers and non-smokers, smoothed across gestational age.

All analyses were conducted using R version 3.2.3.²⁰ Quantile regression was implemented using the quantreg package.²¹ Random forests, Bayesian additive regression trees, and generalized boosted models were implemented using the quantregForest package,²² bartMachine package,²³ and gbm package,²⁴ respectively.

Results

Over the entire MOMI sample, 25%, 46%, 19%, and 10% had one, two, three, or four or more clinical ultrasound visits during the course of follow-up, respectively. The proportion of non- Hispanic black, non-Hispanic white, and Hispanic women was 18%, 73%, and 2%, respectively. Table 1 shows the median and interquartile values of several characteristics in both the MOMI validation subsample and the ODNSR sample. This table shows that infants in the ODNSR sample were very different than those in the MOMI cohort, with lower fetal weights, birth weights, gestational age at birth. Women in the ODNSR sample were also younger than women in the MOMI sample.

Table 1.

Descriptive statistics for 24,670 pregnancies (38,206 ultrasound visits) at the Magee-Womens Hospital, University of Pittsburgh Medical Center, Pittsburgh, PA, 1999–2013, and 240 pregnancies in the ODNSR data from the NICHD Maternal Fetal Medicine Units (MFMU) Network, 1992.

Characteristic	MOMI			ODNSR
	Median	Q1	Q3	Median	Q1	Q3
EFW	1.86	0.89	2.76	0.71	0.58	0.87
Birthweight	3.27	3.64	3.64	0.71	0.59	0.85
MaternalAge	29	24	33	24	21	30
Gestational Age at Birth	39	38	40	25	23	27
Year of Birth	2008	2005	2010	1992	1992	1992

Abbreviations: Q1, First quartile; Q3, Third Quartile; EFW, Estimated Fetal Weight.

eFigure 1 in the eAppendix shows the estimated fetal weight and birth weight distributions over the course of gestation, with solid and dashed lines representing smoothed regression quantiles for the median of birthweight alone, and birthweight + fetal weight. These lines show that, at earlier gestational ages, the median birthweight is lower than the combined birth and fetal weights, in line with results from previous research.²

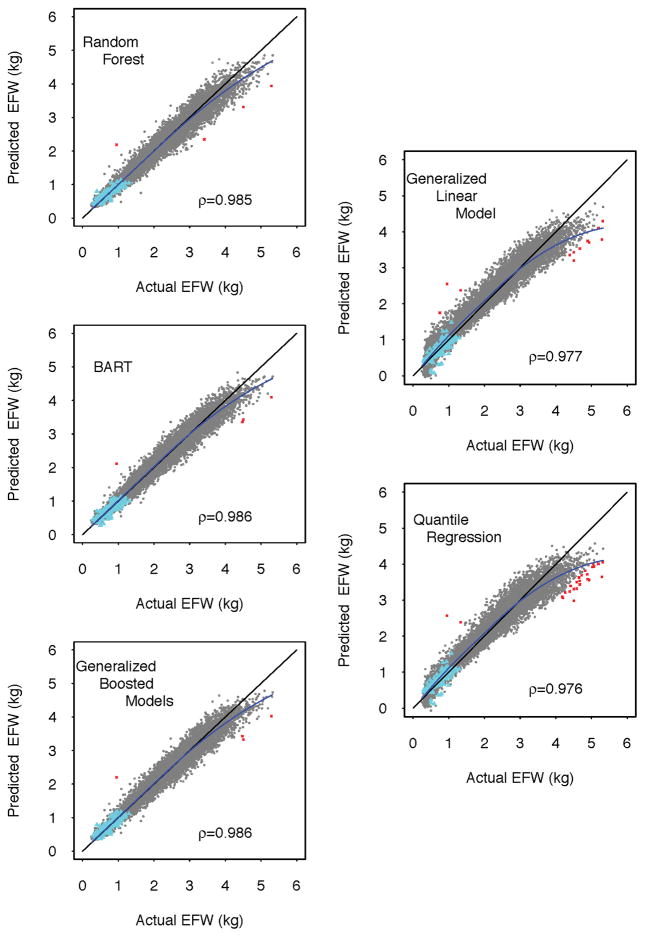
After fitting the regression-based and machine learning algorithms to the development subsample of the MOMI cohort, we generated corresponding predictions for each estimated fetal weight in the validation sub-sample of the MOMI cohort and the ODNSR data. Figure 2 shows scatterplots comparing the actual and predicted fetal weights from these data with each approach, including a kernel regression smoother demonstrating deviations from the diagonal (perfect prediction). These figures suggest overall better performance of machine learning algorithms compared to standard regression approaches. All methods systematically under-predicted estimated fetal weights greater than 3 kg, with larger deviations observed for the regression-based methods. However, regression-based methods systematically over-predicted estimated fetal weights less than 3 kg (as evidenced by the off-diagonal kernel density smoother) whereas the machine learning algorithms yielded unbiased predictions in this region. Predictions in the ODNSR data suggest better out-of-sample performance for machine learning over regression based prediction algorithms.

Figure 2.

Comparison of actual estimated fetal weight to to predicted estimated fetal weight for regression-based (right column) and machine learning (left column) approaches in a validation sub-sample of 8,517 pregnancies (13,354 ultrasound visits) at the Magee-Womens Hospital, University of Pittsburgh Medical Center, Pittsburgh, PA, 2010–2013. Dashed diagonal line represents perfect prediction. Blue lines represents a kernel regression fit to the scatterplots. Red ×’s represent predictions greater than | ± 1| kg of the actual EFW. Cyan ▲’s represent corresponding predictions from 240 pregnancies in the ODNSR sample from the NICHD Maternal Fetal Medicine Units (MFMU) Network, 1992. ρ denotes Pearson’s correlation coefficient for the association between actual and predicted fetal weight.

eTable 1 summarizes the results displayed in Figure 2 using the root mean squared error and median absolute deviation. This table shows that the machine learning algorithms yielded predictions with systematically lower root mean squared error and median absolute deviation values than regression based approaches. In particular, the lowest median of the absolute difference between predicted and actual fetal weights among the regression-based approaches was the quantile regression method, with median absolute deviation = 137.75 grams (95% CIs: 135.70, 140.29). By contrast, Bayesian additive regression trees yielded the lowest overall median absolute deviation = 88.18 grams (95% CIs: 86.25, 90.28), which was not statistically different from generalized boosted model predictions.

A similar pattern was observed in the ODNSR sample predictions (eTable 1), with one exception: the generalized linear model performed similarly to machine learning algorithms in this small sample of pregnancies, yielding median absolute deviation values that were not statistically distinguishable from the machine-learning approaches. However, the same is not true for the corresponding root mean squared error values, which indicates that the generalized linear model yielded several outlying predictions, as confirmed by visual inspection of Figure 2.

The small for gestational age analysis results varied strongly by choice of method. Table e2 shows the number of live-births from the MOMI data that were classified as small for gestational age using a gestational age specific population birthweight standard, and an actual or predicted fetal weight + birthweight standard. As displayed in the first two rows, the number of small for gestational age births identified using the birthweight standard was 1,184 out of 8,517, lower than the actual fetal + birthweight standard of 1,815. A predicted fetal weight standard from all three machine learning approaches yielded results similar to the actual fetal weight birthweight standards. However, both regression-based predicted fetal weight standards yielded a much higher number of pregnancies identified as small for gestational age.

A similar pattern was observed when we estimated the association between smoking status during pregnancy and the risk of small for gestational birth identified using different standards (Table 2). On the risk ratio scale, using the birthweight standard, smoking anytime during pregnancy increased the risk of small for gestational age birth 3.84-fold (95% robust CI: 2.70, 5.47). However, this risk ratio dropped to 1.65 (95% robust CI: 1.50, 1.81) when using the actual fetal + birthweight standard, no different from those obtained using the machine learning-based predicted fetal + birthweight standard. When evaluated using the regression-based predicted fetal + birthweight standard, the risk ratio dropped even further. The same overall pattern was observed on the risk difference scale in terms of the grouping of magnitudes. However, the direction of these associations was reversed, with the birthweight standard yielding the lowest overall association, and the regression-based predicted fetal + birthweight standard yielding the highest association. This reversal is attributable to the variation across method in the baseline risk of small for gestational age birth. Still, the results from the machine-learning based predicted fetal + birthweight standard were no different than those from the actual fetal + birthweight standard.

Table 2.

Risk ratios and differences for the relation between smoking any time during pregnancy (relative to no smoking) and small for gestational age birth defined as birthweight less than the 10th percentile of a national birthweight standard (SGA_B), estimated fetal weight + birthweight standard (SGA_FB), and five different predicted fetal weights + birthweight (SGA_PB) standard in a validation sub-sample of 8,517 pregnancies (13,354 ultrasound visits) at the Magee-Womens Hospital, University of Pittsburgh Medical Center, Pittsburgh, PA, 2010–2013.

Method	Risk Ratio	95% Robust CI		Risk Difference per 100 Live Births	95% Robust CI
SGAB	3.84	2.70	5.47	3.18	2.23	4.17
SGAFB	1.72	1.51	1.78	13.30	10.32	16.28
SGAPB
GLM	1.34	1.23	1.44	14.34	11.26	17.34
QR	1.25	1.16	1.34	13.96	10.87	17.04
RF	1.81	1.62	1.88	13.45	10.87	15.89
BART	1.65	1.50	1.81	13.01	10.12	16.10
GBM	1.72	1.61	1.93	13.87	10.77	16.83

Abbreviations: GLM = generalized linear model; QR = quantile regression; RF = random forest; BART = Bayesian additive regression trees; GBM = generalized boosted models

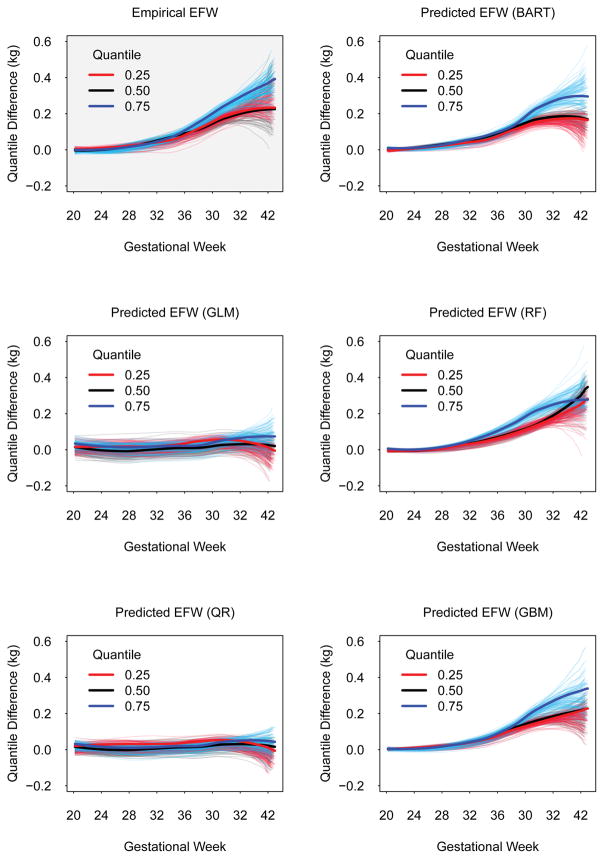
Figure 3 shows quantile differences at the 25th, 50th, and 75th percentiles of the distribution of estimated fetal weight across gestation between smokers and non-smokers. Compared to the smoothed quantile differences in the actual fetal weight + birthweight data (upper left panel, grey background), both generalized linear model and quantile regression model predictions yielded data that showed no differences between smokers and non-smokers at the 25th, 50th, and 75th percentiles. On the other hand, predictions from Bayesian additive regression trees, random forests, and generalized boosted models showed quantile differences that were similar to those obtained in the empirical data. These smoothed quantile differences suggested that: (i) non-smoker fetal weight + birthweight began to deviate from smoker fetal weight + birthweight at roughly 32 weeks of gestation, and (ii) the differences are larger at the 75th percentile of the fetal weight + birthweight distribution, relative to similar differences at the 50th and 25th percentiles.

Figure 3.

Quantile differences in estimated fetal weight across gestational weeks between smokers and non-smokers at the 25th, 50th, and 75th percentiles in a validation sub-sample of 8,517 pregnancies (13,354 ultrasound visits) at the Magee-Womens Hospital, University of Pittsburgh Medical Center, Pittsburgh, PA, 2010–2013. Plot with grey background represents quantile differences estimated using actual fetal weight estimates. Plots with white backgrounds represent quantile differences estimated using predicted fetal weight estimates. Translucent lines represent fits from 100 bootstrap resamples.

Sensitivity analyses were conducted in which development algorithms were trained in various low-risk subsets of the MOMI sample. These results suggest no material changes in these results. Details are provided in the eAppendix.

Discussion

The absence of fetal weight information in population birth records poses several challenges in reproductive epidemiology. Our focus was on the use of machine learning algorithms that take as input maternal and infant birth characteristics, and output predicted fetal weights. We evaluated how predicted fetal weights compare to actual fetal weights by (i) estimating the correlation between predicted and actual fetal weights, (ii) comparing the gestational week specific quantiles of actual and predicted fetal weights, and (iii) examining the relation between smoking status and small-for-gestational-age birth, with the latter defined using actual and predicted data. We found that machine learning algorithms generated fetal weight predictions that closely aligned with actual fetal weight estimates in a sample of future observations from the same population, and in a sample of high-risk pregnancies from an independent population. Furthermore, our analysis of the relation between smoking status and SGA birth when the latter was defined using the combined distributions of birthweight and actual fetal weight were no different from those obtained when using the distributions of birthweight and predicted fetal weight. However, results differed substantially when using the 10th percentile of a national birthweight standard.¹⁸ Overall, these results suggest that machine learning algorithms may be preferable to commonly used population birthweight standards to recover missing fetal weight information in population birth records for the purposes of epidemiologic research.

To evaluate practices commonly employed in reproductive epidemiology, we used a single birthweight standard to define small for gestational age.¹⁸ Other standards are available, including international standards derived from the INTERGROWTH-21^st Project.²⁵ We did not evaluate the INTERGROWTH birthweight standard for three reasons: 1) the standards are only available for gestational weeks 33 to 42, and thus could not be used to define small for gestational age for a large number of gestational weeks in our sample; 2) the 10^th percentile birthweight values for both boys and girls did not meaningfully differ from the national referent values that we used; 3) previous work has shown that the INTERGROWTH standard underestimates the number of small for gestational age infants relative to a more local standard.²⁶

The machine learning algorithms we employed are generally known as ensemble learning methods.⁸ These methods combine (via bagging or boosting) many weak predictors with good local performance to yield an ensemble predictor with strong global performance. We could have additionally combined each ensemble learner and regression-based algorithm into a “SuperLearner” algorithm,²⁸ comprised of a family of weighted combinations of each, with weights chosen to maximize performance. This would have enabled us to automate the evaluation of a much larger set of tuning parameters and model forms.

Our results should be considered in light of certain limitations. First, our approach effectively amounts to imputing missing fetal weight data by combining information available at birth in a given dataset with algorithms trained on data from an external population. As with typical imputation approaches, quantifying the variance of the parameter estimates from a given model should incorporate uncertainty that results from predicting unknown quantities.³¹ In the case of non-parametric data mining and machine learning algorithms, this may be particularly challenging due to what is known as the “curse of dimensionality,”³² and the fact that important “regularity” conditions do not hold.³³ While in our particular case, use of machine learning methods yielded results (including CIs) similar to the true relation (SGA_FB in Table 2) we do not suggest that bootstrapping is a generally valid way of obtaining CIs for data-adaptive techniques.

The regression-based and machine learning based approaches represent only a set of a larger number of approaches that may, in principle, be used to recover missing fetal weight information. Alternative approaches could involve use of novel probability weights with efficient semiparametric estimators such as targeted minimum loss-based estimation,^29,34 or Bayesian data augmentation approaches.³⁰ These latter methods may not be subject to the same limitations resulting from the curse of dimensionality or non-regularity conditions, but their potential for addressing missing fetal weight data in reproductive epidemiology is yet to be explored.

While very different overall, the range of covariate values in the ODNSR data were bounded within the ranges of the corresponding covariates in the MOMI data. Less optimal performance may occur if the regression-based and machine learning algorithms are trained on data that do not overlap with data in which predictions are to be generated. In the MOMI data, many of the ultrasounds were clinically indicated, suggesting covariate distributions may not overlap with those in more general population birth registries. Such “off-support” predictions will likely be as problematic as in the inferential case,³⁵ and thus caution is warranted.

Despite these limitations, we have shown that machine learning algorithms trained on an external dataset hold promise in recovering missing fetal weight information. Such missing information has long been problematic in reproductive and perinatal epidemiology. While several proposals have been made to resolve the problem of missing fetal weight data,^3–7 few are general enough to apply in a wide array of empirical settings. Use of machine learning algorithms only requires the existence of a common set of covariates in both the training and prediction datasets. Additionally, we have shown that using information routinely available in birth cohorts leads to relatively accurate predictions.

ABBREVIATIONS

rMSE

root mean squared error

MAD

median absolute deviation

MOMI

Magee Obstetric Maternal and Infant

ODNSR

Obstetrical Determinants of Neonatal Survival

GLM

generalized linear model

QR

quantile regression

RF

random forest

BART

Bayesian additive regression trees

GBM

generalized boosted models