Gonadotropin-Releasing Hormone (GnRH) Neuron Excitability Is Regulated by Estradiol Feedback and Kisspeptin

Abstract

Gonadotropin-releasing hormone (GnRH) neurons produce the central output controlling fertility and are regulated by steroid feedback. A switch from estradiol negative to positive feedback initiates the GnRH surge, ultimately triggering ovulation. This occurs on a daily basis in ovariectomized, estradiol-treated (OVX+E) mice; GnRH neurons are suppressed in the morning and activated in the afternoon. To test the hypotheses that estradiol and time of day signals alter GnRH neuron responsiveness to stimuli, GFP-identified GnRH neurons in brain slices from OVX+E or OVX female mice were recorded during the morning or afternoon. No differences were observed in baseline membrane potential. Current-clamp revealed GnRH neurons fired more action potentials in response to current injection during positive feedback relative to all other groups, which were not different from each other despite reports of differing ionic conductances. Kisspeptin increased GnRH neuron response in cells from OVX and OVX+E mice in the morning but not afternoon. Paradoxically, excitability in kisspeptin knock-out mice was similar to the maximum observed in control mice but was unchanged by time of day or estradiol. A mathematical model applying a Markov Chain Monte Carlo method to estimate probability distributions for estradiol- and time of day–dependent parameters was used to predict intrinsic properties underlying excitability changes. A single identifiable distribution of solutions accounted for similar GnRH neuron excitability in all groups other than positive feedback despite different underlying conductance properties; this was attributable to interdependence of voltage-gated potassium channel properties. In contrast, redundant solutions may explain positive feedback, perhaps indicative of the importance of this state for species survival.

SIGNIFICANCE STATEMENT Infertility affects 15%–20% of couples; failure to ovulate is a common cause. Understanding how the brain controls ovulation is critical for new developments in both infertility treatment and contraception. Gonadotropin-releasing hormone (GnRH) neurons are the final common pathway for central neural control of ovulation. We studied how estradiol feedback regulates GnRH excitability, a key determinant of neural firing rate using laboratory and computational approaches. GnRH excitability is upregulated during positive feedback, perhaps driving increased neural firing rate at this time. Kisspeptin increased GnRH excitability and was essential for estradiol regulation of excitability. Modeling predicts that multiple combinations of changes to GnRH intrinsic conductances can produce the firing response in positive feedback, suggesting the brain has many ways to induce ovulation.

Introduction

Gonadotropin-releasing hormone (GnRH) neurons are the output pathway for central control of fertility. GnRH initiates pituitary secretion of luteinizing hormone (LH) and follicle-stimulating hormone, thus activating gonadal steroidogenesis. Steroid feedback regulates GnRH release. For most of the reproductive cycle, estradiol negative feedback suppresses GnRH release (Filicori et al., 1986; Moenter et al., 1991). At the end of the follicular phase (proestrus in mice), estradiol switches from suppressing release to inducing a sustained surge of release (Sarkar et al., 1976; Moenter et al., 1991). The GnRH surge drives an LH surge, which induces ovulation.

GnRH surges can be induced by exogenous estradiol (Levine et al., 1985; Moenter et al., 1990). In ovariectomized (OVX) mice with estradiol capsules, GnRH neuron firing and release are suppressed in the morning by estradiol negative feedback (OVX+E AM) and elevated in the afternoon (OVX+E PM) by estradiol positive feedback (Christian et al., 2005; Glanowska et al., 2012). No time of day–dependent shift in GnRH neuron firing rate is observed in OVX mice without estradiol. Both estradiol and time of day regulate GnRH neuron conductances in this daily surge, and other estradiol-induced surge, paradigms (Chu and Moenter, 2006; Zhang et al., 2007, 2009; Sun et al., 2010; Pielecka-Fortuna et al., 2011). Because those studies were done using voltage-clamp approaches to isolate specific currents, it is not clear whether or how the observed changes in conductances alter GnRH membrane potential, specifically excitability (membrane potential response to stimuli) and action potential firing. The changes observed in the conductances studied, and their typical physiologic effects on the membrane potential, led us hypothesize that GnRH neurons are less excitable during negative feedback- and more excitable during positive feedback-compared OVX mice.

Changes in ionic conductances that may alter membrane excitability are likely mediated by estradiol-sensitive afferents because GnRH neurons do not typically express detectable levels of estrogen receptor alpha (ERα), which is required for negative and positive feedback (Hrabovszky et al., 2000, 2001; Couse et al., 2003; Wintermantel et al., 2006; Christian et al., 2008). Anteroventral periventricular kisspeptin neurons, most of which express ERα, may relay estradiol signals to GnRH neurons during positive feedback (Smith et al., 2005, 2006). Kisspeptin directly modulates ionic currents in GnRH neurons and rapidly stimulates GnRH firing (Pielecka-Fortuna et al., 2008, 2011; Zhang et al., 2008, 2013). Anteroventral periventricular kisspeptin neurons exhibit higher firing rates during positive feedback, and endogenous kisspeptin release may enhance GnRH excitability at this time (Zhang et al., 2015; Wang et al., 2016).

We hypothesized that time of day– and estradiol–dependent changes in intrinsic properties render GnRH neurons more excitable during positive feedback and less excitable during negative feedback compared with the open-loop OVX condition. To test this, we used the daily surge paradigm to examine baseline membrane potential and response to current injection of GnRH neurons. To assess whether kisspeptin modulates GnRH neuron excitability, the effects of kisspeptin treatment or deletion of the kisspeptin gene were determined. Both kisspeptin and estradiol feedback target multiple conductances that may drive changes in GnRH neuron excitability. We thus adapted a model GnRH neuron (LeBeau et al., 2000; Moran et al., 2016) to test the contribution of individual conductance targets for estradiol- and kisspeptin-induced alterations in GnRH neuron response. This approach used a Bayesian Markov Chain Monte Carlo (MCMC) method to estimate probability distributions for each parameter and covariances between parameters using data from whole-cell voltage-clamp and current-clamp experiments. MCMC methods are widely used in the physical sciences but have been rarely been applied to integrated biophysical problems, having been used to model single channels or individual whole-cell currents (Rosales et al., 2001; Siekmann et al., 2011, 2012; Merel et al., 2016; Mackay et al., 2017), or cardiomyocyte action potentials (Johnstone et al., 2016a, b). To our knowledge, this is the first application of MCMC to fit multiple currents from whole-cell experiments.

Materials and Methods

All chemicals were purchased from Sigma-Aldrich, unless noted.

Animals.

Transgenic mice expressing GFP under the control of the GnRH promoter (GnRH-GFP) were used (Suter et al., 2000). Kisspeptin knock-out (KO) mice (Lapatto et al., 2007; Chan et al., 2009) were crossed with GnRH-GFP mice to identify GnRH neurons for electrophysiologic recordings. Mice were housed on a 14 h light/10 h dark cycle with lights off at 6:00 P.M. (Eastern Standard Time). Teklad 2916 chow (Envigo) and water were available ad libitum. Adult females within the appropriate age range (65–135 d) were randomly selected from our colony. Ovariectomy was performed under isoflurane (VetOne) anesthesia. At the same time as the surgery for OVX, mice were randomized to either receive a SILASTIC (Dow Corning) capsule containing 0.625 μg 17β-estradiol suspended in sesame oil (OVX+E) or not be treated further (OVX). Bupivacaine (0.25%, APP Pharmaceuticals) was applied to surgical sites to reduce postoperative pain and distress. Electrophysiologic experiments were performed 2–4 d after surgery, and estradiol status was confirmed by measurements of uterine mass of control mice for Figures 1–3 (OVX, n = 31, 45.1 ± 1.5 mg; OVX+E, n = 39, 167.1 ± 2.6 mg; two-tailed unpaired Student's t test, F_(38,30) = 4.13, p < 0.0001) and of kisspeptin KO mice for Figures 4 and 5 (OVX, n = 3, 13.0 ± 2.1; OVX+E, n = 6, 37.8 ± 5.8 mg; two-tailed unpaired Student's t test, F_(5,2) = 15.5, p = 0.02). It is important to point out that this daily surge model does not recapitulate the pattern of estradiol during the cycle. Rather, it effectively induces both negative and positive feedback on LH release in vivo and GnRH neuron activity in the brain slice relative to measurements in OVX mice (Christian et al., 2005; Silveira et al., 2017). This separates two variables (time of day and circulating estradiol level) known to contribute to the generation of the LH surge in mice and other rodents and which were the targets of the present investigations.

Figure 1.

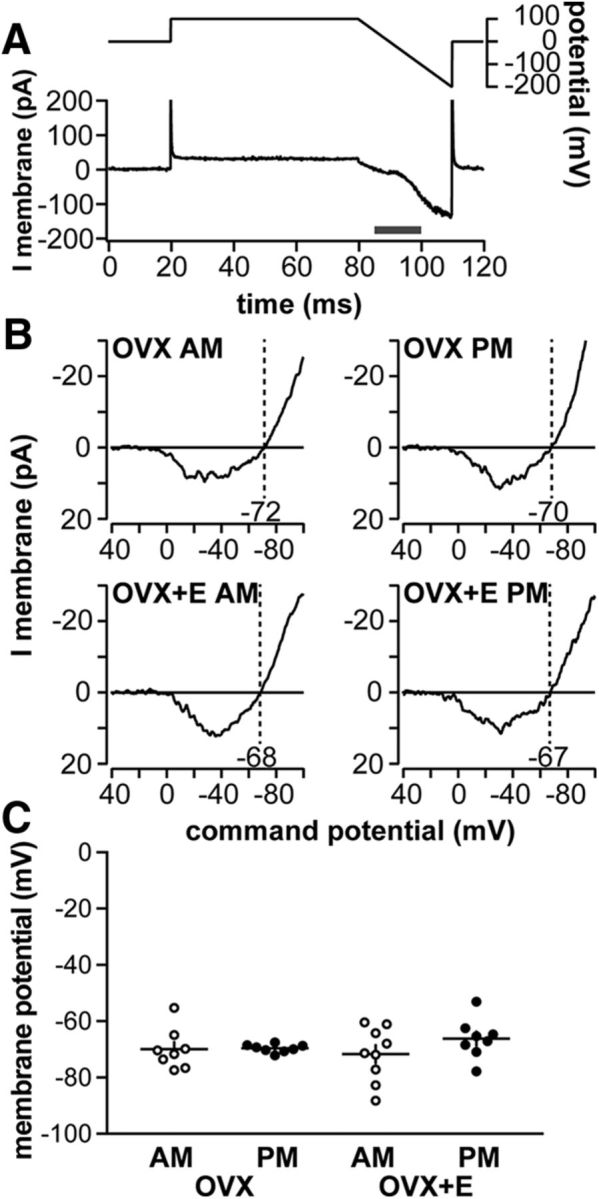
Baseline membrane potential of GnRH neurons is not modulated by time of day or estradiol. A, OCVm recording methodology. Top, Voltage protocol. Bottom, Resulting membrane current. B, Representative leak-subtracted OCVm traces from OVX AM, OVX PM, OVX+E AM, and OVX+E PM neurons. C, No difference in baseline membrane potential (individual values and mean ± SEM, two-way ANOVA/Bonferroni) was observed among experimental groups.

Figure 3.

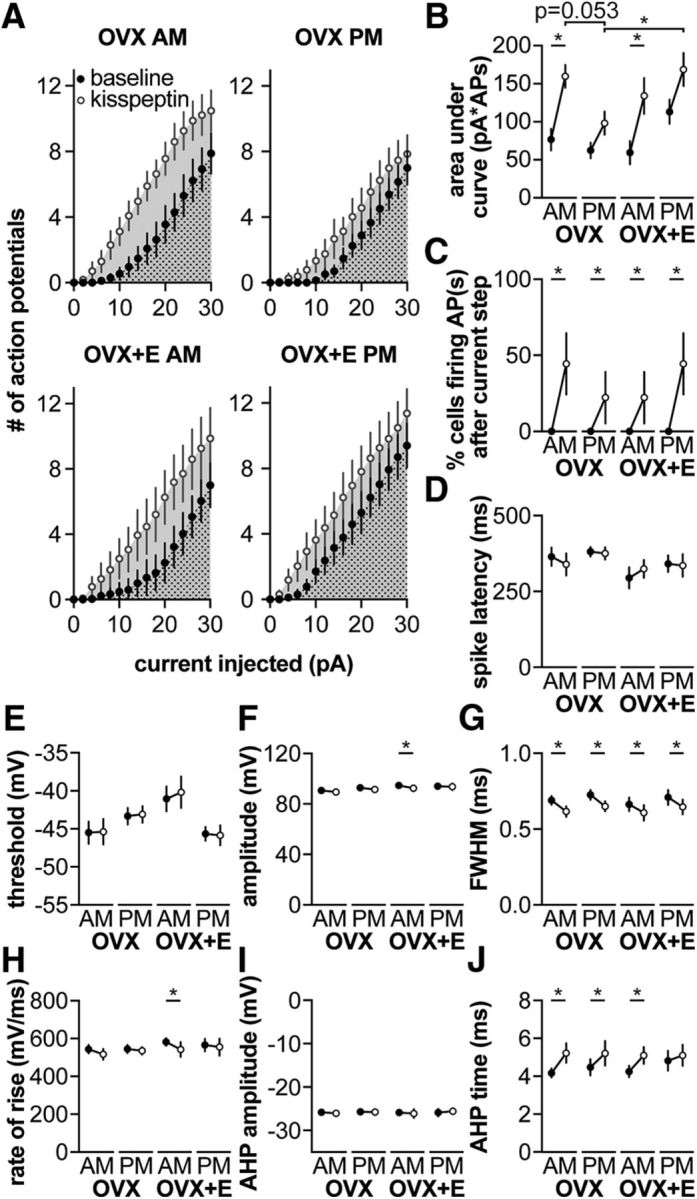
Kisspeptin increases GnRH neuron excitability in a time of day–dependent manner. A, Mean ± 75th percentile CI for spikes elicited during 500 ms current injection (0–30 pA, 2 pA steps) before (black symbols) and during (white symbols) kisspeptin treatment. Dotted area was used to calculate AUC for baseline measurements. Dotted area + solid area was used to calculate AUC for kisspeptin treatment. B–J, Mean ± 75th percentile CI before and during kisspeptin treatment. B, AUC. C, Percentage of cells firing within 1.5 s after termination of the current step. D, Spike latency. E, Threshold. F, Action potential amplitude. G, FWHM. H, Rate of rise. I, AHP amplitude. J, AHP time. When error bars are not visible, they are contained within the symbol. Lines connect means before and during kisspeptin. *p < 0.05, baseline versus kisspeptin (three-way, repeated-measures ANOVA/Bonferroni, or χ²) (C).

Figure 4.

GnRH neuron excitability is independent of time of day and estradiol feedback in kisspeptin KO mice. A, Mean ± SEM number of spikes elicited during 500 ms current injection (0–30 pA, 2 pA steps). B–H, Individual values and mean ± SEM. B, Latency to first spike. C, Action potential threshold. D, Action potential amplitude. E, FWHM. F, Action potential rate of rise. G, AHP amplitude. H, AHP time. *p < 0.05, two-way repeated-measures ANOVA/Bonferroni test (A; group: F_(2,22) = 0.9; current: F_(15,330) = 128.4, p < 0.001; group × current: F_(30,330) = 0.6), one-way ANOVA/Bonferroni (B; F_(2,22) = 0.06; C; F_(2,22) = 0.7; D; F_(2,22) = 3.2, p = 0.06; E; F_(2,22) = 4.0, p < 0.05; G; F_(2,22) = 1.15; H; F_(2,22) = 2.93, p = 0.07) or Kruskal–Wallis/Dunn's (F; F_(2,22) = 2.93, p = 0.07).

Figure 5.

GnRH neuron excitability in kisspeptin KO mice is similar to GnRH excitability during positive feedback in wild-type mice. Mean ± SEM number of spikes elicited during 500 ms current injection (0–30 pA, 2 pA steps) from kisspeptin KO mice (Fig. 4, white circles) and in control mice (Fig. 2, black circles). *p < 0.05, three-way repeated-measures ANOVA/Bonferroni (group: F_(2,54) = 167.2, p < 0.001; kisspeptin KO: F_(1,54) = 10.2, p < 0.01, current: F_(15,810) = 273.5, p < 0.001; group × kisspeptin KO: F_(2,54) = 0.4; group × current: F_(30,810) = 4.1, p < 0.001; kisspeptin KO × current: F_(15,810) = 7.9, p < 0.001; kisspeptin KO × group × current: F_(30,810) = 2.2, p < 0.001).

Brain slice preparation.

All solutions were bubbled with 95% O₂/5% CO₂ throughout the experiments and for at least 15 min before exposure to tissue. Brain slices were prepared either from 7.5 to 9.5 h before lights out (AM recordings) or 1–2.5 h before lights out (PM recordings). The brain was rapidly removed and placed in ice-cold sucrose saline solution containing the following (in mm): 250 sucrose, 3.5 KCl, 26 NaHCO₃, 10 d-glucose, 1.25 Na₂HPO₄, 1.2 MgSO₄, and 3.8 MgCl₂, pH 7.6, 345 mOsm. Coronal (300 μm) slices were cut with a VT1200S Microtome (Leica Biosystems). Slices were incubated in a 1:1 mixture of sucrose saline and ACSF containing the following (in mm): 135 NaCl, 3.5 KCl, 26 NaHCO₃, 10 d-glucose, 1.25 Na₂HPO₄, 1.2 MgSO₄, and 2.5 CaCl₂, pH 7.4, 305 mOsm, for 30 min at room temperature (∼21°C to 23°C). Slices were then transferred to 100% ACSF at room temperature for 0.5–5 h before recording.

Data acquisition.

During recording, slices containing the preoptic area and anterior hypothalamus, which contain the majority of GnRH neuron somata, were placed into a chamber continuously perfused with ACSF at a rate of 2 ml/min with oxygenated ACSF heated to 28.5°C–31.5°C with an inline-heating unit (Warner Instruments). In all recordings, ACSF contained 100 μm picrotoxin, 20 μm d-APV (Tocris), and 20 μm CNQX to block ionotropic GABA and glutamate receptors. GFP-positive cells were visualized with a combination of infrared differential interference contrast and fluorescence microscopy on an Olympus BX51WI microscope. Borosilicate glass capillaries (1.65 mm OD × 1.12 mm ID; World Precision Instruments) were pulled by using a Flaming/Brown P-97 unit (Sutter Instrument) to make recording pipettes. Pipettes measured 2–4.5 mΩ when filled with the following (in mm): 125 K gluconate, 20 KCl, 10 HEPES, 5 EGTA, 0.1 CaCl₂, 4 MgATP, and 0.4 NaGTP, 300 mOsm, pH 7.2 with NaOH. Pipettes were wrapped with Parafilm (Bemis) to reduce capacitive transients; remaining transients were electronically cancelled. Pipettes were placed in contact with a GFP-positive neuron using an MP-285 micromanipulator (Sutter Instrument). All potentials reported were corrected online for liquid junction potential of −14.2 mV (Barry, 1994). Recordings were made with an EPC-10 dual patch-clamp amplifier (HEKA Elektronik) and a Macintosh computer running Patchmaster software (HEKA Elektronik). Experiments were analyzed offline using custom software (DeFazio and Moenter, 2002; DeFazio et al., 2014) written in IgorPro (Wavemetrics).

Experimental design

On-cell measurement of membrane potential (OCVm).

During a recording in the on-cell configuration, the patch of membrane within the pipette is exposed to a potential difference equal to the membrane potential (V_cell) minus the pipette command potential (V_patch = V_cell − V_pipette). Potassium channels within the pipette can be manipulated by varying the pipette potential and the reversal of current through these channels (E_K) used to estimate the membrane potential (Fricker et al., 1999; Verheugen et al., 1999; DeFazio et al., 2002, 2014). This method assumes that the concentration of the potassium in the cell is similar to that in the pipette solution, resulting in a reversal potential for potassium (E_K) near zero. Although the concentration of intracellular potassium in GnRH neurons has not yet been determined, a difference of 15 mm in the typical range of intracellular potassium concentration results in a change in measured membrane potential of only 5 mV using this method. After establishing a >2 GΩ seal, inactivation of potassium channels was reduced by setting V_pipette to 100 mV for 60 ms (V_patch ∼ −170 mV, assuming −70 mV V_cell). Voltage-dependent channels were then activated by ramping the pipette voltage from 100 mV to −150 mV (V_patch ∼ −150 to 200 mV) over 30 ms. During the voltage ramp, potassium channels are opened and generate an initial inward current followed by an outward current. Leak correction was applied by subtracting a linear fit of the current during the ramp before activation of the potassium currents. The ramp potential at which the leak-corrected current is 0 pA reflects the membrane potential of the cell. On-cell measurements were performed in the presence of 1 μm TTX (Tocris) to block action potentials. Membrane currents were sampled at 20 kHz and filtered at 10 kHz. Three to five voltage ramps were averaged for each cell; ramps in which noise prohibited a good linear fit were discarded.

Whole-cell patch-clamp.

After achieving a >1 GΩ seal and the whole-cell configuration, membrane potential was held at −60 mV between protocols. Series resistance (R_s), input resistance (R_in), and holding current (I_hold) were measured every 2–3 min using a 5 mV hyperpolarizing step from −60 mV (mean of 20 repeats, 20 ms duration, sampled at 100 kHz). Only recordings with a R_in of >500 mΩ, I_hold of −35 to 30 pA, stable R_s of <20 mΩ, and a stable C_m between 9.5 and 23 pF were used for analysis.

In current clamp, direct current (<25 pA, 8.6 ± 0.6 pA, n = 109) was adjusted to keep cells within 2 mV of −69 mV. Membrane potential was sampled at 20 kHz and filtered at 7.3 kHz. Bridge balance (95%) was used for most cells; for a few cells, bridge balance was not used but results were similar. To determine GnRH neuron excitability, cells were injected with current from 0 to 30 pA (500 ms, 2 pA steps). This protocol was repeated two to three times per cell and the number of action potentials at each step was averaged. The first spike fired was used to determine the following action potential characteristics: latency from start of the current injection to first spike, firing threshold (first derivative of the voltage trace > 1 mV/s), peak amplitude relative to threshold, full-width at half-maximum (FWHM), rate of rise, and time and amplitude of after-hyperpolarization potential (AHP, the amplitude and time, relative to action potential initiation, of local minimum after the spike peak). To test the effects of kisspeptin, the above was repeated on another set of cells before and during bath application of 10 nm kisspeptin; to control for time of recording, another set of cells was recorded for a similar amount of time but not treated.

To isolate potassium currents in voltage-clamp in cells from control OVX+E AM mice, we blocked voltage-gated Na⁺ and Ca²⁺ channels with 1 μm TTX and 200 μm CdCl₂, respectively. Series resistance was compensated between 55% and 85%. Two distinct voltage-clamp protocols were used to determine inactivation (initial hyperpolarization to −100 mV for 500 ms to remove inactivation, steps from −100 to −10 mV in 10 mV increments for 500 ms, final test pulse of −10 mV for 500 ms), and activation (−100 mV for 500 ms, prepulse of −100 mV or −30 mV, test potentials from −100 to 40 mV, 10 mV increments). Inactivation was complete at −30 mV (i.e., no fast transient current was present in current traces after the −30 mV prepulse). I_A was isolated by subtracting the current after the −30 mV from that of more hyperpolarized pulses. Peak current was normalized and divided by the driving force calculated using Ohm's law rather than the Goldman-Hodgkin-Katz equation to be consistent with the mathematical model. A representative cell was chosen that closely resembled the median activation and inactivation properties of I_A and I_K from our own recordings and from two previous studies (DeFazio and Moenter, 2002; Pielecka-Fortuna et al., 2011).

Statistical analyses.

Data were analyzed using Prism 7 (GraphPad) or SPSS (IBM) and are reported as the mean ± SEM unless otherwise noted. The number of cells per group is indicated by n. No more than two cells were used per animal with at least 4 animals tested per group. An exception was made for kisspeptin KO mice, which are infertile and must be bred from compound heterozygotes. For those groups, no more than three cells per animal and at least 3 animals per group were examined. Data requiring one-way analyses were compared using one-way ANOVA with Bonferroni post hoc analysis or Kruskal–Wallis test with Dunn's post hoc analysis as dictated by data distribution. All data requiring two-way analyses were compared using two-way ANOVA with Bonferroni post hoc analysis; this test is considered sufficiently robust for non-normally as well as normally distributed data (Underwood, 1996). ANOVA analyses did not assume equal subgroup sizes. Percentage values were compared using χ² with Yates correction. Significance was set at p < 0.05, but all p values <0.1 are specified. All data requiring three-way analyses were compared using a three-way ANOVA with Bonferroni post hoc analysis.

Mathematical modeling

Summary.

The mathematical modeling was done in two steps. We started with the model published by Moran et al. (2016). In Step 1, values for individual currents were estimated. We used published voltage-clamp data to estimate the parameters that control the size and timing of ionic currents that are changed in the daily surge model (I_A, I_K, I_HVA, I_LVA). These estimates were loosely constrained by current-clamp data from the present study to make sure action potentials generated by the model looked like those from GnRH neurons. It was also necessary to alter (reestimate) the values used for the fast sodium current underlying action potential firing to achieve this goal. In Step 2, we integrated all the individual currents, along with the current-clamp data (firing at 6 pA steps and action potential shape), to reproduce the firing and action potential characteristics of a GnRH neuron during negative feedback (OVX+E AM). To do this, we allowed four parameters that are dependent on estradiol and time of day to vary (maximum conductance of I_A, I_NaP, and I_HVA, and V_1/2 inactivation of I_A).

We modified a GnRH neuron model developed by Moran and Khadra (Moran et al., 2016) that was itself based upon the original Hodgkin and Huxley GnRH neuron model (LeBeau et al., 2000). In this model, membrane potential is expressed in mV, time is in ms, currents are in pA, and conductances are in nS. The governing equation for membrane potential is described by the following:

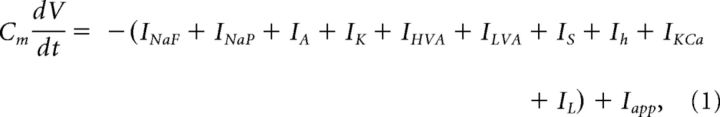where C_m = 20 pF is the cell capacitance (Pielecka-Fortuna et al., 2011), V is the cell membrane potential, and t is the time. I_NaF and I_NaP are fast transient and persistent sodium currents, respectively. I_A is the A-type transient potassium current, and I_K is the delayed-rectifier or sustained potassium current. I_HVA and I_LVA are high-voltage–activated and low-voltage–activated calcium currents. I_S describes a slow inward calcium current. I_h is the hyperpolarization-activated nonspecific cation current. I_KCa is a calcium-dependent potassium current, and I_L is the leak current. I_app is the applied current, which was set to −6 pA to hold the cell at −70 mV.

Individual ionic currents were modeled using Ohm's law I = G(V − E) where G is the conductance, V is the membrane potential, and E is the reversal potential for that ion. (V − E) describes the driving force across the membrane and G is equal to the maximum conductance if all channels are open (g) multiplied by the proportion of open channels. For the majority of currents, the proportion of open channels was estimated using the Hodgkin-Huxley formalism as follows:

where m and h represent activation and inactivation gating variables, and p is the number of independent activation gates. The Hodgkin-Huxley model was also used for the following currents:

In the case of I_A, I_HVA, and I_h, the inactivation variable is the weighted sum of gating variables h_i, which have different voltage-dependent time constants, and represent two different populations of inactivating gates present in the cell membrane:

where f_A = 0.8, f_HVA = 0.2, f_h = 0.384 for h_1A, h_1HVA, and h_1h, respectively.

The activation and inactivation gating variables are governed by the following:

where m_∞ and h_∞ are steady-state activation and inactivation functions and τ is the time constant (which can be voltage-dependent or independent) in ms. Steady-state activation and inactivation functions are of the following form:

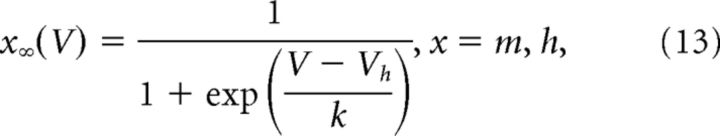V is the membrane potential, V_h is voltage at half-activation or inactivation, and k is the steepness of the steady-state function. In the case of m_k, the steady-state function was raised to the power of 1/4 to increase slope steepness to be consistent with the experimentally derived steady-state activation for I_K (Moran et al., 2016). Our previous work in the daily surge model indicated slopes of the empirical steady-state activation curves for I_K and I_A were ∼1.7 pA/mV and ∼2.1 pA/mV, respectively (Pielecka-Fortuna et al., 2011); reexamination of those data suggest the A-type current may not have been completely inactivated in some cells. We thus made new estimates from individual cells from new voltage-clamp experiments in the daily surge model and from OVX PM and OVX+E PM female mice (DeFazio and Moenter, 2002); these studies indicate the empirical slopes for I_K and I_A are ∼10 pA/mV and ∼15 pA/mV, respectively (estimated using Ohm's law). As a consequence, we did not to raise the steady-state function of m_K to the power of 1/4 to increase slope as in the Moran et al. (2016) model.

Voltage-dependent time constants were estimated from one of the two following functions:

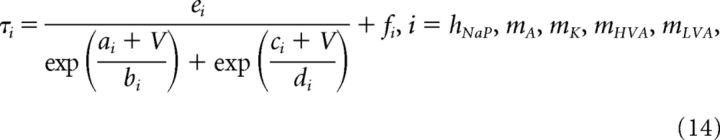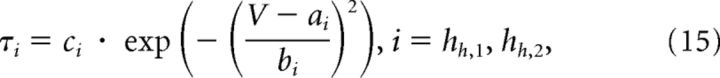where V is the membrane potential and a–e, and f are constants. Parameter estimates for f were close to zero or zero for m_A, m_K, and m_LVA. In the model developed by Moran et al. (2016), the rate of activation (time constant τ_m,HVA) for HVA current was voltage-dependent; however, voltage-clamp data from Sun et al. (2010) indicate that the speed of activation is voltage-independent. The initial parameter estimates for the HVA activation speed using Equation 14 resulted in τ_m,HVA < 0.005 ms from −100 to 100 mV (10 mV steps). Thus, τ_m,HVA for the HVA current activation variable is voltage independent in our adaptation of the model.

Fast transient sodium current is described using a Markov model with each of three subunits having three states, open (O), closed (C), and inactivated (I), as follows:

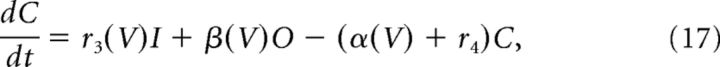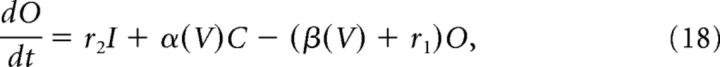V is the membrane potential, r₁, r₂, r₄ are voltage-independent constants, and r₃, α, and β are voltage-dependent constants described by the following:

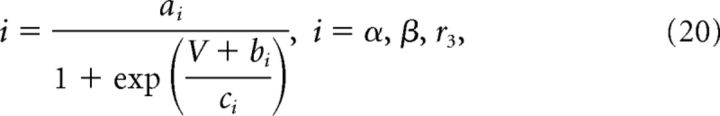where a–c are constants.

Calcium-activated potassium currents were estimated with the following equation:

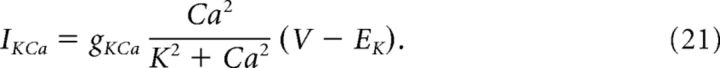Here, K = 1.0 μm, and Ca is the calcium concentration (μm) in the cytosol. Cytosolic calcium increased when calcium entered the cell through voltage-gated channels (I_Ca) and decreased when it was pumped out of the cytosol through calcium-ATPases. Calcium is governed by the following equations:

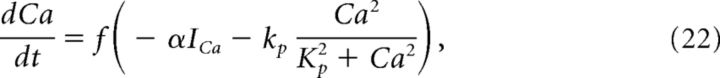where f = 0.0025 is the fraction of unbound calcium in the cytosol, I_Ca is the total calcium current, k_p = 0.265 μm/ms is the maximum pump rate, K_p = 1.2 μm is the concentration of calcium at which half of the pumps are occupied, and α = 0.00185 μm/(pA · ms) is a current to flux conversion factor.

Leak current was estimated with the following function:

Parameter estimation.

Parameter estimation was performed using Goodman and Weare's Affine Invariant MCMC Ensemble sampler, implemented using the emcee package (http://dfm.io/emcee/current/) (Goodman and Weare, 2010; Foreman-Mackey et al., 2013). MCMC methods generated a Markov chain of parameter sets (θ₁, θ₂, …, θ_n), containing m parameters. For each parameter set, a posterior probability (likelihood of set θ_i given the data) is calculated from Bayes' theorem as follows:

where p(θ) is the prior probability for the parameters before observing any data. Because we possessed little prior information regarding parameter values, we chose uniform distributions bounded within physiologic ranges (e.g., −200 to 200 mV for V_1/2 inactivation or activation) as priors for each parameter. p(data|θ) is the likelihood of observing the data if the true parameters were equal to θ. Log probabilities were used to increase computation speed and accuracy. The log likelihood was determined by the following:

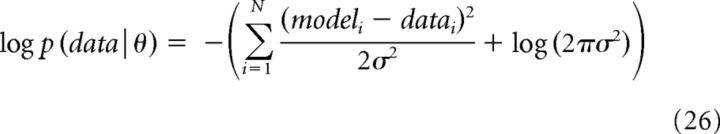where N is the total number of sampled points, i refers to the i_th point, data_i to the i_th point in the data (e.g., the membrane potential or current at i), model_i refers to the to the i_th point in the model having parameter set θ. σ was equal to 0.5.

MCMC methods preferentially sample states with greater likelihoods, generating a posterior probability distribution for each parameter. For each simulation, 100 individual Markov chains (“random walks”) were generated. To increase mixing between samples and avoid individual random walkers from becoming stuck in local minima, a parallel tempering algorithm was used. For MCMC simulations using voltage-clamp data, five “temperatures” were used with each set according to an exponential temperature ladder in which each level increases by a factor of $\sqrt{2}$. For MCMC simulations using current-clamp data, three “temperatures” were used to make computation time manageable.

Previous voltage-clamp experiments have isolated I_A, I_K, I_HVA, and I_LVA in the daily surge model (Sun et al., 2010; Pielecka-Fortuna et al., 2011). Activation and inactivation curves for I_LVA from another estradiol feedback model were used. We used these experiments and experiments measuring I_LVA from another model of estradiol feedback (Zhang et al., 2009) to estimate parameters for I_A, I_K, I_HVA, and I_LVA during negative feedback. For I_HVA and I_LVA, the models were simultaneously fit to activation and inactivation curves as well as time course data from an activation protocol in voltage-clamp. Specific voltage-clamp protocols can be found in Figure 6. Because potassium currents play a large role in determining action potential shape, parameters for I_A and I_K were estimated from both current-clamp and voltage-clamp experiments. For I_A, the model was simultaneously fit to activation and inactivation curves, time course data from an activation protocol in voltage-clamp, and to an average action potential and current versus number of action potentials response curve in current-clamp. For I_K, the model was simultaneously fit to an activation curve, time course data from an activation protocol in voltage-clamp, and to an average action potential and current versus number of action potentials response curve in current-clamp. For I_A, I_HVA, and I_K, parameters were estimated using experiments from a single representative cell. The current versus number of action potentials response curve from a single representative trace was used to provide a discrete number of action potentials at each step. Modeling of current injections was from 0 to 30 pA with 10 pA steps to reduce computation time. Differences in liquid junction potentials across experiments were corrected. To accurately reproduce the upswing of an action potential, it was also necessary to estimate parameters controlling the switch from the closed to open state for I_NaF. These parameters were estimated from current-clamp data alone.

Figure 6.

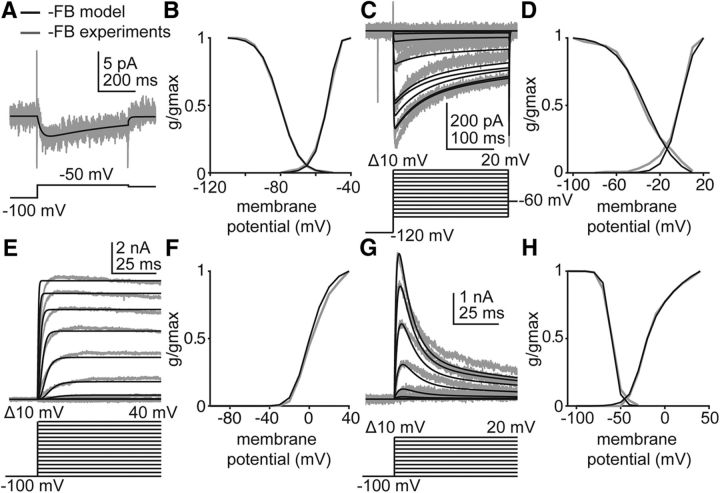
The GnRH neuron model reproduces I_A, I_K, I_HVA, and I_LVA isolated in voltage-clamp experiments performed during negative feedback. Empirical data (gray) and model-simulated current (black) used in Hodgkin-Huxley modeling. Voltage protocols are located beneath the current responses in A, C, E, and G. Only those voltage steps used to estimate parameters for the simulated data are shown. A, I_LVA in response to a depolarizing voltage step in OVXE+ AM mice. Empirical data from Sun et al. (2010). B, Simulated and empirical I_LVA activation and inactivation curves from OVX+E mice during negative feedback. Empirical data from Zhang et al. (2009). C, Simulated and empirical I_HVA in response to depolarizing voltage steps (below current response) during negative feedback. Empirical data from Sun et al. (2010). D, Simulated and empirical I_HVA activation and inactivation curves determined from voltage-clamp experiments. Empirical data from Sun et al. (2010). E, Simulated and empirical I_K in response to depolarizing voltage steps during negative feedback. F, Simulated and empirical activation curves for I_K during negative feedback, determined from activation protocol in E. G, Simulated and empirical I_A during depolarizing voltage steps during negative feedback. H, Simulated and empirical activation and inactivation curves for I_A during negative feedback. Values from these fits populate Table 1, g_vc.

After parameters I_A, I_K, I_HVA, and I_LVA had been individually estimated, we used these new parameters and reestimated time of day– and estradiol–dependent parameters to reproduce average action potential shape during negative feedback and the slope of the current versus number of action potential curves. For this, 6 pA steps from 0 to 30 pA were used as a compromise between computational intensity and not wanting to miss changes occurring between 10 pA steps.

Parameter values are otherwise unchanged from Moran et al. (2016). Maximum conductance values and reversal potentials from voltage-clamp experiments and for negative feedback can be found Table 1, as well as V_1/2 inactivation for I_A. Parameter values for the activation and inactivation variables can be found in Table 2. Parameter values for I_NaF can be found in Table 3.

Table 1.

Parameter values for ionic currents appearing in Equations 2–9^a

	E (mV)	Step 1: gvc (nS)	Step 2: gneg FB (nS)
INaF	54	—	758
INaP	54	—	0.39*
IA	−101	70.2	313*
IK	−101	57	57
ILVA	82.5	0.0679	0.0679
IHVA	82.5	7.31	5.16*
IS	82.5	—	0.18
Ih	−40	—	1
IKCa	−101	—	1.18
IL	−65	—	1

		(mV)	(mV)
IA V1/2 inactivation	—	−60	−69.8*

^aE is the reversal potential. In Step 1, the maximum conductance, g_vc, was estimated from fit (Fig. 6) of voltage-clamp experiments (Zhang et al., 2009; Sun et al., 2010; Pielecka-Fortuna et al., 2011) constrained by current-clamp data (Fig. 2). In Step 2, the maximum conductance, g_{neg FB}, was estimated that reproduces the current-clamp data during negative feedback.

*Parameters that were allowed to vary in Figures 7 and 8.

Table 2.

Parameter values for the activation and inactivation variables appearing in Equations 13–15^a

	INaP		IA			IK	ILVA		IHVA			IS	Ih
	m	h	m	h1	h2	m	m	h	m	h1	h2	m	h1	h2
Vh (mV)	−41.5	−47.4	−29.4b	−60b	−60b	−19.7b	−51.4b	−80.1b	−11b	−36.6b	−36.6b	−45	−77.4	−77.4
k (mV)	−3.0	8.2	−6.64b	4.26b	4.26b	−12.3b	−4.07b	5.5b	−7b	14.6b	14.6b	−12	9.2	9.2
τ (ms)	0.4	Eq. 14	Eq. 14	7.67b	100b	Eq. 14	Eq. 14	250b	0.816b	53.4b	728b	1500	Eq. 15	Eq. 15
a	—	67.3	−2.91b	—	—	23.8b	31.3b	—	—	—	—	—	−89.8	−82.6
b	—	−27.5	25.6b	—	—	18b	10.1b	—	—	—	—	—	11.6	25.7
c	—	67.3	65.3b	—	—	23.8b	31.3b	—	—	—	—	—	35.8	370.9
d	—	27.5	−10.6b	—	—	−18b	−10.1b	—	—	—	—	—	7.6	54.1
e	—	574.5	1	—	—	10.6b	109b	—	—	—	—	—	—	—
f	—	62.6	0.0527b	—	—	0	0.0391b	—	—	—	—	—	—	—

^aV_h and k are the voltage at half-activation or inactivation and the steepness of the steady-state function. τ is the time constant that is voltage-independent for m_Nap, h_1A, h_2A, h_LVA, m_HVA, h_1HVA, h_2HVA, and m_s. For h_NaP, m_A, m_K, m_LVA, h_1h, and h_2h, τ is voltage-dependent and governed by Equation 14 (a, b, c, and d are in mV, e and f are in ms) or Equation 15 (a and b are in mV, and c is in ms).

^bParameters that were reestimated from Moran et al. (2016).

Table 3.

Parameters values for the Markov model of I_NaF (Eqs. 16–19)^a

	α(V)	β(V)	r1	r2	r3(V)	r4
Rate (ms−1)	Eq. 20	Eq. 20	1.0	0.2	Eq. 20	0.05
a (ms−1)	55	60	—	—	30	—
b (mV)	6.4b	32	—	—	77.5	—
c (mV)	−15.9b	10	—	—	12	—

^aα(V) and β(V) describe the transition rates (ms⁻¹) between the closed and open states, r₁ and r₂ describe the transition rates between the open and inactivated states, and r₃(V) and r₄ describe the transition rates between the inactivated and closed states. α(V), β(V), and r₃(V) are voltage-dependent, whereas r₁, r₂, and r₄ are voltage-independent. Maximum conductance was reestimated to be 758 nS.

^bParameters that were restimated from Moran et al. (2016).

Results

GnRH neuron baseline membrane potential is not modulated by time of day or estradiol

GnRH neuron firing rate is decreased during negative feedback (OVX+E AM) and increased during positive feedback (OVX+E PM) relative to OVX controls, which have an intermediate firing level (Christian et al., 2005). Baseline membrane potential can influence firing rate. Estimates of baseline membrane potential were obtained from GFP-identified GnRH neurons in brain slices using an on-cell approach that maintains the native intracellular milieu. Figure 1A shows the voltage protocol used (top) and the membrane current response (bottom) before leak subtraction; Figure 1B shows representative leak-subtracted responses (see Materials and Methods). No time of day– or estradiol–dependent change in baseline membrane potential was observed among groups (Fig. 1C; n = 8 each OVX morning and afternoon, n = 9 each OVX+E morning and afternoon, two-way ANOVA/Bonferroni, p > 0.3, estradiol F_(1,41) = 0.2, time of day F_(1,41) = 2.8, interaction F_(1,41) = 3.2).

GnRH neuron excitability is increased during positive feedback

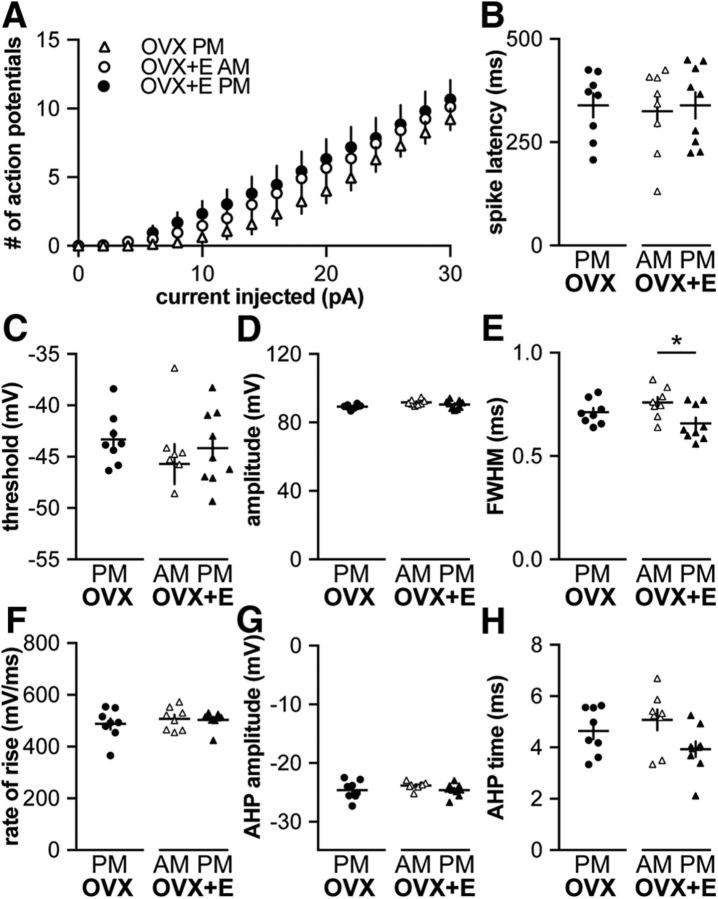
All whole-cell recording parameters are shown in Table 4. In the daily surge model, estradiol and time of day interact to modify calcium and potassium currents. These changes are predicted to make GnRH neurons less excitable during negative feedback and more excitable during positive feedback relative to open-loop (OVX) groups. To investigate directly whether time of day and estradiol modulated GnRH neuron excitability, we measured GnRH neuron response to depolarizing steady-state current injections (0–30 pA, 2 pA steps, 500 ms). Input resistance was not different among groups (Table 4). Current injections were initiated from a mean membrane potential of −69 ± 2 mV, near the value determined in the above experiments. Figure 2A shows representative responses to 12 and 24 pA injections. Once firing was initiated, GnRH neurons from OVX+E PM mice fired more spikes at each current step from 18 to 30 pA compared with all other groups (Fig. 2B; OVX AM, n = 10; OVX PM, n = 9; three-way repeated-measures ANOVA/Bonferroni, p < 0.05). No difference was observed among cells from OVX AM, OVX PM, and OVX+E AM groups (p > 0.15). GnRH neuron excitability, measured as action potential firing response to current injection, is thus increased during positive feedback, consistent with our hypothesis, but not reduced during negative feedback, contrary to our hypothesis.

Table 4.

Whole-cell recording properties for Figures 2–4

Mean ± SEM of GnRH whole-cell passive properties from Figure 2
	OVX AM	OVX PM	OVX+E AM	OVX+E PM
Input resistance (mΩ)	1019 ± 133	897.8 ± 39	955.6 ± 81	992.6 ± 82
Capacitance (pF)	15.5 ± 0.6	17.8 ± 0.8	16.9 ± 0.6	16.3 ± 1.0
Series resistance (mΩ)	11.8 ± 0.9	10.7 ± 0.5	11.4 ± 0.8	12.0 ± 1.0
Holding current (pA)	−0.1 ± 2	−6.4 ± 5	3.3 ± 3	0.3 ± 4
Two-way ANOVA parameters for comparison of GnRH passive properties among groups: cells from OVX AM, OVX PM, OVX+E AM, OVX+E PM (Fig. 2)

	Estradiol	Time of day	Interaction
Input resistance (mΩ)	F(1,41) = 0.03	F(1,41) = 0.2	F(1,41) = 0.7
Capacitance (pF)	F(1,41) = 0.001	F(1,41) = 1.1	F(1,41) = 3.6 (p = 0.07)
Series resistance (mΩ)	F(1,41) = 0.3	F(1,41) = 0.09	F(1,41) = 1.0
Holding current (pA)	F(1,41) = 2.0	F(1,41) = 1.7	F(1,41) = 0.2
Mean ± SEM of GnRH whole-cell passive properties from Figure 3

	OVX AM	OVX PM	OVX+E AM	OVX+E PM
Input resistance (mΩ)
before kisspeptin	1003 ± 111	970.8 ± 59	1097 ± 93	1283 ± 193
during kisspeptin	2061 ± 253	1378 ± 216	1711 ± 314	2302 ± 471
Capacitance (pF)
before kisspeptin	17.3 ± 0.9	16.4 ± 0.9	16.0 ± 0.7	14.4 ± 1.2
during kisspeptin	18.0 ± 1.0	16.9 ± 0.9	16.9 ± 0.6	14.8 ± 1.3
Series resistance (mΩ)
before kisspeptin	10.0 ± 0.5	10.5 ± 0.6	10.8 ± 0.7	10.5 ± 0.4
during kisspeptin	10.4 ± 0.8	10.5 ± 0.8	12.5 ± 1.3	10.8 ± 0.3
Holding current (pA)
before kisspeptin	7.1 ± 3	0.8 ± 3	4.3 ± 3	2.3 ± 2
during kisspeptin	−39 ± 6	−39 ± 5	−25 ± 5	−18 ± 3
Three-way ANOVA F(1,32) values for comparison of GnRH passive properties among groups: cells from OVX PM, OVX+E AM, and OVX+E PM (Fig. 3)

	E2	AM/PM	Kisspeptin	E2 × kisspeptin	AM/PM × kisspeptin	E2 × AM/PM	E2 × kisspeptin × AM/PM
Input resistance (mΩ)	1.1	0.03	39***	0.3	0.4	3.4 (p = 0.07)	3.6 (p = 0.07)
Capacitance (pF)	3.1 (p = 0.09)	2.4	43***	0.03	2.5	0.2	0.3
Series resistance (mΩ)	1.3	0.2	3.3 (p = 0.08)	1.5	2.1	1.0	0.8
Holding current (pA)	5.2*	0.01	283***	21***	3.4 (p = 0.08)	0.7	0.2
Mean ± SEM of GnRH whole-cell passive properties from Figure 4

	OVX PM	OVX+E AM	OVX+E PM
Input resistance (mΩ)	1194 ± 181	1314 ± 208	1531 ± 218
Capacitance (pF)	13.1 ± 1	14.0 ± 1	14.1 ± 0.8
Series resistance (mΩ)	11.9 ± 0.8	11.6 ± 0.9	11.1 ± 0.9
Holding current (pA)	−3.3 ± 3	−3.2 ± 4	−10 ± 3.6
One-way ANOVA parameters for comparison of GnRH passive properties among groups: cells from OVX PM, OVX+E AM, and OVX+E PM (Fig. 4)

Input resistance (mΩ)	KW statistic = 0.6
Capacitance (pF)	F(2,22) = 0.4
Series resistance (mΩ)	KW statistic = 0.6
Holding current (pA)	F(2,22) = 1.3

*p < 0.05;

***p < 0.001.

Figure 2.

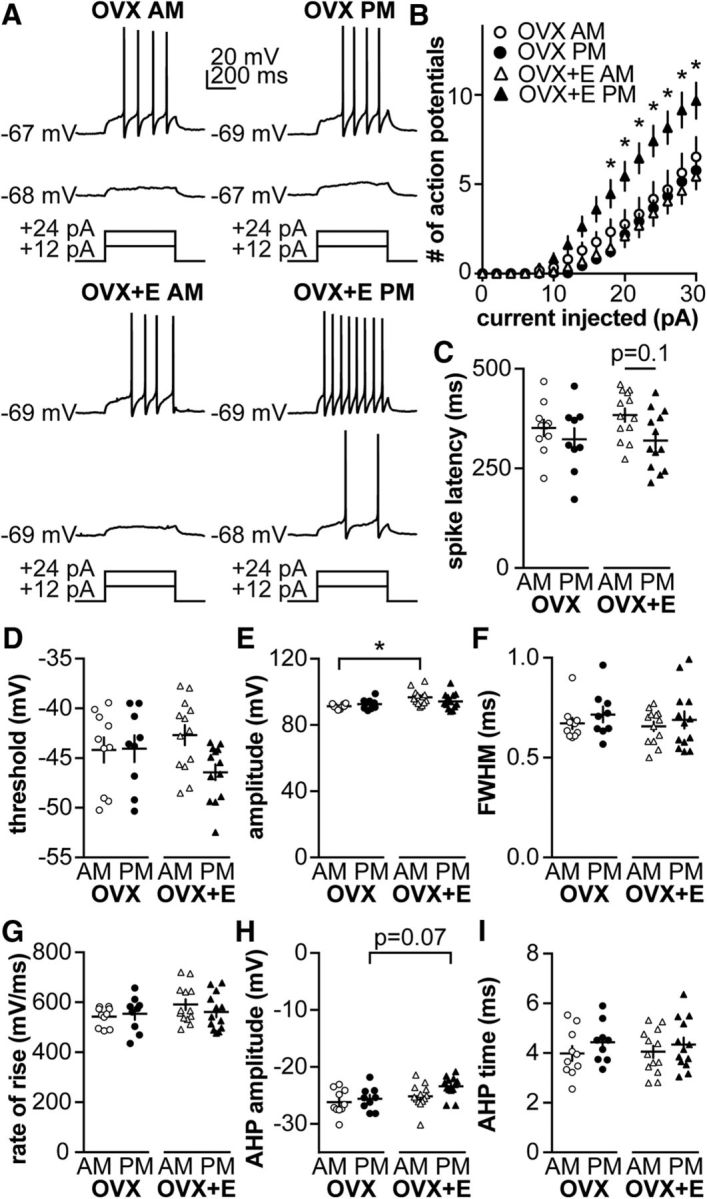
GnRH neuron excitability is increased during positive feedback. A, Representative traces from neurons in each group during 500 ms current injections of 12 and 24 pA (injection protocol below). B, Mean ± SEM spikes elicited for each current injection step. C–I, Individual values and mean ± SEM. C, Latency to first spike. D, Action potential threshold. E, Action potential amplitude. F, FWHM. G, Action potential rate of rise. H, AHP amplitude. I, AHP time. *p < 0.05 versus OVX+E PM, three-way repeated-measures ANOVA/Bonferroni test in B (estradiol: F_(1,41) = 3.5, p = 0.07; time of day: F_(1,41) = 3.7, p = 0.06; current: F_(15,615) = 154, p < 0.001; current × estradiol: F_(15,615) = 2.7, p = 0.1; current × time of day: F_(15,615) = 4.2 p < 0.05, estradiol × time of day: F_(1,41) = 8.9 p < 0.01, current × estradiol × time of day: F_(15,615) = 6.7 p < 0.1) or two-way ANOVA/Bonferroni in C–I.

Despite the marked increase in action potential firing during positive feedback, effects on action potential properties were modest. Estradiol reduced spike amplitude in cells recorded in the AM (Fig. 2E; OVX AM vs OVX+E AM, two-way ANOVA/Bonferroni, p = 0.008; Table 5). Estradiol– and/or time of day–dependent effects on spike latency (Fig. 2C; two-way ANOVA/Bonferroni, p = 0.1, Table 5), firing threshold (Fig. 2D; two-way ANOVA, interaction p = 0.08; Table 5), and AHP amplitude (Fig. 2H; two-way ANOVA/Bonferroni, p = 0.07; Table 5) approached but did not achieve the level set for significance. No time of day– or estradiol–dependent changes were observed in FWHM (Fig. 2F), rate of rise (Fig. 2G), or AHP time (Fig. 2I; two-way ANOVA/Bonferroni, Table 5).

Table 5.

Two-way ANOVA parameters for comparison of action potential characteristics among groups: cells from OVX AM, OVX PM, OVX+E AM, and OVX+E PM

Parameter (figure)	Estradiol	Time of day	Interaction
Spike latency (Fig. 2C)	F(1,41) = 0.5	F(1,41) = 4.7*	F(1,41) = 0.7
Threshold (Fig. 2D)	F(1,41) = 0.2	F(1,41) = 2.8 (p = 0.1)	F(1,41) = 3.2 (p = 0.08)
AP amplitude (Fig. 2E)	F(1,41) = 9.1**	F(1,41) = 0.2	F(1,41) = 2.5
FWHM (Fig. 2F)	F(1,41) = 0.4	F(1,41) = 1.2	F(1,41) = 0.03
Rate of rise (Fig. 2G)	F(1,41) = 1.9	F(1,41) = 0.2	F(1,41) = 1.0
AHP amplitude (Fig. 2H)	F(1,41) = 6.9*	F(1,41) = 3.5 (p = 0.07)	F(1,41) = 0.9
AHP time (Fig. 2I)	F(1,41) = 0.001	F(1,41) = 1.8	F(1,41) = 0.08

*p < 0.05;

**p < 0.01.

Kisspeptin increases GnRH excitability in a time of day–dependent manner

Kisspeptin is a neuromodulator that increases GnRH neuron firing activity and release (Han et al., 2005; Pielecka-Fortuna et al., 2008; Glanowska and Moenter, 2015). To investigate whether kisspeptin increases excitability, we repeated the above experiments before and during bath application of 10 nm kisspeptin. To compare response to kisspeptin among groups (n = 9 each: OVX AM, OVX PM, OVX+E AM, and OVX+E PM), area under the curve (AUC), calculated using the trapezoid rule (Abramowitz and Stegun, 1964), and number of spikes per step was calculated before (Fig. 3A, dotted area) and during kisspeptin treatment (Fig. 3A, dotted plus solid areas). Kisspeptin increased AUC in cells recorded in the AM from both OVX and OVX+E mice (Fig. 3B; three-way repeated-measures ANOVA/Bonferroni, p = 0.003, OVX AM; and p = 0.009, OVX+E AM; Table 6), but had no effect on cells recorded in the PM in either steroid condition (p > 0.1). During kisspeptin treatment, some cells in all groups initiated action potential firing after termination of the current step, whereas no cells studied under control conditions fired at this time (Fig. 3C; χ² with Yates correction, p < 0.0001). To test whether any of these results could be attributed to a spontaneous shift in excitability over the course of recording of this duration, excitability was compared before and during “mock” treatment (n = 2 cells, OVX AM; n = 4, OVX PM; and n = 4, OVX+E AM, which were combined; and n = 5, OVX+E PM). No difference was observed over time (two-way repeated-measures ANOVA/Bonferroni), and no cells fired following termination of the current step, indicating the above observed shifts in firing were kisspeptin-dependent. Kisspeptin increased input resistance and decreased holding current in all groups, except OVX PM (Table 4); this may in part account for increased firing in response to the same current injection, but the difference in response between morning and afternoon, and the occurrence of spikes after termination of current injection indicated some of the changes are attributable to kisspeptin action.

Table 6.

Three-way repeated-measures ANOVA parameters for comparison of GnRH response to current (AUC; Fig. 3B) and action potential characteristics (Fig. 3D–J) before and during kisspeptin treatment among groups: cells from OVX AM, OVX PM, OVX+E AM, and OVX+E PM

	Estradiol	Time of day	Kisspeptin	Kisspeptin × estradiol	Kisspeptin × time of day	Estradiol × time of day	Kisspeptin × estradiol × time of day
AUC (Fig. 3B)	F(1,1) = 0.9	F(1,1) = 0.02	F(1,1) = 38.3***	F(1,1) = 0.08	F(1,1) = 2.7	F(1,1) = 3.9 (p = 0.06)	F(1,1) = 0.5
Spike latency (Fig. 3D)	F(1,32) = 3.4 (p = 0.07)	F(1,32) = 1.5	F(1,32) = 0.02	F(1,32) = 1.1	F(1,32) = 0.1	F(1,32) = 0.003	F(1,32) = 1.1
Threshold (Fig. 3E)	F(1,32) = 0.9	F(1,32) = 1.4	F(1,32) = 0.6	F(1,32) = 0.07	F(1,32) = 0.5	F(1,32) = 9.2**	F(1,32) = 0.8
AP amplitude (Fig. 3F)	F(1,32) = 3.2 (p = 0.08)	F(1,32) = 0.7	F(1,32) = 12.6**	F(1,32) < 0.001	F(1,32) = 1.0	F(1,32) = 0.4	F(1,32) = 1.6
FWHM (Fig. 3G)	F(1,32) = 0.2	F(1,32) = 1.4	F(1,32) = 60.4***	F(1,32) = 0.8	F(1,32) = 0.05	F(1,32) = 0.01	F(1,32) = 0.02
Rate of rise (Fig. 3H)	F(1,32) = 1.1	F(1,32) = 0.02	F(1,32) = 11.3**	F(1,32) = 0.3	F(1,32) = 3.1 (p = 0.09)	F(1,32) = 0.06	F(1,32) = 0.2
AHP amplitude (Fig. 3I)	F(1,32) < 0.001	F(1,32) = 0.2	F(1,32) = 0.03	F(1,32) = 0.09	F(1,32) = 0.4	F(1,32) = 0.003	F(1,32) = 0.1
AHP time (Fig. 3J)	F(1,32) = 0.02	F(1,32) = 0.3	F(1,32) = 43.0***	F(1,32) = 2.2	F(1,32) = 4.0 (p = 0.06)	F(1,32) = 0.04	F(1,32) = 0.3

**p < 0.01;

***p < 0.001.

Kisspeptin modulated some action potential characteristics, reducing action potential FWHM (Fig. 3G) independent of time of day or estradiol (three-way, repeated-measures ANOVA/Bonferroni, all p ≤ 0.01; Table 6). Kisspeptin also delayed the peak of the AHP (AHP time) in cells from all groups, except OVX+E mice recorded in the PM (positive feedback, three-way, repeated-measures ANOVA/Bonferroni, all p ≤ 0.01). In cells from OVX+E mice studied in the AM (negative feedback), kisspeptin decreased action potential amplitude (Fig. 3F; three-way, repeated-measures ANOVA/Bonferroni, p = 0.02) and rate of rise (Fig. 3H; three-way, repeated-measures ANOVA/Bonferroni, p = 0.02). Kisspeptin did not shift spike latency (Fig. 3D), firing threshold (Fig. 3E), or AHP amplitude (Fig. 3I; three-way, repeated-measures ANOVA/Bonferroni). In cells that received “mock” treatment, action potential properties did not shift, with the exception of rate of rise, which was decreased (three-way, repeated-measures ANOVA/Bonferroni, p < 0.02).

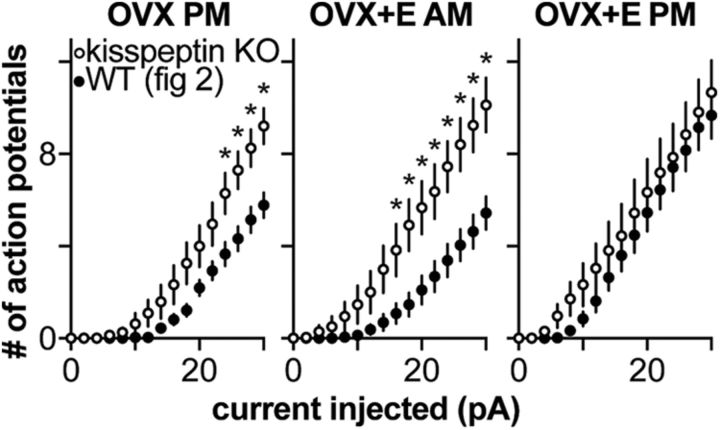
GnRH neuron excitability is independent of estradiol and time of day in kisspeptin KO mice

Because endogenous kisspeptin release is likely to enhance GnRH neuron excitability, we hypothesized that excitability of GnRH neurons would be reduced in the absence of kisspeptin. To test this, we measured GnRH neuron response to current steps (as above) in OVX and OVX+E kisspeptin KO mice. Because these mice are infertile and must be bred from heterozygotes, only three groups were studied (OVX PM, OVX+E AM, and OVX+E PM) as no differences were observed between cells from OVX PM and OVX AM animals in Figure 1 or Figure 2, or in our previous work with this model (Christian et al., 2005; Christian and Moenter, 2007; Sun et al., 2010; Pielecka-Fortuna et al., 2011; Gaskins and Moenter, 2012). GnRH neuron response to current was independent of time of day or estradiol in cells from kisspeptin KO mice (Fig. 4A; OVX PM, n = 8; OVX+E AM, n = 9; and OVX+E PM, n = 9; one-way ANOVA/Bonferroni, p > 0.2). To facilitate comparison of GnRH neuron excitability between KO and control mice, GnRH neuron firing in response to current steps from Figures 1 and 4 are plotted together in Figure 5. GnRH neuron excitability from KO mice is elevated relative to cells from OVX PM and OVX+E AM control mice (Fig. 5; three-way repeated-measures ANOVA/Bonferroni, p < 0.05), but similar to GnRH neuron excitability in OVX+E PM control mice (p > 0.1).

No differences in action potential characteristics were observed among OVX PM, OVX+E AM, and OVX+E PM kisspeptin KO mice (Fig. 4; one-way ANOVA/Bonferroni for Fig. 4B–D,G,H, p > 0.1; and Kruskal–Wallis/Dunn for Fig. 4F, p > 0.1), except for FWHM, in which spike width was decreased in cells from OVX+E AM mice relative to OVX+E PM (one-way ANOVA/Bonferroni, p = 0.03).

The similar firing response of GnRH neurons among negative feedback and OVX groups is effectively modeled by identifiable parameter sets with a strong inverse correlation between gA and V1/2 inactivation of I_A

The above data indicate that GnRH neurons from OVX AM, OVX PM, and OVX+E AM mice have the same action potential firing response to current injections. This was initially surprising because GnRH neurons from the two OVX groups have similar ion channel densities and properties that are different from those of cells from OVX+E AM mice (Sun et al., 2010; Pielecka-Fortuna et al., 2011). These differences led us to the original hypothesis that during negative feedback GnRH neurons exhibit decreased excitability compared with cells from OVX mice. Upon rejection of this hypothesis by the above data, our goal was to examine how individual current properties influenced excitability.

A model GnRH neuron (Moran et al., 2016) was adapted to reproduce the negative feedback state in terms of I_A, I_K, I_HVA, and I_LVA (Fig. 6A–H), all of which have been isolated and characterized in voltage-clamp experiments (Zhang et al., 2009; Sun et al., 2010; Pielecka-Fortuna et al., 2011). These experiments demonstrated that four parameters differed in cells from OVX versus negative feedback animals: the maximum conductances (g) of I_A, I_LVA, and I_NaP and the V_1/2 inactivation of I_A. We used MCMC to estimate the values of these four parameters that best reproduce action potential shape and excitability, permitting only these four parameters to vary. We hypothesized that more than one unimodal distribution of parameter sets would be able to reproduce excitability during negative feedback because empirical channel properties/densities varied despite the same excitability in the above datasets (OVX and negative feedback; Fig. 2). Surprisingly, the model parameters each converged (Fig. 7A–D) to a Gaussian, rather than a non-Gaussian, or multimodal, distribution (Fig. 7E); this model is thus “identifiable.” The hypothesis that more than one distribution of parameter sets would reproduce these data was therefore rejected. Of interest, the joint probability distributions between membrane potential at which ½ of current is inactivated (V_1/2inact) of I_A and g_A were highly dependent on one another (Fig. 7E); as g_A increased, V_1/2 inactivation became more hyperpolarized, thus maintaining the same action potential response to current injection (Fig. 7F,G). In contrast to V_1/2inact of I_A and g_A, values for g_HVA and g_NaP were largely independent of the other parameters (Fig. 7C). Although these parameters vary over a small range, their convergence on a Gaussian distribution indicates that there are indeed preferable parameter values to reproduce the dataset; if these parameters had no influence on the solution, the distribution of possible solutions would be flat.

Figure 7.

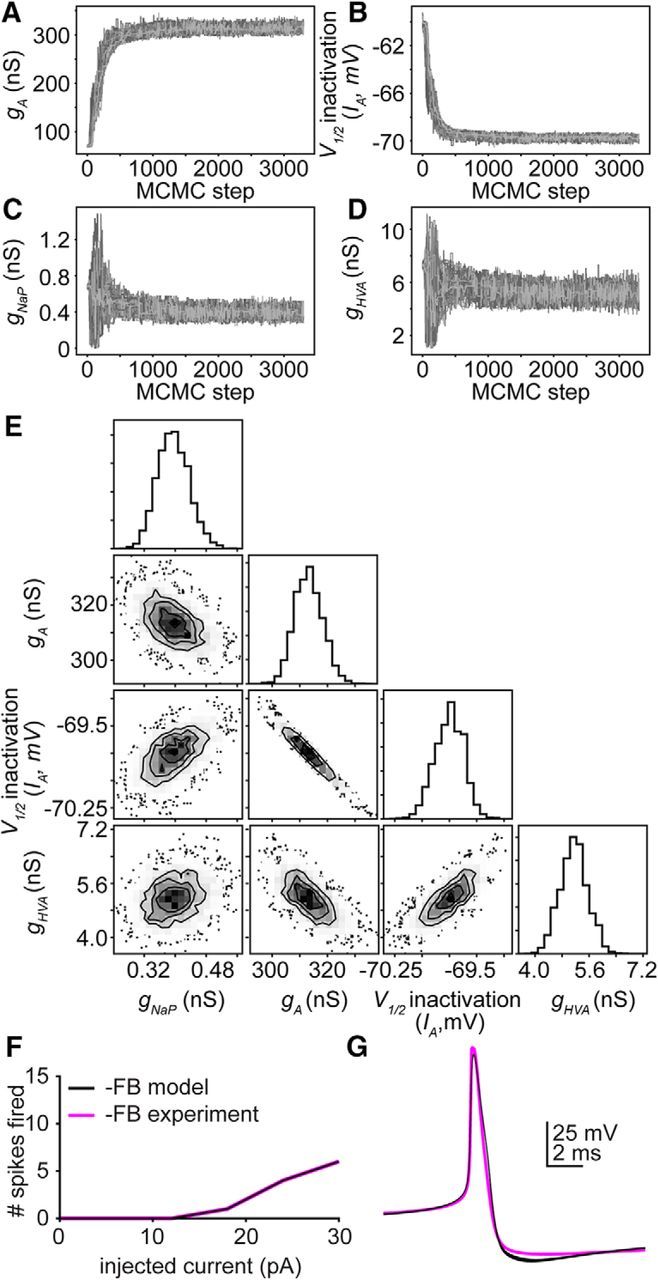
A hyperpolarizing shift in V_1/2 inactivation of I_A can oppose an increase in maximum I_A channel number to prevent changes in excitability. A–D, Convergence plots for parameters: A, g_A. B, V_1/2 inactivation of I_A. C, g_NaP. D, g_HVA. Each line indicates the value of a single walker (of 100) over 3300 iterations. E, Far right panel in each row, individual probability distributions for the parameters g_HVA, V_1/2 inactivation of I_A, g_A, and g_HVA for the simulation in F, G. Two-dimensional probability distributions in the other panels determine whether parameter values vary independently (g_NaP and g_HVA) or dependently (g_A and V_1/2 inactivation of I_A) of one another. F, Ten simulated (black) parameter sets selected along the interdependent distribution for g and V_1/2 inactivation, and a representative empirical GnRH neuron (magenta) responses to 500 ms current injections during negative feedback (0–30 pA, 6 pA steps). G, Ten simulated and empirical action potential waveforms during negative feedback.

We repeated this experiment for two additional excitability curves from cells during negative feedback and for the mean excitability curve for negative feedback from Figure 2. In each case, the four parameters converged to Gaussian distributions, and the joint probabilities between V_1/2inact of I_A and g_A strongly indicate that these parameters are highly dependent on one another (data not shown).

The similar firing response of GnRH neurons within the positive feedback group was not effectively modeled by identifiable parameter sets

Our data demonstrate that GnRH neuron excitability was increased during positive feedback without impacting action potential shape. We used our neuron model to determine which of the steroid-dependent parameters (g_A, g_HVA, and I_A V_1/2 inactivation) examined above were essential for increase in excitability during positive feedback. We used the MCMC method to estimate the best parameter set(s) for reproducing positive feedback excitability without changing action potential shape. In contrast to negative feedback, the MCMC simulations did not converge to a Gaussian distribution for any parameter within the physiologic range (Fig. 8A–E). Simulations were stopped when parameters exited their physiologic range. There were multiple combinations of g_A, g_HVA, and I_A V_1/2 inactivation that provided a good fit to the current-clamp data over large parameter ranges (Fig. 8F,G). These data indicate that, despite the identifiability of the model parameters for OVX+E AM and OVX groups above, this same model running under the same conditions is not identifiable.

Figure 8.

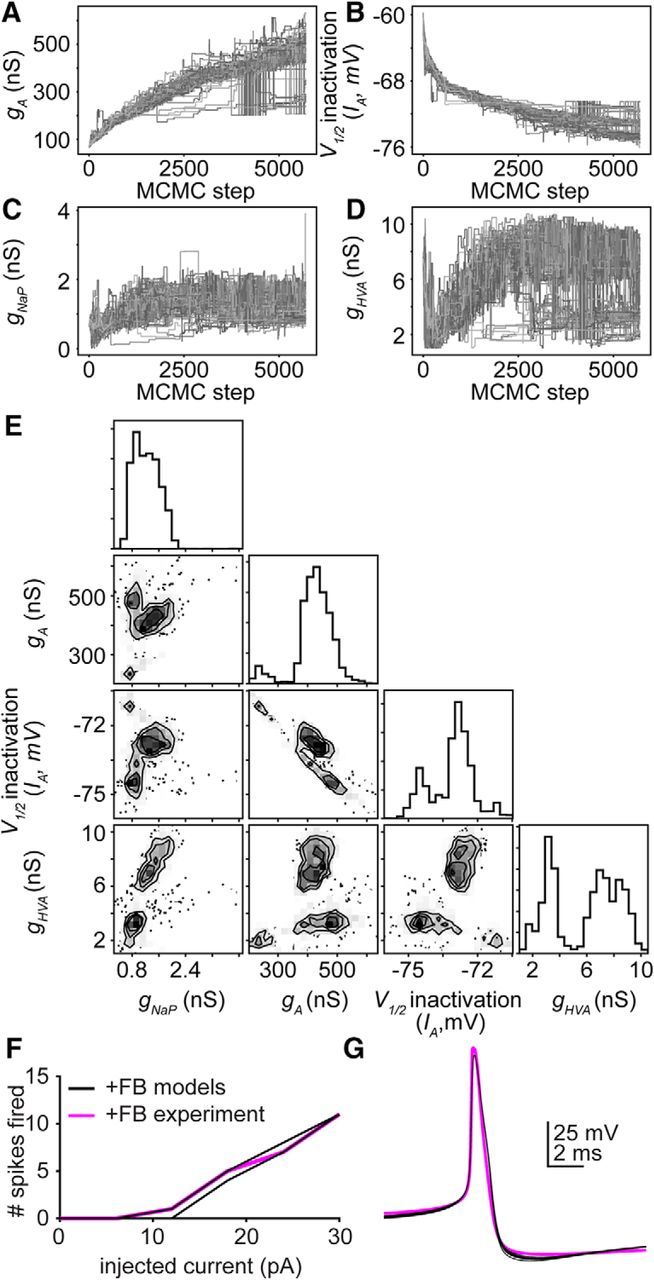
Multiple parameter sets can reproduce increased excitability during positive feedback. A–D, Convergence plots for parameters. A, g_A. B, V_1/2 inactivation of I_A. C, g_NaP. D, g_HVA. Each line indicates the value of a single walker (of 100) over 5700 iterations. E, Far right panel in each row, individual probability distributions for the parameters g_HVA, V_1/2 inactivation of I_A, g_A, and g_HVA for the simulation in F, G. Two-dimensional probability distributions in the other panels determine whether parameter values vary independently or dependently on one another. F, Ten simulated (black, randomselected from parameter sets in A–D) and a representative empirical GnRH neuron (magenta) response to 500 ms current step injections during positive feedback (0–30 pA, 6 pA steps). G, Ten simulated and empirical action potential waveforms during positive feedback.

We repeated this experiment for two additional excitability curves during positive feedback and for the mean excitability curve for positive feedback from Figure 2. In each case, none of the four parameters converge to Gaussian distributions within their physiologic range (data not shown).

Persistent sodium currents can induce spiking after termination of the current step

Kisspeptin induced firing after termination of the current step independent of time of day or estradiol. We were able to reproduce this effect by altering two key parameters for persistent sodium currents in the negative feedback model neuron (Fig. 9A). It was necessary, first, to shift the V_1/2 activation for I_NaP to a more hyperpolarized potential and, second, to decrease the speed at which the activation gate activated/deactivated. This led to the slow activation of I_NaP over the course of the current step, depolarizing the membrane potential, and culminating in a single spike (Fig. 9B). Following the spike, I_NaF was inactivated, the membrane potential dropped, and I_NaP slowly deactivated. Spiking was also increased during the current step, from 6 to 9 action potentials fired during a 30 pA step (Fig. 9A), suggesting that kisspeptin activation of I_NaP may contribute to increased firing during the step as well as after.

Figure 9.

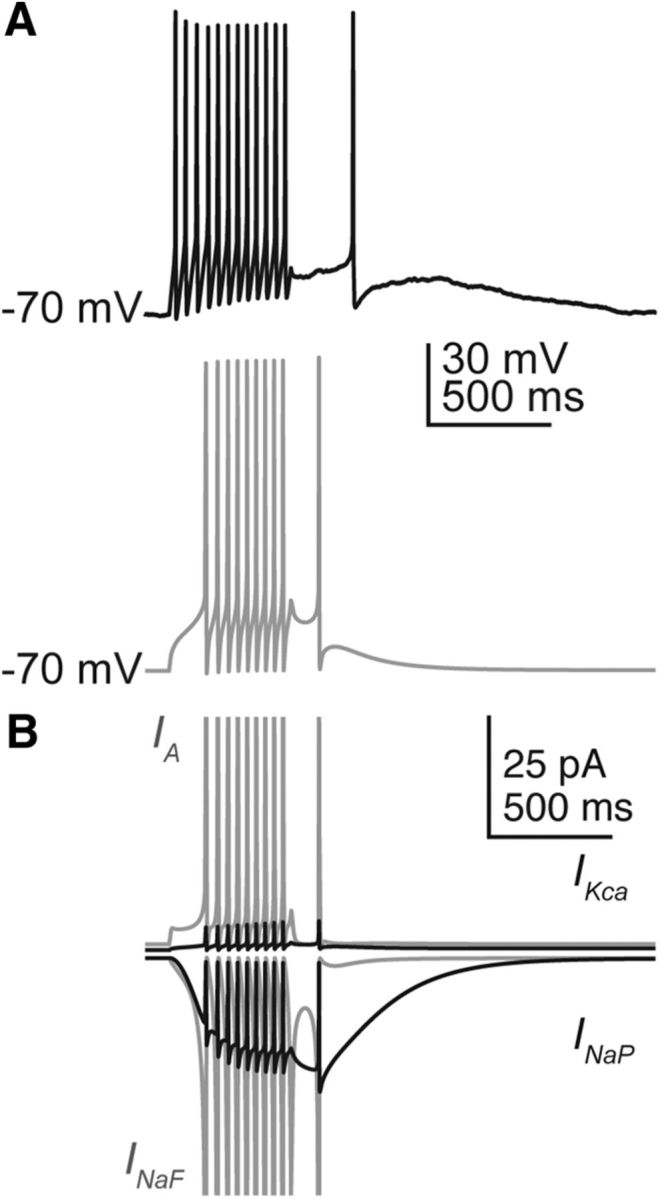
Persistent sodium currents can induce spiking after termination of a current step. A, Spikes can be initiated after the current step in cells from an OVX+EAM mouse (black) and model (gray). B, Individual currents during model membrane response in A, I_A (top gray), I_Kca (top black), I_NaF (bottom gray), and I_NaP (bottom black). Currents for I_NaF and I_A reach >1 nA during an action potential and have been truncated to more clearly observe ionic currents active after termination of the current step.

Discussion

The switch from estradiol negative to positive feedback triggers a surge of GnRH release, ultimately resulting in ovulation. GnRH release at the median eminence to control pituitary output is in part dependent on action potential firing (Glanowska and Moenter, 2015). Intrinsic conductances sculpt whether or not synaptic inputs evoke action potential firing and can also independently initiate spiking. Here we use a daily LH surge model that separates steroid and time of day variables contributing to estradiol feedback to show that GnRH neurons fire more action potentials during positive feedback, that the neuromodulator kisspeptin may play a role in this increase, and use a mathematical model neuron to predict that there are multiple intrinsic mechanisms that can increase excitability during positive feedback.

The increase in excitability observed in GnRH neurons during positive feedback supports and extends previous voltage-clamp experiments done in the same daily LH surge paradigm used in the present work. These studies identified multiple ionic conductances that are modified by both time of day and estradiol. Specifically, rapidly inactivating A-type potassium currents and sustained delayed rectifier potassium currents were increased during negative feedback and decreased during positive feedback (Pielecka-Fortuna et al., 2011); high-voltage–activated calcium currents were increased during positive feedback and suppressed during negative feedback (Sun et al., 2010). In contrast, these currents did not vary in GnRH neurons from OVX mice, and values were typically intermediate to those observed during estradiol negative and positive feedback. In a different estradiol feedback paradigm, low-voltage–activated calcium currents were increased during positive feedback and ATP-sensitive potassium currents were increased during negative feedback (Zhang et al., 2007, 2009). Based on these observations and the typical physiologic effects of these currents on the membrane potential, we expected decreased excitability during negative feedback and increased GnRH neuron excitability during positive feedback compared with cells from OVX mice. The latter hypothesis was supported, but the former was rejected because excitability of GnRH neurons from the negative feedback animal model (OVX+E AM) was not decreased relative to that in cells from OVX mice.

Perhaps the most likely explanation for the similar excitability among these groups is that ionic conductance changes in cells from OVX+E AM mice and OVX mice have opposing effects on one another. Indeed, our model GnRH neuron predicts that the hyperpolarizing shift in I_A V_1/2 inactivation observed in OVX+E AM neurons opposes the increase in I_A current density observed at this time. Changes in other currents examined within the model were unable to compensate for the increase in I_A during negative feedback.

GnRH neuron excitability was markedly increased during estradiol positive feedback, with little effect on action potential shape or spike latency. We used the GnRH neuron model to test whether any individual channel(s) could increase GnRH neuron excitability without modifying action potential shape. Interestingly, and in contrast to negative feedback and open-loop (i.e., OVX) conditions, the model did not converge on unique identifiable parameter sets within the physiologic range. This may suggest that there are multiple yet to be determined mechanisms to increase GnRH neuron excitability during positive feedback; this could increase likelihood of a successful GnRH surge and thus ovulation.

Estradiol- and time of day–dependent effects on intrinsic conductances of GnRH neurons are likely transmitted through the ERα-sensitive network afferent to these cells. The neuromodulator kisspeptin is postulated to play a major role in positive feedback (Oakley et al., 2009). The present work supports and extends these findings by demonstrating that kisspeptin has both time of day–dependent and –independent effects on GnRH neurons. First, kisspeptin increased GnRH neuron excitability during current injection in cells recorded in the morning, but not in cells recorded in the late afternoon, regardless of estradiol status. Second, kisspeptin stimulated spiking after termination of the current stimulus in some cells independent of time of day and estradiol; no spikes were observed after stimulus termination under control conditions. The model GnRH neuron predicts that changes to the activation kinetics of persistent sodium channels may initiate spiking after termination of the current step. Of note, the model also predicts that this change in kinetics would also increase spiking during the current step; this may explain the apparent shift in the excitability curve that did not achieve significance in cells treated with kisspeptin in the afternoon. We postulate that in vivo, endogenous kisspeptin induces two mechanistic changes with different half-lives, such that one effect (increased firing during current injection) persists into the slice preparation, whereas the other effect (increased firing after termination of current injection) does not. The lack of effect of exogenous kisspeptin on firing during the current steps in cells studied in the afternoon would thus be attributable to persistence of the effects of endogenous kisspeptin released before slice preparation on the intrinsic properties of GnRH neurons in the slice. In this regard, kisspeptin acts via mechanisms that typically have longer half-lives, such as changing gene expression (Sukhbaatar et al., 2013; Terasaka et al., 2013; Novaira et al., 2016), and mechanisms with shorter half-lives, including rapid effects on ionic conductances (Zhang et al., 2008, 2013; Pielecka-Fortuna et al., 2011).

Paradoxically, GnRH neuron excitability in kisspeptin KO mice was high, similar to that during estradiol positive feedback in control mice. In contrast to controls, however, neither estradiol nor time of day altered excitability of GnRH neurons from kisspeptin KO mice. Kisspeptin KOs are infertile and do not have estrous cycles or exhibit estradiol positive feedback with increased LH release (Lapatto et al., 2007; Chan et al., 2009). We thus postulated that GnRH neuron excitability would be low in these mice. We reject this hypothesis and offer two possible explanations. First, other mechanisms may compensate to enhance GnRH neuron excitability and release in the absence of kisspeptin. Second, GnRH neurons in kisspeptin KO mice may fail to undergo typical maturation. In this regard, GnRH release frequency in males and firing rate in both sexes are higher before puberty than in adults (Glanowska et al., 2014; Dulka and Moenter, 2017). This typical maturational decline may be regulated by a kisspeptin-dependent circuit.

Interpretation of the present data was facilitated with mathematical modeling. A challenge for modeling biophysical systems is that a model may produce more than one set of parameters that reproduces the data, making the model “unidentifiable.” For many biological models, a single point estimate is given for each parameter, without rigorously determining whether alternative values exist that also reproduce the data. A number of methods have been developed to overcome this problem. Maximum likelihood methods give a mean value and SD for each parameter; large SDs may hint at nonunique solutions. MCMC methods use Bayes' theorem to determine a probability distribution for each parameter, providing not only a mean and SD, but also the shape (e.g., Gaussian, bimodal, uniform) of the distribution (Siekmann et al., 2011). Using voltage-clamp and current-clamp data to constrain our model, the probability distribution for each parameter converged to a Gaussian distribution centered around a single mean value for negative feedback and open-loop conditions. A multimodal or uniform distribution would have suggested that more than one parameter set was able to reproduce the data. When we tried estimating parameters using only activation and inactivation curves, excluding voltage-clamp traces, many parameters displayed almost uniform distributions indicating these data alone were insufficient to constrain the model. It is important to point out that a nonidentifiable solution can also have biological implications. For example, our positive feedback model had access to the same types of data but did not converge within the physiologic range upon a Gaussian distribution of parameters for any of the four variables examined. Similar redundancy was reported to contribute to output among elements of the crustacean stomatogastric ganglion (Prinz et al., 2004). It remains possible that, when more parameters have been empirically determined, future iterations of this model will be able to converge.

MCMC methods also determine whether the predicted values of parameters are dependent or independent of one another. If two parameters are dependent, this can justify fixing one parameter and allowing the other to vary to reduce the total number of parameters in the model. Interdependence can also have a biological significance. In our negative feedback model, I_A V_1/2 inactivation became more hyperpolarized as g_A increased, suggesting that opposing changes observed in negative feedback prevent a decrease in excitability relative to that observed in the open-loop OVX condition. At present, it is not possible to manipulate individual ion channel parameters empirically; modeling and MCMC methods are thus necessary to perform these experiments.

The present studies indicate that multiple parameters interact to regulate GnRH neuron excitability in an estradiol- and time of day–dependent manner. Rigorous parameter estimation of a model neuron provided new insights into possible mechanisms underlying changes in excitability among groups. The possibility of multiple mathematical solutions to positive feedback reminds us to keep in mind that different neurobiological mechanisms may also exist to guarantee reproductive success, including changes to intrinsic properties of GnRH neurons, fast synaptic inputs, and neuromodulators beyond kisspeptin (Gore, 2002; Christian and Moenter, 2010).