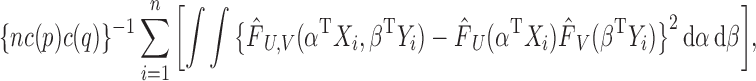Abstract
We propose the use of projection correlation to characterize dependence between two random vectors. Projection correlation has several appealing properties. It equals zero if and only if the two random vectors are independent, it is not sensitive to the dimensions of the two random vectors, it is invariant with respect to the group of orthogonal transformations, and its estimation is free of tuning parameters and does not require moment conditions on the random vectors. We show that the sample estimate of the projection correction is  -consistent if the two random vectors are independent and root-
-consistent if the two random vectors are independent and root-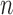 -consistent otherwise. Monte Carlo simulation studies indicate that the projection correlation has higher power than the distance correlation and the ranks of distances in tests of independence, especially when the dimensions are relatively large or the moment conditions required by the distance correlation are violated.
-consistent otherwise. Monte Carlo simulation studies indicate that the projection correlation has higher power than the distance correlation and the ranks of distances in tests of independence, especially when the dimensions are relatively large or the moment conditions required by the distance correlation are violated.
Keywords: Distance correlation, Projection correlation, Ranks of distance
1. Introduction
Let  and
and  be two random vectors. In this paper, we aim to test
be two random vectors. In this paper, we aim to test
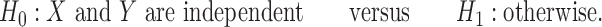 |
Measuring and testing dependence between  and
and 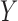 is a fundamental problem in statistics. The Pearson correlation is perhaps the first and the best-known quantity to measure the degree of linear dependence between two univariate random variables. Extensions including Spearman’s (1904) rho, Kendall’s (1938) tau, and those due to Hoeffding (1948) and Blum (1961) can be used to measure nonlinear dependence without moment conditions.
is a fundamental problem in statistics. The Pearson correlation is perhaps the first and the best-known quantity to measure the degree of linear dependence between two univariate random variables. Extensions including Spearman’s (1904) rho, Kendall’s (1938) tau, and those due to Hoeffding (1948) and Blum (1961) can be used to measure nonlinear dependence without moment conditions.
Testing independence has important applications. Two examples from genomics research are testing whether two groups of genes are associated and examining whether certain phenotypes are determined by particular genotypes. In social science research, scientists are interested in understanding potential associations between psychological and physiological characteristics. Wilks (1935) introduced a parametric test based on  , where
, where  ,
, 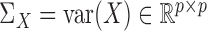 and
and 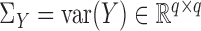 . Throughout
. Throughout 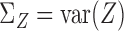 stands for the covariance matrix of
stands for the covariance matrix of  and
and  stands for the determinant of
stands for the determinant of  . Hotelling (1936) suggested the canonical correlation coefficient, which seeks
. Hotelling (1936) suggested the canonical correlation coefficient, which seeks 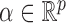 and
and  such that the Pearson correlation between
such that the Pearson correlation between  and
and  is maximized. Both Wilks’s test and the canonical correlation can be used to test for independence between
is maximized. Both Wilks’s test and the canonical correlation can be used to test for independence between 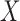 and
and 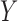 when they follow normal distributions. Nonparametric extensions of Wilks’s test were proposed by Puri & Sen (1971), Hettmansperger & Oja (1994), Gieser & Randles (1997), Taskinen et al. (2003) and Taskinen et al. (2005). These tests can be used to test for independence between
when they follow normal distributions. Nonparametric extensions of Wilks’s test were proposed by Puri & Sen (1971), Hettmansperger & Oja (1994), Gieser & Randles (1997), Taskinen et al. (2003) and Taskinen et al. (2005). These tests can be used to test for independence between  and
and  when they follow elliptically symmetric distributions, but they are inapplicable when the normality or ellipticity assumptions are violated or when the dimensions of
when they follow elliptically symmetric distributions, but they are inapplicable when the normality or ellipticity assumptions are violated or when the dimensions of  and
and  exceed the sample size. In addition, multivariate rank-based tests of independence are ineffective for testing nonmonotone dependence (Székely et al., 2007).
exceed the sample size. In addition, multivariate rank-based tests of independence are ineffective for testing nonmonotone dependence (Székely et al., 2007).
The distance correlation (Székely et al., 2007) can be used to measure and test dependence between 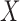 and
and  in arbitrary dimensions without assuming normality or ellipticity. Provided that
in arbitrary dimensions without assuming normality or ellipticity. Provided that 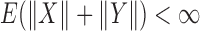 , the distance correlation between
, the distance correlation between  and
and 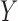 , denoted by
, denoted by 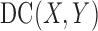 , is nonnegative, and it equals zero if and only if
, is nonnegative, and it equals zero if and only if  and
and  are independent. Throughout, we define
are independent. Throughout, we define  for a vector
for a vector 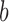 . Székely & Rizzo (2013) observed that the distance correlation may be adversely affected by the dimensions of
. Székely & Rizzo (2013) observed that the distance correlation may be adversely affected by the dimensions of 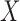 and
and  , and proposed an unbiased estimator of it when
, and proposed an unbiased estimator of it when  and
and 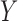 are high-dimensional. In this paper, we shall demonstrate that the distance correlation may be less efficient in detecting nonlinear dependence when the assumption
are high-dimensional. In this paper, we shall demonstrate that the distance correlation may be less efficient in detecting nonlinear dependence when the assumption  is violated. To remove this moment condition, Benjamini et al. (2013) suggested using ranks of distances, but this involves the selection of several tuning parameters, the choice of which is an open problem. The asymptotic properties of a test based on ranks of distances also need further investigation.
is violated. To remove this moment condition, Benjamini et al. (2013) suggested using ranks of distances, but this involves the selection of several tuning parameters, the choice of which is an open problem. The asymptotic properties of a test based on ranks of distances also need further investigation.
We propose using projection correlation to characterize dependence between 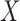 and
and  . Projection correlation first projects the multivariate random vectors into a series of univariate random variables, then detects nonlinear dependence by calculating the Pearson correlation between the dichotomized univariate random variables. The projection correlation between
. Projection correlation first projects the multivariate random vectors into a series of univariate random variables, then detects nonlinear dependence by calculating the Pearson correlation between the dichotomized univariate random variables. The projection correlation between 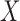 and
and  , denoted by
, denoted by  , is nonnegative and equals zero if and only if
, is nonnegative and equals zero if and only if  and
and  are independent, so it is generally applicable as an index for measuring the degree of nonlinear dependence without moment conditions, normality or ellipticity (Tracz et al., 1992). The projection correlation test for independence is consistent against all dependence alternatives. The projection correlation is free of tuning parameters and is invariant to orthogonal transformation. We shall show that the sample estimator of projection correlation is
are independent, so it is generally applicable as an index for measuring the degree of nonlinear dependence without moment conditions, normality or ellipticity (Tracz et al., 1992). The projection correlation test for independence is consistent against all dependence alternatives. The projection correlation is free of tuning parameters and is invariant to orthogonal transformation. We shall show that the sample estimator of projection correlation is  -consistent if
-consistent if  and
and  are independent and root-
are independent and root-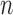 -consistent otherwise. We conduct Monte Carlo studies to evaluate the finite-sample performance of the projection correlation test. The results indicate that the projection correlation is less sensitive to the dimensions of
-consistent otherwise. We conduct Monte Carlo studies to evaluate the finite-sample performance of the projection correlation test. The results indicate that the projection correlation is less sensitive to the dimensions of  and
and 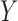 than the distance correlation and even its improved version (Székely & Rizzo, 2013), and is more powerful than both the distance correlation and ranks of distances, especially when the dimensions of
than the distance correlation and even its improved version (Székely & Rizzo, 2013), and is more powerful than both the distance correlation and ranks of distances, especially when the dimensions of 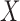 and
and  are relatively large or the moment conditions required by the distance correlation are violated.
are relatively large or the moment conditions required by the distance correlation are violated.
2. Projection correlation
2.1. Motivation
In this section, we propose a new measure of dependence between two random vectors. Testing that  and
and 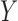 are independent is equivalent to testing whether
are independent is equivalent to testing whether 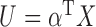 and
and  are independent for all unit vectors
are independent for all unit vectors  and
and  . Let
. Let 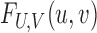 denote the joint distribution of
denote the joint distribution of  , and let
, and let  and
and  denote the marginal distributions of
denote the marginal distributions of 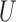 and
and  . Given
. Given 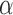 and
and 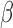 ,
, 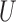 and
and 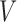 are independent if and only if
are independent if and only if 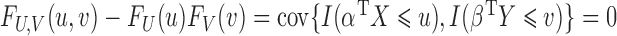 , for all
, for all 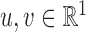 . Therefore, testing whether
. Therefore, testing whether 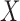 and
and 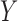 are independent amounts to testing whether
are independent amounts to testing whether
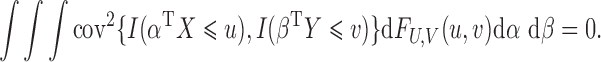 |
(1) |
Suppose that 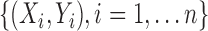 is a random sample of
is a random sample of 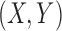 . Using the first five independent copies of
. Using the first five independent copies of 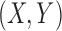 , we rewrite the left-hand side of (1) as
, we rewrite the left-hand side of (1) as
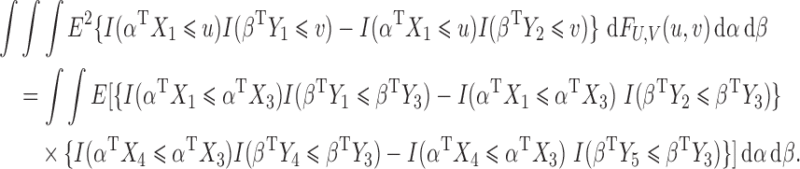 |
Consequently, by Fubini’s theorem, 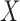 and
and 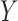 are independent if and only if
are independent if and only if
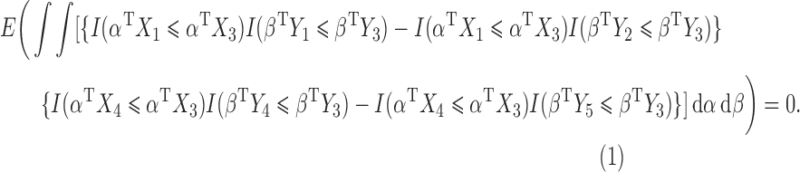 |
(2) |
In general, integration over the  -dimensional space
-dimensional space 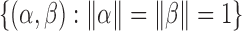 is not straightforward. Lemma 1 enables us to derive an explicit form for (2).
is not straightforward. Lemma 1 enables us to derive an explicit form for (2).
Lemma 1
(Escanciano, 2006). For two arbitrary vectors
, we have
where
,
is the gamma function and
is the inverse cosine function.
Lemma 1 yields an explicit formula for the left-hand side of (2). Ignoring the constants irrelevant to the joint distribution of  , we define the resultant explicit formula as the squared projection covariance between
, we define the resultant explicit formula as the squared projection covariance between  and
and  . To be precise, define
. To be precise, define
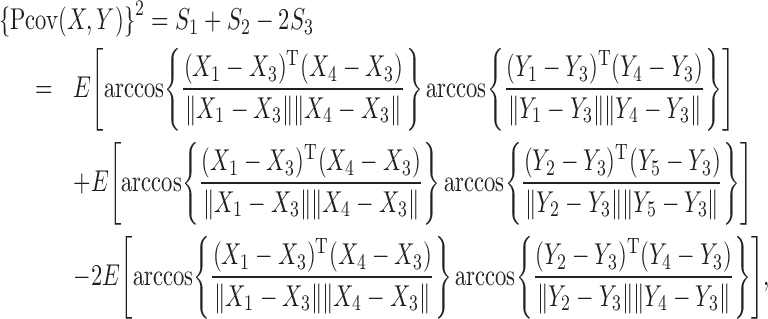 |
(3) |
where  ,
, 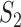 and
and 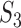 are defined in an obvious manner. We provide details of the derivation of (3) in the Appendix. A distinctive feature of
are defined in an obvious manner. We provide details of the derivation of (3) in the Appendix. A distinctive feature of 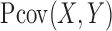 is that it uses only vectors of the form
is that it uses only vectors of the form 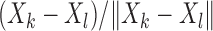 and
and  , whose second moments always equal unity, regardless of the dimensions of the random vectors. This indicates that the projection covariance removes the moment restrictions on
, whose second moments always equal unity, regardless of the dimensions of the random vectors. This indicates that the projection covariance removes the moment restrictions on 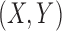 required by the distance correlation.
required by the distance correlation.
Define the projection correlation between 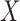 and
and  , denoted by
, denoted by  , as the square root of
, as the square root of
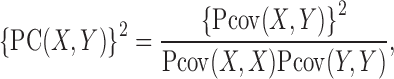 |
and set  if
if  or
or  . Proposition 1 presents the appealing properties of the projection correlation at the population level.
. Proposition 1 presents the appealing properties of the projection correlation at the population level.
Proposition 1.
(i) In general,
. In particular,
if and only if
and
are independent, and
if and only if
almost surely.
(ii) Let
and
be two orthonormal matrices,
and
be two vectors, and
and
be two scalars. Then
.
The first statement indicates that the projection correlation is generally applicable as an index to measure dependence. The second statement implies that, although it is not affine-invariant, the projection correlation is invariant with respect to the group of orthogonal transformations.
2.2. Asymptotic properties
We give two equivalent estimators for 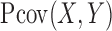 and study their asymptotic properties. The first estimate is built upon the
and study their asymptotic properties. The first estimate is built upon the 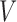 -statistic (Serfling, 1980), given by the square root of
-statistic (Serfling, 1980), given by the square root of
 |
Here 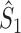 ,
, 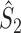 and
and 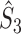 are defined in an obvious fashion and are the estimates of
are defined in an obvious fashion and are the estimates of  ,
,  and
and 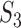 , respectively. The
, respectively. The 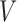 -statistic estimate appears natural, yet it is difficult to calculate (Székely & Rizzo, 2010). Therefore, we give an equivalent form below. Define, for
-statistic estimate appears natural, yet it is difficult to calculate (Székely & Rizzo, 2010). Therefore, we give an equivalent form below. Define, for 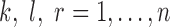 ,
,
 |
To avoid possible confusion, we define 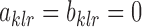 if
if 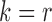 or
or 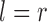 . The second sample estimate of
. The second sample estimate of 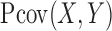 is defined by
is defined by
 |
Accordingly, the sample estimate of 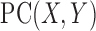 is defined by the square root of
is defined by the square root of
 |
In general, 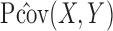 is easier to compute than
is easier to compute than  . Although it may not be immediately obvious that
. Although it may not be immediately obvious that 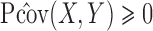 , this fact will become clear from Theorem 1.
, this fact will become clear from Theorem 1.
Theorem 1.
For a given random sample
,
and both equal
where
,
and
stand for the empirical distributions of
,
and
, respectively,
, and
.
The following theorems state the consistency of 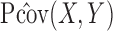 and
and 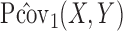 .
.
Theorem 2.
For a given random sample
,
almost surely.
Theorem 3.
(i) If
and
are independent, then as
,
converges in distribution to
where the
depend on the distribution of
and are nonnegative with sum equal to one, and the
are independent standard normal random variables.
(ii) If
and
are not independent, then
converges in distribution to a normal distribution with mean zero and variance
, where the random variable
is defined in (A2). Consequently,
diverges to
.
The projection correlation test is built upon the test statistic  , which converges in distribution to the quadratic form if
, which converges in distribution to the quadratic form if  and
and  are independent and diverges to
are independent and diverges to  otherwise. Theorem 3 suggests that the projection correlation test is consistent against all dependence alternatives without requiring any moment conditions. Because the weights
otherwise. Theorem 3 suggests that the projection correlation test is consistent against all dependence alternatives without requiring any moment conditions. Because the weights  in the quadratic form are unknown, the asymptotic null distribution is intractable. To put the projection correlation test into practice, we approximate the asymptotic null distribution of
in the quadratic form are unknown, the asymptotic null distribution is intractable. To put the projection correlation test into practice, we approximate the asymptotic null distribution of  through a random permutation method. Specifically, we calculate replicates of the test statistic under random permutations of the indices of the
through a random permutation method. Specifically, we calculate replicates of the test statistic under random permutations of the indices of the 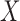 sample or, equivalently, the
sample or, equivalently, the 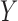 sample. The
sample. The 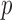 -value obtained from this permutation procedure is defined as the fraction of replicates of the test statistic under random permutations that are at least as large as the observed test statistic. Throughout our simulations, we use 2000 replications and obtain very good control of the Type I error rates. The permutation procedure is computationally feasible owing to the simple form of the test statistic. Computer code for implementing the projection correlation test and the permutation procedure is available from the authors upon request.
-value obtained from this permutation procedure is defined as the fraction of replicates of the test statistic under random permutations that are at least as large as the observed test statistic. Throughout our simulations, we use 2000 replications and obtain very good control of the Type I error rates. The permutation procedure is computationally feasible owing to the simple form of the test statistic. Computer code for implementing the projection correlation test and the permutation procedure is available from the authors upon request.
3. Simulations
In this section, we conduct simulations to compare the performance of independence tests based on the projection correlation, the distance correlation and the ranks of distances (Benjamini et al., 2013). These three tests are consistent and suitable for arbitrary dimensions. Because the distance-correlation-based test is sensitive to the dimensions of random vectors, throughout our simulations we use its improved version recommended by Székely & Rizzo (2013).
We consider three simulated examples in which the dimensions of both  and
and 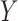 , denoted by
, denoted by 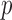 and
and  , respectively, are relatively large for the sample size
, respectively, are relatively large for the sample size  . We set
. We set  for simplicity. In Example 1, we set
for simplicity. In Example 1, we set 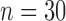 and vary
and vary 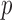 from 15 to 30. In Example 2, we set
from 15 to 30. In Example 2, we set 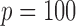 and vary
and vary 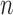 from 10 to 30. We also vary
from 10 to 30. We also vary 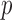 from 30 to 60 and
from 30 to 60 and 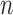 from 10 to 30. In Example 3, we set
from 10 to 30. In Example 3, we set  and vary
and vary 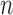 from 20 to 40. The dependence structure is monotone in Example 1 and nonmonotone in Example 2. The dependence structure is much more complicated in Example 3, where the random vectors are drawn from a mixture of distributions.
from 20 to 40. The dependence structure is monotone in Example 1 and nonmonotone in Example 2. The dependence structure is much more complicated in Example 3, where the random vectors are drawn from a mixture of distributions.
All simulations are implemented in R (R Development Core Team, 2017). We implement the test based on distance correlation by calling the dcor.ttest function in the energy package and the test based on ranks of distances by calling the hhg.test function in the HHG package. We repeat each setting 2000 times and report the size and power of the respective tests at significance levels  0·01 and 0·05.
0·01 and 0·05.
Example 1. We consider three scenarios in this example.
(1a) Draw
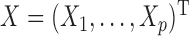 independently from a Cauchy distribution. Let
independently from a Cauchy distribution. Let 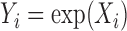 (
( ) and draw
) and draw 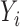 (
(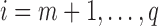 ) independently from a standard normal distribution.
) independently from a standard normal distribution.(1b) This is identical to scenario (1a), except that
 are sampled independently from the Cauchy distribution.
are sampled independently from the Cauchy distribution.(1c) This is identical to scenario (1a), except that
 , for
, for 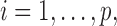 are sampled independently from a standard normal distribution.
are sampled independently from a standard normal distribution.
In the above scenarios, we set  , 2, 4, 6, 8 and 10, where
, 2, 4, 6, 8 and 10, where 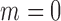 indicates that
indicates that 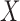 and
and 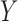 are independent. Table 1 charts the empirical size and power of the tests based on projection correlation, ranks of distances, and distance correlation at significance levels
are independent. Table 1 charts the empirical size and power of the tests based on projection correlation, ranks of distances, and distance correlation at significance levels 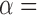 0·01 and 0·05. In all scenarios, the empirical sizes are very close to the significance levels, even when
0·01 and 0·05. In all scenarios, the empirical sizes are very close to the significance levels, even when 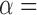 0·01. The test based on projection correlation has higher power than those based on distance correlation or ranks of distances, especially in scenarios (1a) and (1b), where the distributions of the random vectors are all heavy-tailed. The test based on distance correlation fails in the first two scenarios, partly because the moment restrictions required by this test are violated. The test based on ranks of distances is slightly worse than our test based on projection correlation.
0·01. The test based on projection correlation has higher power than those based on distance correlation or ranks of distances, especially in scenarios (1a) and (1b), where the distributions of the random vectors are all heavy-tailed. The test based on distance correlation fails in the first two scenarios, partly because the moment restrictions required by this test are violated. The test based on ranks of distances is slightly worse than our test based on projection correlation.
Table 1.
Empirical size and power 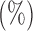 of the tests based on projection correlation, ranks of distances and distance correlation for different
of the tests based on projection correlation, ranks of distances and distance correlation for different  in Example 1 with
in Example 1 with 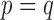 and
and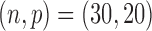 . All numbers reported in this table are multiplied by
. All numbers reported in this table are multiplied by
| Scenario |

|
Test |
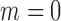
|
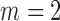
|

|
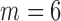
|
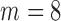
|
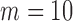
|
|---|---|---|---|---|---|---|---|---|
| (1a) |
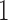
|
Projection correlation | 1·1 | 28·4 | 53·4 | 70·0 | 80·1 | 88·1 |
| Ranks of distances | 0·9 | 2·7 | 8·1 | 20·1 | 36·2 | 52·3 | ||
| Distance correlation | 1·3 | 2·9 | 3·4 | 4·1 | 4·2 | 4·4 | ||
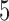
|
Projection correlation | 4·9 | 52·9 | 75·1 | 87·7 | 93·0 | 96·0 | |
| Ranks of distances | 4·9 | 11·2 | 25·1 | 42·2 | 60·4 | 75·2 | ||
| Distance correlation | 6·1 | 5·3 | 5·4 | 6·3 | 6·4 | 6·1 | ||
| (1b) |

|
Projection correlation | 1·2 | 20·8 | 41·7 | 61·5 | 76·3 | 84·8 |
| Ranks of distances | 0·9 | 2·3 | 8·0 | 19·5 | 35·3 | 51·3 | ||
| Distance correlation | 1·4 | 3·0 | 4·0 | 4·2 | 4·5 | 5·0 | ||
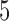
|
Projection correlation | 5·2 | 39·9 | 64·8 | 81·4 | 89·5 | 94·6 | |
| Ranks of distances | 5·2 | 8·3 | 21·1 | 38·8 | 60·4 | 76·1 | ||
| Distance correlation | 4·5 | 4·8 | 5·9 | 5·3 | 5·9 | 6·6 | ||
| (1c) |

|
Projection correlation | 1·0 | 65·1 | 98·8 | 100 | 100 | 100 |
| Ranks of distances | 0·9 | 20·3 | 58·9 | 87·1 | 96·6 | 99·5 | ||
| Distance correlation | 0·9 | 67·0 | 98·3 | 100 | 100 | 100 | ||

|
Projection correlation | 4·5 | 82·0 | 99·6 | 100 | 100 | 100 | |
| Ranks of distances | 4·7 | 37·7 | 79·6 | 96·2 | 99·1 | 100 | ||
| Distance correlation | 5·1 | 82·3 | 99·5 | 100 | 100 | 100 |
We also vary the dimensions of  and
and  from 15 to 30 and fix
from 15 to 30 and fix 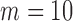 in scenarios (1a) and (1b) and
in scenarios (1a) and (1b) and  in scenario (1c). The simulation results are summarized in Table 2. The power of all tests diminishes quickly as
in scenario (1c). The simulation results are summarized in Table 2. The power of all tests diminishes quickly as  increases. Table 2 indicates that the test based on projection correlation is much less sensitive to the increase of dimensions than the other two tests.
increases. Table 2 indicates that the test based on projection correlation is much less sensitive to the increase of dimensions than the other two tests.
Table 2.
Power
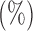 of the tests based on projection correlation, ranks of distances and distance correlation for different
of the tests based on projection correlation, ranks of distances and distance correlation for different
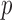 in Example
in Example
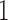 with
with
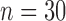 and
and
 . All numbers reported in this table are multiplied by
. All numbers reported in this table are multiplied by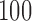
| Scenario |
|
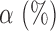
|
Test |
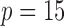
|
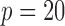
|
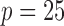
|

|
|---|---|---|---|---|---|---|---|
| (1a) | 10 |

|
Projection correlation | 98·2 | 88·1 | 74·1 | 59·5 |
| Ranks of distances | 81·6 | 52·3 | 35·6 | 24·2 | |||
| Distance correlation | 7·9 | 4·4 | 4·6 | 2·7 | |||
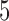
|
Projection correlation | 99·8 | 96·0 | 89·4 | 79·3 | ||
| Ranks of distances | 93·7 | 75·2 | 60·6 | 46·8 | |||
| Distance correlation | 10·5 | 6·1 | 6·0 | 4·0 | |||
| (1b) | 10 |

|
Projection correlation | 97·0 | 84·8 | 70·7 | 54·7 |
| Ranks of distances | 79·8 | 51·3 | 34·9 | 24·8 | |||
| Distance correlation | 7·6 | 5·0 | 3·1 | 2·5 | |||

|
Projection correlation | 99·5 | 94·6 | 87·4 | 77·6 | ||
| Ranks of distances | 93·7 | 76·1 | 60·3 | 45·5 | |||
| Distance correlation | 9·7 | 6·6 | 4·5 | 3·7 | |||
| (1c) | 2 |

|
Projection correlation | 78·1 | 65·1 | 53·1 | 43·1 |
| Ranks of distances | 31·7 | 20·3 | 13·7 | 9·2 | |||
| Distance correlation | 79·5 | 67·0 | 54·1 | 43·4 | |||

|
Projection correlation | 89·7 | 82·0 | 72·2 | 63·3 | ||
| Ranks of distances | 54·2 | 37·7 | 30·4 | 24·6 | |||
| Distance correlation | 90·2 | 82·3 | 73·0 | 63·5 |
Example 2. We draw  independently from the uniform distribution on
independently from the uniform distribution on  . We generate
. We generate  (
(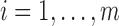 ), where the
), where the 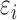 are generated from the Cauchy distribution, and generate
are generated from the Cauchy distribution, and generate  (
( ) independently from the standard normal distribution. This model was also used in Escanciano (2006) for different purposes. In this example,
) independently from the standard normal distribution. This model was also used in Escanciano (2006) for different purposes. In this example, 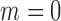 indicates that
indicates that 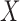 and
and 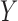 are independent.
are independent.
We first fix 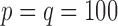 and vary
and vary 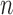 from 10 to 30. The empirical size and power are displayed in Table 3 for
from 10 to 30. The empirical size and power are displayed in Table 3 for 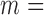 0, 5, 15 and 25 and
0, 5, 15 and 25 and 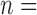 10, 20 and 30. All empirical sizes are close to the significance level. In this example, the moment conditions required by the test based on distance correlation are satisfied. The tests based on projection correlation and on distance correlation are more powerful than that based on ranks of distances, which appears to be very ineffective in this example, partly because the dependence structure is nonmonotone and the dependence strength is very weak.
10, 20 and 30. All empirical sizes are close to the significance level. In this example, the moment conditions required by the test based on distance correlation are satisfied. The tests based on projection correlation and on distance correlation are more powerful than that based on ranks of distances, which appears to be very ineffective in this example, partly because the dependence structure is nonmonotone and the dependence strength is very weak.
Table 3.
Empirical size and power
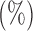 of the tests based on projection correlation, ranks of distances and distance correlation for different
of the tests based on projection correlation, ranks of distances and distance correlation for different
 in Example 2 with
in Example 2 with
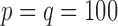

|

|
Test |
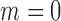
|
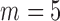
|

|

|
|---|---|---|---|---|---|---|
| 10 |
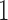
|
Projection correlation | 1·3 | 6·2 | 7·1 | 7·1 |
| Ranks of distances | 1·2 | 1·7 | 2·2 | 1·9 | ||
| Distance correlation | 1·3 | 6·2 | 6·5 | 5·7 | ||
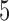
|
Projection correlation | 5·4 | 18·8 | 20·7 | 20·4 | |
| Ranks of distances | 4·3 | 7·6 | 7·3 | 7·2 | ||
| Distance correlation | 5·5 | 16·5 | 18·6 | 17·0 | ||
| 20 |
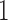
|
Projection correlation | 1·2 | 21·5 | 26·3 | 28·2 |
| Ranks of distances | 0·7 | 4·3 | 4·2 | 4·8 | ||
| Distance correlation | 1·0 | 18·7 | 20·2 | 23·2 | ||

|
Projection correlation | 5·4 | 46·4 | 52·4 | 55·8 | |
| Ranks of distances | 4·4 | 13·4 | 13·1 | 12·5 | ||
| Distance correlation | 5·2 | 40·5 | 43·3 | 45·2 | ||
| 30 |

|
Projection correlation | 1·4 | 50·6 | 63·5 | 63·4 |
| Ranks of distances | 0·9 | 8·2 | 9·3 | 9·5 | ||
| Distance correlation | 1·5 | 42·4 | 51·3 | 51·5 | ||
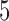
|
Projection correlation | 5·1 | 78·4 | 87·0 | 85·9 | |
| Ranks of distances | 4·7 | 21·0 | 24·1 | 23·0 | ||
| Distance correlation | 5·2 | 69·3 | 75·7 | 76·1 |
Next we fix 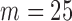 and vary
and vary 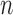 from 10 to 30 and
from 10 to 30 and 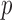 from 30 to 60. Table 4 shows that, provided
from 30 to 60. Table 4 shows that, provided  , say, the test based on projection correlation results in much less power loss across almost all scenarios as the dimensions of
, say, the test based on projection correlation results in much less power loss across almost all scenarios as the dimensions of 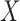 and
and  increase.
increase.
Table 4.
The power
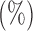 of the tests based on projection correlation, ranks of distances and distance correlation for different
of the tests based on projection correlation, ranks of distances and distance correlation for different
 in Example 2 with
in Example 2 with
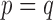
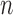
|
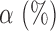
|
Test |
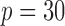
|
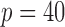
|
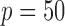
|
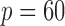
|
|---|---|---|---|---|---|---|
| 10 |
|
Projection correlation | 18·5 | 13·2 | 11·1 | 9·3 |
| Ranks of distances | 4·1 | 2·7 | 2·6 | 2·6 | ||
| Distance correlation | 14·9 | 11·1 | 8·5 | 7·5 | ||
|
Projection correlation | 42·8 | 34·4 | 28·4 | 26·2 | |
| Ranks of distances | 13·1 | 10·6 | 8·8 | 8·7 | ||
| Distance correlation | 34·9 | 27·6 | 23·7 | 21·7 | ||
| 20 |

|
Projection correlation | 79·7 | 67·7 | 53·6 | 47·0 |
| Ranks of distances | 20·1 | 15·9 | 10·8 | 8·7 | ||
| Distance correlation | 66·7 | 55·8 | 42·4 | 37·6 | ||
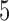
|
Projection correlation | 95·2 | 88·9 | 80·2 | 74·3 | |
| Ranks of distances | 39·6 | 31·8 | 24·5 | 22·3 | ||
| Distance correlation | 86·9 | 79·5 | 69·0 | 62·2 | ||
| 30 |
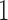
|
Projection correlation | 99·6 | 97·5 | 93·8 | 86·9 |
| Ranks of distances | 49·3 | 33·9 | 25·3 | 19·9 | ||
| Distance correlation | 97·6 | 92·1 | 85·6 | 75·9 | ||
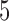
|
Projection correlation | 100 | 99·9 | 99·4 | 97·4 | |
| Ranks of distances | 72·6 | 55·9 | 45·8 | 38·6 | ||
| Distance correlation | 99·7 | 98·1 | 96·1 | 92·2 |
Example 3. This example was used in Benjamini et al. (2013). We fix  and vary
and vary 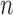 from 20 to 40. We draw
from 20 to 40. We draw 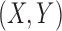 from a mixture distribution with 10 equally likely components. In the
from a mixture distribution with 10 equally likely components. In the 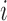 th component, for
th component, for 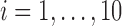 ,
, 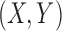 are random vectors
are random vectors  , where
, where 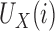 and
and 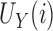 are sampled independently from a multivariate standard normal distribution, and
are sampled independently from a multivariate standard normal distribution, and 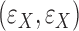 are sampled independently from a multivariate Cauchy or multivariate
are sampled independently from a multivariate Cauchy or multivariate  distribution with three degrees of freedom and the identity correlation matrix. The dependence of
distribution with three degrees of freedom and the identity correlation matrix. The dependence of  and
and 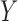 is through the fixed pairs
is through the fixed pairs 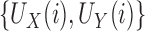 (
(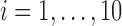 ), such that the data consist of ten clouds around these pairs.
), such that the data consist of ten clouds around these pairs.
The simulations are summarized in Table 5. The dependence of  and
and 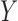 is through the ten equally likely components. The test based on projection correlation performs better than that based on distance correlation, especially when the moment requirements are not satisfied. The improved version of the test based on distance correlation is designed for high dimensions, and its performance appears satisfactory when the moments exist. Again, for the multivariate Cauchy distribution, the test based on projection correlation outperforms that based on distance correlation significantly in this example.
is through the ten equally likely components. The test based on projection correlation performs better than that based on distance correlation, especially when the moment requirements are not satisfied. The improved version of the test based on distance correlation is designed for high dimensions, and its performance appears satisfactory when the moments exist. Again, for the multivariate Cauchy distribution, the test based on projection correlation outperforms that based on distance correlation significantly in this example.
Table 5.
The power
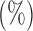 of the tests based on projection correlation, ranks of distances and distance correlation for different
of the tests based on projection correlation, ranks of distances and distance correlation for different 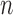 in Example 3 with
in Example 3 with

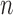
|
Test |
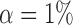
|

|
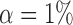
|
||
|---|---|---|---|---|---|---|
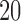
|
Projection correlation | 17·1 | 34·0 | 100 | 100 | |
| Ranks of distances | 1·5 | 6·3 | 5·9 | 16·4 | ||
| Distance correlation | 10·2 | 18·0 | 100 | 100 | ||

|
Projection correlation | 36·7 | 58·7 | 100 | 100 | |
| Ranks of distances | 1·9 | 8·8 | 10·0 | 30·5 | ||
| Distance correlation | 10·3 | 18·2 | 100 | 100 | ||

|
Projection correlation | 59·5 | 81·6 | 100 | 100 | |
| Ranks of distances | 2·1 | 9·2 | 15·3 | 42·4 | ||
| Distance correlation | 9·5 | 17·1 | 100 | 100 |
In our simulations, the test based on projection correlation exhibits a good capability for testing monotone and nonmonotone dependence. Our limited experience indicates that it is very effective, even when the second moments are large or infinite, it is useful for limiting the power loss as the dimensions of random vectors increase, and it is suitable even in high-dimensional cases.
Acknowledgement
The authors would like to thank Ms Amanda Applegate, the associate editor and two reviewers for their constructive comments. Li and Zhong are the corresponding authors. This research was supported by the National Natural Science Foundation of China, National Science Foundation of USA, Chinese Ministry of Education Project of Key Research Institute of Humanities and Social Sciences at Universities, National Institute of Drug Abuse and National Institutes of Health of USA, and National Youth Top-notch Talent Support Program of China.
Appendix
Proofs
We first show that by invoking Lemma 1 repeatedly, the squared projection covariance 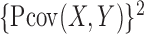 has an explicit form. In other words, we aim to show that
has an explicit form. In other words, we aim to show that
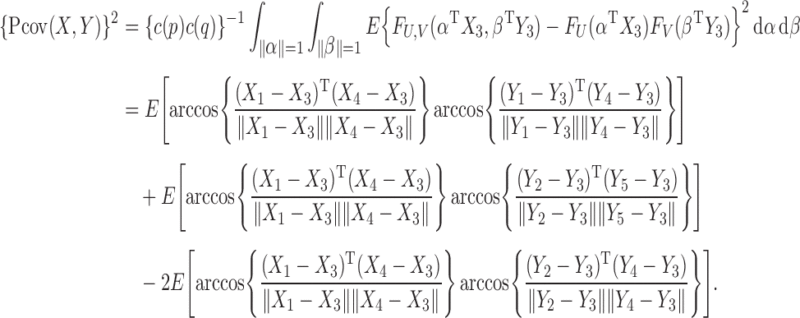 |
For notational clarity. we define
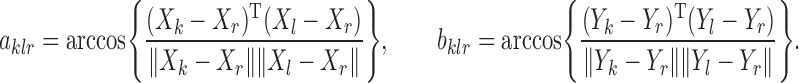 |
All the indices in  and
and 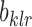 may take value 1, 2, 3, 4 or 5. Invoking Lemma 1 repeatedly, we obtain
may take value 1, 2, 3, 4 or 5. Invoking Lemma 1 repeatedly, we obtain
 |
The last equality follows from  and
and 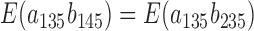 .
.
Proof of Proposition 1
We prove the first assertion. The statement that  is a direct consequence of the Cauchy–Schwarz inequality. By definition,
is a direct consequence of the Cauchy–Schwarz inequality. By definition, 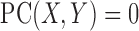 indicates that
indicates that  and
and 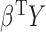 are independent for any
are independent for any 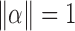 and
and 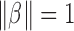 . In other words,
. In other words,  if and only if
if and only if  and
and  are statistically independent. In addition,
are statistically independent. In addition, 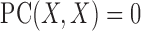 indicates that
indicates that  must be a constant vector, because otherwise
must be a constant vector, because otherwise 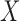 would not be independent of itself.
would not be independent of itself.
By definition, 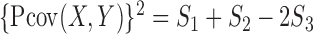 , and all the
, and all the  involve quantities of the form
involve quantities of the form  and
and 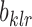 . It is easy to verify that both
. It is easy to verify that both 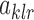 and
and 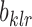 are invariant with respect to orthogonal transformations, which completes the proof of the second assertion.
are invariant with respect to orthogonal transformations, which completes the proof of the second assertion.
Proof of Theorem 1
We first prove that 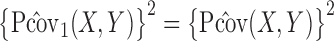 . Recall the definitions of
. Recall the definitions of 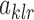 and
and  . Define
. Define
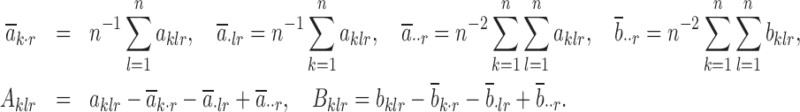 |
We further define
 |
It can be verified that  and
and  . It follows that
. It follows that
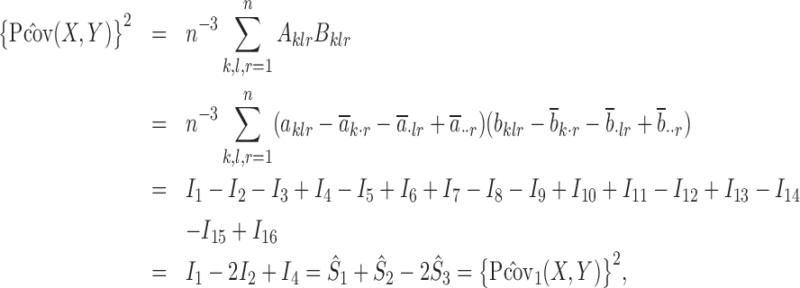 |
which completes the proof of the first part.
Next we prove that 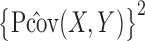 is equal to
is equal to
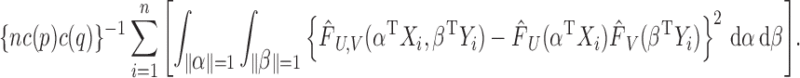 |
Invoking Lemma 1, we have
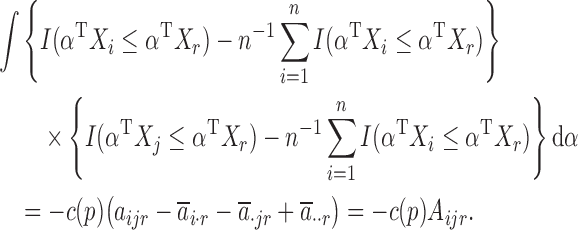 |
Following similar arguments, we obtain
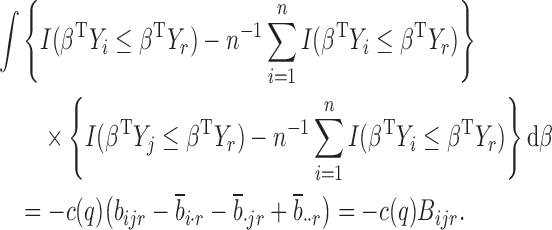 |
The above two results yield
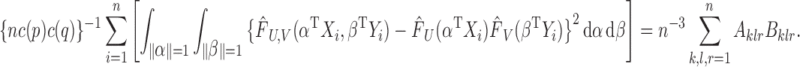 |
The proof of Theorem 1 is complete.
Proof of Theorem 2
By definition, 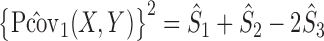 . By the strong law of large numbers for
. By the strong law of large numbers for 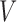 -statistics (Serfling, 1980), it follows that almost surely
-statistics (Serfling, 1980), it follows that almost surely 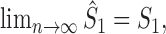
 and
and 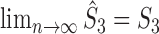 . Therefore,
. Therefore, 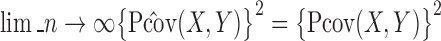 almost surely. This completes the proof.
almost surely. This completes the proof.
Proof of Theorem 3
Define the empirical process
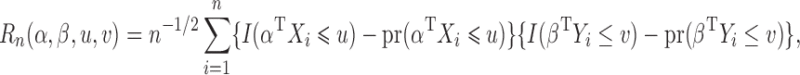 |
where 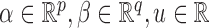 and
and  . When
. When 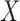 and
and 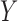 are independent,
are independent,  converges in distribution to a zero-mean Gaussian random process
converges in distribution to a zero-mean Gaussian random process 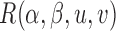 with covariance function
with covariance function
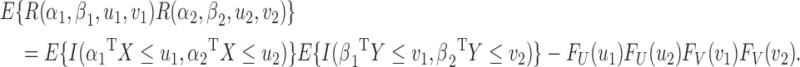 |
Next we define an approximation of  , denoted by
, denoted by 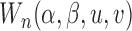 , as follows:
, as follows:
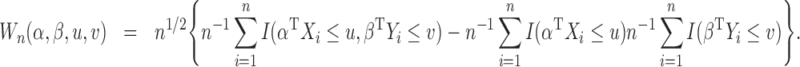 |
We first prove that  holds uniformly for
holds uniformly for  with
with  and
and 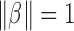 . It is easy to verify that
. It is easy to verify that
 |
Invoking the uniform law of large numbers of Jennrich (1969) or the generalization by Wolfowitz (1954) of the Glivenko–Cantelli theorem, we know that  uniformly for
uniformly for 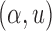 with
with  . Using Theorem 2.5.2 in van der Vaart & Wellner (1996), we can show that
. Using Theorem 2.5.2 in van der Vaart & Wellner (1996), we can show that 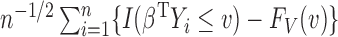 converges to a Gaussian process with zero mean and variance-covariance function
converges to a Gaussian process with zero mean and variance-covariance function 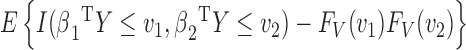 . Therefore,
. Therefore, 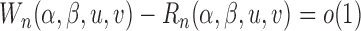 holds uniformly for
holds uniformly for  .
.
Using Theorem 2.5.2 in van der Vaart & Wellner (1996) again, we can show that the finite-dimensional distributions of 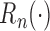 converge to
converge to 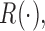 which implies that
which implies that 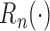 is asymptotically tight. Therefore, for a random continuous functional, Lemma 3.1 in Chang (1990) yields
is asymptotically tight. Therefore, for a random continuous functional, Lemma 3.1 in Chang (1990) yields
 |
and converges in distribution to 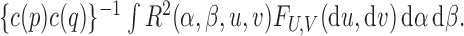 When
When 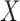 and
and 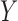 are independent,
are independent,  is a zero-mean process. According to Kuo (1975, Ch. 1, § 2),
is a zero-mean process. According to Kuo (1975, Ch. 1, § 2),
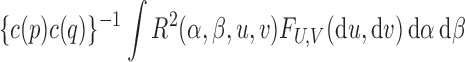 |
(A1) |
follows the same distribution as 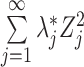 , where the
, where the 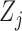 are independent standard normal random variables, and in general, the nonnegative constants
are independent standard normal random variables, and in general, the nonnegative constants  depend on the distribution of
depend on the distribution of  .
.
Next we derive the sum of the 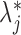 . In view of (A1), we easily find that
. In view of (A1), we easily find that
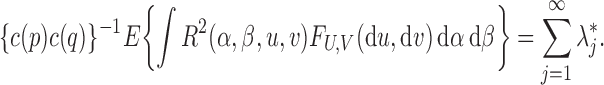 |
Next we calculate the sum of  . If
. If 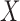 and
and  are independent, then
are independent, then
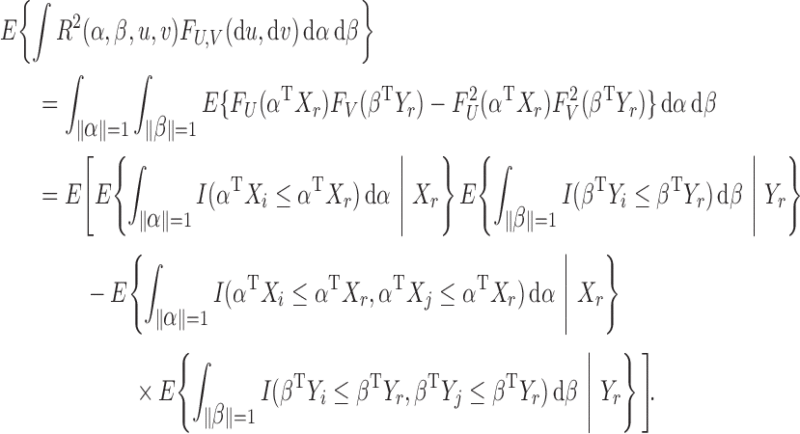 |
Using Lemma 1, the right-hand side of the above equation is equal to
 |
By the strong law of large numbers for 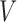 -statistics, we complete the proof of the first part.
-statistics, we complete the proof of the first part.
Next, we deal with the second part. We approximate  with the
with the  -statistics
-statistics 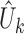 , which can be approximated with their projections. The projections of the
, which can be approximated with their projections. The projections of the 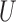 -statistics are averages of independent and identically distributed random variables, and thus the asymptotic normality follows. Define
-statistics are averages of independent and identically distributed random variables, and thus the asymptotic normality follows. Define  to be the number of
to be the number of 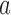 combinations from a set of
combinations from a set of  elements. Define the
elements. Define the  -statistic
-statistic
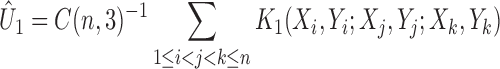 |
with the kernel  , where
, where 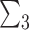 is the permutation of three distinct elements
is the permutation of three distinct elements  . Define the
. Define the  -statistic
-statistic
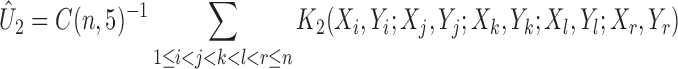 |
with the kernel 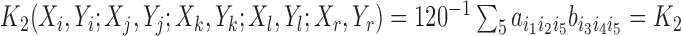 , where
, where  is the permutation of three distinct elements
is the permutation of three distinct elements 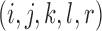 . Define the
. Define the 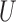 -statistic
-statistic
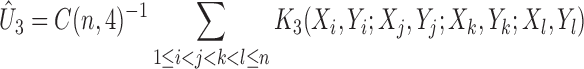 |
with the kernel 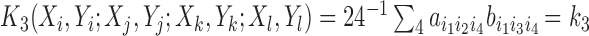 , where
, where 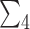 is the permutation of three distinct elements
is the permutation of three distinct elements  . Using standard
. Using standard  - and
- and 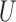 -statistic theory, we have
-statistic theory, we have
 |
where the 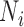 are the centralized projections of the
are the centralized projections of the 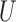 -statistics
-statistics 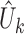 , which are defined as
, which are defined as
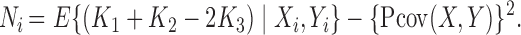 |
(A2) |
All the 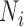 are independent and identically distributed. The second part of Theorem 3 can be proved with the classical central limit theorem
are independent and identically distributed. The second part of Theorem 3 can be proved with the classical central limit theorem
References
- Benjamini, Y., Madar, V. & Stark, P. B. (2013). A consistent multivariate test of association based on ranks of distances. Biometrika 100, 503–10. [Google Scholar]
- Blum, J. R. (1961). Distribution free tests of independence based on the sample distribution function. Ann. Math. Statist. 32, 485–98. [Google Scholar]
- Chang, M. N. (1990). Weak convergence of a self-consistent estimator of the survival function with doubly censored data. Ann. Statist. 18, 391–404. [Google Scholar]
- Escanciano, J. C. (2006). A consistent diagnostic test for regression models using projections. Economet. Theory 22, 1030–51. [Google Scholar]
- Gieser, P. W. & Randles, R. H. (1997). A nonparametric test of independence between two vectors. J. Am. Statist. Assoc. 92, 561–7. [Google Scholar]
- Hettmansperger, T. P. & Oja, H. (1994). Affine invariant multivariate multisample sign tests. J. R. Statist. Soc., B 56, 235–49. [Google Scholar]
- Hoeffding, W. (1948). A non-parametric test of independence. Ann. Math. Statist. 19, 546–57. [Google Scholar]
- Hotelling, H. (1936). Relations between two sets of variates. Biometrika 28, 321–77. [Google Scholar]
- Jennrich, R. I. (1969). Asymptotic properties of non-linear least squares estimators. Ann. Math. Statist. 40, 633–43. [Google Scholar]
- Kendall, M. G. (1938). A new measure of rank correlation. Biometrika 30, 81–93. [Google Scholar]
- Kuo, H. H. (1975). Gaussian Measures in Banach Spaces. Lecture Notes in Mathematics 463. Berlin: Springer. [Google Scholar]
- Puri, M. & Sen, P. (1971). Nonparametric Methods in Multivariate Analysis. New York: Wiley. [Google Scholar]
- R Development Core Team (2017). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. ISBN 3-900051-07-0, http://www.R-project.org.
- Serfling, R. L. (1980). Approximation Theorems in Mathematical Statistics. New York: Wiley. [Google Scholar]
- Spearman, C. (1904). The proof and measurement of association between two things. Am. J. Psychol. 15, 72–101. [PubMed] [Google Scholar]
- Székely, G. J. & Rizzo, M. L. (2010). Brownian distance covariance. Ann. Appl. Statist. 3, 1236–65. [Google Scholar]
-
Székely, G. J. & Rizzo, M. L. (2013). The distance correlation
 -test of independence in high dimension. J. Mult. Anal. 117, 193–213. [Google Scholar]
-test of independence in high dimension. J. Mult. Anal. 117, 193–213. [Google Scholar] - Székely, G. J., Rizzo, M. L. & Bakirov, N. K. (2007). Measuring and testing dependence by correlation of distances. Ann. Statist. 35, 2769–94. [Google Scholar]
- Taskinen, S., Kankainen, A. & Oja, H. (2003). Sign test of independence between two random vectors. Statist. Prob. Lett. 62, 9–21. [Google Scholar]
- Taskinen, S., Oja, H. & Randles, R. H. (2005). Multivariate nonparametric tests of independence. J. Am. Statist. Assoc. 100, 916–25. [Google Scholar]
- Tracz, S. M., Elmore, P. B. & Pohlmann, J. T. (1992). Correlational meta-analysis: Independent and nonindependent cases. Educ. Psychol. Meas. 52, 879–88. [Google Scholar]
- van der Vaart, A. W. & Wellner, J. A. (1996). Weak Convergence and Empirical Processes. New York: Springer. [Google Scholar]
-
Wilks, S. S. (1935). On the independence of
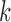 sets of normally distributed statistical variables. Econometrica 3, 309–26. [Google Scholar]
sets of normally distributed statistical variables. Econometrica 3, 309–26. [Google Scholar] - Wolfowitz, J. (1954). Generalization of the theorem of Glivenko–Cantelli. Ann. Math. Statist. 25, 131–8. [Google Scholar]