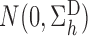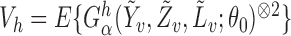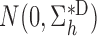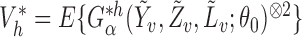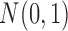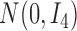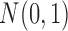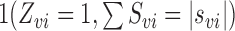Abstract
We consider inference about the causal effect of a treatment or exposure in the presence of interference, i.e., when one individual’s treatment affects the outcome of another individual. In the observational setting where the treatment assignment mechanism is not known, inverse probability-weighted estimators have been proposed when individuals can be partitioned into groups such that there is no interference between individuals in different groups. Unfortunately this assumption, which is sometimes referred to as partial interference, may not hold, and moreover existing weighted estimators may have large variances. In this paper we consider weighted estimators that could be employed when interference is present. We first propose a generalized inverse probability-weighted estimator and two Hájek-type stabilized weighted estimators that allow any form of interference. We derive their asymptotic distributions and propose consistent variance estimators assuming partial interference. Empirical results show that one of the Hájek estimators can have substantially smaller finite-sample variance than the other estimators. The different estimators are illustrated using data on the effects of rotavirus vaccination in Nicaragua.
Keywords: Causal inference, Interference, Inverse probability-weighted estimator, Observational study
1. Introduction
In causal inference it is often assumed that there is no interference between individuals, i.e., that the treatment of one individual does not affect the outcome of another. However, this assumption may not hold. For instance, in infectious disease studies, the vaccination status of one individual may affect whether another individual becomes infected (Halloran & Struchiner, 1995). Similarly, encouraging one individual to vote may increase the likelihood that another individual in the same household will vote (Nickerson, 2008). Interference may also occur between students in the same classroom (Hong & Raudenbush, 2006) or between households in the same neighbourhood (Sobel, 2006), and in myriad other contexts (Rosenbaum, 2007; Luo et al., 2012; Manski, 2013).
Inference in the presence of interference is interesting, because a treatment may have multiple types of effects, but difficult, because individuals may have many potential outcomes. Recently, methods have been developed for the setting where individuals can be partitioned into groups such that there may be interference between individuals in the same group but not between individuals in different groups; this is sometimes called partial interference (Sobel, 2006). Assuming partial interference, Hudgens & Halloran (2008) defined the direct, indirect, total and overall causal effects of a treatment in randomized studies. Inference about these types of causal effects has subsequently been considered by VanderWeele & Tchetgen Tchetgen (2011), VanderWeele et al. (2012), Halloran & Hudgens (2012), Liu & Hudgens (2014) and P. M. Aronow and C. Samii in an unpublished 2013 paper (arXiv:1305.6156), among others. For observational settings where the treatment assignment mechanism is not known, Tchetgen Tchetgen & VanderWeele (2012) proposed inverse probability-weighted estimators of these causal effects based on group-level propensity scores. These weighted estimators can be viewed as a generalization of the usual inverse probability-weighted estimator of the causal effect of a treatment in the absence of interference. However, in general, weighted estimators are known to have relatively large variance. Additionally, in some settings the partial interference assumption may be dubious. In this article we consider alternative weighted-type estimators that allow for general forms of interference and tend to be less variable.
2. Preliminaries
Consider a finite population of 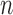 individuals, and suppose that each individual may receive some treatment or exposure. Let
individuals, and suppose that each individual may receive some treatment or exposure. Let 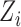 (
(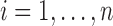 ) be the random variable such that
) be the random variable such that 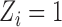 if individual
if individual 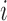 received treatment and
received treatment and 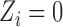 otherwise. Suppose that interference may be present between the
otherwise. Suppose that interference may be present between the 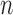 individuals, and define the interference set
individuals, and define the interference set 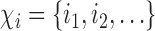 for individual
for individual 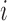 to be an ordered set of all other individuals whose treatment received might affect the outcome of individual
to be an ordered set of all other individuals whose treatment received might affect the outcome of individual 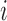 . Assume that there is no interference between individual
. Assume that there is no interference between individual 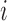 and individuals not in
and individuals not in 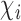 . There may or may not be interference between individual
. There may or may not be interference between individual 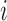 and individuals in
and individuals in 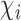 . A central goal of the inferential methods described below is to quantify the extent to which such interference is present. Let
. A central goal of the inferential methods described below is to quantify the extent to which such interference is present. Let 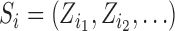 denote the vector of treatment indicators for individuals that possibly interfere with individual
denote the vector of treatment indicators for individuals that possibly interfere with individual 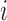 ; that is, the outcome of individual
; that is, the outcome of individual 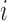 is allowed to depend not only on
is allowed to depend not only on 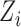 but also on
but also on 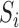 . For example, if the outcome of individual 1 possibly depends on their own treatment status as well as that of individuals 2 and 3 but not on that of individuals
. For example, if the outcome of individual 1 possibly depends on their own treatment status as well as that of individuals 2 and 3 but not on that of individuals 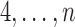 , then
, then 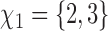 and
and 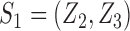 . The interference sets
. The interference sets 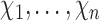 are assumed to be known a priori. Denote possible values of
are assumed to be known a priori. Denote possible values of 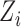 and
and 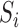 by
by 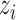 and
and 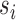 . Let
. Let 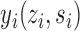 denote the potential outcome of individual
denote the potential outcome of individual 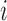 if they receive treatment
if they receive treatment 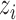 and their interference set receives
and their interference set receives 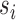 . This potential outcome notation is general enough to encompass any possible interference structure, of which partial interference is a special case. Let
. This potential outcome notation is general enough to encompass any possible interference structure, of which partial interference is a special case. Let 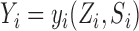 denote the observed outcome. The potential outcomes
denote the observed outcome. The potential outcomes 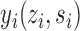 are assumed to be deterministic functions of
are assumed to be deterministic functions of 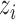 and
and 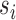 , and the observed outcome
, and the observed outcome 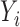 is considered to be random because it depends on the random variables
is considered to be random because it depends on the random variables 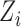 and
and 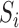 . Let
. Let 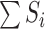 be the sum over all the components of
be the sum over all the components of 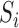 , and let
, and let 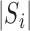 denote the dimension of the vector
denote the dimension of the vector 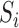 . For example, if
. For example, if 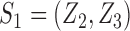 , then
, then 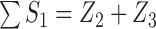 and
and 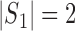 .
.
In the absence of interference, a common causal estimand is the average treatment effect, which contrasts the average outcome for the counterfactual scenario where every individual in the population is treated with that of the counterfactual scenario where every individual in the population is not treated. Similarly, in the presence of interference, causal estimands can be defined in terms of counterfactual scenarios corresponding to different treatment allocation strategies (e.g., Hong & Raudenbush, 2006; Sobel, 2006; Hudgens & Halloran, 2008; Tchetgen Tchetgen & VanderWeele, 2012). For example, the indirect effect, defined formally below, contrasts average outcomes of untreated individuals for the counterfactual scenario where one allocation strategy is adopted in the population with those for the counterfactual scenario where some other allocation strategy is adopted in the population. Such estimands quantify interference, if present, at the population level and can be used to inform policy decisions regarding a treatment or exposure. The allocation strategy of interest will in general depend on the setting.
Here we consider Bernoulli allocation strategies proposed by Tchetgen Tchetgen & Vander-Weele (2012), where strategy 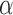 corresponds to the counterfactual scenario in which individuals independently receive treatment with probability
corresponds to the counterfactual scenario in which individuals independently receive treatment with probability 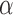 . It is not assumed that the observed treatment indicators
. It is not assumed that the observed treatment indicators 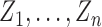 are independent Bernoulli random variables; rather, the distribution of treatment under Bernoulli allocation is used below to define the counterfactual estimands of interest. By analogy, direct standardization of mortality rates could entail using the 2010 United States census age distribution, which may differ from the age distribution giving rise to the observed data. Corresponding to Bernoulli allocation, let
are independent Bernoulli random variables; rather, the distribution of treatment under Bernoulli allocation is used below to define the counterfactual estimands of interest. By analogy, direct standardization of mortality rates could entail using the 2010 United States census age distribution, which may differ from the age distribution giving rise to the observed data. Corresponding to Bernoulli allocation, let 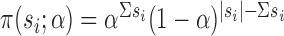 denote the probability of the interference set for individual
denote the probability of the interference set for individual 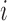 receiving treatment
receiving treatment 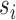 under allocation strategy
under allocation strategy 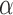 . Let
. Let 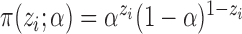 and
and 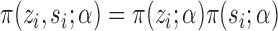 denote, respectively, the probability of individual
denote, respectively, the probability of individual 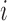 receiving treatment
receiving treatment 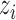 and the probability of individual
and the probability of individual 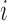 together with their interference set receiving joint treatment
together with their interference set receiving joint treatment 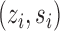 under allocation strategy
under allocation strategy 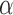 . Define
. Define 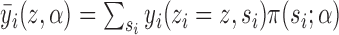 to be the average potential outcome of individual
to be the average potential outcome of individual 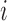 under allocation strategy
under allocation strategy 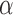 , where the summation is over all
, where the summation is over all 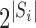 possible values of
possible values of 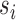 . Returning to the example where
. Returning to the example where 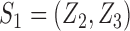 , the average potential outcome of individual 1 is a weighted average of potential outcomes under different combinations of treatment
, the average potential outcome of individual 1 is a weighted average of potential outcomes under different combinations of treatment 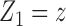 and
and 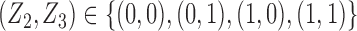 , with the weights being the corresponding probabilities under Bernoulli allocation. Averaging over all individuals, define the population average potential outcome as
, with the weights being the corresponding probabilities under Bernoulli allocation. Averaging over all individuals, define the population average potential outcome as 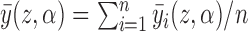 . Similarly, define the marginal average potential outcome for individual
. Similarly, define the marginal average potential outcome for individual 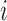 under allocation strategy
under allocation strategy 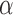 by
by 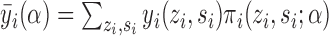 and define the population marginal average potential outcome as
and define the population marginal average potential outcome as 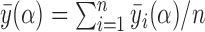 .
.
Various causal effects can be defined by contrasts in the population average potential outcomes. In particular, define the direct effect of treatment under allocation strategy 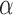 to be
to be 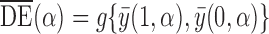 , where
, where 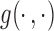 is some continuous contrast function. A commonly used contrast function is
is some continuous contrast function. A commonly used contrast function is 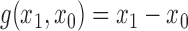 ; in vaccine trials with a binary outcome it is typical to use
; in vaccine trials with a binary outcome it is typical to use 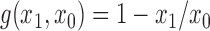 . The direct effect compares the average potential outcomes when an individual receives treatment versus not under allocation strategy
. The direct effect compares the average potential outcomes when an individual receives treatment versus not under allocation strategy 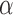 . For two allocation strategies
. For two allocation strategies 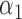 and
and  , let
, let 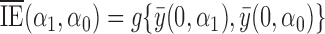 be the indirect or spillover effect, which contrasts average potential outcomes when individuals do not receive treatment under different allocation strategies. In the context of vaccines, the indirect effect is sometimes referred to as herd immunity and describes the effect of the proportion of individuals vaccinated, e.g., 30% versus 50%, on the average outcome among unvaccinated individuals. An indirect effect can also be defined for when individuals receive treatment,
be the indirect or spillover effect, which contrasts average potential outcomes when individuals do not receive treatment under different allocation strategies. In the context of vaccines, the indirect effect is sometimes referred to as herd immunity and describes the effect of the proportion of individuals vaccinated, e.g., 30% versus 50%, on the average outcome among unvaccinated individuals. An indirect effect can also be defined for when individuals receive treatment, 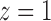 , but for simplicity we do not consider such indirect effects here. The total effect
, but for simplicity we do not consider such indirect effects here. The total effect 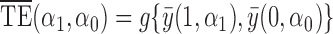 incorporates both direct and indirect effects, and reflects the difference between the average potential outcomes when individuals receive treatment under one allocation strategy versus when they go without treatment under another allocation strategy. Finally, define
incorporates both direct and indirect effects, and reflects the difference between the average potential outcomes when individuals receive treatment under one allocation strategy versus when they go without treatment under another allocation strategy. Finally, define 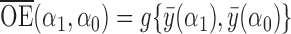 to be the overall effect, which describes the contrast in average outcomes under one allocation strategy relative to another.
to be the overall effect, which describes the contrast in average outcomes under one allocation strategy relative to another.
3. Inverse probability-weighted and hájek-type estimators
In this section we propose inverse probability-weighted and Hájek-type estimators which allow for general interference; that is, no assumption is made regarding the structure or form of interference that might be present. When there is partial interference and the groups are of the same size, the inverse probability-weighted estimators defined below reduce to those proposed by Tchetgen Tchetgen & VanderWeele (2012). Aronow and Samii (arXiv:1305.6156) considered similar estimators in the setting where interference may be present, but where treatment is assigned randomly according to a known experimental design.
Let 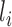 denote a vector of pretreatment covariates of individual
denote a vector of pretreatment covariates of individual 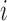 , and let
, and let 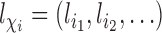 . Assume that conditional on covariates
. Assume that conditional on covariates 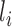 , the treatment allocation for individual
, the treatment allocation for individual 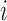 is independent of all potential outcomes and other covariates; that is,
is independent of all potential outcomes and other covariates; that is, 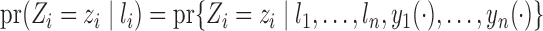 . Likewise, assume
. Likewise, assume 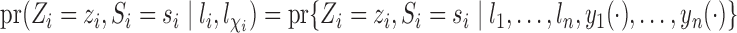 . Define
. Define 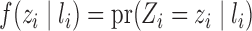 and
and 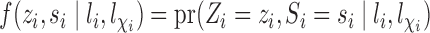 to be the propensity scores of individual
to be the propensity scores of individual 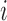 and of individual
and of individual 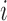 and their interference set, respectively. Assume that
and their interference set, respectively. Assume that 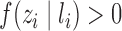 and
and 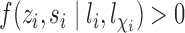 for all
for all 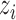 ,
, 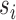 ,
, 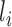 and
and 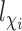 . Define the inverse probability-weighted estimator for treatment
. Define the inverse probability-weighted estimator for treatment 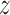 under allocation strategy
under allocation strategy 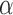 to be
to be
| (1) |
and define the inverse probability-weighted marginal estimator under strategy 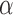 to be
to be
| (2) |
where 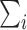 means
means 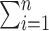 . If the propensity scores are known, then (1) and (2) are unbiased as stated in the following proposition.
. If the propensity scores are known, then (1) and (2) are unbiased as stated in the following proposition.
Proposition 1.
If
is known for all
, then
and
.
In the absence of interference, the Hájek (1971) estimator of the mean of a finite population replaces the denominator 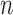 of the Horvitz & Thompson (1952) inverse probability-weighted estimator with the sum of the inverse of the sampling probabilities, which tends to reduce the variance relative to the Horvitz–Thompson estimator. Returning to the current context, let
of the Horvitz & Thompson (1952) inverse probability-weighted estimator with the sum of the inverse of the sampling probabilities, which tends to reduce the variance relative to the Horvitz–Thompson estimator. Returning to the current context, let 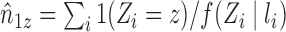 and note that
and note that 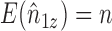 even if interference is present. This suggests replacing
even if interference is present. This suggests replacing 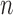 in (1) with
in (1) with 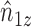 to obtain a stabilized Hájek-type estimator. Alternatively, notice that the weighted estimator (1) involves
to obtain a stabilized Hájek-type estimator. Alternatively, notice that the weighted estimator (1) involves 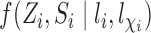 , which suggests replacing
, which suggests replacing 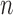 with the unbiased estimator
with the unbiased estimator 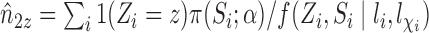 instead. Therefore, we will consider two different Hájek-type estimators of the population average outcome for treatment
instead. Therefore, we will consider two different Hájek-type estimators of the population average outcome for treatment 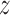 and allocation strategy
and allocation strategy 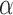 , defined by
, defined by
Here and below we assume that there exists at least one 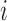 such that
such that 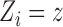 for
for 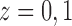 . Similarly, let
. Similarly, let 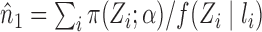 and
and 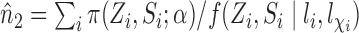 , and note that
, and note that 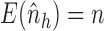
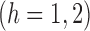 , which suggests the following estimators of the population average marginal outcome for allocation strategy
, which suggests the following estimators of the population average marginal outcome for allocation strategy 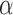 :
:
Note that 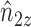 ,
, 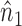 and
and 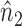 depend on
depend on 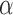 , but we suppress this dependence for notational convenience. In what follows,
, but we suppress this dependence for notational convenience. In what follows, 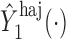 and
and 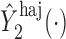 will be referred to as the Hájek 1 and Hájek 2 estimators.
will be referred to as the Hájek 1 and Hájek 2 estimators.
An appealing property of 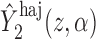 and
and 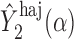 is the preservation of the bounds of the potential outcome
is the preservation of the bounds of the potential outcome 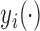 . Specifically, suppose there exist constants
. Specifically, suppose there exist constants 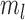 and
and 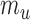 such that
such that 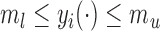
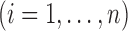 ; then
; then 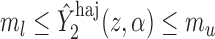 and
and 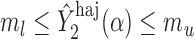 . For example, if
. For example, if 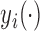 is binary, then
is binary, then 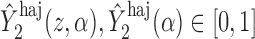 . In contrast, preservation of the bounds is not guaranteed for
. In contrast, preservation of the bounds is not guaranteed for 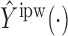 or
or 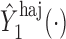 .
.
Another attractive property of the Hájek 2 estimators is preservation of linear transformations of the outcome. In particular, suppose that the observed outcomes 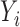 are transformed by the function
are transformed by the function 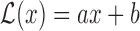
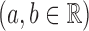 . Then Hájek 2 estimators computed using the transformed responses will equal
. Then Hájek 2 estimators computed using the transformed responses will equal 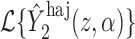 and
and 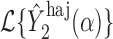 , where
, where 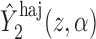 and
and 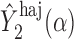 are computed on the original, untransformed observed outcomes. In contrast, the inverse probability-weighted and Hájek 1 estimators have this property only when
are computed on the original, untransformed observed outcomes. In contrast, the inverse probability-weighted and Hájek 1 estimators have this property only when 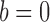 .
.
Define 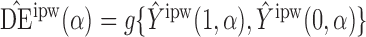 to be the inverse probability-weighted estimator of the direct effect. Define
to be the inverse probability-weighted estimator of the direct effect. Define 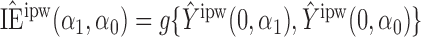 ,
, 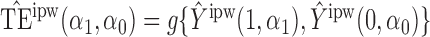 and
and 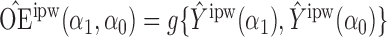 to be the weighted estimators of the indirect, total and overall effects. Hájek-type causal effect estimators are defined similarly. For example, define Hájek-type estimators of the direct effect by
to be the weighted estimators of the indirect, total and overall effects. Hájek-type causal effect estimators are defined similarly. For example, define Hájek-type estimators of the direct effect by 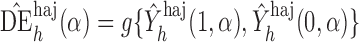
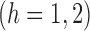 . If the contrast function is
. If the contrast function is 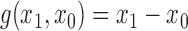 , then by the property described in the preceding paragraph, the values of Hájek 2 causal effect estimators are invariant under location shift. This is not the case for the inverse probability-weighted and Hájek 1 causal effect estimators.
, then by the property described in the preceding paragraph, the values of Hájek 2 causal effect estimators are invariant under location shift. This is not the case for the inverse probability-weighted and Hájek 1 causal effect estimators.
4. Asymptotic distributions
In this section the large-sample properties of the inverse probability-weighted and Hájek-type estimators are derived assuming partial interference. In particular, assume that individuals can be partitioned into groups such that there is no interference between individuals in different groups. Within groups no additional structure is assumed regarding interference, so there may be interference between any two individuals within a group. That is, we assume the following.
Assumption 1.
There exists a partition
of
such that
(
;
).
Let  denote the number of individuals in group
denote the number of individuals in group 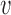 . Let
. Let 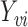 denote the observed outcome for individual
denote the observed outcome for individual 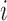 in group
in group 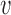 , and write
, and write 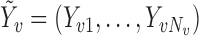 . Let
. Let 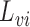 and
and 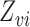 denote the observed covariates and treatment for individual
denote the observed covariates and treatment for individual 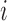 in group
in group 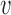 , and define
, and define 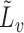 and
and 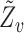 analogously to
analogously to 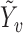 . Assume that
. Assume that 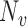 is one of the baseline covariates included in
is one of the baseline covariates included in 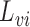 .
.
To derive the large-sample properties of the inverse probability-weighted and Hájek-type estimators, assume that the 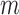 groups are a random sample from an infinite superpopulation of groups such that the observable random variables
groups are a random sample from an infinite superpopulation of groups such that the observable random variables 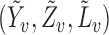
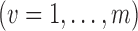 are independent and identically distributed. Let
are independent and identically distributed. Let 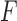 denote the distribution function of
denote the distribution function of 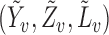 .
.
Let 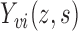 denote the potential outcome for individual
denote the potential outcome for individual 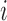 in group
in group 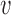 , where
, where 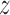 denotes treatment received by individual
denotes treatment received by individual 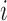 and
and 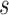 denotes the vector of treatment indicators for all other individuals in group
denotes the vector of treatment indicators for all other individuals in group 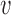 . Unlike in
. Unlike in 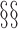 2 and 3, here the potential outcomes are considered random variables because of the assumed random sampling of the
2 and 3, here the potential outcomes are considered random variables because of the assumed random sampling of the 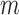 groups from a superpopulation. Denote the observed outcome for individual
groups from a superpopulation. Denote the observed outcome for individual 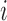 by
by 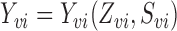 , where
, where 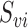 is the subvector of
is the subvector of 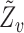 with
with 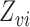 removed. Note that
removed. Note that 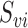 is a function of
is a function of 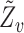 , which for notational simplicity is left implicit. Assume conditional exchangeability, i.e.,
, which for notational simplicity is left implicit. Assume conditional exchangeability, i.e., 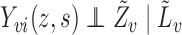 , where
, where 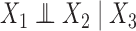 means that
means that 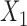 and
and 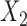 are independent conditional on
are independent conditional on 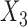 .
.
Under Assumption 1, the inverse probability-weighted estimator for treatment 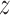 and strategy
and strategy 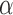 equals
equals
which can be expressed as a solution for 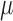 to the estimating equation
to the estimating equation 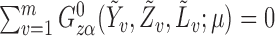 , where
, where
Let 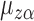 be the solution to
be the solution to 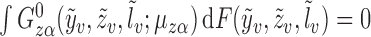 . It is straightforward to show that
. It is straightforward to show that 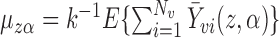 , where
, where 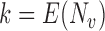 is the mean group size in the superpopulation and
is the mean group size in the superpopulation and 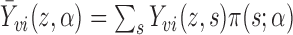 , with the summation being taken over all vectors
, with the summation being taken over all vectors 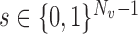 . If
. If 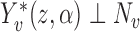 where
where 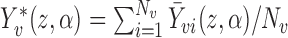 , i.e., if the average potential outcome within a group is independent of the number of individuals within the group, then
, i.e., if the average potential outcome within a group is independent of the number of individuals within the group, then 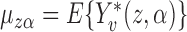 . In other words,
. In other words, 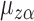 is the mean group average potential outcome in the superpopulation, analogous to
is the mean group average potential outcome in the superpopulation, analogous to 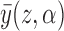 defined in
defined in  2. Define the direct effect in the superpopulation by
2. Define the direct effect in the superpopulation by 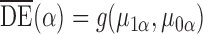 ; the indirect, total and overall effects in the superpopulation can be defined analogously.
; the indirect, total and overall effects in the superpopulation can be defined analogously.
The Hájek-type estimators can also be expressed as solutions to estimation equations. Specifically, under Assumption 1,
where now
It follows that 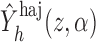 solves
solves 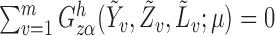 , where
, where
It is straightforward to show that 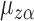 also satisfies
also satisfies 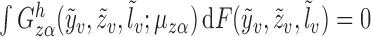
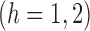 .
.
The asymptotic distributions of the inverse probability-weighted and Hájek-type estimators can be derived from standard estimating equation theory (Stefanski & Boos, 2002; Perez-Heydrich et al., 2014). For example, the proposition below establishes that the three direct effect estimators are asymptotically normal and gives closed-form expressions for the asymptotic variances when the propensity scores are known. The proposition entails the vector estimating equation 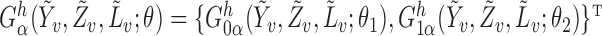 , where
, where 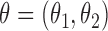 .
.
Proposition 2.
Suppose that Assumption 1 holds, the propensity scores are known, and the regularity assumptions in the Appendix hold. Then
converges in distribution to
and
converges in distribution to
as
, where
with
,
and
; here
.
A comparison between 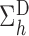
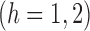 and
and 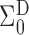 explains why the Hájek-type estimators can vary less than the inverse probability-weighted estimator. For example, suppose that the contrast
explains why the Hájek-type estimators can vary less than the inverse probability-weighted estimator. For example, suppose that the contrast 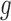 is the difference function. Denote
is the difference function. Denote 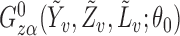 by
by 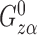 and note that
and note that 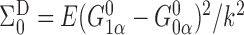 and
and 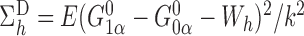
 , where
, where 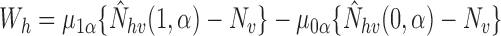 with
with 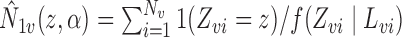 and
and 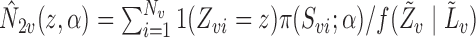 . Thus, the Hájek estimators will have smaller asymptotic variance if and only if
. Thus, the Hájek estimators will have smaller asymptotic variance if and only if 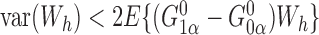 , and so are expected to be less variable when
, and so are expected to be less variable when 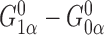 and
and 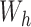 are strongly correlated. In the extreme scenario of
are strongly correlated. In the extreme scenario of 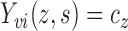
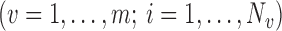 , we have
, we have 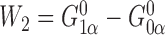 and
and 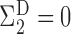 but
but 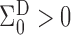 in general.
in general.
In observational studies, the mechanism by which individuals select treatment is in general not known, so that 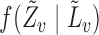 and
and 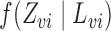 must be estimated in order to construct inverse probability-weighted estimators. In practice, due to the curse of dimensionality, one might assume a parametric model for the propensity scores (Tchetgen Tchetgen & VanderWeele, 2012). Let
must be estimated in order to construct inverse probability-weighted estimators. In practice, due to the curse of dimensionality, one might assume a parametric model for the propensity scores (Tchetgen Tchetgen & VanderWeele, 2012). Let 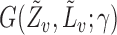 denote the score function for the likelihood under the assumed propensity score model indexed by a finite-dimensional parameter vector
denote the score function for the likelihood under the assumed propensity score model indexed by a finite-dimensional parameter vector 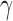 , and let
, and let 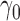 denote the true parameter value, which is the solution to
denote the true parameter value, which is the solution to 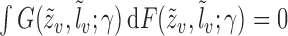 . Now consider the vector estimating equation
. Now consider the vector estimating equation 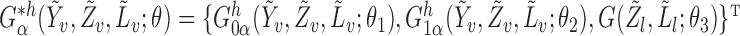
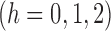 where
where 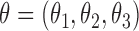 .
.
Proposition 3.
Suppose that Assumption 1 holds, the parametric propensity score model is correctly specified, and the regularity assumptions in the Appendix hold. Then
converges in distribution to
and
converges in distribution to
as
, where
with
,
and
; here
,
denotes the
zero vector, and
is the dimension of
.
Proposition 3 establishes the asymptotic normality of 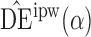 ,
, 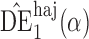 and
and 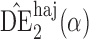 when the propensity score is correctly modelled. The asymptotic variance can be estimated consistently using empirical sandwich estimators, i.e., by replacing
when the propensity score is correctly modelled. The asymptotic variance can be estimated consistently using empirical sandwich estimators, i.e., by replacing 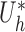 and
and 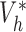 with their empirical counterparts (Stefanski & Boos, 2002). In the Appendix the asymptotic variance of
with their empirical counterparts (Stefanski & Boos, 2002). In the Appendix the asymptotic variance of 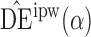 when the propensity score is estimated is shown to be no greater than when the propensity score is known. This is analogous to the well-known result about weighted estimators in the absence of interference; that is, even if the propensity scores are known, it is more efficient to use estimates of the propensity scores when computing inverse probability-weighted estimators. This relationship between the asymptotic variances when the propensity scores are known and when they are unknown but correctly modelled also holds for the Hájek-type estimators. Asymptotic normality of the indirect, total and overall effect estimators can be derived similarly.
when the propensity score is estimated is shown to be no greater than when the propensity score is known. This is analogous to the well-known result about weighted estimators in the absence of interference; that is, even if the propensity scores are known, it is more efficient to use estimates of the propensity scores when computing inverse probability-weighted estimators. This relationship between the asymptotic variances when the propensity scores are known and when they are unknown but correctly modelled also holds for the Hájek-type estimators. Asymptotic normality of the indirect, total and overall effect estimators can be derived similarly.
5. SIMULATION STUDY
A simulation study was conducted to investigate the bias, empirical standard error and average estimated standard error of the different estimators discussed in  4. In the simulations the inverse probability-weighted and Hájek-type effect estimators were computed using the true propensity score, an estimated propensity score based on a correct model, and an estimated propensity score based on a misspecified model. Simulations were conducted under partial interference, i.e., Assumption 1, for both continuous and binary outcomes. The simulation study for a continuous outcome was carried out in the steps described below.
4. In the simulations the inverse probability-weighted and Hájek-type effect estimators were computed using the true propensity score, an estimated propensity score based on a correct model, and an estimated propensity score based on a misspecified model. Simulations were conducted under partial interference, i.e., Assumption 1, for both continuous and binary outcomes. The simulation study for a continuous outcome was carried out in the steps described below.
Step 1.
A random sample of
groups was created as follows. First, the group size
was randomly sampled from
with corresponding probabilities
. For each individual in each group,
was randomly sampled from
. Then the potential outcomes for individual
in group
were set to
.
Step 2.
The covariate vectors
were randomly sampled from
, where
denotes the
identity matrix.
Step 3.
Treatment variables
were simulated from a Bernoulli distribution with mean
, where the random effects
were randomly sampled from
and
.
Step 4.
A correctly specified logistic regression model
and a misspecified logistic regression model
, where
,
,
and
, were fitted to the simulated data.
Step 5.
The causal effect estimators and their corresponding variance estimators were calculated for
and
using the known propensity score, the estimated propensity score from the correctly specified mixed-effects model and the estimated propensity score from the misspecified mixed-effects model.
Step 6.
Steps 1–5 were repeated
times, and the empirical bias, empirical standard error and average estimated standard error were calculated for the estimators in Step 5.
From the potential outcome model specified in Step 1 it follows that 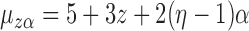 and
and 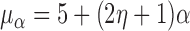 where
where 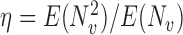 . Hence
. Hence 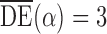 for any
for any 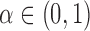 ,
, 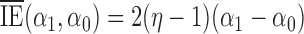 ,
, 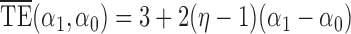 and
and 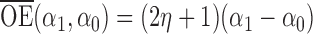 . Simulation results for the direct effect estimators are given in Table 1. All three estimators are approximately unbiased when the propensity scores are known or correctly modelled, but are biased if the propensity scores are incorrectly modelled. For all three estimators the average estimated standard error is also relatively close to the empirical standard error when the propensity scores are known or correctly modelled. Note that
. Simulation results for the direct effect estimators are given in Table 1. All three estimators are approximately unbiased when the propensity scores are known or correctly modelled, but are biased if the propensity scores are incorrectly modelled. For all three estimators the average estimated standard error is also relatively close to the empirical standard error when the propensity scores are known or correctly modelled. Note that 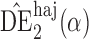 has substantially smaller empirical standard error than
has substantially smaller empirical standard error than 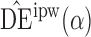 and
and 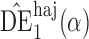 . For example, when
. For example, when 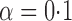 and the propensity scores are known, the empirical standard errors of
and the propensity scores are known, the empirical standard errors of 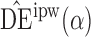 and
and 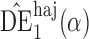 are 1
are 1 4 and 1
4 and 1 5, whereas the empirical standard error of
5, whereas the empirical standard error of 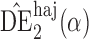 is only 0
is only 0 3. Similar results hold when the propensity scores are treated as unknown and either correctly or incorrectly modelled. The results in Table 1 demonstrate that, as well as having smaller empirical standard error,
3. Similar results hold when the propensity scores are treated as unknown and either correctly or incorrectly modelled. The results in Table 1 demonstrate that, as well as having smaller empirical standard error, 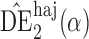 may be more robust than
may be more robust than 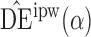 and
and 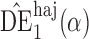 with respect to misspecification of the propensity score model.
with respect to misspecification of the propensity score model.
Table 1.
Empirical bias 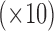 , empirical standard error, and average estimated standard error of the estimators of
, empirical standard error, and average estimated standard error of the estimators of 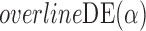 with a continuous outcome
with a continuous outcome
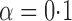
|
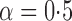
|
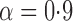
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Known 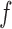
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
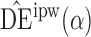
|
0 4 4 |
1 4 4 |
1 4 4 |
0 1 1 |
0 7 7 |
0 7 7 |
0 2 2 |
1 7 7 |
1 7 7 |
||
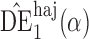
|
0 6 6 |
1 5 5 |
1 5 5 |
0 1 1 |
0 6 6 |
0 6 6 |
0 5 5 |
1 6 6 |
1 6 6 |
||
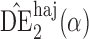
|
0 1 1 |
0 3 3 |
0 3 3 |
0 0 0 |
0 2 2 |
0 2 2 |
0 0 0 |
0 3 3 |
0 3 3 |
||
Correct 
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
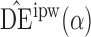
|
4 1 1 |
1 5 5 |
1 4 4 |
0 7 7 |
0 6 6 |
0 6 6 |
7 3 3 |
1 3 3 |
1 3 3 |
||
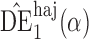
|
3 8 8 |
1 5 5 |
1 5 5 |
0 5 5 |
0 6 6 |
0 8 8 |
7 6 6 |
1 3 3 |
1 5 5 |
||
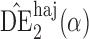
|
0 2 2 |
0 3 3 |
0 3 3 |
0 8 8 |
0 2 2 |
0 2 2 |
0 5 5 |
0 3 3 |
0 3 3 |
||
Mis 
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
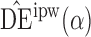
|
0 4 4 |
1e1 | 1e1 | 20 | 1e3 | 1e3 | 10 | 2e2 | 1e2 | ||
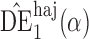
|
5 2 2 |
2e0 | 1e1 | 10 | 1e3 | 1e3 | 30 | 3e2 | 2e2 | ||
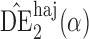
|
0 3 3 |
0 3 3 |
0 3 3 |
0 8 8 |
0 3 3 |
0 3 3 |
0 3 3 |
0 5 5 |
0 5 5 |
||
ESE, empirical standard error; ASE, average estimated standard error; Known  , true propensity score known; Correct
, true propensity score known; Correct 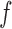 , propensity score unknown but correctly modelled; Mis
, propensity score unknown but correctly modelled; Mis 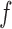 , propensity score incorrectly modelled.
, propensity score incorrectly modelled.
The simulation study described above was repeated for a binary outcome. Specifically, Step 1 was replaced with the following, while all other steps remained the same.
Step 1.
A random sample of
groups was created as follows. First, the group size
was randomly sampled from
with corresponding probabilities
. Then the potential outcomes
were set to 0 with probability 0
2, 1 with probability 0
2, and
with probability 0
6.
For this potential outcome model, 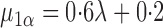 ,
, 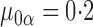 and
and 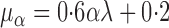 with
with 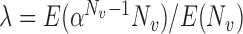 . Simulation results for this scenario are given in Table 2. Similar to the continuous outcome simulations, the empirical standard error for
. Simulation results for this scenario are given in Table 2. Similar to the continuous outcome simulations, the empirical standard error for 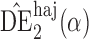 is smaller than that for
is smaller than that for 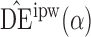 and
and 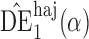 in all three scenarios, and
in all three scenarios, and 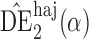 also tends to be more robust with respect to misspecification of the propensity score model than the other two estimators. Similar results, not shown here, were observed for the other causal effect estimators.
also tends to be more robust with respect to misspecification of the propensity score model than the other two estimators. Similar results, not shown here, were observed for the other causal effect estimators.
Table 2.
Empirical bias, empirical standard error, and average estimated standard error of the estimators of 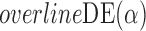 with a binary outcome; all values have been} multiplied by
with a binary outcome; all values have been} multiplied by 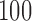
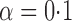
|
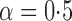
|
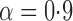
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Known 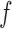
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
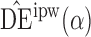
|
0 2 2 |
9 7 7 |
9 7 7 |
0 | 4 7 7 |
4 8 8 |
0 1 1 |
9 3 3 |
9 2 2 |
||
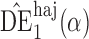
|
0 3 3 |
9 6 6 |
9 7 7 |
0 | 4 6 6 |
4 5 5 |
0 1 1 |
8 4 4 |
8 4 4 |
||
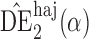
|
0 1 1 |
7 0 0 |
6 9 9 |
0 | 3 9 9 |
3 9 9 |
0 | 5 4 4 |
5 3 3 |
||
Correct 
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
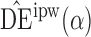
|
1 4 4 |
10 2 2 |
9 8 8 |
0 1 1 |
4 5 5 |
4 3 3 |
3 5 5 |
7 4 4 |
7 2 2 |
||
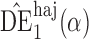
|
1 3 3 |
10 1 1 |
9 8 8 |
0 2 2 |
4 5 5 |
4 5 5 |
3 5 5 |
7 3 3 |
7 5 5 |
||
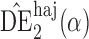
|
0 1 1 |
7 3 3 |
7 1 1 |
0 5 5 |
3 8 8 |
3 6 6 |
0 9 9 |
5 2 2 |
5 0 0 |
||
Mis 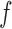
|
Bias | ESE | ASE | Bias | ESE | ASE | Bias | ESE | ASE | ||
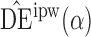
|
1 | 1e2 | 1e2 | 1 | 5e2 | 3e2 | 1e1 | 3e4 | 2e4 | ||
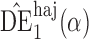
|
1 | 4e1 | 1e2 | 10 | 5e2 | 3e2 | 2e1 | 3e4 | 2e4 | ||
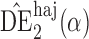
|
0 1 1 |
7 4 4 |
7 3 3 |
1 2 2 |
6 8 8 |
6 4 4 |
1 | 9 7 7 |
9 5 5 |
||
6. Rotavirus vaccine study in nicaragua
Rotavirus diarrhoea is a major health problem in Nicaragua (Espinoza et al., 1997). The pentavalent rotavirus vaccine was introduced in 2006. Nicaraguan infants are offered the vaccine at two, four and six months of age as part of the country’s Expanded Program on Immunization. In 2010, a study to assess the impact of the immunization programme was carried out in León, Nicaragua’s second largest city, with an estimated population in 2010 of close to 200 000. The Health and Demographic Surveillance Site-León was employed to obtain a simple random sample of households from 50 out of 208 randomly selected geographical clusters of equal size in León (Becker-Dreps et al., 2013). For simplicity, in the following analysis the cluster sampling used to obtain these data is ignored. There were 530 households in the study, and any child in a selected household under the age of five was eligible to participate. Information was collected about each household, including water source, sanitation system, maternal education level, and the dates of birth of study participants. Each individual in the study was visited fortnightly by a fieldworker for approximately one year. At each visit information about diarrhoea episodes in the past 14 days was recorded. The primary outcome  was whether a child had at least one diarrhoea episode during the study.
was whether a child had at least one diarrhoea episode during the study.
For each child we assumed their interference set to be other children in the same household. A mixed-effects logistic regression model of the probability of having received all three scheduled doses was fitted conditional on the following baseline covariates: child’s age, categorized as 0–11 months, 12–23 months, or 24–59 months; mother’s education level, categorized as primary education only or at least some secondary education; dirt household floor or not; dry or wet season; household indoor toilet, latrine, or none; indoor municipal water supply or not; and breastfeeding or not. Likelihood ratio tests from the fitted logistic model indicated that the odds of having all three doses of vaccine was higher among children whose mothers were more educated, with 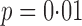 .
.
Effect estimates and estimated standard errors are reported in Table 3 for the inverse probability-weighted and the two Hájek estimators for contrast function 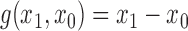 . The Hájek 2 estimates are closer to the null value of zero and, as expected, have 15–20% smaller estimated standard errors than the inverse probability-weighted and Hájek 1 estimates. The direct effect estimates indicate the expected difference in the proportions of children who will acquire rotavirus diarrhoea among vaccinated versus unvaccinated children for a fixed level of vaccine coverage
. The Hájek 2 estimates are closer to the null value of zero and, as expected, have 15–20% smaller estimated standard errors than the inverse probability-weighted and Hájek 1 estimates. The direct effect estimates indicate the expected difference in the proportions of children who will acquire rotavirus diarrhoea among vaccinated versus unvaccinated children for a fixed level of vaccine coverage 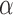 . The estimated direct effects become closer to the null as
. The estimated direct effects become closer to the null as 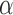 increases, suggesting that the direct protective effect of vaccination decreases as additional children in the household are vaccinated. The indirect effect estimates approximate the expected difference in the proportions of unvaccinated children who will acquire diarrhoea when vaccine coverage is
increases, suggesting that the direct protective effect of vaccination decreases as additional children in the household are vaccinated. The indirect effect estimates approximate the expected difference in the proportions of unvaccinated children who will acquire diarrhoea when vaccine coverage is 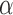 % versus 10%. The total effect estimates indicate the expected difference in the proportions of vaccinated children who will acquire diarrhoea when vaccine coverage is
% versus 10%. The total effect estimates indicate the expected difference in the proportions of vaccinated children who will acquire diarrhoea when vaccine coverage is 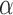 % compared with unvaccinated children when vaccine coverage is 10%. The overall effect estimates provide simple summary comparisons between any two allocation strategies; for example, according to the Hájek 2 estimates, 5
% compared with unvaccinated children when vaccine coverage is 10%. The overall effect estimates provide simple summary comparisons between any two allocation strategies; for example, according to the Hájek 2 estimates, 5 1 fewer cases of diarrhoea per 100 individuals per year would be expected if on average 80% of children in a household were vaccinated than if on average only 10% of children were vaccinated.
1 fewer cases of diarrhoea per 100 individuals per year would be expected if on average 80% of children in a household were vaccinated than if on average only 10% of children were vaccinated.
Table 3.
Effect estimates for the rotavirus vaccine study; all values have been multiplied by 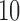
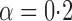
|
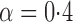
|
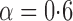
|
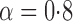
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Est | SE | Est | SE | Est | SE | Est | SE | |||||
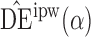
|
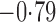
|
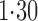
|
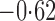
|
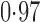
|
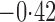
|
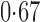
|
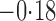
|
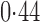
|
||||
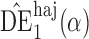
|
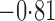
|
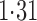
|
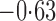
|
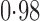
|
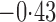
|
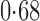
|
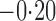
|
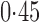
|
||||
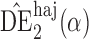
|
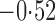
|
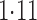
|
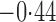
|
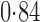
|
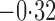
|
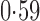
|
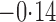
|
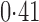
|
||||
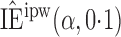
|
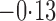
|
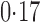
|
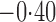
|
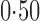
|
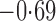
|
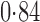
|
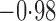
|
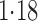
|
||||
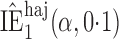
|
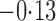
|
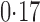
|
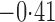
|
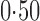
|
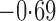
|
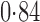
|
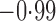
|
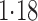
|
||||
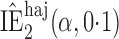
|
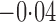
|
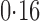
|
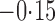
|
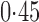
|
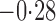
|
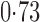
|
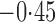
|
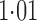
|
||||
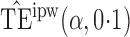
|
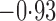
|
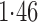
|
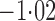
|
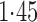
|
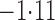
|
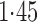
|
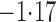
|
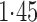
|
||||
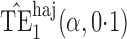
|
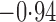
|
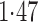
|
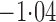
|
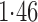
|
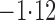
|
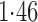
|
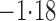
|
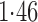
|
||||
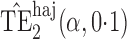
|
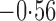
|
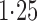
|
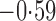
|
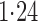
|
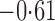
|
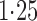
|
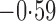
|
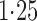
|
||||
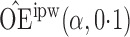
|
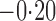
|
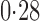
|
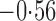
|
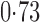
|
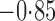
|
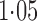
|
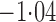
|
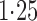
|
||||
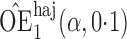
|
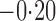
|
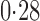
|
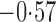
|
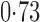
|
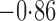
|
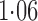
|
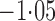
|
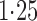
|
||||
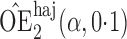
|
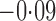
|
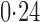
|
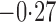
|
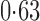
|
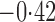
|
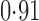
|
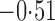
|
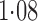
|
||||
Est, point estimate; SE, estimated standard error.
7. Discussion
The inverse probability-weighted estimator and two Hájek-type estimators in  3 allow for any form of interference between individuals, with the former being unbiased in a finite-population model with known propensity scores. Assuming partial interference and random sampling of groups from a superpopulation, all three estimators are consistent and asymptotically normal when the propensity scores are known or correctly modelled. Empirical results demonstrate that the second Hájek estimator can have substantially smaller finite-sample variance than the other two estimators. One avenue of future research entails deriving the estimators’ large-sample properties without assuming partial interference. Another future direction might involve developing estimators which are robust with respect to misspecification of the propensity score model. Throughout this work conditional exchangeability is assumed, i.e., treatment is assumed to be independent of potential outcomes conditional on an observable set of covariates. In future work one could investigate relaxing this assumption, perhaps via sensitivity analysis or instrumental variable methods. Finally, the target parameters in this paper utilize the Bernoulli allocation strategy proposed by Tchetgen Tchetgen & VanderWeele (2012). These estimands consider the counterfactual scenario where individuals independently select treatment with equal probability. In scenarios where interference is present, it is unlikely that individual treatment selections would be independent. Therefore further interference-related research might target alternative parameters.
3 allow for any form of interference between individuals, with the former being unbiased in a finite-population model with known propensity scores. Assuming partial interference and random sampling of groups from a superpopulation, all three estimators are consistent and asymptotically normal when the propensity scores are known or correctly modelled. Empirical results demonstrate that the second Hájek estimator can have substantially smaller finite-sample variance than the other two estimators. One avenue of future research entails deriving the estimators’ large-sample properties without assuming partial interference. Another future direction might involve developing estimators which are robust with respect to misspecification of the propensity score model. Throughout this work conditional exchangeability is assumed, i.e., treatment is assumed to be independent of potential outcomes conditional on an observable set of covariates. In future work one could investigate relaxing this assumption, perhaps via sensitivity analysis or instrumental variable methods. Finally, the target parameters in this paper utilize the Bernoulli allocation strategy proposed by Tchetgen Tchetgen & VanderWeele (2012). These estimands consider the counterfactual scenario where individuals independently select treatment with equal probability. In scenarios where interference is present, it is unlikely that individual treatment selections would be independent. Therefore further interference-related research might target alternative parameters.
Acknowledgments
Acknowledgement
The authors were partially supported by the U.S. National Institutes of Health. The fieldwork was supported by the Thrasher Research Fund. The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors thank M. Elizabeth Halloran, Joseph Rigdon, an associate editor, and a reviewer for helpful comments.
Appendix
Proof of Proposition 1
To show that 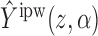 is unbiased, observe that
is unbiased, observe that
That 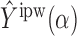 is unbiased can be proved similarly.
is unbiased can be proved similarly.
Proof of Propositions 2 and 3
To prove Proposition 2, assume that there exist constants 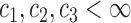 and
and 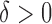 such that
such that 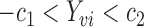 ,
, 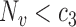 ,
, 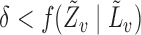 and
and 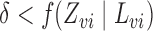 with probability 1. Let
with probability 1. Let 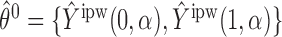 and
and 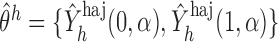 (
(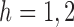 ). Let
). Let 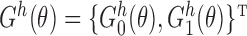 denote the vector estimating equation
denote the vector estimating equation 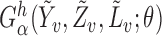 . Let
. Let 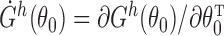 and write
and write 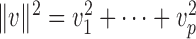 for any vector
for any vector 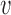 of length
of length 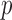 .
.
First we show that the following four conditions hold for 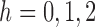 : (i)
: (i) 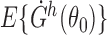 exists and is nonsingular; (ii)
exists and is nonsingular; (ii) 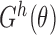 is twice continuously differentiable with respect to
is twice continuously differentiable with respect to 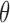 for every
for every 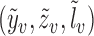 ; (iii)
; (iii) 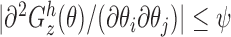 for some integrable measurable function
for some integrable measurable function 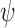 ; and (iv)
; and (iv) 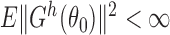 . It is straightforward to show that
. It is straightforward to show that 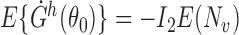 , where
, where 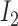 is the
is the 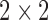 identity matrix, implying (i). Note that
identity matrix, implying (i). Note that 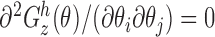 , so (ii) holds and (iii) is satisfied for the function
, so (ii) holds and (iii) is satisfied for the function 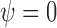 . To show (iv), observe that
. To show (iv), observe that
From the boundedness assumptions on 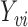 ,
, 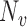 and
and 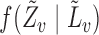 , it follows that
, it follows that 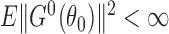 . Similar results can be established for
. Similar results can be established for  .
.
Next, note that 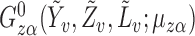 is a linear function of
is a linear function of 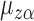 with slope
with slope 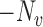 . For
. For 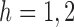 ,
, 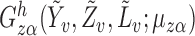 is also a linear function of
is also a linear function of 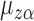 with finite, nonzero slope, because by assumption
with finite, nonzero slope, because by assumption 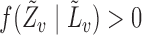 and there exists at least one
and there exists at least one  such that
such that 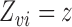 . Hence, the solution for
. Hence, the solution for 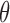 to
to 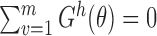 is unique for
is unique for 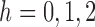 . Therefore, because (i)–(iv) hold, by Theorem 5.4.2 of van der Vaart (1998),
. Therefore, because (i)–(iv) hold, by Theorem 5.4.2 of van der Vaart (1998), 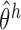 converges in probability to
converges in probability to 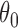 . Proposition 2 then follows from Theorem 5.4.1 of van der Vaart (1998) and the delta method.
. Proposition 2 then follows from Theorem 5.4.1 of van der Vaart (1998) and the delta method.
Similar reasoning can be used to prove Proposition 3 under the following additional assumptions about the parametric propensity score model: 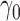 is in an open subset of Euclidean space;
is in an open subset of Euclidean space; 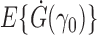 exists and is nonsingular, where
exists and is nonsingular, where 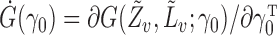 ;
; 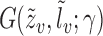 is twice continuously differentiable with respect to
is twice continuously differentiable with respect to 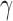 and
and 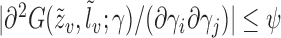 for some integrable measurable function
for some integrable measurable function 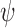 for every
for every 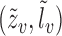 ; and
; and 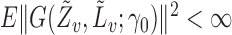 .
.
Proof of reduction in variance with a correctly specified propensity score model
Using block matrix notation, write
where 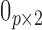 is the
is the 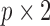 matrix of zeros. It is straightforward to show that
matrix of zeros. It is straightforward to show that 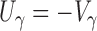 and
and 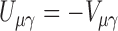 . It follows that
. It follows that
and therefore
where 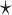 denotes quantities not expressed explicitly. Hence
denotes quantities not expressed explicitly. Hence
Since 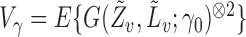 is positive semidefinite, so is
is positive semidefinite, so is 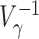 . Therefore
. Therefore 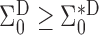 . The same approach can be used to show that
. The same approach can be used to show that 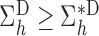 for
for 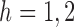 .
.
References
- Becker-Dreps S., MelÉndez M., Liu L., Zambrana L. E., Paniagua M., Weber D. J., Hudgens M. G., CÁceres M., KÄllestÅll C., Morgan D. R. et al. (2013). Community diarrhea incidence before and after rotavirus vaccine introduction in Nicaragua. Am. J. Trop. Med. Hygiene 89, 246–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espinoza F. Paniagua M. Hallander H. Svensson L. & StrannegÅrd Ö.. (1997). Rotavirus infections in young Nicaraguan children. Pediatric Inf. Dis. J. 16, 564–71. [DOI] [PubMed] [Google Scholar]
- HÁjek J. (1971). Comment on a paper by D. Basu. In Foundations of Statistical Inference, Godambe V. & Sprott D. eds. Toronto:Holt, Rinehart and Winston, p. 236. [Google Scholar]
- Halloran M. E. & Hudgens M. G.. (2012). Causal inference for vaccine effects on infectiousness. Int. J. Biostatist. 8, 1–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halloran M. E. & Struchiner C. J.. (1995). Causal inference in infectious diseases. Epidemiology 6, 142–51. [DOI] [PubMed] [Google Scholar]
- Hong G. & Raudenbush S. W.. (2006). Evaluating kindergarten retention policy: A case study of causal inference for multilevel observational data. J. Am. Statist. Assoc. 101, 901–10. [Google Scholar]
- Horvitz D. G. & Thompson D. J.. (1952). A generalization of sampling without replacement from a finite universe. J. Am. Statist. Assoc. 47, 663–85. [Google Scholar]
- Hudgens M. G. & Halloran M. E.. (2008). Toward causal inference with interference. J. Am. Statist. Assoc. 103, 832–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L. & Hudgens M. G.. (2014). Large sample randomization inference of causal effects in the presence of interference. J. Am. Statist. Assoc. 109, 288–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo X. Small D. S. Li C. S. R. & Rosenbaum P. R.. (2012). Inference with interference between units in an fMRI experiment of motor inhibition. J. Am. Statist. Assoc. 107, 530–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manski C. F. (2013). Identification of treatment response with social interactions. Economet. J. 16, S1–23. [Google Scholar]
- Nickerson D. W. (2008). Is voting contagious? Evidence from two field experiments. Am. Polit. Sci. Rev. 102, 49–57. [Google Scholar]
- Perez-Heydrich C. Hudgens M. G. Halloran M. E. Clemens J. D. Ali M. & Emch M. E.. (2014). Assessing effects of cholera vaccination in the presence of interference. Biometrics 70, 731–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum P. R. (2007). Interference between units in randomized experiments. J. Am. Statist. Assoc. 102, 191–200. [Google Scholar]
- Sobel M. E. (2006). What do randomized studies of housing mobility demonstrate? Causal inference in the face of interference. J. Am. Statist. Assoc. 101, 1398–407. [Google Scholar]
- Stefanski L. A. & Boos D. D.. (2002). The calculus of M-estimation. Am. Statistician 56, 29–38. [Google Scholar]
- Tchetgen Tchetgen E. J. & VanderWeele T. J.. (2012). On causal inference in the presence of interference. Statist. Meth. Med. Res. 21, 55–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart A. (1998). Asymptotic Statistics. Cambridge:Cambridge University Press. [Google Scholar]
- VanderWeele T. J. & Tchetgen Tchetgen E. J.. (2011). Effect partitioning under interference in two-stage randomized vaccine trials. Statist. Prob. Lett. 81, 861–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T. J. Tchetgen Tchetgen E. J. & Halloran M. E.. (2012). Components of the indirect effect in vaccine trials: Identification of contagion and infectiousness effects. Epidemiology 23, 751–61. [DOI] [PMC free article] [PubMed] [Google Scholar]