Abstract
We describe a diabatic-at-construction (DAC) strategy for defining diabatic states to determine the adiabatic ground and excited electronic states and their potential energy surfaces using the multistate density functional theory (MSDFT). The DAC approach differs in two fundamental ways from the adiabatic-to-diabatic (ATD) procedures that transform a set of preselected adiabatic electronic states to a new representation. (1) The DAC states are defined in the first computation step to form an active space, whose configuration interaction produces the adiabatic ground and excited states in the second step of MSDFT. Thus, they do not result from a similarity transformation of the adiabatic states as in the ATD procedure; they are the basis for producing the adiabatic states. The appropriateness and completeness of the DAC active space can be validated by comparison with experimental observables of the ground and excited states. (2) The DAC diabatic states are defined using the valence bond characters of the asymptotic dissociation limits of the adiabatic states of interest, and they are strictly maintained at all molecular geometries. Consequently, DAC diabatic states have specific and well-defined physical and chemical meanings that can be used for understanding the nature of the adiabatic states and their energetic components. Here we present results for the four lowest singlet states of LiH and compare them to a well-tested ATD diabatization method, namely the 3-fold way; the comparison reveals both similarities and differences between the ATD diabatic states and the orthogonalized DAC diabatic states. Furthermore, MSDFT can provide a quantitative description of the ground and excited states for LiH with multiple strongly and weakly avoided curve crossings spanning over 10 Å of interatomic separation.
Graphical abstract
1. INTRODUCTION
The diabatic representation of potential energy surfaces (PESs) and their interactions is useful for electronically nonadiabatic processes, especially those involving conical intersections of the adiabatic states, because it provides a smooth description of the PESs and represents their couplings in terms of the smoothly varying off-diagonal matrix elements of the scalar electronic Hamiltonian.1–10 In contrast, the adiabatic PESs, which diagonalize the electronic Hamiltonian, exhibit rapid variations and cuspidal ridges as functions of the nuclear coordinates in these regions, and the adiabatic states are coupled by the vector nuclear momentum operators; these couplings, called nonadiabatic couplings or derivative couplings, are not smooth with singularities at the cuspidal ridges, making them difficult to use in dynamic simulations.11,12 The most common way to treat coupled PESs is by wave function theory (WFT) with multireference (MR) methods; however, accurate calculations are very expensive, usually restricting their applications to small molecules. Density functional theory (DFT) may be the ultimate method in the long term, but the currently available linear-response time-dependent density functional theory (TDDFT) has the wrong dimensionality for conical intersections involving the ground (reference) state.13,14 (This shortcoming can be overcome by modifying the theory,15–17 but we shall not pursue that line of approach in the present article.) The present article considers a combination of DFT and WFT that goes beyond the current Kohn−Sham approximation18 and has advantages compared to using either alone. This article has two objectives: (1) to describe a multistate density functional theory (MSDFT) for constructing quasidiabatic states and (2) to establish a relationship between the diabatic states obtained from MSDFT and those by the 3- fold-way diabatization approach.4,19
The nonadiabatic coupling matrix elements are ⟨ΨI(r;R)|∇R|ΨJ(r;R)⟩, where |ΨI(r;R)⟩ and |ΨI(r;R)⟩ are adiabatic wave functions for states I and J, and r and R specify respectively electronic and nuclear coordinates.20 Diabatic states (sometimes called quasidiabatic states) are those that make the coupling by nuclear momentum operators negligible or as small as possible. In the general case the nonadiabatic couplings cannot be made to completely vanish,21 and the transformation to states that makes them small is not unique. Numerous approaches have been proposed to model diabatic states.10,22–28,8,29–33,4,19,34–41 A thorough comparison of these methods is beyond the scope of this work, but, instead, we roughly classify them into two categories on the basis of the relationship between diabatic and adiabatic states: (1) adiabatic-to-diabatic (ATD) and (2) diabatic-at-construction (DAC).
(1) “Adiabatic-To-Diabatic” via Similarity Transformation
The ATD category involves similarity transformations of adiabatic states to yield orthogonal diabatic states. In some of these methods, the diabatic states when diagonalized exactly reproduce the adiabatic PESs. A prerequisite is a set of adiabatic states, including (usually) the ground state and the relevant excited states, and the resulting diabatic states depend not just on the diabatization method but also on the choice of how many and which states to include in the transformation. Then, a similarity transformation is used to produce a diabatic representation having the desired properties. The adiabatic states can be obtained qualitatively from multiconfiguration self-consistent-field (MCSCF) calculations such as the stateaveraged complete-active-space type (SA-CASSCF),42 but this method does not yield quantitative PESs because of insufficient dynamic correlation. More quantitative results can be obtained by multireference perturbation theory (MRPT)43–45 or multireference configuration interaction (MRCI).46–48 These methods are restricted to relatively small molecules by high computation costs. For larger molecular systems, Kohn−Sham density functional theory (KS-DFT) and linear-response timedependent DFT (TDDFT) are more efficient ways to include dynamic correlation.49 Here we use a multistate approach18,50,51 that extends the approximate density functional theory beyond KS-DFT for applications to photochemistry.
Given a set of adiabatic ground and excited states, one diabatization procedure is to minimize the derivative couplings along a given reaction path by making use of energies, gradients, and derivative couplings at selected points.8,32,33 Another strategy is to approximate the diabatic states according to predefined, smoothly varying orbitals along with the condition of configurational uniformity.4,10,19,34,35 Alternatively, one could carry out orbital-free diabatization by employing dipole moments, quadrupole moments, electrostatic potentials, and transition moments, and these have been used recently and tested on several molecular systems.40,41 Several other ATD diabatization schemes are available, and the reader is referred to recent papers for additional methods and additional references. 52–54
(2) “Diabatic-At-Construction” by Experimental Validation
The diabatic states in the DAC category are often nonorthogonal. For example, they may be chosen on the basis of the electronic configurations of reaction products at the asymptotic dissociation limits, and the valence bond (VB) character of the electronic state may be maintained at all molecular geometries.3,7,50,55–60 Rather than back-transforming the delocalized adiabatic states, the diabatic states are constructed in the first place as the spin-adapted configuration state functions (CSFs) that serve as a basis for direct calculation of the adiabatic ground state and excited states. Although diabatic states are not unique21 and their properties are not physical observables, states of the DAC type can be validated in part by comparison with experiments on observables of the resulting adiabatic ground and excited states. Such comparisons can also provide physically meaningful interpretations of delocalized adiabatic states.
A procedure to construct diabatic states by contracting the eigenvectors from ab initio VB calculations has been described;7 it involves a CSF space of the multiconfiguration self-consistent-field (MCSCF) type. In practice, VB-based diabatic states can be conveniently formulated by blocklocalized molecular orbitals (BLMO) according to the Lewis resonance structures for a given chemical system,61–63 and this has been used in the mixed molecular orbital and valence bond (MOVB) method for studying chemical reactions and charge transfer processes in the context of combined quantum mechanical and molecular mechanical (QM/MM) simulations. 3,56 The use of BLMO or block-localized Kohn−Sham (BLKS) orbitals reduces a large number of valence bond configurations to a manageable number; only those critical to a given system are retained in a way analogous to the spin-coupled valence bond theory.64,65 This method has been extended to density functional theory, in which case it is called multistate density functional theory (MSDFT),18,50,51,66,67 and this is the method that is used in the present work.
A related approach is constrained density functional theory60 that confines the electron density within finite spatial regions to define constrained states. For comparison, localized states are defined in orbital space in MSDFT. The difference is reflected in the computed transfer integrals for electron transfer reactions, where constrained DFT showed,68 incorrectly, nonexponential dependency with donor−acceptor distance and the computed values can vary as large as 5 orders of magnitude with different fractions of Hartree−Fock exchange used in a functional.68 MSDFT does not suffer from electron-transfer contamination of diabatic states found in spatial localization of density, and there is little-to-no dependency on the amount of HF-exchange used.51
The LiH molecule, being the second simplest two-electron chemical bond (after the hydrogen molecule), has been intensively investigated; it has a strong ionic−covalent mixing and a prominent ionic−covalent curve crossing.69–74 In the following, we illustrate the block-localization procedure to form the DAC states by considering the four lowest 1Σ+ states of LiH, which we describe by MSDFT. LiH is chosen because this simple system provides a challenging case for treating avoided state crossings, spanning a coordinate range from the bonding region to more than 10 Å in interatomic separation, and the states of LiH have been extensively studied both experimentally71,75 and theoretically so they provide a good case for validation of the present method.69–71,73,74
The method is explained in sections 2 and 3. In section 4, we compare the computed energetic and geometric results for the adiabatic states with experiments and computational results from accurate wave function theory. This provides a validation of the adequacy of the DAC states as a basis and of the computational accuracy of the MSDFT method. Then we discuss the difference between nonorthogonal and orthogonal diabatic states and some consequences of varying orthogonalization procedures. Differences and similarities are found in the diabatic states obtained by MSDFT18,50,51 and by previous diabatizations.10,40,41
2. METHOD
The MSDFT method18,50 belongs to the “dynamic-then-static” (DTS) scenario described by Liu for treating electron correlation.76,77 There are two computational steps in the DTS approach: (1) the construction and optimization of a set of active states, in which dynamic correlation is first incorporated, and (2) the diagonalization of the configuration interaction (CI) Hamiltonian to include static correlation and to yield the adiabatic ground- and excited-state energies. In the present discussion, it is illustrative to further divide the first step into three stages. (a) We first construct and variationally optimize a set of Nb Slater determinants formed from block-localized orbitals (see below). (b) Then, the determinants are combined to yield Np spin-adapted CSFs {|ΨA⟩;A = 1,⋯,Np}. (c) Finally, the CI matrices of CSFs of the same symmetry are diagonalized, resulting in a set of variational diabatic configuration (VDC) states.7 The state functions in either stage b or stage c, which span the same space and therefore yield identical adiabatic states when diagonalized, constitute what we call a primary space or the active space, and they are used to perform configuration interaction calculations in step 2. The calculations of stage a are labeled block-localized Kohn–Sham density functional theory (BL-KS-DFT or, for short, BLKS). The calculations in all other steps or stages are labeled as multistate density functional theory (MSDFT).
The active states may be regarded as contracted functions from a larger configuration interaction wave function. The DTS scenario is carried out by MSDFT, in which the dynamic correlation in the contracted functions is described by an extension of KS-DFT using the determinants that define the individually localized states in the active space.18,50,51 In this section, we first illustrate the method to construct the diabatic states to form the active space, making use of the four lowest singlet states of LiH as an example. Then, we describe the procedure to determine the effective Hamiltonian in MSDFT.
Step 1(a): Block-Localized Kohn–Sham Density Functional Theory
Although delocalized Kohn–Sham orbitals can be used to construct the determinantal functions of step 1 that form a basis for the CSFs of step 1(b), in the present context where our goal is to define diabatic states, it is more convenient to use localized VB configurations.3,7,56,66 The VB description of Lewis structures is particularly illustrative to understand the asymptotic limits of diabatic states in this work, but one can certainly use the delocalized molecular orbital (MO) picture, as in standard MCSCF approaches, to define spin-adapted configurations.
For an n-electron molecule, the atomic orbital basis functions and electrons of the system are partitioned into MA blocks, also called fragments, according to the Lewis structure of state A. Let nb and μb denote respectively the number of electrons and basis functions in fragment block b (where n1 + ⋯+nMA = n). We use block-localized Kohn–Sham (BLKS) orbitals;50 these are linear combinations of the atomic orbital basis functions restricted to a given block. The determinant function for configuration A is
| (1) |
where  is the antisymmetrizer, NA is a normalization factor, and specifies a product of the BLKS orbitals of block m.3,56
Step 1(b): Construction of CSFs
The qualitative VB description of LiH has been lucidly presented by Mo et al.,55 and their presentation is consistent with findings of the present study. Here, the atomic basis functions are conveniently divided into five blocks, one set of four blocks (the core, 2s, 2pσ, and 3s/3pσ) on Li and one block (1s) on H. Spin-adapted CSFs are constructed by combining several determinants to represent the corresponding covalent and ionic states. Specifically, for LiH, the minimum diabatic representation of the four low-lying 1Σ+ adiabatic states, labeled here (as usual) as the X, A, C, and D states in order of increasing energy, includes seven CSFs, consisting of 12 determinants. They correspond to the ionic and covalent (2s) states and the 2pσ, 3s, and 3pσ excited states of the Li atom
| (2a) |
| (2b) |
| (2c) |
| (2d) |
| (2e) |
| (2f) |
| (2g) |
where φc, φ2s, φ2p, φ3s, and φ3p are the core (1s), valence (2s and 2pσ), and Rydberg-type (3s and 3pσ) BLKS orbitals located on lithium, ϕ1s and ϕH2s are basis orbitals on the hydrogen atom, and ϕ1 and ϕ̅1 respectively indicate single occupation by an electron with respectively α or β spin. Equation 2 defines singlet states that are eigenfunctions of both the Ŝ2 and Ŝz operators, and triplet states can be analogously represented, but for brevity they are not explicitly shown here.
The ionic configuration |Ψ−[(Li−)(H+)]⟩ slightly affects the adiabatic state energies by about 1 kcal/mol (~0.04 eV), but otherwise it does not make significant contributions to bonding. In addition, the 2s-2s bonding interaction between lithium and hydrogen (ϕH2s) is much higher in energy and makes negligible contributions to the low-lying adiabatic states. They are included in test calculations and kept to obtain the adiabatic energies, but we will not further discuss these two states (|Ψ−[(Li−)(H+)]⟩ and |Ψ2s/2s[(Li•)(H•)]⟩).
Step 1(c): Configuration Interaction
In step 1(a), the BLKS determinants were independently optimized as in standard KS-DFT, except that the electron densities are obtained using nonorthogonal orbitals.50 In step 1(b), the singlet (and analogously triplet) CSFs, as given by eqs 2a and 2d–2g, were obtained by diagonalizing the corresponding spincoupled Hamiltonian matrix. These CSFs are not necessarily the diabatic ground and excited states. In step 1(c), to obtain diabatic excited states, the CI matrices of CSFs of the same symmetry, e.g., 2s and 3s and 2pσ and 3pσ, are diagonalized, resulting in a set of variational diabatic configuration (VDC) states.7 The VDC states are also called valence-bond diabatic states, and they are compared in section 4.B to the diabatic states obtained by the 3-fold way from SA(4)-CASSCF and XMC-QDPT calculations as previously reported in refs 10 and 40.
Throughout this article, we use the indices A, B, … to specify the basis configurations from any one of the three stages and I, J, … to indicate adiabatic states.
We note that the choice of fragmental blocks is “natural” and chemically intuitive for bond forming and breaking processes. Thus, the VB-picture is used in this work. For small and medium (~100 atoms) sized molecules, conjugated or not, one can use delocalized orbitals to define configuration space as in MCSCF approaches. For large systems, fragmentation can reduce computational costs. However, for large and extensively conjugated systems (such as graphene), there is probably no simple way to have both efficiency and accuracy both for the ground and excited states. To this end, it is of interest to compare the basis states defined by eq 2 with the spin-coupled valence bond (SCVB) method.64,65 In SCVB, delocalized single-electron orbitals are used among which all spin-coupled configurations are included. In MSDFT, orbitals are block localized, and spin coupling is taken into account only between blocks critical for bonding interactions (e.g., the electron pair involved in the dissociation of a single bond). A single block-localized determinant (BLKS determinant) is employed to approximate the SCVB function for the entire block, greatly reducing the number of configurations in the active space. Importantly, dynamic correlation is incorporated in the reference functions in MSDFT, whereas it is treated as a post-SCF correction in SCVB.64,65
Step 2: Multistate Density Functional Theory
The adiabatic ground and excited state energies in the DTS scenario are obtained, in the second (final) step of the method, by configuration interaction among the basis states defined and optimized in the active space.18,50 In particular, the diagonal matrix elements of the effective Hamiltonian are simply the KSDFT energies for the corresponding states {|ΨA⟩; A = 1,⋯,Np}.50 In the present case of LiH, Np is 7, as constructed from 12 BLKS determinants. It is convenient to first consider the determinant representation to describe the matrix elements as follows50
| (3a) |
where is the electron density of configuration A, determined from the orbitals that form the determinant |ΨA(r;R)⟩. We note that any standard exchange-correlation functional can be used to obtain . In the CSF basis, the matrix elements can be conveniently obtained using the transformation matrix defined by eq 2
| (3b) |
where B specifies a spin-adapted CSF, and A and Ā specify determinants with spin exchanges in eq 2. Note that HAA = HĀĀ, and defined below. If the VDC states are used, a similar transformation will be used with the corresponding transformation matrix.
The off-diagonal matrix elements could in principle be determined by WFT.3,56,78 This would involve the transition density ρAB(r) = ⟨ΨA|ρ̂(r)|ΨB⟩. However, a transition density functional (TDF)18 ETDF[ρAB(r)] between states |ΨA⟩ and |ΨB⟩ does not exist within the KS-DFT framework. ETDF[ρAB(r)] might be derived by multiconfigurational approaches18 and by analogy to methods79 used for electron scattering. Here though, we approximate it in MSDFT by two contributions
| (4) |
where H is the electronic Hamiltonian. The first term in eq 4 is the electronic coupling between the nonorthogonal wave functions, and it is evaluated as an integral between nonorthogonal determinants, which has been used in the MOVB approach.3,56 The second term in eq 4 is a transition density contribution.3,18,50,51,56,67 Note that both exchange and static correlation are included in the first term, whereas only dynamic correlation is in the second term.18 We then approximated the second term of eq 4 by an overlap-weighted average of the KS correlation energies for the two interacting states50,51
| (5) |
where λ is unity in the present work (in later work this parameter or functional could be optimized to fit experimental results), where SAB is the overlap integral ⟨ΨA|ΨB⟩, and where specifies the correlation energy in the corresponding diagonal matrix element (as obtained from the exchange-correlation functional).49
The adiabatic ground and excited states are obtained as the eigenvalues{EI} and eigenvectors CI = {CAI} of the generalized secular equation
| (6) |
where E is a diagonal matrix of the adiabatic energies, and S and C are the overlap matrix and configuration coefficient matrix. The BLKS determinants in eq 2 are used to determine the overlap matrix, and the computational procedure is identical to that used in MOVB.3,56 The densities and energies for the adiabatic states are then given by
| (7) |
| (8) |
Eqs 7 and 8 show that both the ground state (I = 0) and excited states (0 < I < Np) are treated on the same footing. Consequently, the method provides energies for all states described by the basis configurations in the active space, and, unlike linear-response TDDFT, the CI matrix has the correct structure to properly describe all conical intersections (even those involving the ground state) and to treat weakly (and strongly) avoided crossings for nonadiabatic processes.18,50 Eqs 7 and 8 represent a hybrid wave function and density functional theory (WDFT) that goes beyond the Kohn–Sham approximation of DFT from a single determinant for the ground-state density to a multideterminant representation of ground and excited states. It would be interesting to compare MSDFT18,50 to multiconfiguration pair-density functional theory,80 but that is beyond the scope of this article.
3. COMPUTATIONAL DETAILS
In the present study, we consider the four low-lying 1Σ+ states of LiH, which are modeled by the active space defined by eq 2. At interatomic separations near to and shorter than the ground-state minimum, contributions from higher states play an important role in the various adiabatic states, especially for the second and third excited states, S2 (C) and S3 (D), making their detailed behavior even more interesting and complex. The present six (actually seven if the relatively unimportant 2s(H) is counted) CSFs are sufficient for illustrating the complicated electronic couplings in LiH.
The atomic orbital bases are approximated using the aug-cc-pVTZ basis set.81 For Li, the basis set is further divided into four blocks: (1) the 1s-core and 2s valence orbitals, (2) the 2pσ orbitals with σ symmetry along the bond axis direction as well as d-orbitals of the same symmetry, and (3) and (4) the 3s and 3p orbitals representing Rydberg states. All remaining orbitals are grouped into the first block for convenience (a fifth block could be used, but they make no contribution to the bonding energy due to orthogonal symmetry). For the 3s orbital, the standard diffuse function is replaced by the diffuse basis function in the Dunning-Hay basis set82 (this gives a slightly better energy for the 3s state of Li atom from MSDFT calculations), whereas the 3p basis functions are given by the diffuse p functions in the aug-cc-pVTZ basis. Similarly, the aug-cc-pVTZ basis is either used directly for the hydrogen atom, or is separated into two blocks with the diffuse s orbital to represent its Rydberg state. Unless special emphasis is needed, in the remainder of the article, we simply use the standard expression of aug-cc-pVTZ, rather than employing a different notation to represent the small difference in the diffuse basis for lithium. We have not attempted to optimize basis functions specifically to model Rydberg states since this is not the main purpose here; the unoptimized nature of the basis will introduce errors for the upper states. The excitation energies for the 2p (2Po), 3s (2S), and 3p (2Po) states of Li atom are 1.650, 3.493, and 3.822 eV from MSDFT compared with the experimental values of 1.848, 3.373, and 3.834 eV.83 Thus, there is an error of about 0.2 eV in the atomic spectra; this kind of error (due to basis set used) will be transferred to the molecular description.
The configurations defined in eq 2 are built from determinants that are variationally optimized using the hybrid PBE0 density functional;84,85 the computational algorithm has been described previously.50 Either the CSF states7 or the VDC states are subsequently used to solve eq 6, and they yield the same adiabatic ground and excited state energies, but the latter basis can be used in analysis of the DAC states. In principle, the BLKS orbital coefficients and configuration coefficients can be simultaneously optimized as in standard ground-state MCSCF methods, resulting in a set of consistently optimized diabatic configurations (CDC states).7,58 Although the use of CDC states optimized for the ground states can lower the adiabatic ground-state energy, to obtain diabatic excited states useful for bonding analysis it would be preferable to use state-averaged optimization. Since the CDC diabatic states are not variationally optimized, they are not particularly useful for analysis and for understanding of bonding interactions (for example, resonance energy). Thus, we do not further pursue the CDC states in this study.
The computational results are dependent on the functional used since MSDFT relies on a single-determinant functional (SDF), i.e., KS-DFT, for the configurational state. Given a functional used, it defines the condition for the transition density functional (TDF). Therefore, the relative (and absolute) energies of the diabatic (basis) configurations are fully defined by the specific functional used. We have found that the PBE and PBE0 functionals perform well with the MSDFT method, especially for charge transfer processes.51,86
SA-CASSCF42 and MS-CASPT243 calculations are also performed using the standard aug-cc-pVTZ basis set for comparison. Four states are used in the state-average optimization with equal weights, and they are also treated in the multistate perturbation calculation. The Molpro program is used for these WFT calculations,87 while MSDFT is carried out using a locally modified version of the GAMESS program.88 All computations are performed on computer clusters in our laboratory at Jilin University and at the Minnesota Supercomputing Institute.
4. RESULTS AND DISCUSSION
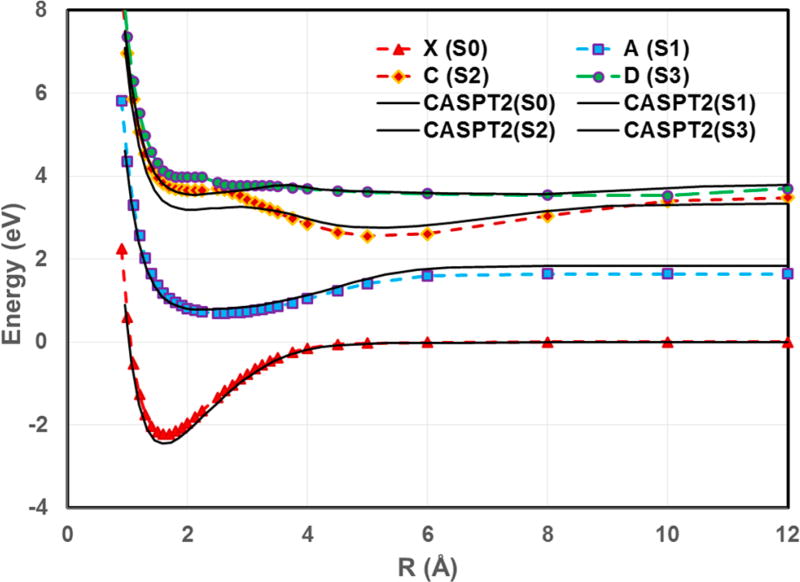
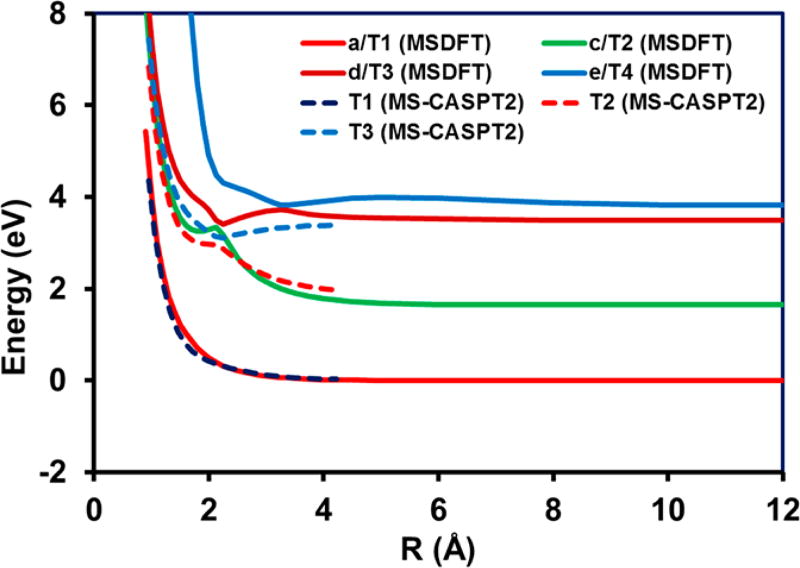
The ground state of LiH is known to be dominated by the ionic configuration, |Ψion[(Li+)(H−)]⟩, whereas the dissociation limit of the ground state consists of two neutral atomic radicals corresponding to the covalent configuration |Ψ2s[(Li•)(H•)]⟩. At short interatomic distances, the excited states are characterized by strong interactions involving several high-lying states, giving rise to further complications. The potential energy curves for the four singlet adiabatic states from MSDFT are shown in Figure 1, along with the MS-CASPT2 results for comparison, and those for the four lowest triplet states are displayed in Figure 2. The main purpose of this section is to show that the present MSDFT method can provide a reasonably quantitative description of the system (≤0.3 eV) and that it can be used to provide insight into the diabatic representation of the potential energy curves.
Figure 1.
Adiabatic potential energy curves for the four lowest 1Σ+ states of LiH as functions of interatomic distance from MSDFT (dashed curves) using the PBE0 density functional and from MS-CASPT2//SA(4)-CASSCF(2,9) calculations (solid curves). The aug-cc-pVTZ basis set with the diffuse s-function replaced by that of the Dunning-Hay basis (simply denoted by aug-cc-pVTZ throughout) is used in all MSDFT computations, whereas the standard aug-cc-pVTZ basis is used in wave function methods.
Figure 2.
Adiabatic potential energy curves for the four lowest 3Σ+ triplet states of LiH (a, c, d, and e in order of increasing energy) as functions of interatomic distance from MSDFT (solid curves) using the PBE0 density functional and from MS-CASPT2/SA(4)-CASSCF (dashed curves). The aug-cc-pVTZ basis set is used in all computations (see caption of Figure 1).
A. Adiabatic Potential Energy Surfaces
We compare the MSDFT potential energy curves to MS-CASPT2 results; both the qualitative trends and quantitative results from MS-CASPT2 calculations agree well with more complete or more accurate studies.69–71,73–75 The present MSDFT method does not involve the high cost of a SA-CASSCF computation, but it includes all dynamic correlation at the stage of diabatic (basis) state construction, yielding results comparable or better than the more expensive MS-CASPT2 calculation. Furthermore, the number of configurations in the active space is smaller in the present method (12 determinants vs 45 in the (2,9)-CAS) – an advantage of the DTS scenario). There is also no complication in MSDFT due to intruder states.
Table 1 summarizes the energies and the corresponding bond distances at the critical points on these potential energy curves. Note that computations are performed using grids with 0.1 to 2 Å intervals (depending on the region), which bracket the precisions of bond distances at the critical points. The global minimum of LiH from MSDFT has a bond length of 1.6 Å with a bond dissociation energy of 2.22 eV, in reasonable agreement with the experimental results (1.596 Å and 2.515 eV)75 and MS-CASPT2 data (1.588 Å and 2.449 eV) as well as MRCI results (Table 1).69,71 The small discrepancy (0.3 eV) in bond energy is primarily due to basis set effects in the MSDFT calculation; the deviation is reduced by 0.1 eV if we switch to the aug-cc-pVQZ basis set. Another key energetic quantity is the bond energy relative to the ionic dissociation limit (7.18 eV); this also agrees well with the experimental value (7.15 eV).75
Table 1.
Bond Energies (De) and Adiabatic Excitation Energies (Te) in eV, and Geometries in Å for the Ground (X) and the First Three Excited States (Denoted as A, C, and D) of LiHd
| propertya | MSDFT | MS-CASPT2 | MRCI69 | expt22,75 | |
|---|---|---|---|---|---|
| S0, X1Σ+ | |||||
| Re | 1.6 | 1.588 | 1.589 | 1.595 | |
| De | 2.223 | 2.449 | 2.522 | 2.515 | |
| LiH → Li+ + H− | 7.180 | 7.151 | |||
| S1(2p), A1Σ+ | |||||
| Re | 2.5 | 2.249 | 2.577 | 2.596 | |
| De | 0.95 | 1.05 | 1.077 | 1.076 | |
| Te | 2.92 | 3.24 | 3.29 | 3.288 | |
| Tvertb | 3.40 | ||||
| S2(3s), C1Σ+ | |||||
| S2(3s), C1Σ+ | |||||
| Re(in) | 2.125 | 2.117 | 2.023 | 2.0289 | |
| Re(o) | 5.0 | 5.29 | 5.384 | 5.3789 | |
| R‡ | 2.5 | 2.91 | |||
|
|
0.12 | 0.06 | |||
| De(in) | −0.17 | 0.14 | 0.16 | ||
| De(o) | 0.95 | 1.08 | 1.15 | 1.0589 | |
| Te(in) | 5.88 | 5.65 | 5.74 | ||
| Te(o) | 4.78 | 5.21 | 4.85 | 4.8322 | |
| S3(3p), D1Σ+ | |||||
| Re(in) | 1.9, 2.75 | 2.1 | 2.822 | ||
| Re(o) | 10 | 7.9 | 10.522 | ||
| De(in) | 0.06 | 0.25 | 0.3322 | ||
| De(o) | 0.29 | 0.24 | 0.3322 | ||
| Te(in) | 6.0 | 6.2 | 5.922 | ||
| Te(o) | 5.7 | 5.922 |
(in) and (o) specify the inner energy minimum and outer energy minimum, respectively.
Vertical excitation energy at ground-state equilibrium geometry.
denotes the barrier higher for dissociation (in eV).
The aug-cc-pVTZ basis set is used in all calculations using the multistate density functional theory (MSDFT) and multistate complete-active-space second-order perturbation theory (MS-CASPT2). The PBE0 density functional is used in MSDFT; the (2,9) active space is employed for MS-CASPT2.
Turning to the excited states, we find that the potential energy curves determined using MSDFT are generally in good agreement with those from MS-CASPT2 as well with those from MRCI studies,69,71 except for states C and D at short bond distances, where the MSDFT energies are about 0.4 eV higher than the MS-CASPT2 values. This difference may be due to limitations in the basis set used to approximate the Rydberg states or to interactions involving high-energy states that are not included in the VB-localized picture. Overall, the computed vertical and adiabatic transition energies to the A, C, and D states agree well with MS-CASPT2 results, typically within 0.2 eV for the former and within 0.3 eV for the latter. An experimental excitation energy for the A state is 3.29 eV, which lies between the computed vertical and adiabatic excitation energies (Table 1).71,75,89
The MSDFT calculations correctly yield a stretched bond for the first excited state. It has an equilibrium distance of near 2.5 Å; this may be compared with the experimental value of 2.596 Å75 and a somewhat shorter bond distance (2.25 Å) from MSCASPT2 (Table 1). The bond energy for the A state is estimated to be 0.95 eV from MSDFT, as compared to 1.08 and 1.05 eV from MS-CASPT2 and experiment.71,75 The C state consists of two energy minima roughly at 2.125 and 5.0 Å on the MSDFT potential energy curves, and the corresponding equilibrium distances are 2.117 and 5.292 Å at the MS-CASPT2 level. The bond energies are 0.6 to 0.9 eV at the longer separation. The inner minimum is produced through interactions involving several states (Figure 1), with primary contributions from the 3s(Li) and 3p(Li) states. Among theoretical studies, comprehensive investigations of the LiH molecule up to the 4p state are given in refs 70, 71, and 74, and the specific features and locations of all avoided crossings found in Figure 1 mirror those reported in earlier work very well. Overall, the agreement in qualitative trends of the potential energy curves and in quantitative energies and geometries between MSDFT and MS-CASPT2 along with experimental data shows that the present MSDFT approach can provide a good description of the ground and excited states for LiH.
The triplet states of LiH have also been studied computationally, although there appears to be little information available from experiment. Representative reports can be found in refs 70 and 71; the weakly avoided crossing between the c (T2) and d (T3) adiabatic states at about 2.1 Å in Figure 2 is clearly shown in the earlier studies. The e (T4) state in Figure 2 has a sharper increase in energy at short distance than that obtained in previous studies;70,71 this suggests that orbital hybridization may be required and basis set limitations may need to be overcome for describing these high-lying Rydberg states.
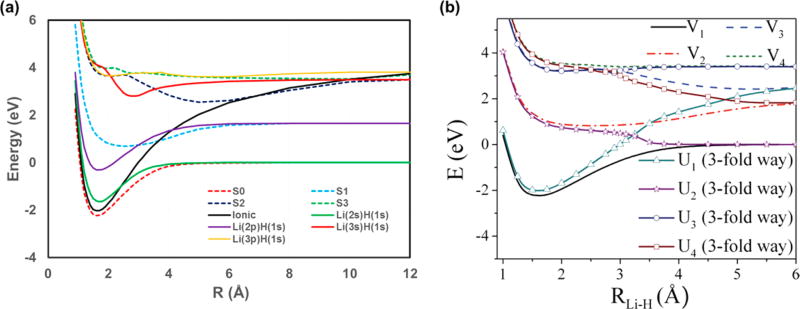
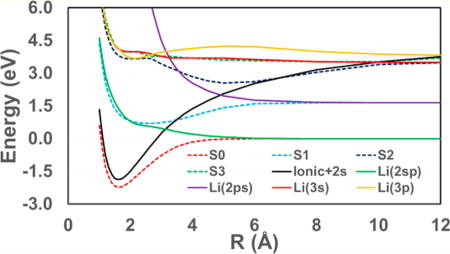
B. Valence-Bond Diabatic States
The potential energy curves for five of the seven VB basis states are shown in Figure 3, excluding the high-energy Li(2s)H(2s) covalent configuration and the reverse ionic state (Li−)(H+) since they make relatively minimal contributions to bonding interactions. These are the block-localized, nonorthogonal VDC states with the upper (Rydberg) states orthogonalized to the low-energy electronic CSFs (eq 2) of the same symmetry. These VB diabatic states approach the dissociation limits of the corresponding adiabatic states by construction. Significantly, the valence characters defined in eq 2 are kept at all geometries.
Figure 3.
(a) Valence-bond diabatic (solid curves) and adiabatic (dashed curves) potential energy curves of LiH as a function of interatomic separation optimized by multistate density functional theory (MSDFT). The PBE0 density functional along with the aug-cc-pVTZ basis set (see Figure 1) is used in all calculations. (b) Diabatic potential energy curves obtained by the three-fold way diabatization approach. Adapted from Figure 5 of ref 40 with permission of the American Institute of Physics.
A most striking observation of Figure 3 is that the ionic state spans the entire relevant energy range, from being the lowest energy diabatic state at the global minimum to becoming the highest energy state at the dissociation limit. The ionic diabatic state crosses at distances about 2.5, 4.2, 10, and >12 Å, respectively, with the 2s, 2pσ, 3s, and 3pσ covalent states of lithium that have been considered. These diabatic crossings also create some of the most intriguing strong nonadiabatic couplings among the adiabatic potential energy curves. For instance, the 2s state indeed transforms smoothly to the adiabatic ground state, X(S0), at the dissociation limit, but the nonorthogonal “pure” atomic covalent state does not start nor approach the first adiabatic excited state, A(S1), at short bond distances. In fact, none of the VB-diabatic states alone can provide an adequate description of the adiabatic surfaces at short bond lengths, except the accidental superposition between the D(S3) adiabatic state and the 3p-diabatic state (see below). The adiabatic states are typically mixtures of at least three major VB states in the present case. This is shown by the adiabatic ground state as an admixture of the dominant Li+H− ionic state with the bonding combination of the 2spσ hybrid of Li and the 1s orbital of hydrogen. The first excited state includes the antibonding combination of the 2s and 2pσ orbtials of Li with 1sH. The loosely bound minimum at about 5 Å on the C(S2) state can be attributed to the strong Coulomb attraction in the ionic VB state.
Note that the 3s and 3pσ VB-diabatic states displayed in Figure 3 are not the variationally optimized energies from the functions defined by eqs 2e and 2f, which are nonorthogonal to the lower states of same symmetry. Their energies in Figure 3 are obtained by configuration interaction involving states with the same symmetry. Consequently, some upper states exhibit effects of coupling, e.g., on the 3s surface (solid-red curve). It is interesting to note that the lithium 2s-3s configuration interaction has little effects on the energy of the 2s valence state, but the overlap-induced increase in energy of the variationally optimized 3s state is more profound (resulting in the solid-red curve).
C. Orthogonal Diabatic States
The diabatic states are typically expressed as orthogonal states,1,58 and in this section we discuss the orthogonalized diabatic states. An example of the diabatic representation of the potential energy curves for LiH from the 3-fold way diabatization method is reproduced in Figure 3b. Orthogonality makes the expression and computation of nonadiabatic dynamics simpler, but in the DAC approach, diabatic state functions are variationally optimized and only states of the same symmetry are orthogonal by configuration interaction; in general, the full VDC basis states are nonorthogonal. Although the adiabatic potential energy curves are similar in Figure 3, the qualitative trends of the nonorthogonal diabatic states from the DAC approach (Figure 3a) and the orthogonal ones (Figure 3b) from the ATD transformation have very different appearances, except the ionic state. One can orthogonalize the VB-diabatic configurations by similarity transformation so that they can be directly used in nonadiabatic dynamics simulations. Is it possible to reproduce similar qualitative features as that expressed in the orthogonal diabatic states in Figure 3b, starting from the nonorthogonal VB states in Figure 3a? If so, what are the main quantitative differences? These are the questions to be addressed in this section.
Unfortunately, orthogonal transformation is not unique from the set of well-defined VB-diabatic states.1,21 Here, we examine several orthogonal transformation procedures and compare the results with the well-tested 3-fold-way diabatization approach. One seemingly appealing approach is the Löwdin transformation using (S)−1/2, where S is the overlap matrix of the VB-diabatic states, which transforms the original vectors into orthogonal ones in a least-squares sense by mixing all configurations. This turns out not to be a good choice since the potential energy curves of the resulting states are severely distorted such that they resemble neither the original diabatic states nor the adiabatic ones (not shown here, but see ref 58 for another system).
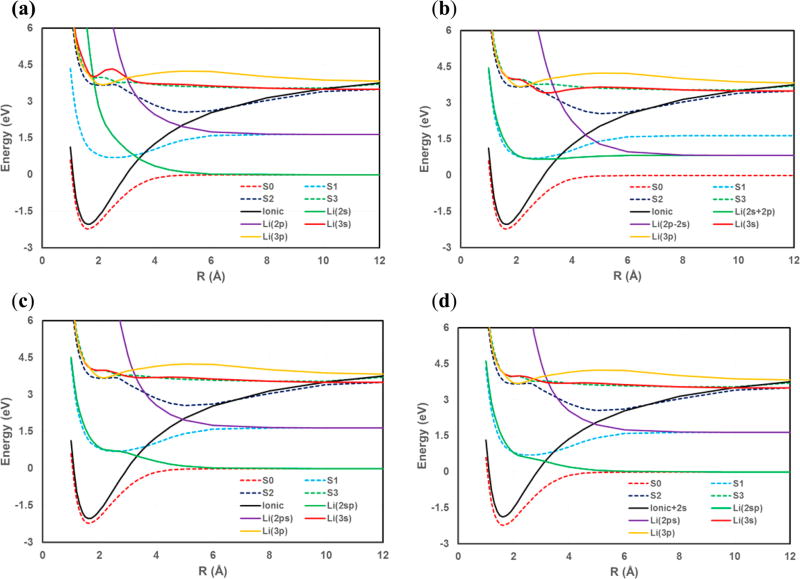
The Gram-Schmidt (GS) orthogonalization method can maximally preserve the characters of each individual state sequentially; here, we follow the order of increasing energy–ionic, 2s, 2p, 3s, 3p, the “reverse ionic”, and the H-2s diabatic states–to describe the four lowest 1Σ+ states of LiH. A set of four different GS transformations of the VB-diabatic states into orthogonal ones, all of which yield the same adiabatic potential energy curves, is shown in Figure 4. They differ in the way of mixing some basis CSFs prior to the GS transformation:
direct GS orthogonalization;
- an equal mixture of 2s and 2p states of Li
where Nb is a normalization factor; - the same sp-mixing as in (b) scaled by the overlap
integral - the inclusion of a small amount (25%) of the 2s-covalent state (also overlap-dependent) in the ionic configuration
Figure 4.
Orthogonalized diabatic (dashed curves) potential energy curves of LiH as a function of interatomic separation, transformed from the nonorthogonal VB-diabatic states in Figure 3(a) by (a) direct Gram-Schmidt (GS) orthogonalization, (b) GS-projection of mixed of 2s and 2p covalent states, (c) 2s-2p mixing scaled by the overlap integral, and (d) as in (c) along with a small amount of 25% 2s state added to the ionic state. The adiabatic potential energy curves are shown as solid curves.
Gram-Schmidt orthogonalization keeping the valence character of the ionic state immediately leads to the familiar curve-crossing features between “neighboring” diabatic states that yield various avoided crossings in the adiabatic curves (Figure 4a). However, the direct GS orthogonalization of the VB diabatic state vectors does not produce a diabatic state closely resembling the first excited state; the latter is formed as a result of antibonding and bonding combinations of the 2s(Li) and 2p(Li) states with hydrogen’s 1s(H), i.e., an sp-hybrid. A simple mixture of 2s(Li) and 2p(Li) configurations is not chemically physical, yielding both states having the same energy at the dissociation limit in Figure 4(b). The sp-hybridization takes place due to chemical bonding interactions at short interatomic distances, which is overlap dependent. As a result, the bonding patterns seen in the 3-fold-way diabatization procedure are reproduced in Figures 4(c) and 4(d) when the 2s-2p mixing is scaled by the overlap integral; Figure 4(d) also includes a small portion of 2s-covalent character in the ionic state.
Figures 4(c) and 4(d) show that the (Li)+(H)− ionic state is dominant in the ground state near the equilibrium geometry, both in the orthogonal diabatic state representation and in the nonorthogonal VB representation in Figure 3(a). The ionic state smoothly transforms to its dissociation limit, crosses with all other diabatic states, and approaches the S3 adiabatic excited state at 12 Å in the present study. The sp-hybrid covalent diabatic state starts from the A(S1) state at short bond lengths and ends at the ground-state dissociation limit as Li• and H•. In the intermediate bonding region on the A(S1) curve, the ionic state is dominant, whose interactions with the 2p(Li)-1s(H) antibonding diabatic state result in an avoided crossing between the S1 and S2 adiabatic states as the covalent configuration decays to the 2p dissociation limit. The two low-lying crossings occur at about 3.125 and 5 Å in Figures 4(c) and 4(d), somewhat longer than those generated by the 3-fold-way diabatization method (2.9 and 3.7 Å) but closer to the minimum-gap positions of the corresponding avoided potential energy curves, and to values of 3.2 and 5.3 Å from a diabatization based on nonadiabatic coupling terms.22 Importantly, all diabatic and adiabatic potential energy surfaces are smooth at all geometries.
The S2 and S3 states possess two avoided crossings: one at an outer range near 10 Å due to the (Li)+(H)− ionic and 3s(Li) interactions and another at the inner distance of about 2.5 Å. The orthogonal diabatic states in Figure 4 (irrespective to the specific orthgonalization details) show that the latter crossing at short distance involves interactions primarily between the 3s(Li) and 3p(Li) states with the participation of the strongly repulsive 2p(Li) state and of 2s(H) character (not shown). These results are consistent with previous analysis of LiH excited states and with the finding that the ionic-3s and 3p state crossings with the ionic state occur at about 10 and 18 Å.22,71,72,90 Figure 4 shows that the nonorthogonal VB states can indeed be orthogonalized to yield diabatic states qualitatively similar to those from the Three-Fold-Way ATD transformation procedure, although the 2p diabatic state is much more repulsive and shows no particular dependence to the higher adiabatic curves. An overlap-dependent mixing of certain VB states before the diagonalization process is needed to represent orbital hybridization. Importantly, the similarity transformation procedure must maintain certain key identities (e.g., the ionic valency and dissociation limits) of the original vectors. We note also that there is no issue concerning phase consistency of the DAC diabatic states,10,34 which is critical in the ATD transformation process; in MSDFT, phases are explicitly expressed, in conjunction with the off-diagonal Hamiltonian matrix elements, in the overlap integral between different states in defining orthogonal as well as nonorthogonal diabatic states.
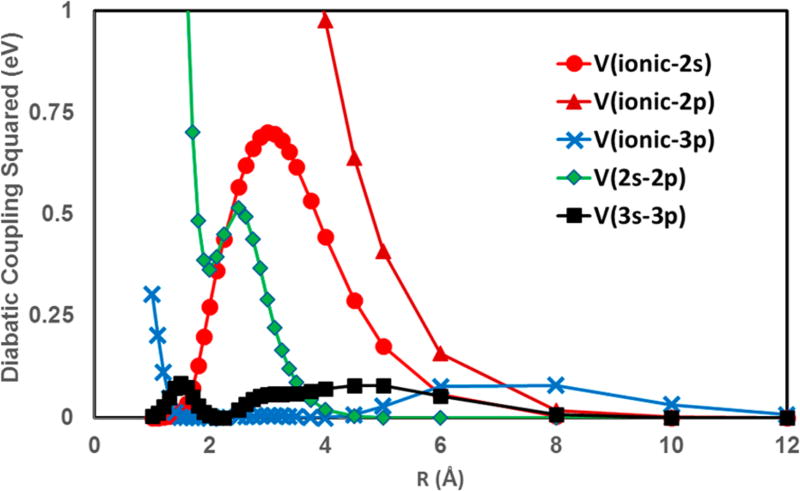
D. Diabatic Coupling
The squared diabatic couplings (i.e., the off-diagonal elements of the diabatic Hamiltonian for the orthogonalized diabatic states) energies are shown in Figure 5 for the diabatic states of Figure 4d. Since there are numerous pairs among the diabatic states in the present MSDFT approach, which is not restricted to only four adiabatic surfaces, for clarity we show only a few selected couplings directly relevant to the avoided crossing interactions. The diabatic states in the present MSDFT approach are all fully coupled, and their diabatic couplings do not necessarily show peaked values near the crossing geometries often found in the ATD transformed diabatic states.10,40,41 This is because, given that the orthogonalization of the VB diabatic states yielded crossings near the minimum gap region of the adiabatic potential energy curves, they still retain their respective valence character. In MSDFT, diabatic interactions do not vanish at short interatomic distances, and they play a crucial role in chemical bond formation in all states. On the other hand, the “diabatic couplings” in the ATD transformation quickly decay to nearly zero away from the avoided crossing geometries. These differences between the ATD transformed states and the present DAC states may have consequences in dynamic simulations of nonadiabatic processes, and further studies of their performances, which are beyond the scope of this article on the PES itself, would be interesting.
Figure 5.
Squared diabatic couplings between selected pairs of orthogonal diabatic states of LiH shown in Figure 4(d) as a function of interatomic separation. All results are determined by MSDFT with the aug-cc-pVTZ basis set (see Figure 1).
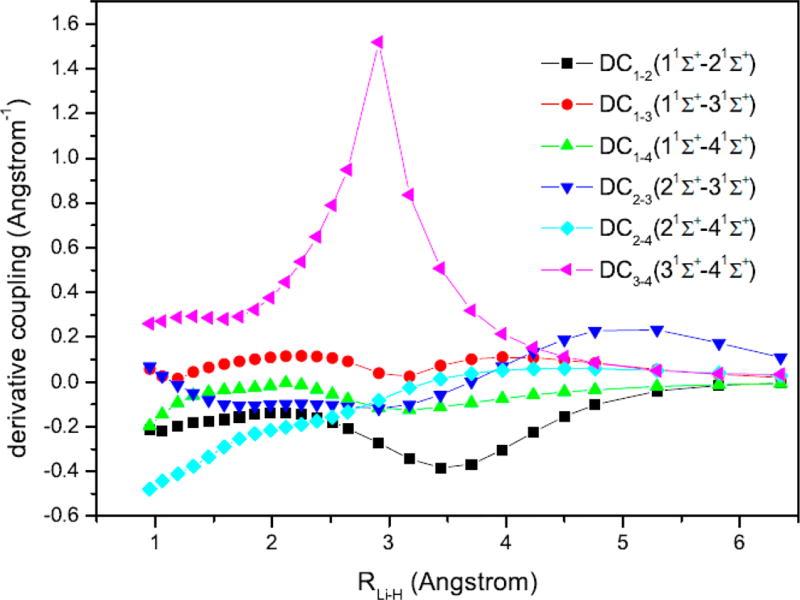
In the present study, we have not attempted to minimize the derivative coupling nor have we examined if the VB-inspired, DAC diabatic states actually minimize derivative coupling. In the present case, as there is only one degree of freedom, we can determine the derivative coupling in the bond dissociation coordinate. The MSDFT derivative coupling results are shown in Figure 6. It would be interesting to examine this property on complex systems.
Figure 6.
Computed derivative coupling values, ⟨ΨI(r;R)|∇R|ΨJ(r;R)⟩ for various states indicated as a function of interatomic separation. All results are determined by MSDFT with the aug-cc-pVTZ basis set (see Figure 1).
5. CONCLUDING REMARKS
Multistate density functional theory (MSDFT) for the calculation of adiabatic and diabatic potentials is presented, and it is illustrated for the extensively studied LiH diatomic molecule. The method represents the ground and excited states and their potential energy curves according to Lewis resonance structures of a given molecular system. The present method belongs to a category called diabatic-at-construction (DAC) strategy, which differs from the more widely used adiabatic-to-diabatic (ATD) transformation procedure. The DAC diabatic states are nonorthogonal, and they are defined (or, the CSFs can be directly used) as the basis states in an active space for configuration interaction to yield the adiabatic states. This is in contrast to the ATD approach, which is based on an orthogonal transformation of a set of preselected adiabatic states and a similarity transformation of their energies. There is no rigorous physical interpretation of any set of diabatic states since they are not unique, but the DAC diabatic states are formulated according to the valence bond characters of the dissociation limits of different adiabatic states, which are strictly maintained at all molecular geometries. Therefore, the DAC diabatic states have well-defined physical and chemical meanings, which provide further insight in the understanding of bonding interactions and for determination of specific energy contributions by energy decomposition analysis.63,67 The adequacy and completeness of such interpretations and energy component analyses can be validated by the results of the electronic couplings among the DAC states.
Qualitative trends of the ATD diabatic states derived by the 3-fold way from the relevant adiabatic states can be reproduced by similarity transformation of the nonorthogonal DAC diabatic states, and comparison between the two reveals certain necessary conditions required for this agreement, including mixing of some VB states and retaining the dissociation limits. Quantitative results on the computed diabatic couplings indicate that the ATD diabatic states represent essentially mixed adiabatic potential energy curves away from the avoided crossing regions with diminished diabatic couplings but peaked values in these regions. On the other hand, orthogonalized DAC diabatic states do not generally exhibit peaked diabatic couplings at the avoided crossings (although some states do), since they are responsible for chemical bonding interactions. It would be interesting in future studies to gain an understanding of the different roles of the different diabatic couplings from the ATD and the DAC states in dynamic simulations.
Supplementary Material
Acknowledgments
The work was supported in part by grants from the National Natural Science Foundation of China (Grant Number 91541124) and the National Institutes of Health (GM46736) to J.G. and by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0015997 (D.G.T.).
Footnotes
ASSOCIATED CONTENT
- Summary of orbital optimization for block-localized Kohn–Sham density functional theory and the numerical data for all figures (PDF)
The authors declare no competing financial interest.
References
- 1.Numrich RW, Truhlar DG. Mixing of ionic and covalent configurations for sodium hydride, potassium hydride, and hydromagnesium(1+). Potential energy curves and couplings between molecular states. J. Phys. Chem. 1975;79:2745–2766. [Google Scholar]
- 2.Yarkony DR. Diabolical conical intersections. Rev. Mod. Phys. 1996;68:985–1013. [Google Scholar]
- 3.Mo Y, Gao J. An Ab Initio Molecular Orbital-Valence Bond (MOVB) Method for Simulating Chemical Reactions in Solution. J. Phys. Chem. A. 2000;104:3012–3020. [Google Scholar]
- 4.Nakamura H, Truhlar DG. The direct calculation of diabatic states based on configurational uniformity. J. Chem. Phys. 2001;115:10353–10372. [Google Scholar]
- 5.Japser AW, Kendrick CA, Mead CA, Truhlar DG. In: In Modern Trends in Chemical Reaction Dynamics: Eperiment and Theory (Part I) Yang X, Liu K, editors. World Scientific; Singapore: 2004. pp. 329–391. [Google Scholar]
- 6.Koppel H. Diabatic representation: methods for the constrution of diabatic electronic states. In: Domcke W, Yarkony DR, Koppel H, editors. Conical Intersections: Electronic Structure, Dynamics and Spectroscopy. World Scientific Publishing Co.; Hackensack, NJ: 2004. pp. 175–204. [Google Scholar]
- 7.Song L, Gao J. On the Construction of Diabatic and Adiabatic Potential Energy Surfaces Based on Ab Initio Valence Bond Theory. J. Phys. Chem. A. 2008;112:12925–12935. doi: 10.1021/jp803050e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhu XL, Yarkony DR. Toward eliminating the electronic structure bottleneck in nonadiabatic dynamics on the fly: An algorithm to fit nonlocal, quasidiabatic, coupled electronic state Hamiltonians based on ab initio electronic structure data. J. Chem. Phys. 2010;132:104101. doi: 10.1063/1.3324982. [DOI] [PubMed] [Google Scholar]
- 9.Domcke W, Yarkony DR. Role of Conical Intersections in Molecular Spectroscopy and Photoinduced Chemical Dynamics. Annu. Rev. Phys. Chem. 2012;63:325–352. doi: 10.1146/annurev-physchem-032210-103522. [DOI] [PubMed] [Google Scholar]
- 10.Li SHL, Truhlar DG, Schmidt MW, Gordon MS. Model space diabatization for quantum photochemistry. J. Chem. Phys. 2015;142:064106. doi: 10.1063/1.4907038. [DOI] [PubMed] [Google Scholar]
- 11.Halvick P, Truhlar DG. A new diabatic representation of the coupled potential energy surfaces for sodium(3p 2P) + molecular hydrogen.fwdarw. sodium(3s 2S) + molecular hydrogen or sodium hydride + atomic hydrogen. J. Chem. Phys. 1992;96:2895–2909. [Google Scholar]
- 12.Jasper AW, Zhu CY, Nangia S, Truhlar DG. Introductory lecture: Nonadiabatic effects in chemical dynamics. Faraday Discuss. 2004;127:1–22. doi: 10.1039/b405601a. [DOI] [PubMed] [Google Scholar]
- 13.Levine BG, Ko C, Quenneville J, Martinez TJ. Conical intersections and double excitations in time-dependent density functional theory. Mol. Phys. 2006;104:1039–1051. [Google Scholar]
- 14.Huix-Rotllant M, Nikiforov A, Thiel W, Filatov M. Description of Conical Intersections with Density Functional Methods. Top. Curr. Chem. 2015;368:445–476. doi: 10.1007/128_2015_631. [DOI] [PubMed] [Google Scholar]
- 15.Li SHL, Marenich AV, Xu XF, Truhlar DG. Configuration Interaction-Corrected Tamm-Dancoff Approximation: A Time-Dependent Density Functional Method with the Correct Dimensionality of Conical Intersections. J. Phys. Chem. Lett. 2014;5:322–328. doi: 10.1021/jz402549p. [DOI] [PubMed] [Google Scholar]
- 16.Yang Y, Shen L, Zhang D, Yang WT. Conical Intersections from Particle-Particle Random Phase and Tamm-Dancoff Approximations. J. Phys. Chem. Lett. 2016;7:2407–2411. doi: 10.1021/acs.jpclett.6b00936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Herbert JM, Zhang X, Morrison AF, Liu J. Beyond Time-Dependent Density Functional Theory Using Only Single Excitations: Methods for Computational Studies of Excited States in Complex Systems. Acc. Chem. Res. 2016;49:931–941. doi: 10.1021/acs.accounts.6b00047. [DOI] [PubMed] [Google Scholar]
- 18.Gao J, Grofe A, Ren H, Bao P. Beyond Kohn-Sham approximation: Hybrid multistate wave function and density functional theory. J. Phys. Chem. Lett. 2016;7:5143–5149. doi: 10.1021/acs.jpclett.6b02455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nakamura H, Truhlar DG. Direct diabatization of electronic states by the fourfold way. II. Dynamical correlation and rearrangement processes. J. Chem. Phys. 2002;117:5576–5593. [Google Scholar]
- 20.Baer M. Beyond Born-Oppenheimer: Electronic Nonadiabatic Coupling Terms and Conical Intersections. Wiley; New York: 2006. [Google Scholar]
- 21.Mead CA, Truhlar DG. Conditions for the definition of a strictly diabatic electronic basis for molecular systems. J. Chem. Phys. 1982;77:6090–6098. [Google Scholar]
- 22.Boutalib A, Gadea FX. Abinitio Adiabatic and Diabatic Potential-Energy Curves of the Lih Molecule. J. Chem. Phys. 1992;97:1144–1156. [Google Scholar]
- 23.Berriche H, Gadea FX. Ab-Initio Adiabatic and Diabatic Permanent Dipoles for the Low-Lying States of the Lih Molecule - a Direct Illustration of the Ionic Character. Chem. Phys. Lett. 1995;247:85–88. [Google Scholar]
- 24.Zhang P, Morokuma K, Wodtke AM. High-level ab initio studies of unimolecular dissociation of the ground-state N-3 radical. J. Chem. Phys. 2005;122:014106. doi: 10.1063/1.1804497. [DOI] [PubMed] [Google Scholar]
- 25.Viel A, Eisfeld W, Evenhuis CR, Manthe U. Photoionization- induced dynamics of the ammonia cation studied by wave packet calculations using curvilinear coordinates. Chem. Phys. 2008;347:331–339. [Google Scholar]
- 26.Mota VC, Varandas AJC. HN2((2)A ’) electronic manifold. II. Ab initio based double-sheeted DMBE potential energy surface via a global diabatization angle. J. Phys. Chem. A. 2008;112:3768–3786. doi: 10.1021/jp710610d. [DOI] [PubMed] [Google Scholar]
- 27.Subotnik JE, Yeganeh S, Cave RJ, Ratner MA. Constructing diabatic states from adiabatic states: Extending generalized Mulliken-Hush to multiple charge centers with Boys localization. J. Chem. Phys. 2008;129:244101. doi: 10.1063/1.3042233. [DOI] [PubMed] [Google Scholar]
- 28.Zhang AJ, Zhang PY, Chu TS, Han KL, He GZ. Quantum dynamical study of the electronic nonadiabaticity in the D +DBr ® BRBr*)+D2 reaction on new diabatic potential energy surfaces. J. Chem. Phys. 2012;137:194305. doi: 10.1063/1.4766355. [DOI] [PubMed] [Google Scholar]
- 29.Domcke W, Woywod C. Direct Construction of Diabatic States in the Casscf Approach - Application to the Conical Intersection of the (1)a(2) and B-1(1) Excited-States of Ozone. Chem. Phys. Lett. 1993;216:362–368. [Google Scholar]
- 30.Godsi O, Evenhuis CR, Collins MA. Interpolation of multidimensional diabatic potential energy matrices. J. Chem. Phys. 2006;125:104105. doi: 10.1063/1.2338912. [DOI] [PubMed] [Google Scholar]
- 31.Ou Q, Bellchambers GD, Furche F, Subotnik JE. First-order derivative couplings between excited states from adiabatic TDDFT response theory. J. Chem. Phys. 2015;142 doi: 10.1063/1.4906941. 142-064114. [DOI] [PubMed] [Google Scholar]
- 32.Zhu XL, Malbon CL, Yarkony DR. An improved quasidiabatic representation of the 1, 2, 3(1)A coupled adiabatic potential energy surfaces of phenol in the full 33 internal coordinates. J. Chem. Phys. 2016;144:124312. doi: 10.1063/1.4944091. [DOI] [PubMed] [Google Scholar]
- 33.Zhu XL, Yarkony DR. Constructing diabatic representations using adiabatic and approximate diabatic data - Coping with diabolical singularities. J. Chem. Phys. 2016;144:044104. doi: 10.1063/1.4939765. [DOI] [PubMed] [Google Scholar]
- 34.Atchity GJ, Ruedenberg K. Determination of diabatic states through enforcement of configurational uniformity. Theor. Chem. Acc. 1997;97:47–58. [Google Scholar]
- 35.Nakamura H, Truhlar DG. Extension of the fourfold way for calculation of global diabatic potential energy surfaces of complex, multiarrangement, non-Born-Oppenheimer systems: Application to HNCO(S-0,S-1) J. Chem. Phys. 2003;118:6816–6829. [Google Scholar]
- 36.Subotnik JE, Vura-Weis J, Sodt AJ, Ratner MA. Predicting Accurate Electronic Excitation Transfer Rates via Marcus Theory with Boys or Edmiston-Ruedenberg Localized Diabatization. J. Phys. Chem. A. 2010;114:8665–8675. doi: 10.1021/jp101235a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Alguire E, Subotnik JE. Diabatic couplings for charge recombination via Boys localization and spin-flip configuration interaction singles. J. Chem. Phys. 2011;135:044114. doi: 10.1063/1.3615493. [DOI] [PubMed] [Google Scholar]
- 38.Simah D, Hartke B, Werner HJ. Photodissociation dynamics of H2S on new coupled ab initio potential energy surfaces. J. Chem. Phys. 1999;111:4523–4534. [Google Scholar]
- 39.Fulscher MP, Serrano-Andres L. Quasi diabatic CASSCF state functions. Mol. Phys. 2002;100:903–909. [Google Scholar]
- 40.Hoyer CE, Parker K, Gagliardi L, Truhlar DG. The DQ and DQ Phi electronic structure diabatization methods: Validation for general applications. J. Chem. Phys. 2016;144:194101. doi: 10.1063/1.4948728. [DOI] [PubMed] [Google Scholar]
- 41.Hoyer CE, Xu XF, Ma DX, Gagliardi L, Truhlar DG. Diabatization based on the dipole and quadrupole: The DQ method. J. Chem. Phys. 2014;141:114104. doi: 10.1063/1.4894472. [DOI] [PubMed] [Google Scholar]
- 42.Siegbahn P, Heiberg A, Roos B, Levy B. Comparison of the Super-Cl and the Newton-Raphson Scheme in the Complete Active Space Scf Method. Phys. Scr. 1980;21:323–327. [Google Scholar]
- 43.Finley J, Malmqvist PA, Roos BO, Serrano-Andres L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998;288:299–306. [Google Scholar]
- 44.Werner HJ, Knowles PJ. A 2nd Order Multiconfiguration SCF Procedure with Optimum Convergence. J. Chem. Phys. 1985;82:5053–5063. [Google Scholar]
- 45.Nakano H, Hirao K, Gordon MS. Analytic energy gradients for multiconfigurational self-consistent field second-order quasidegenerate perturbation theory (MC-QDPT) J. Chem. Phys. 1998;108:5660. [Google Scholar]
- 46.Lischka H, Dallos M, Szalay PG, Yarkony DR, Shepard R. Analytic evaluation of nonadiabatic coupling terms at the MR-CI level. I. Formalism. J. Chem. Phys. 2004;120:7322–7329. doi: 10.1063/1.1668615. [DOI] [PubMed] [Google Scholar]
- 47.Buenker RJ, Peyerimhoff SD, Butscher W. Applicability of Multi-Reference Double-Excitation Ci (Mrd-Ci) Method to Calculation of Electronic Wavefunctions and Comparison with Related Techniques. Mol. Phys. 1978;35:771–791. [Google Scholar]
- 48.Werner H-J, Reinsch E-A. The self-consistent electron pairs method for multiconfiguration reference state functions. J. Chem. Phys. 1982;76:3144–3146. [Google Scholar]
- 49.Cohen AJ, Mori-Sanchez P, Yang WT. Challenges for Density Functional Theory. Chem. Rev. 2012;112:289–320. doi: 10.1021/cr200107z. [DOI] [PubMed] [Google Scholar]
- 50.Cembran A, Song L, Mo Y, Gao J. Block-localized density functional theory (BLDFT), diabatic coupling, and its use in valence bond theory for representing reactive potential energy surfaces. J. Chem. Theory Comput. 2009;5:2702–2716. doi: 10.1021/ct9002898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ren HS, Provorse MR, Bao P, Qu ZX, Gao JL. Multistate Density Functional Theory for Effective Diabatic Electronic Coupling. J. Phys. Chem. Lett. 2016;7:2286–2293. doi: 10.1021/acs.jpclett.6b00915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Venghaus F, Eisfeld W. Block-diagonalization as a tool for the robust diabatization of high-dimensional potential energy surfaces. J. Chem. Phys. 2016;144:114110. doi: 10.1063/1.4943869. [DOI] [PubMed] [Google Scholar]
- 53.Wittenbrink N, Venghaus F, Williams D, Eisfeld W. A new approach for the development of diabatic potential energy surfaces: Hybrid block-diagonalization and diabatization by ansatz. J. Chem. Phys. 2016;145:184108. doi: 10.1063/1.4967258. [DOI] [PubMed] [Google Scholar]
- 54.Tamura H. Diabatization for Time-Dependent Density Functional Theory: Exciton Transfers and Related Conical Intersections. J. Phys. Chem. A. 2016;120:9341–9347. doi: 10.1021/acs.jpca.6b09854. [DOI] [PubMed] [Google Scholar]
- 55.Mo YR, Wu W, Zhang QN. Valence-Bond Description for the Ground-State and Several Low-Lying Excited-States of Lih. J. Mol. Struct.: THEOCHEM. 1993;283:237–249. [Google Scholar]
- 56.Mo Y, Gao J. Ab initio QM/MM simulations with a molecular orbital-valence bond (MOVB) method: application to an SN2 reaction in water. J. Comput. Chem. 2000;21:1458–1469. [Google Scholar]
- 57.Cembran A, Payaka A, Lin YL, Xie WS, Mo YR, Song LC, Gao JL. A Non-Orthogonal Block-Localized Effective Hamiltonian Approach for Chemical and Enzymatic Reactions. J. Chem. Theory Comput. 2010;6:2242–2251. doi: 10.1021/ct1001686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Valero R, Song L, Gao J, Truhlar DG. Perspective on Diabatic Models of Chemical Reactivity as Illustrated by the Gas-Phase SN2 Reaction of Acetate Ion with 1,2-Dichloroethane. J. Chem. Theory Comput. 2009;5:1–22. doi: 10.1021/ct9002459. [Erratum, June 10, 2009]. [DOI] [PubMed] [Google Scholar]
- 59.Kaduk B, Van Voorhis T. Communication: Conical intersections using constrained density functional theory-configuration interaction. J. Chem. Phys. 2010;133:061102. doi: 10.1063/1.3470106. [DOI] [PubMed] [Google Scholar]
- 60.Van Voorhis T, Kowalczyk T, Kaduk B, Wang LP, Cheng CL, Wu Q. The Diabatic Picture of Electron Transfer, Reaction Barriers, and Molecular Dynamics. Annu. Rev. Phys. Chem. 2010;61:149–170. doi: 10.1146/annurev.physchem.012809.103324. [DOI] [PubMed] [Google Scholar]
- 61.Mo Y, Peyerimhoff SD. Theoretical analysis of electronic delocalization. J. Chem. Phys. 1998;109:1687–1697. [Google Scholar]
- 62.Mo Y, Zhang Y, Gao J. A Simple Electrostatic Model for Trisilylamine: Theoretical Examinations of the n→σ Negative Hyperconjugation, pπ→dπ Bonding, and Stereoelectronic Interaction. J. Am. Chem. Soc. 1999;121:5737–5742. [Google Scholar]
- 63.Mo Y, Gao J, Peyerimhoff SD. Energy decomposition analysis of intermolecular interactions using a block-localized wave function approach. J. Chem. Phys. 2000;112:5530–5538. [Google Scholar]
- 64.Cooper DL, Gerratt J, Raimondi M. Applications of spincoupled valence bond theory. Chem. Rev. 1991;91:929–964. [Google Scholar]
- 65.Gerratt J, Cooper DL, Karadakov PB, Raimondi M. Modern valence bond theory. Chem. Soc. Rev. 1997;26:87–100. [Google Scholar]
- 66.Cembran A, Provorse MR, Wang CW, Wu W, Gao JL. The Third Dimension of a More O’Ferrall-Jencks Diagram for Hydrogen Atom Transfer in the Isoelectronic Hydrogen Exchange Reactions of (PhX)2H* with X = O, NH, and CH2. J. Chem. Theory Comput. 2012;8:4347–4358. doi: 10.1021/ct3004595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mo YR, Bao P, Gao JL. Energy decomposition analysis based on a block-localized wavefunction and multistate density functional theory. Phys. Chem. Chem. Phys. 2011;13:6760–6775. doi: 10.1039/c0cp02206c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mavros MG, Van Voorhis T. Communication: CDFT-CI couplings can be unreliable when there is fractional charge transfer. J. Chem. Phys. 2015;143:231102. doi: 10.1063/1.4938103. [DOI] [PubMed] [Google Scholar]
- 69.Gim Y, Lee CW. Studies of singlet Rydberg series of LiH derived from Li(nl) + H(1s), with n ≤ 6 and l ≤ 4. J. Chem. Phys. 2014;141:144313. doi: 10.1063/1.4897564. [DOI] [PubMed] [Google Scholar]
- 70.Gadea FX, Boutalib A. Computation and Assignment of Radial Couplings Using Accurate Diabatic Data for the LiH Molecule. J. Phys. B: At., Mol. Opt. Phys. 1993;26:61–74. [Google Scholar]
- 71.Gadea FX, Leininger T. Accurate ab initio calculations for LiH and its ions, LiH+ and LiH−. Theor. Chem. Acc. 2006;116:566–575. [Google Scholar]
- 72.Bande A, Nakashima H, Nakatsuji H. LiH potential energy curves for ground and excited states with the free complement local Schrodinger equation method. Chem. Phys. Lett. 2010;496:347–350. [Google Scholar]
- 73.Lamoudi N, Bouledroua M, Alioua K, Allouche AR, Aubert-Frecon M. Theoretical investigation of the lithium 2p ← 2s photoabsorption spectra perturbed by atomic hydrogen. Phys. Rev. A: At., Mol., Opt. Phys. 2013;87:052713. [Google Scholar]
- 74.Habli H, Mejrissi L, Ghalla H, Yaghmour SJ, Oujia B, Gadea FX. Ab initio investigation of the electronic and vibrational properties for the (CaLi)(+) ionic molecule. Mol. Phys. 2016;114:1568–1582. [Google Scholar]
- 75.Stwalley WC, Zemke WT. Spectroscopy and Structure of the Lithium Hydride Diatomic-Molecules and Ions. J. Phys. Chem. Ref. Data. 1993;22:87–112. [Google Scholar]
- 76.Liu WJ. Ideas of relativistic quantum chemistry. Mol. Phys. 2010;108:1679–1706. [Google Scholar]
- 77.Liu WJ, Hoffmann MR. iCI: Iterative CI toward Full CI. J. Chem. Theory Comput. 2016;12:1169–1178. doi: 10.1021/acs.jctc.5b01099. [DOI] [PubMed] [Google Scholar]
- 78.King HF, Stanton RE, Kim H, Wyatt RE, Parr RG. Corresponding orbitals and the nonorthogonality problems in molecular quantum mechanics. J. Chem. Phys. 1967;47:1936. [Google Scholar]
- 79.Truhlar DG, Mullaney NA. Semi-Classical Exchange Approximation for Inelastic Electron-Scattering. J. Chem. Phys. 1978;68:1574–1584. [Google Scholar]
- 80.Li Manni G, Carlson RK, Luo SJ, Ma DX, Olsen J, Truhlar DG, Gagliardi L. Multiconfiguration Pair-Density Functional Theory. J. Chem. Theory Comput. 2014;10:3669–3680. doi: 10.1021/ct500483t. [DOI] [PubMed] [Google Scholar]
- 81.Dunning TH., Jr Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989;90:1007–1023. [Google Scholar]
- 82.Dunning TH, Hay PJ. In: Methods of Electronic Structure Theory. Schaefer HF III, editor. Vol. 3. Plenum Press; 1977. pp. 1–28. [Google Scholar]
- 83.Moore CE. Atomic Energy Levels, Nat. Bur. Stand., Circ. No. 467. U.S. GPO; Washington, DC: 1971. [Google Scholar]
- 84.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 85.Adamo C, Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999;110:6158–6170. [Google Scholar]
- 86.Chan W-L, Berkelbach TC, Provorse MR, Monahan NR, Tritsch JR, Hybertsen MS, Reichman DR, Gao J, Zhu X-Y. The quantum coherent mechanism for singlet fission: Experiment and theory. Acc. Chem. Res. 2013;46:1321–1329. doi: 10.1021/ar300286s. [DOI] [PubMed] [Google Scholar]
- 87.Werner HJ, Knowles JR, Knizia G, Manby FR, Schutz M, et al. [accessed Feb 6, 2017];MOLPRO – version 2012.1. 2012 http://www.molpro.net.
- 88.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Matsunaga N, Nguyen KA, Su SJ, Windus TL, Dupuis M, Montgomery JS. General atomic and molecular electronic structure system. J. Comput. Chem. 1993;14:1347–1363. [Google Scholar]
- 89.Huang YL, Luh WT, Jeung GH, Gadea FX. The D 1Σ+ state of 7LiH. J. Chem. Phys. 2000;113:683–689. [Google Scholar]
- 90.Habli H, Ghalla H, Oujia B, Gadea FX. Ab initio study of spectroscopic properties of the calcium hydride molecular ion. Eur. Phys. J. D. 2011;64:5–19. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.