Multiple Overlapping k-Space Junctions for Investigating Translating Objects (MOJITO)

Abstract

It is a well-known property in Fourier transform magnetic resonance imaging (MRI) that rigid body translational motion in image space results in linear phase accumulation in k-space. This work describes Multiple Overlapping k-space Junctions for Investigating Translating Objects (MOJITO), a correction scheme based on phase differences at trajectory intersections caused by 2-D alterations in the position of an object during MR imaging. The algorithm allows both detection and correction of motion artifacts caused by 2-D rigid body translational motion. Although similar in concept to navigator echoes, MOJITO does not require a repeating path through k-space, uses k-space data from a broader region of k-space, and uses the repeated data in image reconstruction; this provides the potential for a highly efficient self-navigating motion correction method. Here, the concept and theoretical basis of MOJITO is demonstrated using the continuous sampling BOWTIE trajectory in simulation and MR experiments. This particular trajectory is selected since it is well suited for such an algorithm due to numerous trajectory intersections. Specifically, the validity of the technique in the presence of noise and off-resonance effects is demonstrated through simulation.

I. Introduction

Continuous sampling [1], [2] in magnetic resonance imaging has been previously described as the extension of the data acquisition window to sample the induced signal throughout the entire image plane gradient application. In the simplest case of Broad Oversampling With TIme Efficiency (BOWTIE) [3], a hybrid Cartesian/radial trajectory [Fig. 1(a)] is produced by sampling overlapping phase encode and dephase/rephase read gradient waveforms [Fig. 1(b)] after slice excitation and refocusing; more complicated 3-D BOWTIE trajectories in which all gradient lobes overlap have also been described. BOWTIE requires unique reconstruction processes (i.e., gridding reconstructions), but results in an increase in signal-to-noise ratio (SNR) without significantly increasing acquisition time when compared to a conventional rectilinear acquisition [3].

Fig. 1.

BOWTIE trajectory (a) with MOJITO intersections and image plane gradient (b) are shown. In (a), the white circles represent the intersection of the radial and Cartesian portions of the BOWTIE PE lines that will be used for motion correction of the dotted PE line with respect to the thick, solid PE line. The black circles represent additional intersections for correction of other PE lines.

However, the utility of magnetic resonance imaging (MRI) may be limited by factors other than SNR, like artifacts resulting from translational or periodic physiologic motion. These motion artifacts may appear as ghosting, streaking, or blurring; their appearance in the image is dependent also upon the k-space trajectory. Many motion correction methods require collection of extra data (e.g., navigator echoes [4]–[6] and adaptive averaging [7]) which may increase acquisition time. Bammer et al. [8] uses spirals, or variable density spiral data as navigator data in which gaps between data points needed for consistency are provided by SENSE parallel imaging methods. Cardiac and respiratory gating methods often use external signals (i.e., ECG or respiratory bellows) to limit the acquisition to periods of relative low motion or consistent temporal location during periodic motion. Self-gating methods [9]–[11] have been proposed to reduce external gating complexity, but these and traditional gating methods only detect motion and cannot retrospectively correct the corrupted data. More recently, the self-navigating PROPELLER trajectory [12] (and the earlier, closely related variant RUKSE [13]) uses the correlation characteristics of the oversampled center of k-space to allow rigid body motion correction resulting from translational and/or rotational motion. However, PROPELLER corrects blocks of data at each time, so the temporal scale over which motion is corrected may be limited. The limitation of the interval over which motion may be corrected is also seen with motion corrections based on detection of discontinuities in k-space [14]. The butterfly trajectory [15], a variation of BOWTIE, repeats one of two short paths through k-space within every TR for self-navigation, yet is unable to correct for rotational motion and the navigator data is not used during image reconstruction. SMASH navigators [16] have been shown to correct motion corrupted data using multiple receiver coil data at no extra time, but may suffer from SMASH fitting errors. Despite these corrections, motion artifacts continue to be problematic in clinical practice.

Here, we describe how the unique traversal of k-space by intersecting k-space trajectories, like BOWTIE, allow correction of rigid body 2-D in-plane translational motion using phase differences at trajectory intersections: a method we have called Multiple Overlapping k-space Junctions for Investigating Translating Objects (MOJITO). Differences in phase are attributed to motion occurring in the interval between the acquisition of intersecting points. Calculated phase differences and known k-space locations are used to calculate a time-dependent representation of motion occurring throughout the acquisition. Unlike conventional navigator techniques, MOJITO allows motion artifact correction consistent with other methods without repeating large portions of k-space and allows the data used to generate the correction to also be used in the reconstruction. Additionally, the MOJITO algorithm with the BOWTIE trajectory takes advantage of continuous sampling of a standard trajectory and allows self-navigating translational motion correction for each line. This study attempts to show that BOWTIE trajectory intersections may be used for in-plane, 2-D translational motion artifact correction using MOJITO via a series of simulations (that include factors like the SNR of the acquired data and field inhomogeneity as variables potentially affecting performance) as well as phantom and in vivo MR experiments.

II. Theory

MOJITO relies on the applicability of the Fourier shift theorem (FST) which limits correctable motion to in-plane translational motion of a rigid body like most other navigator methods. The applicability of the FST not only relies on the type of motion, but also on the assumption that the object does not change (e.g., by deformation or by coil sensitivity). Implications of nonuniform coil sensitivity will be discussed later in this section. MOJITO consists of determining the phase of intersecting points in the k-space trajectory acquired at different times (e.g., during different TRs), calculating the phase differences, solving for object shifts and correcting k-space with respect to a constant reference. These are described more completely below.

A. Fourier Shift Theorem

The standard 2-D MR imaging equation, ignoring relaxation, can be expressed most simply as

$$S(k_x,k_y)=\int \int \rho (x,y)e^{-i2\pi ({\mathit{\text{xk}}}_x+{\mathit{\text{yk}}}_y)}\mathit{\text{dxdy}}$$ (1)

where ρ is the object magnetization (i.e., spin density and relaxation effects), x and y are spatial coordinates, and k_x and k_y are frequency space trajectory coordinates determined by application of magnetic field gradient waveforms. In the presence of motion in the x and/or y direction of amplitude Δx and Δy, respectively, the imaging equation becomes

$$S(k_x,k_y)=e^{-i2\pi (\mathrm{\Delta }{\mathit{\text{xk}}}_x+\mathrm{\Delta }{\mathit{\text{yk}}}_y)}\times \int \int \rho (x,y)e^{-i2\pi ({\mathit{\text{xk}}}_x+{\mathit{\text{yk}}}_y)}\mathit{\text{dxdy}}$$ (2)

according to the FST. Following from (2), the k-space phase difference (Δφ) between two points (separated in time) at the same k-space location (k_x and k_y) in the presence of rigid body 2-D motion can be written as

$$\mathrm{\Delta }\phi =2\pi (k_x{\mathrm{\Delta }}_x+k_y{\mathrm{\Delta }}_y).$$ (3)

This phase difference will be zero in the absence of motion and other phase errors (e.g., field inhomogeneities).

B. BOWTIE Intersections

To calculate a phase shift Δφ, (3) requires the point (k_x, k_y) to be sampled twice; for this analysis, we assume that motion during the intervening interval gives rise to the difference. In the case of navigators, this typically implies the periodic collection of a limited number of phase encode lines. However, in BOWTIE, the intersection of radial and Cartesian components of different data acquisitions provides an inherent method to calculate Δφ without the additional acquisition of navigators.

For example, consider 2-D translational motion occurring between the acquisitions of the two BOWTIE phase encode lines depicted by the thick, dotted and thick solid lines in Fig. 1(a). Suppose one is interested in correcting the effect of motion in the data of the dotted line with respect to the solid line. At intersection 1, two data points, one from the dotted trajectory line (α) and the other from the solid trajectory line (β), are collected and related to signal equations

$$S_{\alpha }(k_{x,1},k_{y,1})=A_{1,\alpha }·\text{exp}(i·{\phi }_{1,\alpha })$$ (4)

$$S_{\beta }(k_{x,1},k_{y,1})=A_{1,\beta }·\text{exp}(i·{\phi }_{1,\beta })$$ (5)

respectively, where A₁ is the magnitude and φ₁ is the phase of the complex signal at k-space location k_x,1 and k_y,1. The phase difference (Δφ₁) between these two points is therefore φ_1,β − φ_1,α = Δφ₁ or, more robustly, is the phase of the multiplication of S_α (k_x,1, k_y,1) and the complex conjugate of S_β (k_x,1, k_y,1). The latter calculation is preferred as it both avoids 2π phase wraps in the difference and also division by zero. The phase difference can be written as

$$\mathrm{\Delta }{\phi }_1=2\pi (k_{x,1}\mathrm{\Delta }{x}_1+k_{y,1}\mathrm{\Delta }{y}_1)$$ (6)

where Δx₁ and Δy₁ describe the relative object shifts between the acquisition of data points S_α (k_x,1, k_y,1) and S_β (k_x,1, k_y,1).

Short sampling times will limit other sources of phase accumulation or signal variation, including motion during the acquisition of a single trajectory line, such that Δx₁ and Δy₁ can approximately describe the change of object location for an entire line in k-space, i.e. when the entire dotted path was acquired compared to the solid path. Therefore, a second equation can be written for intersection 2

$$\mathrm{\Delta }{\phi }_2=2\pi (k_{x,2}\mathrm{\Delta }{x}_1+k_{y,2}\mathrm{\Delta }{y}_1)$$ (7)

which utilizes the same relative changes in position Δx₁ and Δy₁ as intersection 1. Together, (6) and (7) can be solved for the object shifts using simple linear algebra methods.

The calculated shifts (Δx₁ and Δy₁) correct the entire dotted path with respect to the solid path according to the FST

$$S_{\alpha }^{\prime }(k_x,k_y)=S_{\alpha }(k_x,k_y)·\text{exp}(-2\pi i(k_x\mathrm{\Delta }{x}_1+k_y\mathrm{\Delta }{y}_1))$$ (8)

where S_α (k_x, k_y) is the entire BOWTIE path raw data and $S_{\alpha }^{\prime }(k_x,k_y)$ is the corrected BOWTIE path data. This process must then be repeated with different intersections to correct each PE line.

C. BOWTIE Reference Data

The BOWTIE trajectory is well suited for this method of motion correction as it exhibits at least two intersections per PE line (with the exception of the center PE line at k_y = 0). However, because the calculated object shifts describe only relative motion information, every PE line must be corrected with respect to a constant reference over the entire acquisition for an artifact-free image. Here, we assume that at minimum the center three BOWTIE PE lines would provide a constant reference as all other PE lines intersect either k_y = 1 or k_y = −1 twice. The center BOWTIE PE line at k_y = 0 is included in the constant reference because intersections occur only at k_x = k_y = 0 and therefore cannot be corrected using (6) and (7).

In theory, additional reference lines or previously corrected lines allow the inclusion of more intersections and therefore more equations, which can increase the accuracy of the correction. For example, if no motion occurs during the acquisition of the five center k-space lines (or if they were previously corrected), then additional intersections [gray dots, Fig. 1(a)] can also be written as

$$\mathrm{\Delta }{\phi }_j=2\pi (k_{x,j}\mathrm{\Delta }{x}_1+k_{y,j}\mathrm{\Delta }{y}_1)$$ (9)

for the jth intersection. Equation (9) holds for any intersection of the dotted PE line with any other reference line to construct an overdetermined system of equations. However, practically, using previously corrected lines may be problematic in a non-ideal case as errors could propagate throughout the correction.

This overdetermined system of equations can be solved using matrix pseudo-inverse [17] over N intersections. In matrix form

$$\mathit{A}={\mathit{k}}^{-1}\mathbf{\Phi }$$ (10)

where A is the 2 × 1 matrix of Δx and Δy, k⁻¹ is the 2 × N pseudo-inverse matrix of k-space locations, and Φ is the N × 1 matrix of phase differences. The value N will be determined by the number of intersections available per BOWTIE PE line. In the presence of noise, the system can be solved more robustly in the weighted least squares sense as has been previously demonstrated with navigator echoes [18] where the weights are determined by the inverse SNR of the k-space points. The weighted least squares version of (9) can be written as

$$\mathit{A}={({\mathit{k}}^T\mathit{\text{Wk}})}^{-1}{\mathit{k}}^T\mathit{W}\mathbf{\Phi }$$ (11)

where W is a diagonal matrix of weights, T denotes the matrix transpose, and the exponent −1 denotes the matrix inverse.

D. Exact Intersections

Thus far, the analysis has assumed that a particular point in k-space (k_x,j, k_y,j) has been acquired twice at different points in time. Although the BOWTIE trajectory exhibits multiple intersections, the discrete sampling of k-space does not guarantee that a sample will be acquired at the exact k-space locations of the intersections [circles in Fig. 1(a)]. If they do not coincide, the intersection must be interpolated from data points in the vicinity of an intersection. A variety of methods including convolution gridding [19], sinc interpolation [20] and singular value decomposition methods [21] have been developed in nonrectilinear MRI to estimate data at desired k-space locations. This study will predominantly use GRAPPA Operator Regridding (GROG) [22] with multichannel acquisitions to generate intersections from multicoil data which has previously been shown to have similar accuracy when compared to convolution gridding. The rectilinear reference lines provide self-calibration data for GROG. Further, multicoil acquisitions, common in MRI today, increase the level of redundancy by a factor equal to the number of coils, n_c, (e.g., four coils and two intersections yields eights equations and two unknowns). It is important to note that the additional equations are not unique, but rather provide n_c phase differences at one k-space location.

When using multiple coils, it is important to consider the motion of the coil relative to the motion of the object. Bydder et al. defined type 1 motion as object and coil moving together (e.g., a surface coil secured to the object) and type 2 motion as object motion relative to the coil (e.g., a head moving in a stationary head coil) [16]. The same definitions are used here. Type 2 motion may change coil sensitivity maps and coil weights. A changing coil sensitivity map will essentially change the object and therefore violate the Fourier Shift Theorem assumption. This study will focus on the MOJITO method with only type 1 motion.

III. Methods

To test the MOJITO method, a variety of simulations were first performed. In general, simulations used “moving” Shepp–Logan phantoms translating during simulated acquisition of k-space trajectories. To fulfill earlier assumptions, simulated motion occurred only between phase encoding lines for Cartesian and BOWTIE simulations. Simulated data was generated for ideal (i.e., noise free) and Gaussian (white) noise cases. This data was used to calculate translational shifts that were then used to correct data throughout k-space. Differences between the ideal stationary object and reconstructed image were determined in terms of artifact power. An additional measure of performance (residual error), described below, was determined as a function of k-space location and image SNR as noise levels are increased and with variations in background field homogeneity. Specific details are described below.

A. Error Analysis and Notation

Artifact power was calculated as AP = Σ(I_reference − I_test)²/Σ(I_reference)² where the sum is over all image pixels, I_reference is the stationary reference magnitude image, and I_test is the corrected test magnitude image. Artifact power was used as a general image quality metric and is calculated with images uncorrupted by noise since noise affects both reference and test images equally but randomly, and thus would add an unnecessary, systematic term to the artifact power. Residual error was calculated as RE = |Δx_reference − Δx_test|, where Δx_reference is the known motion and Δx_test is the calculated motion. Note that the direction x refers to frequency encoding (FE) direction and the direction y refers to the PE-direction. The labels will be used interchangeably. For simplicity, k-space locations are reported as scaled values such that Δk = 1 and Cartesian values of k occur at integers (i.e., one FOV corresponds to a 2π phase wrap).

B. Cartesian Simulations

To validate (3) in the simplest case (i.e., no gridding), a simulated Shepp–Logan phantom image was transformed to k-space to create two identical 256 × 256 Cartesian data sets. One data set was corrupted by noise and by known sinusoidal motion (1 mm and 5 mm maximum displacement in the FE and PE-direction, respectively). The different displacements were selected in order to avoid phase wrapping at the edges of k-space. The other data set is corrupted only by noise. The added noise was Gaussian white noise with mean of zero and standard deviation of 2 and is added to the real and imaginary k-space. The real world application of this simulation is the acquisition of two data sets for averaging, where the object is motionless during the first acquisition and undergoes sinusoidal motion in the FE and PE direction during the second acquisition. In this case, the reference (the first motionless acquisition) is exactly known and exact intersections (all Cartesian k-space locations) are collected.

Phase differences between the corrupted Cartesian k-space and the original Cartesian k-space at k_x = 1 and −1 for each PE line were used to compute the object shifts using (6) and (7). A noise-free, but motion corrupted k-space was corrected according to the calculated Δx and Δy for each PE line, then 2-D-IFFT into image space for a corrected image. An over-determined case was also tested in simulation using a total of eight phase differences per PE line (i.e., k_x = −4 to 4, not including k_x = 0). Additionally, to examine the relationship between intersection k-space position and correction error, artifact power was calculated for MOJITO corrected images where object shifts were calculated for each PE line using two intersections at increasing ±k_x locations for four noise levels (standard deviation, σ = 0.5, 2, 5, and 10 which correspond to image SNR values of 151, 38, 15, and 7.7, respectively).

C. BOWTIE Simulations

1) SNR Simulation Single Coil

MOJITO BOWTIE simulations were performed by generating BOWTIE k-space data with an inverse nonuniform FFT algorithm [23] assuming a real object with uniform coil sensitivity typical of a birdcage coil [24]. A 256 × 256 Shepp–Logan phantom image was sampled at k-space locations corresponding to 256 radial BOWTIE lines to produce exact intersections (partially represented by light gray filled circles, Fig. 2) to assess the compatibility of the BOWTIE geometry with MOJITO. Essentially, this simulation tested the properties of the intersection location as if the Cartesian and radial lines intersected at k_x = +/ −1. As with the Cartesian simulation, a gridding/interpolation step was not necessary since exact k-space locations were used. Known motion (over phase encode lines) was induced in k-space in the x and y direction. Induced motion was sinusoidal with an amplitude of 6 mm in the x-direction and 3 mm in the y-direction (180° out of phase) and with 2.3 periods completed over 256 PE lines. The nine reference PE lines were uncorrupted by motion for all BOWTIE simulations. Equations (6) and (7) (i.e., only two intersections per PE line) were used to calculate object shifts in the absence and presence of zero mean, Gaussian noise (standard deviation, σ = 0, 5, 10, and 20 which correspond to image space SNR values of 138, 52, 27, and 13, respectively) added to the real and imaginary channels of both the reference and motion corrupted data.

Fig. 2.

Partial simulated BOWTIE trajectory. The rectilinear reference points are shown as open circles. All other circles are radial points. Rectilinear points lie on a Δk = 1 grid, and only partial k-space is shown limited to points within k_x = −5 to 5 and k_y = −4 to 4. The light gray filled points correspond to samples at k_x = −1 and 1 used for simulation of exact point intersections at low spatial frequency. The dark gray filled points correspond to radial points sampled for exact point simulation of intersections at high spatial frequency. And together the circles with black outline correspond to radial points sampled for GROG simulation for the overdetermined simulations.

Noise-free, motion corrupted data was corrected using calculated object shifts. Additionally, mean residual error was calculated over 500 repetitions as a function of k_y at the different noise levels.

2) SNR Simulation Single Coil

A multicoil simulation (n_c = 8) was performed to evaluate the use of GROG with MOJITO for the situation of correcting for inexact intersections of Cartesian and radial points as would typically occur in a real MR acquisition. As with the previous simulation, a Shepp–Logan phantom (with simulated spatially varying complex sensitivity map) was resampled [23] to obtain the desired BOWTIE k-space data (partial k-space shown in Fig. 2). The same motion pattern described above for the single coil simulation was used for the multicoil simulation. Here, BOWTIE points were obtained at k-space locations representing a realistic discrete sampling of the trajectory and therefore gridding was necessary to generate data at exact intersections. For each radial point used in MOJITO, the nearest rectilinear point was gridded to the radial point k-location. Because of the versatility of the selected gridding method, GROG, intersections were defined as any radial point within a reference region (i.e., central 9 PE lines) and within 0.5 pixels in both directions of the nearest rectilinear reference point.

Equation (10) was solved using several combinations of intersections to better understand the noise characteristics of MOJITO. Each intersection consisted of data from all eight coils. A pair of intersections at k_x = −5 and 5 (dark gray filled circles, Fig. 2), a pair of intersections at k_x = −1 and 1 (light gray filled circles, Fig. 2), 40 intersections between k_x = −5 and 5 (black outline circles, Fig. 2, oversampled by a factor of 4 in the k_x direction to simulate closer grid points) per PE line were used to solve for Δx and Δy. Additionally, the weighted least squares version (11) was solved using the same 40 intersections between k_x = −5 and 5. For reference, the exact 40 intersections (no gridding) were also used to solve (11) to compare the effect of GROG. Multicoil images were combined using the square root of the sum of squares over all coils [25] and SNR was measured in these combined images. Average artifact power and residual difference were calculated over 50 repetitions for several noise levels (σ = 0.1, 0.2, 0.5, 1, 2, 3, 4, and 5 corresponding to image SNR of 217, 105, 45, 24, 12, 9, 8, and 7, respectively).

3) Off-Resonance Simulation Single Coil

Any significant source of phase accumulation not due to interview translational motion, such as off-resonance, will result in anomalous phase difference (according to the FST) for a pair of intersecting points leading to error in object shifts. To examine the effects of off-resonance, simulations were performed by performing a slow discrete Fourier transform (DFT) on a simulated Shepp–Logan phantom (single uniform sensitivity coil) according to

$$S(k_x,k_y)=\sum _x\sum _y\rho (x,y)e^{-i\gamma \mathrm{\Delta }{B}_0(x,y)t}{e}^{-i2\pi ({\mathit{\text{xk}}}_x+{\mathit{\text{yk}}}_y)}$$ (12)

where ΔB₀ (x, y) is the generated field map and t is the BOWTIE time acquisition vector (over 5.72 ms). Three sets of exact BOWTIE intersections were simulated with the same field map scaled to represent different levels of off-resonance (maximum approximately 40, 70, and 100 Hz, corresponding to 0.63, 1.1, and 1.6 ppm at 1.5 T, comparable to head imaging). The simulated k-space was oversampled by a factor of four in the k_x direction. The DFT k-space data was corrupted with known motion and the central 26 radial points per PE line were used in an unweighted solution of (10). Artifact power and absolute residual difference were calculated in the absence of noise.

D. Phantom and In Vivo Experiments

MR data was collected with a 12-channel head array (Siemens Medical Solutions, Erlangen, Germany) on a 1.5 T MRI scanner (Siemens Espree, Erlangen, Germany) with a BOWTIE FLASH sequence. A measured trajectory [26] was used to minimize eddy current and gradient nonlinearity effects on k_x and k_y. Only the Cartesian portion of the BOWTIE data was corrected using the calculated object shifts and then 2-D inverse Fourier Transformed to image space. MOJITO correction was performed offline in Matlab (The Mathworks, Natick, MA). The images from individual coil were recombined using a conventional sum of squares algorithm [25]. Final images were cropped for better visualization.

A solid phantom (grapefruit) was used. It allowed us to remove (internal) flow-related effects and consider rigid-body motion alone. An MR compatible track was used to limit rotational and through-plane motion. The phantom was moved during the BOWTIE acquisition in the FE-direction alone and then in a separate acquisition in a combination of FE and PE-direction. Imaging parameters were TE/TR = 5.6 ms/500 ms, flip angle = 15°, slice = 10 mm, FOV = 300 mm² and resolution of 256 × 256. The long TR simply allowed the center reference lines to be acquired while the object was stationary. The extent of motion was small, approximately 1.5 cm, in the FE-direction and 1 cm in the PE-direction to limit the effects of type 2 motion. GROG was calibrated using the center five Cartesian portions of the BOWTIE PE lines which were acquired when the object was stationary. GROGed intersections were limited to radial and Cartesian points spaced no farther than 0.25 * Δk_x apart and within k_x = +/ −80 (i.e., limiting GROG distance and limiting intersections at high spatial frequencies). The weighted least squares solution described by (11) was used to solve for object shifts. Equation (8) was used to correct the remaining 251 nonreference BOWTIE PE lines with the calculated object shifts.

Additionally, motion corrupted BOWTIE data were acquired of an asymptomatic volunteer. Human experiments were conducted in accordance with the institution’s internal review board. Informed consent was obtained. Imaging parameters where the same as the phantom experiment except for use of TR 20 ms. The volunteer was instructed to move in an oscillatory pattern in the frequency-encoding direction. For motion detection, only one reference line and six pairs of GROGed intersections over 12 coils were used. GROG was calibrated using the center 5 PE lines, which were not stationary. All 256 Cartesian BOWTIE PE lines were corrected with the detected Δx’s using (8).

IV. Results

A. Cartesian Simulations

Cartesian image simulation results are shown in Fig. 3. In the absence of noise, simulated motion was detected perfectly (not shown). Although the correction parameters were calculated in the presence of noise, all images shown have no added noise to better highlight residual artifact. For reference, the motion corrupted image is shown in Fig. 3(a) and the MOJITO corrected images are shown in Fig. 3(b) and (c) for two and eight intersections, respectively. Artifact power for images in Fig. 3(a)–(c) was 0.444, 0.335, and 0.327, respectively. Known simulated shifts (solid line) and detected shifts (dots and x’s) are shown in Fig. 3(d). Note that the residual error in Δx is reduced when eight intersections [dots, Fig. 3(d)] versus two intersections [x’s, Fig. 3(d)] were used to fit the motion. Average residual error in Δ_x for lines k_y = −127 to −107 was 2.0 mm and 0.61 mm for two and eight intersections, respectively. The residual error increases where the k-space SNR is low, such as high spatial frequency intersections [27]. The maximum residual error in Δy was approximately 0.9 mm and average residual error was less than 0.025 mm for both 2 and 8 intersections. Fig. 4 generally shows increasing image artifact power as a function of the selected Cartesian “intersections” location (increasing k_x) for several noise levels (σ = 0.5, 2, 5, 10 which correspond to image SNR values of 151, 38, 15, and 7.7, respectively). However, in the range of k_x < 5 the artifact power is decreasing, which suggests that there may be an optimum k-location balancing noise and k-matrix properties.

Fig. 3.

MOJITO Cartesian simulation results. Image (a) shows a motion corrupted Shepp–Logan phantom, (b) shows a MOJITO corrected image using two and (c) eight intersections. Graph (d) depicts calculated shifts in PE (open circles) and FE-direction (x’s and black dots) using 2 (x’s) and 8 (dots) intersections. Solid lines depict the actual object shifts in the PE and FE direction.

Fig. 4.

MOJITO Cartesian artifact power. Artifact power (i.e. level of artifact left uncorrected) is shown for four noise levels for pairs (two intersections) of Cartesian “intersections” at ±k_x. Noise values of σ = 0.5, 2, 5, 10 correspond to image SNR values of 151, 38, 15, and 7.7, respectively.

B. BOWTIE Simulations

1) SNR Simulation Results Single Coil

In the absence of noise, BOWTIE MOJITO simulations calculated object shifts and corrected the image with micrometer precision, the limit of the interpolation methods (not shown). At increasing noise levels (σ = 2, 5, 10, and 20, corresponding to image space SNR values of 138, 52, 27, and 13, respectively), the corrected images exhibited higher residual motion artifact and higher artifact power (0.0012, 0.0124, 0.0512, and 0.1726, respectively, compared to 0.9678 for the uncorrected image). Particularly of note, the residual error in Δy increases for low frequency PE lines (small k_y, Fig. 5) where the matrix k is ill-conditioned. It is well known that a large matrix condition number limits the least squares solution accuracy [28]. The condition number for k is shown in Fig. 5 as the thin, solid line as well as the residual error at each noise level. The k_y locations shown correspond to the center 40 PE lines. The error in Δx was fairly constant over PE lines, increased with increasing noise and the maximum value was 0.16 mm.

Fig. 5.

MOJITO BOWTIE simulation residual error. The average residual error in Δy is plotted for the center 40 BOWTIE PE lines. Also plotted is the condition number (dashed line) of the k matrix. The k_y locations shown correspond to the center 40 BOWTIE PE lines.

2) SNR Simulation Results Multicoil

Fig. 6 shows typical image results from solving for object shifts with 40 intersections between k_x = −5 and 5 [weighted least squares solution, (11)] per PE line at σ = 0.5, 2, and 4 (corresponding to SNR values of 45, 12, and 8, respectively). Like the previous simulations, the correction worsens with increasing noise (i.e., decreasing SNR). Additionally, the five combinations of intersections performed increasingly well (Fig. 7). Average artifact power is shown in Fig. 7(a). The residual difference in Δx was again relatively constant over PE lines for each noise level and is therefore given as the mean residual difference in Fig. 7(b). However, the residual difference in Δy varies with PE line in the same pattern as Fig. 5. To better represent the worse case, the residual difference is given as the maximum residual difference in Δy in Fig. 7(c).

Fig. 6.

MOJITO BOWTIE simulation with GROG. The motion corrupted image is shown in (a). The motion artifact correction in the presence of added zero mean Gaussian noise with standard deviation of 0.5, 2 and 4 to the imaginary and real channels images are shown in (a)–(d), respectively. SNR is 45, 12, and 8 and average artifact power is 0.0027, 0.0506, and 0.198 for images (b)–(d), respectively. Artifact power for the uncorrected image is 0.570. These images correspond to the open circles in Fig. 7.

Fig. 7.

MOJITO BOWTIE simulation with GROG. Average artifact power, mean residual error in Δx, maximum residual error in Δy are shown in (a)–(c), respectively. A pair of intersections at k_x = −5 and 5 (triangles), a pair of intersections at k_x = −1 and 1 (squares), 40 intersections between k_x = −5 and 5 unweighted (dots) and weighted (open circles) per PE line were used to solve for Δx and Δy over 100 repetitions. For reference, the exact 40 intersections results are shown with diamonds. The dotted line in (a) is the artifact power of uncorrected images.

3) Off-Resonance Simulation Results Single Coil

To evaluate the MOJITO method in the presence of object dependent off-resonance effects, simulations were performed with the field map shown in Fig. 8(a). In the presence of no motion, MOJITO inaccurately detected shifts based on the phase differences created by off resonance [Fig. 8(b)]. The calculated shifts in the x-direction show both an offset and a drift away from the expected value while the calculated shifts in the y-direction show a large deviation from expectation for the center PE lines as well as a large discontinuity. In the presence of motion, MOJITO tracks the motion with some precision [Fig. 8(c)], but retains the inaccurate offset and discontinuity seen in the no-motion case. The residual mean errors for Δx and Δy increase with increasing magnitude of off-resonance (Fig. 9).

Fig. 8.

MOJITO BOWTIE simulation with off-resonance. The inhomogeneity field map (in hertz) used in the DFT operation is shown in (a). The graphs in (b) and (c) show the calculated object shifts by MOJITO in the x-direction (dots) and y-direction (open circles). The expected shifts are shown by the thin solid lines where (b) and (c) show calculated object shifts in the absence and presence of motion, respectively. Solid lines show induced motion in the x-direction and the dashed lines show induced motion in the y-direction.

Fig. 9.

Absolute residual error for MOJITO BOWTIE simulation with off-resonance and motion. The two graphs in (a) and (b) show the residual error in object shifts Δx and Δy, respectively, detected by MOJITO in the presence of off-resonance effects at maximum 100 Hz (solid), 70 Hz (dotted), and 40 Hz (dashed).

C. Phantom and In Vivo Results

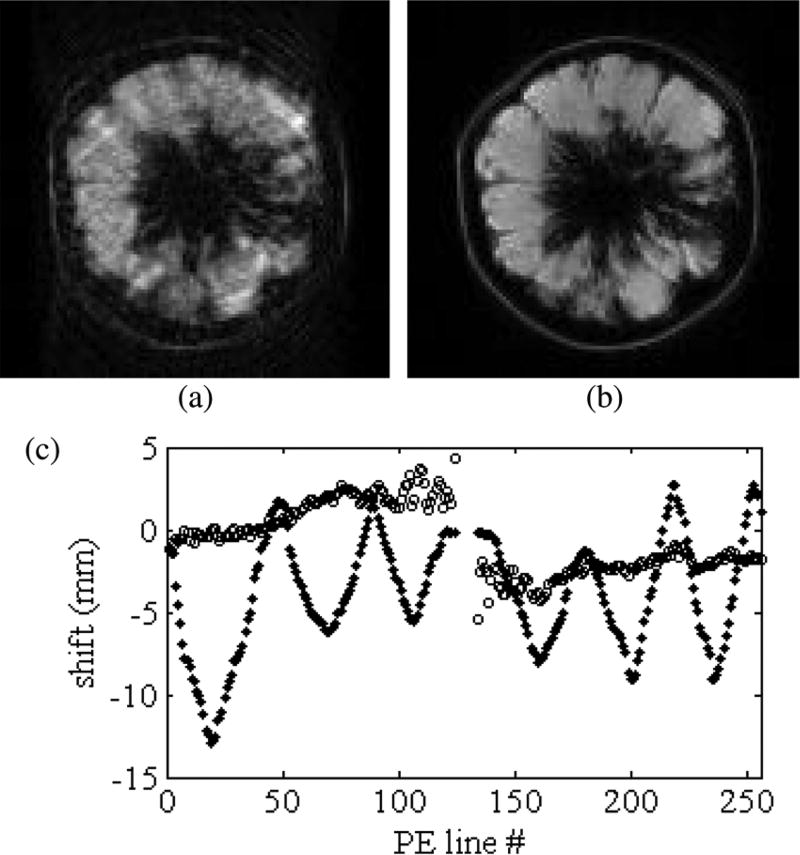
Phantom images for an object moving only in the FE-direction are shown in Fig. 10. The motion corrupted image is shown in Fig. 10(a) and the corrected image (corrected only by FE-direction object shifts) is shown in Fig. 10(b). The detected object shifts (open and closed dots are Δx and Δy, respectively) are shown in Fig. 10(c). The drift and discontinuity [Fig. 10(c)] in the Δy values is very similar to the error seen in the off-resonance simulation shown in Fig. 8. In vivo images are shown in Fig. 11. The motion corrupted image is shown in Fig. 11(a) and the corrected image (corrected only in the FE-direction) is shown in Fig. 11(b). The detected amplitude of motion was found to be approximately 10 cm in the FE-direction for the in vivo image. No correction for translational motion in the PE-direction, incidental rotational or through-plane motion is performed and may account for some of the residual artifact. Since the stationary head coil was used for both experiments, both data sets represent type 2 motion.

Fig. 10.

MOJITO phantom images and object shifts. Image (a) shows a motion corrupted image with motion in the FE-direction (left–right). Image (b) shows the MOJITO corrected image using only Δx. The graph in (c) shows the detected object shifts (Δx in solid dots and Δy in open circles).

Fig. 11.

MOJITO in vivo images. Image (a) shows the motion corrupted image and (b) shows the MOJITO corrected image. Motion is ideally only in the FE-direction (left–right). The images are cropped for better visualization.

V. Discussion

In this study, a novel MRI motion artifact correction method using trajectory intersections was described. The MOJITO algorithm, a self-navigating, k-space based method, is fundamentally different than traditional navigator echo correction methods as it allows motion artifact correction with data acquired along different paths rather than a repeating a specific path through k-space. However, like navigator echo methods, MOJITO is a k-space based phase difference method. The trajectory intersections of a BOWTIE trajectory were used for in-plane, translational motion artifact correction using the MOJITO algorithm. The method was tested in simulation in the presence of noise and off-resonance effects.

The Cartesian simulations showed excellent artifact correction in the absence of noise. The Cartesian simulation showed that increasing the number of intersections (from 2 intersections to 8 intersections, Fig. 3) reduced the residual error and artifact power. Trajectory intersections at high spatial frequencies were more easily corrupted by noise compared to trajectory intersections at low spatial frequencies (Fig. 3), due to low signal. At these high spatial frequency intersections, notice that the error in Δx is larger than the error in Δy in Fig. 3. The chosen intersections occur at k_x = ±1 and k_y = −127 to 128, where error is distributed unevenly between Δx and Δy when k_x and k_y differ. This is best explained by examining the linear algebra solution for (6) and (7) for two intersections. Because k_x,1 = −k_x,2 = 1 and k_y,1 = k_y,2, (6) and (7) also have the relationship [(Δφ₁ − Δφ₂ + 2ε)]/(2k_x,1) = Δx and [(Δφ₁ + Δφ₂ + 2ε)]/(2k_y,1) = Δy, where ε is the expected error in the phase differences. The error in Δx is therefore ε for all intersections, while the error in Δy varies with PE line by ε/k_y,1. At high PE lines, is large (i.e., low k-space signal) yet the error in Δy is only a fraction of ε. Therefore, intersection locations and signal in k-space affect the algorithm’s corruption by noise. This is further shown by Fig. 4 where a minimum artifact power is seen at k_x = 5. Other navigator studies have also noted that the accuracy of phase-based motion corrections methods depends on k-space SNR [6].

The BOWTIE simulation with exact intersections was performed to examine the effects of the BOWTIE intersection geometry on object shift calculation. Like the Cartesian case, the error increased with increasing noise (Fig. 5). However, unlike the Cartesian case the residual error in Δy is not constant for every PE line, suggesting that some accuracy depends on the geometry of BOWTIE intersections. Despite high signal, trajectory intersections at very small k_y locations (< 0.05), as seen in central BOWTIE PE lines, exhibit the highest error in Δy. This sensitivity to noise in one direction is a direct result of the k-space location and can be related to the condition number of the k matrix. These BOWTIE and Cartesian simulations suggest that very high (due to low SNR) and very low (due to low sensitivity) k-space locations in either direction cause susceptibility to error due to noise. Therefore, careful selection of BOWTIE trajectory intersections is necessary for accurate detection of object shifts with MOJITO.

With the MOJITO technique, object displacements are calculated using a number of intersection points in the BOWTIE trajectory (which ranges from 2 to 40 in simulation). Not surprisingly, the results of this study demonstrate that greater accuracy is achieved with a larger number of points. When compared to Cartesian navigators where a full k-space line is available (e.g., 256 points), MOJITO is at an apparent disadvantage. However, in our experience with MOJITO, we found that intersections with low SNR were of little value. The same SNR limitation is shown in the literature for traditional and orbital navigators [6], [18], indicating that performance of the algorithm is more complex than simple dependence on number of available points.

Residual error in the absence of noise for BOWTIE with GROGed intersections was on the order of micrometer or less in both translational directions and therefore is not a dominant source of error. These BOWTIE simulations followed the trend of the Cartesian simulations where low spatial frequency intersections (squares, Fig. 7) performed better than high spatial frequency intersections (triangles, Fig. 7). GROG allowed us to loosely define “intersection” to create an over-determined problem. The performance of the weighted least squares solution is in agreement with similar work using weighted navigator echoes [18].

It can be appreciated that an adequate correction is one that yields object shift errors smaller than image resolution. Clinical images typically achieve resolution of approximately 1 mm. Although exact intersections have the lowest error (diamonds, Fig. 7), the weighted least squares solution using 40 intersections and 8 coils is practical and achieves the desired accuracy with SNR of approximately 12 (in the combined image). This SNR is reasonably achievable with modern technology. These 240 intersections are closely clustered at the center of k-space where SNR is high and in general phase wrapping (of Δφ) can be avoided.

Equation (6), the phase difference calculation, could encounter theoretical challenges due to potential for phase wrapping. Specifically, phase wrapping may lead to confounding results as it is possible to obtain the same phase difference for two different spatial shifts. This problem may be limited by use of intersections at small k_x and k_y (i.e., hence large motions required to create phase wraps) or by assuming the amplitude of motion is small. If phase unwrapping cannot be avoided, then standard phase unwrapping techniques may be used when the SNR is greater than 10 [18] and translational motion is smooth yet this requires further assumptions about the type of motion across multiple views.

Like other MR techniques, the MOJITO method is sensitive to off-resonance effects (Figs. 8 and 9). The detected object shift in the FE-direction is still relatively precise even in the presence of the highest off-resonance tested (100 Hz) where the maximum error was 1.5 mm, not including a systematic 1 mm offset. Such an offset in the shift calculation is a tolerable side effect and will benignly shift the object within the FOV. However, the error in the PE-direction rapidly increases with higher off-resonance [Fig. 9(b)] and is too high without further correction (about 3 mm maximum error for peak inhomogeneity of 40 Hz). In terms of off-resonance, with the field map in Fig. 8(a), even 40 Hz peak inhomogeneity does not meet the 1 mm accuracy limit. A typical range of off-resonance values in our experience and in the literature is approximately ± 100 Hz [29]. Unlike SNR constraints, the off-resonance limit may be unreachable with modern technology without further correction. Previously developed off-resonance correction methods which simultaneously solve for an image, field map, and T2* map [30] or time segmented methods [31] may be the most successful for accurate shift detection with MOJITO. These methods may remove or improve the discontinuity error seen in calculated Δy values at k_y = 0. The ill-conditioned k matrix occurs at small k_x and k_y locations, where even a small error in Δφ causes a large error in Δy. These Δy errors may manifest as a discontinuity because of positive and negative k values surrounding k_y = 0.

The phantom and in vivo images generally agree with the simulation results and show excellent correction for object motion in the FE-direction. The corrected phantom and in vivo images result in obviously sharper borders and more evident detail compared to the uncorrected images. However, the detected PE-direction motion (shown for phantom data in Fig. 10(c)) is corrupted by the same discontinuity and offset seen in the off-resonance simulations (Fig. 8) and excluding detected PE motion from the correction yields qualitatively better results. In an ideal setting, with more uniform field homogeneity the method is likely to perform within the limits of SNR. This suggests that an off-resonance correction method may be useful for more accurate detection of 2-D translational motion under these conditions. Additionally, off-resonance effects caused by shifts due to fat may also be a source of significant anomalous phase error leading to error in calculated object shifts. However, the in vivo image (Fig. 11) shows a reasonable performance even in the presence of fat and regions with large differences in susceptibility (i.e., air/tissue interface in the frontal sinuses). Fat suppression methods in combination with off-resonance correction techniques may further reduce existing errors.

MOJITO is based on three key assumptions. One is that there is no motion during the acquisition of any given phase encode line (i.e., motion occurs between the acquisition of the PE lines), allowing the simplification to the single object shift in (6), (7), and (9). This is enforced by making the sampling time very short, typically around 5–7 ms, so the object would have to be moving rather fast (> 15 cm/s) to invalidate this assumption and move more than 1 mm during the acquisition of a single line. The second assumption is that the phase difference at any intersection is due only to translational motion. This second assumption is violated by phase accumulation due to off-resonance effects or improperly localized data points due to significant eddy currents not compensated by a measured trajectory. Finally, the third assumption is that no motion occurs during the acquisition of the reference lines at the center of k-space (which include a minimum of three lines demonstrated in the in vivo experiments and as many as thirteen lines in the BOWTIE simulations). In this work, the predetermined motion was specifically held to zero during the acquisition of these lines in simulation. Practically, it would be beneficial to employ a rapid acquisition to ensure a motion free condition. However, when a constant reference is not obtained, it may be necessary to fulfill this assumption by performing an additional correction with another method, such as traditional navigator echoes, at the cost of increased acquisition time only for these reference PE lines.

All simulations have assumed type 1 motion. The problem of type 2 motion in the presence of nonuniform coil sensitivity has not yet been formally addressed. However, phantom and in vivo corrected data perform well even in the presence of type 2 motion. Relative motion between the spatially varying coil sensitivities and the object will essentially alter the object and therefore invalidate (3). A phase correction [16] or very small relative motion may allow type 2 motion correction with MOJITO, but has yet to be quantified. A birdcage coil with uniform sensitivity and an alternate method of generating exact intersections, such as convolution gridding, should be explored to avoid such problems. Similarly, the simulated inhomogeneity field map represents object dependent off-resonance such as magnetic susceptibility and off-resonance species. Therefore, the field map presumably moves with the object. Off-resonance effects that are not object dependent may have the same difficulties as type 2 motion, but in practice the main field is very homogeneous (typically varying 5 Hz over 20 cm [32]), likely small enough to ignore.

MOJITO is essentially a self-navigating technique that allows both detection and correction of k-space phase shifts due to in-plane, translational motion. This method demonstrates advantages over some other self-navigating techniques [9], [11] which only allow detection of motion in order to include or exclude data in reconstruction. Unlike navigator methods which repeat a specific path through k-space, such as traditional navigators, orbital navigators and the butterfly trajectory [15], MOJITO allows acquisition of navigator data using any overlapping trajectory which may also be used for image reconstruction. Specifically for BOWTIE, motion corrected radial data may be used in image reconstruction as previously shown for increased SNR [3] or for self-calibrating parallel imaging [33]. BOWTIE’s ability to correct for effects of motion while using all k-space acquired samples in image reconstruction is achieved by continuous sampling (i.e., sampling during the application of image plane gradients) and could be further improved with 3-D BOWTIE. Additionally, the partial radial coverage of k-space may allow rotational motion correction with previously described methods [34], [35].

The BOWTIE trajectory is well suited for this type of motion correction algorithm as it exhibits at least two intersections per line. Unfortunately, many of these intersections occur at relatively high spatial frequencies and therefore have low k-space SNR. Therefore implementation should use the oversampled center data and GROG to obtain high k-space SNR “intersections” and reduce the necessary GROG distance. Oversampling may be accomplished by the intrinsic nature of the trajectory as well as by increasing the sampling rate. Other trajectories with overlapping trajectories such as rosettes [36] or PROPELLER [12] may also contain trajectory intersections appropriate for the MOJITO motion correction algorithm. Rosette trajectory intersections occur on concentric rings in k-space which may give added sensitivity to the MOJITO algorithm by favorably separating intersections in k_x and k_y. However, the rosette trajectory is likely to be as sensitive (if not more sensitive) to off-resonance effects due to long sampling times.

VI. Conclusion

In conclusion, a new motion correction technique was described using k-space trajectory intersections resulting from the BOWTIE trajectory. Intersecting k-space trajectories allow the calculation of phase differences at known k-space locations. The general MOJITO algorithm solves a linear system of equations relating calculated phase differences, known k-space locations, and unknown object shifts. The MOJITO motion artifact correction is fundamentally different than traditional navigator echoes as it allows motion artifact correction with data acquired along different paths rather than a repeating path through k-space. The method has been demonstrated in simulation and preliminary MR experiments to successfully detect in-plane, translational motion using the BOWTIE trajectory in the presence of realistic levels of noise and small off-resonance effects.