Modeling and experimental studies of enhanced cooling by medical gauze for cell cryopreservation by vitrification

Abstract

Vitrification is considered as an important alternative approach to traditional slow freezing method for cryopreservation of cells. A typical cell vitrification procedure involves a non-equilibrium cooling process commonly accomplished in liquid nitrogen, while in which film boiling is believed to greatly hinder heat transfer surrounding the sample, resulting in incomplete vitrification or a much higher critical concentration. In this study, we developed a simple while effective approach, wrapping traditional French-type straw with medical gauze, to greatly enhance convective heat transfer during cooling by suppress film boiling. We further established a coupled heat transfer model for cooling and warming of cell suspensions to investigate the inherent thermodynamic mechanism in this approach. The model describes both the macroscale thermal distributions in extracellular solution and the microscale ice crystallization inside the cells. The simulation indicated that straws wrapped with medical gauze would increase cell survival subject to vitrification cryopreservation by significantly increasing the cooling rate to inhibit intracellular ice formation (IIF). Our experiments on human umbilical vein endothelial cells (HUVECs) further confirmed the predictions in that the cell survival rate was significantly increased by wrapping straws with medical gauze.

1. Introduction

Vitrification has been considered to be the most promising method for successful cryopreservation of cells and tissues [1]. In 1980s, Rall and Fahy introduced vitrification to the preservation of organs and mouse embryos and proposed some emerging principles on the vitrification protocol [2]. Vitrification has tremendous advantages over traditional slow freezing method [1, 3–5]. On one hand, vitrification process is simple and easy to perform. It does not require controlled cooling rate, which is essential to traditional slow freezing method and should be implemented by an expensive controlled rate freezer. On the other hand, vitrification totally avoids the formation of intracellular ice formation (IIF) which is considered to be fundamental to all cryoinjuries. Vitrification experiments for cryopreservation are usually conducted by plunging vitrification devices with cell suspensions into liquid nitrogen (LN₂) [6]. Owing to the large temperature difference between sample and LN₂, this procedure is commonly accompanied by film boiling of LN₂ on device surface [7, 8], which consequently blocks heat transfer surrounding the sample and leads to incomplete vitrification. Some researchers have worked on enhancing heat transfer during cooling in vitrification cryopreservation [8–10]. He et al. suggested that using a quartz micro-capillary would achieve ultra-fast cooling rates and enable vitrification of murine embryonic stem cells at a low concentration of cryoprotectants [9]. Zhou et al. utilized micro-channel array on the surface of vitrification device and reported that an ultra-high heat transfer coefficient can be obtained [8, 10]. However, to our knowledge, little research has been done on eliminating film boiling regime. In order to investigate the inherent thermodynamic mechanism underlying vitrification procedure, a well-established heat transfer model is also needed [11–15]. In 1990s, Boutron carefully investigated the glass-forming tendency in cryoprotective systems and empirically introduced a non-equilibrium model for determination of ice formation in aqueous cryoprotective solutions [16]. This model has been widely used in the simulation of vitrification process. For example, Song et al. successfully optimized the droplet vitrification protocol by adopting this model [7]. Zhou et al. applied this model to demonstrate the efficiency of a novel microfluidic system for cell vitrification [8]. However, in all these studies, they used temperature dependent thermal properties which were measured isothermally. Thus the results might be inaccurate. Besides, Jiao et al. demonstrated that even in a narrow plastic straw, the temperature distribution during cooling could be quite non-uniform depending on the convective heat transfer coefficients [17]. Meanwhile, whether or not a cell is vitrified depends largely on cooling rates. Therefore, thermal non-uniformity of extracellular environments inside straws should be considered.

In this study, we developed a simple while effective approach, wrapping traditional French-type straw with medical gauze, to greatly enhance convective heat transfer during cooling by suppress film boiling. Furthermore, we established a coupled heat transfer model for cooling and warming of cell suspensions to investigate the inherent thermodynamic mechanism in this approach. The simulations indicated that wrapping straws with medical gauze would increase cell survival subject to vitrification preservation. To verify the prediction, we conducted experiments using human umbilical vein endothelial cells (HUVECs) and measured cell membrane integrity after cryopreservation. Finally, the simulative and experimental results were compared and analyzed.

2. Materials and methods

2.1. Modeling of the non-equilibrium crystallizing process

To predict the non-equilibrium crystallizing process, the following equation is used [16]:

$$\frac{d\chi }{dt}=k_a{\chi }^{2/3}\left(1-\chi \right)\left(T_m-T\right)e^{-Q/RT}$$ (1)

where χ is degree of ice crystallization (0<χ<1), t is time, k_a is a characteristic constant, T_m is final temperature of the freezing process, Q is activation energy, and R is gas constant. Corresponding parameters for the model used in this study can be found in a previous research [18].

2.2. Modeling of the heat transfer process

Considering the primary mode of heat transfer in the straw is conduction rather than convection, we adopted the following energy equation to depict the temperature distribution inside the straws [19]:

$$\rho c\frac{\partial T}{\partial t}=k\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\rho L\frac{\partial \chi }{\partial t}$$ (2)

where T is temperature, r is radial coordinate starting from the center of the straw, ρ is density, c is specific heat capacity, k is thermal conductivity, and L is latent heat. To our knowledge, experimental data for thermal properties of supercooled and vitrified water are largely unknown at this time. Therefore, we adopted an approach depicted in [20] to calculate thermal properties.

The convective boundary condition is applied to the straw’s wall:

$$k\frac{\partial T}{\partial r}=h\left(T_{\infty }-T\right)$$ (3)

where h refers to the convective heat transfer coefficient and T_∞ is the temperature of LN₂. The values of h remain largely unknown and are dependent on many factors including the constitutions of solutions in the straw, the material of the straw’s wall as well as its roughness [21]. Thus in the current study the values of h were determined by fitting experimental temperature profiles.

Due to the fact that the heat transfer equation (Eq. 1) is a nonlinear second order partial equation that is highly coupled with that of crystallization (Eq. 2), it is difficult (if not impossible) to obtain analytical solutions of T. In this study, the values of T and χ were calculated simultaneously using numerical methods whereas temperature variations were computed using the method of lines (MOL) [22].

2.3. Modeling of probability of intracellular ice formation

As mentioned before, IIF is the main cause for all cryoinjuries. Thus it is highly correlated with cell viability after cryopreservation. To evaluate the efficiency of vitrification cryopreservation, we considered the probability of IIF (PIF) as an approximate evaluation of the final cell survival rate after cryopreservation. PIF can be estimated using the model as follows [23–25]:

$$P_{\mathit{IIF}}=P_{\mathit{IIF}}^{\mathit{SCN}}+\left(1-P_{\mathit{IIF}}^{\mathit{SCN}}\right)P_{\mathit{IIF}}^{\mathit{VCN}}$$ (4)

$$P_{\mathit{IIF}}^{\mathit{SCN}}=1-\exp \left[-{\displaystyle {\int }_0^t{A}_c{I}_{\mathit{SCN}}dt}\right]$$ (5)

$$P_{\mathit{IIF}}^{\mathit{VCN}}=1-\exp \left[-{\displaystyle {\int }_0^t{V}_c{I}_{\mathit{VCN}}dt}\right]$$ (6)

where t is time, A_c and V_c are cell surface area and volume, respectively, and I is nucleation rate of that can be computed as follows:

$$I^{\mathit{XCN}}={\mathrm{\Omega }}_0^{\mathit{XCN}}\frac{N^{\mathit{XCN}}}{N_0^{\mathit{XCN}}}\frac{{\eta }_0}{\eta }{\left(\frac{T}{T_{f,0}}\right)}^{0.5}\exp \left[\frac{-{\kappa }_0^{\mathit{XCN}}{\left(T_f/T_{f,0}\right)}^4}{{\left(T-T_f\right)}^2{T}^3}\right]$$ (7)

where XCN represents either SCN or VCN, ‘0’ refers to isotonic condition, Ω and κ are thermodynamic and kinetic parameters for nucleation, N is number of water molecules in contact with the substrate, and η and T_f are viscosity and equilibrium freezing temperature of the cytoplasm, respectively.

2.4. Cryopreservation of cells in straws and cell viability detection

On each day of experiment, attached HUVECs in cell culture medium (DMEM with 10% serum and 1% penicillin-streptomycin) were washed with isotonic phosphate buffered saline, trypsinized for 3–5 min, pelleted at 1000 rpm (94×g) for 5 min, and resuspended in cell culture medium for further use. For cryopreservation, cells were resuspended in 1 mL solution made of cell culture medium with 1.5 M 1,2-propanediol as the penetrating cryoprotectant and 0.5 M trehalose as the non-penetrating cryoprotectant for 10 min at 4 °C. The cell suspension was loaded into plastic straw using a syringe and sealed for cooling. The cell suspension was cooled by plunging the straw into LN₂. The straw was then left in LN₂ for ~3 min. The cell suspension was warmed by plunging the plastic straw into water bath at 37 °C for ~3 min. Finally, the suspension was unloaded from the straw into a 1.5 mL centrifuge tube for further use. To determine membrane integrity of cells after cryopreservation, cells were fluorescently stained with acridine orange/ethidium bromide (AO/EB). Cells that have lost membrane integrity will be stained by EB in red.

3. Results and discussions

3.1. Non-cellular experiments

The cooling and warming experiments without cells were firstly carried out. The procedures of the two sets of experiments are as shown in Figure 1(a) and (b) along with corresponding experimental phenomenon. A thermal couple was fixed at the center of the straw (containing 200 μL of 4 M 1,2-propanediol) to record the solution temperature. In the first group, marked as ‘NG’, the straws was plugged directly into LN₂ after sealing. The recorded thermal history is shown in Figure 2(a) (blue circles). The temperature profile can be divided into four regimes (R1–R4 that are separated by points A, B, and C). When the straw is just immersed into LN₂, the temperature difference between LN₂ and the sample is large enough to cause boiling of the LN₂, producing an insulating vapor film that may compromise the heat transfer on the boundary, which is called the “Leidenfrost phenomenon”. As a result, the convective heat transfer coefficient is low in this regime (R1, from the beginning to point A). The vapor film will then break off, leading to a rapid decrease of the temperature (R2, point A to point B), indicating an increased convective heat transfer coefficient. As for the warming part, two regimes are defined probably due to phase change in the sample solution (R3, point B to C, and R4, point C to the end). Similar behavior is observed for the simulations using the coupled heat transfer model (red line). The convective heat transfer coefficients are fitted to be 233, 6.56×10⁴, 4.96×10³, and 501 W/m²/K for R1, R2, R3, and R4, respectively (Table 1, R²=0.99). Figure 2(b) shows the predicted temperature distribution in the cross section of the straw at t=6 s and t=21 s. We can see that the temperature distribution is quite non-uniform in the cooling process and the temperature difference between straw center and boundary is ~25 K. In the experiment, we observed that the solution was approximately transparent when immerged in LN₂ (Figure 1(a)). This is consistent with the simulation showing minimal crystallization in the solution during cooling (Figure 2(c)). Therefore, the solution could be taken as mostly vitrified according to a criteria used in [26] (χ<0.1%). During warming, the solution turned into opaque probably due to devitrification and then became transparent again after 1~2 s (Figure 1(a)). This change in crystallization during and after warming is also shown by the simulation (Figure 2(d)) which indicates the crystallization increases dramatically to 1 at ~19 s due to recrystallization and drops sharply to 0 after warming.

Figure 1.

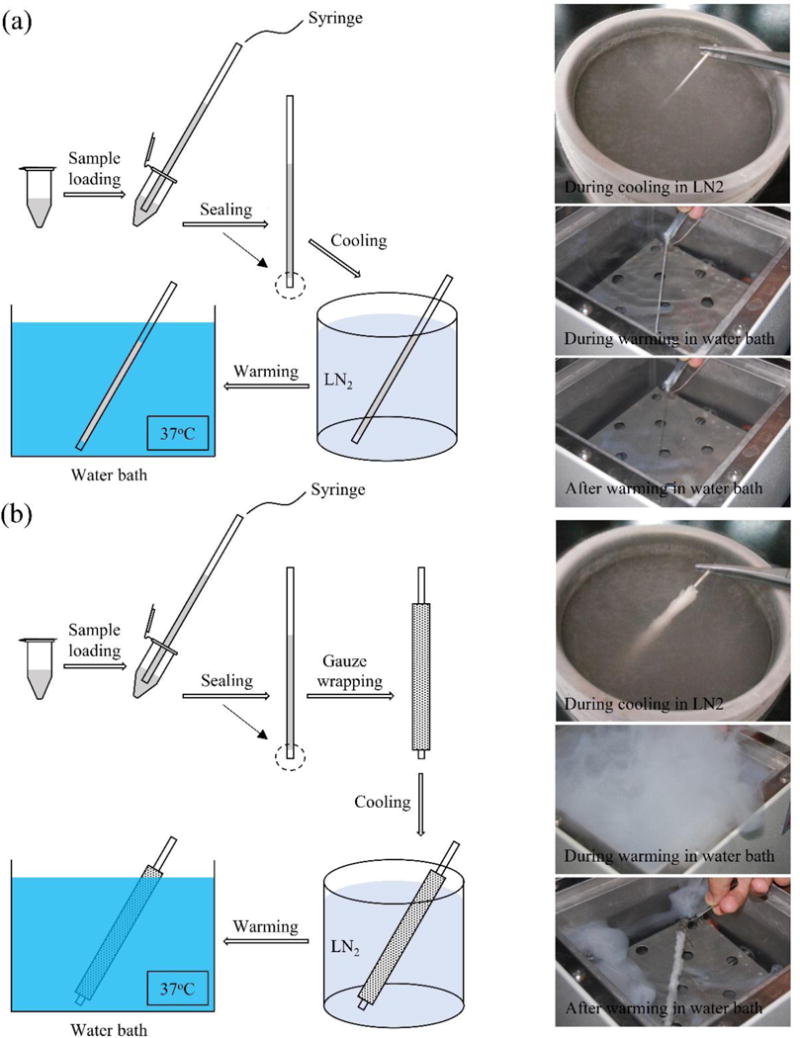
Procedure of the experiment and corresponding experimental phenomenon. (a) and (b) correspond to the ‘NG’ and ‘WG’ group, respectively.

Figure 2.

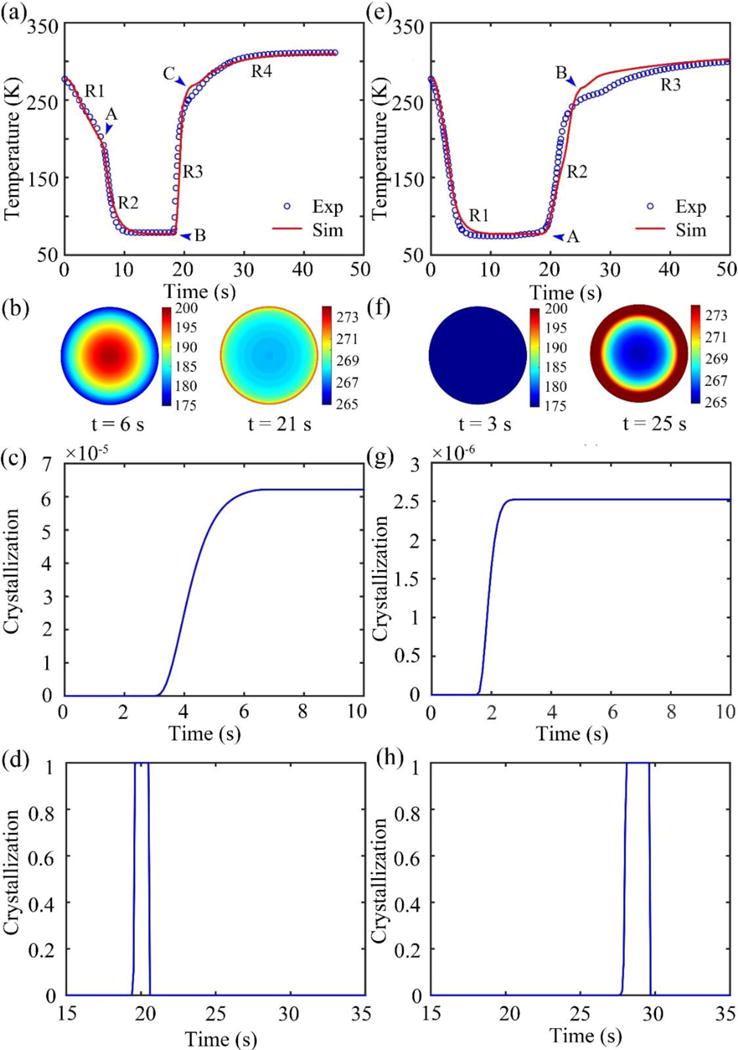
The results of noncellular experiments. (a), (e) The recorded temperature variations (blue circles) and corresponding fitting results (red line). (b), (f) Temperature contour of the cross section. (c), (g) Simulated crystallization curves during cooling. (d), (h) Simulative crystallization curves during warming. (a)–(d) correspond to the ‘NG’ group. (e)–(h) correspond to the ‘WG’ group.

Table 1.

Simulative convective coefficients for both ‘NG’ and ‘WG’ groups.

Group	R1 W/m2/K	R2 W/m2/K	R3 W/m2/K	R4 W/m2/K	R2
NG	233.00	6.56×104	4.96×103	501	0.99
WG	1.21×105	502.59	136.17	–	0.99

Also, another set of experiments, marked as ‘WG’, were conducted. In this group, the straw was wrapped with medical gauze (Figure 1(b)). The recorded thermal history is shown in Figure 2(e) (blue circles). Different from that without gauze, no turning point is clearly observable on the thermal history during cooling, indicating the “Leidenfrost phenomenon” observed for the case without gauze wrapping (Figure 2(a)) is eliminated by wrapping the straw with medical gauze. In other words, the gauze improves heat transfer on the boundary during the cooling process, probably by the so-called “enhanced vapor phase diffusion” effect [27, 28] that has also been noticed in studies on hydrology, atomospheric sciences and food processing [29]. Previous studies observed that due to the existence of porous media, water vapor fluxes were “enhanced” relative to fluxes predicted based on Fick’s law. This is comparative to the vapor of LN₂ in our study. It can be seen that with medical gauze the temperature reduced to the lowest value quickly in ~6 s during cooling which is 4 s faster than the case without gauze (Figure 2(a) and (e)). Although the cooling rate is enhanced, the medical gauze is unfavorable during warming. The warming time for the ‘NG’ group is ~25 s (Figure 2(a)), while it takes nearly 100 s (not shown completely in Figure 2(e)) for the temperature to reach an equilibrium during warming for the ‘WG’ group. The simulated thermal profiles are shown in Figure 2(e) (red line). The convective heat transfer coefficients for the three regimes are fitted to be 1.21×10⁵, 502.59, and 136.17 W/m²/K, respectively (Table 1, R²=0.99). Figure 2(f) shows the predicted temperature distribution in the cross section of the straw at t=3 s and t=25 s. Compared to that in the ‘NG’ group, the temperature gradient is nearly negligible. Besides, similar to the ‘NG’ Group, the amount of crystallization during cooling is low, only ~2×10⁻⁶ according to the simulative results (Figure 2(g)), indicating the solution is mostly vitrified. During the warming process, large quantities of vapor was produced that nothing can be seen clearly (Figure 1(b)). However, from the simulation the crystallization experienced similar changing process as in the ‘NG’ group during warming (Figure 2(h)).

Probability of intracellular ice formation

As shown in Figure 3, we can draw a vertical line from the point where the crystallizing ends. The intersection of the vertical line with the temperature curve can be regarded as the equivalent glass transition temperature (~157 K). Below this temperature, the process of intracellular ice formation should stop. The simulated PIF curves (volume average) are shown in Figure 4(a). It shows that the PIF for the ‘NG’ group is lower than the ‘WG’ group during cooling and warming. The contours of PIF distribution in the cross section at equilibrium are shown in Figure 4(b) and (c) for the ‘NG’ group and ‘WG’ group, respectively. This reduction in PIF is probably due to enhanced heat transfer with the gauze wrapping, indicating cells may suffer less damage in the ‘WG’ group.

Figure 3.

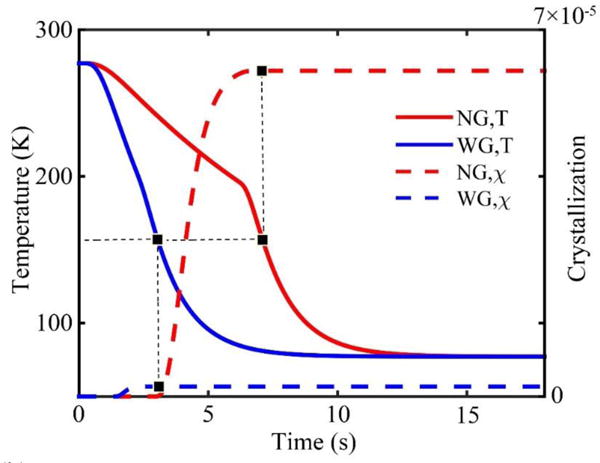
Determination of the equivalent glass transition temperature.

Figure 4.

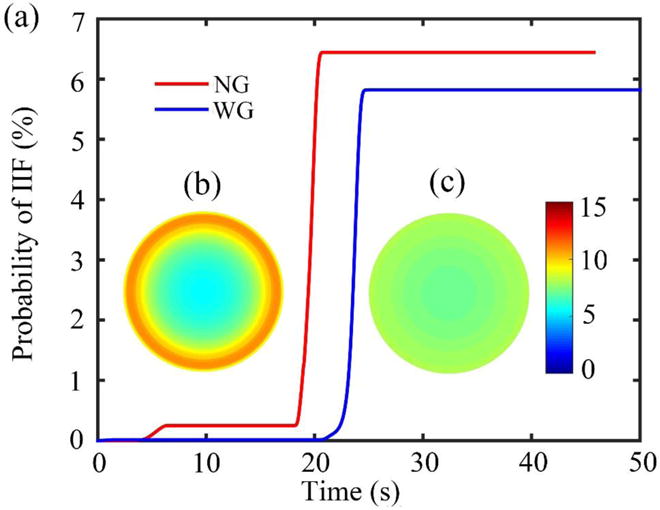
(a) The simulated PIF curves. (b) and (c) The final PIF contour of the cross section ‘NG’ group and ‘WG’ group, respectively.

Cellular experiments and corresponding cell viability

To analyze the enhancement of cell cryopreservation with the medical gauze wrapping, experiments were conducted using HUVECs. It is worth noting that, the gauze was removed in liquid nitrogen before warming so that the warming processes of these experiments are the same for the ‘NG’ and ‘WG’ groups. The experimental procedure for the ‘WG’ group is schematically illustrated in Figure 5. Figure 6 shows the typical fluorescence images to illustrate the membrane integrity of HUVECs after cooling and warming for both in ‘NG’ and ‘WG’ groups. The ‘WG’ group maintained higher cell survival than the ‘NG’ group and the difference is statistically significant (p<0.05). This significant improved cell survival with the gauze wrapping is probably a result of its capability of enhancing the convective heat transfer on the boundary of the straws. However, it is worth noting that both the cell survival rates in these two groups are not higher than 50%. The main reason for this lies in the fact that the warming rate is also important for cryopreservation of cells. Further studies focusing on the enhancement of the warming process are warranted.

Figure 5.

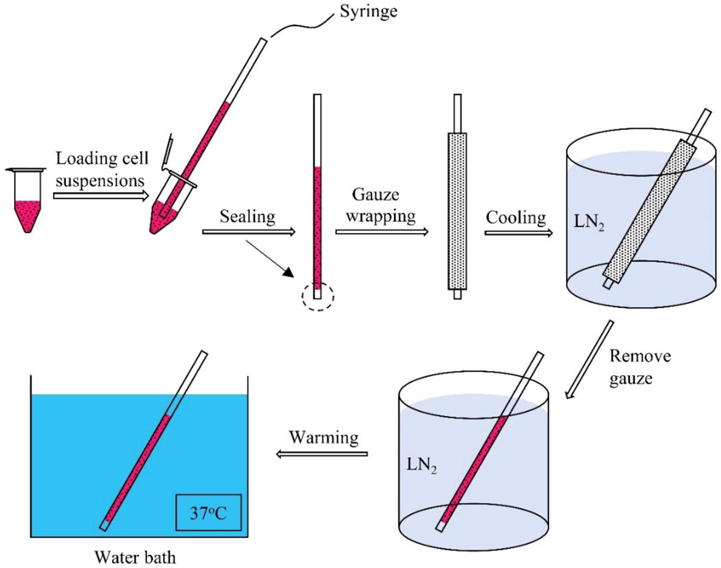
The procedure of the cellular experiments for the ‘WG’ group.

Figure 6.

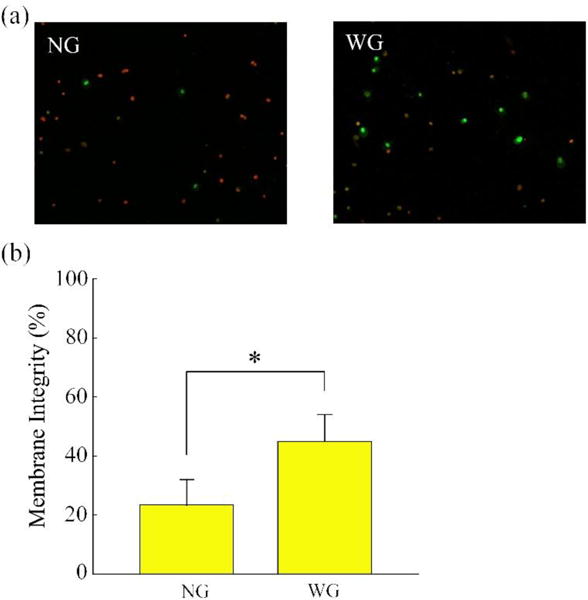
(a) Typical fluorescence images showing the membrane integrity of HUVECs after cooling and warming. (b) Membrane integrity of HUVECs after cooling and warming. *: p<0.05.

4. Conclusions

In summary, we developed an approach of wrapping traditional French-type straw with medical gauze to greatly enhance convective heat transfer during cooling of vitrification cryopreservation. This approach was found to successfully suppress film boiling, due to the “enhanced vapor phase diffusion” effect of the gauze wrapping. A coupled model of heat transfer and crystallization was established to investigate the inherent thermodynamic mechanism in this approach. The simulation indicated that straws with gauze wrapping would increase cell survival subject to vitrification cryopreservation by significantly increasing the cooling rate to inhibit IIF. To confirm our predictions cell experiments using human umbilical vein endothelial cells were conducted to qualify the cell viability after cooling and warming. As a result, straws wrapped with gauze maintained significantly higher cell survival than that without gauze in statistical sense. The computational model and the gauze wrapping technology developed in this study may be valuable to facilitate cell cryopreservation by vitrification with negligible ice formation.

Nomenclature

t

time (s)

T

temperature (K)

k_a

crystallization characteristic constant (s⁻¹K⁻¹)

T_m

final temperature of the freezing process (K)

T_∞

temperature of liquid nitrogen (K)

T_f

equilibrium freezing temperature of the cytoplasm (K)

Q

activation energy (J/mol)

R

gas constant (J/mol/K)

c

specific heat capacity (J/kg/K)

k

thermal conductivity (W/m/K)

r

distance from center of the straw along radial direction (m)

H

latent heat (J/kg)

h

convective heat transfer coefficient (W/m²/K)

A_c

cell surface area (m²)

N

number of water molecules in contract with the substrate (−)

Greek symbols

χ

degree of ice crystallization (−)

ρ

density (kg/m³)

Ω

thermodynamic parameter for nucleation (−)

κ

kinetic parameter for nucleation (−)

η

viscosity of the cytoplasm (Pa·s)

Subscripts

0

isotonic condition