Kernel Methods for Riemannian Analysis of Robust Descriptors of the Cerebral Cortex

Abstract

Typical cerebral cortical analyses rely on spatial normalization and are sensitive to misregistration arising from partial homologies between subject brains and local optima in nonlinear registration. In contrast, we use a descriptor of the 3D cortical sheet (jointly modeling folding and thickness) that is robust to misregistration. Our histogram-based descriptor lies on a Riemannian manifold. We propose new regularized nonlinear methods for (i) detecting group differences, using a Mercer kernel with an implicit lifting map to a reproducing kernel Hilbert space, and (ii) regression against clinical variables, using kernel density estimation. For both methods, we employ kernels that exploit the Riemannian structure. Results on simulated and clinical data shows the improved accuracy and stability of our approach in cortical-sheet analysis.

1 Introduction

Cerebral cortical geometry holds key insights into development, aging, disease progression, and cognition. We propose a new framework to study cortical sheet geometry to detect inter-group differences and regress against clinical variables. Our model subsumes the complementary properties of folding and thickness.

Typical studies of the cortex focus either on folding [19,25,27] or thickness [9,14,23], but not both. They rely on spatial normalization and perform hypothesis tests at every cortical location in the normalized space. However, while the major sulcal patterns are similar across individuals, there is a large variation of the finer-scale cortical folding structure across individuals. This leads to a limited number of homologous features across subject brains [15,16,24], which compromises the precision of the spatial alignment. Moreover, the optimization underlying dense diffeomorphic nonlinear registration is challenged by multiple local optima. Thus, misregistration is inevitable and can inflate the variability of the cortical descriptors and, thereby, reduce the power of subsequent hypothesis tests. To alleviate problems of partial homology and local optima, we use local histogram-based descriptors that are robust to misregistration.

Our histogram-based descriptor lies on a Riemannian manifold. We propose novel Riemannian statistical methods for two typical studies: (i) detecting group differences, using Mercer kernels to fit compact models to non-Gaussian data distributions by implicitly employing a lifting map to a reproducing kernel Hilbert space (RKHS), and (ii) regression against clinical variables, using nonlinear regression via kernel density estimation. Our kernels exploit the Riemannian structure and enable us to effectively deal with (i) nonlinear variations in the data, i.e., within distributions of cortical descriptors, and (ii) dependencies of the cortical descriptors on clinical variables.

We present a new framework for two typical cortical analyses: (i) detecting group differences and (ii) regression against clinical variables. We use a neighborhood-based histogram feature of local cortical geometry, subsuming folding and thickness characteristics, which is robust to misregistration stemming from biology (partial homology) and numerical analysis (local optima). We propose regularized nonlinear models for both analyses, giving compact and reliable model fits, using kernels that exploit the Riemannian structure of the space of histograms. Results on simulated and clinical data shows the improved accuracy and stability of our approach cortical sheet analyses.

2 Related Work

Several cortical studies have focus on its thickness characteristics [9,14,23] or folding characteristics [19,25,27], relying on analyses of cortical features across subjects at every location on the cortical surface (typically, the inner/mid cortical surface). Unlike these studies, we model the 3D cortical sheet including the complementary characteristics of folding and thickness. There are many models for local cortical folding complexity. While [3] uses local curvature measures, [25] represents the cortical surface using spherical wavelets that lead to a set of wavelet coefficients capturing folding at every cortical location. Another method [26] uses spherical harmonic constructions and local fractal dimension to measure folding complexity. In contrast, we capture folding through curvedness and shape index that can lead to easier interpretation. Unlike other approaches, we perform pointwise studies using a local-histogram descriptor combining folding and thickness, which is robust to misregistration. Local histograms were used in [2] without Riemannian analyses and in [1] for linear Riemannian analyses.

Unlike other descriptors [2,3,25,26], our descriptor lies on a Riemannian manifold and we propose novel kernel-based statistical methods that exploit the Riemannian structure. Instead of learning a linear approximation to a manifold (e.g., using isomap) and then using Euclidean statistical analyses in the linearized space, we propose nonlinear statistical analysis directly in the (Riemannian) feature space. For group-difference analysis, we propose a Mercer kernel for modeling the (possibly non-Gaussian) distributions of the histograms within Riemannian space, along with regularized analysis in RKHS. For regression, we propose nonlinear kernel regression directly on the Riemannian manifold [21], and propose a data-driven consistent estimator of the bandwidth parameter.

3 Methods

We first describe our model for the 3D cortical sheet and the robust descriptor of local cortical geometry. We then describe the proposed Riemannian analyses, involving kernel methods, for hypothesis testing to (i) detect group differences in cortical geometry and (ii) regress cortical geometry against clinical variables.

3.1 A Geometrical Model for the Cerebral Cortical Sheet

We use a medial model for the 3D cortical sheet to represent its folding and thickness characteristics. We choose the mid-cortical surface ℳ as the medial surface to model folding. In addition, we use pointwise thickness measurements on the medial surface to model the 3D sheet. At each point m on ℳ, the thickness measurement t(m) gives the locations of the inner and outer (pial) cortical surfaces, at distances t(m)/2 along the inward and outward normals to ℳ at m.

We compute cortical thickness based on an improved version of the diffusion-based method in [11], accounting for partial-volume effects by spatially modulating the diffusion strength proportionately. This also produces the mid-cortical surface ℳ as a level set of the steady-state potential field. For each point m on ℳ, we model the local folding geometry through the principal curvatures determined by the first and second fundamental forms, by fitting a quadratic patch to the local surface around m. The principal curvatures κ_min(m) and κ_max(m) completely describe the local geometry (up to second order and up to a translation and rotation). We reparametrize the 2D space of (κ_min(m), κ_max(m)), via a polar transformation [13], into the orthogonal bases of curvedness C(m) ≔ (κ_min(m)² + κ_max(m)²)^0.5 and shape index $S(m)≔\frac{1}{\pi }\text{arctan }\left(\frac{{\kappa }_{\text{min}}(m)+{\kappa }_{\text{max}}(m)}{{\kappa }_{\text{min}}(m)-{\kappa }_{\text{max}}(m)}\right)$ that meaningfully separate notions of bending and shape for easier interpretation. The curvedness C(m) ≥ 0 measures local patch bending at a particular patch scale/size, and is invariant to location and pose. The shape index S(m) ∈ [−1, 1] is a pure measure of shape, modulo size, location, and pose.

A Robust Local Descriptor of Cortical Folding and Thickness

Nature limits the homology across human brains to about two dozen landmarks in each hemisphere [24]. In typical analyses relying on dense nonlinear diffeomorphic spatial normalization, this partial homology can lead to pointwise correspondences at non-homologous locations, e.g., a gyrus in one brain mapped to a sulcus in another. Such correspondences can inflate the variability of the cortical descriptors and reduce the power of the subsequent hypothesis tests.

One may consider, for a moment, a naive approach to reduce this variability by surface-based spatial smoothing of the descriptors at multiple scales. However, spatial averaging can reduce differences between the smoothed features across corresponding points in subject brains, because multiple spatial distributions of features can all yield the same average. This problem is serious for the brain cortex that is a complex convoluted structure with large variations in the local geometry over small displacements of surface location m. For instance, the value of the shape index drastically changes magnitude and sign as we traverse a surface path from a gyrus (−1) to a sulcus (+1). Curvedness values, along the gyrus-to-sulcus path also changes drastically; from a large positive value to zero (at the inflection point) and back to a large positive value. Cortical thickness also exhibits a variation from gyrus to sulcus, where the crowns of gyri are typically 20% thicker than the fundi of sulci [7]. Indeed, Sect. 4 demonstrates the reduction in the quality of results from smoothing-based multiscale features.

Instead of averaging features across spatial neighborhoods, we propose to use the histograms of neighborhood features, which captures the higher-order statistics of the features. In this way, we extend the notion of histogram-based texture descriptors for images to histogram-based descriptors for the cortical sheet geometry; indeed the cortical sheet exhibits high-frequency spatial variations of features just like a textured image exhibits high-frequency spatial variation of intensity. We propose the local cortical descriptor at location m on the cortical surface to be the joint histogram of shape-index values S(n), curvedness values C(n), and thickness values T(n) at locations n within a spatial neighborhood around location m. The neighborhood size depends on the typical size of regions (not individual points) in the cortex over which homologies can be reliably established (we take this as a region of diameter 1 cm). This histogram is robust to the inevitable misregistration of sulci/gyri at fine scales. Moreover, unlike the neighborhood average that is a scalar, the histogram is a richer descriptor that restricts averaging to each histogram bin.

Riemannian Space of Histograms

We perform statistical analyses using the joint histograms H_i(m) as the local feature descriptor for the cortex at location m for subject i. If the histogram has B bins, then H_i(m) ∈ (ℝ_≥0)^B, ‖H_i(m)‖₁ = 1, and H_i(m) lies on a Riemannian manifold. To measure distance between two histograms H₁(m) and H₂(m), we use the Fisher-Rao distance metric d_ℋ(H₁(m), H₂(m)) ≔ d_𝒮(F₁(m), F₂(m)), where F_i(m) is the square-root histogram that is denoted $\sqrt{H_i(m)}$, with the value in the b-th bin $F_i(m,b)≔\sqrt{H_i(m,b)}$, and d_𝒮(F₁(m), F₂(m)) is the geodesic distance between F₁(m) and F₂(m) on the unit hypersphere 𝕊^B−1.

3.2 Group Analysis Using a Mercer Kernel in Riemannian Space

To detect differences between two groups of histograms, we need models for the distribution of histograms within each group. We propose a parametric and a nonparametric model, and associated test statistics for hypothesis testing.

Parametric Model

Modeling a parametric probability density function (PDF) on a hypersphere entails fundamental trade-offs between model generality and the viability of the underlying parameter estimation. For instance, although Fisher-Bingham PDFs on 𝕊^d are able to model generic anisotropic distributions using O(d²) parameters, their parameter estimation may be intractable [17]. In contrast, parameter estimation for the O(d)-parameter von Mises-Fisher (vMF) PDF is tractable, but that PDF can only model isotropic distributions. We use a tractable approximation of a Normal law on a Riemannian manifold [22], modeling anisotropy through its covariance parameter in the tangent space at the mean. For a group with I subjects, at each cortical location m, we fit the approximate Normal law to the data ${\{\sqrt{H_i(m)}\}}_{i=1}^I$ as follows. We optimize for the Frechet mean μ ∈ 𝕊^B−1 via iterative gradient descent [4], where $\mu ≔{\text{arg min}}_{\nu }{\sum }_{i=1}^I{d}_{𝒮}^2(\nu ,\sqrt{H_i(n)})$ under the constraint ν ∈ 𝕊^B−1. We use the logarithmic map Log_μ(·) to map the square-root histograms ${\{\sqrt{H_i(m)}\}}_{i=1}^I$ to the tangent space at the estimated Frechet mean μ and find the optimal covariance matrix C in closed form [8]. For any histogram H, we define the geodesic Mahalanobis distance between $\sqrt{H}$ and mean μ, given covariance C, as $d_{\mathscr{H}ℳ}(\sqrt{H};\mu ,C)≔{({\text{Log}}_{\mu }{(\sqrt{H})}^{\top }{C}^{-1}{\text{Log}}_{\mu }(\sqrt{H}))}^{0.5}$.

Nonparametric Model

Our nonparametric modeling approach relies on the use of a Mercer kernel to map the square-root histograms on the hypersphere to a RKHS, followed by using (kernel) PCA to fit a multivariate Gaussian distribution to the mapped data in the RKHS. In this way, the Mercer kernel allows us to model nonlinear modes of variation in the data more effectively than the Normal-law approach. The kernel-based strategy has the potential to yield compact fits to the data, thereby being able to detect subtle differences, and detect cortical regions, more accurately. For this purpose, we choose a real-valued Mercer kernel that exploits the Riemannian structure of the space of histograms, which is the vMF Mercer kernel defined on the Riemannian space of histograms as follows: $K_{\text{vMF}}(H_1,H_2;\gamma )≔\text{exp}(\gamma \langle \sqrt{H_1},\sqrt{H_2}\rangle )$, where γ > 0 is a regularization parameter. We set γ to be the average of all intra-group pairwise inner products between the square-root histograms in the dataset.

Let the associated lifting map for the Mercer kernel be Φ(·) that maps H to Φ(H) ≔ k(·, H) in a RKHS ℱ. Consider two vectors in RKHS: $f≔{\sum }_{i=1}^I{\alpha }_i\Phi (H_i)$ and $f\prime ≔{\sum }_{j=1}^J{\beta }_j\Phi (H_j)$. The inner product ${\langle f,f\prime \rangle }_{ℱ}≔{\sum }_{i=1}^I{\sum }_{j=1}^J{\alpha }_i{\beta }_j{K}_{\text{vMF}}(H_i,H_j)$. The norm ${\Vert f\Vert }_{ℱ}≔\sqrt{{\langle f,f\rangle }_{ℱ}}$. When f, f′ ∈ ℱ\{0}, let f ⊗ f′ be the rank-one operator defined as f ⊗ f′(g) ≔ 〈f′, g〉_ℱf. The model fit via kernel PCA, to a sample of size N, gives a mean μ and a covariance operator C. The Mahalanobis distance relies on a regularized sample inverse-covariance operator [18] $C^{-1}≔{\sum }_{q=1}^Q(1/{\lambda }_q){\upsilon }_q\otimes {\upsilon }_q$, where λ_q is the q-th largest eigenvalue of the covariance operator C, υ_q is the corresponding eigenfunction, and Q < N is a regularization parameter. We choose Q to be the number of principal eigenfunctions that capture 90% of the energy in the eigenspectrum. Then, the square-root inverse-covariance operator is $C^{-1/2}≔{\sum }_q(1/\sqrt{{\lambda }_q}){\upsilon }_q\otimes {\upsilon }_q$ and the Mahalanobis distance of point f ∈ ℱ from mean μ ∈ ℱ is d_ℱℳ(f; μ, C) ≔ ‖C^−1/2(f − μ)‖_ℱ.

Test Statistics

For both parametric and nonparametric models, at each cortical location m, for two cohorts ${\{H_i^X(m)\}}_{i=1}^I$ and ${\{H_j^Y(m)\}}_{j=1}^J$, we obtain the means μ^X (m), μ^Y (m) and covariances C^X (m), C^Y (m). For the parametric model the means lie on the hypersphere and the covariances are defined on the tangent spaces at the means. For the nonparametric model, the means and the covariance operators lie in the RKHS associated with the Mercer kernel. To perform hypothesis testing for significant differences between the groups, we need test statistics for the parametric and nonparametric models. For both models, we propose a test statistic t(m) to measure the dissimilarity between the two cohort distributions by adding the squared Mahalanobis geodesic distance between the group means with respect to each group covariance, i.e., $t(m)≔d_{·ℳ}^2({\mu }^X(m);{\mu }^Y(m),C^Y(m))+d_{·ℳ}^2({\mu }^Y(m);{\mu }^X(m),C^X(m))$. The Hotelling’s 2-sample T² test statistic used in the usual Euclidean multivariate Gaussian case may be inapplicable in our parametric Riemannian case because the covariances C^X (m) and C^Y (m) are defined in two different (tangent) spaces.

3.3 Kernel Regression in Riemannian Space

To regress local cortical geometry against a clinical variable, we need a regressor in the Riemannian space of histograms. We propose a nonlinear regressor that relies on principles on kernel density estimation.

Regression Model

We propose an extension of the Nadaraya-Watson nonlinear kernel regressor [10] to the Riemannian space of histograms [21], with the kernel PDF as PK(H; μ, c) ≔ (1/η) exp(cd_ℋ(H, μ)), where H and μ are histograms, μ is the mean parameter, c is the concentration parameter, and η is the normalization constant. Interestingly, this kernel PDF is equivalent to the vMF PDF on the hypersphere associated with square-root histograms. Given a cohort comprising the independent variables as the joint histograms ${\{H_i(m)\}}_{i=1}^I$ and the dependent variable as the clinical score ${\{S_i\}}_{i=1}^I$ the clinical score S for an arbitrary histogram H is given by $r(H;{\{H_i,S_i\}}_{i=1}^I,c)≔\frac{{\sum }_{i=1}^I{P}_K(H;H_i,c)S_i}{{\sum }_{i=1}^I{P}_K(H;H_i,c)}$.

Data-driven selection of the bandwidth parameter 1/c is critical for reliable regression. We propose a leave-one-out (LOO) cross validation approach [10] to automatically optimize the bandwidth parameter based on the structure underlying the data. We optimize c by brute force; we first compute the mean squared error, in the LOO regression estimates across the dataset, for a sequence of discretized parameter values and then select the parameter value that minimizes this error. This estimate c_CV is guaranteed to be consistent [10].

Test Statistic

At each location m on the cortex, we want to test the hypothesis that the clinical variable is dependent on the local cortical descriptor. If the null hypothesis was true, i.e., the clinical variable was independent of the local cortical geometry, then the optimal regressor would be a constant function. We compare the sets of residual errors across the dataset $\{S_j-\hat{r}{(H_j(m);{\{H_i(m),S_i\}}_{i=1}^I\}}_{j=1}^I$, resulting under two regressors r̂(·), i.e., (i) the constant-function regressor r̂(H) = δ and (ii) the kernel regressor $\hat{r}(H)=r(H;{\{H_i(m),S_i\}}_{i=1}^I,c_{\text{CV}})$. If the null hypothesis was true, then the two regressors will produce residuals that would appear to be drawn from the same distribution. If the null hypothesis was false, then the residuals from the kernel regressor would be significantly smaller than those from the constant-function regressor. Thus, we propose the test statistic as the well-known F statistic, i.e., the ratio of the sample variances of the two sets of residuals.

3.4 Permutation Testing and Stability Analysis Using Resampling

Voxel-wise parametric hypothesis testing in the framework of general linear models runs a test at each voxel and adjusts p-values to control for Type-I error arising from multiple comparisons, using Gaussian field theory. However, such parametric approaches make strong assumptions on the data distributions and the dependencies within neighborhoods. In contrast, permutation tests are nonparametric, rely on the generic assumption of exchangeability, lead to stronger control over Type-1 error, are more robust to deviations of the data and effects of processing from an assumed model, and yield multiple-comparison adjusted p values (controlling family-wise error rate through the permutation-distribution of the extremal test statistic). Under the null hypothesis, assuming exchangeability, in mappings between (i) cortical descriptors and (ii) group labels/clinical scores, we use permutation-based resampling to empirically compute the null distribution of the extremal (across all cortical locations) test-statistic values proposed in Sects. 3.2 and 3.3, to compute p values. To evaluate the stability of the p values under variation in cohorts, we compute a set of p values by bootstrap sampling the original cohort and analyzing the associated variation.

4 Results and Discussion

We evaluate our framework on MRI volumes from 2 large datasets: (i) OASIS, for the group-difference study, and (ii) Human Connectome Project (HCP), for the regression study. We use BrainSuite (http://brainsuite.org/) for computing the tissue segmentation, thickness (Fig. 1(a)), mid-cortical surface, shape index (Fig. 1(b)), curvedness (Fig. 1(c)), and spatial normalization [12].

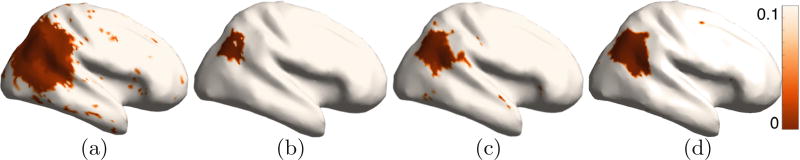
Fig. 1.

Cortical sheet model. Computed values of the cortical (a) thickness, (b) shape index, and (c) curvedness, at each point on the mid-cortical surface. Simulating cortical effects. (d) Selected region for simulating group effects.

Group-Difference Study: Validation with Simulated Differences

We randomly assigned 140 control subjects to 2 groups of 90 and 50 subjects. We treat the larger group as normal, mimicking practical scenarios. For the 50 subjects, we simulated both cortical thinning (eroding the cortex segmentation) and flattening (smoothing the cortex segmentation) in a part of the right parietal lobe (Fig. 1(d)). This (i) reduced thickness and curvedness values and (ii) increased the concentration of shape index values around ±0.5 (corresponding to gyral ridges and sulcal valleys). We then tested for differences between cortices of these 2 cohorts. We compare our approach, i.e., using local joint-histogram descriptors and nonparametric kernel-based Riemannian statistical analysis (Sect. 3.2), against 3 other approaches: (i) multiscale joint descriptors of shape index, curvedness, and thickness (Sect. 3.1), with Euclidean analysis, (ii) histogram descriptors with Euclidean multivariate-Gaussian analysis, ignoring the Riemannian structure, and (iii) histogram descriptors with Riemannian parametric Normal-law modeling (Sect. 3.2).

The detection of group differences with multiscale descriptors (Fig. 2(a)) leads to many false positives. While the histogram-based Euclidean analysis (Fig. 2(b)) detects a region much smaller than the actual (false negatives), the histogram-based Riemannian Normal-law analysis detects a region larger than the actual (false positives). Detection accuracy is best with the proposed approach of Riemannian analysis with Mercer kernels (Fig. 2(d)) that leads to a compact region with very few false positives/negatives. The stability of all histogram-based analyses (Fig. 3) is significantly higher (lower variation in p values) than the multiscale-descriptor analysis. The stability of the proposed approach (Fig. 3(d)), in the affected region in the parietal lobe, is higher than the other histogram-based approaches (Fig. 2(b) and (c)).

Fig. 2.

Group-difference study: validation with simulated differences. permutation test p values with the following features: (a) joint multiscale descriptor, (b) joint histogram descriptor with Euclidean analysis, (c) joint histogram descriptor with Riemannian normal-law analysis, (d) joint histogram descriptor with Riemannian kernel-based analysis (proposed).

Fig. 3.

Group-difference study: simulated differences, stability analysis. Standard deviation of p values, via bootstrap sampling, for: (a) joint multiscale descriptor, (b) joint histogram descriptor with Euclidean analysis, (c) joint histogram descriptor with Riemannian normal-law analysis, (d) joint histogram descriptor with Riemannian kernel-based analysis (proposed).

Group-Difference Study: MCI Data

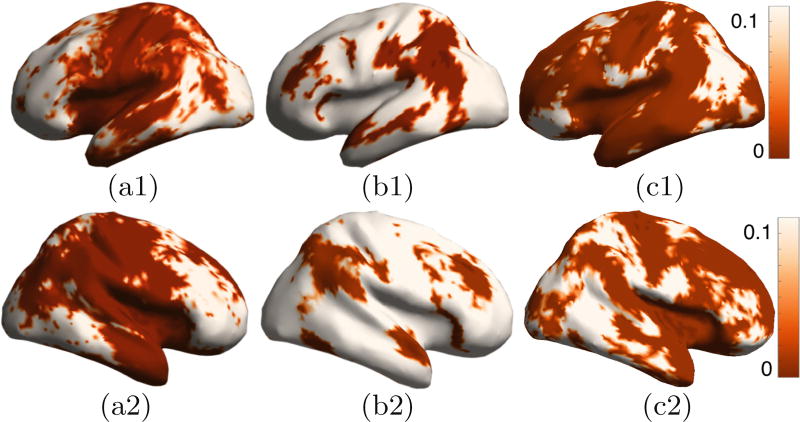
We tested for differences in 2 cohorts from the OASIS dataset: (i) 140 control subjects and (ii) 28 subjects with mild cognitive impairment (MCI) with a clinical dementia rating of 1. The histogram-based descriptors (Fig. 5(b) and (c)) give more stable results than the multiscale descriptors (Fig. 5(a)). The proposed kernel-based approach (Fig. 4(c)) is able to detect differences in more brain lobes, without significant reduction in stability, as compared to the histogram-based Riemannian Normal-law approach (Fig. 4(b)).

Fig. 5.

Group-difference study: MCI, stability analysis. Standard deviation of permutation test p values, via bootstrap sampling, for: (a1), (a2) joint multiscale descriptor, (b1), (b2) joint histogram descriptor with Riemannian normal-law analysis, (c1), (c2) joint histogram with Riemannian kernel-based analysis (proposed).

Fig. 4.

Group-difference study: MCI. Permutation test p values with: (a1), (a2) joint multiscale descriptor, (b1), (b2) joint histogram descriptor with Riemannian Normal-law analysis, (c1), (c2) joint histogram descriptor with Riemannian kernel-based analysis (proposed).

Regression Study: Validation with Simulated Effects

We took 200 MRI volumes from the HCP dataset along with clinical scores on a task. First, we randomly reassign the scores to subjects, to eliminate any existing dependencies between the score and cortical geometry. Then, for all the subjects, we simulated subtle relationships between the scores and the geometry of a part of the right parietal lobe (Fig. 1(d)), by cortical thinning (eroding the cortex segmentation) and flattening (smoothing the cortex segmentation) in amounts directly related to the score.

We compare our approach, i.e., using local joint-histogram descriptors and nonlinear kernel regression on Riemannian space (Sect. 3.3) with cross-validation based data-driven bandwidth estimation, against 3 other approaches: (i) multiscale joint descriptors (Sect. 3.1) with linear regression, (ii) multiscale joint descriptors with nonlinear regression with data-driven bandwidth estimation, and (iii) histogram descriptors with linear regression, ignoring Riemannian structure.

Linear regression with multiscale descriptors performs poorly, wrongly indicating relationships (Fig. 6(a)) with the entire cortex and with the worst stability under bootstrap sampling of the cohort (Fig. 7(a)). With multiscale descriptors, nonlinear regression improves over linear regression, but still leads to many false positive and false negatives (Fig. 6(b)) and has less stability (Fig. 7(b)) than histogram-based descriptors. Histogram-based descriptors perform much better that multiscale descriptors, yielding a coherent region with few false positives (Fig. 6(c) and (d)) and greater stability (Fig. 7(c) and (d)). Our histogram-based nonlinear-regression on Riemannian space, along with automatic bandwidth selection, yields the most stable results (Fig. 7(d)). Our data-driven bandwidth-parameter estimation, at every cortical location, is important in adding to the stability of the nonlinear regression approaches.

Fig. 6.

Regression study: validation with simulated effects. Permutation test p values for: (a) joint multiscale descriptor with linear regression, (b) joint multiscale descriptor with kernel regression, (c) joint histogram descriptor with linear regression, (d) joint histogram descriptor with kernel regression in Riemannian space (proposed).

Fig. 7.

Regression study: simulated effects, stability analysis. Standard deviation of p values, via bootstrap sampling, for: (a) joint multiscale descriptor with linear regression, (b) joint multiscale descriptor with kernel regression, (c) joint histogram descriptor with linear regression, (d) joint histogram descriptor with kernel regression in Riemannian space (proposed).

Regression: Task Score, Stability Analysis

We tested for dependencies between local cortical structure and the task score (average of language-based story and mathematics tasks) on 200 subjects in the HCP dataset. Analogous to the other results in the paper, the histogram-based descriptors (Fig. 9) give far more stable results. The proposed histogram-based approaches, with linear regression ignoring Riemannian structure (Fig. 8(a) and (b)) and nonlinear kernel regression in Riemannian space (Fig. 8(c) and (d)), seem to show dependencies of the task scores on the cortical structure around the insular and opercular regions and near language areas. Recent studies on language processing, using functional imaging, in the brain seem to indicate insula to play an important role in language processing [5,6,20]. The insula shares reciprocal functional and structural connections with linguistic, motor, limbic, and sensory brain areas.

Fig. 9.

Regression study: task score, stability analysis. Standard deviation of permutation test p values, via bootstrap sampling, for the: (a) joint multiscale descriptor with linear regression, (b) joint multiscale descriptor with kernel regression, (c) and (d) joint histogram descriptor with kernel regression in Riemannian space, with data-driven bandwidth selection (proposed).

Fig. 8.

Regression study: task score. Permutation test p values for the joint histogram descriptor with: (a) and (b) linear regression, and (c) and (d) kernel regression in Riemannian space, with data-driven bandwidth selection (proposed).

Conclusion

We propose a framework for analysis of cortical geometry to (i) detect group differences and (ii) regress against clinical variables. We use a cortical descriptor that is robust to fine-scale misregistration, having a Riemannian structure. We propose novel regularized nonlinear models for analyses, giving compact and reliable model fits, using kernels that exploit the Riemannian structure. Our results show improved robustness and accuracy relative to (i) multiscale descriptors and (ii) linear analyses.