A GPU-based symmetric non-rigid image registration method in human lung

Abstract

Background and Objective

Quantitative computed tomography (QCT) of the lungs plays an increasing role in identifying sub-phenotypes of pathologies previously lumped into broad categories such as COPD and Asthma. Methods for image matching and linking multiple lung volumes have proven useful in linking structure to function and in the identification of regional longitudinal changes. Here, we seek to improve the accuracy of image matching via the use of a symmetric multi-level non-rigid registration employing an inverse consistent (IC) transformation whereby images are registered both in the forward and reverse directions.

Methods

To develop the symmetric method, two similarity measures, the sum of squared intensity difference (SSD) and the sum of squared tissue volume difference (SSTVD), were used. The method is based on a novel generic mathematical framework to include forward and backward transformations, simultaneously, eliminating the need to compute the inverse transformation. Two implementations were used to assess the proposed method: A two-dimensional (2-D) implementation using synthetic examples with SSD, and a multi-core CPU and Graphics Processing Units (GPU) implementation with SSTVD for three-dimensional (3-D) human lung datasets (6 normal adults studied at total lung capacity (TLC) and functional residual capacity (FRC)). Success was evaluated in terms of the IC transformation consistency serving to link TLC to FRC.

Results

2-D registration on synthetic images, using both symmetric and non-symmetric SSD methods, and comparison of displacement fields showed that the symmetric method gave a symmetrical grid shape and reduced IC errors, with the mean values of IC errors decreased by 37%. Results for both symmetric and non-symmetric transformations of human datasets showed the symmetric method gave better results for IC errors in all cases, with mean values of IC errors for the symmetric method lower than the non-symmetric methods using both SSD and SSTVD. The GPU version demonstrated an average of 43 times speedup and ∼5.2 times speedup over the single-thread and twelve-threaded CPU versions, respectively. Run times with the GPU were as fast as 2 minutes.

Conclusions

The symmetric method improved the inverse consistency, aiding the use of image registration in the QCT-based evaluation of the lung.

1. Introduction

Image registration is a key process in medical image analysis used to determine the optimal correspondence between images in a common coordinate system when trying to match images collected at different times or using different imaging modalities [1]. The correspondence provides a model to predict deformation in various human organs, such as the human lung. In the study of the lung, image registration has been applied to both normal and diseased lungs [2,3] with the goal of tracking the motion and regional deformation [4–6], linking dynamic (four dimensional) lung datasets together [7] and differentiating emphysema from small airways disease in smoking-associated chronic obstructive pulmonary disease (COPD) [8].

The result of image registration yields a transformation mapping between two images, being referred to as the fixed and moving images, respectively. Registration involves three principal components: a transformation model, a similarity measure and an optimization step. The transformation model defines how one image can be transformed or deformed in order to match another image. The similarity measure quantifies the degree of matching between two images within a common coordinate system. It is desirable that each point in the moving image has only one correspondent point as its counterpart in the fixed image. This assumption means the forward transformation, which maps the fixed image to the moving image, and the backward transformation, mapping the moving image to the fixed image, should be inverses of one another, a feature referred to as inverse consistency (IC). IC evaluates how well the transformation derived from image registration satisfies inverse consistency conditions [9,10]. However, in usual computational usage the inverse consistency condition is not satisfied in various image registration techniques and therefore registration results are transformation direction-dependent, causing inconsistent forward and backward transformations [11].

Several image registration methods have been proposed to address the issue of inverse consistency. Christensen and Johnson [12] proposed a non-parametric image registration method to overcome the inconsistency issue. Their method is based on jointly estimating the transformation in both registration directions, as well as imposing an inverse consistency constraint. Another approach was proposed by Ashburner et al. [13], who used Bayesian statistics to achieve a maximum a posteriori estimate of the deformation field. Also, Cachier and Rey [14] proposed an approach to reduce the asymmetry of registration by introducing inversion-invariant similarity and smoothness energies. Another interesting method was proposed by Rogelj and Kovačič [11]. They improved registration's inverse consistency by defining a symmetric image interdependence function measuring the image similarity in both transformation directions. Papiez et al. [15] used a Newton-Raphson like method to symmetrize the cost function to satisfy the IC condition directly, while Aganj et al. [16] targeted the non-uniformity of the cost function as the underlying cause of asymmetry by adding “an adaptive quasi-volume” constraint, where non-uniformity occurs when a cost function is divided into two parts with different weights in a symmetrization process. Also Vercauteren et al. [17] proposed non-parametric image registration method that imposes the “symmetric forces variant” as a constraint in diffeomorphic demons to achieve IC. Reaungamornrat et al. [18] proposed the MIND Demons algorithm for symmetric image registration in spinal interventions. They used a constrained symmetric energy function to estimate diffeomorphisms between two images.

Due to the ability of symmetric image registration to provide improved registration results in terms of inverse consistency and because medical image analysis demands high quality registration results, it is desirable to have the feature of symmetry in transformation direction. For example, symmetric methods can be used to improve image registration of the human lung that is complicated due to its non-rigid motion. Xu and Li [19] proposed a 4D image registration algorithm for dynamic volumetric lung images using two 4D B-spline functions, indicating a forward and inverse parameterization. Reaungamornrat et al. [18] used MR-To-CT symmetric image registration in spinal intervention using a symmetric constrain.

In this paper, we propose a novel mathematical framework for symmetric registration based on free-form deformation transformation (FFD) models [20]. The aim of this method is to eliminate or decrease sensitivity and dependence of the image registration method to transformation direction without explicit need for the inverse transformation in such a way that final form of similarity measure does not depend on inverse of transformation. We implement this framework for a cubic B-spline transformation model with two different similarity measures: 1) the sum of squared intensity difference (SSD) for two-dimensional (2-D) synthetic images 2) a physiologically meaningful similarity measure, the sum of squared tissue volume differences (SSTVD), for pairs of three-dimensional (3-D) computed tomography (CT) datasets of the human lung. The datasets were acquired at total lung capacity (TLC) and functional residual capacity (FRC). In order to ensure a one-to-one mapping for large deformation, the maximum displacement of control nodes was constrained [21], thus requiring solving for a sequence of invertible B-splines in a multi-level and multiresolution framework. The proposed symmetric method was assessed in two ways: 1) with 2-D synthetic examples using SSD in order to validate the model, and 2) with 3-D lung CT datasets using SSTVD because of its volume preserving nature. The time required for performing registration is very important in practical medical usages [22]. We follow the method proposed recently by Ellingwood et al. [23] for faster GPU and multi-threaded CPU implementations of multi-level SSTVD method for 3-D cases, and a comparison of performance results is included in the result section.

2. Methods

Given two images I_f and I_m, referred to as the fixed and moving images, respectively, where I_f (x): Ω → ℛ, x ∈ Ω ⊂ ℛ³ and I_m(y′): Ω′ → ℛ, y′ ∈ Ω′ ⊂ ℛ³ these images can be considered as continuous functions of intensity at corresponding voxel coordinates. The aim of symmetric registration is to find a transformation function T(x, ϕ) mapping one image to another by calculating forward, T_F, and backward,T_F, transformations simultaneously in order to decrease the dependence on registration direction. This can be accomplished by the symmetrization of the similarity measure so that information of both forward and backward transformations is included in the related cost function [11].

2.1. Transformation model

We adopt cubic B-splines as the transformation model to use in conjuction with the symmetric measure presented in the next section. Cubic B-splines are one of the most common parametric transformation models for nonrigid image registration [20,24]. A key property of cubic B-splines is that they are locally controlled and, thus, computationally efficient even for a large number of control nodes. Furthermore, the cubic B-spline can be very efficiently implemented on the GPU [25].

Denote as Φ a n_x × n_y × n_z grid of uniformly-spaced FFD control nodes, referred to as the control grid, overlaying a discrete and uniformly spaced grid of voxel intensity values, denoted as Ω, with a size of N_x × N_y × N_z voxels. The displacement of the ijkth control node is denoted by ϕ_i,j,k, and used to parameterize the transformation. The distances between the control nodes in the x, y, and z directions are denoted by δ_x, δ_y, and δ_z, respectively. The 3-D cubic B-spline transformation T is defined for each voxel coordinate x = (x, y, z) with respect to 4^d surrounding the displacement vectors of control nodes ϕ (the number of dimensions d = 3) as:

$$\mathit{T}(\mathit{x},\mathit{\varphi })=\mathit{x}+\sum _{l=0}^3\sum _{m=0}^3\sum _{n=0}^3{B}_l(u)B_m(\nu )B_n(w){\mathit{\varphi }}_{i+l,j+m,k+n}$$ (1)

where i = ⌊x/δ_x⌋ − 1, j = ⌊y/δ_y⌋ − 1, k = ⌊z/δ_z⌋ − 1 are the indices of the first of the control nodes surrounding the voxel to be used for the FFD transformation. u = x/δ_x − (i + 1), v = y/δ_y − (j + 1), w = z/δ_z − (k + 1) denote the local physical coordinates of the voxel, normalized between 0 and 1. The uniform cubic B-spline basis functions B₀ through B₃ are defined for the x direction (and similarly for y and z) as:

$$\begin{array}{c}{B}_0(u)=\frac{{(1-u)}^3}{6},\\ B_1(u)=\frac{3u^3-6u^2+4}{6},\\ B_2(u)=\frac{-3u^3+3u^2+3u+1}{6},\\ B_3(u)=\frac{u^3}{6}\end{array}$$ (2)

where 0 ≤ u ≤ 1. These basis functions are defined on limited support, allowing for efficient computation of the transformation function. In addition they are C² continuous, allowing analytic calculation and continuity of first-order derivatives of the transformation function [3]. In order to minimize the symmetric similarity measure function, we need to calculate its gradient and the Jacobian matrix of the transformation (the Jacobian matrix is defined as the derivative matrix of the transformation). Since the cubic B-spline transform is the tensor product of independent one-dimensional functions, the entries of the Jacobian matrix of the transformation can be analytically calculated. Computation of these derivatives is very similar to computing the transformation itself, applying the product rule from calculus and replacing as approprite basis functions B₀ to B₃ by their respective derivatives as

$$\begin{array}{c}d{B}_0(u)/\mathit{\text{du}}=(-u^2+2u-1)/2,\\ d{B}_1(u)/\mathit{\text{du}}=(3u^2-4u)/2,\\ d{B}_2(u)/\mathit{\text{du}}=(-3u^2+2u+1)/2,\\ d{B}_3(u)/\mathit{\text{du}}=u^2/2\end{array}$$ (3)

2.2. Symmetrization of similarity measure

2.2.1. Sum of squared intensity difference

Given a pair of N-dimensional images I_f and I_m, a commonly used similarity measure, the sum of squared intensity difference (SSD), is defined as

$$C_{\mathit{\text{SSD}}}(\mathit{\varphi })=\sum _{x\in \mathrm{\Omega }}{[I_f(\mathit{x})-I_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2$$ (4)

where x = (x₁ … x_N) and y = T[x, ϕ] is the corresponding transformed point from the fixed to the moving image. A symmetric version of the SSD similarity measure E(ϕ), can be defined as

$$E(\mathit{\varphi })=\frac{1}{2}\sum _{\mathit{x}\in \mathrm{\Omega }}{[I_f(\mathit{x})-I_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2+\frac{1}{2}\sum _{y^{\prime }\in {\mathrm{\Omega }}^{\prime }}{[I_m({\mathbf{y}}^{\prime })-I_f({\mathit{T}}^{-\mathbf{1}}[{\mathit{y}}^{\prime },\mathit{\varphi }])]}^2$$ (5)

Where Ω and Ω′ are the domains in images I_f and I_m, respectively. In order to ensure symmetry of the similarity measure, we force the backward transformation as the exact inverse of the forward transformation. To calculate Eq. (5), we choose the sample point y′ as the forward transformed point of x, i.e., y′ = y = T [x, ϕ] and x = T⁻¹ [y′, ϕ]. Thus, we could rewrite Eq. (5) as

$$E(\mathit{\varphi })=\frac{1}{2}\sum _{\mathit{x}\in \mathrm{\Omega }}{[I_f(\mathit{x})-I_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2+\frac{1}{2}\sum _{x\in \mathrm{\Omega }}{[I_m(\mathbf{y})-I_f({\mathit{T}}^{-\mathbf{1}}[\mathit{y},\mathit{\varphi }])]}^2$$ (6)

Where both x and y are elements in the same set of Ω. For optimization, we need to calculate the gradient of the cost function, Eq. (6), with respect to the transformation parameter ϕ as

$$\frac{\partial E}{\partial \mathit{\varphi }}=-\sum _{\mathit{x}\in \mathrm{\Omega }}[I_f(\mathit{x})-I_m(\mathit{T}[\mathit{x},\mathit{\varphi }])][\nabla I_m(\mathit{y})\cdot \frac{\partial (\mathit{T}[\mathit{x},\mathit{\varphi }])}{\partial \mathit{\varphi }}-\nabla I_f(\mathit{x})\cdot \frac{\partial ({\mathit{T}}^{-1}[\mathit{y},\mathit{\varphi }])}{\partial \mathit{\varphi }}]$$ (7)

where (or ∇I_m(y) (or ∇I_f(x)) is the intensity gradient of the moving (or fixed) images. It is straightforward to calculate ∂T/∂ϕ with the defined forward transformation. ∂T⁻¹/∂ϕ is derived by use of the chain rule for partial derivatives and noting that the fixed image coordinates x are independent of the displacement vectors of control nodes ϕ, and that y is identified with the forward transformed point of x, y = T [x, ϕ]:

$$0=\frac{d\mathit{x}}{d\mathit{\varphi }}=\frac{\partial {\mathit{T}}^{-\mathbf{1}}}{\partial \mathit{y}}\frac{\partial \mathit{y}}{\partial \mathit{\varphi }}+\frac{\partial {\mathit{T}}^{-\mathbf{1}}}{\partial \mathit{\varphi }}=[J_{T^{-1}}]\frac{\partial \mathit{T}[\mathit{x},\mathit{\varphi }]}{\partial \mathit{\varphi }}+\frac{\partial {\mathit{T}}^{-\mathbf{1}}}{\partial \mathit{\varphi }}$$ (8)

where [J_T⁻¹] is the Jacobian matrix of the transformation T⁻¹ . The Jacobian value J_T is defined as the determinant of the derivative matrix of the transformation respect to voxel coordinate x [3]. The Jacobian matrix of the inverse transformation is the inverse of the Jacobian matrix of the transformation. Using the inverse function theorem, we can recast Eq. (7) in terms of the forward transformation by making use of the substitution from Eq. (8) as

$$\frac{\partial {\mathit{T}}^{-\mathbf{1}}}{\partial \mathit{\varphi }}=-{[J_T]}^{-1}\frac{\partial \mathit{T}}{\partial \mathit{\varphi }}$$ (9)

So Eq. (7) can be rewritten as

$$\frac{\partial E}{\partial \mathit{\varphi }}=-\sum _{\mathit{x}\in \mathrm{\Omega }}[I_f(\mathit{x})-I_m(\mathit{y})]\{\nabla I_m(\mathit{y})+\nabla I_f(\mathit{x})\cdot {[J_T]}^{-1}\}\cdot \frac{\partial T}{\partial \mathit{\varphi }}$$ (10)

Eq. (10) does not explicitly require the inverse transformation of T. The framework presented above is a generic form for intensity-based symmetric registration and can be applied to both non-parametric and parametric transformation models with complicated similarity measures, such as mutual information, normalized correlation coefficient and the sum of squared local tissue volume difference (SSTVD).

2.2.2. Sum of squared tissue volume difference

The similarity measure SSTVD, proposed by Yin et al. [3], has been demonstrated to successfully improve registration of lung images, particularly in regions with large deformations. It takes into account changes in the reconstructed Hounsfield unit (scaled attenuation coefficient, HU) due to inflation in lung motion. The Hounsfield units can be used to estimate the amount of air or tissue in each voxel [26]. SSTVD extends the SSD similarity measure to address intensity changes in respiratory motion between intra-subject volumetric lung CT images by including air and tissue volume information. This measure is defined as

$$C_{\mathit{\text{SSTVD}}}(\mathit{\varphi })=\sum _{x\in \mathrm{\Omega }}{[{\nu }_f(\mathit{x}){\stackrel{\sim }{I}}_f(\mathit{x})-{\nu }_m(\mathit{T}[\mathit{x},\mathit{\varphi }]){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2$$ (11)

where ν_f and ν_m are the local volumes of corresponding regions in the fixed and moving images, respectively. In addition, Ĩ the tissue fraction estimated from the Hounsfield unit can be calculated as

$$\stackrel{\sim }{I}(\mathit{x})=\frac{I(\mathit{x})-{\mathit{\text{HU}}}_{\mathit{\text{air}}}}{{\mathit{\text{HU}}}_{\mathit{\text{tissue}}}-{\mathit{\text{HU}}}_{\mathit{\text{air}}}}$$ (12)

where the HUs of air and tissue are taken as HU_air = −1000 and HU_tissue = 55, respectively [26,27]. The Jacobian value measures contraction or expansion in lung motion, revealing local expansion if J_T > 1 and local contraction if 0 < J_T > 1. To avoid non-invertible transformation, the Jacobian value must be positive, which is enforced by constraints on the displacement of B-spline control nodes [21]. Also, v_m (T [x, ϕ]) can be calculated from the Jacobian value as

$${\nu }_m(\mathit{T}[\mathit{x},\mathit{\varphi }])=J_T(\mathit{x},\mathit{\varphi }){\nu }_f(\mathit{x})$$ (13)

With Eq. (13), Eq. (11) can be rewritten as

$$C_{\mathit{\text{SSTVD}}}(\mathit{\varphi })=\sum _{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x}){[{\stackrel{\sim }{I}}_f(\mathit{x})-J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2$$ (14)

We recast Eq. (14) so that the matching between the reference and moving images is symmetric. Eq. (14) can be rewritten to define the symmetric similarity measure E(ϕ) with SSTVD as

$$E(\mathit{\varphi })=\frac{1}{2}\sum _{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x}){[{\stackrel{\sim }{I}}_f(\mathit{x})-J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2+\frac{1}{2}\sum _{y^{\prime }\in {\mathrm{\Omega }}^{\prime }}{{\nu }_m}^2({\mathit{y}}^{\prime }){[{\stackrel{\sim }{I}}_m({\mathit{y}}^{\prime })-J_{T^{-1}}({\mathit{y}}^{\prime },\mathit{\varphi }){\stackrel{\sim }{I}}_f({\mathit{T}}^{-\mathbf{1}}[{\mathit{y}}^{\prime },\mathit{\varphi }])]}^2$$ (15)

where Ω is the fixed image domain, Ω′ is the moving image domain, Ĩ_f and Ĩ_m are the fixed and moving tissue fraction estimated from the Hounsfield Unit (HU), T is the forward transformation, T⁻¹ is the backward transformation, and J_T and J_T⁻¹ are the respective Jacobian values of the forward and backward transformations. The cost function includes information of forward and backward transformations simultaneously to determine registration parameters during optimization, defining the symmetric similarity criteria. For optimization, the gradient of the similarity function with respect to the transformation parameter ϕ is needed, and expressed as:

$$\frac{\partial E}{\partial \mathit{\varphi }}=\sum _{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x})[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])-{\stackrel{\sim }{I}}_f(\mathit{x})]{\nabla }_{\mathit{\varphi }}[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]+\sum _{y^{\prime }\in {\mathrm{\Omega }}^{\prime }}{{\nu }_m}^2({\mathit{y}}^{\prime })[J_{T^{-1}}({\mathit{y}}^{\prime },\mathit{\varphi }){\stackrel{\sim }{I}}_f({\mathit{T}}^{-\mathbf{1}}[{\mathit{y}}^{\prime },\mathit{\varphi }])-{\stackrel{\sim }{I}}_m({\mathit{y}}^{\prime })]{\nabla }_{\mathit{\varphi }}[J_{T^{-1}}({\mathit{y}}^{\prime },\mathit{\varphi }){\stackrel{\sim }{I}}_f({\mathit{T}}^{-\mathbf{1}}[{\mathit{y}}^{\prime },\mathit{\varphi }])]$$ (16)

where ${\nabla }_{\mathit{\varphi }}=(\frac{\partial }{\partial {\varphi }_x},\frac{\partial }{\partial {\varphi }_y},\frac{\partial }{\partial {\varphi }_z})$. Based on the constraints [21] that the transformation is invertible, we make the assumption that we can choose the sample point y′ as the forward transformed point of x, that is y′ = y = T [x, ϕ] and x = T⁻¹ [y′, ϕ]. By making this assumption, we can recast both the cost function and cost gradient in terms of the fixed image domain, leaving the variable x as the independent variable and removing explicit reference to the backward transformation and y variable. Using Eq. (9), Eq. (16) gives

$$\frac{\partial E}{\partial \mathit{\varphi }}=\sum _{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x})[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})-{\stackrel{\sim }{I}}_f(\mathit{x})]\{{\nabla }_{\mathit{\varphi }}[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})]+J_T(\mathit{x},\mathit{\varphi }){\nabla }_{\mathit{\varphi }}[J_{T^{-1}}(\mathit{y},\mathit{\varphi }){\stackrel{\sim }{I}}_f(\mathit{x})]\}$$ (17)

The constraints mentioned in [21] require that the displacements ϕ in each direction and the B-spline grid spacing δ fit the condition ϕ < δ/K where k = 2.479472335. This leads to the need for a multi-level registration strategy, consisting of a sequence of B-spline grids beginning with a coarse grid of control nodes, and transitioning to finer grids of more closely space grids. The coarse grids with farther spacing between control nodes capture global deformations, while the finer grids capture local deformations. A composite transformation operation links the registration results between levels, see Ellingwood et al. [23] for more details.

2.3. Optimization

Image registration is an optimization problem and needs an efficient optimization algorithm to minimize the cost function with coresponding transformation parameters. But in all cases, due to the ill-posed nature of registration, the optimization process should be constrained to avoid folding in the moving image. This may result in inconsistent deformation and a less physiologically meaningful deformed image [28]. Therefore, adding a penalizing term to the similarity measure is important due to its ability to enforce topology preservation in registration process. This can be accomplished by adding regularization terms to the related similarity measure. In other words, the optimization process defines the similarity energy S(ϕ) to be optimized as a linear combination of a similarity measure E(ϕ) and a regularization term F(ϕ) as

$$S(\mathit{\varphi })=E(\mathit{\varphi })+\lambda F(\mathit{\varphi })$$ (18)

where λ > 0 is a weighting parameter. The weight λ = 0.5 was used in this work. Possible regularization models such as linear elasticity [29], viscous fluid [30], and analytic regularization for landmark-based registration [31] have been developed to regularize the transformation. In this work, we used an unbiased registration constraint [32] as

$$F(\mathit{\varphi })=\sum _{x\in \mathrm{\Omega }}(J_T(\mathit{x},\mathit{\varphi })-1){log}_{10}(J_T(\mathit{x},\mathit{\varphi })$$ (19)

which is based on a log-normal distribution of the Jacobian determinants. The inverse consistency property of this method was shown in the study of unbiased fluid registration methods [33]. A limited-memory quasi-Newton minimization method with bounds on the variables, L-BFGS-B [34] is used along with the multiresolution strategy to improve the computational efficiency and avoid local minima [3,23]. With the SSTVD measure and using Eq. (17), Eq. (18) and Eq. (19), we have the gradient of S(ϕ) as

$$\begin{gathered} \frac{\partial S}{\partial \mathit{\varphi }}=\sum _{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x})[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y}) \\ -{\stackrel{\sim }{I}}_f(\mathit{x})]\{{\nabla }_{\mathit{\varphi }}[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})]+J_T(\mathit{x},\mathit{\varphi }){\nabla }_{\mathit{\varphi }}[J_{T^{-1}}(\mathit{y},\mathit{\varphi }){\stackrel{\sim }{I}}_f(\mathit{x})]\} \\ +(1+{log}_{10}(J_T(\mathit{x},\mathit{\varphi }))-1/J_T(\mathit{x},\mathit{\varphi })) \end{gathered}$$ (20)

2.4. Inverse consistency error

The symmetric method can be evaluated via inverse consistency error (ICE). ICE is defined as an average distance between the original point and its mapped point in the reference image after two subsequent forward and backward transformations (T_F ∘ T_R or T_R ∘ T_F) to the moving image. Therefore ICE can give an evaluation criteria for a consistent pointwise correspondence mapping between the reference and moving images [15,35]. It is defined as

$$\mathit{\text{ICE}}=\Vert \mathit{x}-(T_R\circ T_F)(\mathit{x})\Vert$$ (21)

where T_F and T_R are the forward and backward transformations, respectively. The maximum of ICE is also defined as

$$\mathit{\text{maxICE}}=\mathit{max}(\Vert \mathit{y}-(T_F\circ T_R)(\mathit{y})\Vert )\text{or}\mathit{max}(\Vert \mathit{x}-(T_R\circ T_F)(\mathit{x})\Vert )$$ (22)

The averaged ICE for forward and backward transformations between the fixed and moving images provides a criterion to assess the symmetry condition of a similarity measure.

2.5. GPU and Multi-threaded CPU Implementation

The implementation of GPU and multi-threaded CPU versions was developed extending the procedure reported in Ellingwood et al. [23] (Fig. (1)). The procedure involved two key steps in designing an effective GPU implementation. First, the uniformly spaced grid of control nodes for parameterizing the cubic B-spline transformation was aligned with the uniformly spaced voxel grid (partitioning it into tiles of equal numbers of voxels). Due to the uniform spacing of the voxels, corresponding voxels within tiles share the same local coordinates (normalized between 0 and 1). B-spline product weights could then be precomputed for a single tile, with computation required only one time during initialization, and stored in a lookup table (LUT) for reuse, creating tremendous computational and memory efficiencies. Second, in order to maintain the uniform spacing of the voxel grid necessary to utilize the B-spline LUTs for subsequent resolution levels of registration within the multi-level framework, a diffeomorphic multi-level transform composite (DMTC) method was utilized (see Ellingwood et al. [23] for details). Implementation of the GPU version of the symmetric SSTVD method required additional memory storage and computation for the gradient of the moving image. A pseudo-code is included in the supplementary section 5.1 for clarity; see Ellingwood et al. [23] for a detailed description. Registration accuracy results for DMTC based on annotated landmarks also are included in section 3.4.

Fig. 1.

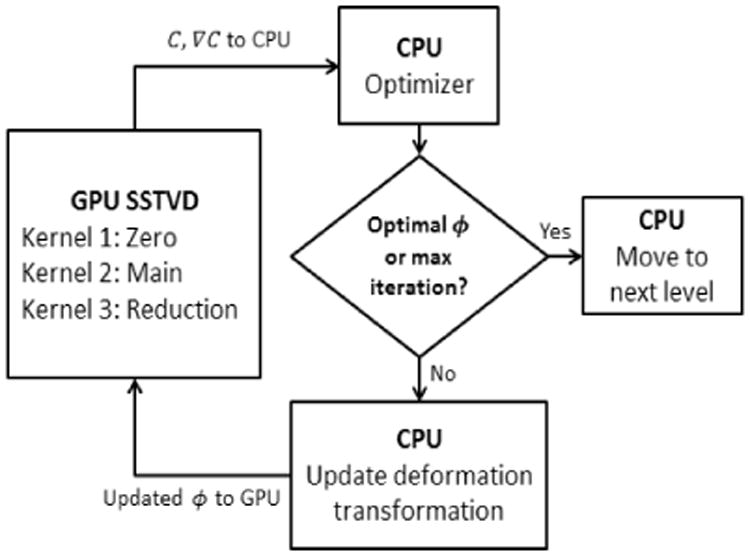
Division of work between CPU and GPU during the SSTVD computations [23].

3. Results

Two sets of experiments were performed to evaluate the symmetric registration method. First, registration of synthetic data sets consisting of two 2-D images (so-called Circle to C-shape test) was assessed based on the symmetric SSD method. Second, lung CT datasets from six normal human subjects (previously described by Yin et al. [3]) were used to assess the proposed SSTVD symmetric similarity method. For these subjects, two volumetric scans were acquired with a Siemens Sensation 64 multi-detector row CT scanner (Forchheim, Germany) during breath-holds near FRC and TLC in the same scanning session for each subject. The University Institutional Review Board approved the scanning protocol. Each volumetric dataset contains 550-760 image sections with a section spacing from 0.5 to 0.7 mm and a reconstruction matrix of 512 × 512 pixels. In-plane pixel spatial resolution is approximately 0.6 × 0.6 mm². The software Apollo (VIDA Diagnostics, Coralville, Iowa) was used to segment the lungs and lobes of CT images.

3.1. Assessment based on 2-D synthetic objects

Fig. 2(a) shows the synthetic data of 2-D Circle and C-shape images from the classical registration example, each of size 256 × 256 pixels with pixel size of 1.0mm × 1.0mm. A composite transform consisting of eight levels of B-splines was used to describe the deformation. Also the displacement field and transformed shape of the deformed grid space were compared for non-symmetric and symmetric SSD similarity measures and depicted in Fig. 2(b) and Fig. 2(c). The symmetries of these methods were quantified by inverse consistency error. Results for forward and backward deformations and their related ICE values are tabulated in Table 1 for two different ICE ranges.

Fig. 2.

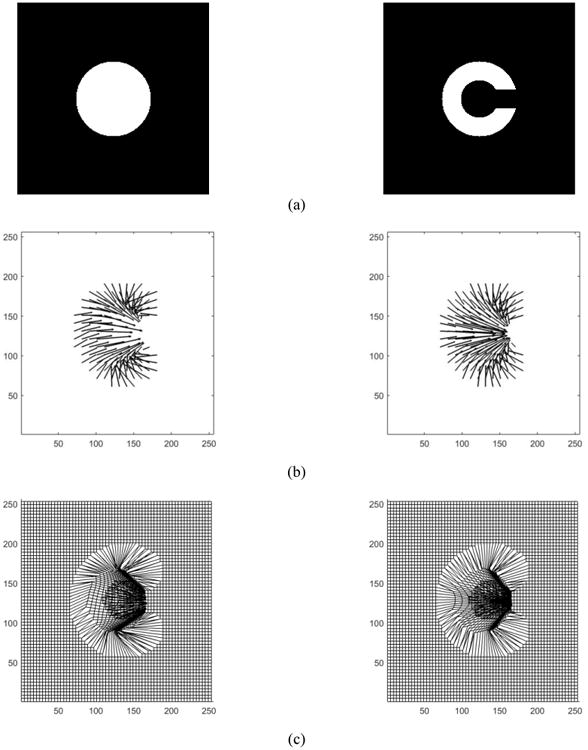
Classical Circle to C-shape experiment (a) and Registration displacement field and transformation grid shape for non-symmetric and symmetric for C-shape as the fixed image: (b) Displacement vector field non-symmetric (left) vs. symmetric (right) (c) Transformation shape in deformed grid space for non-symmetric (left) vs. symmetric (right).

Table 1.

Comparison results for mean of ICE values for 2-D non-symmetric vs. symmetric SSD method (C-shape as the fixed image) and their error ranges (percentage of the voxel numbers with ICE less than 40 and greater than 40 mm divided by the total pixel number).

	Method-SSD		ICE range	Error range [%]
Non-Symmetric	Mean [mm]	36.32	ICE < 40	67.9
			ICE > 40	32.1
Symmetric
	Mean [mm]	22.87	ICE < 40	97.5
			ICE > 40	2.4

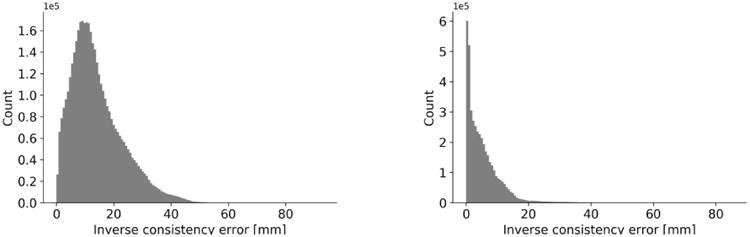
Clearly, from Table 1 the mean values of ICE are lower in the symmetric method than the non-symmetric method. In addition, the symmetric method yields a more symmetrical grid shape as seen in Fig. 2(b) and Fig. 2(c). The distributions and histograms of ICE for non-symmetric and symmetric methods are shown in Fig. 3(b).

Fig. 3.

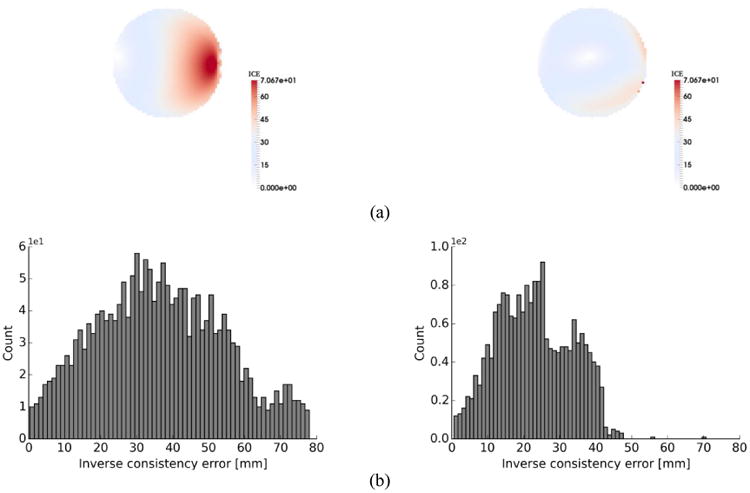
(a) distribution of inverse consistency error for non-symmetric (left) vs. symmetric (right) method for SSD registration of Circle and C-shape (C-shape as the fixed image) (b) histogram of inverse consistency error for non-symmetric (left) vs. symmetric method (right) for SSD.

3.2. Validation for 3-D lung CT datasets

Mean of ICE values in different ranges (ICE < 15 mm and ICE > 30 mm) for forward and backward (non-symmetric) and symmetric methods for both SSD and SSTVD are tabulated in Table 2. Fig. 4 shows an example of histograms for ICE values with SSD and SSTVD similarity measures for both non-symmetric and symmetric methods to illustrate the distribution of different ICE values. The ICE contours for non-symmetric and symmetric methods for both SSD and SSTVD within the sagittal planes of the lung are displayed in Fig. 5.

Table 2.

The mean of ICE for forward (T_F), backward (T_R) and symmetric (T_S) methods (TLC as the fixed image) and their error ranges (percentage of the voxel numbers with ICE less than 15 and greater than 30 mm divided by the total pixel number).

Experiment	SSD	Mean [mm]	Error range [%]		SSTVD	Mean [mm]	Error range [%]
			< 15 mm	> 30 mm			< 15 mm	> 30 mm
Case 1	TF	23.36	35.0	28.9	TF	6.78	88.8	2.9
	TR	31.24	28.1	47.5	TR	20.40	49.9	30.8
	TS	16.77	44.4	5.9	TS	5.53	90.9	2.5
Case 2	TF	14.83	56.5	8.7	TF	6.43	90.1	0.8
	TR	25.23	46.2	29.1	TR	19.93	61.9	28
	TS	11.62	70.6	0.9	TS	5.56	95.0	0.7
Case 3	TF	14.16	62.2	6.4	TF	5.44	89.1	1.0
	TR	23.74	50.3	29.3	TR	17.05	63.8	24.1
	TS	11.56	70.2	0.44	TS	4.96	96.1	0.2
Case 4	TF	12.81	60.3	1.0	TF	6.22	80.0	1.1
	TR	25.48	46.4	36.33	TR	18.77	54.2	27.6
	TS	12.07	66.6	0.8	TS	5.532	92.2	0.9
Case 5	TF	21.01	37.7	23.3	TF	9.03	83.7	1.3
	TR	28.03	34.1	36.5	TR	19.40	53.5	23
	TS	16.41	45.9	4.69	TS	5.57	95.4	0.84
Case 6	TF	24.48	36.7	33.7	TF	10.60	75.4	4.3
	TR	33.10	31.7	39.2	TR	23.52	45.3	30.5
	TS	18.06	41.3	12.52	TS	7.10	91.5	1.7

Fig. 4.

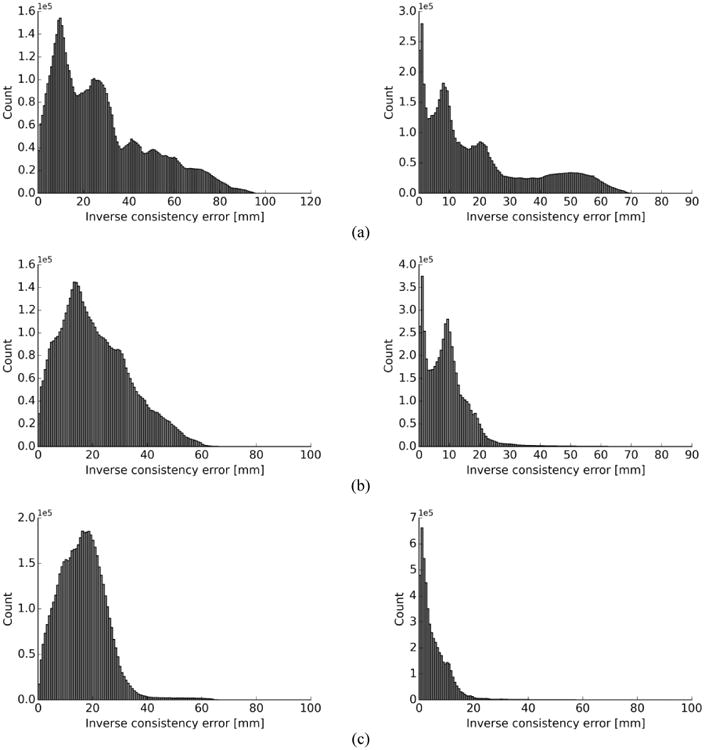
Distribution of inverse consistency error for non-symmetric (backward and forward) vs. symmetric (TLC as the fixed image) for SSD (left) vs. SSTVD (right) for (a) forward (b) backward (c) symmetric transformations.

Fig. 5.

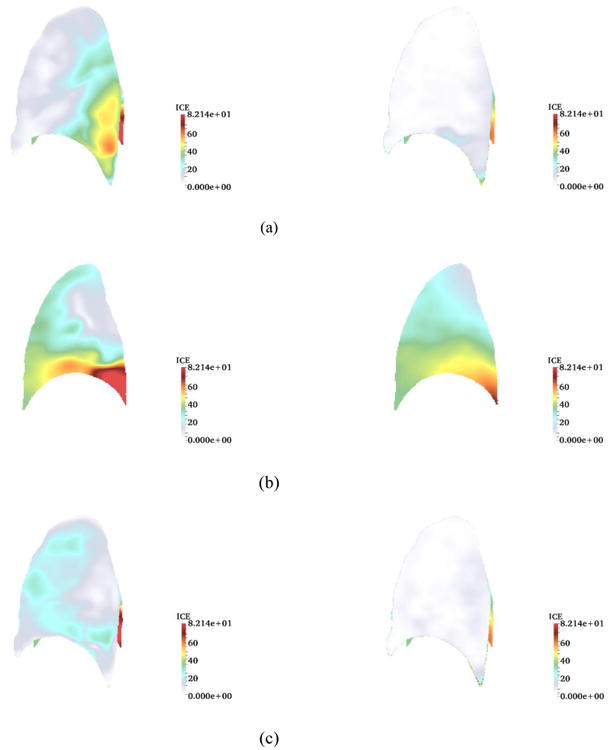
Inverse consistency error [mm] for non-symmetric vs. symmetric method (TLC as the fixed image) for sagittal plane. SSD (left) vs. SSTVD (right) for (a) forward (b) backward (c) symmetric transformations.

3.3. GPU performance results of symmetric method

During code testing, we determined the cost and cost-gradient computations for the similarity measure were responsible for over 60% of the total computational time for the symmetric image registration code (optimization taking most of the remaining 40%, pseudo-code for implementation of the symmetric method is presented in the section 5.1). The vast amount of data-parallelism present within this component of the code indicated it was well-suited for GPU implementation. The procedure developed in Ellingwood et al. [23] was followed and is discussed in section 2.5.

The GPU version of symmetric registration method was run on a Nvidia Tesla K40 GPU on the XSEDE supercomputing resource Maverick, a supercomputer dedicated to high-performance GPGPU computing and data visualization at the Texas Advanced Computing Center (TACC) at the University of Texas. The Tesla K40 consists of 15 streaming multiprocessors of 192 Cuda cores each, for a total 2880 Cuda cores, and total memory (DRAM) of 12GB with bandwidth 288 GB/sec. The results for the GPU implementation were verified against those of the single-threaded CPU implementation, with the CPU implementation serving as the reference.

The performance results for the GPU implementation (using a Nvidia Tesla K40) are compared to single and twelve-threaded CPU results (run an Intel Xeon E5-2620 6-core CPU clocked at 2.1 GHz) and reported in two ways – total times and speedup per resolution level. The results in Fig. 6 show the speedup factors per level of registration, where speedup factor is defined as the time_{serial CPU}/time_GPU. At every level, the GPU performs better than each of the multithreaded CPU versions. Greatest speedup occurs for GPU over CPU at the highest resolution level, where the GPU version demonstrated an average of 43 times speedup and nearly 5.1 times speedup over the single-thread and twelve-threaded CPU versions, respectively.

Fig. 6.

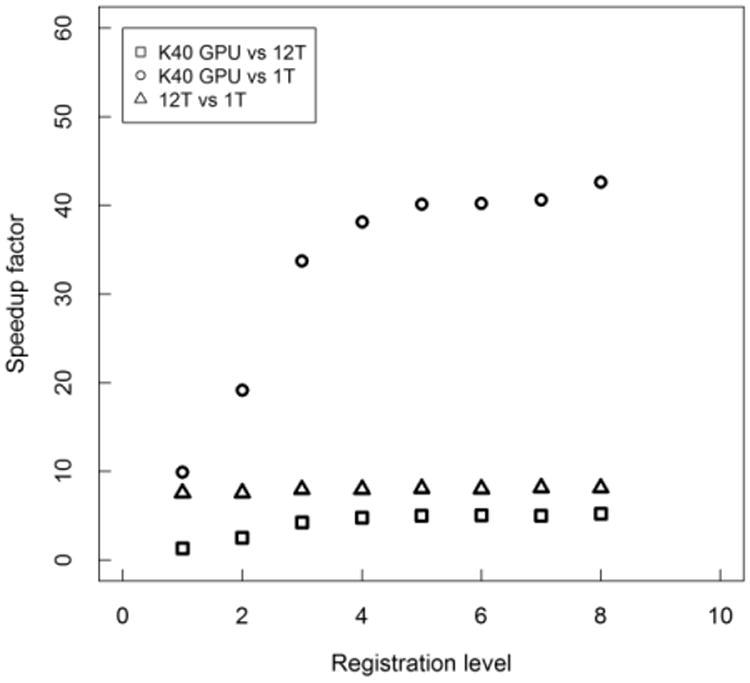
Speedup factors for the accelerated symmetric cost and cost-gradient component of code, comparing the GPU implementation to single- and twelve-threaded (1T, 12T) CPU versions. Values shown are averaged for subjects at each of the 8 levels of the image pyramid. Image results for B-Spline grid spacing so that the number of voxels in a tile are multiples of 4 per direction.

For total times, registration time (cost, cost gradient, and optimization) and isolated cost and cost gradient computations, totaled over all resolution levels, are compared. As shown in Table 3, total time decreased substantially with use of GPU as compared to twelve-threaded CPU results. The Tesla K40 substantially improved the runtime performance over the single-threaded version for total registration time (13.7 times faster) and the isolated cost plus cost gradient total time targeted for GPU acceleration (38 times faster). The GPU performance is also better than the 12-threaded version, performing 1.8 times faster in total registration time and 5 times faster in total cost plus cost gradient time. Scalability of the multi-threaded CPU version flattens after 12 threads, yielding performance only slightly better for 24 threads compared to 12 threads.

Table 3.

Total registration time and total cost and gradient computational time for GPU and CPU implementations of symmetric SSTVD. Note: Time is totaled over all 8 levels of registration and averaged for subjects.

Version	Total Registration Time [min]	Total Cost and Cost Gradient Time [min]
K40* GPU	9.0	2.0
12T CPU	16.1	9.8
1T CPU	123.5	75.3

^*K40 GPU information: Total memory: 12GB, Memory bandwidth: 288 GB/se with 15 streaming multiprocessors (SMX) consisting of 192 Cuda cores.

3.4. Landmark validation

Landmarks located at vessel bifurcation of TLC and FRC of six normal human subjects [3] are used to assess registration accuracy. These landmarks are picked up based on a semi-automatic landmark annotation system [36] and each pair included 120-210 landmarks. A comparison of landmark errors between SSTVD and SSD methods, averaged over six subjects is shown in Table 4. The landmark error shows the distance between corresponding landmarks in the TLC to FRC before registration and after registration. The landmark distances are averaged together based on initial distance (s) of 20, 40, 60 mm.

Table 4.

Averaged landmark errors between SSTVD and SSD method for six normal human subjects.

	Non-Symmetric			Symmetric
Initial distance s [mm]	SSD [mm]	SSTVD [mm]	p value	SSD [mm]	SSTVD [mm]	p value
s < 20	8.09±3.42	1.2±1.1	≪ 0.0001	7.18±4.02	1.19±1.2	≪ 0.0001
20 ≤ s < 40	11.31±4.24	2.48±3.32	≪ 0.0001	10.44±6.17	2.05±1.3	≪ 0.0001
40 ≤ s < 60	17.36±9.01	3.04±2.63	≪ 0.0001	17.01±4.90	2.72±2.43	≪ 0.0001
s ≥ 60	26.67±5.35	2.93±2.59	≪ 0.0001	25.0±7.15	2.84±2.81	≪ 0.0001

A comparison of landmark errors showed that both symmetric and non-symmetric SSTVD methods decreased the landmarks error to less than 3 mm for all initial distance, where for s < 20 mm, 20 ≤ s < 40 mm, 40 ≤ s < 60 and s ≥ 60, both non-symmetric and symmetric SSD yielded the landmark errors about 7 mm, 10 mm, 17 mm and 25 mm, respectively. This means that both non-symmetric and symmetric SSTVD methods showed very good accuracy for image registration. Although the accuracy of symmetric SSTVD method appears to be slightly better than that of non-symmetric one, their difference is statistically insignificant (p value > 0.05).

4. Discussion

We have presented a novel generic framework for an intensity-based symmetric registration method that can be applied to parametric transformation models and can be extended to more complicated similarity measures. This method was implemented by using a cubic B-spline transformation and then solved by minimizing the symmetric form of the similarity measures (SSD and SSTVD) along with the regularization term included for topology preservation. Invertibility of each B-spline was achieved by imposing displacement constraint of the control nodes.

To evaluate the proposed methods, we first performed registration on a classical Circle to C-shape experiment (Fig. 2(a)) by using both symmetric and non-symmetric SSD methods. Comparison of displacement vector fields and transformation grid shape in Fig. 2(b) and Fig. 2(c) shows that both symmetric and non-symmetric methods gave almost the same displacement fields where the symmetric SSD demonstrated a regular invertible transformation with more symmetrical grid shape than the non-symmetric. Furthermore, the results of ICE (Table 1) show that the symmetric method improved the consistency issue, demonstrated by decreasing the mean values of ICE errors by 37%. This improvement is more evident from the histograms in Fig. 3(b), where the symmetric method shifted higher ICE values to the lower ranges so that percentage of voxels with ICE < 40 mm is approximately 98% of the total voxels number, compared to just 68% for the non-symmetric method. However, there are some high ICE values (less than 2.5% of total voxels number) which occurred at the object boundaries as seen in Fig. 3(a). One possible reason is that the balancing of the similarity measure and the regularization terms in the optimization process can cause these errors at the object edges. This happened for both symmetric and non-symmetric methods because the penalizing (regularization) term prevents the fixed image to completely transform into the moving image trying to preserve the image registration topology.

Results for 3-D cases for both symmetric and non-symmetric (forward and backward) transformations are tabulated in Table 2. Values are based on the mean value of ICE and also error range, which is defined as the percentage of the voxel numbers with ICE less than or greater than a specific value (ICE < 15 mm and ICE > 30 mm ranges were chosen for both symmetric and non-symmetric cases so that a common measure can be used in comparison of the results for all the subjects). The symmetric method gave better results in terms of ICE improvement so that in all cases, the mean values of ICE for the symmetric method were lower than their counterparts, forward and backward transformations (non-symmetric methods) for both SSD and SSTVD. Also, mean values of ICE with SSTVD were significantly lower than those of SSD. This is consistent with the fact that the SSTVD method accounts for the change of intensity and therefore gives a more precise similarity measure criterion and consequently lower ICE (Yin et al. [3]). Also for both SSD and SSTVD, ICE values for backward transformation were higher than forward transformation because in the case of backward transformation, mean values of ICE were calculated within the FRC domain as the fixed image having lower resolution than TLC. Impact of the symmetric method on decreasing error ranges for both SSD and SSTVD can be seen from the histograms in Fig. 4. It should be noted that, even though the inverse consistency constraint was not imposed directly in the related cost function, the symmetric method showed a significant improvement for ICE by decreasing the number of voxels with high ICE values for both SSD and SSTVD. As expected, SSTVD was more effective at decreasing error ranges than SSD. For instance, for all cases, the symmetric SSTVD method decreased the percentage of voxels with ICE > 30 mm to less than maximum 2.5% of the total number of voxels, and simultaneously increased the percentage of voxels with ICE < 15 mm to more than minimum 91% of the total voxels number, while these values for SSD were 12.5% and 70.6%, respectively for the same error range criterion. Histograms in Fig. 4 show that the symmetric method not only decreased ICE for both SSD and SSTVD, but also decreased the range of higher ICE values significantly so that ICE values shifted toward the lower values. Fig. 5 shows an example of a distribution of ICE values in the sagittal plane of the lung with both SSD and SSTVD methods for forward, backward and symmetric transformations. The region with higher ICE values lies near the diaphragm. This happens due to larger displacement errors in regions near the diaphragm which is consistent with the fact that registration errors in the regions near the diaphragm are greater than other regions as reported by Yin et al. [3]. As seen from Fig. 5, both symmetric SSD and SSTVD methods decreased ICE, especially in the basal part of lung (near the diaphragm) where the SSTVD method was more effective in decreasing ICE in regions with large deformation. However, similar to the 2-D cases, there are some high ICE values (less than 1% for all subjects) at the edge of the lung as a result of a trade-off between the regularization part and the similarity measure.

5. Conclusion

We symmetrized the cost function into forward and backward transformations and recast the gradient of the cost function in such a way that it only depends on forward transformation. Therefore the cost function does not explicitly require the inverse transformation of T which results in a simpler form of the gradient of the cost function. We have demonstrated, in both 2-D synthetic images and 3-D lung data sets, that the symmetric method greatly improves the inverse consistency and also its GPU version can be used as a powerful technique with significant increase in speedup factor for lung volume registration. While we have focused upon lung imaging, the generic nature of the proposed approach can be potentially applied to other organs.

Biographies

Ching-Long Lin is professor of mechanical and industrial engineering, faculty research engineer at IIHR—Hydroscience & Engineering, and researcher at the Iowa Institute for Biomedical Imaging and a Fellow of the American Society of Mechanical Engineers (ASME).

Professor Lin's current research at the College of Engineering focuses on multiscale simulation of gas flow and particle transport in the human lungs, medical imaging, turbulent flow in complex geometry, fluid-structure interaction, and parallel computing.

6. Appendix: Supplementary Material

6.1. Symmetric registration Pseudo-code

A pseudo code of the symmetric implementation in the image registration code is presented for clarification of the main kernel structure. Calculations of the transformation, the cost and cost-gradient computations for the SSTVD similarity measure are included in the pseudo code of the symmetric function. The pseudo code focuses on the symmetric implementation and the details of GPU implementation are excluded. For more details on GPU implementation and its Pseudo-code, please see Ellingwood et al. [23]. For parallelization process, tiles are assigned to blocks and the main kernel partitions the tile into sub-tiles of 64 voxels in 3D, and then each voxel is assigned a thread.

Pseudo code: Main kernel for symmetric SSTVD function

1. // Get block index B and thread index T

2. // Allocate shared memory for Cost

3. // Allocate shared memory for temp Cost gradient values

4. // Allocate shared memory for temp Cost gradient bins

5. // Partition tile into subsets of 64 voxels, begin loop over these subsets with index pTile For pTile = 0 to TileSize/64

6. // B maps corresponds to voxel tile

7. // T maps to voxel within subset pTile with coordinate x = (x,y,z)

8. // Compute local voxel coordinates and local indices within tile B

9. u = x/δ_x − ⌊x/δ_x⌋, v = y/δ_y − ⌊y/δ_y⌋, w = z/δ_z − ⌊z/δ_z⌋

10. i = ⌊x/δ_x⌋ − 1, j = ⌊y/δ_y⌋ − 1, k = ⌊z/δ_z⌋ − 1

11. // Compute transformation function

12. Compute transformation T_i [x, ϕ] for x = (x,y,z) where T_i is the current transformation from DMTC [23]

13. Compute D^T (D is defined as the determinant of derivative matrix of deformation)

14. // Compute Jacobian value J_T

15. J_T [x, ϕ] = det(D^T)

16. // For multilevel B-spline technique for compute current level transformation and warping image at the previous level i.

17. T_c [x, ϕ] = Warping (T_i [x, ϕ])

18. J_ω [x, ϕ] = Interpolate(T_i [x, ϕ], Image J_ω)

19. J_TC [x, ϕ] = J_ω [x, ϕ]J_Ti [x, ϕ]

20. // Calculation of symmetric similarity measure

21. $\frac{\partial {\mathit{T}}^{-\mathbf{1}}}{\partial \mathit{\varphi }}=-{[J_T]}^{-1}\frac{\partial \mathit{T}}{\partial \mathit{\varphi }}$

22. // Compute SSTVD similarity measure

23. // The process repeats for each sub-tile within the tile, accumulating the cost gradient partial sums in shared memory.

24. // C_SSTVD(ϕ)+ = Σ_x∈Ω [v_f(x)Ĩ_f(x) − v_m(T [x, ϕ])Ĩ_m(T [x, ϕ])]²

25. // Compute and summation of symmetric SSTVD similarity measure.

26. $E(\mathrm{\varphi })+=\frac{1}{2}{\sum }_{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x}){[{\stackrel{\sim }{I}}_f(\mathit{x})-J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{T}[\mathit{x},\mathit{\varphi }])]}^2+\frac{1}{2}{\sum }_{y^{\prime }\in {\mathrm{\Omega }}^{\prime }}{{\nu }_m}^2({\mathit{y}}^{\prime }){[{\stackrel{\sim }{I}}_m({\mathit{y}}^{\prime })-J_{T^{-1}}({\mathit{y}}^{\prime },\mathit{\varphi }){\stackrel{\sim }{I}}_f({\mathit{T}}^{-\mathbf{1}}[{\mathit{y}}^{\prime },\mathit{\varphi }])]}^2$

27. // Compute the derivative of symmetric similarity measure

28. // Setting y′ = y = T [x, ϕ] and x = T⁻¹ [y′, ϕ] yields the following:

29. $\frac{\partial E}{\partial \mathrm{\varphi }}+={\sum }_{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x})[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})-{\stackrel{\sim }{I}}_f(\mathit{x})]\{{\nabla }_{\mathit{\varphi }}[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})]+J_T(\mathit{x},\mathit{\varphi }){\nabla }_{\mathit{\varphi }}[J_{T^{-1}}(\mathit{y},\mathit{\varphi }){\stackrel{\sim }{I}}_f(\mathit{x})]\}$

30. // Final form of symmetric similarity measure after adding regularization term

31. $\frac{\partial S}{\partial \mathrm{\varphi }}+={\sum }_{x\in \mathrm{\Omega }}{{\nu }_f}^2(\mathit{x})[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})-{\stackrel{\sim }{I}}_f(\mathit{x})]\{{\nabla }_{\mathit{\varphi }}[J_T(\mathit{x},\mathit{\varphi }){\stackrel{\sim }{I}}_m(\mathit{y})]+J_T(\mathit{x},\mathit{\varphi }){\nabla }_{\mathit{\varphi }}[J_{T^{-1}}(\mathit{y},\mathit{\varphi }){\stackrel{\sim }{I}}_f(\mathit{x})]\}+(1+{log}_{10}(J_T(\mathit{x},\mathit{\varphi }))-1/J_T(\mathit{x},\mathit{\varphi }))$

6.2. Inverse consistency error (ICE) for two patient from SPIROMICS study

To examine the robustness of our symmetric method, we applied our method to assess ICE for a smoker patient from Subpopulations and intermediate outcome measures in COPD study (SPIROMICS) [37]. SPIROMICS study uses residual volume (RV) instead on FRC which makes calculation of ICE even more changing due to smaller size of RV. The symmetric method successfully decrease the ICE for both SSD and SSTVD methods. The histograms of ICE and their contours were shown in Fig. 7 and Fig. 8.

Fig. 7.

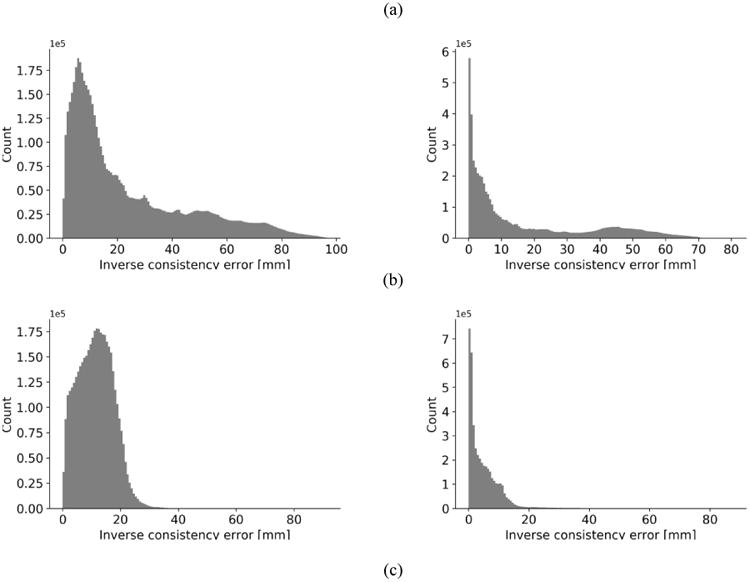
Distribution of inverse consistency error for non-symmetric (backward and forward) vs. symmetric (TLC as the fixed image) of a smoker patient for SSD (left) vs. SSTVD (right) for (a) forward (b) backward (c) symmetric transformations.

Fig. 8.

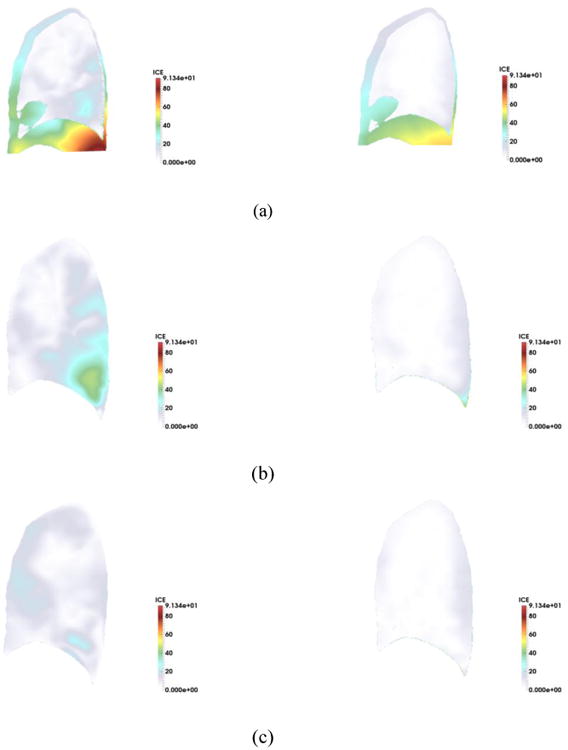
Inverse consistency error [mm] for non-symmetric vs. symmetric method (TLC as the fixed image) for sagittal plane. SSD (left) vs. SSTVD (right) for (a) forward (b) backward (c) symmetric transformations.