Beyond the margin recipe: the probability of correct target dosage and tumor control in the presence of a dose limiting structure

Abstract

In the past, hypothetical spherical target volumes and ideally conformal dose distributions were analyzed to establish the safety of planning target volume (PTV) margins. In this work we extended these models to estimate how alternative methods of shaping dose distributions could lead to clinical improvements. Based on a spherical clinical target volume (CTV) and Gaussian distributions of systematic and random geometrical uncertainties, idealized 3D dose distributions were optimized to exhibit specific stochastic properties. A nearby spherical organ at risk (OAR) was introduced to explore the benefit of non-spherical dose distributions.

Optimizing for the same minimum dose safety criterion as implied by the generally accepted use of a PTV, the extent of the high dose region in one direction could be reduced by half provided that dose in other directions is sufficiently compensated. Further reduction of this unilateral dosimetric margin decreased the target dose confidence, however the actual minimum CTV dose at 90% confidence typically exceeded the minimum PTV dose by 20% of prescription.

Incorporation of smooth dose-effect relations within the optimization led to more concentrated dose distributions compared to the use of a PTV, with an improved balance between the probability of tumor cell kill and the risk of geometrical miss, and lower dose to surrounding tissues. Tumor control rate improvements in excess of 20% were found to be common for equal integral dose, while at the same time evading a nearby OAR. These results were robust against uncertainties in dose-effect relations and target heterogeneity, and did not depend on ‘shoulders’ or ‘horns’ in the dose distributions.

1. Introduction

Dose distributions in photon radiotherapy are in general largely invariant under geometrical variations, therefore the application of a PTV margin (ICRU 2010) along with a uniform dose prescription provides a high confidence of reaching the intended dose to the CTV. However, such margins lead to large volumes of healthy tissue irradiated to a high dose, thus preventing tumor dose escalation (Craft et al 2016). Alternative plan optimization techniques based on probabilities (Unkelbach and Oelfke 2004, Baum et al 2006, Witte et al 2007, Gordon et al 2010, Fredriksson and Bokrantz 2016) may provide a superior balance between tumor control and toxicity, but have not reached the clinical photon therapy routine so far and therefore clinical evidence is not available. The dose volume histogram (DVH) of the PTV is meant to be representative of the CTV DVH when geometric uncertainties are considered, lending it a widely recognized value and an intuitive clarity. The various alternative approaches differ in their details of implementation, and require a more involved interpretation to estimate associated benefits and/or risks. Comparison between methods is difficult, since each implementation is based on its own set of principles.

The original work leading to the van Herk et al (2000) PTV margin recipe aimed to derive a generic guarantee of safety in the worst case by considering a spherical CTV in the presence geometrical uncertainties, using idealized uniform spherical dose distributions. The result was a PTV margin providing a certain confidence of reaching a given minimum dose in the CTV. Here we extended these investigations, performing optimizations of idealized dose distributions for a spherical target under geometric uncertainties in the presence of a nearby OAR, allowing the dose distributions to become non-uniform and non-spherical. We focused on two simplifications inherent to the PTV concept:

• Geometrical rigidity All volume elements contained within a PTV are considered equally important during plan optimization and plan evaluation. Nonetheless, the probability that a geometric error causes an element of volume to be occupied by the CTV is smaller near the surface than it is deeper inside the PTV.

• Dose-response simplicity Minimum achieved CTV dose would fully determine the effectiveness of the treatment if dose above the prescription level would offer no additional control, and dose below this value would be fully ineffective. In reality, dose-effect relations are not expected to show such discontinuities.

Using the optimized dose distributions, we investigated geometrical rigidity by determining to what extent a loss of CTV dose confidence can be prevented in the case of PTV-OAR overlap by adding dose elsewhere. To establish the PTV's dose-response simplicity we incorporated sigmoid tumor control probability (TCP) models. This way the probabilities of geometric miss and of biological control could be combined to enable a balanced deposition of dose. The performance of such dose distributions in terms of the expected tumor control was determined for a range of TCP model parameters, and considering heterogeneous distributions of the disease within the CTV. By comparing with the performance of a PTV based dose distribution, a baseline quantification could be provided of the potential clinical risks and benefits of PTV-less treatment planning, irrespective of plan optimization or delivery technique.

Alternative probability based planning methods aiming for an improved compromise between toxicity and tumor control will necessarily fail the PTV's strict minimum dose safety requirements. With this work we aim to support future clinical implementation of such methods, by providing quantitative yet generic estimates of the potential clinical benefit of PTV-less planning.

2. Methods and materials

A spherical 50 mm diameter CTV was considered. Isotropic Gaussian distributions of systematic (preparation) and random (execution) translational uncertainties were assumed with SDs Σ = σ = 3 mm in each direction. Using a 3.2 mm (water equivalent) Gaussian penumbra, a 9.4 mm PTV margin then leads to a 90% confidence of at least 95% of dose prescription to the CTV (van Herk et al 2000), which was set at D_pres = 60 Gy over 30 fractions. Dose to a nearby 50 mm spherical OAR was limited to a maximum of 30 Gy. The OAR was placed at various distances, but to serve simplicity, geometric uncertainties of the OAR were not considered for optimization or evaluation.

2.1. Dose optimization

Starting with a uniform PTV-based dose distribution on a 3 mm resolution cubic grid with sides of 37 voxels centered on the PTV, further optimizations were performed in which the dose in each voxel was allowed to vary individually, without consideration of delivery technique (such as an external beam set-up). To allow efficient optimizations the CTV, OAR, and the error kernels were discretized on the dose grid resolution. Random errors were treated as a dose blurring, systematic errors as CTV displacements in units of the dose grid resolution (Bohoslavsky et al 2013). For dose grid voxels which were partially covered by the CTV or OAR, the fractional coverage was determined and used as voxel weight.

As voxel-wise dose optimization might result in a penumbra shape steeper than physically possible, an intermediate step was used to prevent such unrealistic dose distributions. The random error kernel was first convolved with the penumbra, leading to a wider blurring kernel used during optimization: ${\sigma }_{\text{opt}}=\sqrt{{\sigma }^2+{\sigma }_{\text{Pen}}^2}$. A dose distribution generated in this way optimally compensates for the increased blurring, but potentially has unrealistic steepness. By then blurring such a dose distribution with the penumbra width σ_pen, a distribution results which can no longer be too steep, and which has a shape optimally compensating for further blurring with the kernel width σ of the random errors.

Cost functions including gradient computations were implemented in C⁺⁺. A downhill gradient method with small step size was used which showed slow convergence, but good consistency over consecutive optimization runs.

Since no PTV was used, conventional strategies to reach conformity (e.g. rings around the PTV) did not apply. To limit unnecessary dose, a quadratic cost function limiting the mean dose to the entire grid was implemented. This would be reasonable for a tumor embedded in a parallel OAR, and allowed the penumbra shape to be optimized without introducing discontinuous spatial behavior. In external beam delivery all dose needs to be brought in through healthy tissues, therefore the limitation of integral dose in these synthetic distributions should correspond to a limitation of overall toxicities for realistic dose distributions based on these. Non-negativity and an optional maximum dose constraint were built into the optimization routines.

A probabilistic minimum dose cost function was implemented to allow optimization for a given confidence of minimum CTV dose. Cost values for the blurred dose were computed for each displaced CTV position according to the systematic kernel, and sorted by cost value. Then, voxels of the systematic error kernel with highest associated cost values were cropped away until a 90% probability content remained. Final cost was computed as a probability weighted sum over the remaining systematic error positions (Bohoslavsky et al 2013).

Non-linear tumor dose-effect relations were represented using a generic sigmoid curve

$$\text{TCP}(D)={(1+{\left(\frac{D_{50}}{D}\right)}^k)}^{-1},$$ (1)

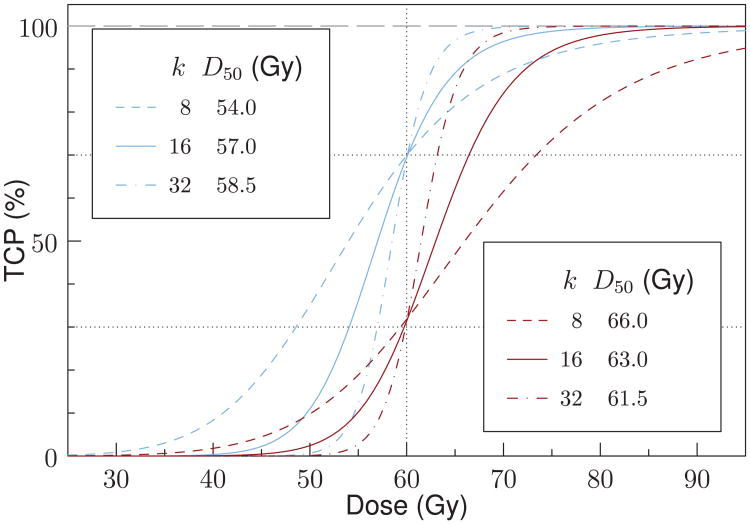
with D₅₀ the dose at 50% tumor control and k a steepness parameter (Bentzen and Tucker 1997). A few combinations for which the TCP at 60 Gy is either close to 30% or to 70% were used (Kim and Tome 2006). Figure 1 shows the dose-effect curves for these combinations. A cost function was constructed which evaluated cost based on the expectation value of TCP (Witte et al 2007). All dose optimizations assumed a homogeneous CTV, i.e. the same k and D₅₀ values for each voxel.

Figure 1.

Generic sigmoid curves representing non-linear tumor dose-effect relations. Combinations of steepness parameters k and dose levels D₅₀ were chosen such that at 60 Gy the TCP is close to either 70% (blue lines), or 30% (red lines).

2.2. Dose evaluation

A Monte Carlo sampling method was used to accurately evaluate optimized dose distributions in terms of their stochastic properties (van Herk et al 2002, Witte et al 2014), without requiring the discretization used to speed up optimization. 10 000 samples were taken from the distribution of systematic errors, and for each systematic error 30 daily random errors were sampled and consecutively added. A cloud of 50 000 random points described the CTV, and was shifted with respect to the dose according to the resulting error vectors. Dose to each transformed point was evaluated using trilinear interpolation on the dose grid. The probability of receiving at least 0.95D_pres to 99.99% of the CTV was evaluated, as well as the expectation of TCP for the various combinations of k and D₅₀.

OAR maximum dose was evaluated excluding 1% of the volume receiving highest dose, based on 10⁶ random points in the OAR at its fxed position.

2.3. Iterative plan optimization

The optimized dose distributions depend on the various weights and constraints of the cost functions, but it is not possible to predict their stochastic properties (as determined by the Monte Carlo evaluations) beforehand. To be able to arrive at a dose distribution which e.g. provides 90.0% confdence of 95% minimum CTV dose at given mean integral and maximum OAR doses, an iterative plan optimization loop was scripted in the Perl language. Using an initial set of parameter values the optimizer is allowed to finish, the dose re-scaled to the same mean dose as the PTV based distribution, and the Monte Carlo evaluation performed. Based on these results the constraints for mean integral dose and maximum OAR dose are adjusted, and the optimization re-started from the PTV-based distribution. Iterations continued until the intended stochastic target and/or OAR dose levels were reached within 1% (if simultaneously attainable).

3. Results

3.1. Geometrical rigidity

Figure 2(a) shows a PTV-based distribution using a 9.4 mm margin, providing 90.0% confdence of receiving 95.0% of dose prescription in 99.99% of the CTV. The 95% iso-dose contour (dashed) overlaps with the PTV contour.

Figure 2.

Central slices through 60 Gy prescription dose distributions (a) based on the PTV; (b) optimized to reach a 90% confdence of 95% dose prescription in the CTV under geometric errors with Σ=σ =3 mm while minimizing integral dose, using 60 Gy; (c) 64.2 Gy; (d) without maximum dose constraint. Dose to the stationary OAR was limited to 30 Gy, and the OAR was brought in as close as possible while still reaching a 90% CTV dose confidence. (e) Dose profiles in the OAR direction. (f) DVHs of the PTV.

In panel figure 2(b) the optimized dose distribution is shown for which the OAR was placed as close as possible to the PTV while still attaining a 90% CTV dose confidence, using a strict maximum dose constraint equal to the prescription dose value of 60 Gy, and minimizing integral dose. A dent in the 95% iso-dose contour to a depth of one third of the PTV margin is seen next to the OAR position, however there is a shallow dose fall-off toward the 50% level and the OAR can only approach the PTV to a distance of 3 mm. In reaction, the 95% isodose contour expanded in other directions by a tiny amount (the PTV delineation is slightly more visible inside the 95% iso-dose line).

In panel figure 2(c) a 7% overdose is allowed, and as a result the OAR can now touch the PTV surface while maintaining CTV dose confidence. The dent in the 95% iso-dose line increased and now exceeds half the PTV margin; nonetheless, only 1.5 cc (<1%) of the PTV had dose lower than 95%. The 95% iso-dose surface expanded outside the PTV in the other directions and dose increased inside the 95% iso-surface near the OAR, while the steepness of the dose fall-off toward the OAR was increased.

The dose sculpting mechanism to compensate for geometric errors is illustrated in its most extreme form in figure 2(d), for which optimization was performed without imposing a maximum dose constraint. The dent in the 95% iso-dose line is not as deep as in panel figure 2(c), but the steepness of the dose fall-off toward the OAR increased and a bow wavelike hot region with dose values exceeding 90 Gy was raised. As a result the OAR could be placed 3 mm into the PTV without reducing the CTV dose confidence below 90%, but in view of the extreme hot spot the resulting dose distribution would likely not be considered clinically acceptable.

Figure 2(e) shows dose profiles along the central line for these situations, illustrating the donut-like regions of increased dose above prescription level and the very high dose values in the hot region of dose figure 2(d). The dose fall-off toward the OAR at the 95% dose level is steepest for dose figure 2(d).

Figure 2(f) shows DVHs for the PTV. The DVHs illustrate an increased concentration of dose for higher allowed maximum doses: the fraction of PTV receiving 95% dose decreases, while volumes receiving higher than prescribed dose increase.

The appearance of the hot regions can be understood as deconvolution of the dose for the blurring effects of random errors (Lind et al 1993, Lof et al 1998, Unkelbach and Oelfke 2004) and penumbra (Sharpe et al 2000): the optimizer sets up a dose fall-off which is essentially too steep, resulting in a nearby cold region, and then relies on dose blurring to transport excess dose from the hot region next to it to compensate.

Further dose optimizations were performed using a clinically acceptable 107% maximum dose constraint (ICRU 1993). The OAR was placed increasingly deeper into the PTV at 1 mm steps. Optimization still penalized less than 90% confidence of CTV dose, but due to the OAR position this 90% was no longer met in the optimized dose distributions. Figure 3 shows the evaluation results for the confidence of 95% minimum dose to the CTV, and of the minimum CTV dose at 90% confidence as a function of OAR position. Figure 3(a) indicates that the 95% dose confidence reduces to approximately 50% if the OAR is 5 mm inside the PTV, and vanishes as it is in by the full margin size (i.e. touching the CTV in its nominal position). In the latter case the dose at 90% confidence (figure 3(b), solid line) is close to 50% of prescription, reflecting the 50% maximum dose limit on the OAR.

Figure 3.

Dose distributions optimized for minimum CTV dose confidence with an OAR (D_max = 0.5D_presc) placed at various distances. Overdosage was allowed up to 7% over prescription level. (a) The resulting confidence of reaching at least 95% of prescription dose in the CTV. (b) The minimum CTV dose at 90% confidence (solid), and minimum PTV dose (dashed).

Even with the OAR at a large distance the minimum dose in 99.99% of the PTV (figure 3(b), dotted line) falls below 95%, reflecting the increased concentration (and reduced integral) of dose and associated increased steepness of the dose fall-off at the 95% level made possible by allowing 7% overdosage. As the OAR is brought closer, the minimum PTV dose starts dropping ≈2 mm before the dose at 90% confidence does, and typically underestimates the dose at 90% confidence by 20% to 30% of prescription.

3.2. Dose-response simplicity

To investigate the best way to redistribute the available dose, given the non-linear relation between dose and effect described by the TCP model, further dose optimizations were performed using a cost function maximizing the expectation of TCP. No maximum dose constraints were applied, but rather the integral dose to the entire dose grid was kept at the same level as for the PTV based distribution in figure 2(a). This should lead to dose distributions with similar overall toxicities, without explicitly having to deal with normal tissues other than the spherical OAR. Using a TCP model with moderate steepness (k = 16, D₅₀ = 57 Gy) this PTV based dose distribution evaluates to a 69.6% expected TCP, almost equal to the 69.7% TCP for a uniform 60 Gy dose (i.e. full body). TCP loss due to geometrical miss is thus highly unlikely for the PTV based dose distribution. (Note that the computations use DVH representations with a finite bin width, as a result these values are slightly higher than the theoretical value of 69.4% computed by substituting D = 60 Gy in equation (1)).

The prevention of geometric miss is served by spreading out dose beyond the CTV periphery, while on the other hand the prevention of local recurrence is served by concentrating dose such that a larger fraction of the tumor ends up at a higher position on the TCP curve. When directly incorporating the expectation of TCP as an objective, the optimizer can strike a balance between these rivaling effects. The result (figure 4(a)) was a more concentrated dose distribution than for the PTV, cutting through the PTV surface at lower dose values (figure 4(e)). Also, dose deconvolution features presented as a set of concentric high dose shells (rings in the image). Monte Carlo setup error simulations of this dose distribution resulted in a TCP of 99.9%. The introduction of an OAR overlapping the PTV by 5 mm (figure 4(b)) again lead to a bow wave-like hot region, but also caused the concentric shells to disappear. Expected TCP for this situation was 99.8%.

Figure 4.

Dose distributions optimizing expected TCP for a homogeneous CTV with k = 16, D₅₀ = 57 Gy. Integral dose was forced to equal that of the PTV-based distribution at 60 Gy prescription (figure 2(a)). For geometric errors Σ=σ=3 mm the dose shows (a) concentric shells in the absence of an OAR, but instead (b) a single hot region if an OAR is placed at small distance. These features disappear (c) and (d) for single fraction treatment. Two possible locations of a 1 cc tumor focus are identified as foc_A and foc_B. (e) Dose profiles in the OAR direction. (f) DVHs of the PTV.

There may be preference to avoid the deconvolution features in an optimized dose distribution if the sensitivity to the size of random errors assumed is unknown. This circumvents potential treatment outcome deterioration that might occur should the realized randomness differ greatly from that assumed or if random variations do not occur. Furthermore, dose blurring may be an inadequate approximation for the cumulative effect in hypo-fractionated treatments, instead requiring explicit per-fraction sampling. While our implementation does not allow explicit optimization for a low number of treatment fractions, it is possible to optimize for single fraction treatment as the most extreme case of hypo-fractionation. In such a case a single daily error (which is a sample from the random error distribution σ) is added to the systematic error (sampled from Σ), and the result is a purely systematic error with distribution $\mathrm{\sum }\prime =\sqrt{{\mathrm{\sum }}^2+{\sigma }^2}$. Optimization using the Σ′ error distribution resulted in dose distributions without deconvolution features, with expected TCP values of respectively 99.5% and 99.1% for the cases without OAR (figure 4(c)) and with an OAR overlapping the PTV by 5 mm (figure 4(d)). Application of such a dose distribution in fractionated treatment would accommodate a worst-case approach for the random errors, i.e. optimizing for the (unlikely) event that all random errors point equally far in the same direction for each fraction.

While the expected TCP results thus acquired were excellent, they assumed that adequate model parameters were available for optimization and evaluation of the dose distributions. To test the sensitivity of outcome on model parameter uncertainties, we considered various cross-combinations of optimization and evaluation parameters. Optimizations were performed for TCP parameter combinations resulting in 70% TCP at 60 Gy (highest curves in figure 1), assuming either many fractions or a single one (i.e. with and without deconvolution features). Doses were optimized without OAR, and with 5 and 10 mm OAR-PTV overlap. Evaluations were performed assuming a treatment schedule of 30 fractions, and TCP parameters leading to 70% and to 30% TCP_{60 Gy} (highest and lowest curves in figure 1), respectively. To estimate the effect of CTV heterogeneity, evaluations were furthermore performed for the case in which all clonogenic cells were concentrated in a single 1 cc focus inside the CTV. Two locations for such a focus were tested, one toward the OAR (foc_A, see figure 4) and one in the opposite hemisphere (foc_B), both touching the CTV surface from the inside. For the latter, cross-combinations of parameter values were omitted for brevity.

For a homogeneous CTV all optimized dose distributions outperformed the PTV in terms of expected TCP, with a TCP increase always exceeding 22% for 70% TCP_{60 GY}, and always exceeding 39% for 30% TCP60 Gy (table 1). This included those cases in which the OAR had 10 mm overlap with the PTV, using dose distributions without deconvolution features (optimized for a single treatment fraction, yet delivered fractionally). Also, this included dose distributions optimized for dose-effect parameters that did not match those used during evaluation.

Table 1.

Expected TCP for various combinations of model parameters used during optimization (k^opt, $D_{50}^{\text{opt}}$) and evaluation (k^eval, $D_{50}^{\text{eval}}$); results for corresponding values are printed boldface. Optimization was performed for (a) many fractions and (b) single fraction treatment, keeping the integral dose equal to a uniform 60 Gy PTV based dose distribution. For each case three doses were optimized: without OAR (‘None’), and with 30 Gy maximum dose for an OAR overlapping the PTV by 5 and 10 mm, respectively. Evaluations using 30 treatment fractions were performed for a homogeneous CTV, or assuming all clonogenic cells were concentrated within either of two 1 cc tumor foci (figure 4).

a Many fc.			Homogeneous CTV						focA						focB
kopt	$D_{50}^{\text{opt}}$	keval	8	16	32	8	16	32	8	16	32	8	16	32	16
		$D_{50}^{\text{eval}}$	54.0	57.0	58.5	66.0	63.0	61.5	54.0	57.0	58.5	66.0	63.0	61.5	57.0
8	54.0	None	99.4	99.6	99.3	97.7	99.3	99.1	99.6	99.9	99.8	98.2	99.7	99.7	99.9
		5mm	99.4	99.6	99.3	97.7	99.3	99.1	99.6	99.8	99.7	98.2	99.7	99.6	99.9
		10mm	97.8	97.6	95.5	93.4	96.3	94.6	85.9	81.0	74.3	76.0	75.8	71.5	99.9
16	57.0	None	98.5	99.9	99.9	93.0	99.5	99.8	98.7	99.9	99.9	93.3	99.7	99.9	99.9
		5mm	98.1	99.8	99.8	91.4	99.2	99.6	98.6	99.7	99.6	93.8	99.4	99.5	99.9
		10mm	96.5	97.6	95.8	87.6	96.0	95.0	85.6	81.2	74.2	75.9	76.3	72.0	99.8
32	58.5	None	94.9	99.3	100	81.4	97.4	99.9	95.7	99.5	100	81.7	97.6	99.9	99.5
		5mm	92.9	98.5	99.7	72.6	93.2	99.4	96.2	99.1	99.2	84.9	97.2	90.0	98.6
		10mm	92.6	96.6	95.7	73.7	91.5	94.8	85.1	80.6	73.9	74.5	75.6	71.3	98.6
PTV			69.9	69.5	69.3	31.8	31.5	31.3	70.0	69.6	69.5	31.9	31.6	31.6	69.6
b Single fc.			Homogeneous CTV						focA						focB
kopt	$D_{50}^{\text{opt}}$	keval	8	16	32	8	16	32	8	16	32	8	16	32	16
		$D_{50}^{\text{eval}}$	54.0	57.0	58.5	66.0	63.0	61.5	54.0	57.0	58.5	66.0	63.0	61.5	57.0
8	54.0	None	98.5	99.7	99.6	93.4	99.0	99.4	98.9	99.9	99.9	94.4	99.6	99.8	99.9
		5mm	97.8	99.5	99.5	90.7	98.4	99.1	97.2	98.6	98.0	89.5	96.9	97.4	99.8
		10mm	95.6	96.5	94.0	84.9	93.8	92.6	80.6	74.6	67.6	61.8	65.5	61.6	99.8
16	57.0	None	96.6	99.5	99.8	85.2	98.0	99.6	97.1	99.7	100	86.1	98.5	99.9	99.7
		5mm	95.5	99.1	99.5	81.3	96.5	99.1	94.0	97.2	96.7	78.4	93.0	95.4	99.5
		10mm	94.5	96.2	93.8	81.0	92.9	92.3	78.0	73.1	65.1	57.2	62.6	59.4	99.7
32	58.5	None	95.6	99.5	99.8	71.6	92.5	99.3	93.3	98.5	99.9	72.7	93.1	99.6	98.5
		5mm	92.5	98.2	99.4	72.0	92.5	98.7	90.1	95.3	94.9	68.0	86.9	92.9	98.6
		10mm	92.1	95.4	93.5	72.7	89.7	91.6	73.3	71.0	60.7	50.2	57.5	56.2	99.1
PTV			69.9	69.5	69.3	31.8	31.5	31.3	70.0	69.6	69.5	31.9	31.6	31.6	69.6

For tumors concentrated in a focus the TCP increase was always larger than 25%, except in the case of maximum OAR overlap and an unfavorable location of the focus toward the OAR. This situation still led to an increased TCP for most parameter combinations, however for the steepest dose-effect relation with 70% TCP_{60 GY}, and for dose optimized without deconvolution features, a loss of TCP up to 9% compared to the un-edited PTV could be observed.

TCP based optimization assuming a shallow dose-effect relation (k = 8) performed well even when evaluated using a much steeper dose-effect curve (k = 32). TCP loss compared to the dose optimized using the true steep dose-effect ranged between 0.1% and 2.3% depending on OAR overlap, while for single fraction optimization the TCP results could even be improved by assuming a shallower TCP dose-effect relation. On the other hand, incorrectly assuming a steep dose-effect during optimization led to decreased TCP results if the true dose-effect turned out much shallower.

Provided that accurate dose-effect parameters could be established for a homogeneous CTV (boldface in table 1), the assumption of single fraction treatment during optimization as a mechanism to suppress deconvolution features resulted in a TCP loss relative to the corresponding dose optimized including dose blurring (i.e. involving hot shells/spots) of less than 1% in the absence of an OAR, and up to 3% for the case of maximum OAR overlap. This illustrates the small effect of random errors or blurring on the dose distributions.

TCP results for a tumor focus away from the OAR direction typically slightly exceeded those for a homogeneous CTV. Although a large fraction of the clonogenic cells in such a focus are close to the edge of the high dose region and end up at a low dose if a shift toward the gradient occurs, shifts in the opposite direction bring all tumor cells deeper into high dose. For a homogeneous CTV all possible shifts move some part of the clonogenic cells toward lower dose. Apparently the effects balance out in favor of the tumor focus.

A last set of evaluations were performed for error distributions exceeding those used for optimization to determine how much larger Σ and σ could be compared to the values used during optimization yet still yield TCP greater than or equal to the TCP provided by the PTV. For both planning and evaluation, we used a moderately steep dose-effect relation with k = 16. A multiplicative factor Σ′ = aΣ, σ′ = aσ was introduced during plan evaluation. For a homogeneous CTV, superior TCP resulted for a ≤ 2.2 regardless of deconvolution features or OAR overlap. For the foc_A near the OAR the resulting factor was usually larger than 2.5, except for the case of maximum OAR overlap without deconvolution which resulted in a factor of 1.3. So in the worst case, for clonogenic cells which happen to be at the least favorable location, and for geometric errors 30% larger than anticipated, the TCP is reduced to the same level as a PTV based plan.

4. Discussion

Over decades of clinical use the PTV concept has acquired such a central role in the radiotherapy chain it is very difficult to scratch its surface indeed. Supported by the mathematical elegance and simplicity of the van Herk et al (2000) recipe, the use of a proper PTV margin is synonymous with a safe treatment. In this work we followed the same methodology leading to this formula to show that treatment can be safe without having to adhere strictly to the PTV. Moreover, we were able to assess the extent to which the PTV's fat-dose paradigm (Deasy and Jeong 2011) is in fact hampering a balanced deposition of dose. An estimate could thus be provided of the envelope within which planning methods without a PTV can operate, much in the way the original margin recipe provided a worst case estimate for PTV-based treatment plans.

An improved, non-conformal deposition of dose provided equal target dose confidence while sparing an OAR overlapping the PTV. In clinical practice the PTV is often hand-edited to spare a nearby OAR, however a quantitative risk assessment of such ad-hoc alterations is usually lacking. We now provide a theoretical upper limit for the freedom planners can take when altering their treatment volumes without sacrificing tumor dose confidence. For a strictly uniform dose distribution at prescription level an indentation of the 95% dose level by one third of the margin size is feasible. If over-dosage up to 107% of prescription is used to set up a steeper dose fall-off toward the OAR, the depth of indentation may reach half the margin size. The excess dose required outside the PTV in other directions to compensate is small, and could well already be present in a clinical plan with realistic conformity.

Furthermore, more concentrated dose distributions at equal integral dose were presented which could spare a nearby OAR, and at the same time provide higher expected tumor control than the PTV. This is in line with previous observations, stating that even when using a PTV it is often beneficial to reduce margins and allow higher maximum doses to increase tumor control while at the same time decreasing toxicity (Engelsman et al 2001). Improvements of the expected TCP were rarely less than 20%, and were proven to be robust against variations in biological parameters, unfavorable cell distributions within the CTV, and underestimated geometrical uncertainties. The benefits were shown not to depend on the deconvolution features inherent to some probability based dose optimization techniques. The optimized dose distributions should be expected to cause less toxicity since dose to the OAR (at its static position) and to the surroundings was decreased. However, the occurrence of a hot region close to the OAR may increase the risk of toxicity due to its geometric variations, which were not considered. This risk could have been balanced against tumor control by introducing a Normal Tissue Complication Probability (NTCP) model for the OAR during planning, and including its geometric variations (Witte et al 2007), however this was beyond the scope of the current work. Our static OAR could still be interpreted as the dose avoidance region for a smaller highly serial OAR including its Planning organ at Risk Volume (PRV) margin. While this would change the interpretation of the distance to the OAR, it would not change the resulting shapes of the optimized dose distributions, or the listed results for CTV dose confidence and TCP expectation.

To our knowledge this is the first time the balance between the probabilities of cell kill and of tumor miss have been quantified in a generic way. Such quantifications may help to estimate the actual clinical cost associated with the choice of PTV as planning tool, and the predominance of homogeneous dose distributions, without the need to explicitly evaluate competing planning strategies. By highlighting the shortcomings of the current planning tool set, we hope to pave the way for future clinical implementations of PTV-less planning techniques which provide a superior clinical balance.

Spherical target volumes and idealized dose distributions with perfect conformity were previously used to derive margin recipes because these provide a worst case for clinical situations: in practice entry beams and imperfect conformity add dose, enhancing the target dose confidence. This argument also applies to the current work, and can be extended: plan optimization techniques that do not rely on the PTV can acknowledge unavoidable dose due to limitations of the delivery system, and, due to increased target coverage induced by unavoidable dose, potentially reduce dose elsewhere.

The TCP function we applied (equation (1)) was not necessarily intended to be mechanistically or clinically realistic (Webb and Nahum 1993, Zaider and Minerbo 2000, Jeong et al 2013), but merely served as the simplified parameterization of a smooth non-linear relation between dose and effect. Non-linear dose accumulation over fractions could have been considered explicitly during evaluation, but would effectively only have resulted in variations of the shape and steepness of the TCP curve. As our results hold for a wide range of slopes of the assumed dose-effect relation, and for variations between the curves used for optimization and evaluation, it follows that exactly how dose and effect relate is not crucial. Rather, we can find a better place in the treatment planning solution space than provided by the PTV by merely acknowledging that there is a smooth, moderately steep relation between the two.

While optimizations were only performed for an assumed homogeneous CTV, the lack of a PTV in fact allows one to incorporate imaging based information about tumor heterogeneity and/or estimated distributions of sub-clinical disease (Groenendaal et al 2012) in treatment planning much more easily (Witte et al 2011). In general, a CTV is formed by adding a margin around the gross tumor, and the density of cells should decrease toward the CTV surface. This reduces the consequence of a geometric CTV miss, and further enhances the benefit of a more concentrated deposition of dose over the more spread out dose of the PTV.

Simulating a 1 cc tumor focus inside a 50 mm diameter CTV, we were able to show that even without knowledge of the focus location, a probability based deposition of dose should be expected to offer better control than the PTV. For deep seated foci an improved TCP for the more concentrated dose is evident, and even peripheral foci will generally benefit. The TCP gains in these cases more than compensate the small TCP loss that results in the most unfavorable, unlikely situation of a tumor focus adjacent to the OAR, with a steep dose-effect relation.

To keep our analyses tractable, we introduced a single spherical OAR with the same size as the CTV. In complicated planning geometries, as are regularly encountered in head-and-neck cancer patients, the vicinity of multiple serially reacting OARs would reduce the degrees of freedom in redistributing the dose, complicating the translation of our results to such cases. Eventually, full probability based planning should provide the best trade-offs in these complicated circumstances.

The analyses we presented assumed 3 mm Σ and σ geometric uncertainties which would warrant the use of a 9.4 mm PTV margin. Smaller uncertainties would leave a smaller opportunity for improvement. In the limiting case of vanishing geometric uncertainties the probability based dose redistribution would only handle penumbra effects, and (for a uniform CTV) result in a dose more closely resembling that of the PTV (with, in that case, zero margin). If uncertainties were overestimated during planning, the true population averaged TCP would be higher than expected for the concentrated probability based dose distributions; we have shown that the PTV based distributions only suffer very little from the expected geometric miss, and will therefore only benefit very little from the lack of it. The probability based dose distributions could be at a disadvantage when uncertainties turn out considerably larger than planned for, however evaluations indicated that they are generally still to be preferred over the PTV for uncertainties more than two times as large as anticipated.

5. Conclusions

CTV minimum dose coverage confidence can be maintained while meeting an adjacent OAR maximum dose constraint without requiring full PTV coverage. Allowance of PTV overdose enabled a retraction of the 95% iso-dose by half the margin size in a single direction without compromising CTV coverage confidence. The PTV minimum dose regularly underestimates the true CTV minimum dose at 90% confidence by 20% of the prescription. The use of more concentrated non-uniform dose distributions improves the balance between the probability of tumor cell kill and the risk of geometrical miss. Despite uncertainties in dose-effect relations and target heterogeneity, a 20% tumor control rate improvement seems feasible while decreasing dose to a nearby OAR and surrounding tissues. Dose deconvolution features (‘shoulders’ or ‘horns’) are not required to reach this gain.