Modeling Individual Differences in the Go/No-go Task with a Diffusion Model

Abstract

The go/no-go task is one in which there are two choices, but the subject responds only to one of them, waiting out a time-out for the other choice. The task has a long history in psychology and modern applications in the clinical/neuropsychological domain. In this article we fit a diffusion model to both experimental and simulated data. The model is the same as the two-choice model and assumes that there are two decision boundaries and termination at one of them produces a response and at the other, the subject waits out the trial. In prior modeling, both two-choice and go/no-go data were fit simultaneously and only group data were fit. Here the model is fit to just go/no-go data for individual subjects. This allows analyses of individual differences which is important for clinical applications. First, we fit the standard two-choice model to two-choice data and fit the go/no-go model to RTs from one of the choices and accuracy from the two-choice data. Parameter values were similar between the models and had high correlations. The go/no-go model was also fit to data from a go/no-go version of the task with the same subjects as the two-choice task. A simulation study with ranges of parameter values that are obtained in practice showed similar parameter recovery between the two-choice and go/no-go models. Results show that a diffusion model with an implicit (no response) boundary can be fit to data with almost the same accuracy as fitting the two-choice model to two-choice data.

In standard two-choice tasks, subjects are asked to make a categorical decision that requires one of two responses. In go/no-go tasks, subjects are presented with the same categorical decision, but they are instructed to make a response to only one of the choices ("go" trials) and not to the other ("no-go" trials). On no-go trials, the next trial begins after some fixed time-out such as 1500 ms. In this article, we show how a sequential sampling model for decision-making, the standard diffusion model (Gomez, Ratcliff, & Perea, 2007; Ratcliff, 1978; Ratcliff & McKoon, 2008), explains data from go/no-go tasks and how the model can provide a different understanding of individuals’ failures to inhibit responses on no-go trials than can be drawn directly from data.

Gomez et al. (2007) tested several variants of the diffusion model for three go/no-go tasks (including the numerosity discrimination task used in the studies reported here). In the diffusion model for two-choice tasks, information from a stimulus is accumulated from a starting point to one or the other of two boundaries, one for each choice, and a response is made when the accumulated information reaches one of the boundaries. In Gomez et al.’s variants of the model, the decision process is the same except that when the no-go boundary is reached, no response is made. Thus, the go/no-go model is essentially the same as the two-choice model except that RT distribution data is not used for go/no-go responses. Here we use the term "go/no-go model" to refer to the model applied to go/no-go data in order to discriminate it from application of the two-choice model.

Gomez et al. believed that the parameters of the go/no-go model were not sufficiently constrained unless they were jointly determined by two-choice data collected with the same subjects in the same experimental session. In other words, they believed that without the two-choice data, the parameters recovered from fitting the go/no-go task alone would be inaccurate. As a result, they did not fit the go/no-go data alone and therefore could not examine whether parameters changed between the two tasks. They also analyzed the data only at the group level, not at the level of individual subjects.

In this article, we show that the diffusion model can, in fact, be used to estimate parameters for go/no-go data alone and we show that it can recover parameters for individual subjects. Removing the need for go/no-go tasks to be combined with two-choice tasks is especially important for clinical research where there is often a limited amount of time for data collection and where individuals may not have the stamina for lengthy sessions of data collection.

Go/no-go tasks have been widely used to study inhibitory control in a range of clinical disorders, most notably Attention Deficit Hyperactivity Disorder (ADHD) (Metin, Roeyers, Wiersema, van der Meere, & Sonuga-Barke, 2012), but also autism (Geurts, van den Bergh, & Ruzzano, 2014), bipolar disorder (Elliott et al., 2004), schizophrenia (Ford et al., 2004), Tourette’s (Roessner et al., 2008), depression (Boggio et al., 2007), Post Traumatic Stress Disorder (PTSD), and mild traumatic brain injury (Dimoska-Di Marco et al., 2011). The frequency with which an individual makes a "go" response to a no-go stimulus is taken as an index of that individual’s inhibitory control.

Indeed, poor ADHD-related performance on go/no-go tasks (and related stop-signal-reaction time tasks) has been instrumental in defining executive dysfunction as a core cognitive mechanism in ADHD (Metin, et al., 2012; Nigg, Willcutt, Doyle, & Sonuga-Barke, 2005; Willcutt, Doyle, Nigg, Faraone, & Pennington, 2005). The source of deficits has not been determined, but in this population, poor performance has been variously attributed to deficits in arousal (Sergeant, 2000), a motivational aversion to delay (Sonuga-Barke, 2002), and executive dyscontrol (Nigg, 2001).

In the standard go/no-go task, the proportion of go stimuli is larger than the proportion of no-go stimuli, e.g., up to 80:20. This means that the simplest way for the diffusion model to explain the data is to assume bias toward go stimuli. Bias can be implemented in several ways, as we describe below and as are tested in Experiments 1 and 2. We also examined another task from clinical research, the continuous performance task (CPT), in which the proportion of go stimuli is less than the proportion of no-go stimuli, e.g., as few as 20:80 (see the meta-analysis by Huang-Pollock, Karalunas, Tam, & Moore, 2012). Thus, for the CPT, and in contrast to the go/no-go task, the frequency with which an individual can successfully detect a rare target over time represents that person’s ability to maintain a state of readiness to respond (i.e., vigilance or sustained attention). Together, the go/no-go and CPT tasks are two of the most widely used computer-administered tests of cognitive performance in the clinical literature. We conducted experiments using the go/no-go task and we used simulations to examine both the CPT task the go/no-go task.

For both the go/no-go task and the CPT, error rates and Signal Detection Theory (SDT) parameters (d’ and β) derived from hit and false alarm rates for "go" responses have historically been the primary variables of interest. However, in most clinical research, the go and no-go stimuli are quite distinctive (e.g., letters versus numbers), with the consequence that false alarm and miss rates are often too low for estimates of d’ and β to be reliable (the diffusion model can mitigate this problem if there are some conditions with higher error rates, Ratcliff, 2008). Furthermore, accuracy and RTs sometimes provide conflicting views of performance. A greater bias toward making "go" responses to no-go stimuli (relative to a control group or to what might occur in a two-choice version of the task) suggests a deficit in performance, but faster responses to go stimuli suggests no deficit or even an advantage. Such reduction in RT is often interpreted as indicative of normative performance, or even enhanced processing efficiency. Current sequential sampling models like the diffusion model can resolve seemingly contradictory results like these. They integrate the two dependent variables within a single decision process. For the purposes of clinical research, model-based analyses may allow the field to move beyond simply documenting performance deficits to a better understanding of the processes responsible for them.

Each of the two experiments we describe here used both the go/no-go and the two-choice tasks. Subjects were asked to decide whether the number of asterisks displayed on a PC screen was larger than 50 or smaller than 51. For the go/no-go task, the probability of a no-go ("small") stimulus was .25 and for the two-choice task, the probability of that stimulus was .5 (typical values for these two tasks). For no-go decisions, there was a 1500 ms time-out before the next trial began. The two experiments differed only in that for Experiment 1, there was a 300 ms delay between a "go" response and the next stimulus (with an additional 300 ms after an error), whereas in Experiment 2, a delay was added so that the total time for "go" responses from the stimulus to the next trial was the same as for "no-go" responses.

We analyzed the data in two ways. First, we fit the two-choice model to the two-choice data and, separately, fit the go/no-go model to the two-choice data. The go/no-go model is the same as the two-choice model except that the no-go boundary is implicit, which means it is fit to RTs and choice probabilities for go choices but only choice probabilities for no-go choices. Because the only difference between the two-choice and go/no-go models is for the go/no-go model, choice proportions and not RTs are fit for no-go stimuli, the parameters of the models that produce the best fits to the data should be the same (or nearly the same). Results showed that the parameters of the go/no-go and two-choice models that produced the best fits to the data were nearly the same. Assuming that the two-choice model recovers parameter values well, (as it does when it is fit to simulated data, Ratcliff & Childers, 2015, and to experimental data), then if the go/no-go model produces the same values, it can be concluded that the go/no-go model, by itself, adequately recovers the parameter values. In addition, correlations of the parameter values across subjects should be the high for the fits of the two models to the same data (i.e., individual differences should be consistent).

In the experiments reported here, examination of parameter recovery was limited by the ranges of individual differences in the experiments. To test the generality of parameter recovery beyond that range, we used simulations with a range of parameter values that match those that have been found in the fits of the two-choice model to other experimental data. The results showed good parameter recovery for both models.

The Standard Two-Choice Diffusion Model

The standard two-choice diffusion model is designed to explain the cognitive processes involved in making simple two-choice decisions, decisions that take place in under a second or two, and to explain all the data for the decisions: accuracy, mean RTs for correct responses, mean RTs for errors, and the full distributions of RTs (their shapes and locations) for correct responses and errors. Decisions are made by a noisy process that accumulates information over time from a starting point toward one of the two boundaries. The rate of accumulation of information is called drift rate and it is determined by the quality of the information extracted from the stimulus in perceptual tasks and the quality of match between the test item and memory in lexical decision and memory tasks. In Figure 1A, the boundaries are a and 0, the starting point is z, and the drift rates are shown for two conditions, one for which correct decisions are at the top boundary (drift rate v₁) and one for which correct decisions are at the bottom boundary (drift rate v₂). Processes outside the decision process such as stimulus encoding and response execution are combined into one component of the model, labeled "nondecision" time, with mean T_er. Total RT is the sum of the time to reach a boundary and the nondecision time. The noise in the accumulation of information, "within-trial" variability (Gaussian distributed noise), results in decision processes with the same mean drift rate terminating at different times (producing RT distributions) and sometimes at the wrong boundary (producing errors).

Figure 1.

An illustration of the two-choice model (A) and the go/no-go model (B). In the go/no-go model, when the implicit boundary is reached, the subject waits until the next trial begins. The starting point is at z, the boundaries at 0 and a, and the drift rates are v₁ and v₂. For the go/no-go model, trials with drift rate v₁ have correct responses that are go trials and trials with drift rate v₂ have error responses that are go trials. Panels C, D, and E show some of the main ways that model parameters might change to account for the difference between the two-choice task and the go/no-go task (dotted lines). C shows a change in starting point to bias to the go boundary. D shows a bias in drift rates with the go drift rates (v_1g and v_2g) with an added constant relative to the two-choice versions (v₁ and v₂). E shows a bias and a reduction in discriminability (the dotted lines show a small difference in drift rates than the solid lines). Results from experiments can have combinations of these as well as changes in the nondecision time.

The values of the components of processing are assumed to vary from trial to trial, under the assumption that subjects cannot accurately set the same parameter values from one trial to another (e.g., Laming, 1968; Ratcliff, 1978). Across-trial variability in drift rate is normally distributed with SD η, across-trial variability in starting point is uniformly distributed with range s_z, and across-trial variability in the nondecision component is uniformly distributed with range s_t. Across-trial variability in drift rate and starting point allow the model to fit the relative speeds of correct and error responses (Ratcliff et al., 1999; Ratcliff & McKoon, 2008). In signal detection theory, which deals only with accuracy, all sources of across-trial variability are collapsed into one parameter, the variability in information across trials. In contrast, with the diffusion model, the separate sources of across-trial variability are identified.

Boundary settings, nondecision time, starting point, the drift rates for each condition, and the across-trial variabilities in drift rate, nondecision time, and starting point, are all identifiable. When data are simulated from the model (with numbers of observations approximately those that would be obtained in real experiments) and the model is fit to the data, the parameters that were used to generate the data are well recovered (Ratcliff & Tuerlinckx, 2002). The success of parameter identifiability comes in part from the tight constraint that the model account for the full distributions of RTs for correct and error responses (Ratcliff, 2002).

The Go/No-Go Model

Figure 1B illustrates the go/no-go model. Biases toward "go" responses can come about in the three ways shown in Figures 1C, 1D, and 1E, or combinations of them. We stress that these are biases in the decision process. They are not failures of "executive control," the dysfunction often postulated in clinical studies, but rather they are factors that are inherent in the decision process. In Figure 1C, the starting point is set closer to the go than the no-go boundary, as shown by the dashed line. In Figure 1D, the drift rates are all shifted to be an equal amount toward the go boundary; this represents a shift in the criterion that divides positive from negative drift rates (a shift in this criterion is the same as a shift in the criterion in SDT, Ratcliff, 1985; Ratcliff & McKoon, 2008).

In the data from Experiments 1 and 2, there was both a shift in the drift rate criterion and a reduction (relative to the two-choice data) in the differences between drift rates across experimental conditions. This is illustrated in Figure 1E. The reduction in the drift rate differences is exactly analogous to a reduction in d’ in SDT. It could occur if the need for only a single response or the higher proportion of go stimuli led to less effort and hence poorer encoding of stimuli.

Experiments 1 and 2

The experiments used the numerosity discrimination task described above (Ratcliff, Thapar, & McKoon, 2001, 2010; Gomez et al., 2007, Experiment 5). The advantage of discrimination tasks like this is that difficulty can be manipulated so that accuracy varies from near-chance to near-ceiling, which provides more constraints on the models than would a reduced range. For both experiments, half the trials were two-choice and the other half go/no-go.

For the go/no-go trials in the first experiment, the next trial began 300 ms after a "go" response was made and so there was a time advantage to making a "go" response. This procedure is often used in clinical studies with the intention of encouraging the establishment of a bias to produce "go" responses, which has been thought necessary for testing inhibitory control. In the second experiment, the time bias for go responses was eliminated by introducing a delay after a "go" response that made the total time from the onset of one stimulus to the onset of the next the same for go and no-go trials.

Method

Subjects

College students at The Ohio State University participated in the experiments for credit in an introductory psychology class, each for one 60-min session. There were 39 subjects in Experiment 1 and 31 in Experiment 2. We aimed for 32 in each experiment, but the research assistants ran over in the first experiment and did not make 32 in the second. All the subject-sessions were completed before the data were examined.

Procedure

Stimuli were displayed on the screen of a desktop computer and responses were collected from a keyboard. On each trial, an array of white asterisks was displayed against a black background. The asterisks filled random positions in a 10x10 array in the center of the screen subtending a visual angle of 17.5 degrees both horizontally and vertically. The task was to decide whether the number of asterisks was "small" (39–48) or "large" (52–61).

In both experiments, there were 22 blocks of 80 trials per block, 10 for the two-choice task and 12 for go/no-go task. For approximately half the subjects, the two-choice blocks were administered first in the experiment and then the go/no-go blocks, and for the other half, the order was reversed.

For the two-choice task, there were four trials of each number of asterisks per block in random order. The correct response was "large" for half the trials and "small" for the other half. For the go/no-go task, there were six trials of each number of asterisks for which the correct response was "large" and two trials of each number for which the correct response was "small," all in random order. The proportions of the stimuli for each task were explained to the subjects at the beginning of the experiments and a message reminding them of the relevant proportion was given at the beginning of each block.

For the two-choice trials, subjects were instructed to press the "?/" key on the keyboard for "large" and the "z" key for "small." For the go/no-go trials, they were instructed to press the space bar on the keyboard for a "large" response but to make no response if the number was small. Subjects were instructed to respond as quickly and accurately as possible.

For the two-choice task for both experiments, the screen was cleared following a response, then there was a 300 ms blank screen, and then, if the response was correct, the next stimulus was presented. If the response was incorrect, "ERROR" was displayed for 300 ms, then the 300 ms blank screen, and then the next stimulus. To deter fast guessing, a "TOO FAST" message was displayed for 500 ms if a response time was under 280 ms.

For the go/no-go task in Experiment 1, if the space bar was pressed in response to a "large" stimulus, then there was a 300 ms blank screen and then the next stimulus. If the space bar was not pressed for a "large" stimulus, the stimulus remained on the screen until the trial timed out at 1500 ms, then "ERROR" was displayed for 300 ms, then a blank screen for 300 ms, and then the next stimulus. If the RT was under 280 ms, "TOO FAST" was displayed for 500 ms, then a 300 ms blank screen, and then the next stimulus. If the stimulus was "small" and a subject waited out the 1500 ms delay (the stimulus remained on the screen), then after the delay, a blank screen was displayed for 300 ms, and then the next stimulus.

For the go/no-go task in Experiment 2, the amount of time between trials for "go" and "no-go" responses was equated. The procedure was otherwise the same: If the space bar was pressed in response to a "large" stimulus (a correct "go" response), then there was a delay until 1500 ms had elapsed since the presentation of the stimulus (the stimulus remained on the screen), then there was a 300 ms blank screen, and then the next stimulus. If the space bar was not pressed for a "large" stimulus, then the 1500 ms interval was followed by "ERROR" for 300 ms, then a blank screen for 300 ms, and then the next stimulus. If there was no response to a "small" stimulus, the 1500 ms interval was followed by a blank screen for 300 ms, then the next stimulus. If the stimulus was "small" and the space bar was pressed, then after the 1500 ms interval, "ERROR" was displayed for 300 ms, and then the next stimulus.

Results

Responses with RTs shorter than 300 ms were eliminated from analyses of the data. (For cutoffs of 250, 350, and 400 ms, the parameters recovered by the models were almost identical to those for 300 ms.) Stimulus conditions were grouped into two easy conditions (39–43 and 57–61 asterisks) and two difficult conditions (44–48 and 52–56 asterisks). Response proportions and mean RTs for the four conditions for the two-choice and go/no-go data for the two experiments are shown in Table 1. Here, we summarize the RT and choice probability data and later we describe how the models fit the data.

Table 1.

Response proportions and mean RTs for Experiments 1 and 2.

		Experiment 1			Experiment 2
Task	Condition	Pr “Large”	Mean RT “Large”	Mean RT “Small”	Pr “Large”	Mean RT “Large”	Mean RT “Small”
Go/no-go	easy/small/no-go	0.263	579		0.210	675
	difficult/small/no-go	0.556	649		0.474	695
	difficult/large/go	0.928	597		0.882	639
	easy/large/go	0.981	550		0.934	589
Two- choice	easy/small	0.119	663	669	0.121	735	684
	difficult/small	0.335	705	723	0.318	768	747
	difficult/large	0.803	674	727	0.784	706	786
	easy/large	0.918	623	661	0.896	650	755

For the two-choice task in both experiments, there was a slight bias to respond "large" and RTs were shorter for correct "large" responses than correct "small" responses. Error responses were slower than correct responses except for small stimuli in Experiment 1.

For the go/no-go task in both experiments, mean RTs were shorter for "go" responses relative to "large" responses in the two-choice task. There was a strong bias toward "go" responses, which might be interpreted in terms of inhibitory control: subjects frequently failed in the executive control that should have led them to inhibit "go" responses to small stimuli. Below, the diffusion model gives a different interpretation.

Fitting the diffusion model

In fitting the two-choice model, the values of all the parameters, including the variability parameters, are estimated simultaneously, for all the data from all the conditions of an experiment. To fit the model to the data, the RT distributions were represented by 9 quantiles, the .1, .2, .3, …, .9 quantiles. The quantiles and the response proportions were entered into the minimization routine and the diffusion model was used to generate the predicted cumulative probability of a response occurring by that quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a chi-square computation, these are the expected proportions, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .2, …, .9, and 1.0, which are .1, .1, .1, …, and .1). The proportions are multiplied by the number of observations in the condition (this produces values of the proportions weighted by accuracy) to give observed (O) and expected (E) frequencies and summing over (O-E)2/E for all conditions gives a single chi-square value to be minimized. The number of degrees of freedom in the data are the 20 proportions between and outside the quantiles (10 each for correct and error responses) minus 1 (because the sum must equal 1) multiplied by the number of conditions in the data. The model was fit to the data for each subject individually using a chi-square minimization method as described by Ratcliff and Tuerlinckx (2002). Later we use a G-square statistic that is asymptotically equivalent to the chi-square statistic, G²=2ΣOln(O/E).

A difference in this method of fitting the data and that used by Gomez et al. (2007) is that they used 5 quantile RTs but we used 9 quantiles. Ratcliff and Childers (2015) compared the use of 5 versus 9 quantile RTs and found little difference in parameter recovery for the two-choice model. This suggests that any differences between this study and that of Gomez et al. are not likely due to the number of quantiles used in fitting.

When the number of observations for a condition was less than 11 (usually for error responses), the RT distribution for a condition was divided at its median and the model was fit by predicting the cumulative probability of responses above and below the median. This reduced the number of degrees of freedom from 10 to 2 for that condition.

For the go/no-go model, the fitting method was the same except that for "no-go" responses (correct "no-go" responses and error "go" responses), a single bin was used for the contribution to chi-square, namely, (O-E)2/E, where O is the observed frequency of "no-go" responses and E is the expected frequency of "no-go" responses. Thus, for each condition, the number of degrees of freedom was 10-1 for the RT bins for the "go" responses plus 1 for the "no-go" responses. We also used this single bin when the number of observations in an error condition was less than 4.

In fits to both go/no-go and two-choice data, with stimuli of all levels of difficulty intermixed within blocks of trials, the only parameter that can differ across difficulty levels is drift rate. To change boundary settings, subjects would have to discover what level of difficulty a stimulus represented, then change the boundary settings, and then run the decision process. This is implausible in tasks with RTs in the hundreds of ms. So parameters other than drift rates are set to the same values across conditions of the experiment.

There is one complication that occurs when the best-fitting parameters of the model predict RTs for "go" responses longer than the no-go time out value, 1500 ms. Strictly speaking, the probability density for these responses should be moved to the no-go category. This would have the effect of reducing the predicted .9 quantile RTs (especially for the misses in the .9 quantiles for the larger values). But in the fits reported here (Figures 2 and 3), there were only 15/693 and 24/ 479 0.9 quantile RTs greater than 1400 ms, so there would be little effect on parameter values. If there were more predicted values near the no-go time out value, the modeling would have to be adjusted.

Figure 2.

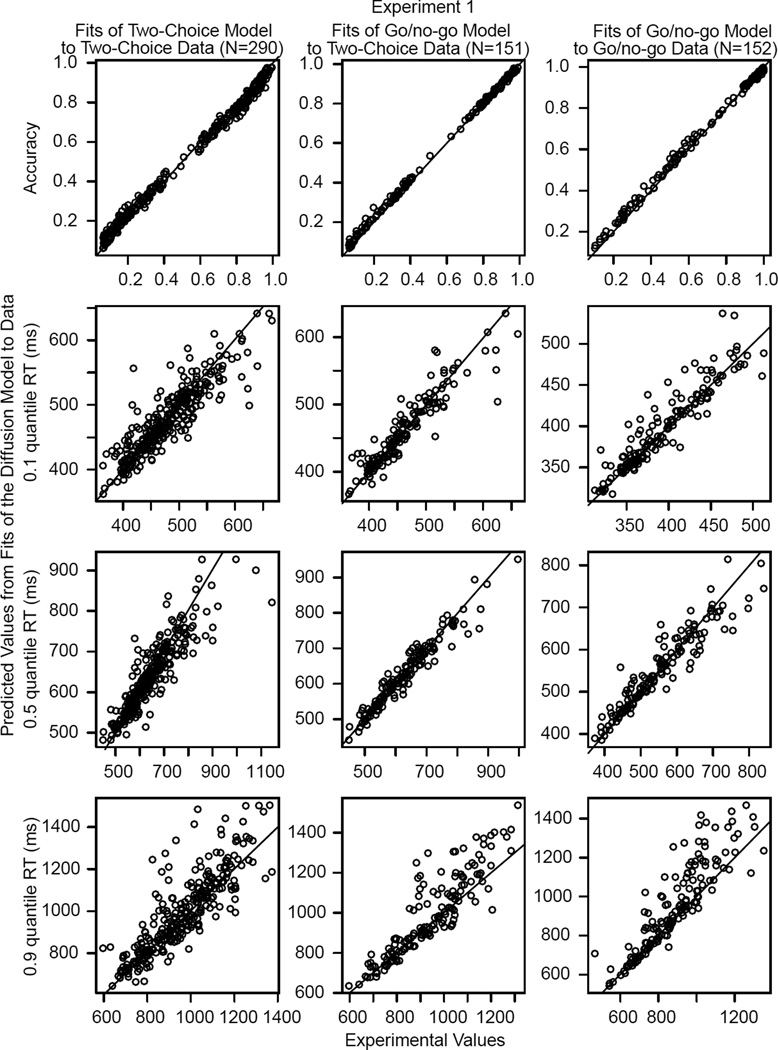
Plots of accuracy and the .1, .5 (median), and .9 RT quantiles for data (x-axis) and predicted values from fits of the diffusion model (y-axis) for Experiment 1. The points are the values for individual subjects and for conditions for correct and error responses with more than 11 observations per value. The left column shows plots for the fits of the two-choice model to two-choice data, the middle column shows fits of the go/no-go model to half the two-choice data, and the right column shows fits of the go/no-go model to go/no-go data. The N in the column head represents the number of points in the plots in the column.

Figure 3.

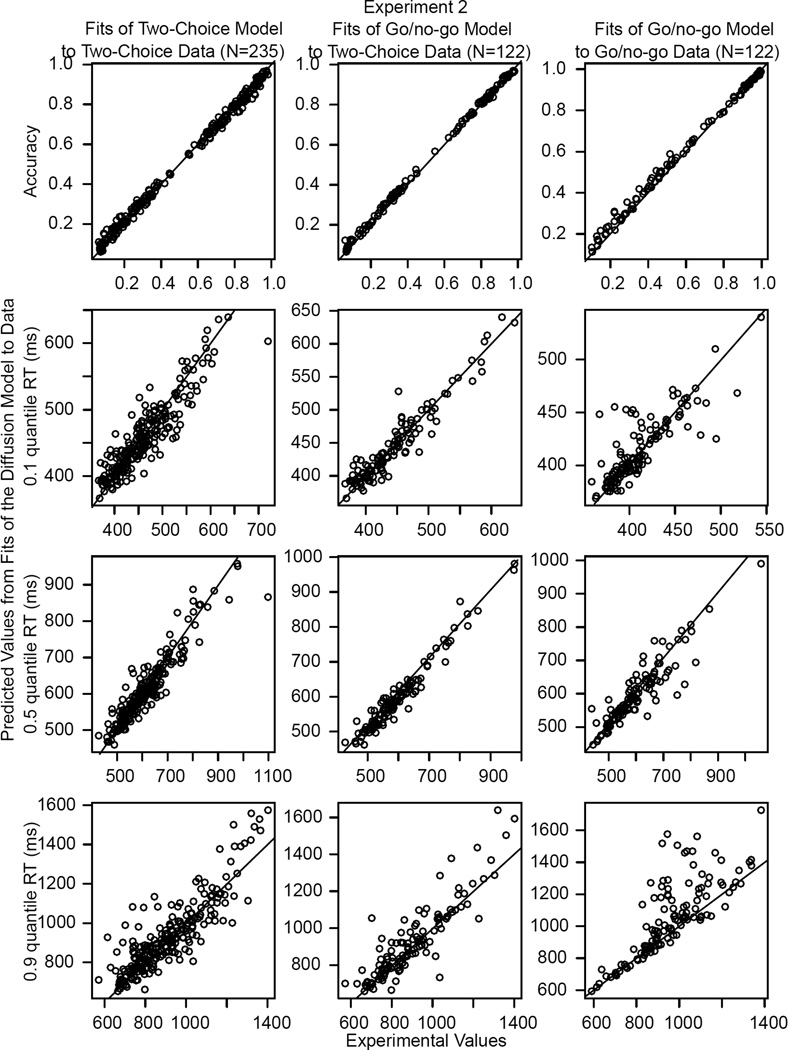
The same plot as that in Figure 2 for Experiment 2.

Fitting the two-choice model and the go/no-go model to the two-choice data

The question for this analysis was whether the go/no-go model could recover parameter values that were close to those from the two-choice model, as it should, given that it is applied to the same data as the two-choice model except that only choice probability is used for no-go responses. We addressed this first by fitting the two-choice model to the two-choice data and found that it fit the data well (as described later). Then we fit the go/no-go model to the two-choice data and compared the best-fitting parameter values from the two models. We found that they were nearly the same, and so concluded that the go/no-go model does, in fact, recover values that are consistent with the two-choice model. In the next paragraphs, we give these results in detail.

The parameter values from the best fits to the data are shown in Table 2. Although some of the differences between the parameters for the two-choice model and those for the go/no-go model were significant, as listed below, they were small relative to the sizes of their values. The reason for differences was that there were less data for the go/no-go model (no RTs for no-go decisions).

Table 2.

Mean diffusion model parameters for fits of go/no-go model and two-choice model

Experiment and task	Model fitted	a	Ter	η	sz	st	z	Bias to the go bound	v1	v2	v3	v4	χ2
1:go/no-go	go/no-go	0.139	0.379	0.098	0.068	0.171	0.084	0.608	−0.162	−0.008	0.223	0.341	44.0
1: two- choice	go/no-go	0.124	0.425	0.125	0.043	0.194	0.063	0.508	−0.251	−0.085	0.179	0.308	38.6
	two-choice	0.121	0.442	0.137	0.040	0.202	0.067	0.553	−0.273	−0.115	0.135	0.274	85.5
2: go/no-go	go/no-go	0.145	0.363	0.101	0.068	0.143	0.077	0.523	−0.133	−0.011	0.202	0.294	46.8
2: two- choice	go/no-go	0.118	0.423	0.132	0.048	0.194	0.062	0.525	−0.258	−0.102	0.163	0.282	34.9
	two-choice	0.114	0.433	0.133	0.052	0.201	0.062	0.544	−0.270	−0.112	0.147	0.275	87.8
	one-boundary	0.600	0.482	0.290	0.038	0.263	0.556	-	−0.529	−0.265	0.145	0.338	51.2

Experiment 1 has no delay before next trial for go responses. Experiment 2 has the same 1500 ms total time before next trial for both go responses and time out no-go responses. a=boundary separation, z=starting point, T_er=nondecision component of response time, η =standard deviation in drift across trials, s_z=range of the distribution of starting point (z), s_t = range of the distribution of nondecision times, and χ² is the chi-square goodness of fit measure. Drift rates for small stimuli are v₁ and v₂ and drift rates for large stimuli are v₃ and v₄. Easy conditions and v₁ and v₄ and difficult conditions are v₂ and v₃. For the go/no-go task, v₁ and v₂ are for no-go stimuli and v₁ and v₂ are for go stimuli. The bias to the go boundary is (z-a)a.

We used t-values to test for significance of the differences for all model parameters except drift rates. The degrees of freedom for paired t-tests were 38 for Experiment 1 and 30 for Experiment 2, with critical values for a two-tailed test of 2.02 and 2.04, respectively. The differences in boundary separation between the two models (0.003 and 0.004 for Experiments 1 and 2, respectively) were significant for both experiments (t= 2.05 and 2.22 for the two experiments, respectively). The small differences in starting points between the two models (0.004 for Experiment 1, 0.000 for Experiment 2), were significant only for Experiment 1 (t=3.00 and t=0.17, for the two experiments, respectively). The small differences in nondecision times (17 ms and 10 ms for the two experiments, respectively) were also significant for Experiment 1 but not Experiment 2 (t=4.83 and t=1.97, respectively.) There were no significant differences in the across-trial variability parameters (these parameters have more variability in their estimates, Ratcliff & Tuerlinckx, 2002).

For drift rates, two-factor within-subject ANOVA’s were carried out. One factor was difficulty: drift rates were lower for the difficult conditions than the easy conditions for both experiments (F= 383.83, df=3,114, for Experiment 1 and F=332.53, df=3,90, for Experiment 2). The other factor was the two models. The interactions between difficulty and the two models were not significant ((F=1.71, df=3,114, for Experiment 1 and F=0.20, df=3,90 for Experiment 2).

For Experiment 1, the differences between the models in drift rates were modest (relative to the sizes of the drift rates) but significant. The differences were 0.022 for v₁, 0.030 for v₂, 0.044 v_3, and 0.034 for v₄ (F=49.15, df=1,38). The differences were approximately the same size across difficulty (as shown by the non-significant interaction), indicating a shift in the drift rate criterion toward go responses but not a decrease in discriminability (Figure 1D, not Figure 1E). For Experiment 2, the differences between the two models were close to zero: 0.012 for v₁, 0.011 for v₂, 0.014 v₃, and 0.007 for v₄ (F=1.84, df=1,30).

To further test the equivalence of the parameter estimates, we examined effect size using Rouder et al’s (2009) online Bayesian t-test which provides a convenient way of assessing evidence for and against the null hypothesis based on effect size assumptions. For Ns of 39 and 31, a t of 2 gives about equal evidence for the null and alternative hypotheses, a t of 0.3 gives a Bayes factor of about 5 in favor of the null, and a t of 3 gives a Bayes factor of about 10 in favor of the alternative (using Rouder et al.’s default effect size). These values lead to the same conclusion as for the tests above, that there is relatively weak evidence for the alternative hypothesis for most of the differences in recovered parameters between the two models.

Fitting the two-choice model to the two-choice data and the go/no-go model to the go/no-go data

In this section we examine which parameters change between the go/no-go and two-choice tasks. For the go/no-go task relative to the two-choice task, the main results were shorter nondecision times, wider boundary separation, and smaller differences between the drift rates for the different conditions.

For Experiment 1, comparing the go/no-go task to the two-choice task, nondecision times were shorter, the starting point moved modestly closer to the go boundary (Figure 1C), and boundary separation was modestly larger. For drift rates there were two differences (Figure 1E): the differences between drift rates for the four conditions of the experiment were smaller for the go/no-go than the two-choice data and they were shifted toward the go boundary (i.e., a change in the drift criterion). Experiment 2 differed from Experiment 1 only in that the starting point did not move significantly closer to the go boundary.

For boundary separation, the difference between the two models was 0.018 for Experiment 1 and 0.031 for Experiment 2, and t=5.59 and t=8.18 for the two experiments, respectively. For starting points, the differences between the two models were 0.017 for Experiment 1 and 0.015 for Experiment 2, t=5.18 and t=4.63, respectively. For nondecision times, the differences were 63 ms and 70 ms and t=9.98 for t=8.93, for the two experiments, respectively. The differences in all of the across-trial variability parameters in Experiment 1 were significant, t=3.73, 4.85, and 2.12 for η, s_z, and s_t, respectively). For Experiment 2, only the s_t difference was significant, t=1.84, 1.95, and 2.80 for η, s_z, and s_t, respectively).

The Bayesian t-tests suggest that there is strong evidence for the alternative hypothesis for most of the differences between model parameters for the fits of the go/no-go model to the go/no-go data and the two-choice model to the two-choice data.

The differences between the models in their estimates of drift rates were 0.111 for v1, 0.107 for v2, 0.088 for v3, and 0.067 for v4 for Experiment 1 and 0.137 for v1, 0.101 for v2, 0.055 for v3, and 0.019 for v4 for Experiment 2.

The drift rates differed significantly across the four conditions as would be expected, F=574.64, df=3,114, for Experiment 1 and F=341.58, df=3,90, for Experiment 2. They also differed significantly between the two tasks, F=155.52, df=1,38 for Experiment 1 and 53.19, df=1,30, for Experiment 2, and the interaction between conditions and tasks was significant, (F=3.00, df=3,114 for Experiment 1, and F=12.81, df=3,90 for Experiment 2). This shows a reduction in the differences between drift rates for the go/no-go task relative to the two-choice task which represents poorer evidence being used in the decision (the effect was relatively small for Experiment 1 and larger for Experiment 2).

Quality of fits

The behaviors of model parameters can only be interpreted if the model fits the data adequately. Figures 2 and 3 show the experimental values and the models’ predicted values for accuracy and the .1, .5, and .9 quantile RTs for Experiments 1 and 2, respectively. There is one slightly misleading aspect of the figures, which is that the density of points along the diagonal is quite high and this makes it look as though there are many deviations. However, the proportions of misses were low. For example, for the .1 quantile, almost all of the predictions matched the data within 40 ms. For Experiment 1, there were 37 misses of more than 40 ms out of 290 data points for fits of the two-choice model to the two-choice data, 11 out of 151 for fits of the go/no-go model to the two-choice data, and 10 out of 152 for fits of the go/no-go model to the go/no-go data. The corresponding results for Experiment 2 were 24 out of 235, 4 out of 122, and 11 out of 122.

There were 76 degrees of freedom in the data used for fitting for the two-choice task and 40 for the go/no-go task. These come from 10 bins between the 9 quantiles for the four conditions (plus one for the go/no-go task because the proportion of errors is also fit). There are 11 parameters for both models: four drift rates, boundary separation (a), starting point (z), nondecision time, and across-trial variability in drift rate, starting point, and nondecision time. The 11 parameters reduce the degrees of freedom to 65 for the two-choice model and 29 for the go/no-go model. The critical chi-square value for a one-tailed test is 89.2 for the two-choice model and 45.7 for the go/no-go model. The mean chi-square values in Table 2 are close to the critical values. These are quite reasonable fits relative to other published results (e.g., Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff et al., 2010, 2011).

We also estimated a parameter for the proportion of responses delayed by processes other than those of interest, for example, losses of attention (Ratcliff & Tuerlinckx, 2002). The estimates of the proportions of them for the experiments here did not exceed .005, so they are not mentioned further.

The main systematic deviations between predictions and data were for fits of the go/no-go model to the .9 quantile go/no-go RTs for Experiment 2, for which the predicted values were larger than the data. This is likely because subjects tended to respond before the time-out at 1500 ms (some of the predicted values are larger than this time-out value). We discuss this further later.

Correlations among model parameters

When the go/no-go and two-choice models are fit to two-choice data, the only difference is that the go/no-go model uses only choice proportions for the no-go boundary, not RTs. It follows that the parameter values recovered for the two models should be nearly the same, which the results above indicated they are. Another way to verify that the recovered values are nearly the same is to examine correlations between them, which can be done because the differences among subjects in the values of the parameters were larger than the variability in the estimates.

The correlations are shown in Table 3. The correlations between parameters for Experiments 1 and 2, were, for boundary separation .91 and .91, for nondecision time .93 and .80, for starting point .77 and .60, and the correlations between the eight drift rates (correlations were computed for each drift rate separately for each experiment) were greater than .61. The smallest correlation for the six across-trial variability parameters (three parameters for each of the two experiments) was greater than .59. These strong correlations support the conclusion that the go/no-go model applied to the two-choice data recovers parameter values similar to those recovered by the two-choice model: the go/no-go model produces parameter values that maintain all of the correct relationships among conditions and individuals that the two-choice model does.

Table 3.

Correlations between the two-choice model fit to the two-choice data, the go/no-go model fit to go/ no-go data, and the go/no-go model fit to half the two-choice data.

Experiment and task pair	a	Ter	η	sz	st	z	v1	v2	v3	v4
1: 2-choice&go/no- go fit to 2-choice	0.911	0.932	0.612	0.591	0.937	0.773	0.851	0.726	0.782	0.865
1: 2-choice&go/no- go	0.389	0.650	0.213	0.136	0.252	−0.077	0.474	0.214	0.518	0.459
2: 2-choice&go/no- go fit to 2-choice	0.911	0.795	0.629	0.638	0.874	0.600	0.609	0.620	0.824	0.895
2: 2-choice&go/no- go	0.335	0.552	−0.286	−0.090	0.119	−0.227	0.381	0.038	0.448	0.429

Note. For the key to model parameter names, see the footnote to Table 2.

When the go/no-go model was fit to the go/no-go data and the two-choice model was fit to the two-choice data, there was also reasonable consistency in drift rates (correlations averaging .46) for the conditions in which the correct response was "large" for the two-choice data and "go" for the go/no-go data. For the conditions in which the correct responses were "small" and "no-go," there was less consistency (correlations averaging .28) because RT data were not fit for the "no-go" response and there were fewer observations for the no-go stimuli. The correlations, shown in Table 3, for Experiments 1 and 2, were, for boundary separation .39 and .34, for nondecision time .65 and .55, for starting point −.07 and −.22, and for the eight drift rates, they were between .04 and .52. The correlations for the six across-trial variability parameters were between −.28 and .25. The inconsistency for the across-trial variability parameters is expected because the standard deviations on their estimates are much larger than those for the other parameters (Ratcliff & Tuerlinckx, 2002).

The results for the fits to the go/no-go data and two-choice data show consistency in nondecision time and drift rates (especially the go drift rates, v₃ and v₄, see Table 3), and to a smaller degree, boundary separation. This suggests consistency in the main model parameters which suggests similar processing in the two tasks across individuals (see also Gomez et al., 2007).

Simulation Study

To examine whether the go/no-go model could fit data with wider ranges of parameter values than for the two experiments presented here, we conducted a simulation study using the 18 combinations of parameter values shown in Table 4 to generate two-choice data. The values were chosen to span much of the range of values that has been observed in fits of the two-choice model to two-choice data in other experiments (e.g., Matzke & Wagenmakers, 2009; Ratcliff & Childers, 2015).

Table 4.

Model parameters used in the simulations

a	Ter	η	sz	z	st	v1	v2	v3	v4
0.08	0.4	0.08	0.02	0.024	0.1	0.1	0.2	−0.1	−0.3
		0.2		0.04	0.25
				0.056
0.2	0.4	0.08	0.02	0.06	0.1	0.1	0.2	−0.1	−0.3
		0.2		0.1	0.25
				0.14

Note: For the key to model parameter names, see the footnote to Table 2. All combinations of the model parameters, η, z, a, and s_t were used leading to 24 combinations of parameter values. The numbers of observations were 175, 175, 350, and 350 corresponding to drift rates v₁-v₄ respectively.

In clinical uses of the go/no-go task, the number of observations for go trials is usually larger than the number for no-go trials, as it was in our experiments, and in uses of the CPT task, the number for go trials is smaller than the number for no-go trials. In order to produce simulated data that could mimic the proportions of trials for both tasks, we generated data with 350 trials for one stimulus type and 175 trials for the other type. For the go/no-go task, the 350 trials were treated as go stimuli and the 175 as no-go. For the CPT, it was the reverse, the 350 trials were treated as no-go stimuli and the 175 as go. For the go/no-go task, both accuracy and RTs were examined for the 350-trial stimuli and only accuracy for the 175-trial stimuli. For the CPT, both were examined for the 175-trial stimuli and only accuracy for the 350-trial stimuli. (Unequal probabilities have also been examined in two-choice tasks, Leite & Ratcliff, 2011; Mulder et al., 2012; Ratcliff, 1985.) To anticipate, we found that fits to the go/no-go data (larger numbers of observations) produces parameter values with a little more variability than the two-choice model, but fits to the CPT data (smaller numbers of observations) produces values with substantially more variability.

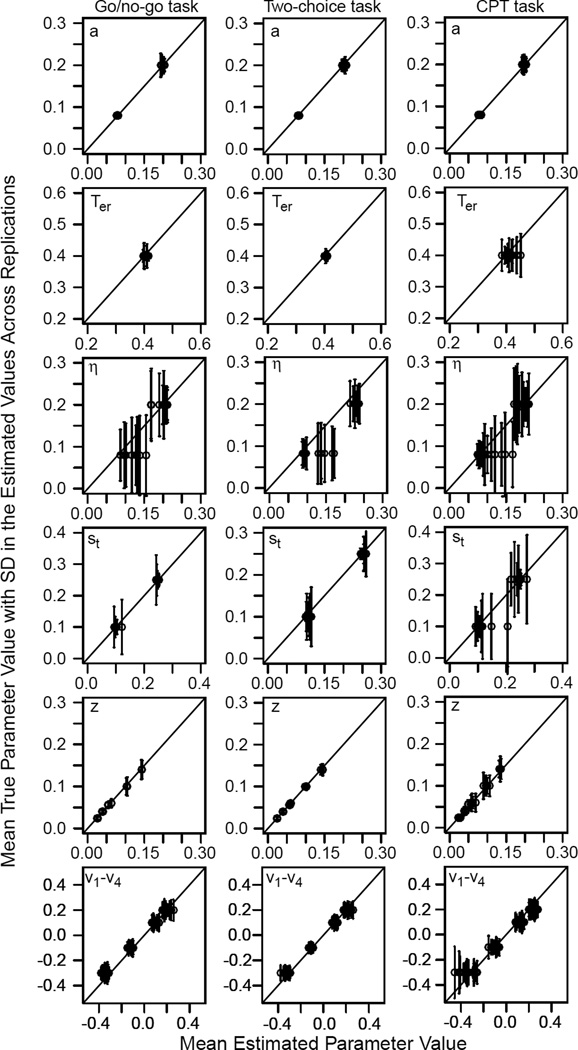
We generated 64 sets of simulated two-choice data for each of the 18 combinations of parameter values, a total of 1050 observations (using the random walk method, Tuerlinckx et al., 2001; Ratcliff & Childers, 2015). For each of the parameters for each of the combinations, we computed the mean and standard deviation of the recovered value. These are plotted in Figure 4. The value of the parameter used to generate the data is located on the y-axis, the mean of the recovered value is plotted on the x-axis, and plus and minus 1 SD error bars are plotted over the mean of the recovered value. When a parameter is estimated accurately, the points will lie on the diagonal line (intercept 0, slope 1) and the error bars will be small. When there is bias in an estimated value, the points will lie to the left or right of the diagonal line. When the parameters are estimated with high variability, the vertical error bars will be large.

Figure 4.

Plots showing parameter recovery for the simulation study. On the x-axis is plotted the mean of the parameter values and on the y-axis, in a horizontal row at the value of the parameter used to generate the simulated data is plotted 1 SD error bars. Movement away from the vertical line on the x-axis represents bias in the recovered parameter values and a large spread of the error bars represents high variability in the recovered parameter values.

We first fit the two-choice model to the data (accuracy and RTs for both types of stimuli). Boundary separation, starting point, nondecision time, and drift rates were recovered well. There were some biases in across-trial variability in drift rate and the SDs were larger for the across-trial variability parameters than the other parameters.

We fit the go/no-go model to quantile RTs for the stimulus type with the higher probability (correct responses for the conditions with drift rates v₃ and v₄) and accuracy for the stimulus type with the lower probability v₁ and v₂, "go/no-go task"). There was somewhat more variability in the recovered values than for the two-choice model, but the important result is that biases in the values were not greater than for the two-choice model.

For the CPT task, we reversed the application of the go/no-go model-- the model was fit to accuracy only for the stimulus type with the higher probability and RT quantiles for the stimulus type with the lower probability. This meant that, compared to the go/no-go task, there was half as much data for the stimulus type for which both accuracy and RTs were used. This led to larger standard deviations in the recovered parameter values and biases in nondecision times (the recovered values were longer than the generating values by up to 50 ms) and in across-trial variability in nondecision time.

To summarize, with 1050 observations and a 2:1 ratio of go stimuli to no-go stimuli, the model parameters were recovered almost as well for the go/no-go model as for the two-choice model. But the model parameters were less well recovered for the simulated CPT data.

Fitting Two-Choice and Go/No-Go Data Simultaneously

Gomez et al. (2007) fit the diffusion model to two-choice and go/no-go data at the same time. They found that drift rates were the same for the two tasks or were shifted only by a constant, that boundary separation and starting point were either the same or only modestly different, and that nondecision time was shorter for the go/no-go task. These findings are somewhat different from what we found in Experiments 1 and 2 when we applied the two-choice model to the two-choice data and the go/no-go model to the go/no-go data. We found a reduction in the differences in drift rates across conditions for the go/no-go data but not the two-choice data, a bias toward the go boundary for the go/no-go data, and shorter nondecision times for the go/no-go data. The difference in the findings for the starting point is likely due to a difference in the probability of go stimuli, .50 for Gomez et al. and .75 for our experiments. However, the differences in drift rates require further examination.

For comparison to Gomez et al., we performed the same analysis they did for Experiments 1 and 2 except that we fit the data for individual subjects, not averaged data. We used the G-square multinomial likelihood goodness of fit statistic to allow likelihood ratio tests as well as AIC and BIC tests, which penalize goodness of fit to different degrees as a function of number of parameters. AIC = −G²+2k, where k, where k is the number of parameters, and BIC = −G²+kln(N), where N is the number of observations.

We compared three sets of assumptions (similar to those in Gomez et al.) to determine which gave the best fits of the model to the data; in each, across-trial variability in drift, nondecision time, and starting point were assumed to be the same across tasks. The first set (A) assumed that nondecision time, starting point, and boundary separation but not drift rates were different between the two tasks; the second set (B) assumed that nondecision time, starting point, and boundary separation were different and drift rates were assumed different by a constant amount that was the same for all conditions (i.e., a change in drift criterion); and the third set (C) assumed that nondecision time, starting point, and boundary separation were different and drift rates were allowed to be unconstrained-- they could be the same or different between the tasks and they could be different by different amounts for different conditions. The pattern we found for Experiments 1 and 2 when we fit the go/no-go model to the go/no-go data and the two-choice model to the two-choice data is consistent with C; the differences in drift rates between conditions were smaller for go/no-go than two-choice.

The results of fitting the two-choice and go/no-go data together are shown in Tables 5 and 6. Mean G-square goodness of fit and AIC preferred the set with free drift rates (set C), but BIC penalizes goodness of fit more heavily than AIC for numbers of parameters and it preferred drift rates the same for Experiment 1 (set A) and different by only a constant amount for Experiment 2 (set B). Thus the results for BIC match those of Gomez et al.

Table 5.

Model parameters for joint fits to go/no-go and two-choice data

Experiment and model assumptions	Task	a	Ter	η	sz	st	z	v1	v2	v3	v4	G2
1: Drift rates the same	g/ng	0.147	0.396	0.110	0.044	0.201	0.104	−0.246	−0.082	0.170	0.290	153.3
	2-ch	0.120	0.436	0.110	0.044	0.201	0.064	−0.246	−0.082	0.170	0.290	-
1: Drift criterion	g/ng	0.143	0.384	0.121	0.054	0.194	0.092	−0.211	−0.042	0.222	0.347	144.4
	2-ch	0.122	0.440	0.121	0.054	0.194	0.068	−0.278	−0.109	0.155	0.280	-
1: Drift rates free	g/ng	0.143	0.382	0.116	0.054	0.190	0.091	−0.203	−0.035	0.215	0.336	133.4
	2-ch	0.123	0.439	0.116	0.054	0.190	0.068	−0.278	−0.115	0.152	0.281	-
2: Drift rates the same	g/ng	0.149	0.381	0.110	0.050	0.180	0.094	−0.229	−0.084	0.158	0.257	154.1
	2-ch	0.115	0.423	0.110	0.050	0.180	0.061	−0.229	−0.084	0.158	0.257	-
2: Drift criterion	g/ng	0.148	0.368	0.125	0.059	0.173	0.083	−0.203	−0.054	0.199	0.300	144.2
	2-ch	0.117	0.427	0.125	0.059	0.173	0.064	−0.255	−0.106	0.147	0.248	-
2: Drift rates free	g/ng	0.147	0.362	0.117	0.059	0.173	0.081	−0.168	−0.036	0.198	0.289	130.4
	2-ch	0.117	0.429	0.117	0.059	0.173	0.064	−0.271	−0.119	0.146	0.267	-

Note: For the key to model parameter names, see the footnote to Table 2. Parameter values in italics denote parameters that are the same for the two tasks. For each model, the values of boundary separation, a, starting point, z, and nondecision time T_er were free to vary. The model parameters, η , s_z ,and s_t were fixed across all the sets of assumptions. For the drift criterion model, drift rates differ between the two tasks by a constant.

Table 6.

Goodness of fit for joint fits to go/no-go and two-choice data

Experiment and model assumptions	Mean G2	Mean AIC	Mean BIC	NAIC	NBIC	LR test: number different from A	LR test: number different from B
1: Drift rates same (A)	153.3	179.3	248.9	4	19
1: Drift criterion (B)	144.4	172.4	250.0	10	16	23
1: Drift rates free (C)	133.4	167.4	259.9	25	4	29	17
2: Drift rates same (A)	154.1	180.1	250.1	4	14
2: Drift criterion (B)	144.2	172.2	247.5	9	13	18
2: Drift rates free (C)	130.4	164.4	255.8	18	4	23	17

Note. N_AIC and N_BIC show the number of subjects best fit by each model. The last two columns show the number of subjects for which the difference in G-square between the two models was significant. For fits to the two-choice and go/no-go data, a, z, T_er differ, but the across trial variability parameters are the same. For the key to the model parameters, see the footnote to Table 2, and for the model assumptions see Table 5.

These issues become more complicated when fits to individual subjects are examined. Strictly speaking, model selection should be done on a subject-by-subject basis and there is no consensus on how to combine AIC or BIC values across subjects. This means that the data from some subjects would be assumed to come from one set of assumptions and the data from other subjects from a different set, as shown by the results in Table 6.

It might appear that hierarchical models could provide a way out of this problem, but they assume that all subjects behave in the same way and so impose the same set of assumptions on all subjects. It may be possible to use mixed models in which different subjects use different processes (e.g., Bartlema et al., 2014), but to implement such modeling would require a great deal of new research to develop the method and examine whether it works in the framework of diffusion models of RT and choice.

In much modeling in cognitive psychology, the exact absolute values of parameters are rarely important, but relative values are. In neuropsychological and educational testing, reliable values for individuals are necessary for comparisons to individual-difference measures. The relevant issue here is whether fitting the go/no-go and two-choice tasks together distorts differences among individual subjects compared to fitting the data separately. To address this, we computed correlations between parameters for the two cases-- the parameter values for fitting them together in Table 5 and the parameter values for fitting them separately in Table 2. The result was strong positive correlations: for boundary separation, the mean of the correlations for Experiments 1 and 2 was 0.81; for nondecision time, it was 0.79; and for drift rates, it was 0.66 (we correlated the drift rates for each of the four difficulty levels for the two tasks and two experiments and then took the mean of those 16 values).

There are three important results from these analyses. First, estimates of the values of the diffusion model parameters produced by fitting the go/no-go and two-choice models together are quite similar to the values produced when they are fit separately. Second, the findings here are similar to those in Gomez et al. (2007) in that BIC preferred models with constant differences across conditions in drift rates for go/go-no and two-choice data, but here we show that the AIC and G-square statistics preferred a model in which differences in drift rates were lower for the go/ no-go task. Third, these choices as a function of the statistic were different for different subjects. Fourth, it should be stressed that estimates of the values of the diffusion model parameters produced by fitting the go/no-go and two-choice models together are quite similar to the values produced when they are fit separately and individual differences are consistent across the two fitting methods.

Discussion

With the research in this article, we successfully modeled behavior for the go/no-go and CPT tasks, two widely used tasks in the clinical and cognitive literatures. The go/no-go model that we used is the same as the standard two-choice model except that subjects are to make no response to no-go stimuli so the data for them are only choice probabilities, not RTs. The question with which we began was whether application of the go/no-go model to go/no-go data could recover parameter values for individual subjects -- drift rates, boundary separation, starting point, and nondecision time-- and whether it could do so without the constraints imposed by fitting go/no-go data simultaneously with two-choice data.

We showed good recovery of parameters in three ways. First, when the go/no-go model is applied to two-choice data, it should recover the same (or nearly the same) parameter values as the two-choice model applied to the two-choice data and we found that this was the case (correlations in drift rate, boundary separation, and nondecision times all between .60 and .93). Second, when go/no-go data are collected in the same experiment with the same subjects as two-choice data, the recovered parameter values should correlate, and they did (correlations in drift rates for "go" responses, boundary separation, and nondecision time were all between .33 and .65). Third, when we tested the model with simulations across a greater range of parameter values than in Experiments 1 and 2, it recovered the values that generated the simulated data well (Figure 5). We also conducted simulations of data from the CPT procedure and found again that parameter values were well-recovered, although with more variability than the go/no-go and two-choice procedures.

In the two experiments we conducted, there was a bias to respond "go" to no-go stimuli, that is, subjects were more likely to respond "go" to a no-go stimulus than they were to the same stimulus in the two-choice task. In the diffusion model, this bias can be realized in several ways (Figure 1C, 1D, and 1E). For Experiment 1, where the next trial began immediately after a "go" response, the starting point moved toward the go boundary, drift rates shifted toward the go boundary, and the differences among the drift rates were reduced. For Experiment 2, where there was a delay after a "go" response that made the total time between trials the same as for "no-go" responses, both boundaries moved away from the starting point and there was a reduction in the differences among drift rates. For both experiments, drift rates for "no-go" responses were closer to zero than for the two-choice task (similar to Figure 1E). For both experiments, nondecision times were shorter for the go/no-go task than for the two-choice task.

The diffusion model’s explanation of bias toward "go" responses contrasts with that in the clinical literature where the bias has usually been interpreted in terms of a failure of inhibition. By the diffusion model account, the go bias is a quantitative bias expressed within the decision process and not a modulation of an inhibitory control process, although it might be possible to make the two accounts compatible if the inhibitory control process was defined as one which modulates decision criteria and biases drift rates.

The diffusion model integrates all the data from two-choice, go/no-go, and CPT tasks into the same decision process and, in so doing, it accounts for all the data: the shapes and locations of the distributions of correct and error RTs, accuracy, and the relative speeds of correct and error responses. When the go/no-go and CPT tasks are used in the clinical literature, typically only accuracy data are considered. However, as pointed out above, accuracy and RT data can lead to different conclusions about performance.

A key additional feature of diffusion model analyses is that they recover parameters for individual subjects (Ratcliff, Thapar, & McKoon, 2006, 2010; Ratcliff & Childers, 2015). This is an important advance because it allows the possibility of examining relationships among model parameters across subjects to explain, for example, why speed and accuracy are often not correlated across subjects (Ratcliff et al., 2010; Ratcliff, Thompson, & McKoon, 2015) and it gives a means of examining relationships between model parameters and clinical outcome or neuropsychological measures for both normal and special populations.

There is one aspect of the go/no-go task that could be problematic with clinical populations (or uncooperative subjects). There appears to be no way to detect a strategy in which subjects hit the go button on some proportion of the trials without processing the stimulus, in other words a biased (to go responses) guessing strategy. In the two-choice task, such fast guesses produce chance accuracy for responses under some lower cutoff, for example, 300 ms. In data analyses with the two-choice task, we would eliminate subjects if they had more than 5 or 10% of responses lower than 300 ms with chance accuracy. Perhaps one way to see if this might be a problem for go/ no-go data would be to run the two-choice task with some subjects and make sure that the estimate of non-decision time was not more than 50–80 ms shorter for the go/no-go data versus the two-choice data. At the very least, if a subject produced a number of responses with RTs less than say 150–200 ms, then RT distributions need to be examined. If they show bimodality or a long flat left tail, then it may be possible to place a cutoff that eliminates those fast responses. Such data should be treated with caution and the subject possibly eliminated from modeling. On the other hand, it may be possible to make assumptions about the distribution of fast guesses and develop a mixture model that allows estimates of the proportion of fast guesses (see the contaminant distribution assumptions in Ratcliff & Tuerlinckx, 2002, and the random guess contaminant assumption in Ratcliff & Van Dongen, 2009).

Huang-Pollock et al. (2012) conducted a meta-analysis of CPT data for ADHD individuals and applied the diffusion model to the data. They found that sustained attention deficits in that population could be attributed to lower drift rates. However, they used the EZ-diffusion technique (Wagenmakers, van der Maas, & Grasman, 2007; see also Ratcliff, 2008) to model the data. The EZ technique’s estimates of parameter values are based only on the mean and variance of RTs for correct responses and the probability of an error for each condition of an experiment separately, and it produces estimates of only drift rates, boundary separation (not bias) and nondecision time. The EZ technique lends itself well to situations (as in a meta-analysis) in which full RT distributions are not available, but it cannot be falsified because it exactly transforms the three data values into the three model parameters. Furthermore, contrary to go/no-go findings, the technique requires the assumption that the decision boundaries are equidistant from the starting point. Thus, although slower drift rates for ADHD individuals have now been documented in several studies (Karalunas & Huang-Pollock, 2013; Karalunas, Huang-Pollock, & Nigg, 2012; Weigard & Huang-Pollock, 2014; Weigard, Huang-Pollock, & Brown, 2016), it is now possible to obtain a more conclusive interpretation of the cause of ADHD-related poor vigilance in CPT tasks using the full go/no-go diffusion model to directly fit RT distributions (Endres, Donkin, & Finn, 2014).

Huang-Pollock et al. (in press) used the diffusion model methods and tasks presented here to compare children with ADHD and non-ADHD control children. They manipulated the rate of events in two experiments. In one experiemnt, the next stimulus was presented immdiately after a response, in the other experiment, there was a time out after a go response to make the total time from the stimulus onset to the next trial the same for go and no-go trials as in Experiments 1 and 2 here. Diffusion model fits were conducted as for Experiments 1 and 2. For children with ADHD versus controls at the slow event rate, drift rate for go stimuli and starting point were lower and for the fast event rate, drift rates were lower for no-go stimuli (leading to an increased error rate, "go" responses, on no-go trials). For the slow versus fast event rate, for children with ADHD, nondecision time, boundary separation, and drift rate for no-go stimuli were lower and there was an increased bias toward the go boundary in the starting point. For the control children, there was only a decrease in nondecision time. Thus, although faster event rates increased bias towards go decisions, children with ADHD, the decrease in drift rate for ‘Äúno-go’ Äù decisions results in an increase of incorrect "go" responses.

Gomez et al. (2007) also examined a single-boundary model in which there was a boundary for go decisions but no boundary for no-go decisions. They found that relative to parameters for fits of the two-choice model to two-choice data, drift rates were much higher for the single boundary model, across trial variability in drift rate was higher, and the model predicted wider RT distributions than occurred in the data. We performed a similar analysis on the data from Experiment 2 by fitting the go/no-go model with the no-go boundary a large distance from the starting point (which means that almost no processes terminated at this boundary). Boundary separation a=0.6, and starting point z was allowed to vary freely (a-z is the distance to the go-boundary). Results were very similar to those in Gomez et al. with parameters shown in the bottom row of Table 2. Drift rates for no-go conditions were dramatically more negative and goodness of fit was considerably worse than those for fits to the data of the two-choice model and the go/no-go model with an implicit boundary. More negative drift rates imply that no-go stimuli would generate twice as much negative evidence than for the two-choice task. Examination of RT distributions showed that the mean .9 quantile RT for the one boundary model missed the data by about 300 ms. Thus, our analyses of the single boundary model (cf. Trueblood et al., 2011) were quite similar to those in Gomez et al. (2007).

Our results provide the basis for model-based analyses of go/no-go data from a variety of tasks that use the go/no-go procedure (e.g., memory, lexical decision, numeracy, Gomez et al., 2007) without the need to collect two-choice data. The results also show that the go/no-go model recovers individual differences that are needed in clinical and neuropsychological applications. This modeling approach offers different interpretations of differences in go/no-go performance with disorders such as ADHD by suggesting that they may result from biases in processing rather then some failure of inhibitory processing. It also may be that other tasks that seem to require conflict or inhibition mechanisms can be reinterpreted in different ways with model based analyses (e.g., White, Ratcliff, & Starns, 2011). These results show that it will be possible to provide a theoretically based analysis of deficits measured by using the go/no-go task that resolves the differences in interpretations provided by accuracy and RT measures.