Reconstructing time-to-event data from published Kaplan–Meier curves

Abstract

Hazard ratios can be approximated by data extracted from published Kaplan–Meier curves. Recently, this curve approach has been extended beyond hazard-ratio approximation with the capability of constructing time-to-event data at the individual level. In this article, we introduce a command, ipdfc, to implement the reconstruction method to convert Kaplan–Meier curves to time-to-event data. We give examples to illustrate how to use the command.

1. Introduction

The hazard ratio is often recommended as an appropriate effect measure in the analysis of randomized controlled trials with time-to-event outcomes (Parmar, Torri, and Stewart 1989; Deeks, Higgins, and Altman 2008) and has become the de facto standard approach to analysis. In meta-analysis of aggregated time-to-event data across trials, an essential step is to extract the (log) hazard ratio and its variance from published trial reports. Various extraction methods have been described (Parmar, Torri, and Stewart 1989; Williamson et al. 2002; Tierney et al. 2007), including direct and indirect estimates of hazard ratios based on 95% confidence intervals (CIs), p-values for the log-rank test or the Mantel–Haenszel test, and regression coefficients in the Cox proportional hazards model. An approximation to hazard ratios can also be derived by a “curve approach”, as described by Parmar, Torri, and Stewart (1989) and Tierney et al. (2007). The curve approach uses the extracted ordinate (y) and abscissa (x) values from the Kaplan–Meier curve to calculate hazard ratios for each time interval for which the number of patients at risk was reported. The overall hazard ratio during the follow-up phase is then derived by a weighted sum of the individual estimates of hazard ratios across time intervals, with the weights inversely proportional to the variance of each estimate (Parmar, Torri, and Stewart 1989).

The curve approach has been extended (Guyot et al. 2012) beyond the estimation of hazard ratios to the reconstruction of time-to-event data at the individual level. The availability of reconstructed individual-level data allows one to fit alternative models in secondary analyses if desired. Because nonproportional hazards are increasingly reported in trials, alternative measures (such as restricted mean survival time) that do not require the proportional-hazards assumption may have a more intuitive interpretation under nonproportional hazards (Royston and Parmar 2011). Because the proportionalhazards assumption may not be satisfied for all trials in a meta-analysis, alternative effect measures to hazard ratios may be more appropriate in such settings (Wei et al. 2015). However, by definition, newly developed effect measures are not reported in earlier trial publications. The use of these measures therefore relies either on collaborative sharing of individual-level data or on methods that enable reconstruction of such data from trial reports.

The reconstruction algorithm was written as an R function (Guyot et al. 2012). In this article, we present an implementation of this algorithm with improvements by introducing a command, ipdfc, that has the following features:

• Uses the curve approach to reconstructing individual-level time-to-event data based on the published Kaplan–Meier curves.

• Uses the number of patients at risk, as reported in the trial publication.

• Can identify which extracted time points correspond to the lower and upper endpoint of each time interval in the risk table.

• Can use survival probabilities, survival percentages, failure probabilities, or failure percentages as data input.

• Incorporates correction of monotonicity violators in the extracted data for survival probabilities, survival percentages, failure probabilities, or failure percentages.

In the following section, we briefly overview the methods underpinning the ipdfc command introduced in this article. We then give detailed descriptions of syntax and options. We then demonstrate its application in two examples from trial publications and assess the approximation accuracy by comparing summary statistics between the reconstructed data and the original publications. We close with a discussion.

2. Methods

2.1. Extracting data from published Kaplan–Meier curves

The reconstruction of time-to-event observations is based on data extracted from published Kaplan–Meier curves. In such curves, the x values usually represent the follow-up time since randomization; the y values may represent the survival probabilities, survival percentages, failure probabilities, or failure percentages at the corresponding time points, as specified in the trial publication. These measures can be transformed arithmetically into survival probabilities. In addition to data from curves, the number of patients randomized into each arm of a trial should be extracted from publications.

The DigitizeIt (http://www.digitizeit.de/) software application is a suitable tool for extracting data from a graphical image. Data extraction using this software is far more rapid, detailed, accurate, and reliable than manually applying pencil and ruler methods to a reduced image of the graph. If a curve is displayed as a clearly defined, unbroken line, DigitizeIt can automatically read off the x and y values at a large number of time points. This helps ensure the good quality of data required as input in the reconstruction of time-to-event observations. However, if the curve is presented as a broken (for example, dashed) line, the operator must extract data semi-manually by clicking on individual points on the curve using a mouse. Because each click returns only one data point, many clicks must be made to obtain sufficient data when there are many jumps in the curve. In contrast, within a specific time interval where there are few events or where the survival curves are flat, little information is available and correspondingly few clicks are required.

In addition, it is important to extract the number of patients at risk for each arm at regular time intervals during the follow-up. This information, usually known as the risk table, is often presented beneath the published Kaplan–Meier curves. The accuracy of the approximated time-to-event data can be improved by incorporating information provided in the risk table (Tierney et al. 2007).

2.2. Adjusting monotonicity violators

Because a survival function is by definition monotone decreasing with time, the y values extracted from a survival curve should also be monotone when ordered by the corresponding x values. However, there may be violators among the extracted data such that the monotonicity constraint is not satisfied. This is due to publication quality of the curves or errors in controlling the mouse clicks (Guyot et al. 2012). The reconstruction algorithm involves estimating survival functions. Monotonicity violators can lead to incorrect estimates for the number of events, and subsequently incorrect estimates of the survival function, which prevents the reconstruction from working. It is therefore crucial to correct the values for violators to ensure monotonicity. Because violators are often multiple, a systematic method is required.

With the ipdfc command, we incorporate alternative methods for the correction of violators. The first method, isotonic regression (Barlow et al. 1972), may help to detect violators and correct their values by using a pool-adjacent-violators algorithm. Adjacent violators occur where a pair of adjacent times and corresponding survival probabilities is inappropriately ordered, for example, time = (1.0, 1.1), survival = (0.91, 0.92). Briefly, the pool-adjacent-violators algorithm replaces the adjacent violators with their mean so that the data satisfy the monotonicity constraint. The technique has been recently coded in a command called irax (van Putten and Royston 2017), which can be called in our command. We also consider an alternative. We replace the value of a violator with the value of its adjacent violator such that the corrected data satisfy the monotonicity. We expect that using either method will lead to similar results because the absolute difference between the values of adjacent violators is often too small to have a material influence on the resulting data.

2.3. Algorithm to reconstruct survival data

We now briefly describe the algorithm underpinning the ipdfc command. We start with introducing notations. Let S_k denote survival probabilities at time t_k, where k = 1, 2, . . . , K and K is the total number of data points extracted. The survival probabilities S_k and the corresponding time t_k may be extracted from the respective y and x coordinates of a Kaplan–Meier curve. Let nrisk_i denote the number of patients at risk at time trisk_i, where i = 1, . . . , T, with T as the number of intervals where the number of patients at risk is reported. The number of extracted data points, K, is often much greater than T, the total number of intervals at the risk table. If the risk table is not reported, we have T = 1.

The four quantities S_k, t_k, nrisk_i, and trisk_i are the required input in the algorithm. As mentioned above, the number of patients at risk, if available, should be included in the algorithm. Otherwise, if T = 1, the number of patients randomized to each arm should be included in the algorithm. The total number of events, D, can also be used in the reconstruction.

In the algorithm, we will estimate the following quantities: the number of censoring, ĉ_k; the number of events, d̂_k ; the censoring time, ${\widehat{ctime}}_k;$ and the event time, ${\widehat{dtime}}_k.$ To estimate these quantities, we implement the algorithm described in Guyot et al. (2012) by adding three new components for improvements. First, we calculate lower_i and upper_i by using the input data t_k, trisk_i. Here, lower_i and upper_i are respectively the indices for the first and last time points extracted from the time interval [trisk_i, trisk_i+1]. For each of these time intervals, lower_i is equal to min{k : t_k ≥ trisk_i}, and upper_i is equal to max{k : t_k ≤ trisk_i+1}. Thus, lower_i and upper_i are not required as data input like the R code of Guyot et al. (2012). Second, we adjust the values of monotonicity violators by using isotonic regression or its alternative as just described. Third, we extend the algorithm to the situation where the number at risk is reported at the last time interval, at which we allow the calculation of the number of censoring following the same methods as those for the other intervals. The full algorithm is given in the appendix of this article.

3. The ipdfc command

3.1. Syntax

ipdfc, surv(varname) tstart(varname) trisk(varname) nrisk(varname) generate(varname1 varname2) saving(filename[ , replace] ) [probability failure isotonic totevents(#)]

This syntax converts data extracted from a Kaplan–Meier curve to time-to-event data. The syntax does not handle more than one sample at a time. When dealing with a trial having more than one arm, the syntax converts data extracted from one curve at a time to time-to-event data for the respective arm. This should be done for all arms individually, and further data management is needed to amalgamate the data from all arms of a trial, if the data are from a trial. We will illustrate this in the examples given later in this article.

3.2. Options

surv(varname) specifies the data extracted from the ordinate (y axis) of a published Kaplan–Meier curve. The data may be survival probabilities, survival percentages, failure probabilities, or failure percentages. By default, varname is assumed to contain survival percentages. surv() is required.

tstart(varname) specifies the time since randomization as extracted from the abscissa (x axis) of a published Kaplan–Meier curve. The time could be in any units (for example, days, months, or years), as specified in the publication. tstart() is required.

trisk(varname) specifies the times corresponding to the numbers of patients at risk in nrisk(). Set trisk() as 0 only if the total number of patients in the sample is known. trisk() is required.

nrisk(varname) supplies the number of patients at risk for each time in trisk(). Both trisk() and nrisk() are often found in a risk table displayed beneath published Kaplan–Meier curves. If no risk table is available, specify nrisk() as the number of patients in the sample, and specify trisk() as 0. nrisk() is required.

generate(varname1 varname2) generates the time-to-event outputs extracted from the input information. varname1 and varname2 specify two new variables, the time to an event and an event indicator (1 = event, 0 = censored). For example, specifying generate(time event) would create time as the time to event and event as the event indicator. generate() is required.

saving(filename[ , replace ]) saves the reconstructed survival data to filename.dta.replace allows the file to be replaced if it already exists. saving() is required.

probability signifies that varname in surv() contains probabilities rather than the default percentages.

failure signifies that varname in surv() contains failure information rather than the default survival information.

isotonic uses isotonic regression to adjust values that violate the time-related monotonicity in surv(). By default, an alternative, simpler method is used to correct the values of violators by replacing the value of a violator with the value of its adjacent violator.

totevents(#) is the total number of events and is used to adjust the number of observations censored in the final interval of the risk table.

4. Illustrative examples

4.1. Example 1: Head and neck cancer trial

Our first example is a two-arm randomized controlled trial published in Bonner et al. (2006). A total of 424 participants with locoregionally advanced head and neck cancer were randomized to receive either radiotherapy plus cetuximab or radiotherapy alone. The primary outcome was the duration of locoregional control. Both Kaplan–Meier curves and the hazard ratio were reported. This example was first used in Guyot et al. (2012) to illustrate the application of the reconstruction method. Here we use ipdfc to reconstruct the survival data and to illustrate how it performs compared with Guyot et al. (2012) and with the results in the original publication. We run the steps for each arm separately to obtain arm-specific data based on the associated Kaplan–Meier curve from the trial report.

We read in a text file for the control arm by calling import delimited.

 . import delimited using “head_and_neck_arm0.txt”
 (4 vars, 102 obs)

The text file contains four variables: ts and s as the data extracted from the x axis and y axis of a curve, and trisk() and nrisk() from the risk table.

We regenerate data for the control group by calling ipdfc.

 . ipdfc, surv(s) tstart(ts) trisk(trisk) nrisk(nrisk) isotonic
 > generate(t_ipd event_ipd) saving(temp0)

Because the extracted y values are survival percentages in this example, we need not use either probability or failure to convert s. However, we use the option isotonic to evoke isotonic regression to correct monotonicity violators. The regenerated survival data are stored in the file temp0.dta.

We run the following steps for the treatment group:

 . import delimited using “head_and_neck_arm1.txt”, clear
 (4 vars, 87 obs)
 . ipdfc, surv(s) tstart(ts) trisk(trisk) nrisk(nrisk) isotonic
 > generate(t_ipd event_ipd) saving(temp1)

The regenerated survival data are stored in the file temp1.dta.

The data simulated from both arms are then combined and specified with an arm indicator.

 . use temp0, clear
 . gen byte arm = 0
 . append using temp1
 . replace arm = 1 if missing(arm)
 (213 real changes made)

In the amalgamated data, there are three variables—t_ipd, event_ipd, and arm—which are time to event, event indicator, and arm indicator, respectively. We label the arm indicator as Radiotherapy and Radiotherapy plus cetuximab, as specified in the trial publication.

 . label define ARM 0 “Radiotherapy” 1 “Radiotherapy plus cetuximab”
 . label values arm ARM

We set time as the time to failure.

 . stset t_ipd, failure(event_ipd)

      (output omitted)

By calling sts graph, we reconstruct the survival curves (see figure 1).

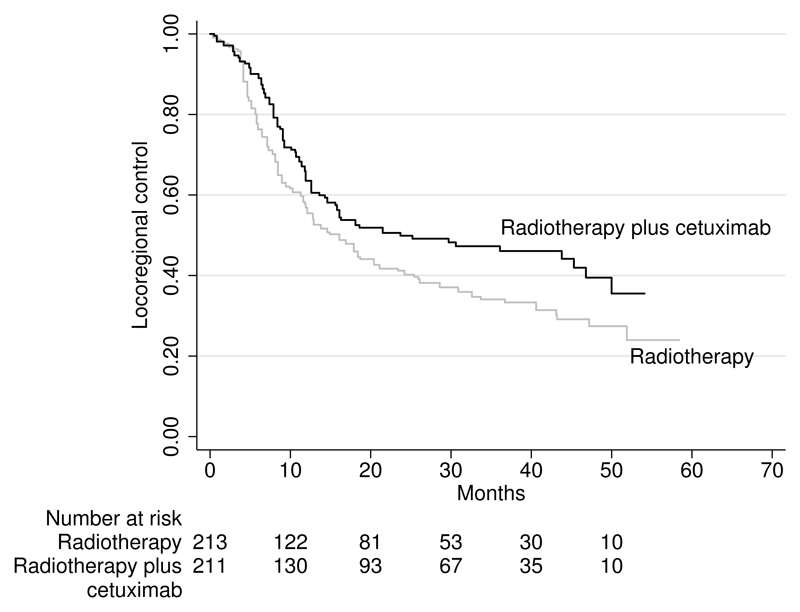
Figure 1.

Reconstructed Kaplan–Meier curves for locoregional control among patients with head and neck cancer (Bonner et al. 2006). Patients are randomized to receive radiotherapy plus cetuximab or radiotherapy alone.

 . sts graph, by(arm) title("") xlabel(0(10)70) ylabel(0(0.2)1)
 > risktable(0(10)50, order(2 “Radiotherapy” 1 “Radiotherapy plus”))
 > xtitle(“Months”) l2title(“Locoregional control”)
 > scheme(sj) graphregion(fcolor(white))
 > plot1opts(lpattern(solid) lcolor(gs12))
 > plot2opts(lpattern(solid) lcolor(black))
 > text(-0.38 -9.4 “cetuximab”)
 > legend(off)
 > text (0.52 53 “Radiotherapy plus cetuximab”) text(0.20 60 “Radiotherapy”)
          failure _d: event_ipd
    analysis time _t: t_ipd

The survival analysis is carried out by calling stcox arm.

 . stcox arm
          failure _d: event_ipd
    analysis time _t: t_ipd
 Iteration 0:	log likelihood = -1323.3427
 Iteration 1:	log likelihood = -1320.1905
 Iteration 2:	log likelihood = -1320.1899
 Refining estimates:
 Iteration 0:	log likelihood = -1320.1899
 Cox regression -- Breslow method for ties 


No. of subjects =         424

Number of obs =          424


No. of failures =         241




Time at risk    = 8412.821523






LR chi2(1)    =         6.31


Log likelihood  =  -1320.1899

Prob > chi2   =        0.0120



          _t
  Haz. Ratio
  Std. Err.
z
P>|z|
  [95% Conf. Interval]



arm
.7208993
  .0947487
-2.49
0.013
  .5571859    .9327152

The reconstructed Kaplan–Meier curves (see figure 1) look similar to the published curves (Bonner et al. 2006). There is only a small discrepancy in the numbers of patients at risk in the radiotherapy plus cetuximab arm. For this arm, based on the reconstructed data, the numbers of patients at risk are 211, 130, 93, 67, 35, and 10, which are similar though not identical to 211, 143, 101, 66, 35, and 9 in the original publication. The discrepancy in the risk table between the approximation (figure 1) and the original publication is very small for the radiotherapy arm.

In table 1, we report percentages of patients surviving one, two, and three years; median duration of locoregional control; and hazard-ratio estimates. The estimates of percentage of surviving and median time to event are close to those in the original publication. The hazard ratio (0.72, 95% ci: [0.56, 0.93]) estimated by our command is close to the hazard ratio (0.73, 95% ci: [0.57, 0.94]) estimated by Guyot et al. (2012). Because we digitize the data independently of Guyot et al. (2012), we do not expect to obtain identical data nor identical results. Though not identical, both approximated hazard ratios are similar to the published hazard ratio (0.68, 95% ci: [0.52, 0.89]).

Table 1.

Example 1. Comparison of summary measures estimated from publication and their corresponding reconstructed data

	Original publication	Guyot et al. (2012)	ipdfc
Radiotherapy arm		Percent [95% CI]	Percent [95% CI]
Percent surviving one year	55	56.1 [49.6, 63.3]	56.9 [49.9, 63.2]
Percent surviving two years	41	41.1 [34.7, 48.6]	40.9 [34.2, 47.5]
Percent surviving three years	34	34.7 [28.4, 42.5]	33.5 [27.1, 40.1]
Median duration	14.9	14.9 [11.9, 23.0]	16.1 [11.9, 20.4]
Radiotherapy plus cetuximab arm		Percent [95% CI]	Percent [95% CI]
Survival rate at one year	63	64.0 [57.8, 70.9]	65.4 [58.2, 71.6]
Survival rate at two years	50	50.4 [43.9, 57.8]	51.0 [43.3, 58.6]
Survival rate at three years	47	46.7 [40.1, 54.4]	49.6 [40.4, 55.7]
Median duration	24.4	24.3 [15.7, 45.7]	23.7 [15.6, 46.8]
Hazard ratio with 95% CI
	0.68 [0.52, 0.89]	0.73 [0.57, 0.94]	0.72 [0.56, 0.93]

4.2. Example 2: ICON7 trial

Our second example is icon7, a two-arm randomized controlled trial in advanced ovarian cancer (Perren et al. 2011). A total of 1,528 women were randomized to receive either standard chemotherapy plus bevacizumab or standard chemotherapy alone. From the analysis based on data with 30 months follow-up, Perren et al. (2011) concluded that bevacizumab improved progression-free survival in this population, with hazard ratio 0.81 (95% ci: [0.70, 0.94]; P = 0.004 from a log-rank test). Perren et al. (2011) found significant nonproportional hazards (P < 0.001) of the treatment effect. Kaplan–Meier curves and the associated risk table for progression-free survival were reported in their figure 2a, on which we base our reconstruction of the survival data using ipdfc. Also, we use the total number of events, tot, because it is available.

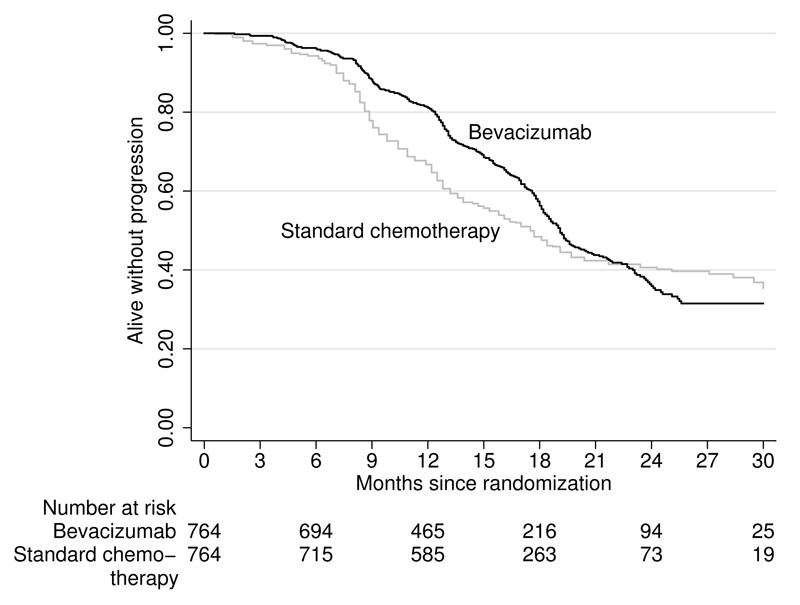
Figure 2.

Reconstructed Kaplan–Meier curves for progression-free survival according to treatment group in icon7 (Perren et al. 2011). Patients are randomized to receive standard chemotherapy plus bevacizumab or standard chemotherapy alone.

 . local tot0 = 464
 . local tot1 = 470
 . import delimited using “icon7_data_arm0.txt”, clear 
 (4 vars, 86 obs)
 . ipdfc, surv(s) tstart(ts) trisk(trisk) nrisk(nrisk) probability isotonic
 > tot(`tot0´) generate(t_ipd event_ipd) saving(temp0)
 . import delimited using “icon7_data_arm1.txt”, clear
  (4 vars, 473 obs)
 . ipdfc, surv(s) tstart(ts) trisk(trisk) nrisk(nrisk) probability isotonic
 > tot(`tot1´) generate(t_ipd event_ipd) saving(temp1)

In this example, the extracted y values are survival probabilities. According to the above codes, we use the probability option to specify that surv(s) represents survival probabilities rather than survival percentages.

The reconstructed Kaplan–Meier curves in figure 2 look similar to those in the original publication (Perren et al. 2011). The number of patients at risk is also well approximated, with most numbers identical to those in the original publication. The little discrepancies lie in 6 months and 12 months. The numbers of patients at risk are 694 at 6 months and 465 at 12 months based on the approximated data, which compared similarly though not identically to the original publication numbers of 693 at 6 months and 464 at 12 months. The estimated hazard ratios, median survival time, and p-values from the log-rank test are also similar to those in the original publication. See table 2 for a comparison of summary measures.

Table 2.

Example 2. Comparison of summary measures estimated from publication and their corresponding reconstructed data

	Original publication	Reconstructed data
Log-rank test	P = 0.004	P = 0.009
Nonproportional hazard test	P < 0.001	P < 0.001
Hazard ratio	0.81 (95% ci: [0.70, 0.94])	0.83 (95% ci: [0.72, 0.96])
Median survival time
Chemotherapy arm	17.3	17.5 (95% ci: [16.1, 18.7])
Bevacizumab arm	19.0	19.1 (95% ci: [18.3, 19.9])

4.3. Example 3: EUROPA trial

Our third example, europa, is a two-arm randomized placebo-controlled trial evaluating the efficacy of perindopril in reduction of cardiovascular events among patients with stable coronary artery disease (Fox 2003). In this trial, 12,218 patients were randomly assigned perindopril 8 mg once daily (n = 6110) or placebo (n = 6108). Kaplan–Meier curves and the associated risk table were presented in figure 2 of the trial report. In Fox (2003), the Cox proportional hazards model was used, but the hazard-ratio estimate was not reported. It was reported in Fox (2003) that perindopril treatment was associated with a significant reduction in the composite events (cardiovascular mortality, nonfatal myocardial infarction, and resuscitated cardiac arrest), with p-value = 0.0003 from a log-rank test and absolute risk reduction of 1.9%.

We extracted the failure percentages and the associated time points, respectively, from the y axis and the x axis of the Kaplan–Meier curves in Fox’s (2003) figure 2. In the following codes, we use the option failure to specify that the input data are failure percentages instead of the default survival percentages.

 . import delimited using “europa_data_arm0.txt”, clear 
 (4 vars, 743 obs)
 . ipdfc, surv(s) failure isotonic tstart(ts) trisk(trisk) nrisk(nrisk)
 > generate(t_ipd event_ipd) saving(temp0)
 . import delimited using “europa_data_arm1.txt”, clear
 (4 vars, 650 obs)
 . ipdfc, surv(s) failure isotonic tstart(ts) trisk(trisk) nrisk(nrisk)
 > generate(t_ipd event_ipd) saving(temp1)

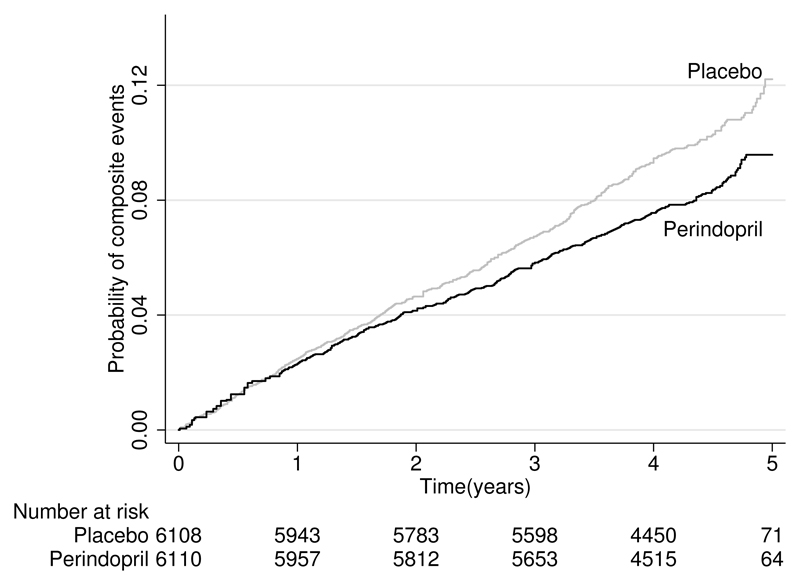
The Kaplan–Meier curves from the reconstructed data are presented in figure 3. The reconstructed curves appear nearly identical to the original. The reconstructed curves correctly reflect that the benefit of perindopril treatment began to appear at one year and gradually increased throughout the follow-up of the trial. The numbers of patients at risk are also very similar to the reported values, with only a small discrepancy in the placebo arm in two years of follow-up (5,781 in the original report versus 5,783 in the reconstructed data).

Figure 3.

Reconstructed Kaplan–Meier curves for time to first occurrence of event. Patients are randomly assigned to perindopril treatment or placebo in the europa trial (Fox 2003).

Using the reconstructed data, we obtain p-value = 0.0006 from a log-rank test (see table 3). Similar to the original report, this result also suggests that perindopril treatment was associated with a significant reduction in the composite events. We estimate the absolute risk reduction as 1.82%, similar to the 1.9% in the original publication. We are able to obtain the 95% ci [0.80, 2.84] for this based on the reconstructed data. Using the Cox proportional hazards model, we obtain the hazard-ratio estimate 0.81 (95% ci: [0.72, 0.91]). Table 3 shows that the correction of monotonicity violators by isotonic regression and by the default method lead to very similar results.

Table 3.

Example 3. Comparison of summary measures estimated from publication and their corresponding reconstructed data

	Publication	ipdfc with isotonic	ipdfc without isotonic
Log-rank test	P = 0.0003	P = 0.0006	P = 0.0006
Absolute risk reduction (95% CI)	1.9%	1.82% [0.80, 2.84]	1.80% [0.80, 2.82]
Hazard ratio (95% CI)	not applicable	0.81 [0.72, 0.91]	0.81 [0.72, 0.92]

The availability of Kaplan–Meier curves has enabled us to reconstruct the time-to-event data and calculate the hazard ratio, which was not reported for this trial. This would be particularly helpful if this trial was included in a meta-analysis where the hazard ratio is used as an effect measure.

5. Discussion

In this article, we provide a command, ipdfc, to implement the algorithm of reconstructing time-to-event data based on the information extracted from published Kaplan–Meier curves. Our command has greater flexibility, incorporating several additional features. It requires fewer inputs, automatically corrects data inconsistency that violates monotonicity, and allows one to use the number of patients at risk at the final interval, if reported.

Example 1 shows that the estimates of summary statistics (table 1) based on ipdfc are similar to those by Guyot et al. (2012). Some estimates are better approximations than others. The approximations to median times to event are very close to those in the original publication (Perren et al. 2011). The approximated hazard ratio is also close, but not identical, to that reported in the original publication. This small discrepancy is possibly due to the numbers and positioning of events not being entirely accurately estimated by the algorithm.

Although nonproportional hazards are evident in icon7, the reconstructed Kaplan–Meier curves and hazard-ratio estimate are in reasonable agreement with those from the trial publication (see table 2). This suggests that nonproportional hazards may not much affect the approximation accuracy. However, further empirical evaluation of ipdfc in a larger number of trials, with or without obvious nonproportional hazards, is desirable; this is a topic for further research.

Where hazard ratios are not reported but Kaplan–Meier curves are available, ipdfc is particularly helpful because it enables the reconstruction of time-to-event data and hence allows for reanalysis of the data. For the europa trial, we are able to obtain the estimate of the hazard ratio and obtain the 95% ci for the absolute risk reduction, both of which were not reported in the trial publication. It is shown that the recovered Kaplan–Meier curves and the associated risk table are both very similar to the originals. This is perhaps due to the large sample size in this trial, and the accuracy of the reconstructed data increases accordingly.

We conclude that ipdfc appears to perform quite well in regenerating survival data, sufficient to produce reasonable approximations to summary statistics in time-to-event analysis.

Biography

About the authors

Yinghui Wei is a statistician with research interests including statistical methods for medicine and health as well as statistical computing and algorithms. Her current work centers on survival analysis, meta-analysis, hierarchical models, and infectious diseases epidemiology.

Patrick Royston is a medical statistician with 40 years of experience, with a strong interest in biostatistical methods and in statistical computing and algorithms. He works largely in methodological issues in the design and analysis of clinical trials and observational studies. He is currently focusing on alternative outcome measures and tests of treatment effects in trials with a time-to-event outcome, on parametric modeling of survival data, and on novel clinical trial designs.