Abstract
Purpose
Functional MRI (fMRI) blood-oxygen level dependent (BOLD) signals result not only from neuronal activation, but also from non-neuronal physiological processes. These changes, especially in the low frequency domain (0.01-0.2 Hz), can significantly confound inferences about neuronal processes. It is crucial to effectively identify these nuisance low frequency oscillations (LFOs).
Method
A high temporal resolution (TR~0.5 s) fMRI resting state study was conducted with simultaneous physiological measurements to compare LFOs measured directly by near-infrared spectroscopy (NIRS) in the periphery and three methods that model LFOs from respiration or cardiac signal: 1) the respiration volume per time (RVT), 2) the respiratory variation (RVRRF) and 3) the cardiac variation method (HRCRF). The LFO noise regressors derived from these methods were compared temporally and spatially as well as in their denoising efficiency.
Results
Methods were not highly correlated with one another, temporally or spatially. The set of two NIRS LFOs combined explained over 13% of BOLD signal variance and explained equal or more variance than HRCRF and RVRRF or RVT combined (in 14 of 16 participants).
Conclusion
LFOs collected using NIRS in the periphery contain distinct temporal and spatial information about the LFOs in BOLD fMRI that is not contained in current low frequency denoising methods derived from respiration and cardiac pulsation.
Keywords: Low frequency oscillations, BOLD fMRI denoising, NIRS, respiration, cardiac, multiband
Introduction
Functional MRI (fMRI) blood-oxygen level dependent (BOLD) contrast (1) is a composite measurement of hemodynamic properties of blood flow, volume, and tissue and vessel oxygenation, changing in response to neural activity (2). However neuronal activations are not the only factor impacting BOLD signals. Low-frequency oscillations (LFOs) in the range of 0.01-0.2 Hz are commonly observed in functional imaging studies and some are attributed to baseline brain activity. However some are non-neuronal and closely related to autonomic physiological changes. These signals are unrelated to neural activity and can confound inferences made from BOLD signals about neuronal processes. These confounding signals are believed to stem from various physiological procedures, including: aliased signals from higher frequency signals such as respiration and cardiac pulsations (3), variations in heart rate and respiratory volumes (4,5), global LFOs possibly related to autoregulation (6), Mayer waves (7), vasomotion from oscillations in the vascular tone (8), and non-task-related neuronal activity (9). Physiological noise can account for 20-70 % of the BOLD signal variance, depending on acquisition and locations of the voxels (10).
Various physiological noise modeling methods have been developed to account for nuisance signals. Most involve simultaneously measuring physiological data such as respiration or heart rate and using variations of these timecourses as noise regressors in a general linear model analysis of the BOLD data. However, the relationship between these faster processes and the noise in the slower LF band is poorly understood. It is important to note that these modeling methods were designed primarily to model noise in undersampled datasets. Until recently, whole head fMRI experiments with repetition times shorter than 2 s were unpractical. Therefore, cardiac and respiratory signals were always aliased in fMRI data, so the “LFO” component in the fMRI data was a combination of “true” LFOs and aliased physiological signals. While these modeling methods remove a great deal of physiological noise, it was not possible to determine what fraction was truly LFO. Recent developments in fast imaging techniques have made routine acquisition of sub-second TR whole brain data possible (11,12) and have allowed us to address this question directly.
Our group has developed a BOLD physiological denoising method that utilizes LFOs in blood oxygenation measured directly in the periphery with near-infrared spectroscopy (NIRS). NIRS has a number of advantages for measuring systemic LFOs. First, NIRS directly measures concentration changes in oxy- (Δ[HbO]) and deoxy-hemoglobin (Δ[Hb]) independently at high temporal resolution (12.5-25 Hz); therefore, LFOs can be clearly separated spectrally. Second, peripheral (e.g. fingertip) NIRS measures these variations with no contamination from neuronal activity and therefore will not remove activations of interest. Finally, these NIRS signals can be used directly to regress out BOLD noise without further modeling, as BOLD is known to depend directly on the same concentration variations as NIRS and highly correlated with the global BOLD signal (13).
In this study we sought to determine how closely the LFO signals generated by various physiological modeling methods matched our direct measurement of the systemic LFO signals, and further to determine how well each of these matched the observed BOLD LFOs. Specifically, we compared, pairwise: 1) our near-infrared spectroscopy (NIRS) method utilizing LFOs measured in the periphery (13); 2) the Respiration Volume per Time (RVT) method, which models respiratory depth in the LF range (4); 3) the Respiratory Variation method (RVRRF) which models LFOs as Respiration Variation (RV) convolved with the respiratory response function (RRF) (5,14); and 4) The Cardiac Variation method (HRCRF) which models LFOs as heart rate (HR) variations convolved with the cardiac response function (CRF) (5). In order to unambiguously compare the LF regressors generated by the various methods, we ensured that aliased signals do not play a critical role by using an extremely fast ‘multiband’ fMRI acquisition (11,12) (TR~0.5 s) to achieve whole brain coverage at high temporal resolution.
In summary, the purpose of this study is to determine whether the different methods account for the same LF physiological noise both temporally and spatially, and whether the methods remove different physiological noise in the BOLD fMRI data when aliasing does not play a critical role.
Methods
Sixteen healthy participants provided informed consent for BOLD fMRI brain imaging with concurrent physiological measures and participated in the study (10 male, 6 female, average age 36±13 years, with two participants being measured twice, totaling 18 measurements). They were asked to lie quietly in the scanner and view a gray screen with a fixation point in the center. The resting state scans lasted 390 and 600 s. The Institutional Review Board at McLean Hospital approved the protocol and participants were compensated for their participation.
fMRI
All MR data was acquired on a Siemens TIM Trio 3 Tesla (T) scanner (Siemens Medical Systems, Malvern, PA) using a 32-channel phased array head matrix coil. First, a high-resolution localizer image was obtained [MPRAGE, repetition time/inversion time/echo time (TR/TI/TE)= 2530/1100/3.31, 256 × 256 × 128 voxels over a 256 × 256 × 170 mm sagittal slab, GRAPPA factor of 2]. Afterwards, multiband EPI data were obtained (University of Minnesota sequence cmrr_mbep2d_bold R008 (11,12)) with the following parameters: TR/TE = 400/30 ms (N=8) and TR/TE = 520/30 (N=10) flip angle 43 degrees, matrix 64 × 64 on a 220 × 220 mm field of view (FOV), multiband factor=6 (this multiband factor was a compromise value in order to minimize the TR with sufficient spatial coverage required the high multiband factor), thirty 3.0 mm slices with 0.5 mm gap parallel to the AC–PC (anterior commissure– posterior commissure) line extending down from the top of the brain. Initially 390 s were acquired (N=13). This was later increased to 600 s (N=5) when collection progressed, and we became interested in how resting state signals evolved over time.
The initial preprocessing steps were performed in FSL (15). Motion correction (MCFLIRT), slice time correction, spatial smoothing (FWHM 5 mm) and highpass filtering (100 s cut off) were performed. The data were registered linearly to the main structural image (BBR) and standard space (12 DOF). Ten volumes in the beginning of the temporal timecourse were discarded to allow for T1 relaxation.
Pulse Oximeter and Respiratory belt
Heart rate and respiration were continuously monitored at 50 Hz with the built-in photoplethysmograph (pulse oximeter) and pneumatic respiratory belt. While the exact internals of commercial plethysmographs vary, the low frequency oscillation used in this manuscript is always filtered out to optimize cardiac frequency signals. Moreover, only one signal is returned (probably total hemoglobin variation), rather than separate waveforms for oxy- and deoxy- hemoglobin. Three LFO timecourses were calculated from the raw respiration and cardiac signals (see Fig. 1); heart rate variation (HRCHR), respiration variation (RVRRF) (5) and the respiration volume timecourse (RVT) (4).
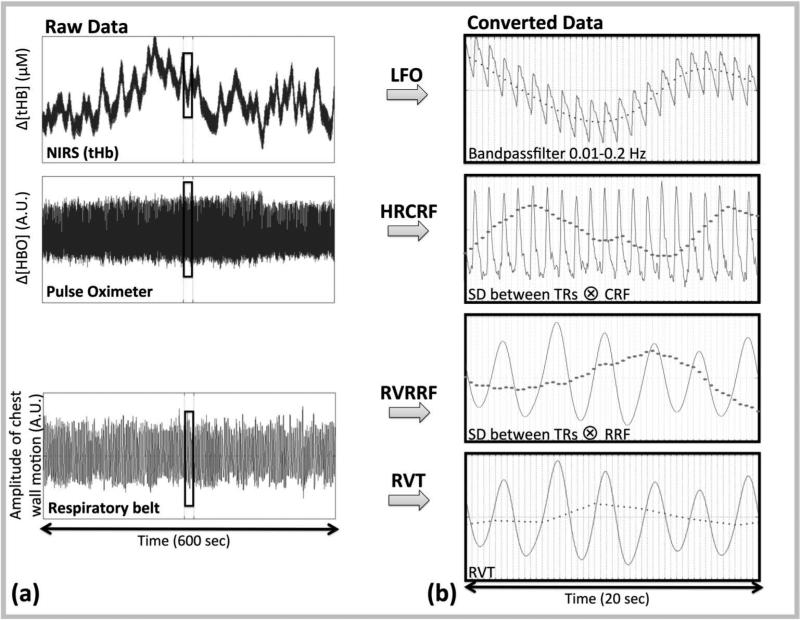
Figure 1. Steps for temporal and spatial analysis.
(a) The raw signals from the NIRS, Pulse Oximeter and Respiratory belt acquisition are shown in the first column. (b) Four methods were used to convert these raw signals into LFO noise regressors (dotted line in second column): 1) The NIRS LFO method which involved, direct measurements of LFOs in the periphery using NIRS (13), 2) the cardiac variation method (HRCRF) (5), 3) the respiratory variation method (RVRRF) (5) and 4) the respiration volume per time (RVT) method (4). The LFO noise regressors were then downsampled to the acquisition TR (0.4 s) and compared both temporally, and spatially (via their maximum correlation map).
HRCRF and RVRRF as described by Chang et al. (5) were derived as following. The cardiac and respiration signal's (Fig. 1(a)) standard deviation was calculated on a sliding window of 3 TRs as described in the reference (here 1.2 s). Since our TR was different, we also used a sliding window of 6 s, which is the exact window described previously (5), and which is better matched to physiological timescales. We decided to use 6 s, to maximize the explained variance (Sup. Fig. S1). Next, the same signal was convolved with the corresponding response function, CRF (5) (Formula 1) for the HRCRF and RRF (14) (Formula 2) to generate the RVRFF timecourse. Lastly, the signal was filtered to 0.01-0.2 Hz with a zero-delay Fourier-domain bandpass filter. The detailed procedures were carried out using PhLEM (16) in MATLAB (The Mathworks, Natick, MA). Analysis options were set to “variation model” (rvhr option in PhLEM) and the corresponding TR (Fig. 1(b), Fig. 2). Other parameters such as smoothing were set as described in Verstynen and Deshpande (16). We did not deconvolve individually per voxel but delayed the deconvolved regressor derived by the PhLEM software (16) and included voxel-specific time delays.
| [1] |
| [2] |
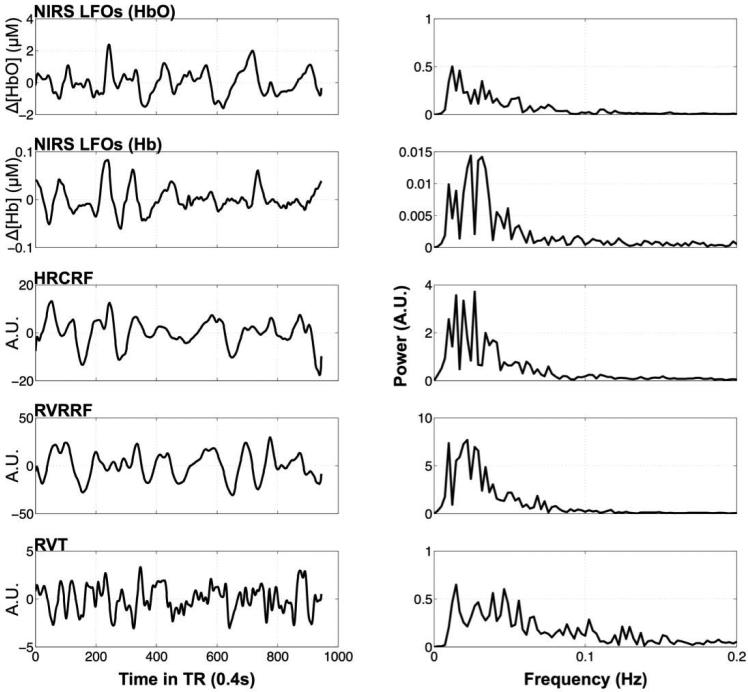
Figure 2. Example timecourses and their frequency distributions.
Timecourses (first column) of one participant downsampled to the TR of 0.4 s and their frequency distributions (second column) are depicted for each method (row) in the following order: NIRS Δ[HbO] and Δ[Hb] LFOs, the cardiac variation method, HRCRF, and the two respiration variation methods RVRRF and RVT.
The RVT timecourse was derived from the respiratory belt signal (Fig 1(a)). RVT is defined as the difference between maximum (Vmax) and minimum (Vmin) belt position between the peaks of inspiration (Formula 3). The maxima and minima of the respiratory belt signal were identified using a peak detection algorithm (peakdet in MATLAB) and then downsampled to the scan TR for temporal correlation. Lastly, the signal was filtered to 0.01-0.2 Hz with a zero-delay Fourier-domain bandpass filter (Fig.1(b), Fig. 2).
| [3] |
NIRS
We used the near-infrared tissue imager (Imagent, ISS, Champaign, IL) for the peripheral NIRS measurement (left middle finger or toe for two subjects for whom the finger measurement was not well adjusted). MRI-compatible probes with one collection and one pair of illumination fibers (690 and 830 nm) were separated by 1.5 cm. NIRS data were recorded at 12.5-25 Hz continuously during and several minutes before and after the fMRI acquisition. The NIRS instrument recorded TR trigger pulses for data alignment. Raw NIRS timecourses were converted into Δ[HbO], Δ[Hb] and total hemoglobin concentration change (Δ[tHb]) using the modified Beer-Lambert law (17) in MATLAB (Fig. 1(a)). For the differential pathlength factors, we used published values of 6.51 at 690 nm and 5.86 at 830 nm (18). The low-frequency component (0.01-0.2 Hz) was obtained by using a zero-delay Fourier-domain bandpass filter in MATLAB (Fig. 1(b), Fig 2).
Analysis
To determine the temporal correlation (rt) between the LFO timecourses, NIRS LFOs (Δ[HbO], Δ[Hb], and Δ[tHb]) were cross-correlated pairwise with each of the model-based methods (RVRRF, HRCRF, and RVT) for each participant (xcorr function in MATLAB). Optimum correlation search was restricted to 40 s delay (timeshifts: −20 to +20 s) to ensure meaningful correlations (a hemoglobin molecule circles the entire body in ~14.7 s (19)). Mean and standard deviation of the maximum cross-correlation across participants was calculated.
Determining significance of the correlations between timeseries with the processing steps we applied here is somewhat problematic. Conventional methods to statistically test the correlation employ the t-transformation (t, Equation 4) and fisher-z transformation (z-fisher, Equation 5.1 with 5.2) (20) for correlation value r between the timeseries xt and yt, t=1,...T and Zeta as the expected mean.
| [4] |
| [5.1] |
| [5.2] |
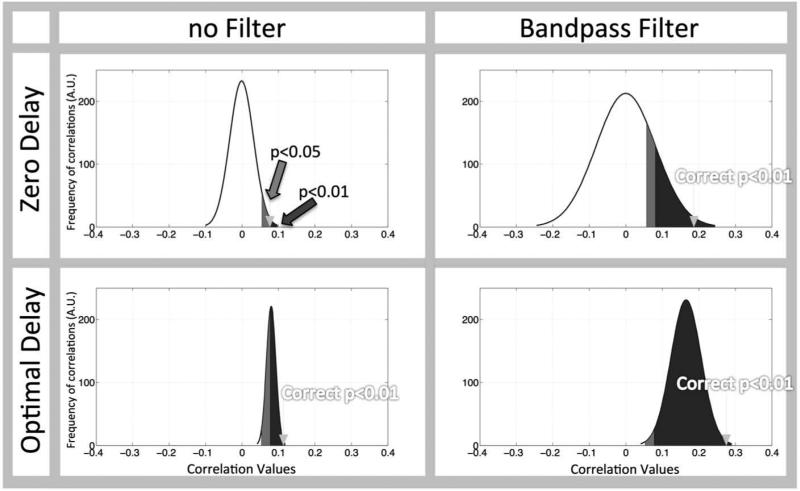
However this calculation seriously overestimates significance when processing steps such as bandpass filtering and optimal delay search are used, which they are in our method. Fig. 3 shows the effects of filtering and optimal delaying signals on the correlation distribution of two random timecourses. It is clear that the correlation distribution resulting from our processing steps (Fig. 3 (lower, right panel)) is altered relative to the normal correlation distribution (Fig. 3 (upper, left panel)) due to the filtering process (which broadens the distribution) and the use of the optimal delay for the maximum correlation (which will cause bias towards positive correlation values). Conventional correction greatly underestimates the significance thresholds, rendering all correlations done with our processing steps “significant” with a P<0.05. This type of distribution is not well characterized in the literature (more detail in Sup. Fig. S2). As a result, we must estimate the distribution to determine where our threshold correlation should lie (Fig. 3, arrow) using a Monte Carlo simulation. We can then find the 99 percentile from the random correlation distribution and get the corresponding correlation value, which then can be used as threshold for P<0.01. A correlation value of rt>0.28 is required for the parameters we used. We chose to use the more conservative significance criterion at P<0.01 to avoid false positives with our processing methods.
Figure 3. Standard statistical methods to evaluate correlations with bandpass filtering and optimal delayed signals are suboptimal.
Two completely random signals, resampled to 2.5 Hz (0.4 s) were generated over 1000 trials. The effects of bandpass filtering (0.01-0.2 Hz) as well as applying the optimal delay are shown as a distribution curve of the actual correlation between these completely random signals for each case (the black curve shows the smoothed histogram). “Significant” outcomes, when standard statistical methods are used, are shown for a one-sided alpha=0.05 (light grey shaded area) and alpha of 0.01 (dark grey shaded area) are shown. The correct threshold for the correlation distributions with an alpha=0.01 is marked with an arrow. The panel showing ‘Zero Delay’ and ‘no Filter’ is the only case in which the thresholds found with the conventional statistical methods and those found from the actual correlation distribution agree (the arrow and the dark shaded area).
A more straightforward and potentially more generally applicable alternative method for estimating the level of spurious correlation is to use a ‘sham NIRS’ correlation to establish a baseline correlation level. We generated the ‘sham NIRS’ timecourse by correlating the correctly aligned NIRS data from one subject with the asynchronous (recorded 700 s later) NIRS data from all other subjects. This correlation also takes the spectral characteristics of the real NIRS data into account and establishes a suitable baseline for spurious correlations (see Fig. 4(a), sham NIRS comparison vs. dotted line (equal to Fig. 3, arrow in lower, right panel). A one-sided independent sample t-test at alpha=0.01 (aligned condition > sham condition) (ttest2 function in MATLAB) between sham NIRS and the real correlation coefficients was then calculated because the aligned and sham conditions were taken from different participants.
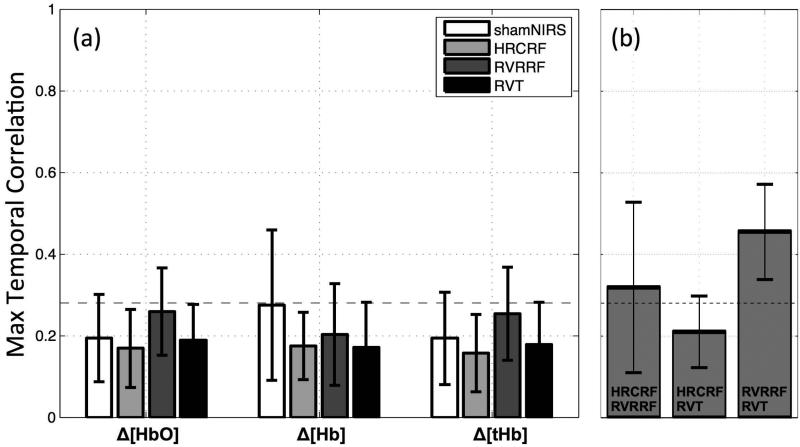
Figure 4. NIRS LFOs contain distinct temporal information.
(a) The mean maximal temporal correlation coefficients within subjects (r) between the NIRS LFO signal and the LFOs modeled by three other physiological BOLD denoising methods (grey shades) as well as the sham correlation (NIRS timecourse shifted 700 s in time correlated with the correctly aligned NIRS timecourse, white squares, error bars represent standard deviations). Significant correlations (P<0.01, one sided independent sample t-test) were not found. The dotted horizontal line was drawn for the upper limit of the confidence interval of random correlations (rt=0.28) at alpha=0.01. (b) The mean maximal temporal correlation coefficients (r) between the LFOs models HRCRF, RVRRF and RVT. The dotted horizontal line was drawn for the upper limit of the confidence interval of random correlations (rt=0.28) at alpha=0.01.
To evaluate whether our correlation is influenced by TR (0.4 s and 0.520 s), length of the scan, and motion artifacts, we preformed a linear regression (fitlm in MATLAB) with the above mentioned parameters as regressors. The average motion as well as the maximum motion artifact of each participant was used in the model.
For the spatial overlap (rs) between the methods, each of the model-based LFO and the NIRS timecourse, were used as input to the fast implementation of the timelag-dependent analysis approach called regressor interpolation at progressive time delays (RapidTiDe) (21). For each LFO method tested, we calculated the maximum cross-correlations between the BOLD signal in the LF range (0.01-0.2 Hz) in each voxel and the timecourse of the LF regressor generated by that LF method. This resulted in a maximum correlation map depicting the brain regions and the corresponding highest correlation between the LFO regressor and the BOLD LF signal. The maximum correlation maps for each participant were then thresholded with the previously calculated threshold for at rt>0.28. Overlap between spatial maps for each of the four LFO methods were calculated per participant, as well as sham condition maps, in which NIRS LFO signals of the other subjects were shifted 700 s after the end of the relevant scan times and used as regressor instead of the correctly aligned and correct subject. Spatial overlap was calculated over the entire brain matter by using the dice similarity coefficient (DSC) (22). In short, the DSC measures the spatial overlap between two target regions A and B (DSC(A,B)= 2(A∩B)/(A+B) with ∩ as the intersection). The DSC ranges between 0 and 1, with 0 meaning no overlap and 1 perfect spatial overlap. The mean and standard deviation of this overlap across participants was calculated. In addition a comparison between the sham NIRS correlation and the proper correlation was performed in the same way as done in the temporal correlation. The explained variance of the BOLD fMRI signal was calculated by squaring the maximum correlation maps for each participant (fslmaths –sqr (FSL)).
Results
Temporal Correlations
The mean temporal correlations and standard deviations between the NIRS LFO signal and the other LFO methods as well as the sham correlation (white) can be seen in Fig. 4(a). In addition a dotted horizontal line was drawn for the upper limit of the confidence interval for random correlations (rt=0.28). Due to the low concentration of deoxy-hemoglobin in normally perfused peripheral tissue, the Δ[HbO] signal dominates the Δ[tHb] signal therefore Δ[tHb] will not be discussed separately. On average, the correlation values between the NIRS LFO timecourse and the LFO timecourses modeled from physiological data did not exceed the threshold rt=0.28. Highest but non-significant correlations were found between NIRS Δ[HbO] and RVRRF (rt=0.26±0.11), which corresponds to a shared variance between the signals of only 6%; the majority of the signal power is not shared. Sham correlations averaged around rt=0.19±0.1 (for Δ[HbO]) and 0.28±0.18 (for Δ[Hb]). Motion (0.0057 ± 0.04 mm, with maximum 0.12 mm and minimum −0.09 mm), neither the TR nor the length of scan had any significant influence on the correlation values (at P<0.05). Between the LF models HRCRF, RVRRF and RVT we found mean correlations of rt=0.32±0.2 (HRCRF and RVRRF), rt=0.2±0.09 (HRCRF and RVT) and rt=0.45±0.12 (RVRRF and RVT) (Fig.4 (b).
In summary, in the temporal domain, mean correlations between the LFO timecourses generated using NIRS versus the other model-based LFO methods were low. Highest correlations were found between models of RVT and RVRRF.
Spatial Correlation
The groupwise mean spatial distribution by each LFO method is depicted in Fig. 5. Spatial overlap in the grey matter between the NIRS LFOs and other model-based LFO methods (HRCRF and RVRRF and RVT) are shown in Fig. 6. As in Fig. 4(a), the mean and standard deviation of all spatial overlap (rs) across participants (grey shades) and the sham correlation (white) are depicted. No DSC exceeded that of the sham condition significantly (P<0.01, one sided independent sample t-test with the hypotheses that the real correlation is greater than the sham correlation). Average spatial correlations were low between the NIRS LFOs and other model-based LF methods (rs< 0.3). Comparisons between NIRS Δ[HbO] and RVRRF (rs=0.29±0.14) showed the highest spatial overlap. NIRS Δ[HbO] and NIRS Δ[Hb] had low spatial correlations (rs=0.29±0.18). Between the LF models HRCRF, RVRRF and RVT we found mean correlations of rt=0.20±0.14 (HRCRF and RVRRF), rt=0.19±0.11 (HRCRF and RVT) and rt=0.30±0.15 (RVRRF and RVT) (not shown).
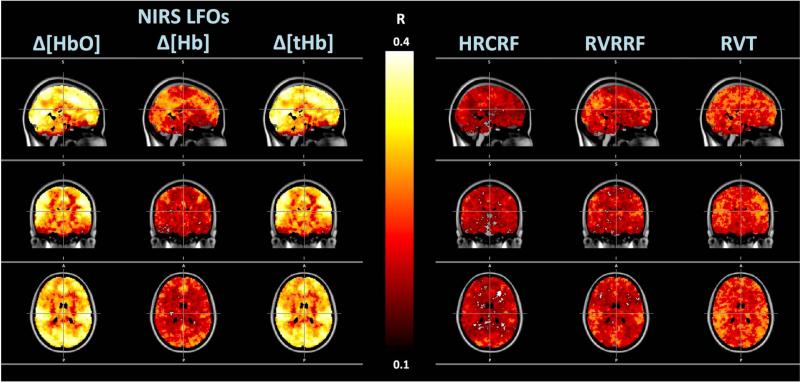
Figure 5. Spatial Distribution.
Maximum correlation maps showing the maximum correlation between the BOLD data and the different LFO timecourses. Columns 1-6 from left to right show the spatial distribution and magnitude of correlations between BOLD data and (1) NIRS LFOs Δ[HbO], (2) Δ[Hb] and (3) Δ[tHB], the cardiac variation method HRCRF (4), and the respiration variation methods RVRRF (5) and RVT (6).
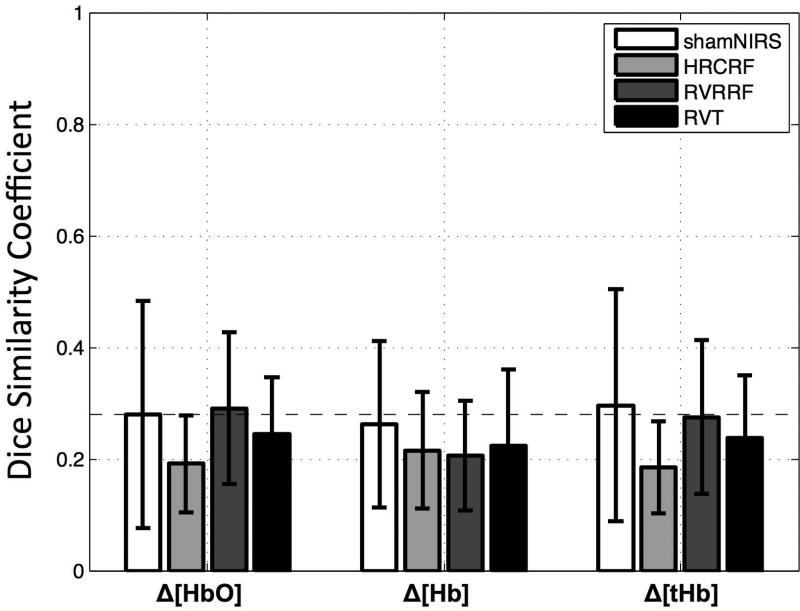
Figure 6. NIRS LFOs contain distinct spatial information.
The dice similarity coefficient (DSC) or spatial overlap (also referred in the text as rs) between the NIRS LFO signal and the other model-based LFO methods are shown in grey shades along with the sham correlation (NIRS timecourse shifted 700s in time correlated with the correctly aligned NIRS timecourse, white). Error bars represent standard deviations. No significant correlations (P<0.01, one sided independent sample t-test) in comparison to the sham correlation were found. The dotted horizontal line as shown in the temporal correlation was added for comparison (upper limit of the confidence interval of random correlations (rt=0.28) at alpha=0.01).
In summary, spatial correlations between the methods were low and comparable to the temporal results.
Explained Variances
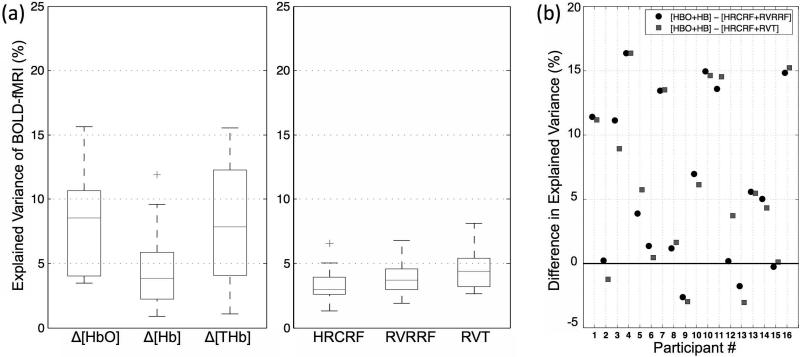
The BOLD fMRI variance explained by the LFO methods in the grey matter is shown in Fig. 7(a) as boxplots. When considering the mean, standard deviation (and the median), NIRS Δ[HbO], NIRS Δ[Hb], HRCRF, RVRRF and RVT explained BOLD fMRI variance with 8.5±3.8 (8.6 %), 4.6±3.0 (3.9 %), 3.3±1.2 (3.0 %), 4.0±1.5 (3.7 %) and 4.5±1.5 (4.4 %), respectively. TR only affected RVRRF significantly (P=0.0057). In summary, LFO denoising methods can account for approximately 3-12% of the variance present in the BOLD signal. For most participants, NIRS -based methods accounted for more BOLD variance than either HRCRF and RVRRF or HRCRF and RVT combined, explaining up to 16% more BOLD variance. For 2 participants the combined RVT and HRCRF or the combined RVRRF and HRCRF performed marginally better (less than 5%) (Fig. 7(b)).The 3-4 % BOLD fMRI variance can be explained by sham NIRS, the number drops to 1-2 % with the thresholded (rt=0.28, P<0.01).
Figure 7. NIRS LFOs contain information highly correlated with BOLD fMRI.
(a) BOLD fMRI variance explained by the LFO methods in the grey matter as boxplots from left to right: NIRS Δ[HbO], Δ[Hb] and Δ[tHB] LFOs, the cardiac variation method HRCRF, and the two respiration variation methods RVRRF and RVT. The median is indicated with a horizontal line in the boxplots, and the outlier by a ‘+’. (b) Difference in explained BOLD fMRI variance between NIRS Δ[HbO] and Δ[Hb] (HBO+HB) combined and the respiration and cardiac variation models combined (HRCRF+RVRRF and HRCRF+RVT) per participant. The respiration and cardiac based models combined explained variance (%) was subtracted from the NIRS LFOs. Positive values indicate that the NIRS LFOs performed better and negative values indicate that respiration and cardiac based models performed better.
Discussion
To answer the question of whether the LFOs measured by NIRS in the periphery are the same as those derived from the methods of Birn et al. (4) and Chang et al. (5), we performed both temporal comparisons of the denoising timecourses, and spatial comparisons of patterns of variance reduction when each of these methods were used to denoise fMRI. We optimized the comparison by using voxel-specific time delays for all methods to account for different arrival times of the signals at different parts of the brain. In addition we used a very short TR (~0.5 s) to prevent aliasing of respiratory and cardiac pulsation into the LFOs of the BOLD signal, which allowed us to study the LFOs uncontaminated by the aliased high frequency physiological signals.
Temporal comparison
The results suggest that NIRS measures are substantially different from model-based LFO method outcomes and are likely to account for a novel subset of the physiological noise contained within BOLD data. We also found very small temporal and spatial similarity between these methods and NIRS LFOs which were not significant according to our statistical assessment; However the correlation between NIRS Δ[HbO] and RVRRF differed from the sham correlation.
Possible underlying similarities reflecting this difference may be attributed to variations of the CO2 level. As mentioned previously, respiration based LFO models are constructed to account for fluctuations in CO2. NIRS Δ[HbO] is also closely related to cerebral blood volume, modulated by CO2 concentration, implying a closer relationship of NIRS Δ[HbO] to volume effects from respiration. This is not the case with cardiac based methods. Although both the cardiac pressure wave and Δ[HbO] have a close relationship with blood flow (24), the cardiac model discussed here is not simply a downsampled version of the cardiac signal. The mechanisms controlling cardiac variance are, as discussed, not well understood but may be partly due to neuronal activity linked with changes in levels of arousal (3).
In summary, we have temporally compared NIRS LFOs with the regressors generated by three popular methods derived from respiration and cardiac pulsation. Our main finding is that there are distinct components in the NIRS LFO not present in the evaluated cardiac and respiration variation methods.
Spatial comparison
Spatial correlations were similar to the ones seen in the temporal comparison (Fig. 6). Knowing that NIRS follows the vascular system closely (6,25), it is surprising to see these low spatial correlations when we normally assume that various components are likely tied to the same parts of the vascular system. This would be plausible, as the various physiological signals all travel with the blood through the vasculature. Because we introduced voxel-specific delays for each method, we expected that the pathway of the signals through the vasculature would be more pronounced as a result of this optimization. This is possible because BOLD signal reflects the changes in blood flow, volume and oxygenation. Many physiological processes can affect the signal simultaneously. In other words, the BOLD signal is the sum of many physiological oscillations. Each process will influence unique brain regions. However, these regions can have some overlapping. Moreover, it also depends on the blood content in different voxels. For the voxel that has high blood content, it might correlate better with several processes. The lack of these spatial correlations shows clearly the distinction between the methods and their various application methods. Our results are in accordance with earlier studies (26) in which we showed the contribution of NIRS LFOs in resting state analysis. Whereas NIRS LFOs where more prominent in sensory resting state networks (26), Birn et al. (27) and Chang et al. (28) have shown high contributions of the respiratory and cardiac variations in the default mode network, which is less contaminated by NIRS LFOs.
We also found slightly different spatial distributions of the RVT method than seen in previous evaluations of the method (4). In particular we did not see ventricular activation, which was previously reported. This might be due to the short TR, which might remove the T1 effects and therefore does not show ventricular “activation”. However ventricular “activations” have also been associated with motion, which are closely related to respiration; the extremely short TR allows motion due to respiration to be removed directly (see Methods). Further analysis of these differences and their consequences is needed.
In summary the spatial results are consistent with the temporal results suggesting that NIRS LFOs contain unique temporal as well as spatial information.
Variance explained by different methods
A relevant question is: how do these distinct LFOs correlate temporally with the BOLD fMRI? We found that NIRS LFOs explained a substantial amount of the variance of the resting state BOLD fMRI LF signal (Fig. 7 (a)) over widespread regions of the brain (Fig. 5). In the grey matter alone NIRS Δ[HbO] accounted for 8.5 % and NIRS Δ[Hb] for 4.6 % of BOLD variance. Moreover, the BOLD variance explained by NIRS Δ[HbO] and NIRS Δ[Hb] is additive because both are temporally different signals which do not occupy the same locations in space (rs=0.29 ). This adds to around 14% of the BOLD variance in the LF domain that can be explained by directly measured peripheral NIRS LFOs “uncontaminated” by neuronal signal or higher frequency physiological variations.
In this study we showed results, which were partly consistent and partly inconsistent with previous studies. For instance, in previous studies, denoising with RVT reduced variation from 1.41 to 1.25 % and improved Z scores on average by an additional 8 % (from 7.9 to 8.5) (2). It is hard to compare our results, but we found only low explained variance. One factor might have been the longer TR of 2 s, adding additional nuisance from aliased signals that are undersampled with long TRs. Another factor might be that in in contrast to our study, previous evaluation held breathing constant at ~0.3 Hz (4).
When comparing our results of RVRRF and HRCRF to the ones of Chang et al. (5) we found similar results in that HRCRF accounted for less explained variance than RVRRF (Fig. 7(a)). We also found the least overlap between the HRCFR model and other models (Fig. 4(b)), and highest similarity between the RVT and RVRRF model (Fig. 4(b)), reported earlier by Chang et al. (5). However Chang et al. (5) found that in a resting state study with TR=2 s, the RVRRF model explained variance in 7.6 % of the brain, explaining ~8.9 % of variance across these voxels, which was increased by adding the HRCFR model to 23.5 % of the brain with 12.9 % explained variance across these significant voxels.
In contrast, we found very little correlation between the HRCRF model and the BOLD fMRI signal. Schmueli et al. (29), found also only 1 % explained variance (beyond RV and RETROICOR regressors), with the HR signal using time delays with best results at 30-42 s (positive correlations). In our current study, we restricted delays to 20 s, which might have contributed to the low results. In addition we only partly used the convolution model proposed by Chang et al. (5) (deconvolve individually per voxel) but delayed the deconvolved regressor from Verstynen and Deshpande (16). However we did incorporate time delays. Another difference is the evaluation of explained variance, which was the explained variance in regions selected on the basis of significant impact of the regressors (5). When we used this method on the current dataset, the sham regressors would explain with more than 12% fMRI BOLD variance (not shown), which would be misleading.
In summary, NIRS LFOs do not only contain distinct temporal and spatial information in comparison to these respiration and cardiac based methods, but more importantly, contain information highly correlated with BOLD fMRI. However the question remains what these pure LFOs signals are if they are not related to direct variations of either cardiac or respiration signals.
NIRS LFOs are derived from direct quantitative measurement of hemoglobin concentration and oxygenation, which are factors that directly affect BOLD fMRI. As expected, using NIRS to directly measure changes in a subset of the same hemodynamic parameters that contribute to the BOLD fMRI signal is a more direct method of accounting for BOLD variance compared to methods that are based on modeling relationships between physiological processes less closely related to BOLD signal. Additionally, other LFO methods focus only on a single physiological process such as the respiratory or cardiac cycle and its associated variance. The great advantage of NIRS is that it allows direct measurements of these BOLD-related peripheral signals regardless of their complicated and/or multiple origins. So even though NIRS LFOs may not be directly related to the models presented in this paper, they might still be related to these physiological processes through some other more complicated models. For instance recent studies have emphasized the link between LFOs and slow changes in cerebral autoregulatory processes such as mean arterial blood pressure, vasomotion (a marker of elasticity of blood vessels allowing for the change in diameter of vessels) as well as carbon dioxide changes.
Spontaneous LFOs at around 0.1 Hz are associated to mean arterial pressure, lagging in time (also referred to as Mayer waves (7,31)) and have recently been coupled autoregulation mechanism (30), in particular around <0.1 (32-34). These studies showed high correlations between mean arterial blood pressure and cerebral intravascular oxygenation when using NIRS to monitor cerebral circulation and blood flow. However Mayer waves are characterized by being symmetrical in large parts of the brain (34), which seems to contradict the dynamically evolving character of the NIRS LFOs which has been described in several papers of ours before (6,25).
Numerous studies have also associated these processes with NIRS LFOs with vasomotion (34-36), referring to oscillations in the vascular tone, thought to be generated within the vessel walls. The relationship has been further supported by research into oscillatory intracellular calcium. As part of the underlying mechanism of vasomotion, calcium concentration changes have been linked closely to LFOs of deoxy- and oxyhemoglobin in both large and blood vessels and capillaries with lags of 5-6 s (37). However vasomotion is characterized by localized changes (8,34), which again does not agree with the global nature of the NIRS LFOs we measure (25).
Carbon dioxide changes are partial pressure fluctuations of end-tidal carbon dioxide, inducing changes in cerebral blood flow and volume, which have been associated with NIRS measurements (34). However they are characterized in a frequency domain in which the evaluated NIRS LFOs are less dominant, namely 0-0.05 Hz (we did not evaluate lower than 0.01 Hz). This does not exclude that the effects of these changes or other ones named above are partly contained in the NIRS LFOs we measure or that a secondary effect might be related, but it does show that we are not measuring this effect solely.
In summary all these underlying physiological processes may be contributing to the distinct portion of the NIRS LFOs that is not well-modeled by the respiratory or cardiac methods. However none of these processes seem to be solely responsible for the variance measured with NIRS LFOs. At last we would like to mention that LFOs can have an active role indirectly related to neuronal activity (e.g. as a result of local vascular anatomy (38)). However we have also found that the NIRS LFOs we evaluated here, can increase the z-scores for task activation (21), which indicates that most of the removed variance is indeed more nuisance.
Conclusion
We directly compared measured peripheral NIRS LFOs with three currently utilized methods for modeling LF nuisance signals in BOLD fMRI data using respiratory and cardiac variation signals. We found that 1) peripheral NIRS LFOs contain temporal and spatial information that are unique compared to three commonly used LF physiological denoising methods which are based on modeling the LFOs from respiration and cardiac variation, 2) peripheral NIRS LFOs explain a significant amount of BOLD variance exceeding across widespread brain areas; 3) peripheral NIRS LFOs explain distinct BOLD fMRI variance, which does not result from aliasing of undersampled physiological signals. This distinct information can be obtained using NIRS LFOs measured directly in the periphery, which can be used to significantly reduce the variance in BOLD fMRI data related to non-neuronal signals.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health R21 DA027877(BF), R21 DA032746(BF) and K25 DA031769 (YT).
References
- 1.Ogawa S, Lee TM, Nayak AS, Glynn P. Oxygenation-sensitive contrast in magnetic resonance image of rodent brain at high magnetic fields. Magn Reson Med. 1990;14(1):68–78. doi: 10.1002/mrm.1910140108. [DOI] [PubMed] [Google Scholar]
- 2.Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magnetic Resonance in Medicine. 1998;39(6):855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- 3.Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med. 2000;44(1):162–7. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 4.Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory- variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage. 2006;31(4):1536–48. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- 5.Chang C, Cunningham JP, Glover GH. Influence of heart rate on the BOLD signal: the cardiac response function. Neuroimage. 2009;44(3):857–69. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tong Y, Hocke LM, Frederick B. Isolating the sources of widespread physiological fluctuations in functional near-infrared spectroscopy signals. J Biomed Opt. 2011;16(10):106005. doi: 10.1117/1.3638128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Julien C. The enigma of Mayer waves: facts and models. Cardiovascular research. 2006;70(1):12. doi: 10.1016/j.cardiores.2005.11.008. [DOI] [PubMed] [Google Scholar]
- 8.Aalkjaer C, Boedtkjer D, Matchkov V. Vasomotion - what is currently thought? Acta Physiol (Oxf) 2011;202(3):253–69. doi: 10.1111/j.1748-1716.2011.02320.x. [DOI] [PubMed] [Google Scholar]
- 9.Buzsaki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304(5679):1926–9. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- 10.Triantafyllou C, Hoge RD, Krueger G, Wiggins CJ, Potthast A, Wiggins GC, Wald LL. Comparison of physiological noise at 1.5 T, 3 T and 7 T and optimization of fMRI acquisition parameters. Neuroimage. 2005;26(1):243–50. doi: 10.1016/j.neuroimage.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 11.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One. 2010;5(12):e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63(5):1144–53. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tong Y, Hocke LM, Licata SC, Frederick B. Low-frequency oscillations measured in the periphery with near-infrared spectroscopy are strongly correlated with blood oxygen level-dependent functional magnetic resonance imaging signals. J Biomed Opt. 2012;17(10):106004. doi: 10.1117/1.JBO.17.10.106004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Birn RM, Smith MA, Jones TB, Bandettini PA. The respiration response function: the temporal dynamics of fMRI signal fluctuations related to changes in respiration. Neuroimage. 2008;40(2):644–54. doi: 10.1016/j.neuroimage.2007.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. others. [DOI] [PubMed] [Google Scholar]
- 16.Verstynen TD, Deshpande V. Using pulse oximetry to account for high and low frequency physiological artifacts in the BOLD signal. Neuroimage. 2011;55(4):1633–44. doi: 10.1016/j.neuroimage.2010.11.090. [DOI] [PubMed] [Google Scholar]
- 17.Delpy DT, Cope M, van der Zee P, Arridge S, Wray S, Wyatt J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys Med Biol. 1988;33(12):1433–42. doi: 10.1088/0031-9155/33/12/008. [DOI] [PubMed] [Google Scholar]
- 18.Duncan A, Meek JH, Clemence M, Elwell CE, Tyszczuk L, Cope M, Delpy DT. Optical pathlength measurements on adult head, calf and forearm and the head of the newborn infant using phase resolved optical spectroscopy. Phys Med Biol. 1995;40(2):295–304. doi: 10.1088/0031-9155/40/2/007. [DOI] [PubMed] [Google Scholar]
- 19.Sutton GC, Karnell J, Nylin G. Studies on the rapidity of complete blood circulation in man. Am Heart J. 1950;39(5):741–8. doi: 10.1016/0002-8703(50)90134-7. [DOI] [PubMed] [Google Scholar]
- 20.Fisher RA. Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika. 1915:507–521. [Google Scholar]
- 21.Frederick B, Nickerson LD, Tong Y. Physiological denoising of BOLD fMRI data using Regressor Interpolation at Progressive Time Delays (RIPTiDe) processing of concurrent fMRI and near-infrared spectroscopy (NIRS). Neuroimage. 2012;60(3):1913–23. doi: 10.1016/j.neuroimage.2012.01.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zou KH, Warfield SK, Bharatha A, Tempany CM, Kaus MR, Haker SJ, Wells WM, 3rd, Jolesz FA, Kikinis R. Statistical validation of image segmentation quality based on a spatial overlap index. Acad Radiol. 2004;11(2):178–89. doi: 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hoshi Y, Kobayashi N, Tamura M. Interpretation of near-infrared spectroscopy signals: a study with a newly developed perfused rat brain model. J Appl Physiol. 2001;90(5):1657–62. doi: 10.1152/jappl.2001.90.5.1657. [DOI] [PubMed] [Google Scholar]
- 24.Huppert TJ, Diamond SG, Franceschini MA, Boas DA. Hom ER: a review of time-series analysis methods for near-infrared spectroscopy of the brain. Applied Optics. 2009;48(10):D280–D298. doi: 10.1364/ao.48.00d280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tong Y, Frederick BD. Time lag dependent multimodal processing of concurrent fMRI and near-infrared spectroscopy (NIRS) data suggests a global circulatory origin for low-frequency oscillation signals in human brain. Neuroimage. 2010;53(2):553–64. doi: 10.1016/j.neuroimage.2010.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tong Y, Hocke LM, Nickerson LD, Licata SC, Lindsey KP, Frederick BD. Evaluating the effects of systemic low frequency oscillations measured in the periphery on the independent component analysis results of resting state networks. Neuroimage. 2013;76C:202–215. doi: 10.1016/j.neuroimage.2013.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Birn RM, Murphy K, Bandettini PA. The effect of respiration variations on independent component analysis results of resting state functional connectivity. Hum Brain Mapp. 2008;29(7):740–50. doi: 10.1002/hbm.20577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chang C, Glover GH. Effects of model-based physiological noise correction on default mode network anti-correlations and correlations. Neuroimage. 2009;47(4):1448–59. doi: 10.1016/j.neuroimage.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. Neuroimage. 2007;38(2):306–20. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tsuji M, Saul JP, du Plessis A, Eichenwald E, Sobh J, Crocker R, Volpe JJ. Cerebral intravascular oxygenation correlates with mean arterial pressure in critically ill premature infants. Pediatrics. 2000;106(4):625–32. doi: 10.1542/peds.106.4.625. [DOI] [PubMed] [Google Scholar]
- 31.Mayer S. Mathematisch naturwissenschaftliche Classe. Vol. 74. Sitzungsberichte Akademie der Wissenschaften in Wien; Anatomie: 1876. Studien zur Physiologie des Herzens und der Blutgefässe 6. Abhandlung: Über spontane Blutdruckschwankungen. pp. 281–307. [Google Scholar]
- 32.Obrig H, Neufang M, Wenzel R, Kohl M, Steinbrink J, Einhaupl K, Villringer A. Spontaneous low frequency oscillations of cerebral hemodynamics and metabolism in human adults. Neuroimage. 2000;12(6):623–39. doi: 10.1006/nimg.2000.0657. [DOI] [PubMed] [Google Scholar]
- 33.van Beek AH, Claassen JA, Rikkert MG, Jansen RW. Cerebral autoregulation: an overview of current concepts and methodology with special focus on the elderly. J Cereb Blood Flow Metab. 2008;28(6):1071–85. doi: 10.1038/jcbfm.2008.13. [DOI] [PubMed] [Google Scholar]
- 34.Sassaroli A, Pierro ML, Bergethon PR, Fantini S. Low-Frequency Spontaneous Oscillations of Cerebral Hemodynamics Investigated With Near-Infrared Spectroscopy: A Review. IEEE Journal of Selected Topics in Quantum Electronics. 2012;18(4):1478–1492. [Google Scholar]
- 35.Muller MW, Osterreich M. A comparison of dynamic cerebral autoregulation across changes in cerebral blood flow velocity for 200 s. Front Physiol. 2014;5:327. doi: 10.3389/fphys.2014.00327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang R, Zuckerman JH, Giller CA, Levine BD. Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol. 1998;274(1 Pt 2):H233–41. doi: 10.1152/ajpheart.1998.274.1.h233. [DOI] [PubMed] [Google Scholar]
- 37.Du C, Volkow ND, Koretsky AP, Pan Y. Low-frequency calcium oscillations accompany deoxyhemoglobin oscillations in rat somatosensory cortex. Proc Natl Acad Sci U S A. 2014;111(43):E4677–86. doi: 10.1073/pnas.1410800111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tong Y, Hocke LM, Fan X, Janes AC, Frederick B. Can apparent resting state connectivity arise from systemic fluctuations? Front Hum Neurosci. 2015;9:285. doi: 10.3389/fnhum.2015.00285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Davey CE, Grayden DB, Egan GF, Johnston LA. Filtering induces correlation in fMRI resting state data. Neuroimage. 2013;64:728–40. doi: 10.1016/j.neuroimage.2012.08.022. [DOI] [PubMed] [Google Scholar]
- 40.Tukey JW. Some thoughts on clinical trials, especially problems of multiplicity. Science. 1977;198(4318):679–84. doi: 10.1126/science.333584. [DOI] [PubMed] [Google Scholar]
- 41.Olden JD, Neff BD. Cross-correlation bias in lag analysis of aquatic time series. Marine Biology. 2001;138(5):1063–1070. [Google Scholar]
- 42.Hochberg Y, Benjamini Y. More powerful procedures for multiple significance testing. Stat Med. 1990;9(7):811–8. doi: 10.1002/sim.4780090710. [DOI] [PubMed] [Google Scholar]
- 43.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995:289–300. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.