Segmentation of Lumen and Outer wall of Abdominal Aortic Aneurysms from 3D Black-Blood MRI with a Registration Based Geodesic Active Contour Model

Abstract

Segmentation of the geometric morphology of abdominal aortic aneurysm is important for interventional planning. However, the segmentation of both the lumen and the outer wall of aneurysm in magnetic resonance (MR) image remains challenging. This study proposes a registration based segmentation methodology for efficiently segmenting MR images of abdominal aortic aneurysms. The proposed methodology first registers the contrast enhanced MR angiography (CE-MRA) and black-blood MR images, and then uses the Hough transform and geometric active contours to extract the vessel lumen by delineating the inner vessel wall directly from the CE-MRA. The proposed registration based geometric active contour is applied to black-blood MR images to generate the outer wall contour. The inner and outer vessel wall are then fused presenting the complete vessel lumen and wall segmentation. The results obtained from 19 cases showed that the proposed registration based geometric active contour model was efficient and comparable to manual segmentation and provided a high segmentation accuracy with an average Dice value reaching 89.79%.

1. Introduction

Abdominal Aortic Aneurysm (AAA) is the direct cause of more than 15,000 deaths each year in the United States and is the cause of 1.3% of all deaths among men aged 65–85 years in developed countries (Sakalihasan et al., 2005; Upchurch and Schaub, 2006). Most AAAs are not detected because AAA disease is usually asymptomatic; patients generally exhibit no major symptoms until the aneurysm ruptures (Cornuz et al., 2004). As the abdominal aorta is the largest blood vessel in the body, rupture can lead to massive internal bleeding and mortality rates approach 90% if rupture occurs outside of the hospital setting (Mozaffarian et al., 2016).

Surgical planning, such as surgical resection or percutaneous stent-graft deployment, is highly dependent on the geometric characteristics of the aneurysm (Whitaker, 2001; Czermak et al., 2001; Malaspinas et al., 2016). Segmentation of AAA for evaluating its geometric characteristics therefore plays an important role in medical treatment. It enables the reconstruction of three-dimensional (3D) patient-specific geometries, which can help provide measurements at various stages of treatment. In particular, these geometries can facilitate the assessment of rupture risk, which is normally based on aneurysm size and shape. Additionally, the change in aneurysm volume can be used as an indicator of rupture risk in preoperative or postoperative follow-up studies (Wever et al., 2000; Pollock et al., 2002).

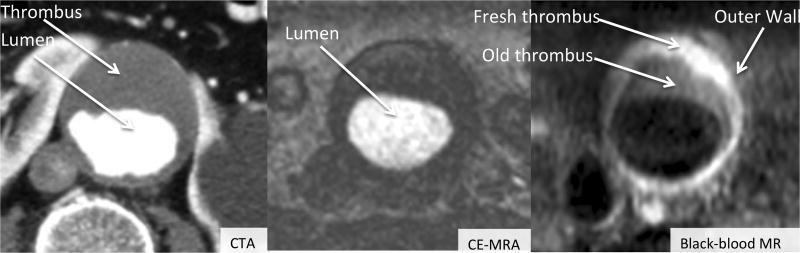
Two-dimensional ultrasound, Computed Tomography Angiography (CTA) and Magnetic Resonance Imaging (MRI) are widely used in the diagnosis, treatment evaluation, and monitoring of AAAs (US Preventive Services Task Force, 2005). However, 2D ultrasound is limited by inter-operator variability and is limited in capturing 3D anatomy; CTA requires radiation and iodinated contrast, and therefore is not a suitable imaging modality for longitudinal monitoring; traditional MRI has limited coverage, coarse through-plane resolution and degraded image quality due to flow artifacts (Nguyen et al., 2014; Richards et al., 2011; Liu et al., 2017). In distinction to that, 3D black-blood MRI is promising for the assessment of the AAA wall as it is non-invasive, provides high isotropic resolution, and allows volumetric measurements of the lumen and outer wall (see Fig. 1), which have been shown to be more predictive of clinical outcomes (Mihai et al., 2010; Zhu et al., 2014). Therefore, segmentation of the lumen and outer wall from 3D black-blood MR images is an important step in generating volumetric measurements of AAA. However, a slice-wise manual delineation and segmentation of the aneurysm lumen and outer wall from high resolution MR black-blood image is extremely time-consuming, tedious, and, as it can take a skilled radiologist more than 30 minutes (Dehmeshki et al., 2009), is prone to fatigue errors. Accordingly, development of an efficient computer-aided method for AAA lumen and outer wall segmentation is important for clinical evaluation and treatment.

Figure 1.

Typical diseased aortas taken from three types of images: CTA, CE-MRA and black-blood MR, respectively. From CE-MRA, the shape, the size and the grayscale of the lumen are easy to detect. The lumen and the thrombus can be segmented from the CTA image. Lumen, fresh thrombus, old thrombus and the outer wall can be differentiated in black-blood MR images.

1.1. Previous studies

Algorithms for segmenting aneurysms can be broadly divided into two categories: methods that segment only the lumen boundary (Loncaric et al., 2000), and techniques that segment both the lumen and the outer wall (including the thrombus) (de Bruijne et al., 2004; Wang et al., 2011, 2016). The focus of this work is on methods for multilevel segmentation of AAAs. (de Bruijne et al., 2002) used an active shape model for segmenting lumen and thrombus in AAAs from CTA data. (Olabarriaga et al., 2005) proposed using a gray-level modeling approach with a non-parametric pattern classification technique to segment thrombus. That system estimates a rough initial surface, and then refines it using a level set segmentation scheme and was reported in (Zhuge et al., 2006). A method based on intensity histograms and neural networks involving segmentation of contrast enhanced CTA was proposed in (Shum et al., 2010). In the recent work of (Chen et al., 2014), the Lattice Boltzmann Geodesic Active Contour Method (LBGM) was used on the anisotropic diffusion of the filtered CTA image to detect the lumen and thrombus.

All the methods mentioned above have been applied to CTA data for aneurysm segmentation. Aneurysm segmentation from MRI is much more difficult than from CTA, because the MR wall boundary is not as distinct as it is on CTA. Only one recent study (Ukwatta et al., 2015) has been reported using black-blood MR data. That study proposed a semi-automated algorithm to jointly segment the lumen and outer wall from 3D femoral artery black-blood MRI. To the best of our knowledge, the work from our group (Zhu et al., 2016) was the first study evaluating 3D black-blood MRI techniques in patients with AAA disease. This report is the first to investigate segmentation of the AAA lumen and outer wall using 3D black-blood MR images.

1.2. Contributions

The present paper is focused on the segmentation of both the lumen and outer wall of AAAs. We propose a multilevel segmentation methodology based on the combined use of the mutual information and the geometric active contour (GAC) to segment the lumen and outer wall. In this approach, the mutual information based registration equation is adapted to image segmentation problems by integrating an extra term in the GAC model. More precisely, we first segment the lumen of AAAs using GAC from the CE-MRA; once the lumen is segmented, we then perform the segmentation of the outer wall with the aid of the registration based GAC method. In this study, segmentation accuracy was assessed using manual segmentation as the reference standard. Furthermore, two previously published segmentation methods were compared with our proposed registration based geometric active contour (RGAC) method on the same data sets.

2. Segmentation methodology

2.1. Overview of the segmentation scheme

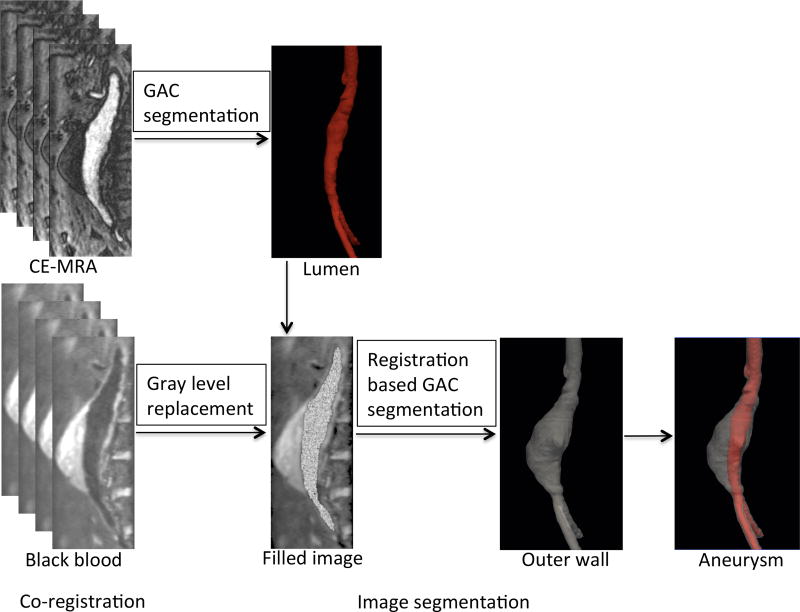
The methodology proposed herein consists in first co-registering CE-MRA and black-blood MR images using a Siemens LEONARDO workstation (Syngo software, Siemens Healthineers, USA) and then segmenting the aneurysm (both lumen and outer wall as indicated in Fig. 1) using the GAC and RGAC methods, respectively.

The proposed multilevel segmentation methodology first uses the Hough transform (Hough and Paul, 1962) and GAC to segment the lumen directly from the CE-MRA images. The gray level values of the lumen region are then replaced with the mean value outside it. This operation gives gray level values similar to the total aneurysm, which makes it easier to segment the aneurysm as one object. The outer wall is a diffuse object with low contrast relative to neighboring tissues, and it is therefore difficult to delineate the outer wall. The proposed RGAC method is then used to segment the outer wall of AAAs. After manual delineation of the outer wall in the first slice, the method automatically detects the contour in subsequent slices, using the result from the previous slice as a reference. If an obtained contour is not sufficiently accurate, the user can intervene and provide an additional manual reference contour. The segmentation scheme is shown in Fig. 2.

Figure 2.

Lumen and Outer wall segmentation scheme. The scheme consists of two parts: co-registration and image segmentation.

2.2. Co-registration

Black-blood MRI of the aneurysm vessel wall and CE-MRA of the lumen were acquired in succession to minimize the effect of patient motion between scan acquisitions. In order to correct for any motion that may have occurred, a semiautomatic registration was performed using the Siemens LEONARDO workstation with Syngo software (Siemens Healthineers, USA). First, both black-blood MRI and CE-MRA image sequences were imported and overlaid in InSpace, an interface for manual and automatic registration. Window and level were adjusted for each sequence to appropriately visualize the lumen and vessel wall. Next, an automatic registration and a manual refinement were performed using a series of incremental translations and rotations to ensure that the lumen, as measured by the CE-MRA, was completely confined to the area within the vessel wall, as depicted by the black-blood MRI. In this step, the 3D/3D registration we used between black-blood MRI and CE-MRA is only a rigid registration. For this registration, the selected features are anatomical landmarks such as the renal arteries, celiac and SMA arteries. Finally, after the two 3D image volumes were satisfactorily aligned from the level of the renal arteries to the iliac bifurcation, axial reformats were generated for each image sequence using 1.3mm image spacing (this amounts to 85–100 slices, depending on the coverage needed between the anatomical landmarks). These co-registered, axial reformats were used as the input for the subsequent image segmentation.

2.3. Image pre-processing and segmentation

Pre-processing such as denoising, and contrast enhancement may greatly improve the segmentation results. Since the Signal-to-Noise Ratio (SNR) from black-blood MR images of AAA is high (Zhu et al., 2016), in the present study we only use the image processing function to enhance the contrast level. The global contrast enhanced filter applied the same level of enhancement for all CE-MRA images for both lumen segmentation and on the filled images (shown in Fig. 2) for outer wall segmentation.

The first step for image segmentation is to locate the center point of the vessel of interest. We use the Hough transform to find lumen locations with near circular contours in the middle slice of the image. Once that location is found, it is used as the initial contour in the GAC segmentation method to obtain the entire luminal region.

2.3.1. GAC segmentation

In a recent study (Chen et al., 2014), the authors segmented the lumen and thrombus using a GAC related method. After comparing different methods, they suggested that the GAC related method has higher accuracy for aneurysm segmentation. In (Caselles et al., 1997), the authors defined the GAC model as energy-minimizing splines guided by external constraint forces that pull them toward features such as edges. They also defined an internal energy term that is used to impose a smoothness constraint on the moving curve. The GAC is based on designing a speed term such that the evolving front gradually attains zero speed as it gets closer to the object boundaries and eventually comes to a stop. The speed term may depend on the boundary of the front while it can also make use of the information inside the region enclosed by the evolving front. We briefly describe the GAC model. Let C(q) : [0, 1] → R² be a parameterized planar curve and let I : [0, a] × [0, b] → R⁺ be a given image in which we want to detect the object boundaries. In the GAC formalism, the evolving curve C is represented as the zero level set of a Lipschitz-continuous function ϕ (subsequently used in eq.(4) and eq.(9)) that satisfies

$$\{\begin{array}{cc}\varphi (x,y)>0,\hfill & (x,y)\in I_{\mathit{\text{in}}}\hfill \\ \varphi (x,y)<0,\hfill & (x,y)\in I_{\mathit{\text{out}}}\hfill \\ \varphi (x,y)=0,\hfill & (x,y)\in C\hfill \end{array}$$ (1)

where I_in and I_out are regions inside and outside the closed contour C. The classical GAC approach associates the curve C with an energy given by

$$E(C)=\alpha {\int }_0^1{|C\prime (q)|}^2\mathit{\text{dq}}-\lambda {\int }_0^1|\nabla I(C(q))|\mathit{\text{dq}},$$ (2)

where α and λ are real positive constants. The first term controls the smoothness of the contours to be detected (internal energy), while the second term is responsible for attracting the contour towards the object in the image (external energy). By minimizing the functional eq.(2), we try to locate the curve at the points of maxima |∇I|, while keeping certain smoothness in the curve. Eq. (2) can be extended by generalizing the edge detector part in the following way: Let g : [0,+∞] → R⁺ be a strictly decreasing function such that g(r) → 0 as r → ∞. Hence, −|∇I| can be replaced by g|∇I|², obtaining a general energy functional given by

$$E(C)=\alpha {\int }_0^1{|C\prime (q)|}^2\mathit{\text{dq}}+\lambda {\int }_0^{1}g{(|\nabla I(C(q))|)}^2\mathit{\text{dq}}={\int }_0^1(E_{\mathit{\text{int}}}(C(q))+E_{\mathit{\text{ext}}}(C(q)))\mathit{\text{dq}}.$$ (3)

This energy functional can be minimized by solving the following gradient flow (Li et al., 2010)

$$\frac{\partial \varphi }{\partial t}=\mu [\mathrm{\Delta }\varphi -\mathit{\text{div}}(\frac{\nabla \varphi }{|\nabla \varphi |})]+\lambda \delta (\varphi )\mathit{\text{div}}(g\frac{\nabla \varphi }{|\nabla \varphi |})+\nu g\delta (\varphi ),$$ (4)

where μ, λ and ν are coefficient for each term. Δ is the Laplacian operator and g is the edge indicator function defined by

$$g=\frac{1}{1+{|\nabla G_{\sigma }\ast I|}^2},$$ (5)

where G_σ is the Gaussian kernel with standard deviation σ. In eq.(4), the first term is a penalty term used to penalize the deviation of ϕ from a signed distance function during its evolution, and the other two terms represent the gradient flow of the energy function.

2.3.2. Gray level replacement

According to the GAC segmentation method, the lumen region marked as L is segmented. In order to segment the entire AAA (outer wall segmentation) as one object, the gray level of the vessel wall is assigned to region L. We first add a one-pixel-thick layer to L to create a new region D (note that for simplicity, only a one-pixel-thick layer is needed). Following that, the gray level values of region L are replaced by the mean value of region B, where B = D\L. For each pixel, the new gray level of the lumen can be defined as follows

$$l_{\mathit{\text{new}}}=\frac{\sum b_i}{n}+\epsilon R,i\in [1,n]$$ (6)

where l_new represents the mean gray level for each pixel from region L, b_i represents the gray level for each pixel from region B, ε is an infinitesimally small number and R is random noise.

2.3.3. RGAC segmentation

It is difficult to generate an outer wall delineation because of the low contrast with respect to neighboring tissues. In the present study, we propose a new RGAC model to estimate the outer wall with the energy formulation of RGAC that can be expressed by adding a registration-based term and a prior shape term to the GAC formulation

$$E=c{E}_{\mathit{\text{GAC}}}+r{E}_{\mathit{\text{registration}}}+s{E}_{\mathit{\text{similarity}}},$$ (7)

where r, c and s are the weights, which correspond to the positive parameters that balance the influence of these three terms. E_GAC controls the contour of the segmentation moving towards a local minimum of energy (see eq.(4)), E_registration controls the registration between the previous reference slice and subsequent slice on the filled image (shown in Fig. 2) (Thirion, 1998; Wang et al., 2005)

$$E_{\mathit{\text{registration}}}=\int \int {(M(x+m,y+n)-S(x,y))}^2\mathit{\text{dxdy}},$$ (8)

with M the moving image (the subsequent slice), S the static image (the previous reference slice), transformation field describing the translation in m and n of every pixel from its original position x and y. E_similarity represents the shape term. The shape term we incorporate in the energy functional measures the non-overlapping areas between the prior shape and the evolving shape. ϕ_e and ϕ denote the distance function of the prior shape and the evolving level set shape representation. This energy function can be expressed as (Riklin-Raviv et al., 2007)

$$E_{\mathit{\text{similarity}}}=\int \int {(\varphi (x,y)-{\varphi }_e(x,y))}^{2}H(\varphi )\mathit{\text{dxdy}},$$ (9)

where H is the Heaviside function.

3. Experiments and results

The experiments were performed on an OS X system with an Intel Core i7 CPU and 8 GB RAM. The data were processed using in-house developed MATLAB^® software. Manual segmentation, including drawing contours (Region of Interest- ROI) of the lumen and outer wall in axial slices, was performed using MeVisLab software by a trained radiologist with 6 years of experience.

3.1. Patient MR imaging data

A total of 19 datasets, comprised of 3D CE-MRA and 3D black-blood MR images, were acquired from 10 patients with AAA (9 patients had 6 month follow up studies). All the patient studies were conducted following IRB approval of the University of California San Francisco (reference number: 10-03248). All patients underwent 3D CE-MRA and 3D T1 weighted black-blood MR on a 3T Siemens Skyra scanner (Siemens Healthcare, Germany) (Zhu et al., 2016). The acquisition parameters for 3D CE-MRA were:TR/TE=3.09ms/1.11ms, band width=500Hz/pixel, 88 coronal slices, 38×38cm² field of view, 1.2mm slice thickness and 320×320 image matrix, scan time 30 seconds; the scan parameters for black-blood imaging were: TR/TE=800~1040/20ms, band width=781Hz/pixel, echo train length (ETL)=60, echo spacing=3.58ms, duration of echo train=215ms, 44~60 coronal slices, 32×32cm² field of view, 1.3mm slice thickness and 256×256 image matrix, scan time 7.1~9 minutes.

3.2. Parameter settings for segmentation

According to (Li et al., 2010), we set μ = 0.2, λ = 5, ν = −3.0 and the time step as 1 in eq.(4). The other parameters in eq.(4), such as δ, div and Δ, were chosen as Dirac function, divergence operator and Laplacian operator. The parameters in eq.(6) and eq.(7) should be chosen carefully, since they can influence the accuracy of the final results. The parameter settings used in this study were chosen empirically by processing images with three types of aneurysms (occlusive thrombus, initial thrombus and no thrombus) from 6 aneurysm cases (3 intracranial, 3 AAA, 60 slices in total). By testing on different slices, it was found that the given set of parameters in Table 1 can be used for images over a broad range of image characteristics. For eq.(6), random noise was added and ε was set to 15% of the mean value of region B. For eq.(7), r, c and s are the weights that balance the influence of the registration-based term, gradient-based term, and shape-based term, respectively. The parameters should be determined based on specific aims. For this study, the segmentation of ellipse-like objects (i.e. 2D AAA and intracranial aneurysm (IA) images), r and c need to be larger than s. Reasonable ranges for r and c are ≥ 0.5 while s and ε should be < 0.3. The settings of all the parameters are summarized in Table 1.

Table 1.

List of segmentation parameters

μ = 0.2, λ = 5, ν = −3.0, timestep = 1, $g=\frac{1}{1+{|\nabla G_{\sigma }\ast I|}^2}$

$\epsilon =0.15\frac{\sum b_i}{n}$, r = 1, c = 0.5, s = 0

The first S is from manual segmentation.

In addition to the manual segmentation and the proposed RGAC segmentation algorithm, we also applied two other previously developed segmentation algorithms for comparison. Based on a recent study (Chen et al., 2014), anisotropic diffusion preprocessing together with the LBGM was proposed for estimation of the aneurysm edges, which is the main challenge in aneurysm delineation. They first compared the LBGM method with GAC and Distance Regularized Level Set Evolution (DRLSE), and showed both DRLSE and LBGM can generate similar segmentation results and regulate the level set functions effectively. They then compared the LBGM method with the narrow-band level set method and the Chan-Vese model on aneurysm cases, and demonstrated the LBGM method provides the best segmentation result. Since the previous comparison were performed on different types of method (region-based segmentation, gradient-based segmentation and local-based segmentation), we chose the best two methods including DRLSE and LBGM used for segmentation of lumen and thrombus. Some of the crucial algorithm parameters are listed as follows:

• DRLSE: The coefficients of the distance regularization, weighted length, and area terms are 0.2, 5, and −3, respectively.

• LBGM: The D2Q5 model is used in the lattice Boltzmann method (LBM) simulation. The segmentation scheme we used to compare with the proposed methodology is the same one proposed in the study (Chen et al., 2014). The anisotropic diffusion is first implemented for image denoising and the Canny operator is used to detect the edge map of the denoised image. After this preprocessing, the LBGM is implemented to segment the lumen and thrombus.

3.3. Evaluation criteria

The results are evaluated by comparing the proposed segmentation with the reference standard using the “Dice coefficient” defined as the fraction of the intersection of R_A and R_M to their sum (Dice, 1945)

$$\mathit{\text{Dice}}\%=\frac{2|R_A\cap R_M|}{|R_A|+|R_M|}\times 100\%,$$ (10)

where R_A is the proposed segmentation result and R_M is the reference standard from manual segmentation. | | denotes the number of pixels in the corresponding volume. The greater the Dice coefficient is, the better the match of segmentation results between two methods (1 indicates perfect overlap, and 0 means no overlap). Moreover, the coefficient of variation (CV) was also calculated, which is a statistical measure of the precision of segmentation.

$$\mathit{\text{CV}}=\frac{d}{a}\times 100\%,$$ (11)

where d represents the standard deviation and a is the average Dice value. Also, the volume difference ϒ was defined as follows

$$\mathrm{\Upsilon }=\frac{|V_A-V_M|}{\frac{1}{2}(V_A+V_M)}\times 100\%,$$ (12)

where V_A is the volume of the proposed segmentation result and V_M is the volume of the reference standard.

3.4. Repeatability and reproducibility

Manual registration and an initial manual contour are used in this proposed method, which may potentially influence the final results. However, we note that manual registration and the initial manual contour do not affect the lumen segmentation, which is delineated prior to this step. The coefficients of repeatability and reproducibility were computed from the standard deviations of the differences between the results made with different manual registrations and initial manual contours.

Following automatic registration using Syngo software, two investigators manually refined the registration results twice. The proposed methodology was performed on these four co-registered CE-MRA and black-blood MR images. The Dice value of outer wall segmentation for these four cases is 93.24% in our experiments, which indicates negligible influence caused by manual processing.

In order to test the influence of dependence of outer wall segmentation on the selection of the initial manual contour, we performed an experiment that consisted of generating four different initial manual contours. This was performed on one randomly selected slice from our database. An initial manual contour was drawn by our primary radiology reader (Contour 1), and independently by a second radiologist (contour 2). In addition, we processed Contour 1 by eroding it by one pixel (to form Contour 3) and dilating it by one pixel (to form Contour 4). We then performed a quantitative comparison of the generated areas of the adjacent slices that resulted from these four different initial manual contours (Table 2). The average Dice value and CV value for these different contours are 92.46±1.11%. This indicates that the proposed method has good repeatability and reproducibility.

Table 2.

Quantitative comparisons (Dice and CV) for each slice with different manual initial contour.

Dice value	Contour 1	Contour 2	Coutour 3	Coutour4
Slice No. 63	93.19	92.92	92.46	93.26
64	93.93	94.18	93.79	94.70
65	92.15	92.59	92.13	93.20
66	91.58	92.02	90.99	93.06
67	92.73	92.81	91.94	93.36
68	100	95.11	88.94	92.25
69	90.45	89.74	91.90	89.77
70	92.78	92.56	91.07	92.97
71	92.71	92.20	91.77	92.90
72	91.55	91.33	90.67	92.26
73	92.47	92.25	91.11	93.00
Dice±CV	93.04±7.83	92.51±4.38	91.52±3.82	92.79±3.76

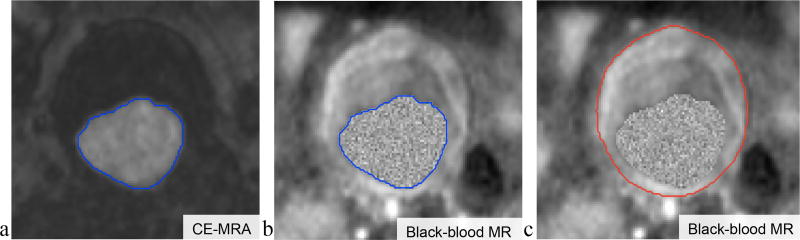
Fig. 3 (a–c) illustrates the intermediate results of the proposed segmentation method. As can be observed, after the GAC segmentation (with an initial contour obtained from the Hough transform), the lumen contour is obtained from CE-MRA images (Fig. 3a). With CE-MRA and black-blood images co-registered using the Siemens LEONARDO workstation, the segmented lumen contour from the CE-MRA can be superimposed on the black-blood MR image as shown in Fig. 3b. The lumen region in the black-blood MR image was filled with a gray level replacement (Fig. 3b), which makes the lumen and outer wall a single entity. The outer wall contour can then be generated using the proposed RGAC segmentation in Fig. 3c.

Figure 3.

a. AAA lumen segmentation contour obtained using the GAC method on CE-MRA images; b. lumen region shown in black-blood MR image after CE-MRA and black-blood image co-registration; c. the outer wall contour obtained using the RGAC segmentation method on black-blood MR image.

We performed experiments to test the impact of selecting different initial contours for the proposed RGAC segmentation, including manually drawing the initial contour or automatically obtaining the initial contour using the Hough transform. Two different slices, one with a nearly circular contour and the other non-circular, were selected as initial slices for the Hough transform. The corresponding RGAC segmentations using these initial contours were compared with the manual segmentation, and their Dice values were 92.27%, 90.37% and 84.16% respectively. This demonstrates that the segmentation that uses the automatic initial contour based on the Hough transform might be heavily dependent on the vessel shape (Dice value of 84.16% vs 90.37%). In this study, we therefore chose to use the manual contour as the initial contour in the proposed RGAC segmentation to assure high accuracy and less dependence on the vessel geometry.

Currently manual segmentation has been used as the gold standard (and is used as the reference standard in this study). The adequacy of using manual measurements of AAAs for determining truth has been shown in (Weiss et al., 2001) and (Li et al., 2004). In this study, two radiologists have reached consensus on the definition of contours by drawing manual contours for 25 slices selected from 5 AAA cases, and briefly reviewing all 19 cases. Subsequently, one radiologist drew manual contours for each slice of all AAA cases. There were nearly one hundred slices for each AAA case, and nearly two thousand slices for all cases. We have implemented a MevisLab (http://www.mevislab.de/) based tool to help the radiologists draw the manual contours. The radiologist drew the manual contours two times for all 19 cases. The intra-observer variability was 5.07 ± 3.74% and 5.98 ± 4.11% for lumen and outer wall respectively.

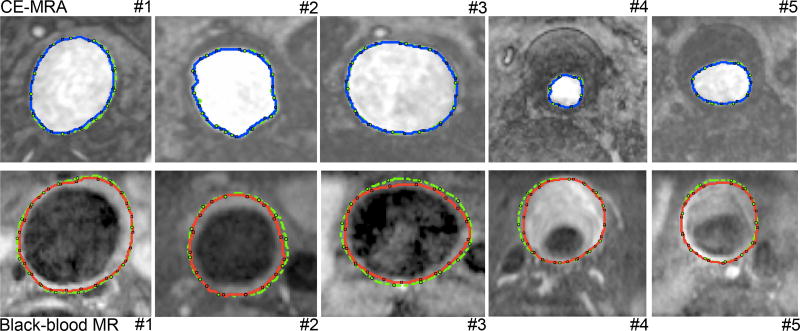
We then applied the above-illustrated RGAC segmentation algorithm to 19 AAA cases (nearly two thousand slices). Both AAA lumen and outer wall were successfully segmented using the proposed RGAC method with results similar to those with the manual delineation, as demonstrated in Fig. 4, which shows segmentations obtained with the manual and the proposed methods from 5 representative patients. For quantitative comparison, the average Dice and CV values reached 89.79% and 2.46% respectively, which demonstrated comparable and stable segmentation was achieved with the proposed method compared to the manual segmentation on different cases. For extreme cases, the radiologist needed to take several neighboring slices into consideration in order to segment one slice. Segmentation of only the AAA outer wall on one slice took a radiologist up to as much as 1.5 minutes, while the algorithm proposed here can achieve a comparable contour within 35 seconds (on a 2.2 GHz Intel laptop with 8GB RAM).

Figure 4.

AAA lumen (top row) and outer wall (bottom row) segmentations. The blue and red contours correspond to the lumen and outer wall segmentations respectively using the proposed RGAC method; and green contours correspond to the manual segmentations.

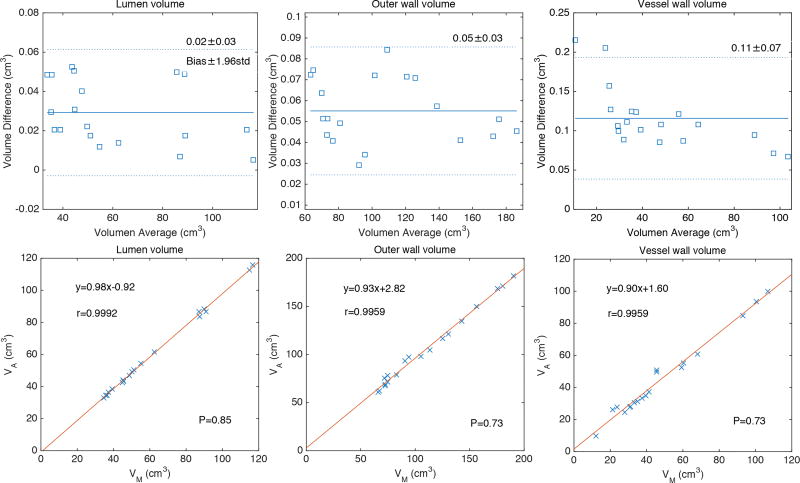
We defined the lumen volume and the outer wall volume as the volumes enclosed in the lumen and outer wall boundaries, respectively. The vessel wall volume refers to the volume enclosed between the lumen boundary and the outer wall boundary. The volume and volume difference between the proposed segmentation and manual segmentation were also compared in the present study. The Bland-Altman (Bland and Altman, 1999) and the linear regression plot of the volume measurements were used to evaluate the association and difference between the two segmentation results. The correlation coefficients, linear fitting slope and offsets, mean bias and confidence intervals (±1.96×std) were calculated and reported in Fig. 5. The P-value was used to determine statistical significance (Fig. 5).

Figure 5.

Bland-Altman and linear regression plots of the volume measurements of lumen, outer wall and vessel wall obtained with manual and proposed segmentation methods on the 19 AAA cases.

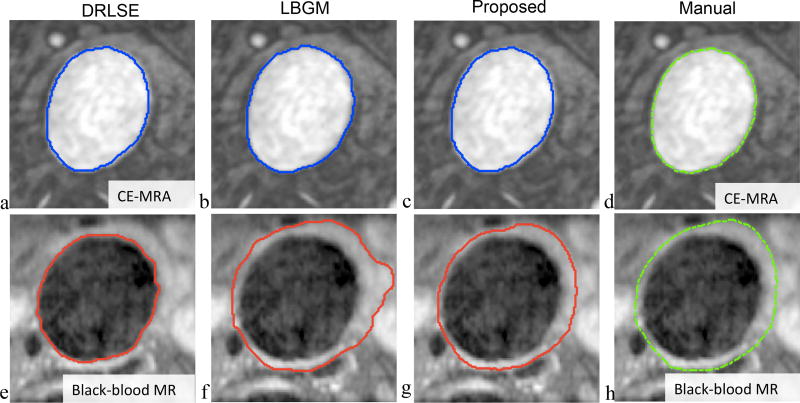
Fig. 6 shows the segmentations that were obtained with DRLSE, LBGM, proposed RGAC and manual segmentation methods from a representative case. Compared to manual segmentation, the proposed method achieved similar segmentation results on both the lumen and outer wall, while DRLSE did not locate the vessel wall and LBGM had obvious errors at the vessel wall edge where the signal ambiguity is high and difficult to segment. The quantitative evaluation for different segmentation methods is summarized in Table 3. Based on Dice and CV, all methods achieved similar performance on lumen segmentation, while the proposed RGAC method outperformed the other two methods on vessel wall segmentation (average Dice and CV values on vessel wall segmentation were 55.56±24.74%, 78.58±6.92% and 89.79±2.46% for DRLSE, LBGM and RGAC respectively).

Figure 6.

Lumen (top row) and outer wall (bottom row) segmentation results with different methods (columns). a&c: DRLSE, b&f: LBGM, c&g: the proposed method, and d&h: manual.

Table 3.

Quantitative comparisons (Dice and CV) between different segmentation methods and the manual method.

	Case No.	1	2	3	4	5	6	7
Lumen	DRLSE	95.61	94.80	96.74	94.73	97.46	94.57	94.29
	LBGM	95.37	95.14	96.29	94.19	96.85	94.43	93.28
	Proposed	95.61	94.80	96.74	94.73	97.46	94.57	94.29
Outer wall	DRLSE	50.27	68.69	65.61	72.12	48.04	50.19	66.63
	LBGM	83.63	80.14	81.51	85.17	72.85	67.34	85.09
	Proposed	92.53	89.27	88.39	91.74	92.27	89.54	88.24
	Case No.	8	9	10	11	12	13	14
Lumen	DRLSE	95.92	95.02	95.77	95.79	94.37	95.88	95.25
	LBGM	95.31	94.76	95.25	94.71	95.87	95.32	95.06
	Proposed	95.92	95.02	95.77	95.79	94.37	95.88	95.25
Outer wall	DRLSE	48.33	38.19	24.29	53.03	67.32	82.79	65.98
	LBGM	78.29	74.42	76.51	81.56	79.98	78.3	83.69
	Proposed	85.47	88.15	93.24	91.05	89.64	89.73	92.34
	Case No.	15	16	17	18	19	Average
Lumen	DRLSE	97.34	95.15	94.70	95.83	94.35	95.45±0.97
	LBGM	96.72	94.86	94.52	95.36	94.29	95.13±0.8
	Proposed	97.34	95.15	94.70	95.83	94.35	95.45±0.97
Outer wall	DRLSE	46.39	51.51	66.35	49.58	40.41	55.56±24.74
	LBGM	84.08	65.42	81.39	78.32	75.36	78.58±6.92
	Proposed	92.37	89.18	88.05	85.35	89.52	89.79±2.46

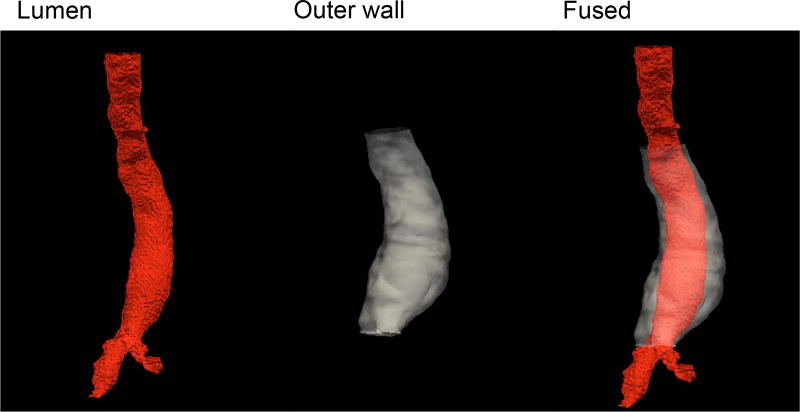
Fig. 7 shows the 3D volume rendering visualization of segmentation of the AAA lumen and outer wall, as well as the fused display based on the two segmentations.

Figure 7.

AAA 3D volume rendering achieved with the proposed RGAC segmentations on lumen (left), and outer wall (middle). Also shown is the fused display.

4. Discussion

It has been well demonstrated that the rupture risk, surgical planning and postoperative follow-up of an AAA depends strongly on its geometry (Mozaffarian et al., 2016). The segmentation of an AAA provides quantitative measurements of the geometrical characteristics, including the aneurysm diameter and volume, which are the critical parameters clinicians use for making decisions on whether to pursue clinical interventions or monitor aneurysm growth.

In this study, we proposed a multilevel segmentation method to assess the geometrical characteristics of AAAs including the lumen from CE-MRA and the outer wall from black-blood MR images. The low contrast between surrounding tissue and vessels that are close to the outer wall are the principal cause of difficulty in the segmentation of AAA. The proposed RGAC method was developed to address this problem: a registration term and a similarity term are added to the original GAC energy formulation. The GAC term is used to control the main segmentation contour based on the image gradient, while the registration and similarity terms are used to control the segmentation contour based on the correlation between the current and reference contours. The latter two terms were intentionally used to separate the outer wall from the surrounding vessels. Bland-Altman and linear regression plots of the volume measurements of lumen, outer wall and vessel wall demonstrated that volume measurements by the manual and by the proposed segmentation methods are significantly correlated. The volume differences between the manual and proposed segmentation methods are not significant.

We generated the lumen segmentation from CE-MRA instead of black-blood MR because the former is used clinically for estimating luminal diameters. To improve the outer wall segmentation, which is initialized using the lumen segmentation, we co-registered the CE-MRA and black-blood MR images using a Siemens LEONARDO workstation. The co-registration took no more than two minutes for each case.

The results obtained from 19 cases showed that the RGAC model was efficient and provided comparable segmentation to that obtained with the manual method, by providing a high segmentation accuracy with an average Dice value of 89.79 ±2.46%. Computation times for the DRLSE, LBGM and RGAC models are of the order of 20s, 35s, and 35s per slice, respectively. Although the DRLSE method has the shortest computation time, it is ineffective in segmenting the outer wall. The LBGM and RGAC models are similarly effective in AAA segmentation, but the latter provided better accuracy.

We are aware that our method has some limitations. First, the proposed RGAC algorithm requires manual delineation of the outer wall of an initial contour in the first slice. In this study, we have used a manual initial contour for AAA segmentation but, in the future, will further explore how to achieve an accurate automatic initial contour regardless of the vessel geometry. One approach would be to automatically generate this initial contour, as in the work of (Adame et al., 2006), where an ellipse was used to match the outer wall and the contour was then refined by means of dynamic programming. Since accuracy is important for providing clinical guidance, and manual contouring of the initial slice has been demonstrated to be reproducible, we employed manual initial contouring in the present study. Second, the proposed RGAC algorithm detects the outer wall contour in subsequent slices, relying on the result from the previous reference slice. An accumulating error could occur and affect the accuracy. In future, to reduce this error, we plan to investigate the use of multiple location initial reference contours or the development of an adaptive iterative algorithm to find more accurate contours for local reference slices.

We also plan to evaluate our developed method on a larger patient data base to reach a better understanding of the generalizability of the approach and to explore its potential for providing improved accuracy of measurements for better treatments in other anatomic regions, such as IAs. This methodology will be applied to assess how aneurysms evolve over time, using objective measures of the change of the lumen and outer wall volumes as a determining metric.

5. Conclusions

The segmentation of AAAs that assesses both the lumen and the outer wall remains a challenge because of the high-intensity lumen and the adjacent low-contrast outer wall. To solve this problem, we have proposed a RGAC segmentation method to efficiently delineate the entire lumen and the contour of the outer wall. Our results show that the proposed method accurately segments both the lumen and the outer wall. Visually, the segmented aneurysm contours are similar to those defined by radiologists. Quantitatively, the average segmentation marching factor (SMF) value obtained with the proposed method reaches a Dice value of 89.79 ±2.46%, demonstrating good segmentation accuracy.

Highlights.

• MR image segmentation is performed on abdominal aortic aneurysm lumen and outer wall.

• Novel segmentation is proposed using image registration and shape terms in the model.

• The repeatability and reproducibility of the proposed method are validated.