Predictive Mapping of the Biotic Condition of Conterminous-USA Rivers and Streams

Abstract

Understanding and mapping the spatial variation in stream biological condition could provide an important tool for conservation, assessment, and restoration of stream ecosystems. The USEPA’s 2008-2009 National Rivers and Streams Assessment (NRSA) summarizes the percent of stream lengths within the conterminous US that are in good, fair, or poor biological condition based on a multimetric index of benthic invertebrate assemblages. However, condition is usually summarized at regional or national scales, and these assessments do not provide substantial insight into the spatial distribution of conditions at unsampled locations. We used random forests to model and predict the probable condition of several million kilometers of streams across the conterminous US based on nearby and upstream landscape features, including human-related alterations to watersheds. To do so, we linked NRSA sample sites to the USEPA’s StreamCat Dataset; a database of several hundred landscape metrics for all 1:100,000-scale streams and their associated watersheds within the conterminous US. The StreamCat data provided geospatial indicators of nearby and upstream land use, land cover, climate, and other landscape features for modeling. Nationally, the model correctly predicted the biological condition class of 75% of NRSA sites. Although model evaluations suggested good discrimination among condition classes, we present maps as predicted probabilities of good condition, given upstream and nearby landscape settings. Inversely, the maps can be interpreted as the probability of a stream being in poor condition, given human-related watershed alterations. These predictions are available for download from the USEPA’s StreamCat website (https://www.epa.gov/national-aquatic-resource-surveys/streamcat). Finally, we illustrate how these predictions could be used to prioritize streams for conservation or restoration.

INTRODUCTION

Biological assessments have long been integral to many state, regional, and national monitoring programs of rivers and streams (Reynoldson et al. 1995, Barbour et al. 1999, Smith et al. 1999, European Community 2000), and their use is expanding globally (e.g., Oliveira et al. 2011, Chen et al. 2014, Chowdhury et al. 2016, Kabore et al. 2016, Summya et al. 2016). Assessments are often conducted and summarized within ecological or political boundaries to provide a snapshot of biological condition during a specific time period. However, this approach does not provide information on the spatial distribution of these conditions within assessed regions beyond the set of streams used to develop the assessment. Furthermore, these sample sites are a relatively small proportion of total stream lengths within a region. For example, the US Environmental Protection Agency’s (USEPA) 2008-2009 National Rivers and Stream Assessment (NRSA) used samples from 1,924 sites to represent the condition of 1.9 million kilometers of streams within the US (USEPA 2016a). The limited spatial information these summaries provide within assessment units has limited their use for guiding specific management or restoration activities (Angradi et al. 2008). Spatially-explicit maps of biological condition could provide important insight into where streams at high risk of impairment occur, as well as streams in good biological condition for conservation (Carlisle et al. 2009, Maloney et al. 2009). Here, we leverage an existing assessment conducted for the conterminous US (CONUS) to model and predict the probable biological condition of rivers and streams nationally. The predictions are available for download from the USEPA StreamCat website (https://www.epa.gov/national-aquatic-resource-surveys/streamcat).

Research over the last several decades has focused on improving the repeatability, comparability, representativeness, accuracy, precision, and interpretation of biological assessments (e.g., Barbour et al. 1992, Karr 1999, Hawkins et al. 2000, Cao et al. 2007, Herlihy et al. 2008, Stoddard et al. 2008, Mazor et al. 2016). Of the various methods for assessing the biological condition of streams, multimetric indices (MMI) of benthic macroinvertebrates are among the most common (Buss et al. 2014). An MMI is a composite index produced from several metrics calculated using taxonomic data from sampled sites. These metrics are selected to represent differing aspects of a biological community that are considered to be key indicators of stream health (Karr 1999). These metrics often include measures of pollution tolerance, taxonomic diversity, feeding habits, and behavior (Stoddard et al. 2008). The selection of metrics for an MMI can be driven by specific objectives, such as the desire for metrics that are responsive to particular stressors (e.g., nutrients; McCormick et al. 2001). Stoddard et al. (2008) developed a method of metric selection that maximized the repeatability of the process, while maintaining the original intent of MMIs to characterize key aspects of the biological community and, hence, the condition of streams (see MMI development in Methods). The USEPA followed the approach of Stoddard et al. (2008) to conduct the 2008-2009 NRSA and we used the results of this assessment in the present study.

Recently, several studies have used geospatial indicators of human activity within watersheds to model the results of previously-conducted bioassessments (e.g., Maloney et al. 2009, Waite et al. 2010, May et al. 2015, Schnier et al. 2016). For example, Carlisle et al. (2009) related the results of a biological assessment of sites from the US Geological Survey’s National Water Quality Assessment Program to watershed characteristics, such as upstream agriculture. Carlisle et al. (2009) demonstrated the feasibility of producing a model of biological condition at a large spatial extent based on land use information. Extending these models to produce spatially explicit maps of predicted biological condition could be a powerful tool for prioritizing and focusing limited resources for monitoring, restoration, or protection programs (Carlisle et al. 2009, Maloney et al. 2009). However, prediction to new, unsampled locations based on watershed features requires the delineation of watershed boundaries and calculation of the same suite of watershed metrics that were used to develop the models. The technical challenge of delineating and calculating upstream metrics for thousands to millions of watersheds across a large geographic extent is prohibitive and has limited the widespread use of such models for mapping, except at regional or state scales (e.g., Maloney et al. 2009).

Recent advances in characterizing watershed information in large, nationwide datasets provide the opportunity to apply such models to produce national maps (e.g., Esselman et al. 2011). Specifically, the USEPA’s StreamCat Dataset (Hill et al. 2016) provides a framework for applying models of biological condition and producing spatially explicit maps of predictions. This dataset contains a suite of both natural and anthropogenic watershed features for 2.65 million stream segments within the CONUS that can be linked to the 1:100,000 scale NHDPlusV2. The NHDPlusV2 improves upon NHD Plus Version 1 with respect to network topology, spatial detail, and catchment delineations (McKay et al. 2012). The set of metrics contained within StreamCat were selected based on a literature review of studies that related the biological condition of streams to geospatial indicators of land use (Hill et al. 2016).

In this paper, our objective was to model and predict the probable biological condition of streams across the CONUS based on anthropogenic and natural watershed features. We describe the development of this model and its application to several million stream segments. We used random forest (RF) modeling to achieve these predictions (Breiman 2001). Although RFs have been used extensively in ecology in recent years, few studies have explored how data structure and study design can affect predictions made by such models. We tested several modeling options to identify an approach that produced the most precise and unbiased predictions; a set of analyses that we think provide a template for similar modeling efforts. See Fox et al. (2017) for additional details on model development, evaluation, and selection. Although other studies have focused primarily on model development and the interpretation of the response variable to predictors (e.g., Carlisle et al. 2009), our focus, and main contribution, was the application of a model to produce a national map of biological condition. Hence, we do not provide extensive interpretation of model results here, but we do provide several model diagnostics that are commonly used for interpretation as supplemental materials to this article. Finally, another major objective of this study was to produce a model and map of predicted biological condition with transparent and open methods. Therefore, all code used in this study is provided in supplemental materials (Appendix S1).

METHODS

Summary of approach

We used previously-defined classes of stream biological condition as the response variable in an empirical model to predict the probable condition of all perennial streams within the CONUS. The condition classes were obtained from the NRSA benthic invertebrate MMI as a part of USEPA’s National Aquatic Resource Surveys (USEPA 2016a). We related geospatial indicators of anthropogenic watershed alterations and natural features to these condition classes with RF modeling (Breiman 2001). We obtained these geospatial indicators from the StreamCat Dataset; a publically-available, nationally-consistent data source (Hill et al. 2016). In our modeling, we used predictor variables that represented both natural and anthropogenic features because natural factors have been shown to influence the response of stream biotic conditions to anthropogenic stressors, that is, the response of biological condition can depend on the context of the natural setting within which streams reside (Poff et al. 2006, Carlisle et al. 2009, Maloney et al. 2009). This CONUS-wide dataset allowed the application of the model to predict the probability of individual streams being in good biological condition. We present maps and summaries of these predictions by each of the nine USEPA National Aquatic Resource Surveys reporting regions (Fig. 1). In addition, these predictions are available for download as part of the StreamCat Dataset (https://www.epa.gov/national-aquatic-resource-surveys/streamcat). We have made all of our code available in supplemental materials that parallel the methods and results described here (Appendix S1).

Figure 1.

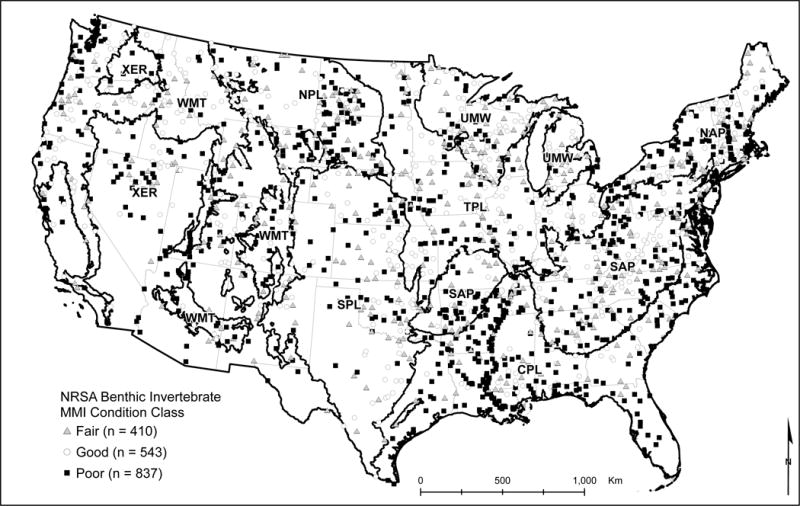
Map of USEPA’s National Aquatic Resource Surveys assessment regions and National Rivers and Streams Assessment (NRSA) sample sites. Regional abbreviations: CPL = Coastal Plains; NAP = Northern Appalachians; NPL = Northern Plains; SAP = Southern Appalachians; SPL = Southern Plains; TPL = Temperate Plains; UMW = Upper Midwest; WMT = Western Mountains; XER = Xeric.

Data

Benthic invertebrate sampling and processing

Barbour et al. (1999), USEPA (2006), and USEPA (2016a) provide the protocols used by the USEPA to sample, process, and standardize benthic macroinvertebrate data as part of the 2008-2009 NRSA. Briefly, The USEPA sampled 1,924 streams from across the CONUS (Fig. 1). At each sample site, crews used a standardized protocol (Barbour et al. 1999) to collect benthic macroinvertebrates. When available, 500 individuals were identified to the lowest taxonomic resolution possible (usually genus) in a laboratory and then standardized to 300 individuals by re-sampling without replacement before analysis (Vinson and Hawkins 1996).

MMI development

Following Stoddard et al. (2008), the USEPA used these resampled data to calculate a suite of metric scores that were the basis of the MMI. Potential metrics were classified into 6 categories depending on the aspect of the benthic invertebrate assemblage they characterized: (1) taxonomic composition, (2) evenness/diversity, (3) feeding groups, (4) dominant behaviors (e.g., percent of taxa that are burrowers), (5) taxonomic richness, and (6) pollution tolerance (Stoddard et al. 2008). These candidate metrics were then filtered to identify metrics that had a reasonable range of values and were repeatable when recalculated at a subset of sites that were revisited within the same sample period. Of the metrics that passed these filters, an iterative process was then used to select a metric from each of the six categories that best discriminated between a set of best-case and worst-case samples, while minimizing redundancy among selected metrics (i.e., r < |0.71|). The six selected metrics were then rescaled (range = 0-10), summed, and then rescaled again (range = 0-100) to facilitate interpretation (see Stoddard et al. 2008). These composite metrics (MMIs) were then classified into three condition classes (good, fair, or poor) by comparing scores with the distribution of MMI scores at a set of regional reference sites (Stoddard et al. 2006). The USEPA used percentiles of <5^th, 5^th-25^th, >25^th of reference site MMI scores as thresholds to classify assessed sites as being in poor, fair, or good condition, respectively (Herlihy et al. 2008). This process was repeated to produce an MMI assessment for each of the nine assessment regions (Fig. 1) with a unique set of metrics and reference sites used in each region. For example, the Western Mountain MMI was comprised of (1) % of taxa comprised of Ephemeroptera, Plecoptera, and Trichoptera (EPT), (2) % of individuals in top five taxa, (3) scraper richness, (4) % clinger taxa, (5) EPT taxonomic richness, and (6) % pollution tolerant taxa (metrics listed in the same order as their categories above). In contrast, the Upper Midwest region MMI only shared EPT taxonomic richness as a common metric with the Western Mountains (see Table 1 in Stoddard et al. 2008).

Of the 1,924 sampled sites, a sufficient number of benthic invertebrate individuals and taxa were collected at 1,883 sites to apply an MMI assessment. Of these 1,883 assessed sites, we withheld 5% of sites (randomly selected) from each region for external evaluation (n = 93), leaving 1,790 for modeling.

Predictor variables

We used the USEPA’s StreamCat Dataset (Hill et al. 2016) as a source of independent variables to model and map predicted stream condition. StreamCat provides spatial summaries of landscape information for more than 2.65 million stream segments within the CONUS. StreamCat was built on, and works within, the NHDPlusV2 geospatial framework. StreamCat data are available at two scales: local catchments and full-contributing watersheds (Fig. 2A). In addition, for a select set of landscape features, Hill et al. (2016) used 100-meter buffers to characterize near-stream conditions, such as the percent of the buffer comprised of urban and agriculture land uses. StreamCat data include summaries of anthropogenic metrics, such as watershed urbanization, agriculture, land surface imperviousness, road densities, mines, dams, and human population and housing-unit densities (see Appendix S2 for a complete list of predictor variables). Natural metrics include summaries of topography, soils, lithology, and hydrology (see Hill et al. 2016 for a complete description of catchment and watershed metrics). The initial set of metrics included in StreamCat were based on a literature review of previous studies that identified landscape metrics that were of ecological relevance to streams (Hill et al. 2016). In total, we used 198 catchment and watershed metrics for modeling (Appendix S2). Some of these metrics were manipulations of existing StreamCat data. For example, we used the percent of the watershed comprised of agriculture as a predictor in the model which we derived by summing NLCD crop and hay land-use classes (see Appendix S2). Other predictors have been added to StreamCat since publication that we hypothesized could explain the biological conditions of streams, including anthropogenic nitrogen loading to the landscape (Sobota et al. 2013), base-flow index (Wolock 2003), and forest loss (Hansen et al. 2013).

Figure 2.

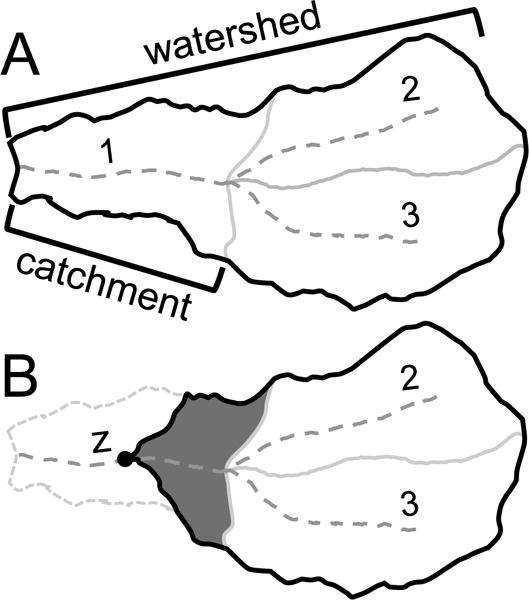
(A) The NHDPlusV2 geospatial framework that is composed of streams (dashed grey lines), local catchments, and full contributing watersheds. We used StreamCat data at both scales for modeling. (B) We used digital elevations models to delineate just the portion of the local catchment that was upstream from each sample point (dark grey above point labeled “z”). In this example, information from catchments 2 and 3 would then be linked to the split catchment to produce site-specific watershed data.

Sample-specific watersheds

Many NRSA sample sites fell well above the outlet of the NHDPlusV2 stream segments (Fig. 2B). These outlets, therefore, did not accurately represent contributing areas or upstream landscape features of NRSA sites. We adjusted the catchment boundary to NRSA sample locations with rasters that represent flow across land surfaces (available for download as part of the NHDPlusV2; McKay et al. 2012). We used these flow rasters to delineate upstream contributing areas within these local catchment, thereby creating a site-specific catchment for these samples (i.e., dark grey area in Fig. 2B). We then overlaid these site-specific catchments onto the same set of geospatial layers used by Hill et al. (2016), and topologically linked them to upstream catchments (i.e., catchments 2 and 3 in Fig. 2B) to calculate a suite of predictors for each NRSA site that matched the set of StreamCat metrics described above and in Appendix S2.

Model development

We used RFs (Breiman 2001) to model and predict the probability of streams being in good biological condition. All analyses were conducted with the randomForest package (Liaw and Wiener 2002) in R statistical software (R Development Core Team 2014). In classification models, RF uses the majority of votes from classification trees in the forest to predict group membership. Alternatively, RF can return the proportion of votes for each class and these proportions can be interpreted as predicted probabilities. Other attractive features of RF models are the ability to handle non-linear relationships, insensitivity to correlated predictors and overfitting, the ability to model interactions among predictor variables, and several diagnostic tools, such as variable importance and partial dependence plots (Cutler et al. 2007).

RF models have very few “tunable” parameters (Segal and Xiao 2011). The main features of RFs that can be adjusted are the number of individual classification trees that compose a forest and the number of randomly-selected variables to test at each split during the development of each tree; however, RF is insensitive to each (Cutler et al. 2007, Fox et al. 2017). Development of a CONUS-wide predictions of biological condition required several key decisions that are not normally described in papers using RF. It was unknown how these decisions would affect the accuracy and precision of modeled and mapped results because few studies have attempted to make spatially-explicit predictions to unsampled locations at such a large spatial scale (see Maloney et al. 2009 for a regional example). Below, we describe each key modeling decision we tested. The code and output in Appendix S1 parallels the modeling decisions described in this section.

National versus regional models

We compared a single, national model with models that were developed for each of the nine regions (i.e., a unique model for each region in Fig. 1). Ideally, a single model could be used to predict stream condition within the CONUS. However, the occurrence and prevalence of land uses differed among regions and the response of biological condition to these land uses may differ by region. Additionally, it was uncertain how differences in MMI development and reference site quality among the nine regions would affect predictions made by a single, national model. NRSA used a unique benthic invertebrate MMI for each of the nine regions to assess streams. That is, the individual metrics that composed each MMI varied from region to region. For example, only one of the six metrics used to develop regional MMIs (taxonomic richness of mayflies, stoneflies, and caddisflies) was common between the Western Mountain and Upper Midwest regions (Stoddard et al. 2008). In addition, each MMI in each region used a unique set of reference sites to assess the condition of NRSA sites to create the condition classes we used in modeling. Reference sites represent streams in the best available condition (Stoddard et al. 2006); however, reference-site quality is known to vary substantially between regions and may affect the ability of a single, national model to produce accurate and unbiased predictions (Ode et al. 2008, Ode et al. 2016).

Treatment of fair sites

Of the 1,790 sites used in modeling, 23% (n = 410) were assessed by NRSA to be in fair condition. In practice, these sites had MMI scores that were between the 5^th and 25^th percentiles of reference-site MMI scores and were considered by the NRSA to be “somewhat different from the reference sites” (USEPA 2016a). Fox et al. (2017) tested a multinomial model of condition with good, fair, and poor classes in random forest model. They found that the model could only correctly predict the condition of 24% of fair sites (see Supplement 2 of Fox et al. 2017). However, it was unclear if fair sites should be excluded from modeling completely or if they could be grouped with either good sites or poor sites to provide information for modeling. Preliminary analyses indicated that watershed characteristics (e.g., upstream urbanization) of fair sites may be more similar to good sites than poor sites, but these analyses were inconclusive (not shown here). We compared three models to determine the effect of retaining or excluding fair sites on model performance. These models (1) excluded fair sites, (2) grouped fair sites with good sites, or (3) grouped fair sites with poor sites.

Balanced versus imbalanced observations

Poor sites outnumbered good and fair sites both nationally and in most regions. When confronted with imbalanced response data, many statistical classifiers, including RF, can produce biased predictions (Haibo and Garcia 2009). We developed and compared RF models with balanced and imbalanced observations across condition classes. To create balanced models, we forced RF to have an equal number of observations across condition classes by down-sampling the majority class to match the number of observations in the minority class during the construction of each tree within the forest (see Appendix S1). In this way, all observations were used in the development of an RF but equal class sizes are used during the construction of each tree within the forest.

Model selection and evaluation

We used RF out-of-bag (OOB) predictions to develop performance metrics for comparing model decisions and for evaluating the final model. Through bootstrapping, RF withholds about one-third of observations during the construction of each classification tree and produces OOB predictions from these withheld data. OOB predictions are considered a reasonable approximation of predictions made with an independent dataset (Cutler et al. 2007). To evaluate each modeling option, we examined boxplots of predicted probabilities of good biological condition [henceforth Pr(good)] versus observed NRSA condition. These plots helped to identify prediction biases produced by certain modeling options. Ideally, an accurate and precise model should produce predicted probabilities that fall above 0.5 for true good sites and below 0.5 for true poor sites. In addition, we calculated the percent of sites correctly classified (PCC) as being in good or poor condition, including model sensitivity (PCC of true good sites) and model specificity (PCC of true poor sites). Unbiased models should balance model sensitivity and specificity. Finally, we calculated the area under a receiver operating curve (AUC), which compares all pairwise combinations of true good and true poor sites and reports the proportion of times that the Pr(good) of each true good sites was greater than the Pr(good) of each true poor sites (Fielding and Bell 1997, Hosmer and Lemeshow 2004). A model with AUC = 0.5 cannot distinguish between true good and true poor sites. In contrast, a model with AUC = 1.0 indicates that all true good sites had Pr(good) values that were higher than all true poor sites. Models with AUC > 0.7 and AUC > 0.8 are considered “acceptable” and “excellent”, respectively (Hosmer and Lemeshow 2004). For space, we present the diagnostic plot or table that provided the clearest guidance on final model decisions (Appendix S1 contains all code and plots from this analysis). A companion paper to this study by Fox et al. (2017) provides an examination of variable reduction with RFs. Fox et al. (2017) found that variable selection did not substantially affect model performance, relative to the model decisions explored here. Rather, variable selection tended to introduce instability in predicted probabilities (Fox et al. 2017). Thus, we used all 198 predictors in our RF models. For the final model, we also calculated a national PCC and AUC with the randomly-selected sites that were withheld as an external evaluation.

We used the variable importance measure provided with the R randomForest package (Liaw and Wiener 2002) to compare the 10 most important predictors in each of the final models across regions. Random forest can assess the contribution of each predictor to model performance by permuting variable values when they are selected within individual trees (Breiman 2001). The change in model performance when variables are permuted is interpreted as the relative contribution of that variable to the model. We used 3,000 trees for each RF model because the stability of variable importance measures increases with the number of trees (Wang et al. 2016).

RESULTS

The selected model: (1) was composed of nine regional models, (2) excluded fair sites, and (3) used a balanced set of good and poor sites to build each tree. We first describe the results of each test used to identify this final set of model characteristics. To present the isolated effect of each decision, we show the results of each test with all other options set to their final characteristics. For example, to show how using a national model versus nine regional models affected model performance, we set options (2) and (3) to the characteristics described above. We next describe the performance of the final model nationally and by region, and present the national map that was produced using these three characteristics. To construct the national map, we applied the model to just those NHD stream segments designated as perennial. That is, we excluded intermittent streams from the national map because they are outside of the NRSA sampling frame.

Model decisions

Regional models outperformed a single, national model

Substantial bias in the single, national model was apparent in several regions. For example, almost all Pr(good) values produced by the national model in the Coastal Plains region were below 0.5, even for sites that were assessed by NRSA to be in good condition (Fig. 3A). The opposite pattern was observed for sites in the Western Mountains region, where the model over predicted Pr(good) values of true poor sites (Fig. 3B). The national model did not produce biased predictions in all regions. For example, model sensitivity and specificity were balanced within the Temperate Plains region (Table 1A). However, regional models greatly reduced prediction bias for several regions (e.g., Figs. 3C-D). We, therefore, used regional models to map biological condition.

Figure 3.

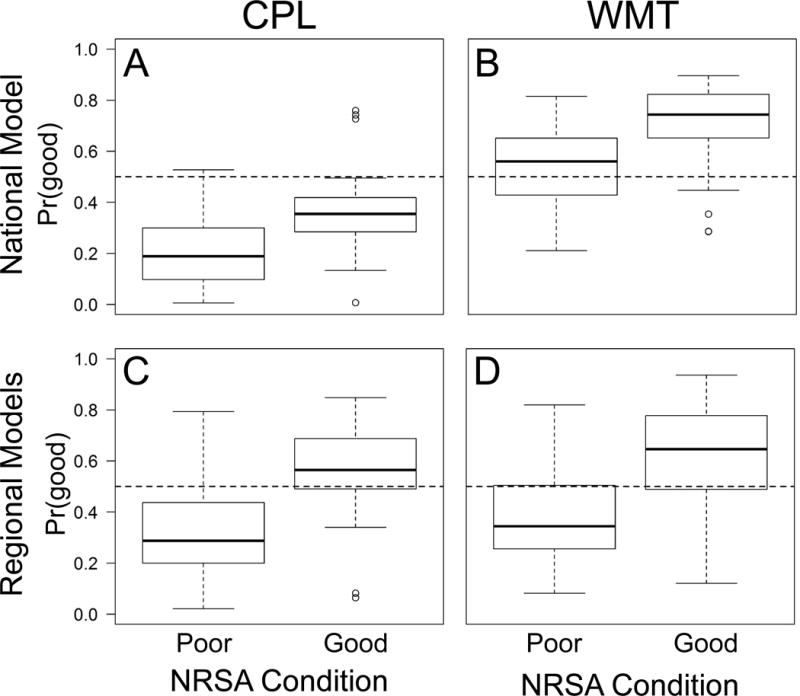
Boxplots of predicted probabilities of good biological condition [Pr(good)] for a single, national model (A-B) and for region-specific models (C-D) versus observed NRSA condition. Horizontal dashed lines represent Pr = 0.5. Regional abbreviations: CPL = Coastal Plains; WMT = Western Mountains. NRSA Condition = the condition assigned by the National Rivers and Streams Assessment and used as the response variable in our models.

Table 1.

Random forest out-of-bag model performance for the conterminous US (CONUS) and by National Aquatic Resource Surveys region for each modeling option. Region acronyms: SAP = Southern Appalachians; CPL = Coastal Plains; WMT = Western Mountains; XER = Xeric; SPL = Southern Plains; NAP = Northern Appalachians; UMW = Upper Midwest; TPL = Temperate Plains; NPL = Northern Plains. Abbreviations: PCC = Percent correctly classified; Specificity = Percent of true poor sites correctly classified; Sensitivity = Percent of true good sites correctly classified; AUC = Area under the receiver operating curve.

A. Single National Model, Fair Sites Excluded, Balanced Observations
	CONUS	SAP	CPL	WMT	XER	SPL	NAP	UMW	TPL	NPL
PCC	77	73	85	67	78	70	80	77	82	79
Sensitivity	76	68	23	90	80	67	83	95	82	68
Specificity	78	76	98	45	77	74	79	30	81	87
AUC	0.84	0.82	0.79	0.81	0.83	0.79	0.87	0.73	0.87	0.88
B. Regional Models, Good and Fair Sites Combined, Balanced Observations
	CONUS	SAP	CPL	WMT	XER	SPL	NAP	UMW	TPL	NPL
PCC	73	72	71	73	69	71	81	65	72	77
Sensitivity	83	86	74	81	79	84	92	82	86	90
Specificity	66	64	71	66	62	54	74	22	55	68
AUC	0.83	0.84	0.84	0.79	0.76	0.78	0.9	0.71	0.82	0.88
C. Regional Models, Poor and Fair Sites Combined, Balanced Observations
	CONUS	SAP	CPL	WMT	XER	SPL	NAP	UMW	TPL	NPL
PCC	74	71	79	74	72	70	81	64	73	80
Sensitivity	62	41	63	63	59	59	71	63	69	73
Specificity	83	89	83	83	80	85	87	65	79	84
AUC	0.82	0.79	0.83	0.80	0.77	0.80	0.86	0.71	0.83	0.86
D. Regional Models, Fair Sites Excluded, Imbalanced Observations
	CONUS	SAP	CPL	WMT	XER	SPL	NAP	UMW	TPL	NPL
PCC	77	73	84	75	70	73	82	74	77	82
Sensitivity	70	48	26	74	56	82	67	92	84	79
Specificity	83	88	97	76	80	61	91	26	67	84
AUC	0.84	0.81	0.81	0.80	0.76	0.81	0.85	0.71	0.84	0.86
E. Selected Approach – Regional Models, Fair Sites Excluded, Balanced Observations
	CONUS	SAP	CPL	WMT	XER	SPL	NAP	UMW	TPL	NPL
PCC	75	72	76	73	69	75	71	71	79	82
Sensitivity	73	63	66	75	62	77	75	77	81	81
Specificity	77	77	79	72	73	72	85	56	77	83
AUC	0.84	0.82	0.84	0.80	0.77	0.80	0.86	0.72	0.72	0.88

Excluding fair sites improved model precision and bias

Excluding fair sites from modeling improved the balance between model sensitivity and specificity across most regions and the CONUS (cf. specificity and sensitivity of Table 1B-C to 1E). Grouping fair sites with good sites improved model sensitivities but reduced model specificities (Table 1B). The inverse was true for sensitivities and specificities when fair sites were grouped with poor sites (Table 1C). The improvements in model performance that were observed through exclusion of fair site were not as marked as those observed through the development of regional models. However, these improvements were consistent across most regions and we excluded fair sites from the final set of regional models.

Balancing response data reduced model bias

Forcing models to have the same number of good and poor sites in each tree reduced biases in predicted probabilities for regions where these imbalances were large. For example, in the Coastal Plains region, imbalanced response data produced Pr(good) values with compressed ranges relative to models that used balanced observations, although some compression of Pr(good) values was still apparent after balancing (Fig. 4, cf. Tables 1D and 1E). For the final set of regional models, we balanced good and poor observations.

Figure 4.

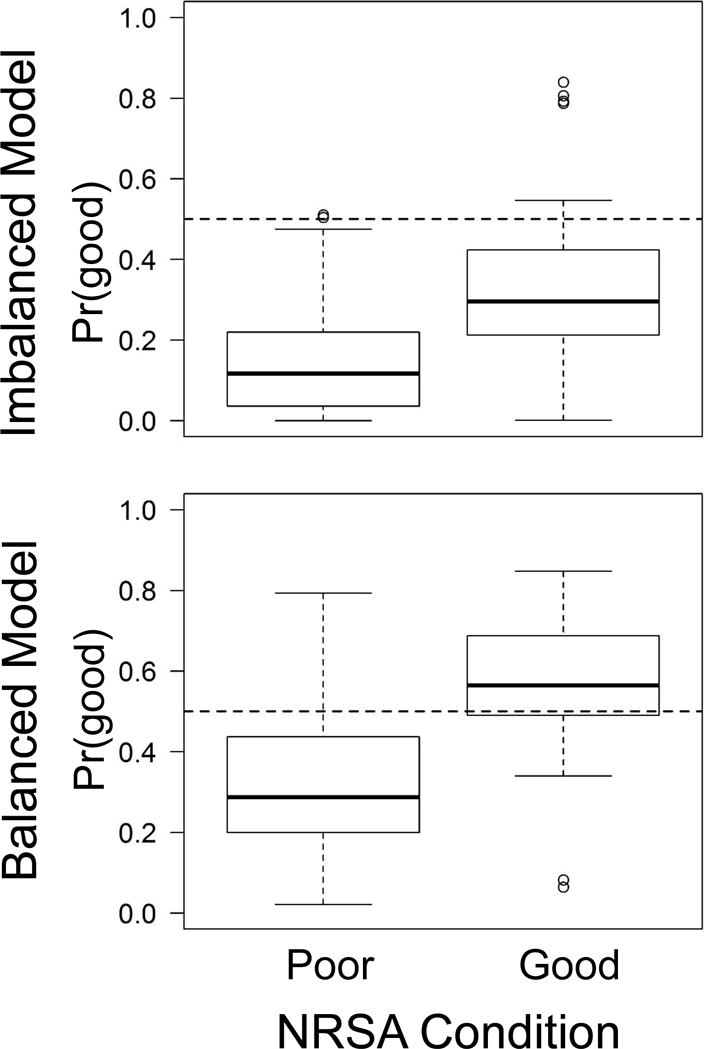
Boxplots of predicted probabilities of good biological condition [Pr(good)] for the Coastal Plains (CPL) region. Horizontal dashed lines represent Pr = 0.5. The imbalanced model allowed random forest to build trees with random samples of good (n = 37) and poor (n = 197) sites. The balanced model down-sampled the majority class (i.e., poor) when generating random selections for each tree such that equal numbers of good and poor sites were used in tree development.

Final model performance

OOB evaluations suggested excellent model performance, both nationally and for most regions. Nationally, the PCC for the benthic invertebrate MMI was 75%. Poor sites were correctly predicted at a slightly higher rate than good sites (77% versus 73%, respectively). Regionally, the PCC ranged from 69% in the XER region to 82% in the Northern Plains region (Table 1E). Regional boxplots showed Pr(good) values that were unbiased, i.e., generally centered on Pr(0.5) (see Fig. 3C-D for example). Nationally, the model had excellent performance as measured with AUC (0.84) (Table 1E). Regionally, AUC values ranged from 0.72 (Upper Midwest and Temperature Plains) to 0.88 (Northern Plains).

Model performance among the withheld validation sites generally paralleled the OOB evaluations. Of the 93 validations sites, 71 were classified as good or poor by NRSA (i.e., we did not use fair sites for this evaluation). Among these 71 sites, model AUC was 0.81, similar to the OOB AUC of 0.84. In contrast, PCC of good and poor sites were 61% and 85%, respectively, and were less balanced than the OOB sensitivity and specificity (cf. OOB PCC in Table 1E). There were too few sites withheld to evaluate model performance regionally with these data.

Final model and predicted biological condition

Important predictors

Of the top ten predictors across the nine regions, 19 were local catchment predictors and the remaining 71 were watershed-level predictors; highlighting the importance of understanding the full watershed context of streams. Despite substantial differences in important predictors and their rankings across the nine regional models, several types of metrics recurred throughout. This result was not surprising because the selection of StreamCat metrics was based on a literature review of landscape metrics that have been shown to influence stream biological condition (Hill et al. 2016).

Natural metrics comprised more than half of the top ten importance-ranked predictors across all nine regional models (i.e., 46 or 90 predictor variables). Across many regions watershed area, runoff, and a topographic wetness index were among the most important natural factors (see Appendix S3 for variable importance plots of the top ten predictors in each region). However, correlations among these three predictors were small and likely represented different aspects of stream hydrology or topographic position (e.g., r² = 0.06 between runoff and watershed area). Four of the nine regional models had watershed area within the within the top ten importance-ranked predictors. In general, larger watershed areas had a positive relationship with Pr(good) values (see partial dependence plots for WsAreaSqKm in Appendix S3). This relationship may seem counterintuitive given the paradigm of healthy headwaters that transition to valley reaches with an array of human-related pressures. However, first order streams make up 39% of total stream lengths within the NRSA sampling frame. The vast majority of these streams occur in valleys and are subjected to human-related pressures at their initiation. In contrast, mid- to large-order streams often flow from relatively intact headwaters and retain some features of this water quality well within valleys that experience human-related alterations (personal communication with Dr. Alan Herlihy, 4 December 2015). Climate metrics were also among the most important natural metrics across all models. Air temperature occurred within the top ten predictors in six of nine regional models. In all cases, Pr(good) was negatively with warmer temperatures, except in the Temperature Plains. Precipitation metrics were important in the Xeric, Western Mountain, and Norther Plains regions and in all cases Pr(good) was associated with more precipitation.

Urbanization and agriculture were the most common anthropogenic metrics across all models. In all cases, the relationship between these metrics and Pr(good) was negative (Appendix S3) and is consistent with other studies of this type (e.g., Carlisle et al. 2009, Falcone et al. 2010). Urbanization was important for all models and these measures of urbanization included a variety of metrics (e.g., % of watershed comprised of urban land use, housing unit or population density, number of road-stream crossings weighted by the slope of the stream segment). In addition, a composite metric of disturbance (i.e., the sum of all agriculture and urbanization within the watershed or within the riparian buffer) was within top ten importance-ranked predictors in four of the nine regional models.

Various metrics of water impoundment (i.e., dam density and volume) were important in four regions, but the direction of the relationship with biological condition depended on the region. Water impoundments were negatively associated with Pr(good) in the Northern Appalachian and Xeric regions but were positively related with Pr(good) in the Northern and Temperate Plains regions (Appendix S3). The Northern Appalachian and Xeric regions are mountainous regions and the types, sizes, and thus the impacts of dams likely differ from those found in the plains and may explain the differing responses among these regions.

The directions of relationships for other anthropogenic metrics also differed from what was expected. For example, mine density within the watershed was within the top ten predictors in the Temperate Plains region and the partial dependence plot showed a positive relationship with Pr(good) (Appendix S3). This pattern is in contrast to numerous other studies that have demonstrated that mining can negatively affect stream ecosystems (Nuttle et al. 2017). However, this mining metric only quantifies the density of mines based on the US Geological Survey point layer of active mines and mineral plants (https://mrdata.usgs.gov/mineplant/) and does not contain information regarding the size or type of mining activity. We cannot explain the direction of this relationship with this study, but mining density within this region was also positively associated with the organic matter content of soils (r² = 0.22, p < 0.0001); a natural metric that showed positive relationships with condition in the Southern Appalachian and Southern Plains regions. The relationship between Pr(good) and forest loss was also initially counterintuitive. Forest loss occurred within the top ten predictors of three regions; the Northern and Southern Plains and the Upper Midwest. We had excluded percent of the watershed comprised of forested land cover (NLCD) as a predictor during preliminary analyses because it failed to capture recent alterations in forest cover and instead included forest loss. However, in the Upper Midwest and Southern Plains regions, greater forest loss is positively and significantly associated with percent forest cover within the watershed (r² = 0.22 and 0.44, respectively; p < 0.001 for both) and may simply be acting as a surrogate for the presence of forest cover within these models. It is unlikely that forest loss in the Southern Plains region is acting as a major stressor because it comprised a small percentage of any watershed (i.e., maximum ≈ 4%).

Summary and map of predicted conditions

For the CONUS, mean (weighted by stream lengths) predicted Pr(good) was 0.47 (SD = 0.19). However, regional values of mean Pr(good) differed by up to 0.21 (Table 2). Specifically, the mean Pr(good) in the Coastal Plains was 0.37 (SD = 0.16) while the mean Pr(good) in the Western Mountains was 0.58 (SD = 0.18). Length-weighted medians of Pr(good) by region and for the CONUS did not differ substantially from length-weighted means (Table 2). These variations in regional Pr(good) could not be explained by simple associations with dominant land uses. For example, the mean Pr(good) among regions was weakly, and non-significantly associated with variations in agricultural land use (i.e., percent crops within watersheds) among regions (r² = 0.07, p = 0.49) and supports the findings that the importance of variables were region-specific (see section Important predictors above).

Table 2.

Mean, standard deviation, and median of predicted probabilities of good biological condition by EPA National Aquatic Resource Survey (NARS) reporting region (see Fig. 1) and for the conterminous US (CONUS). NARS regions are in ascending order of mean predicted probability. Means and standard deviations are weighted by the length (km) of NHDPlusV2 stream segment. Regional abbreviations: CPL = Coastal Plains; NAP = Northern Appalachians; NPL = Northern Plains; SAP = Southern Appalachians; SPL = Southern Plains; TPL = Temperate Plains; UMW = Upper Midwest; WMT = Western Mountains; XER = Xeric.

NARS Region	Mean (St. Dev.)	Median
CPL	0.37 (0.16)	0.34
NPL	0.42 (0.19)	0.39
TPL	0.43 (0.17)	0.42
SAP	0.44 (0.15)	0.45
XER	0.44 (0.16)	0.44
UMW	0.49 (0.17)	0.49
NAP	0.51 (0.22)	0.51
SPL	0.53 (0.19)	0.54
WMT	0.58 (0.18)	0.60
CONUS	0.47 (0.19)	0.46

Distinct shifts in catchment-specific values of Pr(good) were visible at several regional boundaries. For example, the border between the Southern Appalachian and Coastal Plains regions was marked by a shift from lower to higher values of Pr(good), respectively (Fig. 5). Notably, in the Potomac watershed (Fig. 6), catchments in Coastal Plains were comprised of similar or higher amounts of urbanization than catchments in Southern Appalachian at the regional boundary. However, Coastal Plains streams at the border were predicted to have higher Pr(good) than Southern Appalachian streams. This pattern may reflect, in part, the relative quality of reference sites used to develop the NRSA benthic invertebrate MMIs for these regions and the fact that a unique model was developed for each of the nine regions.

Figure 5.

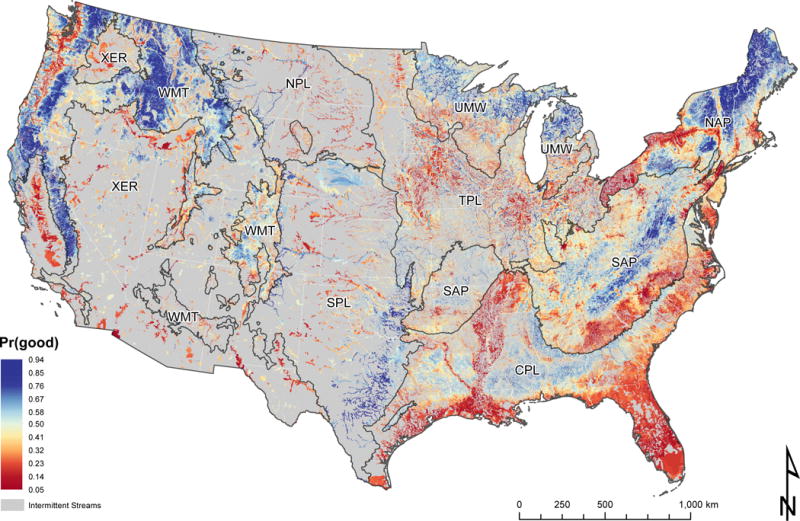
National map of predicted probabilities of good biological condition [Pr(good)]. Grey regions represent catchments for which NHD flow type is “intermittent”. To improve the visibility of individual stream segments, we mapped values to the incremental NHDPlusV21 catchments in which each segment occurred. Regional abbreviations: CPL = Coastal Plains; NAP = Northern Appalachians; NPL = Northern Plains; SAP = Southern Appalachians; SPL = Southern Plains; TPL = Temperate Plains; UMW = Upper Midwest; WMT = Western Mountains; XER = Xeric.

Figure 6.

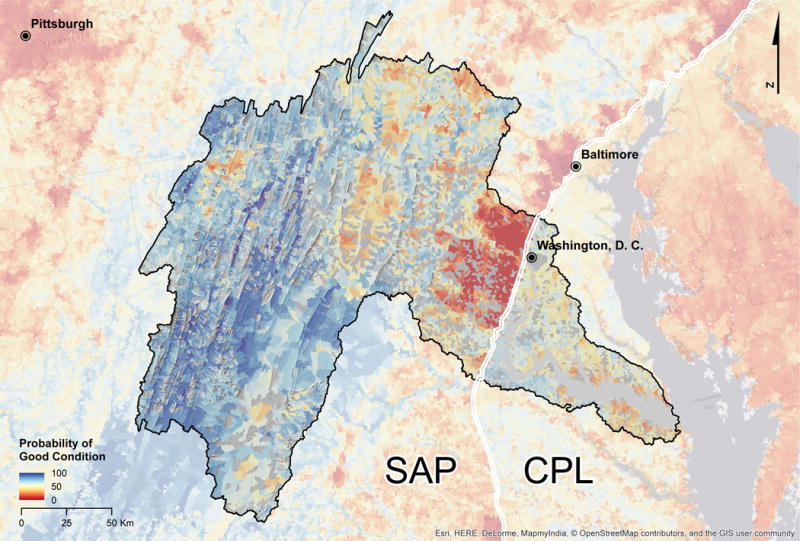
Map detail of predicted probabilities of good biological condition within the Potomac River watershed. Washington D.C. and Baltimore are at the border between the Southern Appalachian and Coastal Plains assessment regions. To improve the visibility of individual stream segments, we mapped values to the incremental NHDPlusV21 catchments in which each segment occurred.

Within regions, the condition map identified several distinct geographic patterns in Pr(good) values. Streams within the northern portion of the Upper Midwest region had higher predicted Pr(good) values than the southern portion of the region (Fig. 5). Likewise, a north-south band of streams with higher values of Pr(good) in the Southern Appalachian region gave way to streams with lower values of Pr(good) in the southeastern edge of the region (Fig. 5). These shifts from higher to lower values of Pr(good) often coincided with changes in major land use. For example, the pattern of higher to lower Pr(good) values in Upper Midwest coincided with an increase in the percent of watersheds comprised of agriculture (cf. Fig. 5 with Appendix S4: Figure S1). Overall, areas dominated by agriculture were generally associated with lower values of Pr(good), including the Central Valley, California (Xeric), the Willamette Valley, Oregon (Western Mountains), the Corn Belt region (Temperature Plains), and parts of the Lower Mississippi Basin (Coastal Plains) (Fig. 5).

In many regions, such as the Western Mountain and Xeric regions, small headwater streams had similar or higher mean Pr(good) values as higher order streams. However, in some regions, headwater streams had substantially lower Pr(good) values than higher order streams. For example, first order streams in the Temperate Plains had mean (length-weighted) Pr(good) values of 0.31 (SD = 0.1) versus a mean of 0.55 (SD = 0.13) in streams of 4^th order and greater. However, this association with watershed size was context dependent. In the Northern Plains region, larger rivers that received much of their flow from the Bitterroot Mountains (western edge of Northern Plains; Fig 7) continued to have higher values of Pr(good) relative to adjacent first-order streams despite passing through land that is dominated by agriculture (Fig. 5). This pattern of rivers in some regions maintaining good biological condition well within locations dominated by human-related land uses was corroborated by scientists that developed the benthic invertebrate MMI for NRSA (personal communication with Dr. Alan Herlihy, 4 December 2015) and in a plot of model response to watershed area in these regions (see Appendix S3 for RF partial dependence plots of watershed area).

Figure 7.

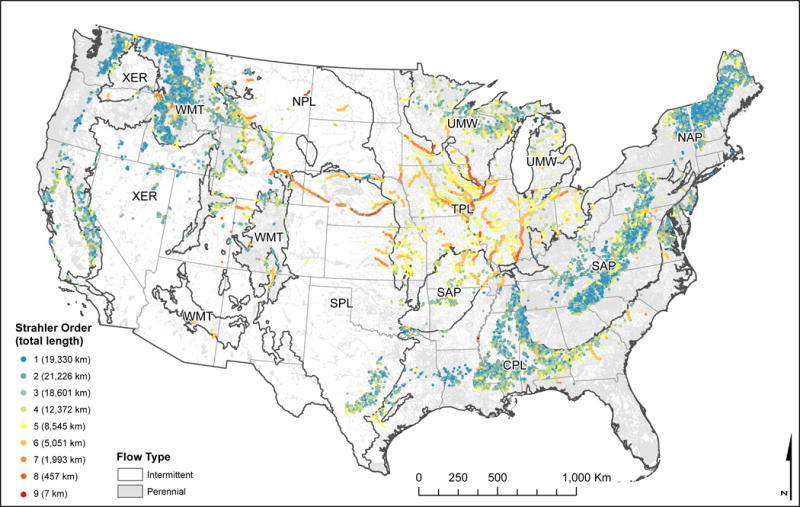
Map of streams that met the criteria of our illustrative query to identify candidate streams for conservation. The query identified streams with predicted probabilities of good [Pr(good)] biological condition within the upper 95^th percentile of Pr(good) values in each National Aquatic Resource Survey region.

DISCUSSION

The use of landscape information to model and predict the biological condition of unsampled streams is important because understanding the spatial variation in these conditions can improve our ability to assess, manage, protect, and restore these ecosystems (Carlisle et al. 2009, Villeneuve et al. 2015). However, the widespread use of such predictions to guide these activities has not been possible until now because technical challenges have prevented their application to large spatial extents. We think that our study provides an important advancement of these efforts. Furthermore, we think our map provides unique information regarding the probable biological condition of streams that we have made publically available (https://www.epa.gov/national-aquatic-resource-surveys/streamcat). The predictions take advantage of the ability of RF to model non-linear relationships and interactions among predictor variables. For example, Pr(good) values have relatively low correlations with the percentage of watersheds composed of agriculture and urbanization alone and does not appear to be a simple, linear reflection of these land uses (Table 3).

Table 3.

Coefficients of determination (r-squared) between predicted probability of good condition and the percent of each watershed composed of urbanization, agriculture, and the index of watershed integrity (Thornbrugh et al. in review). National Aquatic Resource Surveys (NARS) region abbreviations: CPL = Coastal Plains; NAP = Northern Appalachians; NPL = Northern Plains; SAP = Southern Appalachians; SPL = Southern Plains; TPL = Temperate Plains; UMW = Upper Midwest; WMT = Western Mountains; XER = Xeric.

NARS Region	Coefficient of determination (r2)
	Urb	Ag	IWI
CPL	0.09	0.13	0.14
NAP	0.24	0.16	0.44
NPL	0.00	0.10	0.09
SAP	0.19	0.07	0.26
SPL	0.04	0.08	0.09
TPL	0.03	0.01	0.04
UMW	0.10	0.24	0.27
WMT	0.09	0.11	0.27
XER	0.05	0.06	0.13

In this discussion, we consider several factors regarding the interpretation, accuracy, and application of our models and map. We first consider the interpretation of our predictions within the context of NRSA MMIs. Next, we compare the performance of our predictions to the performance of previous modeling efforts to provide context into the advances we were able to make here. Third, nationally-consistent datasets within the CONUS have allowed the development of at least two additional national maps of relevance to river ecosystems. We compare our approach and map to those related efforts. We next consider how our map could be used to support the identification of sites for conservation and restoration. Our model decisions identified behaviors within the predicted probabilities that may provide insight into ecological modeling generally (e.g., species distribution modeling) and for NRSA, specifically. We discuss these behaviors and their implications for future modeling and assessments. Finally, we made predictions to streams within the current NRSA sampling frame because these assessments are intended for perennially flowing waters. This decision excluded intermittent streams (~59% of streams) from the map and we close by considering the implications of excluding these systems from assessments and our modeling in this study.

Ecological interpretation of Pr(good)

To interpret the predictions made by our models, it is important to consider the MMIs used in the NRSA. They represent an attempt to maintain the original intent of MMIs to characterize key aspects of the biological community (sensu Karr 1981), while maximizing the reproducibility, consistency, and discrimination ability of the assessment (Herlihy et al. 2008, Stoddard et al. 2008). Thus, six categories of metrics that represented key taxonomic and autecological features of streams were used to develop each regional MMI, even though individual metrics within these categories could differ among regions (Table 1 in Stoddard et al. 2008). NRSA compares MMI scores of assessed sites to the statistical distribution of MMI scores at a set of regional reference sites. A site that falls outside of this distribution can be thought of as having aspects of these six categories of metrics that are sufficiently different from the set of regional reference sites that it can be considered as being in poor condition.

There are at least two factors that limit the interpretation of the predictions made by our models. First, the composite nature of MMIs make their direct interpretation difficult, i.e., it is difficult to parse why particular streams failed the assessment without decomposing MMIs to their individual metric scores. Second, metrics selection for the NRSA MMIs was done independently of any stressors (e.g., fine sediments). This approach is in contrast to other MMI assessments that selected metrics based on their responsiveness to specific stressors (e.g., McCormick et al. 2001), which can aid in MMI interpretation. For our modeling, we used the binary classes of good and poor condition to predict the probability of good condition. Thus, predictions produced by our model represents the probability that a stream segment shares metric characteristics with reference sites of that region, given the local catchment and watershed pressures we can currently measure with geospatial data.

Comparison with previous models

Placing the performance of our predictions in context with previous studies provides insight into the advances we were able to make here. Our modeling achieved similar or better performance than several previous efforts, but at a much larger spatial extent. Carlisle et al. (2009) provides the clearest comparison to our study because they used sample sites from across the mid-western and eastern US. Carlisle et al. (2009) developed two models to predict biological condition as determined by two previously-developed biological assessments (i.e., RIVPACS assessments; Moss et al. 1987, Hawkins et al. 2000) for the eastern highlands and the eastern lowlands. The highland and lowland models each correctly predicted the condition classes of 87% and 77% of sites, respectively. These PCC values are similar to those achieved by our models for similar regions of the country (cf. Tables 1 and 2 of Carlisle et al. 2009 and PCC in our Table 1E). However, the PCC values reported by Carlisle et al. (2009) had highly imbalanced model specificity and sensitivity. For example, Carlisle et al. (2009) reported that the eastern highland model had specificity and sensitivity values of 51% and 96%, respectively. In contrast, our models generally achieved more balanced specificities and sensitivities (Table 1E). The dissimilar sensitivity and specificity values observed in the models of Carlisle et al. (2009) suggest that their probabilities may have been biased due to imbalances in their response data. Our analysis showed that balancing classes during model construction can substantially reduce such biases. In addition to Carlisle et al. (2009), our models compared well with models developed for: southern California (Brown et al. 2012; specificity = 69-75% and sensitivity = 78-87%), Maryland (Maloney et al. 2009; RF model PCC = 46.4-49.2% and AUC = 0.64-0.69), and France (Villeneuve et al. 2015; PCC = 74-79% and AUC = 0.80-0.85).

Comparison with other national mapping efforts

The advent of nationally-consistent watershed data (e.g., StreamCat; Hill et al. 2016) allows for the rapid application of conceptual and analytical results to millions of stream kilometers within the US. We know of at least two efforts that have been conducted at a similar spatial scale to our map of Pr(good). First, the National Fish Habitat Action Plan provides an example of producing national maps of ecological relevance to streams. While not explicitly modeling biological condition, Esselman et al. (2011) developed indices of anthropogenic stress on fish habitats that were calibrated with the distributions of sensitive fish species. These calibrated indices were then aggregated and applied to the National Hydrography Dataset (NHD) Plus Version 1 (USEPA and USGS 2005) to produce a national map of relative disturbance to fish habitats. While there are similarities between our map and that of Esselman et al. (2011), substantial differences exist between the two efforts (cf. Fig. 6 of Esselman et al. 2011 and our Fig. 5). Both maps show the western mountains as being in good condition (i.e., low disturbance in the map of Esselman et al. 2011). In addition, both maps suggest high levels of disturbance in eastern Texas and Florida. In contrast, in the Southern Appalachian region, our map shows the Appalachian Mountains as having high Pr(good) relative to lower-lying areas. No such pattern is apparent in the map of Esselman et al. (2011). Our map differed from the map of (Esselman et al. 2011) in some regions for at least three reasons. First, the two studies used different taxonomic groups (i.e., benthic macroinvertebrates versus fish) and indices derived from different taxonomic groups can produce differing assessments, even when similar statistical and assessment techniques are used (Hawkins et al. 2010). Second, the statistical approaches and objectives of the two studies differed substantially. Esselman et al. (2011) used the slopes from linear regressions between a set of fish assemblage indices and geospatial indicators of disturbance as weights within a cumulative disturbance metric (Esselman et al. 2011). In contrast, our approach, that used RF modeling, made no assumptions of linearity and directly related the assessment to natural and anthropogenic geospatial metrics. Finally, our approach was based on reference sites within nine separate regions whereas the map of Esselman et al. (2011) was developed without regionalization.

In another example of a national map, we conducted a related effort (Thornbrugh et al. in review) using the StreamCat Dataset and NHDPlusV2 to apply the definition of watershed integrity proposed by Flotemersch et al. (2015) (index of watershed integrity; henceforth IWI). In addition, the definition of Flotemersch et al. (2015) was extended to local catchments within the NHDPlusV2 (see Fig. 2A for definitions of catchments and watersheds) to generate a national map of catchment integrity (ICI; index of catchment integrity). IWI and ICI are applications of a conceptual framework that uses anthropogenic factors (e.g., road-stream crossings) to map the risk of low watershed and catchment integrities. That is, they are conceptual indices and are not calibrated from empirical relationships. Thornbrugh et al. (in review) assumed linear declines in index scores with increasing measures of human-related activity within catchments and watersheds. In contrast, our map of Pr(good) is empirical (i.e., we used RF modeling) and incorporates potential non-linear or threshold relationships between NRSA benthic MMI classes and landscape features. This difference in approach to produce the IWI and Pr(good) results in very low correlations between these two maps (Table 3). Additionally, the map of Thornbrugh et al. (in review) differ in what they portray. NRSA data represent particular river reaches that were sampled during yrs. 2008-2009 and the assessment is a snapshot of instream conditions of perennially flowing waters. Our map excluded up to 59% of streams within the NHD that were designated as intermittent because they were not part of the NRSA sampling frame (see Intermittent streams below). In contrast, the IWI and ICI use human-related stressors on the landscape as indicators of whole watershed or catchment integrity. In other words, they are landscape indices that do not make assumptions regarding the type of flow occurring within streams. In this way, they can be applied to both perennial and intermittent catchments.

How can our map be used to support conservation and restoration?

A major challenge in conservation and restoration of streams is determining where to best place limited financial resources towards these efforts. Our map of Pr(good) could provide an important tool for guiding these efforts within the US. For example, if the goal of a land manager is to identify and conserve streams that are in good biological condition, our map can be queried to select streams that meet these criteria. As an illustration, we selected streams that were within the upper 95^th percentile of Pr(good) values within each region and mapped them by their Strahler stream order (Fig. 7). Within several regions (e.g., Western Mountains), 1^st order streams showed the highest potential for conservation. In contrast, 5^th – 8^th order streams showed the highest potential for conservation in the Temperate Plains region. Managers could use this type of information to develop strategies to maintain the biological integrity of these streams and rivers. In the Western Mountains region, many of these streams occur on Federal land and their condition could be maintained through careful management of extractive land uses. In the Temperate Plains region, a strategy to maintain the biological condition of these rivers could include working with local land owners to plant and preserve riparian corridors in agricultural lands; a major land use category within this region. Furthermore, tributaries to these rivers could be restored to support the good condition predicted at these locations and to expand the distribution of streams in good biological condition from those identified in this query.

To maximize the likelihood of successful restoration, additional information could be used in conjunction with our predictions. Restoration is most likely to be successful where the cause of stream impairment can be tied to local activity, but the upstream watershed remains relatively intact (Harmon et al. 2012, Kail et al. 2015). Furthermore, likelihood of post-restoration improvements in biological condition increase if nearby reaches are in good biological condition and can act as a source of native taxa for recolonization of restored reaches (Lake et al. 2007, Palmer et al. 2014). Stream segments within the NHD that fit these criteria can be identified with queries of the ICI and IWI maps of Thornbrugh et al. (in review) and our map of Pr(good). First, NHD segments with both low Pr(good) and low ICI values could represent biologically impaired stream reaches where local factors (i.e., low ICI) contribute to this impairment. This query could be further refined by identifying those stream segments with high IWI values, suggesting an intact contributing watershed. Thus, the predicted biological impairment in these streams is likely due to local conditions and not to chronic upstream impairment. Finally, this pool of candidate streams could be further filtered by identifying those that have neighboring streams with high Pr(good), thus increasing the likelihood of dispersal of native taxa from nearby reaches. We applied an example of these criteria to the ICI, IWI, and our map of Pr(good). In this illustration we selected non-headwater streams with Pr(good) < 0.5 and ICI < 0.60 (i.e., the 1^st quartile of ICI values), but with IWI > 0.75 (i.e., higher IWI than the national average). For headwater streams, we excluded the criteria of IWI > 0.75 because the catchment and watershed are the same geographic unit (Fig. 2), and restoration of the ICI would result in a commensurate increase in IWI as well. This query identified more than 7,300 km of streams within the CONUS that met these criteria (see Table 4 and Fig. 8). Notably, more than half of these stream lengths (4,659 km) were within the Temperate Plains region alone and were almost entirely comprised of 1^st order catchments (Fig. 8), suggesting that local restoration efforts could substantially improve biological conditions within the upper Mississippi Basin. Additional geospatial (e.g., land ownership) and local information (e.g., stakeholder interactions) could be used to further refine this list of candidate streams. Although this approach may overlook worthwhile restoration efforts that do not meet the above criteria, it provides an objective and easily implemented way to prioritize candidate streams. These approaches to identify streams for potential conservation or restoration are flexible because we mapped predicted probabilities of good condition rather than condition classes. In this way, these criteria can be adjusted to expand or restrict the pool of candidate streams as needed.

Table 4.

Kilometers of river by region and within the CONUS that met the criteria of an example query to identify stream reaches with (1) low probability of being good biological condition (Pr(good) < 0.5), (2) low index of catchment integrity (ICI < 0.60; the 1^st quartile of national ICI values), (3) high watershed integrity (IWI > 0.75; mean of national IWI values), and (4) either an upstream or downstream adjacent reach with high probability (Pr(good) > 0.5) of being in good biological condition. For headwater streams, the criteria of IWI > 0.75 was ignored because the local catchment and watershed are the same geographic unit and we assumed that restoration of catchments integrity would result in a commensurate increase in IWI. These criteria can be adjusted to be more or less inclusive to refine a list of candidate streams. National Aquatic Resource Surveys (NARS) region abbreviations: CPL = Coastal Plains; NAP = Northern Appalachians; NPL = Northern Plains; SAP = Southern Appalachians; SPL = Southern Plains; TPL = Temperate Plains; UMW = Upper Midwest; WMT = Western Mountains; XER = Xeric.

NARS Region	Km of River
CPL	8.5
NAP	179
NPL	39
SAP	1,983
SPL	116
TPL	4,659
UMW	235
WMT	4
XER	197
CONUS	7,331

Figure 8.

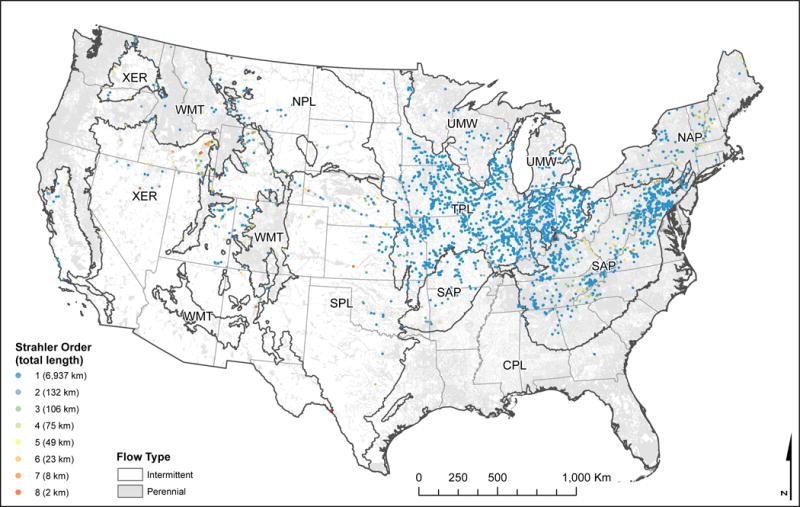
Map of streams that met the criteria of our illustrative query to identify candidate streams for restoration. The query first identified streams with predicted probabilities of good [Pr(good)] biological condition < 0.5 and an index of catchment integrity (ICI) < 0.60 (the 1^st quartile of ICI values). The query then identified streams with index of watershed integrity (IWI) values > 0.75 (i.e., higher than mean national IWI). First (Strahler) order streams were excluded from this second query because for these streams ICI and IWI are equivalent and restoration of the catchment should result in the restoration of the watershed. The final query identified streams with an upstream or downstream neighbor with Pr(good) > 0.5, thus improving the likelihood of dispersal of desired taxa from neighboring streams.

Model decisions and implications

The model decisions we explored in this study substantially affected predictions produced by the final models and may provide insight into improving other ecological models. For example, several studies have examined the effect of variable selection on RF model performances (Evans et al. 2010). However, in an examination of model selection with the same data used here, Fox et al. (2017) showed that variable selection played a negligible role in model performance and can lead to unstable predictions that vary greatly with the removal or addition of a single variable. Instead, we found that balancing the number good and poor sites during model development, excluding fair sites, and developing regional models improved model bias and precision. Parallels to these decisions may be found in other ecological modeling contexts. One such parallel is imbalanced detections of occurrence in species distribution modeling (Haibo and Garcia 2009) and balancing observations in RFs should improve the sensitivity and specificity of these models. In addition, the availability of biological datasets has increased and their aggregation has become a common practice in ecological modeling. However, this scenario may be similar to our attempt at developing a single, national model and care must be taken to ensure consistency among datasets to avoid biased predictions.

The behavior of predictions under certain model decisions could provide important insight into NRSA. Although the NRSA MMI is a national assessment, it may be viewed as an aggregation of nine regional assessments with imperfect comparability. This interpretation is supported by the greater success of regional models in balancing prediction specificity and sensitivity over the single, national model for most regions (i.e., Table 1E). The biased predictions produced by the national model may be due to differences among regions in: (1) reference site quality (Ode et al. 2016) and (2) base invertebrate metrics that composed regional MMIs (Ode et al. 2008, Mazor et al. 2016). Variation in reference site quality is a major challenge in developing precise and accurate assessments (Herlihy et al. 2008). Reference site selection represents a balance between: (1) identifying sites that are both representative of streams within a region and are minimally impaired by human activity, and (2) obtaining enough sites to provide statistical power for comparisons (Stoddard et al. 2006, Ode et al. 2016); a challenge that is highlighted by our results. Developing a single MMI or MMIs that are consistent and comparable across regions is a second challenge faced by practitioners because the taxonomic and autecological features that define streams in good biological condition also vary naturally both within and across regions (Cao et al. 2007, Mazor et al. 2016). The development of nine regional models ameliorated biases across regions, but produced sharp changes in predicted condition at regional borders (Fig. 6) and this pattern further supports the use and interpretation of NRSA MMIs on a regional, rather than national, basis. Our study does not provide a way to disentangle these two potential sources of bias in the national model. However, similar modeling of the NRSA RIVPACS assessment (Moss et al. 1987) could provide insight into this question because this assessment compares the ratio of observed taxa to those expected under reference conditions. This observed-to-expected (O/E) ratio represents taxonomic loss and can be standardized to allow comparison across regions (Hawkins 2006).

Intermittent streams

NRSA, as currently implemented, only includes streams that are designated by the NHD as perennial, and therefore excludes the majority (59%) of stream channels within the CONUS from its assessments. The percentage of excluded stream lengths can be as high as 88% in the Northern Plains (Fig. 5). Non-perennial streams often compose a large proportion of stream networks and they can strongly influence water quality and biological assemblages of downstream, perennial waters (Acuña et al. 2014, USEPA 2015). For example, dry tributaries can supply cold hyporheic flow to mainstem reaches and provide thermal refugia for cold-water taxa (Ebersole et al. 2015). The expansion and contraction of intermittent streams can influence the amount and timing of nutrient delivery to downstream reaches (von Schiller et al. 2011). In addition, the drying and re-wetting dynamics of intermittent streams can result in a diverse mix of habitats that can simultaneously support lotic, lentic, and terrestrial species (Datry et al. 2016). However the extreme hydrologic variation of intermittent streams may also exacerbate the effects of land use on their biotic communities (Cooper et al. 2013). Historically, intermittent streams have not received the same attention as perennial streams, but our awareness and understanding of the important role intermittent streams play in the quality and ecology of perennial streams is growing (Datry et al. 2016; also see special issue of Freshwater Biology [volume 61, issue 8] on intermittent streams). A comprehensive assessment of the Nation’s stream networks would require that these streams be assessed (Leigh et al. 2016). However, significant challenges still exist in assessing intermittent streams due to our limited ecological understanding of these systems. For example, we currently lack a standardized set of tools to effectively assess and monitor intermittent streams and such tools are just now being developed (e.g., Mazor et al. 2014). Perennial and intermittent stream assessments and management are further complicated by the imperfect application of these designations within the NHD framework (Fritz et al. 2013). Improvements in the accurate designation of perennial and intermittent streams are needed to correctly target and accurately assess streams using relevant assessment techniques. It will be important to continue such work if we are to assess and monitor all streams within the US and provide predictions for the remainder of streams within our map.

CONCLUDING REMARKS

Through modeling, we leveraged the EPA’s NRSA to predict the probability of streams being in good biological condition across the CONUS. This study provides an important proof-of-concept and approach for using this type of survey data to predict stream condition at large scales with geospatial information. This study provided insight into the NRSA design and how future assessments might be improved to be more representative of both perennial and intermittent streams. Specifically, intermittent streams compose a substantial proportion of streams within the CONUS and current assessment programs do not assess these important systems. Benthic invertebrate MMIs are just one of several biological assessments conducted as part of NRSA, including and O/E assessment of benthic invertebrates and MMI and O/E assessments for fish. Models of these assessments could provide additional insight into the distribution of conditions across different taxonomic groups and assessment techniques and how each responds to human-related alterations to watersheds. Furthermore, future assessments, such as the forthcoming 2013-2014 NRSA, could increase the coverage of observed conditions to improve models and further evaluate model performance.