Improving the Hospital Quality of Care during Winter Periods by Optimizing Budget Allocation Between Rotavirus Vaccination and Bed Expansion

Abstract

Background

During each winter the hospital quality of care (QoC) in pediatric wards decreases due to a surge in pediatric infectious diseases leading to overcrowded units. Bed occupancy rates often surpass the good hospital bed management threshold of 85%, which can result in poor conditions in the workplace. This study explores how QoC-scores could be improved by investing in additional beds and/or better vaccination programs against vaccine-preventable infectious diseases.

Methods

The Cobb–Douglas model was selected to define the improvement in QoC (%) as a function of two strategies (rotavirus vaccination coverage [%] and addition of extra hospital beds [% of existing beds]), allowing improvement-isocurves to be produced. Subsequently, budget minimization was applied to determine the combination of the two strategies needed to reach a given QoC improvement at the lowest cost. Data from Jessa Hospital (Hasselt, Belgium) were chosen as an example. The annual population in the catchment area to be vaccinated was 7000 children; the winter period was 90 days with 34 pediatric beds available. Rotavirus vaccination cost per course was €118.26 and the daily cost of a pediatric bed was €436.53. The target QoC increase was fixed at 50%. The model was first built with baseline parameter values.

Results

The model predicted that a combination of 64% vaccine coverage and 39% extra hospital beds (≈ 13 extra beds) in winter would improve QoC-scores by 50% for the minimum budget allocation.

Conclusion

The model allows determination of the most efficient allocation of the healthcare budget between rotavirus vaccination and bed expansion for improving QoC-scores during the annual epidemic winter seasons.

Key Points for Decision Makers

Hospital quality of care (QoC)-scores decrease in the winter due to the surge of pediatric infectious diseases.

Modelling the optimization of the healthcare budget could help to identify the balance between treatment and prevention to improve the QoC-scores to a fixed amount.

The model is able to predict which combination of the two competing strategies is the most efficient for improving the QoC-scores in pediatric hospital units during the rotavirus seasonal peak.

Background

Infectious diseases in children remain a serious health problem in hospital care during each winter period in high-income countries despite the application of strict hygienic measures and better treatment procedures. Respiratory diseases and acute gastroenteritis (AGE) peak during winter leading to overcrowded pediatric wards with high bed occupancy rates exceeding 85% on average, which is the threshold for operating efficiently in hospital bed-management [1–3]. The temporary shock in bed-demand reduces the quality of care (QoC) because of high occupancies, discharges, and unplanned returns of patients but also because of stress in healthcare workers expressed through sick leave, extra working hours, and the enrollment of interim workers [4]. Among the covariates underlying the two principal factors (bed- and staff-management) defining the hospital QoC-scores, high bed occupancy is the main driver [4]. In addition, a high concentration of infections in hospital care will result in increased nosocomial infections and in antimicrobial resistance (AMR) [2, 4–7].

To adequately tackle this annual problem one may consider building more infrastructures but that might not totally resolve the issue of nosocomial infection and AMR [8, 9]. One should also think outside the hospital infrastructure and introduce vaccination against infections that may decrease the patient hospital inflow [5, 10, 11]. The latter was observed after introducing rotavirus vaccination in 2006 in Belgium, which resulted in a highly significant improvement of the hospital QoC during the peak season [4].

Thus, only a limited number of interventions allow enhancement of a sustainable improvement in the QoC-scores translating into more treatment with a higher number of beds in the department or sharing beds with other departments, better prevention through large vaccination programs, or a combination of both. The question we would like to answer here is which is the best balance to choose between the options of treatment and prevention to maintain the substantial improvement in QoC-scores during the infection peak periods while minimizing the budget investment [12].

Data from one pediatric ward in Belgium (Jessa Hospital, Hasselt, Belgium) was analyzed with pre-vaccination data as a starting point [4]. Rotavirus disease was selected as the example of an infectious disease to control. The infection has its seasonal peak in the winter, causing dramatic increases in bed occupancy rates, and vaccines are available on the market to prevent it [13].

Methods

Quality of Care (QoC)-Isocurve Model

The baseline model developed is non-linear and multivariate, similar to the Cobb–Douglas function [14] where the output is the fixed achievement of improvement in QoC-scores ($\text{QoC}$), during the winter periods in a pediatric ward. The two influencing variables are the extra treatment (H), expressed as extra beds as a percentage of the existing number of beds, and extra prevention ($V$), expressed as absolute or extra vaccine coverage rates in the age group to be vaccinated, that is the annual birth cohort of infants below 1 year old (see Sect. 2.5) [15]. The relative contribution of each of the two variables to the QoC-score improvement is investigated. The relationship between the output ($\text{QoC}$, measured in percentage improvement) and the influencing variables ($V$ and $H$, also measured in percentage change) is considered to be positive, increasing, and concave, and is expressed as Eq. 1:

$$\text{QoC}=A·V^{\mathit{\alpha }}·H^{\mathit{\beta }},$$ 1

where $A$ is a scaling parameter and $\mathit{\alpha }$ and $\mathit{\beta }$ are the relative contribution parameters of $V$ and $H$ in the QoC-score improvement. The values of $\mathit{\alpha }$ and $\mathit{\beta }$ should be between 0 and 1, bounds excluded, to have positive but diminishing marginal factor returns (i.e., concavity). We consider these values as arbitrary throughout the article, as explained in Sect. 2.5. Consequently, the model and its subsequent illustration are more theoretical.

In a previous work, the hospital QoC-score was defined and quantified as a composite index resulting from the addition of two principal factors extracted from exploratory factor analysis taking into account ten underlying covariates that reflect the management of hospital beds and of medical staff. Among these covariates, bed occupancy was found to be the main driver of the QoC-score [4]. The hospital QoC-score improvement can vary from 0 to 100%, with 0% indicating no improvement and 100% the highest improvement. Given a certain amount of QoC improvement to be reached ($X$), the level of $H$ and $V$ can be calculated using Eq. 2:

$$H={\left(\frac{X}{A}\right)}^{\frac{1}{\mathit{\beta }}}·V^{-\frac{\mathit{\alpha }}{\mathit{\beta }}}.$$ 2

Equation 2 is the expression of a QoC-isocurve representing all possible combinations of $V$ and $H$ associated with a constant QoC-score improvement, $\text{QoC}=X$. It is used as an equality constraint in the optimization process.

Optimization Process

The subsequent step formulates the optimization model, which is defined by an objective function to be optimized through decision variables and subject to some specific constraint(s) [16, 17]. Our objective function here is the budget to be minimized, which is influenced by the two decision variables: $V$ and $H$. The constraint has been set to reach a 50% improvement in QoC-score: $X=50\%$ in Eq. 2.

The budget function ($B$) is calculated using Eq. 3:

$$B=C_V·V+C_H·H,$$ 3

where $C_V$ and $C_H$ are the costs at 100% prevention and at 100% treatment, respectively. The constrained optimization model is expressed using Eq. 4:

$$\underset{\left\{V,H\right\}}{\text{min}}B=C_V·V+C_H·H\text{subject to}H={\left(\frac{X}{A}\right)}^{\frac{1}{\mathit{\beta }}}·V^{-\frac{\mathit{\alpha }}{\mathit{\beta }}}.$$ 4

A graphical output is generated to illustrate the results.

Data Input

Rotavirus vaccination was selected to illustrate the working of the previous model construct. A Belgium hospital (Jessa Hospital) was chosen as the vaccine was introduced in Belgium in 2006. The perspective considered is the healthcare payer. Table 1 summarizes the data inputs.

Table 1.

Input variables and values in the model

Input data	Value	Source
$A$	1	Baseline assumption, neutral scaling factor
$\mathit{\alpha }$	0.5	Baseline assumption, equal contribution to the QoC improvement
$\mathit{\beta }$	0.5	Baseline assumption, equal contribution to the QoC improvement
QoC-score improvement (X)	+ 50%	Baseline constraint
Birth cohort in the catchment area	7000 children aged < 1 year old	Estimated from [18]
Existing number of beds	34 pediatric beds available	[4]
Seasonality	90 days (1 January–31 March)	[4]
Rotavirus vaccine cost per course	€118.26	Computed from [19]
Average cost of 1 hospital bed per day	€436.53	Estimated from [20]

€ 2016 euros, QoC quality of care

The rotavirus vaccine cost per course is for a two-dose vaccine (i.e., €118.26 = 2 × (71.03 − 11.90)), which has been available in Belgium since June 2006 and is partially reimbursed (i.e., co-payment is €11.90 per dose) [19]. The cost of one hospital bed per day is the average cost of a day at the Jessa Hospital for acute care, which was reimbursed in 2016 at €436.53/day [20]. The input data are used to calculate the costs of 100% prevention ($C_V$) and 100% treatment ($C_H$) plugged into the budget function: C _V = 7000 × 118.26 = €827,820, and C _H = 34 × 90 × 436.53 = €1,335,782.

Data Output

The final data output is the lowest budget (€) reached with the percentages of $V$ and $H$ needed to achieve the QoC improvement target of 50%.

Model Assumptions

A no-vaccination condition is initially considered so that absolute vaccine coverage equals the relative increase in coverage (i.e., extra vaccination). The rationale underlying this assumption is that a new birth cohort must be vaccinated every year. In other words, the vaccine coverage reflects vaccination in the annual birth cohort of infants below 1 year old and not in the population of children below 5 years old.

$\mathit{\alpha }$ and $\mathit{\beta }$ are equal, i.e., $V$ and $H$ have the same impact on the QoC improvement. This was fixed arbitrarily in order not to favor either of the two variables, $V$ and $H$. This assumption implies that the minimum budget will be allocated equally between vaccination and bed expansion.

No specific vaccine administration cost is included as the vaccine will be co-administered with other vaccines such as the hexavalent (diphtheria–tetanus–pertussis–polio–Haemophilus influenzae type B–hepatitis B) or pneumococcal vaccines as recommended in Belgium [15, 21, 22].

Full compliance with the two-dose vaccination schedule is assumed, but the benefit of vaccination in the function of the vaccine coverage resulting in a herd effect is not considered in the equations.

No prevention ($V=0$) and/or no extra treatment ($H=0$) leads to no improvement in the QoC-score ($\text{QoC}=0$). The proportion of both $V$ and $H$ should be increased to improve the QoC-score (essentiality condition).

The function exhibits diminishing marginal factor returns for $V$ and $H$: the more one factor is used, the less it will be productive in terms of adding a same effect to the QoC-score improvement.

Constant returns to scale (i.e., $\mathit{\alpha }+\mathit{\beta }=1$) are assumed for both factors: doubling the quantity of each factor would result in exactly the same proportional improvement in QoC scores. We will relax this assumption in the sensitivity analysis.

The total cost of $V$ and $H$ enters the budget function linearly. One may suspect that the cost of $V$ could be convex in function of the coverage rate, i.e., a higher coverage is more difficult and costly to achieve. However, evidence from the Belgium data showed that a high rotavirus vaccine coverage (> 85%) is reached in the first years of vaccine introduction [11]. The cost of $V$ is therefore considered linear in the budget function. The cost of adding more beds is also linear in the percentage of extra beds considered, including medical staff and building costs [20].

Sensitivity and Scenario Analyses

In the one-way sensitivity analyses data inputs are varied by ± 25% and the impact on outcome measures is assessed, i.e., optimal allocation between prevention and treatment as well as the minimum budget needed. Moreover, since the baseline relative contributions of vaccination and extra beds to the hospital QoC-score improvement are set arbitrarily, and are therefore not estimated from observed data, sensitivity of model outputs with respect to these parameters is also assessed. In particular, the values of $\mathit{\alpha }$ and $\mathit{\beta }$ are tested over six different scenarios, including the baseline values to ease the comparison, as shown in Table 2. Scenario III reflects a higher contribution to improvement in QoC-scores from vaccination versus extra hospital beds. To relax the assumption of constant returns to scale (i.e., $\mathit{\alpha }+\mathit{\beta }=1$), scenarios IV and V reflected equal relative contributions to QoC-score improvement while considering decreasing (i.e., $\mathit{\alpha }+\mathit{\beta }<1$) or increasing (i.e., $\mathit{\alpha }+\mathit{\beta }>1$) returns to scale, respectively. Scenario VI also assumes increasing returns to scale but reflects a higher contribution of $V$, for instance to account for potential additional benefits such as herd protection and reduction in AMR and nosocomial infections.

Table 2.

Testing the range of values for parameters $\mathit{\alpha }$ and $\mathit{\beta }$ in different scenarios

Scenario	Parameters	Interpretation
I	$\mathit{\alpha }=0.25$ and $\mathit{\beta }=0.75$	Higher contribution of treatment, constant returns to scale
II (baseline)	$\mathit{\alpha }=$ $\mathit{\beta }=0.5$	Equal contributions, constant returns to scale
III	$\mathit{\alpha }=0.75$ and $\mathit{\beta }=0.25$	Higher contribution of prevention, constant returns to scale
IV	$\mathit{\alpha }=$ $\mathit{\beta }=0.45$	Equal contributions, decreasing returns to scale
V	$\mathit{\alpha }=$ $\mathit{\beta }=0.55$	Equal contributions, increasing returns to scale
VI	$\mathit{\alpha }=0.55$ and $\mathit{\beta }=0.5$	Higher contribution of prevention, increasing returns to scale

$\mathit{\alpha }$ and $\mathit{\beta }$ the relative contribution parameters of prevention and treatment, respectively

In Eq. 1, the scaling parameter$A$ is said to be neutral [23], meaning that a change in $A$ does not change the ratio of marginal product of $V$ to marginal product of $H$ for a given $V$-to-$H$ ratio. Since variation in $A$ and subsequent variation in optimal allocation components is perfectly inversely proportional, there is no need to vary $A$ in sensitivity analyses.

Similarly, due to the baseline assumption of constant returns to scale a ceteris paribus variation in targeted QoC improvement will generate an exactly proportional variation in the optimal allocation components. For example, increasing the QoC improvement target from 50 to 75% (i.e., a 50%—or 25% point—increase) would also generate a 50% increase in the optimal vaccine coverage, extra hospital beds, and minimum budget needed. However, the impact of such an increase in model outcomes is assessed for illustration purposes only since the Belgian study reported an improvement of more than 100% in hospital QoC-scores after the introduction of rotavirus vaccination [4]. Finally, since the vaccine coverage achieved is above 85% when introducing the rotavirus vaccination in Belgium [11], the corresponding percentage of extra beds needed to reach a 50% QoC-score improvement is also calculated.

All calculations are conducted using MATLAB R2016a (The MathWorks, Inc., Natick, MA, USA), except for the one-way sensitivity analysis on data inputs which is done in MS Excel (Microsoft Corporation, Redmond, WA, USA).

Results

Model Output

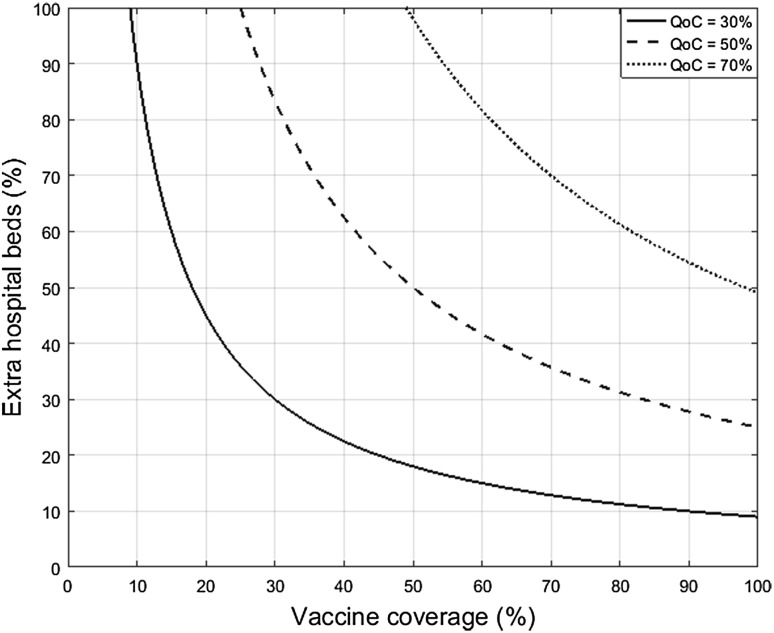
Figure 1 presents the QoC-isocurves for three improvement rates in hospital QoC-score (i.e., $\text{QoC}=$ + 30, + 50, and + 70%), with a higher improvement in hospital QoC-scores when moving to the top right of the graph. The curves are obtained by setting the parameters to baseline values in Eq. 2, described as $A=1$ (neutral scale) and $\mathit{\alpha }=\mathit{\beta }=0.5$ (equal contribution of $V$ and $H$).

Fig. 1.

Example of QoC-isocurves with baseline calibration for three different growth rates of the hospital QoC-score (i.e., $\text{QoC}=$ + 30, + 50, and + 70%). QoC hospital quality of care growth

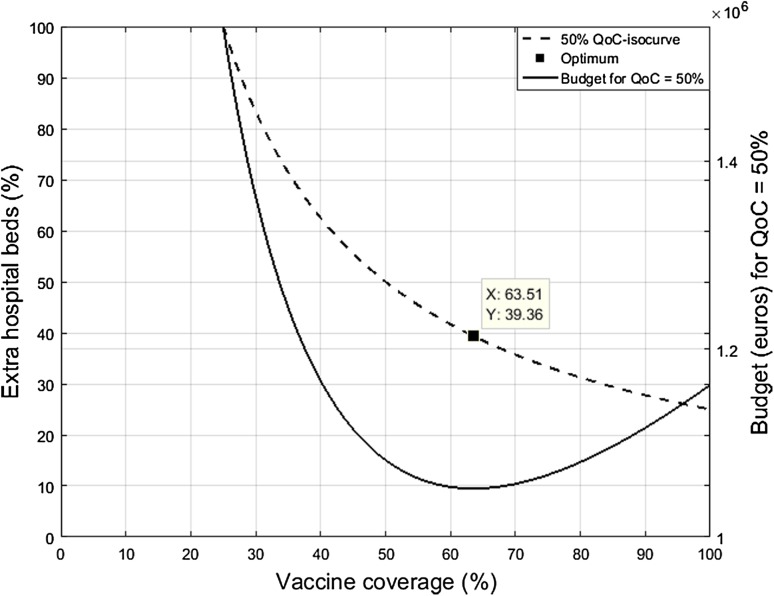
In the subsequent analysis the target improvement in hospital QoC-score is 50%, presented as the dashed QoC-isocurve of Fig. 1. Using the aforementioned data and the baseline parameter values, Fig. 2 shows the solution of the budget optimization model described by Eq. 4. To reach a 50% improvement in hospital QoC-score the minimum budget between rotavirus vaccination and rotavirus gastroenteritis (RVGE) treatment covers a combination of 63.51% vaccine coverage (V) and 39.36% extra hospital beds (H) (+ 13 extra beds) during the winter peak. This combination represents a total annual budget of €1,051,564. V ($\mathit{\alpha }$) and H ($\mathit{\beta }$) are assumed to contribute equally (50–50%) to the QoC-score improvement and, subsequently, to the minimum budget as well. In other words, the same amount of money is spent on vaccination and bed expansion. However, Fig. 2 shows that the budget curve increases faster with more H than with a higher V. Therefore, vaccination could be the most efficient option to achieve the target QoC-score improvement: an increase in H costs more than an increase in V for the same improvement in QoC-scores.

Fig. 2.

Budget-minimizing allocation between rotavirus vaccination and rotavirus gastroenteritis treatment. QoC hospital quality of care growth

Sensitivity Analysis

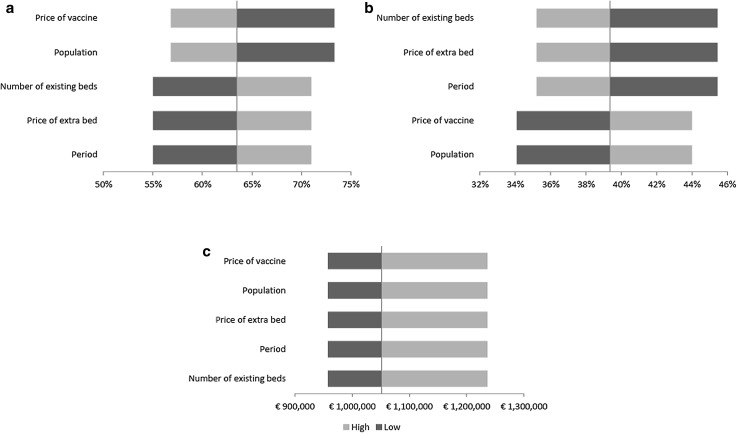
Results of the one-way sensitivity analyses are presented in Fig. 3 showing the impact of varying inputs by ± 25% on the three model outputs. The most influential factors related to optimal V are those in the composition of $C_V$, namely the vaccine cost per course and the size of the population to vaccinate. Similarly, the optimal percentage of H is most influenced by the components of $C_H$, the number of existing beds, the price of an extra bed, and the length of the evaluation period considered. Since the input data enter the calculation of the budget in the same way (through $C_V$ and $C_H$), variation in the minimum budget remained constant.

Fig. 3.

Tornado diagrams: sensitivity analyses showing the impact of varying inputs by ±  25% on three outcomes: a optimal vaccination coverage; b optimal extra hospital beds; and c minimum budget

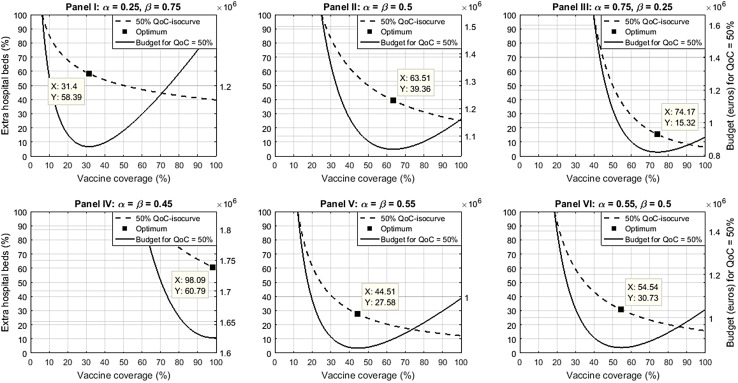
Figure 4 presents the budget-minimizing allocation for rotavirus vaccination and RVGE treatment for each of the six scenarios in the sensitivity analysis. Although the variations of $\mathit{\alpha }$ and $\mathit{\beta }$ in panels I and III are quantitatively the same around the baseline scenario (panel II), the resulting variation in the optimal combination of prevention and treatment is not symmetric. For instance, when $\mathit{\alpha }$ is reduced from 0.5 to 0.25, the optimal vaccine coverage decreases from 63.51 to 31.40% (i.e., a 50.56% decrease) (panel I), but when $\mathit{\beta }$ is reduced from 0.5 to 0.25, the optimal extra hospital beds decreases from 39.36 to 15.32% (i.e., a 61.08% decrease), a higher relative decrease for the optimal percentage of extra hospital beds (panel III).

Fig. 4.

Sensitivity analysis of model parameters ($\mathit{\alpha }$ and $\mathit{\beta }$). The budget-minimizing allocation is presented between rotavirus vaccination and rotavirus gastroenteritis treatment for each of the six scenarios of the sensitivity analysis. $\mathit{\alpha }$ and $\mathit{\beta }$ the relative contribution parameters of prevention and treatment, respectively, QoC hospital quality of care score

When considering decreasing returns to scale with $\mathit{\alpha }=\mathit{\beta }=0.45$ (panel IV), the optimal values of prevention and treatment needed to reach the same QoC-score improvement of 50% are 98.09% vaccine coverage and 60.79% extra beds (i.e., a 54.45% relative increase for both). In contrast, considering increasing returns to scale with $\mathit{\alpha }=\mathit{\beta }=0.55$ (panel V) imply a relative decrease of 29.93%, from 63.51 to 44.51% and from 39.36 to 27.58% in the optimal values of V and H, respectively. Considering a higher contribution of V versus H and increasing returns to scale with $\mathit{\alpha }=0.55$ and $\mathit{\beta }=0.5$ (panel VI) imply a V value of 54.54% and an H value of 30.73%, i.e., a lower relative decrease in optimal vaccine coverage.

In all scenarios the same evolution is observed as in Fig. 2, with a much steeper budget rise (solid curves) for increases of H than for increases in V, when deviating from the optimal combination (shown on the dashed curves).

To achieve the same objective while keeping V at 85%, as observed in Belgium post-vaccine introduction, the corresponding percentage of H is 29.41% (+ 10 extra beds), leading to a total budget of €1,096,524. Finally, the minimum budget allocation that would achieve a 75% improvement in hospital QoC-score is a combination of 95.27% vaccine coverage and 59.04% extra hospital beds (+ 20 extra beds [rounded]) during the winter season, representing a minimum budget of €1,577,346.

Discussion

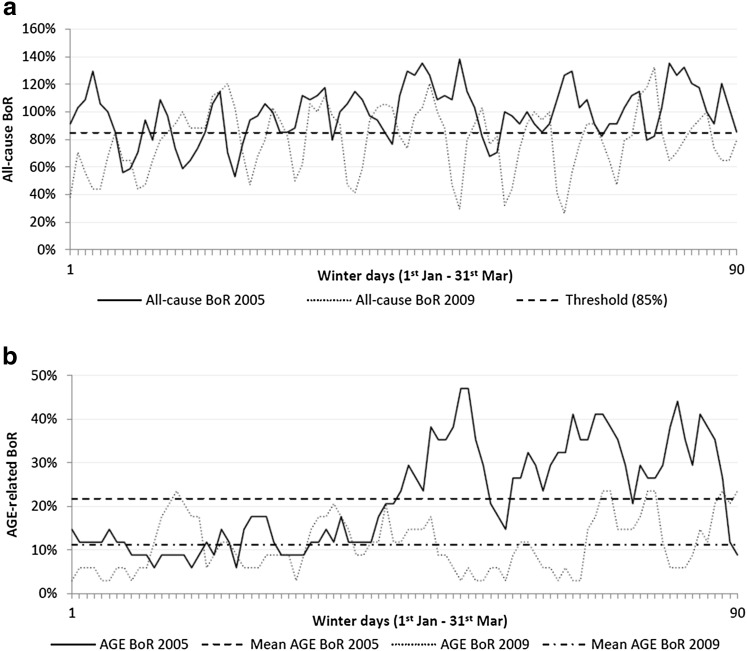
A new way to analyze and optimize the healthcare budget for reaching specific health goals is presented here using a Cobb–Douglas-like power function [14]. Here, that function measures and combines extra treatment (more beds) with extra prevention (more vaccination) to get a substantial fixed improvement in hospital QoC-scores at the lowest investment needed [24, 25]. Previous studies have shown that the QoC in pediatric wards during winter periods is low [2, 4]. Many respiratory and gastroenteritis infections occur during those periods, leading to overcrowded pediatric units with high transmission rates of infections among those children [6, 11, 26]. Figure 5a shows for Jessa Hospital that the all-cause bed occupancy rates on average exceed the 85% threshold of safe and efficient operations during winter seasons [1–3]. The problem is recurrent yearly and only a few sustainable options can solve the issue: extra beds and/or reducing the bed demand through prevention. The baseline model setting presented here indicates that the minimum budget equally distributed among prevention and treatment is optimally allocated when it combines 64% coverage of rotavirus vaccination with 39% extra hospital beds for RVGE treatment during the peak periods, obtaining a 50% QoC improvement. The budget needed to be spent annually is around €1.05 million. The cost difference between vaccine coverage ($C_V$) and extra hospital beds ($C_H$) drives the results in their optimal budget allocation.

Fig. 5.

All-cause and acute gastroenteritis-related daily bed occupancy rates in the pediatric unit (acute care) at Jessa Hospital (Hasselt, Belgium) during winter periods (1 January– 31 March) pre- versus post-vaccine introduction: a all-cause bed occupancy rate; and b acute gastroenteritis-related bed occupancy rate. AGE acute gastroenteritis, BoR bed occupancy rate

The present study also suggests that building more beds may result in only a partial solution for the recurrent healthcare problem as the infection is still kept within the hospital facility but is now spread over a larger space, and thus still causing a high risk of nosocomial infection and AMR [9]. Therefore, a better solution needs a more sustainable approach to benefit the hospital units. The way to achieving this is by reducing the infection influx entering the hospital. Vaccination should therefore be considered in this context.

The target to improve the QoC-scores in this exercise has been set at 50%. However, the QoC-scores of the pediatric ward in the Belgian study improved by more than 100% after introducing the vaccine [4]. Vaccination alone could therefore easily be sufficient to reach the improvement level proposed in our exercise. Our analysis is thus quite conservative. However, the purpose of the exercise is to demonstrate new ways of presenting the economic value of vaccine prevention as opposed to extra treatment, solving an existing and specific healthcare problem [27]. It gives the decision maker another analysis framework when he/she needs to invest in one or another option for achieving specific healthcare goals. The results of the exercise indicate that increased childhood vaccination could prevent or even reduce pediatric treatment care. This is now reflected in rotavirus vaccination post-implementation data, showing that when current-day pricing and herd effects are accounted for, the vaccination is cost effective and can even be cost saving [28]. The trade-off between vaccination and adding extra beds may in the future become the trade-off between vaccination and bed reduction in order to improve the QoC at a reasonable extra cost if more vaccination options against other infections are available.

The limitation of the present research is the use of a production-like function to solve a healthcare problem with only two variables. The selection of only two variables is intentional as prevention and treatment are restricted to vaccine coverage (V) and extra hospital beds (H). Yet, prevention could also include hygiene measures (e.g., hand washing) and treatment could include transportation to other hospitals. Other demand-side strategies to increase capacity, while keeping the existing number of beds and reducing demand (e.g., rescheduled elective stays, transfer of patients, etc.), could also have been considered. Since those other options would only account for a marginal part of the costs and are expected to have a marginal impact on the QoC-scores compared with extra hospital beds and vaccination [4, 5, 29–31], they have not been included in the analysis.

The advantages of using a generalized form of the Cobb–Douglas function is that the equation is convenient to work with as it has nice mathematical properties and can easily be translated into an econometric model [32]. In the analysis presented here, the labour component of the original function has been replaced by prevention. The reason for doing this is twofold. First, the cost of an extra bed includes medical staff costs. Second, as shown in Fig. 5, there is a significant decrease in AGE-related bed occupancy rates after the introduction of rotavirus vaccination. Combining these factors using a multivariate power function, such as the Cobb–Douglas one, seemed appropriate since vaccination and extra hospital beds interact together and may have a significantly positive, eventually diminishing, marginal impact on hospital QoC-scores.

In the baseline setting the model assumed that $A=1$ (neutral scaling factor) and $\mathit{\alpha }=\mathit{\beta }=0.5$ (i.e., prevention and treatment contribute equally to the QoC-score improvement). Keeping $\mathit{\alpha }+\mathit{\beta }=1$ implies that the Cobb–Douglas function is first-order homogeneous in $V$ and $H$ with constant returns to scale and diminishing factor returns (i.e., $\mathit{\alpha },\mathit{\beta }\in (0,1)$). Changing $V$ and $H$ by the same positive factor would result in an exactly proportional change in output. Furthermore, because the analysis omitted other factors that could influence the hospital QoC-score (e.g., income, location, hygiene promotion in hospitals, etc.), improvement is only determined by the model design of prevention through vaccination and treatment through extra hospital beds.

The time horizon of the model is 90 days per year, corresponding to the winter period during which the problem of low QoC-scores appears. This restricted period of evaluation should not be seen as a limitation in the process of QoC-score improvement. The latter is a dynamic process over several years with annual peaks that decrease over time depending on the vaccine coverage rates. Moreover, starting each year from a no vaccination situation seems reasonable as the rotavirus epidemic takes place every year during each winter period, and the vaccination of each new birth cohort each year must be maintained. Therefore, starting from a no vaccination situation and considering the 90-day winter period only does not seem too restrictive.

Based on the limitations of the work presented here, the challenge for future research is to collect the data that more precisely estimate the parameters of the model function developed using appropriate econometric techniques for quantifying the contribution of each factor in improving QoC-scores while calibrating the model to a specific region or hospital. The model could handle multiple variables simultaneously, introducing other relevant factors, including interactions, which could be another possibility for further research development [33]. Other specifications such as generalized additive models (GAMs) or transcendental logarithmic (translog) functions could also be considered to contrast with the function we have here, avoiding making explicit assumptions on factor and scale returns. However, GAMs and translog functions are less easily translatable into an econometric model. The exercise was tested using a GAM function (i.e., $\text{QoC}=V^{\mathit{\gamma }}+H^{\mathit{\gamma }}$) but the results were not robust to small variations in the parameters.

Conclusion

A production-like function model and a budget optimization model were applied to evaluate how treatment or prevention could improve QoC-scores in hospital bed management. These models could become an easy application tool to guide decision makers in their investment decisions. The analysis does not require a large number of data and the interpretation of the results is straightforward. The models help clarify the dilemma of investing in an optimal mix of both treatment and prevention that will find the right balance between those two forces in healthcare development programs, and thus improving the QoC-scores in the hospital environment.

Author contributions

All authors participated in the design, implementation, or analysis, and interpretation, of the study, and the development of this manuscript. All authors had full access to the data and gave final approval before submission. Thibaut Dort will act as the overall guarantor of the study and manuscript.

Compliance with Ethical Standards

Data availability statement

All data used in this manuscript are either detailed in the methods or can be found in the referenced literature. The MATLAB^® codes of the model and sensitivity analysis on parameters are also available from the corresponding author on a reasonable request.

Funding

GlaxoSmithKline Biologicals S.A. funded this study (GSK study identifier: HO-13-14103) and all costs related to the development of this manuscript.

Conflict of interest

TD reports consulting fees to his institution, Keyrus Management S.A., from the GSK group of companies. NS reports consulting fees to her institution, Keyrus Biopharma, from the GSK group of companies. TD and NS also report receiving travel to congress and accommodation from the GSK group of companies. BS is an employee of the GSK group of companies and holds shares in this company as part of his employee remuneration.

Ethics approval and consent to participate

Ethical approval was not required for this study as it is entirely based on publicly available data and did not include personal data.