Quantitative Two-Dimensional Ultrashort Echo Time Magnetization Transfer (2D UTE-MT) Imaging of Cortical Bone

Abstract

Purpose

To investigate quantitative 2D ultrashort echo time magnetization transfer (UTE-MT) imaging in ex-vivo bovine cortical bone and in-vivo human tibial cortical bone.

Methods

Data were acquired from 5 fresh bovine cortical bone samples and 5 healthy volunteer tibial cortical bones using a 2D UTE-MT sequence on a clinical 3T scanner. The 2D UTE-MT sequence employed four or five MT powers with five frequency offsets. Results were analyzed with a two-pool quantitative MT model, providing measurements of macromolecular fraction (f), macromolecular proton transverse relaxation times (T_2m), proton exchange rates from water/macromolecular to the macromolecular/water pool (RM_0m/RM_0w) and spin-lattice relaxation rate of water pool (R_1w). Besides, a sequential air-drying study for a small bovine cortical bone chip was used to investigate whether above MT modeling parameters were sensitive to the water loss.

Results

Mean fresh bovine cortical bone values for f, T_2m, R_1w, RM_0m, and RM_0w were 59.9±7.3%, 14.6±0.3 μs, 9.9±2.4 s⁻¹, 17.9±3.6 s⁻¹ and 11.8±2.0 s⁻¹, respectively. Mean in vivo human cortical bone values for f, T_2m, R_1w, RM_0m and RM_0w were 54.5±4.9%, 15.4±0.6 μs, 8.9±1.1 s⁻¹, 11.5±3.5 s⁻¹ and 9.5±1.9 s⁻¹, respectively. Besides, the sequential air-drying study shows that f, RM_0m and R_1w were increased with longer drying time.

Conclusion

UTE-MT two-pool modeling provides novel and useful quantitative information for cortical bone.

Introduction

Osteoporotic fractures, such as of the hip and vertebra, have a very high morbidity and mortality (1). With a lifetime risk of approximately 40–50% for women and 13–22% for men, osteoporotic fractures are generally defined as occurring at sites of low bone mineral density (BMD) (2). Although BMD is considered the standard measure for the diagnosis of osteoporosis and assessment of fracture risk, several studies have demonstrated that BMD cannot be used as the sole predictor of bone strength. In particular, changes in BMD have been shown to account for < 50% of variation in whole bone strength (3), with the majority of fragility fractures occurring in patients with a T-score > −2.5 (4, 5). Identification of more sensitive determinants of bone strength using magnetic resonance imaging (MRI) has consequently been an active area of interest.

Due to the short T₂ components of bone matrix, clinical MRI systems are generally limited to the imaging of the marrow space. While high resolution MRI has been shown to detect age and disease-induced changes in trabecular morphology (6), the use of ultrashort echo time (UTE) pulse sequences has allowed for the quantitative evaluation of cortical bone (7–10). Water content and T₂* measurements have been shown to correlate with cortical bone porosity and failure properties (8, 10). Despite that, protons with extremely fast transverse relaxation, such as tightly bound water and collagen protons, remain undetectable even when UTE is employed. Magnetization transfer (MT) imaging has therefore been investigated as a potential method to indirectly assess these “invisible” proton pools.

The MT technique generates unique contrast and quantitative information in MRI by exploiting coupling processes between macromolecular and mobile protons. MT imaging uses an off-resonance radiofrequency (RF) pulse to preferentially saturate macromolecular protons. Since macromolecular protons can influence the spin state of mobile protons, this off-resonance saturation can be subsequently transferred to mobile protons and thereby be measured by MRI. The extent of magnetization transfer between these two pools of protons depends on their rate of exchange (11). In combination with UTE (UTE-MT), MT has been studied as a quantitative measure of short T₂ tissues (12, 13). More recently, magnetization transfer ratios (MTR) using the UTE-MT technique have been shown to be sensitive to cortical bone porosity, as determined by μCT, and biomechanical function (14).

To improve the sensitivity and reproducibility of MT metrics in cortical bone, we sought to explore a more quantitative modeling of MT phenomena in combination with UTE. We aimed to optimize acquisition protocols and better understand MT behavior in ex vivo bovine and in vivo healthy human tibial cortical bone. Our purpose was to establish methods enabling UTE-MT two-pool modeling measurements that might potentiate new surrogate markers for cortical bone strength.

Methods

Two-Pool MT Modeling

Two-pool MT modeling was performed to measure macromolecular fraction (f), water proton transverse relaxation time (T_2w), macromolecular proton transverse relaxation time (T_2m), proton exchange from water to macromolecular pool (RM_0m), and proton exchange from the macromolecular to water pools (RM_0w). Two-pool UTE-MT modeling was largely based on the previously described Ramani model (15), in which the MT pulse was treated as a rectangular continuous wave (CW) signal with the same mean saturating power as the experimentally used shaped pulse, or the so-called continuous wave power equivalent (CWPE) approximation. The angular frequency of precession w_CWPE induced by the off-resonance MT pulse was used to measure the amplitude of the B₁ field. The UTE-MT signal was modeled by the following equation (15):

$$S=g{M}_{0w}\frac{R_{1m}\left[\frac{R{M}_{0w}f}{R_{1w}(1-f)}\right]+R_{\mathit{RFm}}+R_{1m}+R{M}_{0w}}{\left[\frac{R{M}_{0w}f}{R_{1w}(1-f)}\right](R_{1m}+R_{\mathit{RFm}})+\left(1+{\left[\frac{w_{\text{CWPE}}}{2\pi \mathrm{\Delta }f}\right]}^2\left[\frac{1}{R_{1w}{T}_{2w}}\right]\right)(R_{\mathit{RFm}}+R_{1m}+R{M}_{0w})}$$ [1]

where M_om and M_ow are the fully relaxed magnetizations of macromolecular and water pools, respectively. f is defined as $\frac{M_{0m}}{M_{0m}+M_{0w}}$. R_1m and R_1w are the corresponding longitudinal rate constants. g is an amplitude scaling factor. R is the first-order magnetization exchange rate constant between the two pools. R_RFm is the loss rate of longitudinal magnetization of the macromolecular pool due to the RF saturation of the MT pulse. Here we employ a Gaussian lineshape for the macromolecular proton pool in cortical bone due to its extremely short T₂ value (16). Additional details regarding the UTE-MT two-pool modeling used in this study have been previously reported (17).

Pulse Sequence

The 2D UTE-MT sequence employs an MT preparation pulse followed by a basic 2D UTE data acquisition. The basic 2D UTE sequence uses a hard pulse or a short half pulse excitation followed by 2D radial ramp sampling. Fast transmit/receive switching allows for a minimal nominal TE of around 10 μs (14). The MT preparation pulse is a Fermi pulse with a duration of 8 ms, a spectral bandwidth of 0.8 kHz, a maximal B₁ of 24μT and a maximal saturation flip angle of 1740°. The Fermi pulse was employed because it provided an improved spectral profile compared with a rectangular pulse and higher efficiency compared with conventional Gaussian or sinc pulses, facilitating MT modeling of cortical bone, which has an extremely short apparent transverse relaxation time or T₂*. 2D UTE-MT data were acquired with a series of MT pulse frequency offsets (Δf) and powers (ω₁) for two-pool MT modeling.

Ex Vivo UTE-MT Imaging

In total, five mature bovine femoral and tibial midshafts from freshly slaughtered animals were obtained from a local slaughterhouse and cleaned of external muscle and soft tissue. A bovine cross-section with approximate thickness of 4 cm was cut from each specimen using a low-speed diamond saw (Isomet 1000, Buehler) with constant water irrigation, and stored in phosphate buffered saline (PBS) solution for 24 hours prior to use. A wrist coil (BC-10, Medspira, Minneapolis, MN) was used for both signal excitation and reception. The 2D non-selective UTE-MT imaging protocol included: TR=100 ms, TE=10 μs, FOV=8×8 cm², hard excitation pulse (32 μs) with a flip angle =10°, acquisition matrix=128×128, five MT powers (300°, 600°, 900°, 1200° and 1500°) and five MT frequency offsets (2, 5, 10, 20 and 50 kHz), with a total of 25 different MT datasets. The total scan time was about 17.5 min. T₁ values were measured with the same UTE sequence except without MT preparation using a rectangular excitation pulse (duration = 80 μs) with a flip angle=25° and multiple TRs (i.e. 24, 50, 100, 200, 400, 600, 800 ms). Then T₁ was calculated by fitting the following equation (18, 19):

$$S=S_0{e}^{-\frac{TE}{T_2^{\ast }}}\frac{1-e^{-\frac{TR}{T_1}}}{1-cos(\theta )e^{-\frac{TR}{T_1}}}$$ [2]

Where S₀ is the signal intensity in the equilibrium state and TE is a constant. Therefore, the first two elements in the above equation can be combined into a constant when fitting. Total scan time was about 15.2 min.

A sequential air-drying study was also performed to investigate whether UTE-MT modeling parameters are sensitive to the water content loss in cortical bone. A bovine cortical bone chip was cut with approximate dimensions of 18×12×5 mm³. The bone chip was immersed in PBS for 30 mins before the first experiment. The second and third experiments were conducted after one and three hours of air-drying in a 22°C condition, respectively. A 30 ml birdcage coil was used for both RF transmission and signal reception. The sequence parameters were identical to the above bovine cortical bone sample study.

Reproducibility was investigated for the two-pool UTE-MT modeling of cortical bone with three measurements. The MRI system was reset before each measurement and the same slice location was used for all the measurements. Mean and standard deviation values of the three independent measurements were calculated.

In Vivo UTE-MT Imaging

The 2D UTE-MT sequence was also applied to the tibial midshaft of five healthy volunteers (all males, 28–43 years old, mean/standard deviation=32.6±6.4 y) for two-pool modeling. Written informed consent approved by our Institutional Review Board was obtained prior to their participation in this study. An 8-channel knee coil was used for signal excitation and reception. The protocol was similar to that for the bovine specimens, except for the use of a soft half pulse excitation with variable rate selective excitation (VERSE) (pulse duration=472μs, pulse bandwidth=2.7 kHz), FOV=10×10cm², slice thickness of 7mm, acquisition matrix=192×192, and four MT powers (600°, 900°, 1200° and 1500°) for a total scan time of 14 min. T₁ value was measured with a similar 2D selective UTE sequence (flip angle=25°) and TRs=10, 40, 70, 100, and 150 ms for a scan time of 2.6 min.

Data Analysis

The analysis algorithm was written in MATLAB 2012a (MathWorks Inc., Natick, MA, USA) and was executed offline on the DICOM images obtained by the 2D UTE-MT protocols described above. Two-pool UTE-MT modeling was performed on the bovine femoral midshaft and human tibial midshaft cortical bones, and was performed pixelwise (i.e. quantitative mapping) as well as by using the mean values of regions of interest (ROIs) placed in each image separately. Mean and standard deviation of macromolecular proton fractions, relaxation times, exchange rates and water longitudinal relaxation rates were calculated and summarized.

Results

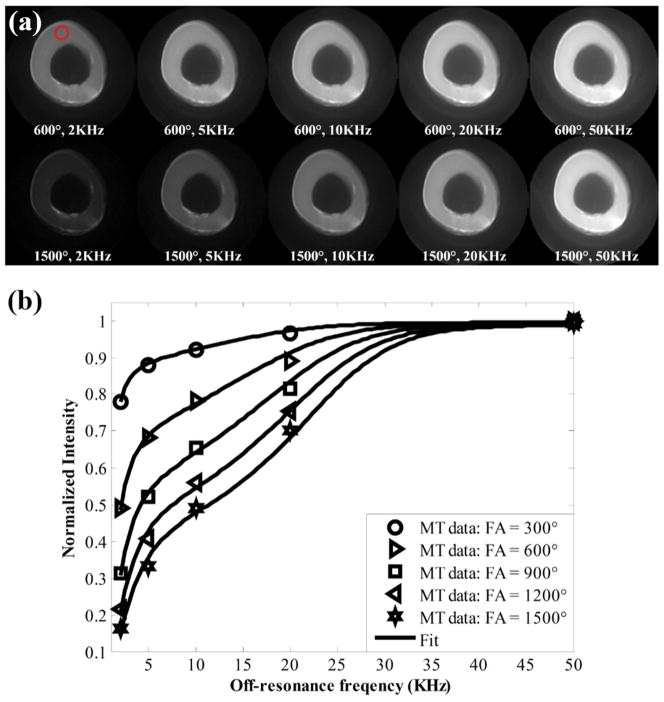
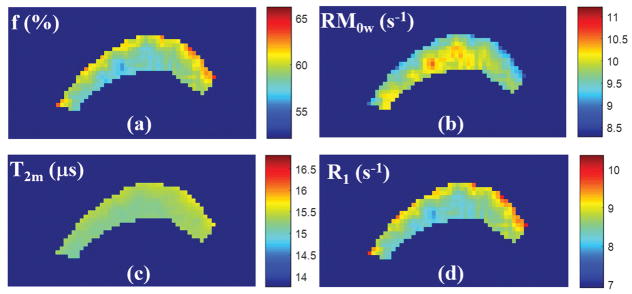
Figure 1 shows 2D UTE-MT images from an ex vivo bovine cortical bone sample with different MT flip angles and off-resonance frequencies. Increased cortical bone signal intensity is observed at low MT flip angles and high off-resonance frequencies. The excellent fitting curves demonstrate the validity of using the 2D UTE-MT sequence to model MT effect in cortical bone which has extremely short T2 and shows as signal void when imaged with conventional clinical sequences. Color maps of select MT modeling parameters from another bovine cortical bone specimen are presented in Figure 2. The parameter distributions of MT modeling can be seen in the analyzed region.

Figure 1.

(a) Representative MT images from an ex vivo bovine cortical bone specimen obtained with MT flip angles of 600° and 900° at increasing off-resonance frequencies of 2, 5,10, 20, and 50 kHz. (b) Fitting curves for cortical bone signal intensity versus off-resonance frequency for multiple MT flip angles are shown. Increased cortical bone signal intensity is observed at low MT flip angles and high off-resonance frequencies. Red circle in top left MT image (600°, 2 kHz) (a) shows region of interest used for signal intensity measurement.

Figure 2.

Color mapping of MT modeling parameters from an ex vivo bovine cortical bone specimen, including macromolecular fraction (f) (a), proton exchange rate from the macromolecular to water pools (RM_0w) (b), T₂ relaxation time of the macromolecular pool (T_2m) (c), and spin-lattice relaxation rate of the water pool (R_1w) (d). Color maps demonstrate good homogeneity of MT modeling values within cortical bone. Color bar indicates the gradation of MT modeling measures.

For the reproducibility study, mean and stand deviation values of three independent measurements for f, T_2m, R_1w, RM_0m, and RM_0w were 56.1 ± 1.0%, 14.2 ± 0.02 s⁻¹, 16.9 ± 0.8 s⁻¹, 13.2 ± 0.1 s⁻¹ and 8.9 ± 0.4 s⁻¹, respectively, demonstrating excellent reproducibility of the 2D UTE-MT modeling technique.

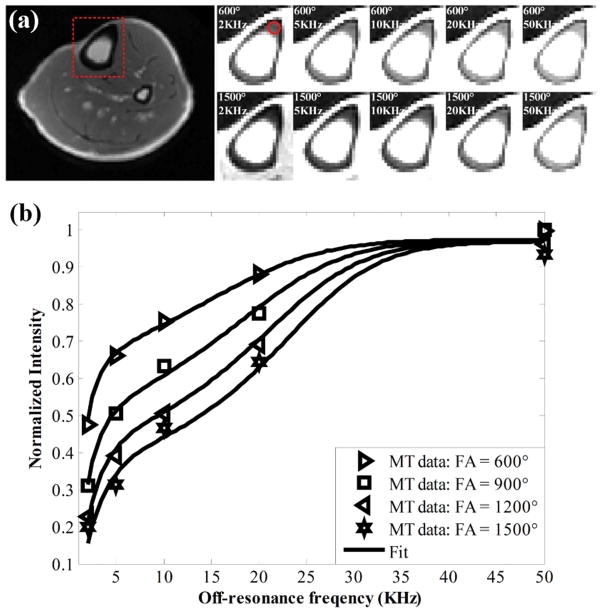
UTE-MT images from in vivo human cortical bone are shown in Figure 3. Representative images at MT flips angles of 600° and 1500° show increased cortical bone signal intensity with lower MT power and higher off-resonance frequencies. Again, excellent curve fitting was achieved for all 2D UTE-MT data acquired with different MT flip angles and off-resonance frequencies, suggesting the feasibility for fast MT modeling of cortical bone in vivo.

Figure 3.

(a) Representative MT images from in vivo human tibial cortical bone obtained with MT flip angles of 600° and 900° at increasing off-resonance frequencies of 2, 5, 10, 20, and 50 kHz. (b) Fitting curves for cortical bone signal intensity versus off-resonance frequency for multiple MT flip angles are shown. Similar to bovine cortical bone, increased signal intensity is evident at low MT flip angles and high off-resonance frequencies. Red dashed box in far-left image (a) shows field of view selection for MT analysis. Red circle in top left MT image (600°, 2 kHz) (a) shows region of interest used for signal intensity measurement.

Quantitative MT modeling measurements of ex vivo and in vivo cortical bone are presented in Tables 1 and 2, respectively. Mean bovine cortical bone values for f, T_2m, R_1w, RM_0m, RM_0w, and residual of fitting were 59.9 ± 7.3%, 14.6 ± 0.3 μs, 9.9 ± 2.4 s⁻¹, 17.9 ± 3.6 s⁻¹, 11.8 ± 2.0 s⁻¹, and 1.8 ± 0.1%, respectively. Mean human cortical bone values for f, T_2m, R_1w, RM_0m, RM_0w, and residual of fitting were 54.5 ± 4.9%, 15.4 ± 0.6 μs, 8.9 ± 1.1 s⁻¹, 11.5 ± 3.5 s⁻¹, 9.5 ± 1.9 s⁻¹, and 2.7 ± 0.3%, respectively.

Table 1.

Quantitative MT modeling measurements^* for ex vivo bovine cortical bone (N = 5).

	f (%)	T2m (μs)	R1w (s−1)	RM0m (s−1)	RM0w (s−1)	Residuals (%)
1	57.4	14.5	8.9	15.5	11.5	1.7
2	59.6	14.7	9.5	16.2	11	1.7
3	71.4	14.8	13.9	24.3	9.7	1.9
4	59.6	14.7	9.4	17.2	11.7	1.8
5	51.5	14.1	7.6	16.1	15.2	1.9

^*f = macromolecular fraction; T_2m = T₂ relaxation time of macromolecular pool; R_1w = spin-lattice relaxation rate of water pool; RM_0m = proton exchange rate from water to macromolecular pool; RM_0w = proton exchange rate from macromolecular to water pool, Residuals = Residual of fitting.

Table 2.

Quantitative MT modeling measurements^* for in vivo human tibial cortical bone (N = 5).

	f (%)	T2m (μs)	R1w (s−1)	RM0m (s−1)	RM0w (s−1)	Residuals (%)
1	61.3	15.5	10.6	13.6	8.6	2.9
2	54.2	16.0	9.4	8.6	7.3	2.3
3	51.1	15.6	8.1	10.1	9.7	2.8
4	48.8	15.5	7.8	8.8	9.3	2.5
5	56.9	14.4	8.7	16.6	12.5	2.9

^*f = macromolecular fraction; T_2m = T₂ relaxation time of macromolecular pool; R_1w = spin-lattice relaxation rate of water pool; RM_0m = proton exchange rate from water to macromolecular pool; RM_0w = proton exchange rate from macromolecular to water pool, Residuals = Residual of fitting.

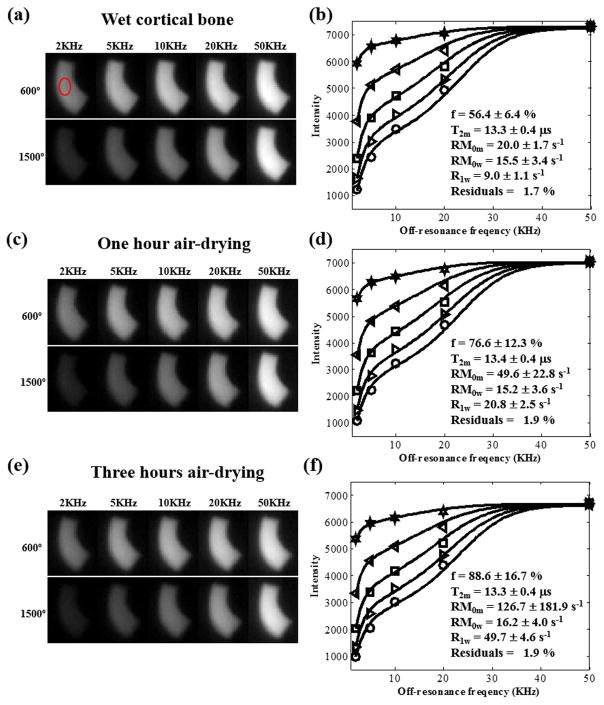
Figure 4 shows the results of the sequential air-drying study. f, RM_0m and R_1w were increased with longer drying time. In addition, almost no changes were observed in T_2m.

Figure 4.

(a), (c) and (e) are representative MT images from the sequential air-drying bovine cortical bone study (i.e. wet bone, one hour of drying and three hours of drying) obtained with MT flip angles of 600° and 900° at increasing off-resonance frequencies of 2, 5,10, 20, and 50 kHz. (b), (d) and (f) are corresponding fitting curves for cortical bone signal intensity versus off-resonance frequency for multiple MT flip angles are shown. Red circle in top left MT image (600°, 2 kHz) (a) shows region of interest used for signal intensity measurement. The sequential MT modeling results are also shown in (b), (d) and (f).

Discussion

In this study, we demonstrated that a quantitative model of MT can be performed in ex vivo bovine and in vivo human cortical bone with suitable estimates of model parameters. We found the two-pool model to appropriately describe the acquired signal as a function of off-resonance RF power and frequency with good fit.

Several pools of proton signal in cortical bone have been identified, which differ considerably in their transverse relaxation times. Horch et al. postulated six biophysical origins of NMR signal in cortical bone, including collagen methylene, collagen amides/hydroxides, mineral hydroxides/water, collagen-bound water, pore space water, and lipid methylene (20). Since most MRI techniques of cortical bone are dominated by signal from collagen-bound water and to a lesser extent pore water, most prior studies have focused on these proton pools (21–23). Several studies have shown that cortical porosity, such as from increased bone turnover or age-related bone loss, is a major determinant of bone mechanical strength (24–28). Hence, identifying potential surrogate measures of cortical porosity has been an area of considerable interest, especially using UTE techniques. For example, subsequent in vivo studies have validated the use of UTE MRI techniques for the assessment of bound and pore water (29, 30). More recently, UTE MRI has been combined with MT technique (UTE-MT) to not only assess cortical bone water, but also the extremely short T₂ macromolecular proton pool (15, 31).

Despite the potential advantages of UTE-MT over other methods of bone quantification, UTE-MT measurements are intrinsically semi-quantitative (14). Several variables can influence MTR, including main magnetic field and RF homogeneities, inherent tissue T₁ and T₂ relaxation times, and pulse sequence application. Well established in CNS applications (32, 33), models detailing the MT process have been developed that are implementation independent with few recent studies describing this technique in musculoskeletal applications, such as in Achilles tendon and muscle (17, 34). To our knowledge, however, UTE-MT using two-pool modeling has not been previously reported in cortical bone.

Quantitative UTE-MT parameters obtained were f, T_2m, R_1w, RM_0m, and RM_0w. Previous studies show that all the MT modeling parameters are independent and can be uniquely determined (15, 16). These parameters are expected to provide information on various tissue properties. Higher MT powers can saturate macromolecular protons more effectively, allowing more accurate MT modeling. However, proper consideration should be given to the MT powers that are used because higher MT power will generate higher specific absorption ratio (SAR), which can be problematic, especially for in vivo studies. Powers up to 1500° with a TR of 100 ms represents a good balance between high saturation efficiency and SAR limitation for in vivo imaging of the tibial midshaft. For MT modeling, the acquired data with a wide range of saturation including high saturation to non-saturation conditions are needed for accurate modeling since there are a total of five fitting parameters. The macromolecular components have a broad lineshape with a T₂ around a few microseconds. Thus, a wide range of off-resonance frequencies from 2 KHz to 50 KHz and MT powers from 300° to 1500° can generate a broad range of signal saturation. To achieve relatively accurate MT modeling, the lowest off-resonance frequency is chosen in order to minimize direct saturation of the water pool. Therefore, the lowest off-resonance frequency for MT modeling of short T₂ tissues such as cortical bone (minimal off-resonance frequency offset of 2KHz) is higher than that of long T₂ tissues such as white matter and optic nerve (i.e. 1KHz).

The bound or macromolecular fraction is a measure particularly unique to quantitative MT modeling. We observed mean macromolecular fractions of 59.9 ± 7.3% and 54.5 ± 4.9% in ex vivo bovine and in vivo human tibial cortical bone, respectively. The corollary of these results is in keeping with previous measures of total water content (17.4–24.8%) among in vivo human tibial cortical bone studies (10, 35, 36). Based on NMR experiments in human cortical bone, greater than 80% of signal contributions from this observed proton fraction would be expected to correspond with collagen methylene (20). Since serum and urine collagen degradation products seen with increased bone resorption may be confounded by various factors such as circadian rhythm, fracture healing and others (37), cortical bone bound fraction might be complementary to existing methods used for treatment monitoring and fracture risk prediction. The disease specificity of such a measure however must be determined in patient studies prior to forming a conclusion on the clinical use of quantitative UTE-MT in cortical bone.

For the sequential air-drying study, f, RM_0m and R_1w are increased with longer drying time. f is increasing due to more water loss with a longer drying time. With air-drying, free water can be lost much more quickly than bound water (38). As a result, bound water will represent a higher fraction of the water pool. Besides, exchange rates R, RM_0m and R_1w of bound water content are higher than that of free water content. So both RM_0m and R_1w increase with longer drying time. No significant change in RM_0w was observed because of the compromise of the increasing R and decreasing M_0w. There is no change in T_2m because the short period of air-drying does not affect the macromolecular proton pool much. Further air-drying studies would be interesting to investigate the changes of free water, bound water and macromolecular proton contents when combined with UTE-MT modeling and UTE bi-component analysis (38).

Furthermore, the five MT modeling parameters including f, T_2m, R_1w, RM_0m, and RM_0w can be potentially useful biomarkers, especially considering that those biomarkers are insensitive to the magic angle effect (17). Conventional T₂ and T_1rho may increase by several fold when the collagen fibers are reoriented from 0° to 55° (the magic angle) relative to the B₀ field (39), while the MT modeling parameters are relatively constant with less than 10% increase near the magic angle (17). The UTE-MT modeling parameters may be useful in the diagnosis and treatment monitoring of osteoporosis, where the macromolecular proton fraction is expected to inversely correlate with cortical porosity. Other MT modeling parameters such as relaxation times and exchange rates may also be correlated with bone properties. Further validation studies on cortical bone samples to correlate UTE MT modeling parameters with micro-CT measurements (cortical porosity, bone mineral content and bone mineral density), and biomechanics including elastic (modulus, yield stress and strain) and failure (ultimate stress, failure strain and energy) properties are still under investigation. The fitted parameter T_2w is known to be less accurate, as has been discussed in greater detail in Ref. 40. Lack of consideration of the excitation pulse for this MT model and low duty-cycle of the UTE-MT sequence due to SAR limitation can both lead to inaccurate T_2w estimation. For 2D UTE-MT modeling of cortical bone, T_2w may be subject to increased error due to the simplification of both bound water and free water into a single water pool. Another way is to measure T_2w with fast multi-echo UTE sequences. The curves did not fit the experimental data perfectly, which is probably due to the two-pool approximation. In fact, there are many proton pools in bone tissues including a free water pool, a bound water pool, and a macromolecular pool. Therefore, a two-pool model may not be accurate but just a reasonable approximation where bound water and free water are simplified as one water pool. In addition, there were also biases between the fitting curves and the experimental data for 2D UTE-MT modeling. However, these biases were also present in the Ramani model, which was used to evaluate the cerebral cortex and a multiple sclerosis (MS) lesion (see Fig. 2 in Ref. 15). Though a slight fitting bias exists, their results show that the MT modeling parameters can be good biomarkers to distinguish between normal white matter and MS lesions. We hope the 2D UTE-MT modeling parameters can similarly provide clinically useful biomarkers of cortical bone properties such as cortical porosity and biomechanical properties. Clearly a lot more research remains to be performed.

Fat has a much higher signal intensity than cortical bone and will also lead to off-resonance and Gibbs ringing artifacts. Therefore, the MT modeling parameters may be affected by fat. Recently, Smith et al. reported that with increased fat fraction, both macromolecular fractions and exchange rates are decreased but T₂ relaxations are increased by numerical simulation (41). To reduce the fat contamination induced errors, they incorporate Dixon multi-echo fat-water separation for fat-free MT modeling. Incorporating fat-water separation methods into UTE-MT modeling can potentially resolve this issue, and will be investigated in future studies.

Simulations have been performed to investigate the effects of B₁ inhomogeneity on MT modeling. From our simulations, if B₁ changes by 5%, the T₁ value measured with the variable TR method will change by 9.3% and MT parameters including f, RM_0m, RM_0w and R_1w will change by 2.3%, 8.9%, 12.9% and 8.7% respectively. There is almost no change for T_2m. Therefore, B₁ variation can lead to increased errors in MT quantification, especially for RM_0m, RM_0w and R_1w. On the other hand, a smaller degree of error is observed for f and T_2m due to B₁ inhomogeneity. To fully address the errors induced by B₁ variation, correction techniques are needed for accurate MT quantification with a measured B₁ map (42).

There are several limitations to this study. First, we had a small sample size for both ex vivo and in vivo groups. Second, imaging time was clinically prohibitive and longer compared to other bone water quantification methods, including semi-quantitative UTE-MT MTR measurements (12, 14, 37). Some potential strategies to reduce scan time for clinical use include employing fewer datasets, selecting MT powers and frequency offsets using Cramer-Rao lower bounds theory (43), and compressed sensing reconstruction (44). Third, consideration must be given to the level of RF power deposition generated by acquiring MT data at different MT pulse powers and off-resonance frequencies. This may ultimately impact the dynamic range of quantitative UTE-MT acquisitions. Lastly, most of the previously reported quantitative MT models assume only two pools of protons (water and macromolecular protons) (13, 15, 16), theoretically however, a three-pool model (free water, bound water, and macromolecular protons) would be more accurate than the two-pool model for evaluating biological tissues (45).

In conclusion, we provided preliminary data for UTE-MT modeling in ex vivo bovine and healthy adult cortical bone. This technique allows for a more comprehensive assessment of the MT process than previously reported by MTR measurement alone and lays the ground work for future studies into disease-based changes in MT parameters. We believe that UTE-MT modeling has the potential to provide a complementary quantitative approach to the diagnosis and treatment of conditions associated with impaired bone quality.