Improving pediatric protein binding estimates: An evaluation of α1-acid glycoprotein maturation in healthy and infected subjects

Abstract

Background and objective

Differences in plasma protein concentrations observed between children and adults can alter the extent of xenobiotic binding in plasma, resulting in divergent patterns of exposure. This study serves to quantify the ontogeny of α-1-acid glycoprotein (AAG) in both healthy and infected subjects.

Methods

Data pertaining to AAG from healthy subjects were compiled over 26 different publications. For subjects diagnosed or suspected of infection, AAG concentrations were obtained from 214 individuals acquired over 3 clinical investigations. The analysis evaluated use of linear, power, exponential, log-linear, and sigmoid Emax models to describe the ontogeny of AAG. Utility of the derived ontogeny equation for estimation of pediatric fraction unbound (fu) was evaluated using average-fold error (AFE) and absolute average-fold error (AAFE) as measures of bias and precision, respectively. A comparison to fu estimates derived using a previously proposed linear equation was also instituted.

Results

The sigmoid Emax model provided the comparatively best depiction of AAG ontogeny in both healthy and infected subjects. Despite median AAG concentrations in infected subjects being more than 2-fold greater than those observed in healthy subjects, a similar ontogeny pattern was observed when concentrations were normalized toward adult levels. For estimation of pediatric fu, the AAG ontogeny equation derived from this work (AFE 0.99; AAFE 1.24) provided a superior predictive performance in comparison to the previous equation (AFE 0.74; AAFE 1.45).

Conclusion

The current investigation depicts a proficient modality for estimation of protein binding in pediatrics and will, therefore, aid in reducing uncertainty associated with pediatric pharmacokinetic predictions.

1. Introduction

Plasma protein binding is a key physiological process capable of imparting influence on both pharmacokinetic (PK) and pharmacodynamic (PD) properties of xenobiotics. As such, measures of plasma protein binding are typically considered an intrinsic component for scaling PK data from preclinical species or in-vitro systems towards humans [1]. Between children and adults, developmental differences in the concentration of plasma proteins have been documented [2]. As the extent of xenobiotic-protein binding exhibits a direct relationship to the concentration of plasma proteins, differences in protein binding between children and adults are expected [3]. Correspondingly, quantitative descriptions of the ontogeny of plasma proteins represent a central component of scaling PK between different maturational stages (i.e. intraspecies scaling) [4].

Human serum albumin (HSA) and α-1-acid glycoprotein (AAG) are the two major proteins present in serum with binding capacities towards a wide variety xenobiotics [5]. Whereas HSA is typically associated with binding acidic exogenous compounds, AAG displays a high affinity towards basic lipophilic compounds [6, 7]. AAG is comprised of a highly glycosylated single polypeptide chain [5] with a molecular weight ranging between 41–43 kDa [8]. Binding of xenobiotics is facilitated by the presence of a single ligand-binding site per AAG molecule [6, 9]. In humans, the majority of AAG is present as either 2 or 3 genetic variants [10]. Furthermore, differences in ligand binding properties between specific variants have been documented in the literature [11, 12]. For several therapeutic compounds including imipramine, propranolol, lidocaine, methadone, and chlorpromazine, AAG represents the major constituent modulating plasma binding [3]. In healthy subjects, plasma concentrations of AAG range from ≈50–130 mg/dL [5]. However, as an acute-phase reactant, AAG concentrations can increase 3–5 fold in response to pathologies such as Crohn’s disease, myocardial infarction, infection, burns, and malignancy [7, 13]. In comparison, decreased AAG concentrations are associated with pregnancy, oral contraceptive use, and infancy [13].

A highly cited evaluation of changes in plasma AAG concentrations associated with normal growth and development was published by McNamara and Alcorn in 2002 [2]. Using data compiled from three separate publications, the authors derived a quantitative equation (i.e. linear model) describing the relationship between postnatal age (PNA) and plasma AAG concentrations from birth to adulthood. Despite providing suitable estimates for older subjects, the use of a linear model appeared to overestimate AAG concentrations amongst the most developmentally immature subjects (i.e. newborns) [2]. In addition, an alternative ontogeny equation was proposed by Johnson et al. [14], who utilized a sigmoid Emax function to describe the relationship between age and plasma AAG levels. However, both the aforementioned works exclusively focused on normal/healthy subjects; whereas, utilization of therapeutic compounds is typically focused towards subjects with disease. As AAG is an acute-phase reactant, it is unclear whether these ontogeny equations can provide a suitable modality for estimating differences in AAG concentrations between pediatric and adult subjects with disease.

This work will serve to quantitatively describe of the ontogeny of serum AAG in normal (healthy) individuals as well as an additional cohort of subjects diagnosed or suspected of bacterial infection (infected). Pediatric fraction unbound in plasma (fu) data for compounds exhibiting preferential binding to AAG will be used to compare the predictive capacity of the ontogeny equation derived from this work to McNamara and Alcorn’s [2] seminal equation.

2. Methods

The present analysis evaluating the ontogeny of AAG in humans (from birth to adulthood) was divided into three corresponding subsections: (i) evaluation of AAG ontogeny in normal subjects, (ii) evaluation of AAG ontogeny in subjects with known or suspected infections, and (iii) comparison of the predictive performance of our prospectively derived ontogeny equation to previously proposed models [2].

2.1 Ontogeny of AAG in healthy (normal) subjects

To assess the relationship between age and plasma AAG concentrations in healthy (normal) subjects, the analysis utilized primary literature sources attained from the PubMed database (last accessed August 2016). Data pertaining to subjects with disease states known to alter plasma AAG levels (i.e. Crohn’s disease, myocardial infarction, infection, burns, and malignancy) were excluded from the analysis. Investigations quantitatively denoting the age of participants in addition to plasma/serum AAG concentrations expressed in terms of central tendency (i.e. mean or median) and spread (i.e. standard deviation, standard error of the mean, or percentiles) were included. Investigations reporting AAG levels among different subject groups were permitted to contribute multiple data points to the analysis. Publications that expressed data graphically were converted to numerical values using GetData Graph Digitizer (v2.26).

To introduce a degree of consistency between studies conducted over various publication dates, protein concentrations were normalized toward certified reference material (CRM) 470 values, a widely circulated serum protein calibrant developed in 1993 [15], using the following process. For investigations conducted between 1973 to 1993 or those utilizing protein standards manufactured during these aforementioned years, protein standards were assumed to conform to United States National Reference Preparation for Serum Proteins (USNRP) lot 12-0575C values. AAG concentrations were subsequently normalized towards CRM470 values using a proportional transfer value [16]. For investigations conducted after 1993, protein standards were assumed to conform to CRM470 values. As such, no adjustment was made. Studies conducted prior to 1973 were excluded from the analysis due to the assumed diversity in protein standards available prior to this year [17]. Quantitative assays utilized between studies varied and included radial immunodiffusion, nephelometry, turbidimetry, HPLC, and immunoelectrophoresis. Due to the inherent difficulty of assessing quantitative equivalence between specific assays conducted in different laboratories over various periods of time, an overarching assumption that AAG concentrations were equivalent between assay types was used.

In human plasma, AAG concentrations are log-normally distributed [18]. Considering this distributional assumption, the analysis, which complied data obtained from various investigations, required AAG concentrations to be expressed using log-normal parameters such as the geometric mean and log-normal standard error (log-normal standard deviation/ $\sqrt{n}$). For the majority of investigations, AAG concentrations were reported using an arithmetic mean and standard deviation. For these studies, estimates of the geometric mean (μ_geo) and log-normal standard error (SE_LN) were determined using the following equations [19]

$${\mu }_{\mathit{geo}}=\frac{m}{\sqrt{1+\frac{S{D}^2}{m^2}}}$$ (Eq.1)

$$S{E}_{LN}=\sqrt{\frac{ln\left(1+\frac{S{D}^2}{m^2}\right)}{n}}$$ (Eq.2)

where m is the arithmetic mean, SD is arithmetic standard deviation, and n is the number of individuals examined. Two investigations [20, 21] expressed AAG concentrations in terms of percentiles (5^th, 50^th, and 95^th; or 2.5^th, 50^th and 97.5^th). For these studies, the median (i.e. 50^th percentile) was assumed to be equivalent to the geometric mean [22]. Using the assumption that log-transformation of plasma AAG concentrations results in a normal distribution, the log-normal standard error was estimated using the following equation

$$S{E}_{LN}=\frac{ln(\mathit{Upper})-ln(\mathit{Lower})}{2\ast T_{\#,n-1}\ast \sqrt{n}}$$ (Eq.3)

where Upper refers to the 95^th or 97.5^th AAG percentile, Lower refers to the 2.5^th or 5^th AAG percentile, and T_#,n−1 is the one-sided critical t-value (probability 0.95 or 0.975) associated with n-1 degrees of freedom. One investigation [23] graphically expressed neonatal AAG concentrations using arithmetic means and standard errors of the mean (SEM) without denoting the number of subjects assessed at each time-point. For this study, the geometric mean was estimated using equation 1 with an approximate SD value derived from additional figures from the same manuscript depicting the upper limit of normal AAG values (mean +2SD). Based on the approximation that the coefficient of variation (CV=SD/m) of a log-normally distributed variable is equal to the log-normal standard deviation [24], an estimate of the log-normal standard error was derived using the right-hand component of equation 4.

$$S{E}_{LN}\sim \frac{CV}{\sqrt{n}}=\frac{SD/m}{\sqrt{n}}=\frac{\mathit{SEM}}{m}$$ (Eq.4)

To quantitatively describe the functional relationship between age and plasma AAG levels, a variety of models were assessed: linear, power, exponential, linear-log, and sigmoid Emax. Gestational ages (GA) for neonatal (preterm and term) and infant subjects’ were not a universally reported among all investigations. As such, PNA was utilized as the primary age descriptor within this analysis. The functional form of each model is denoted in Table 1. Parameter estimation was conducted using a maximum likelihood estimation (MLE) technique with minimization of the objective function value (the negative two log-likelihood) achieved via the fminunc algorithm in Matlab R2015a (The Mathworks Inc., Natick, MA). Model fits were weighted using the squared reciprocal of log-normal standard errors associated with each study group (1/SE_LN²). To impart a log-normal error structure, parameter estimation was performed using log-transformed values for observed (i.e. study specific μ_geo) and predicted AAG concentrations with PNA, in days, serving as the sole covariate for all fitted models (Table 1). Since predicted plasma AAG concentrations at birth (i.e. PNA = 0 days) under the power and sigmoid Emax model return a value of 0, the fitting algorithm, which log-transforms predictions, fails to compute (i.e. Ln(0) = undefined). In addition, the linear-log model is undefined at birth. To circumvent these operational issues, the PNA for subject groups assessed at birth (PNA = 0) were adjusted to a PNA of 1 day. This modification was deemed defensible as the μ_geo of AAG concentrations observed among subjects assessed at birth and those observed during the first day of life were similar within our dataset (19.92 vs. 17.67 mg/dL, respectively). Model selection was performed using a combination of the Akaike Information Criterion (AIC) and a visual inspection of observed study data overlaid with predicted AAG concentrations to assess curve shape.

Table 1.

Ontogeny models investigated

Model	Equation1
Linear2	(a * AGE) + b
Power2	b *AGEa
Exponential2	b * ea * AGE
Linear-Log2	b + [a *ln(AGE)]
Sigmoid Emax3	$\frac{{\mathit{AAG}}_{\mathit{max}}\ast {\mathit{AGE}}^P}{T{M_{50}}^P+{\mathit{AGE}}^P}$

¹the covariate AGE was specified using either postnatal age (days) or postmenstrual age (weeks)

²a and b denote estimable parameters associated with the linear, power, exponential, and linear-log models

³AAG_max (maximum plasma AAG concentration [mg/dL]), TM₅₀(age at 50% AAG_max [days or weeks]), and P (Hill coefficient) denote estimable parameters associated with the sigmoid Emax model

2.2 Ontogeny of AAG in subjects with diagnosed or suspected of infection

To evaluate of the relationship between age and plasma AAG concentrations in patients diagnosed or suspected of infection, individual subject data were compiled over three clinical trials: The Pharmacokinetics of Anti-Staphylococcal Antibiotics in Infants Clinical Trial (Staph Trio; NICHD-2012-STA01, ClinicalTrials.gov NCT01728363; IND 115,396) [25], Pharmacokinetics of Understudied Drugs Administered to Children per Standard of Care (PTN POPS; NICHD-2011-POP01, ClinicalTrials.gov NCT01431326; IND 113,645) [26], and Safety and Pharmacokinetics of Multiple-Dose Intravenous and Oral Clindamycin in Pediatric Subjects with BMI ≥ 85th Percentile (CLIN01; NICHD-2012-CLN01, ClinicalTrials.gov NCT01744730; IND 115,396) [27]. The dataset consisted of a subset subjects being treated with the antibiotic clindamycin in whom plasma AAG concentrations were ascertained. Age was denoted as PNA; however, gestational age was also recorded for subjects less than 3 months old. Inclusion/exclusion criteria specific to each investigation is described in Table 2.

Table 2.

Key inclusion/exclusion criteria for the three of studies that reported AAG levels among purportedly infected subjects. (note: the below criteria denote those that were considered for inclusion in our analysis and not necessarily for enrollment purposes for the respective studies)

Study	Inclusion Criteria	Exclusion Criteria
STA01a	-suspected systemic infection or receiving clindamycin as per standard or care for treatment of an infectious pathogen -<30 weeks gestational age and <121 days postnatal age	-urine output <0.5 ml/kg/hr -serum creatinine >1.7 mg/dL - history of allergic reaction to clindamycin
PTN POPSb	- patients diagnosed with anaerobic bacteria, Pneumococci, Staphylocci, or Streptococci infections; infections (other types); necrotizing enterocolitis; or skin or soft tissue infections who received clindamycin -<21 years of age	-pregnancy
CLIN01c	-suspected/confirmed infection or receiving clindamycin as per standard or care for treatment of an infectious pathogen -negative serum pregnancy test (if female and has reached menarche) within 24 hours prior to first study drug -body mass index ≥ 85th percentile for age and sex based on the Centers for Disease Control recommendations -2-<18 years of age	-aspartate aminotransferase (AST) >120 units/L* -alanine aminotransferase (ALT) >210 units/L* -total bilirubin >3 mg/dL* -serum creatinine >2 mg/dL* -receiving neuromuscular blocking agents* -history of allergic reaction to clindamycin* -receiving potent CYP3A4 inhibitors, CYP3A4 inducers, inotropes/pressors, or St. John’s Wort -receiving extracorporeal life support -post cardiac bypass (within 24 hours) *denotes criteria applicable to patients who were not already receiving clindamycin a per standard of care at time of enrollment

^aThe Pharmacokinetics of Anti-Staphylococcal Antibiotics in Infants Clinical Trial (Staph Trio; NICHD-2012-STA01, ClinicalTrials.gov NCT01728363; IND 115,396)

^bPharmacokinetics of Understudied Drugs Administered to Children per Standard of Care (PTN POPS; NICHD-2011-POP01, ClinicalTrials.gov NCT01431326; IND 113,645)

^cSafety and Pharmacokinetics of Multiple-Dose Intravenous and Oral Clindamycin in Pediatric Subjects with BMI ≥ 85th Percentile (CLIN01; NICHD-2012-CLN01, ClinicalTrials.gov NCT01744730; IND 115,396)

A similar assessment as described in the previous section was instituted to select the most suitable quantitative equation (Table 1) to describe the relationship between plasma AAG levels and PNA. Parameter estimates were obtained via MLE using a log-normal error model with minimization of the objective function value achieved using the previously described computational approach. Confidence intervals associated with estimated AAG concentrations were tabulated using the delta method (asymptotic theory) [24].

An evaluation of the use of an alternative age descriptor, post-menstrual age (PMA = PNA + GA), was also conducted using this dataset. Parameter estimates were obtained in a similar manner as depicted above but using PMA, in weeks, instead of PNA. For subjects greater than 3 months of age, PMA was calculated assuming a GA of 40 weeks. The AIC and standard deviation of log-normalized residuals (≈RMSE) between models utilizing PMA and PNA were utilized to assess the goodness of fit associated with each age descriptor.

2.3 Prediction of pediatric fu: a comparison of the AAG ontogeny equation derived from this study to previously proposed models

Estimates of pediatric fu (fu_ped) were tabulated from observed adult fu (fu_adult) values and the ratio of pediatric-to-adult plasma protein concentrations $(\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}})$ using the following equation proposed by McNamara and Alcorn [2].

$$f{u}_{\mathit{ped}}=\frac{1}{1+\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}\frac{(1-f{u}_{\mathit{adult}})}{f{u}_{\mathit{adult}}}}$$ (Eq 5)

To obtain $(\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}})$ ratios as required by Equation 5, the derived AAG ontogeny equations, which were formulated in terms of absolute plasma concentrations (mg/dL), were simply divided by estimated adult AAG values. The above process also denotes how AAG estimates derived from Johnson et al.’s [14] ontogeny equation were converted to estimates of fu_ped.

A set of experimentally determined fu_ped values also complied by McNamara and Alcorn [2] were utilized to assess the predictive accuracy of estimates. The dataset consisted of 17 pairs of age-specific fu values (pediatric and adult) for 11 xenobiotics exhibiting specific affinity towards AAG. Observed fu values were predominantly determined in plasma samples from healthy or control subjects. Correspondingly, estimates of fu_ped were derived using observed fu_adult values from the dataset and $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$ ratios pertaining to the ontogeny of AAG in healthy subjects. Overall predictive performance was evaluated using the average-fold error (AFE) and absolute average-fold error (AAFE) as measures of bias and precision, respectively. The equations for both measures are given below

$$\mathit{AFE}={10}^{\frac{1}{n}{\displaystyle \sum \text{log}(\frac{\mathit{pred}}{\mathit{obs}})}}$$ (Eq 6)

$$\mathit{AAFE}={10}^{\frac{1}{n}{\displaystyle \sum |\text{log}(\frac{\mathit{pred}}{\mathit{obs}})|}}$$ (Eq 7)

where obs is the observed fu_ped value from the dataset and pred is the predicted fu value based on equation 5. The predictive accuracy of fu_ped estimates derived using McNamara and Alcorn’s [2] seminal AAG ontogeny equation as well as Johnson et al.’s [14] equation were tabulated for comparison. Furthermore, as an alternative measure of goodness of fit, the concordance correlation coefficient [28] for fu_ped estimates derived by the model from this analysis and McNamara and Alcorn’s linear model were tabulated and compared.

3. Results

The ontogeny of plasma AAG in healthy (control) subjects was evaluated using data from 26 separate studies complied from the literature [13, 18, 20, 21, 23, 29–49]. The analysis included AAG concentrations from subject groups that ranged in average (postnatal) age from 0 days (i.e. newborns) to 79 years. Data from each subject group was weighted by observed log-normalized standard error values (weight = 1/SE_LN²). In comparison to other models fit using PNA, the sigmoid Emax model was associated with the lowest AIC value (52.84) and depicted a curve shape that was visually congruent with observed AAG concentrations (Figure 1). AIC values associated with competing models were as follows: 184.43 (linear), 95.72 (power), 189.17 (exponential), and 70.70 (linear-log). Table 3 denotes parameter estimates and associated standard errors for the sigmoid Emax model. The AAG_max (93.17 mg/dL) depicts the geometric mean (or median) of plasma AAG concentrations in healthy adults. Comparatively, the model estimates median AAG concentrations to be approximately 3.8 fold lower (i.e. 24.67 mg/dL) during the first day of life (day =1).

Figure 1.

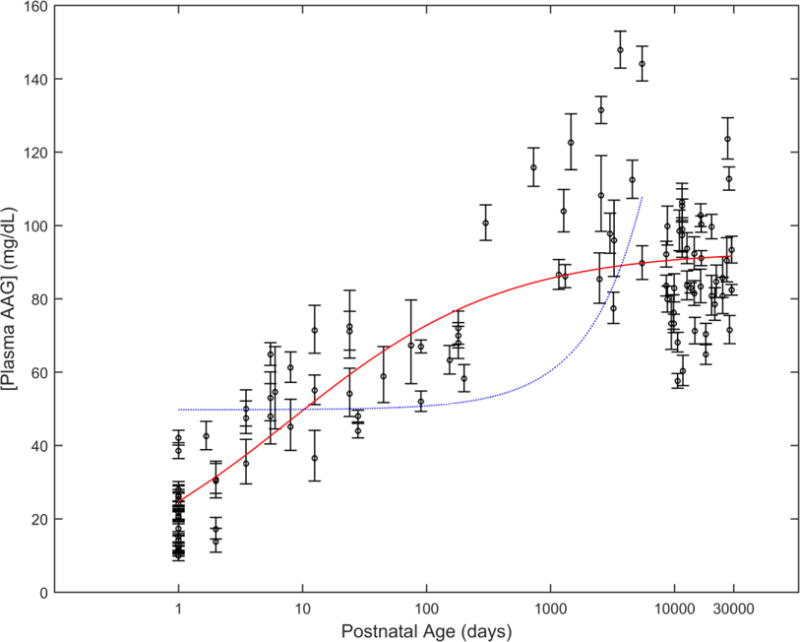
Ontogeny of AAG among healthy subjects. Concentrations, normalized to CRM470 values, are depicted using estimated geometric mean values (o) for each study group. Geometric error bars depict the log-normal SE associated with each study cohort. Predicted AAG concentrations based on a sigmoid Emax model (solid line - red), as derived from this work, and a linear model (dashed line - blue), as proposed by McNamara and Alcorn (assuming adult plasma AAG concentrations ≈ 93.17 mg/dL) [2], are denoted. Observed data were compiled from the following publications: [13, 18, 20, 21, 23, 29–49].

Table 3.

Parameter estimates (sigmoid E_max model) describing the relationship between postnatal age (days) and AAG (mg/dL) in healthy subjects

AAGmax [mg/dL] Estimate (SEa)	TM50 [days] Estimate (SEa)	P Estimate (SEa)
93.17 (3.16)	7.76 (2.57)	0.498 (0.068)

^aStandard-Error

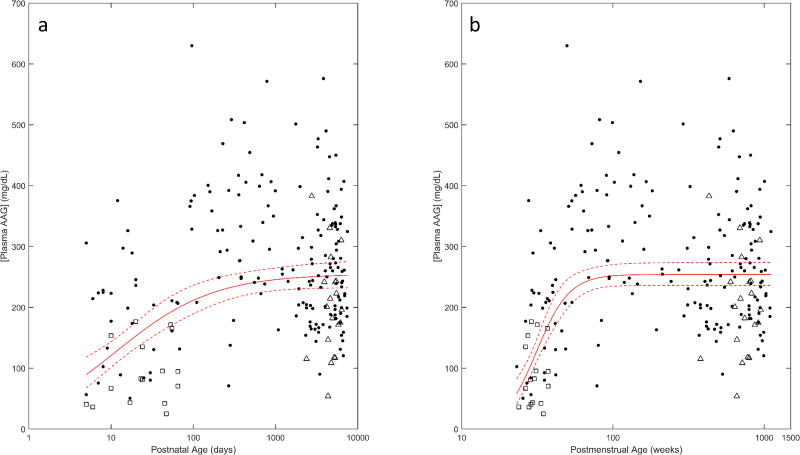
Two-hundred and fourteen individual AAG concentrations complied over 3 separate clinical trials were utilized to evaluate the ontogeny of AAG in subjects diagnosed or suspected of infection. The dataset included 20 subjects from the CLIN01 trial, 177 from the PTN POPS trial, and 17 from the Staph Trio trial. Individuals ranged in PNA from 5 days to 20.5 years. As in healthy subjects, the sigmoid Emax model provided the best fit between PNA and AAG concentrations as determined by the AIC (319.24) and visual examination of curve shape (Figure 2a). In comparison, AIC values associated with the linear, power, exponential, and linear-log models were 359.87, 334.61, 360.34, and 329.76, respectively. Parameter estimates and standard errors associated with the sigmoid Emax model using the covariate PNA are denoted in Table 4. For subjects diagnosed or suspected of infection, the estimated geometric mean of AAG level among adults (AAG_max; 254.71 mg/dL) was comparatively higher than values observed in healthy (normal) adults. This trend towards increased AAG concentrations was depicted throughout the entire developmental age range. For example, at 5 days old, median AAG concentrations were estimated to be 89.41 mg/dL in infected individuals compared to 41.51 mg/dL in healthy subjects. On average, AAG concentrations from the Staph-Trio trial, which contributed data pertaining to premature born (< 30 weeks GA) neonates and infants less than 3 months PNA, appeared to be overestimated by the sigmoid Emax model fit using PNA (□ in Figure 2a). A similar pattern was also seen for children from the CLIN01 trial, all of whom were either overweight or obese (≥85^th percentile of weight for age and sex) (Δ in Figure 2a).

Figure 2.

AAG ontogeny with respect to (A) PNA and (B) PMA in subjects diagnosed or suspected of infection. Median (i.e. geometric mean) AAG concentrations (solid lines) and associated 95% CI (dashed lines) as estimated using a sigmoid Emax model are depicted. Subjects from the each clinical trial (Staph Trio, □; PTN POPS ●;CLIN01 Δ) are denoted separately.

Table 4.

Parameter estimates (sigmoid E_max model) describing the relationship between age (postnatal or postmenstrual) and AAG (mg/dL) in subjects with suspected or confirmed infections

Age descriptor	AAGmax [mg/dL] Estimate (SEa)	TM50 [days or weeks] Estimate (SEa)	P Estimate (SEa)
Postnatal age (PNA)	254.71 (12.25)	11.53 (3.11) [days]	0.735 (0.167)
Postmenstrual age (PMA)	254.37 (9.49)	31.33 (1.31) [weeks]	3.97 (0.714)

^aStandard-Error

Figure 2b depicts the ontogeny of AAG derived using a sigmoid Emax model employing PMA as its primary covariate for subjects diagnosed or suspected of infection. The model was associated with an AIC value of 291.02, which was comparatively lower than the previous model fit using PNA. In addition, use of PMA was associated with a lower standard deviation of log-normalized residuals (≈RMSE) in comparison to PNA (0.4710 vs. 0.5031, respectively). Correspondingly, PMA was deemed as the preferable age descriptor for defining the ontogeny of AAG within this subset of subjects. Parameter estimates and standard errors for the sigmoid Emax model fit to PMA are denoted in Table 4. The estimated AAG_max (254.37 mg/dL) was similar in value to that of the PNA model; however, estimates of the age at 50% AAG_max (TM₅₀) and the hill coefficient (P) were expectedly different between models due to the use of varying age descriptors. Additionally, use of PMA decreased the degree of overprediction associated with AAG estimates for premature born children from the Staph-Trio trial (□ in Figure 2b). Though, similar to the PNA model, AAG estimates for subjects from the CLIN01 trial were overestimated using the PMA model (Δ in Figure 2b).

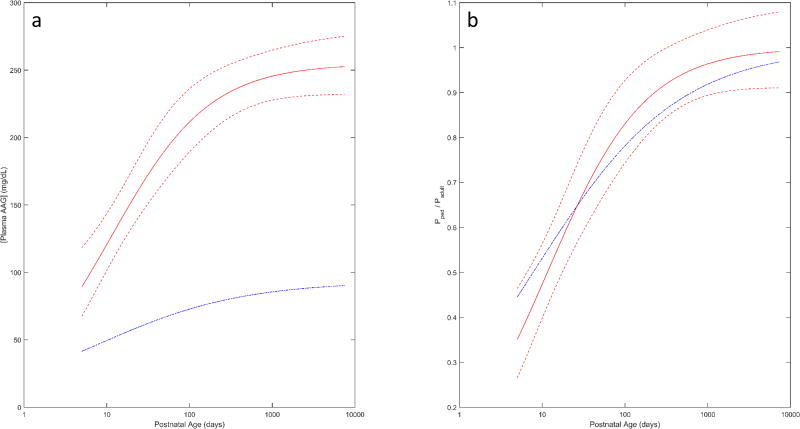
A graphical comparison of model predicted AAG concentrations between healthy subjects and those diagnosed or suspected of infection is displayed in Figure 3a. The comparison employed models parameterized in terms of PNA as the analysis in healthy subjects did not assess ontogeny with regards to PMA. The span of postnatal ages depicted were limited to the age range of purportedly infected subjects (i.e. 5 days to 20.5 years). Normalizing AAG concentrations towards the adult levels provides an estimate of the fractional attainment of adult AAG concentrations (i.e. $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$). Average estimates of $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$ ratios in healthy subjects fell within the 95% CI of values associated with subjects diagnosed or suspected of infection for the assessed age range (5 days to 20.5 years). As a result, it was asserted that the developmental trajectory of the $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$ ratio was not substantially different between healthy and infected subjects (Figure 3b).

Figure 3.

(A) Comparison of median (geometric mean) AAG concentrations with respect to PNA in healthy (blue dotted line) and infected subjects (Median-red solid line; 95% CI – red dashed line), as estimated by separate sigmoid Emax models. (B) Comparison of normalized estimates of AAG concentrations (i.e. normalized to adult AAG values) with respect to PNA in healthy (blue dotted line) and infected subjects (Median- red solid line; 95% CI –red dashed line). AAG estimates are depicted for postnatal ages ranging between 5 days and 20.5 years.

Overall bias associated with use of the derived AAG ontogeny model among healthy subjects, parameterized using PNA, at estimating 17 separate fu_ped values was very low. On average, estimates underpredicted observed values by 1% (AFE = 0.99). The model was associated with a precision (AAFE) of 1.24, indicating that on average individual predictions were within 24% of observed values. Johnson et al.’s [14] ontogeny equation performed quite similarly in terms of bias (AFE = 0.95) and precision (AAFE = 1.24). In contrast, the use of McNamara and Alcorn’s [2] linear equation for estimating fu_ped was associated with a larger degree of underprediction (AFE = 0.74) and poorer precision (AAFE = 1.45). A graphical comparison of fu_ped predictions derived from the sigmoid Emax model developed in the current analysis to McNamara and Alcorn’s [2] linear model is depicted in Figure 4. The sigmoid Emax model provided predictions that were in closer agreement to observed values as illustrated by their proximity to the line of identity. This newly developed model was associated with a higher concordance correlation coefficient in comparison to the linear model (0.851 vs. 0.652, respectively).

Figure 4.

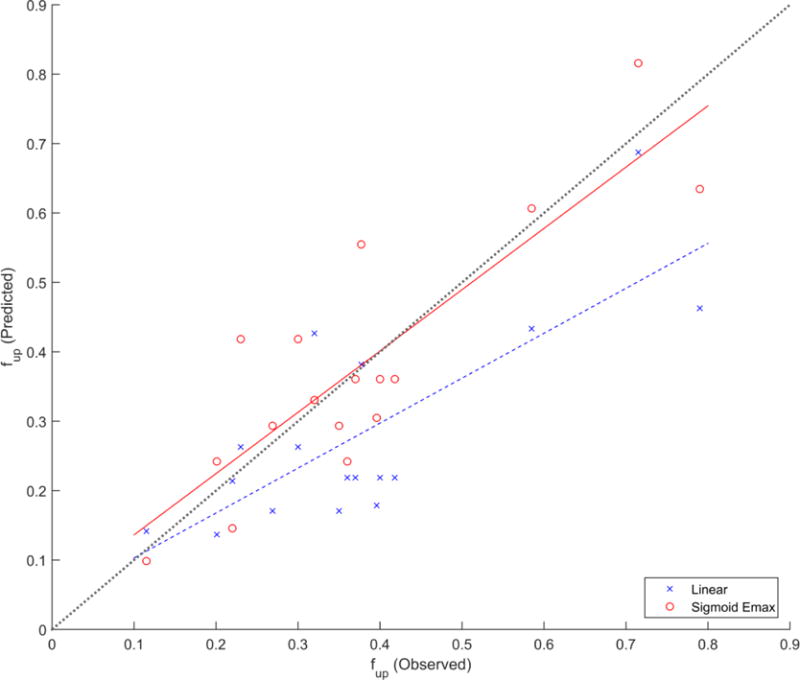
Predictive performance of McNamara and Alcorn’s (linear) equation vs. the sigmoid Emax equation derived from this analysis at estimating observed pediatric fraction unbound (f_up; n=17) values. Solid and dashed lines depict the lines of best fit (i.e. linear regression) for estimates derived from the sigmoid Emax and linear equations, respectively. The line of identity (dotted) is superimposed for reference.

4. Discussion

For estimation of AAG concentrations among subjects diagnosed or suspected of infection, the analysis supported use of PMA as a comparatively better age descriptor than PNA. With use of PMA, estimated AAG concentrations were notably less biased for the subset of premature children from the Staph-Trio trial (Figure 2). Use of PMA as an alternative age descriptor for assessment of the ontogeny of AAG among healthy individuals was precluded as not all studies with neonatal subjects reported GA, thus preventing tabulation of PMA [29, 41]. Several investigations, however, have documented lower AAG concentrations among premature newborns in comparison to purportedly normal term newborns [23, 39, 43]. As use of PMA provides some capacity to account for prematurity, it is postulated that models using this age descriptor among healthy subjects will exhibit a better fit to AAG concentrations in comparison to PNA. Therefore, it is prudent that prospective studies exploring the trajectory of AAG in healthy individuals document GA among their youngest subjects to permit for PMA calculation.

As an acute-phase reactant, AAG levels increase in response to injury, inflammation, or infection [8]. The magnitude of increase has been related to factors such as the severity of disease [44] and type of infection (i.e. meningitis vs. pneumonia) [50]. Furthermore, normalization of AAG levels appear to follow the clinical course of infection [23]. Data utilized to evaluate the ontogeny of AAG in subjects diagnosed or suspected of infection did not provide sufficient information to stratify individuals based on infection type, severity, or time course of infection. As such, assessed subjects displayed a high degree of inter-subject variability in terms of AAG concentrations, making prediction of individual AAG levels precarious. However, for the purposes of scaling PK parameters from adults to pediatrics, the relative difference in AAG concentrations between these two age groups is the measure of interest [4, 51]. The current work demonstrates that, on average, the relative ontogeny profile of $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$ in infected subjects followed a similar trajectory to that observed among healthy subjects (Figure 3b). Correspondingly, it could be asserted that scaling of fu, as determined according to equation 5, from healthy or infected adults toward pediatric subjects within the same respective clinical state (e.g. infected adult → infected child) could be determined using a single ontogeny profile for $\frac{P_{\mathit{ped}}}{P_{\mathit{adult}}}$ (e.g. use of the profile pertaining to healthy subjects).

Median AAG estimates among purportedly infected, overweight and obese children from the CLIN01 trial (n=20) were slightly over-predicted by sigmoid Emax models incorporating PNA or PMA. This raises the notion of AAG concentrations differing between overweight and normal weight children - an observation that has been documented among ‘healthy’ adults [52]. However, as the dataset pertaining to infected subjects did not contain information relating to potential cofounders (e.g. infection type, severity, and time course of infection), establishing an association between the attributes (i.e. obesity) of subjects from one specific trial (CLIN01) and AAG may lack external validity and was, therefore, was not pursued.

Based on an observed dataset containing 17 fu_ped values, estimates of fu derived using the proposed AAG ontogeny equation from healthy (control) subjects were associated with a low bias (AFE = 0.99) and relative accurate precision (AAFE = 1.24). Discontinuity between observed and predicted fu values can be related to numerous etiologies; however, an understanding of the assumptions associated with fu prediction in pediatrics can provide some insight. Predictions of fu_ped were derived using equation 5, as previously depicted by McNamara and Alcorn [2]. With use of this equation, several assumptions are inherently presumed: 1, plasma protein binding is linear (i.e. nonsaturable ligand concentrations); 2, ligand-protein binding properties are the same between children and adults (i.e. number of binding sites per protein and affinity constants are constant with age), and 3, AAG is the principal protein responsible for plasma protein binding. Violation of any of these assumptions can result in deviation between observed and predicted values. With plasma concentrations up to 50-fold lower than albumin and exhibiting only a single binding site [5], AAG is frequently termed as a low capacity protein [3]. Resultantly, therapeutic concentrations that drugs are commonly dosed towards (i.e. 1 – 10 μM) may result in saturation of AAG [5]. This propensity for saturation is expected to be especially prominent among neonatal subjects, where concentrations of AAG are considerably lower than adults. One previous study exploring protein binding of lidocaine among pediatric plasma samples asserted that age-related differences in the binding capacity of AAG between neonates and older children could be responsible for the inconsistency of fu values between the groups [39]. However, this postulation requires further study to be corroborated. Differential protein binding properties between variants of AAG have been documented in the literature [11, 12]. Unfortunately, the datasets utilized within this analysis did not stratify AAG into specific genetic variants; therefore, developmental changes in variant concentrations and their influence on protein binding estimation were not assessed. Furthermore, some xenobiotics may display affinity for more than one plasma protein. For example, the opioid antagonist naloxone displays affinity for both albumin and AAG [29]. As equation 5 only considers changes to a single protein, estimates of fu_ped for such compounds may be biased.

Compared to the ontogeny model proposed in this study, fu_ped estimates derived from McNamara and Alcorn’s [2] AAG ontogeny equation were associated with a higher degree of bias and lower precision. On average, McNamara and Alcorn’s equation underpredicted observed fu values by 26% (AFE = 0.74). The author’s utilized a linear equation to describe the ontogeny of AAG (Figure 1; age is displayed on a log scale). Unfortunately, this functional form does not provide an appropriate depiction of AAG concentrations among the most developmentally immature subjects. For example, in neonates, the equation provided estimates of AAG concentrations that were well above observed data points. Therefore, considering that ≈80% (14/17) of fu values within the observed dataset were from neonatal subjects, the finding that fu_ped estimates derived using McNamara and Alcorn’s equation were associated with an underprediction bias was not unexpected.

Considering the importance of protein binding on modulating key PK parameters such as clearance and volume of distribution [53], an inherent understanding of how plasma proteins change as a function of age is fundamentally required to derive age-specific estimates of the time-course of drug exposure in children. With ever widening acceptance of the use of physiologically-based pharmacokinetic (PBPK) models for scaling xenobiotic exposures from adults to pediatrics [4, 54], the findings of this analysis can be readily integrated into common practice. PBPK models represent a bottom-up approach that integrates components of organism physiology with xenobiotic-specific parameters to foster a priori predictions of systemic as well as tissue-specific exposures [51]. Thus, within such models there exists an intuitive link between the quality of input parameters (i.e. physiological and xenobiotic-specific parameters) and the accuracy of model-predicted exposures. PBPK models typically parameterize the magnitude of xenobiotic-protein binding using fu. By providing superior estimates of fu_ped, the ontogeny model derived from this work can be used in conjunction with PBPK modeling techniques to improve their predictive capacity among pediatrics. This could prospectively permit for such models to function as the primary exploratory investigation of pediatric drug PK, allowing clinical investigations to function on a confirmatory basis.

The use of a sigmoid Emax model for defining the ontogeny of AAG concentrations is not unique to this investigation. Johnson et al. [14] previously conducted an analysis of plasma AAG levels as a function of age. The authors’ found that a sigmoid Emax model suitably described the data. Derived parameter estimates were not considerably different from parameters reported among healthy subjects from the current study. Estimates of AAG_max, TM₅₀, and P were 88.7 mg/dL, 8.89 days, and 0.38, respectively. As a result, it was unsurprising that Johnson et al.’s model was associated with a similar predictive capacity as the model derived from the current analysis with regards to estimating fu_ped. However, in comparison to Johnson et al.’s publication, which collated AAG data from a limited set of investigations [2, 13], our analysis offers a more comprehensive examination of the available literature with data compiled over 26 separate investigations. The present study also considered a wider variety of prospective models and provided an evaluation of the predictive performance of the derived ontogeny equation at estimating fu_ped, an important parameter utilized for PK scaling. In addition, the assessment of AAG ontogeny among subjects diagnosed or suspected of infection represents a component unique to the current work.

This analysis represents one of the most comprehensive examinations of published literature characterizing plasma AAG levels in healthy subjects from birth to adulthood. However, despite compiling AAG data from 26 studies conducted over a wide range of countries, the majority of data was assumedly directed towards a Caucasian population. For example, only one study was conducted in a country where the population is primarily of Asian descent (i.e. Japan) [37]. The remaining investigations, conducted in France, Canada, the Netherlands, USA, Australia, Greece, Denmark, Germany, England, and Belgium, were subsequently postulated to contain a high proportion of Caucasian subjects. Within adults, inter-ethnic differences in AAG levels have been documented. In one study, AAG concentrations were denoted to be 20% higher in Caucasians compared to African Americans [55]. Another investigation measuring AAG concentrations in Chinese and Caucasian volunteers found 25% higher levels among Caucasians [56]. Considering the demographics of individuals within the examined studies, the analysis was incapable of investigating for the presence of interethnic differences among healthy subjects; therefore, presented results are primarily reflective of AAG concentrations within a Caucasian population. Racial demographics of individuals included in the analysis of AAG ontogeny among subjects diagnosed or suspected of infection was 76% White, 16% African American, and 8% Other. A secondary analysis was conducted based on the depicted sigmoid Emax model using the covariate PMA (base model) to assess whether inclusion of a binary race covariate (Non-White 0; White 1) could enhance model fit. However, inclusion of race in a proportional manner resulted in a similar AIC to the base model (291.84 vs. 291.02, respectively). As such, use of the covariate race was not considered to be beneficial for estimation of AAG among our sample of purportedly infected subjects.

In this study, the ontogeny of AAG among healthy subjects was assessed using AAG concentration data averaged over multiple subjects from separate publications. Analyses of this type of can be influenced by the presence of an aggregation bias (ecological fallacy). This bias arises from the loss of information associated with aggregating individual data, leading to distortion of the relationship that exists between individual subjects and the variable of interest [57]. Despite this, use of aggregated data within the analysis was deemed reasonable as the majority of publications failed to report individualized data. In addition, the ontogeny models derived from this investigation should not be consider to entail wider applicability towards other plasma proteins (e.g. albumin), which can follow alternative ontogeny patterns [2].

Conclusion

The current investigation sought to quantitatively describe the ontogeny of AAG in both healthy subjects and those diagnosed or suspected of infection. A sigmoid Emax model was found to best describe the developmental trajectory of AAG in both groups of subjects (healthy and infected). As an acute-phase reactant, plasma AAG levels increase in response injury, inflammation, and infection [7]. Though a profound dissimilarity in median AAG concentrations between healthy and infected subjects was observed, the analysis depicted a similar ontogeny pattern when AAG levels were normalized toward adult values. Furthermore, the derived ontogeny equation demonstrated a proficient predictive capacity for estimation of fu_ped. As developmental changes in plasma protein binding (i.e. fu) can translate into significant alterations in compound distribution and clearance, this work will aid in reducing uncertainty associated with pediatric PK predictions.

Key points.

• We present a mathematical description of how plasma concentrations of α1-acid glycoprotein (AAG), a major plasma protein responsible for binding a wide range of drugs, change between children and adults.

• Developmental differences in plasma protein concentrations affect the magnitude of free drug available in plasma, often leading to changes in drug pharmacokinetics (PK).

• In addition to describing the developmental profile of AAG in healthy and infected subjects, the study demonstrates the utility of these profiles for estimating pediatric fraction unbound in plasma, a key parameter for fostering PK predictions in children.