Artificial intelligence exploration of unstable protocells leads to predictable properties and discovery of collective behavior

Significance

Exploring and understanding the emergence of complex behaviors is difficult even in “simple” chemical systems since the dynamics can rest on a knife edge between stability and instability. Herein, we study the complex dynamics of a simple protocell system, comprising four-component oil droplets in an aqueous environment using an automated platform equipped with artificial intelligence. The system autonomously selects and performs oil-in-water droplet experiments, and then records and classifies the behavior of the droplets using image recognition. The data acquired are then used to build predictive models of the system. Physical properties such as viscosity, surface tension, and density are related to behaviors, as well as to droplet behavioral niches, such as collective swarming.

Abstract

Protocell models are used to investigate how cells might have first assembled on Earth. Some, like oil-in-water droplets, can be seemingly simple models, while able to exhibit complex and unpredictable behaviors. How such simple oil-in-water systems can come together to yield complex and life-like behaviors remains a key question. Herein, we illustrate how the combination of automated experimentation and image processing, physicochemical analysis, and machine learning allows significant advances to be made in understanding the driving forces behind oil-in-water droplet behaviors. Utilizing >7,000 experiments collected using an autonomous robotic platform, we illustrate how smart automation cannot only help with exploration, optimization, and discovery of new behaviors, but can also be core to developing fundamental understanding of such systems. Using this process, we were able to relate droplet formulation to behavior via predicted physical properties, and to identify and predict more occurrences of a rare collective droplet behavior, droplet swarming. Proton NMR spectroscopic and qualitative pH methods enabled us to better understand oil dissolution, chemical change, phase transitions, and droplet and aqueous phase flows, illustrating the utility of the combination of smart-automation and traditional analytical chemistry techniques. We further extended our study for the simultaneous exploration of both the oil and aqueous phases using a robotic platform. Overall, this work shows that the combination of chemistry, robotics, and artificial intelligence enables discovery, prediction, and mechanistic understanding in ways that no one approach could achieve alone.

There is great interest in oil-in-water droplets both as protocell models and as simple systems that display an astonishingly delicate set of behaviors that rest on a sensitive knife edge between stability and instability (1). They have been shown to exhibit cell-like properties including movement, division, and chemotaxis while inherently satisfying the need for a protocell to be compartmentalized (2–5). The understanding of the driving forces influencing these droplets is limited, although Marangoni instabilities, imbalances in surface tension initiated by symmetry breaking, are thought to play a key role (6). Indeed, along with autocatalytic systems (7–9), chemical gardens (10, 11), and other protocell models (12, 13), these systems together illustrate how the combination of relatively few components and phase boundaries can lead to complex and “life-like” outcomes. Chemotaxis (14, 15) movement in response to chemical stimuli such as a pH or salt concentration gradient has also been observed in simple oil-in-water droplet systems (3, 4, 16–18). These droplet behaviors are thought to be driven by Marangoni instabilities originating from surface tension asymmetry and by the relative solubilities of the oil- and aqueous-phase components (6, 19).

The use of automation and image analysis in the exploration of protocell and droplet systems has been shown to be a powerful way to investigate the behaviors observed for a four-component oil-in-water droplet system (2). This is because these platforms are now easy to design and construct using affordable and open-source hardware and software. For example, bespoke closed-loop systems can be used for the robotic exploration and assisted evolution of physicochemical systems, expanding from the fields of engineering and robotics, and inspired from the realm of biology (20–24). The variation in droplet behaviors as their composition varies can be vast and unpredictable, despite having only a small number of inputs. For example (2), when using only four oil inputs droplets could move rapidly, remain stationary, divide into many smaller droplets, deform, or display a whole range of behaviors. The issue is that the systems seem so complex that deriving mechanistic and predictive information seems far from reach, especially when utilizing smart-automation or standard chemical analytical techniques alone.

Herein, we first apply classic analytical chemistry techniques and machine learning to try to expand understanding of our oil-in-water droplet system and to develop analytical methods universally applicable to such systems. The droplets are composed of four oils [octanoic acid, diethyl phthalate (DEP), 1-octanol, and 1-pentanol] and are placed in a high-pH surfactant-containing aqueous phase. The utilization of machine learning for the prediction of the surface tension and viscosity of the oil mixtures enables the correlation of these to droplet behaviors, and unlocks the dataset collected during optimization to enable mechanistic insight. pH indicators are shown to be a method suitable for visualizing the flow of material within and outside the oil droplets while ¹H NMR spectroscopy is used to quantify the level of oil dissolution in the aqueous phase. Furthermore, we present a chemorobotic platform developed to allow us to study how the chemical environment of the droplets (i.e., the aqueous phase) influences the droplet’s behaviors by adding up to six aqueous-phase constituents. Using the platform we screen for interesting droplet behaviors and utilize a genetic algorithm to optimize both the oil- and aqueous phases simultaneously, thus showing that the coevolution of an entity with its environment allows the discovery of behavioral niches unreachable by independent evolution. Fundamentally, the combination of automated experimentation and data generation, physicochemical analysis, and machine learning has allowed significant advances to be made in understanding the driving forces behind droplet behaviors and moved us closer to being able to predict them. Furthermore, we were able to demonstrate the general utility of evolutionary algorithms, machine learning, and data visualization for understanding complex systems defined by several inputs, which cannot feasibly be modeled.

Results

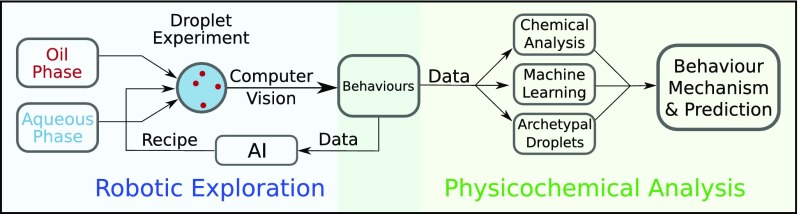
Our system comprises oil droplets (composed of octanoic acid, DEP, 1-octanol, and 1-pentanol) placed into a surfactant-containing aqueous phase by a robotic assistant. The droplet behavior is recorded, analyzed by computer vision, and fed back to generate the next experiments via a genetic algorithm, in a closed-loop system (Fig. 1). Using this system, 7,767 experiments were previously undertaken aimed at exploring the behaviors possible in this system and optimizing for three––movement, division, and vibration. This represented a vast underexplored dataset which we wanted to exploit to try and investigate the mechanisms behind the behaviors observed in our system. Furthermore, we have now expanded the system to allow the simultaneous variation of the aqueous phase.

Fig. 1.

Summary of the workflow presented herein. During robotic exploration, oil droplets are placed into a surfactant-containing aqueous phase by a robotic assistant. The droplet behavior is recorded, analyzed by computer vision, and fed back to generate the next experiments via a genetic algorithm, in a closed-loop system. The recipes and data generated from this process are then used for physicochemical analysis, where traditional chemical analysis, machine learning, and archetypal droplet experiments are used to study the behavioral mechanisms and to predict droplet behaviors.

Chemical Analysis.

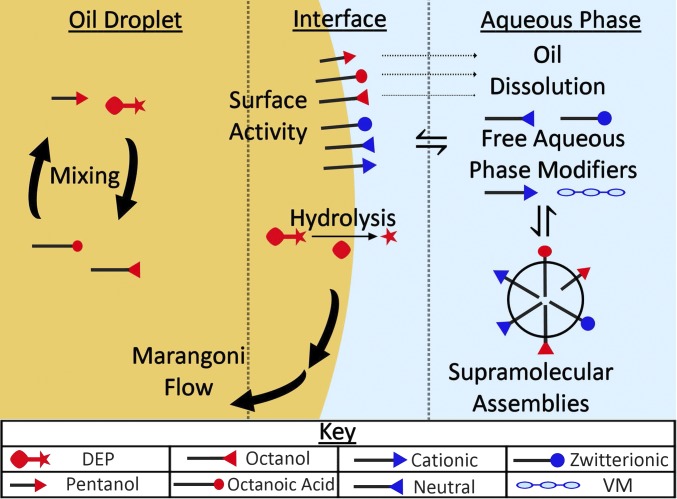
We hypothesized that the various behavioral effects observed in the previously reported system are due to a trade-off between different oil properties (e.g., density, surface tension, and viscosity) and oil dissolution (Fig. 2). We targeted our investigations on a select number of archetypal formulations known to exhibit behaviors representative of what is possible in the system. In the subsequent sections we present analysis of the oil density, dynamic viscosity, and surface tension, showing how these properties can be related to droplet behavior. To do this we utilize machine-learning techniques––the utility of which is rapidly being demonstrated across the physical sciences (25–28). Phenolphthalein is used to investigate phase mixing and material flows while ¹H NMR spectroscopy enables quantification of oil dissolution in the aqueous phase.

Fig. 2.

Summary of the different physical and chemical processes thought to be occurring in our oil-in-water droplet system. VM, viscosity modifier.

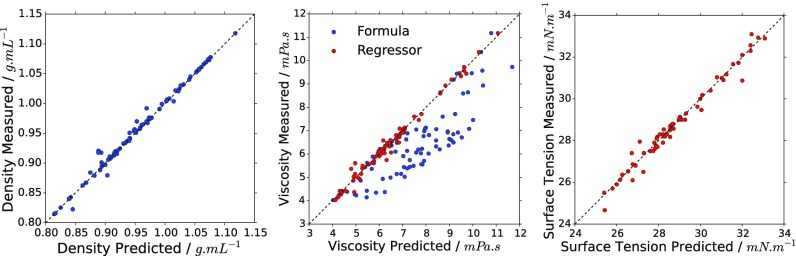
A number of oil formulations were prepared and their density, dynamic viscosity, and surface tension measured, with the intention of testing for any correlation between these physical properties and droplet behavior. From this initial dataset, it was clear that for density a simple weighted mean was sufficient for predicting mixed oil formulation densities (Fig. 3). For viscosity, however, an Arrhenius-based method yielded unsatisfactory results for dynamic viscosity prediction while no appropriate method for surface tension prediction of oil mixtures could be found. As such, machine-learning regression was utilized for the prediction of the physical properties of all of the formulations previously tested––some 7,767 experiments––and mined for trends.

Fig. 3.

Plots of the predicted density (Left), dynamic viscosity (Center), and surface tension (Right) against their measured values. Blue points are predicted using weighted mean (density) and Arrhenius-based method (viscosity) while red values are predicted using an SVM regressor.

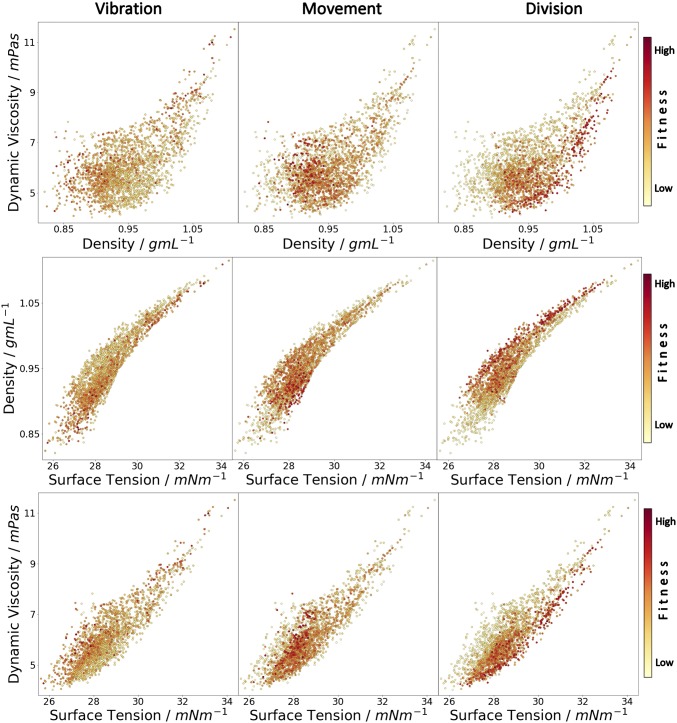
Fig. 4 reveals definite correlations between the physical properties of a given oil mixture and how the droplets behave. These plots are presented in full in Movie S1. For example, oil formulations expressing high levels of division usually have a high density for their surface tension and viscosity and a high surface tension for their viscosity. Similarly, high movement is expressed for formulations with a broad range of intermediate physical properties while vibration occurs at the opposite end of the physical property space to division. These trends were confirmed using a machine-learning approach to predict the behavioral trends from oil physical properties, as shown in SI Appendix, Fig. S6 and Movie S1. This is significant as it allows us to build a property to behavior model that fills the gaps between observations.

Fig. 4.

Impact of dynamic viscosity, density, and surface tension on droplet behavior: movement (Left), vibration (Center), and division (Right). Each dot is an experiment; the color is proportional to the intensity of the behavior.

To test whether we could use physical properties in a predictive manner, we identified two nonoverlapping regions in the physical property space where a swarming behavior (see Automated Experiments) appeared to be favored. The physical properties of these formulations were predicted and used to select similar recipes that had not previously been analyzed by eye. By repeating these experiments, 20 of the 53 exhibited swarming in both repeats (SI Appendix, Fig. S9), demonstrating that our predicted physical properties could be used to discover more instances of a rare behavior. Both regions occurred at low viscosity and surface tension, but one at significantly higher density (0.92–0.96 g mL⁻¹ vs. 0.85–0.88 g mL⁻¹). Prediction of physical properties is therefore a useful tool for both identifying general trends and for identifying new recipes that display a previously observed behavior.

To investigate phase mixing and material flows, we added a pH indicator––phenolphthalein––to the oil phase. Upon droplet placement the clear, neutral indicator may be deprotonated and turn pink. These experiments confirmed that there is aqueous–oil phase mixing going in both directions; both the oil and aqueous phase end up stained pink, while clouds of pink were often seen to diffuse out of the droplets. Furthermore, vastly different effects between the different oils were observed, for example, DEP tends to favor mixing at the boundary and gentler internal mixing while pentanol favors rapid internal mixing, as illustrated in Movie S2. They also show the complexity of the system; the fact that such complex behaviors can be exhibited in such simple systems is remarkable. Movie S3 shows the Sudan III (red dye) and phenolphthalein (pH indicator) versions of the same four-component formulations and illustrates how much more information is accessible using the indicator. While the presence of the indicator will have some effect on the droplet properties, these movies demonstrate that the effect is minimal. In some cases droplets expel white or pink material and influence the behavior of nearby droplets, suggesting that matter expelled from the droplets affected the Marangoni forces resulting in chemotaxis. This visualization of the “tethering” of droplets is both interesting and surprising. The indicator observations were fairly consistent for the same formulation, but different formulations with a high fitness for a particular behavior did not exhibit identical indicator phenomena.

Hypothesizing that oil dissolution could play a role in droplet behavior, we developed an experimental procedure to quantify the amount of each oil dissolved in the bulk aqueous phase. Interestingly, ethanol was present in the aqueous phase, due to the hydrolysis of DEP, showing that, even in this simple system, both physical and chemical processes take place. Initially, we focused on droplets containing either a single oil or a 1:1 (vol/vol) mixture of two oils.

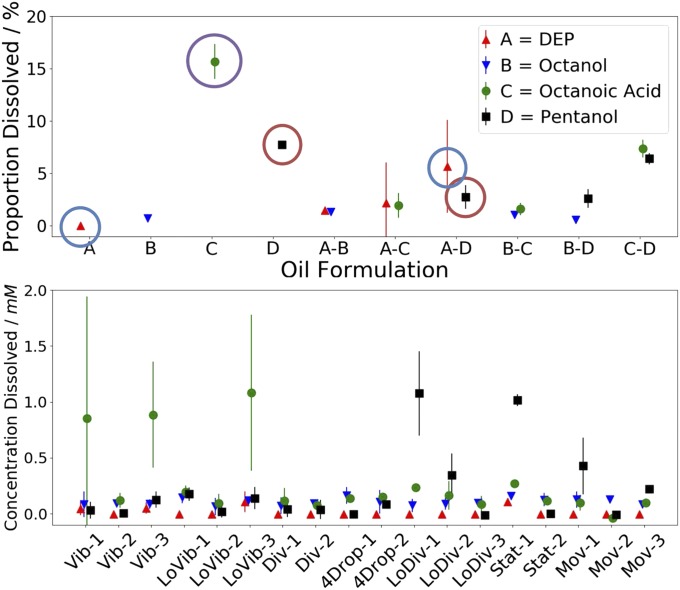
As can be seen from Fig. 5, there are significant variations in the levels of oil dissolution depending on the oil formulation present. When placed alone, octanoic acid and pentanol dissolve to significant levels (red and purple circles), while DEP is not seen to dissolve at all (blue circle), as expected given the oils’ aqueous solubilities. The trends for the binary mixtures are not, however, as predictable. Octanoic acid and pentanol promote the dissolution of the other oils, while simultaneously their own dissolution is lower. Octanoic acid is seen to dissolve at low levels when mixed with DEP, octanol, or even pentanol. These observations could either be due to molecular-scale interactions or due to droplet behavior. On observing how each of the binary oil droplets behaves, however, there does not appear to be a direct link between oil dissolution and droplet behavior in these cases. For those cases with large error bars, it is thought this is due to spatiotemporal variations in the oil concentration within each experiment.

Fig. 5.

Plots showing the concentration of oil dissolved in the aqueous phase for various formulations 1 min after 4 × 4 µL droplets are placed in 3.5 mL aqueous phase. (Top) The proportion of the oil present dissolved for droplets composed of a single oil or 1:1 (vol/vol) mixture of two oils, i.e., point A-B, corresponds to the oil-dissolution levels when a 1:1 (vol/vol) mixture of DEP and octanol is used as the droplet formulation. (Bottom) The concentration oil dissolved for full four-oil formulations, categorized by the high- or low fitnesses they show for certain behaviors. Key: Vib, LoVib: high or low vibration fitness. Div, LoDiv: high or low division fitness. 4Drops: division fitness of 4; i.e., four droplets present after 1 min. Mov, Stat: high or low movement fitness. Error bars show SD.

For full formulations the levels of oil dissolution are similar, but for a few outliers. These formulations represent a vast range of droplet behaviors, thus implying that the level of oil dissolution does not play a key role in defining droplet behavior. There are some exceptions, however. For example, three formulations show significantly higher levels of octanoic acid dissolution than the rest of the formulations. On viewing the phenolphthalein indicator movies of these formulations, these are also the only formulations that show a tethering interaction between droplets, thus implying there is a link between octanoic acid dissolution and this interaction, potentially with octanoic acid aqueous-phase supramolecular assemblies playing a key role. The level of pentanol dissolution is also seen to vary significantly, although in almost all cases this is just a reflection of the changing level of pentanol in the formulation, as pentanol has a relatively high water solubility. It is very surprising to learn that oil dissolution does not play a key role in the quantified droplet behaviors, but can be linked to other observed effects, especially given the fact that oil dissolution was previously thought to be one of the key drivers for symmetry breakage and droplet behavior in this and other systems (2).

Automated Experiments.

To investigate how the chemical environment of the droplets (i.e., the aqueous phase) influences their behavior, we wished to enable the simultaneous variation and optimization of both the aqueous and oil phases. A robotic platform was designed to automatically undertake droplet experiments with variable aqueous and oil phases, with droplet analysis via video recording (SI Appendix, Fig. S11 and Movie S4). Six aqueous-phase modifiers were chosen for use on the automated platform: the cationic surfactants TTAB and CTAB; the nonionic surfactants Brij O10 and Triton X-100; the zwitterionic surfactant DDMAB, and poly(ethylene glycol) (Mn = 400). These were chosen due to their varied chemical structures, properties, effects on droplets, and compatibility. To identify the droplet behaviors possible in this system, 393 random recipes were tested. Movement and division, as previously observed with the single aqueous-phase system, were again the most prevalent droplet behaviors. Remarkably, several other behaviors were identified: swarming, fusion, pulsing, and sorting (Movie S5).

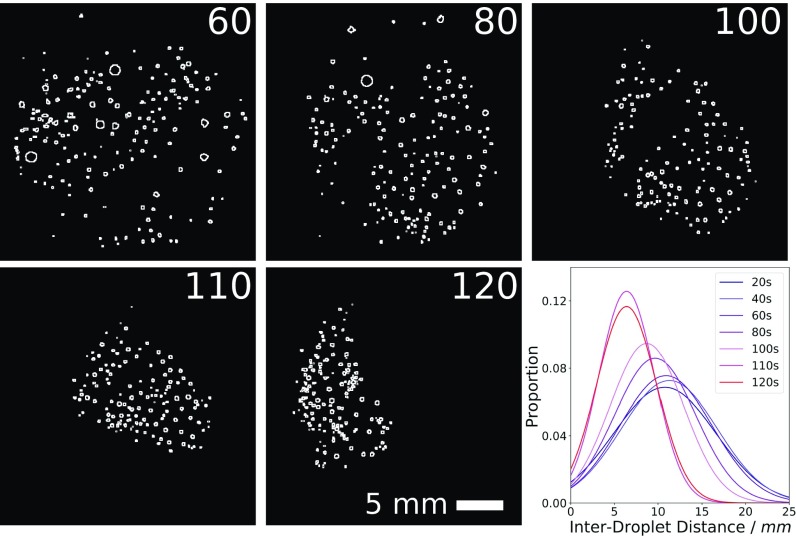
“Swarming” was observed when the droplets divided into a large number of small droplets on placement, maintaining a close proximity to each other while appearing to move in concert, as illustrated in Fig. 6. Interestingly, if a larger droplet approached the swarm of smaller droplets, the direction and shape of the whole swarm changed in response to repulsive interactions. From our analysis work we have some understanding of the driving forces behind this swarming behavior. Initially, a large number of droplets must be present––hence the formulation must be unstable, leading to rapid division. Following this, small droplets either move collectively, apparently driven by bulk surface tension variations “carrying” the droplets together, or the smaller droplets are “herded” by larger droplets, whose more definite movements through the swarm cause the swarm to shift around the larger droplet. Often, there is a period of rapid division at the beginning of the experiment followed by a period of swarming and then the repeated fusion of the small droplets.

Fig. 6.

Movie snapshots of a swarming formulation, converted into black and white outlines using ImageJ. Numbers in the corners correspond to the experiment time in seconds since the experiment started. Initially there are relatively few droplets, fairly evenly spaced (0–60 s). These then divide and swarm, to give more droplets closer together. At around 100–105 s, the rapid dissolution of a droplet stuck to the edge of the dish (not shown) leads to a much tighter-knit swarm, with an average interdroplet distance of only around 6.4 mm. The variation in interdroplet distance is also seen to decrease. Images processed using ImageJ (29).

Droplet “fusion” had previously been observed in the TTAB-only system, but it was very rare owing to the stabilizing boundary formed by the cationic surfactant. It would, however, be a desirable behavior for oil droplets to exhibit, especially if it can be controlled, due to the possibility of controlling a chemical reaction between two components dissolved in two separate droplets. Electrostatic repulsion plays a role in the prevention of fusion, in addition to surfactant gradients induced by the decrease of distance between droplets resulting in Marangoni forces against the direction of movement (30). These forces can be reduced by ion pairing between oppositely charged ions (e.g., quaternary ammonium surfactant and octanoate). Clusters of many smaller droplets provide greater surface area for the deprotonation of octanoic acid, which combined with cationic surfactants in the aqueous phase forms a catanionic system. Indeed, fusion is far more commonly observed for smaller droplets and division for larger droplets, implying there may be an intermediate optimal radius in many cases. As surfactant concentrations vary, fluctuations in interfacial tension mean that division could be favored in one location in the dish and fusion in another (31). Some droplet formulations give droplets which may fuse if they happen by chance to collide with each other, i.e., they have no significant repulsive or attractive forces, while others exhibit attraction to each other and experience a change of trajectory before fusion. “Pulsing” droplets exhibit constant, rapid changes in diameter as the droplets shrink and grow periodically. This is in contrast to vibration, which involves rapid changes in a droplet’s direction of movement. When droplets were attracted to the walls of the Petri dish they sometimes also exhibited movement around the edge of the dish, division or fusion. This also often resulted in droplet “sorting,” in which the droplets spread themselves evenly around the circumference of the dish due to repulsive interactions between the droplets.

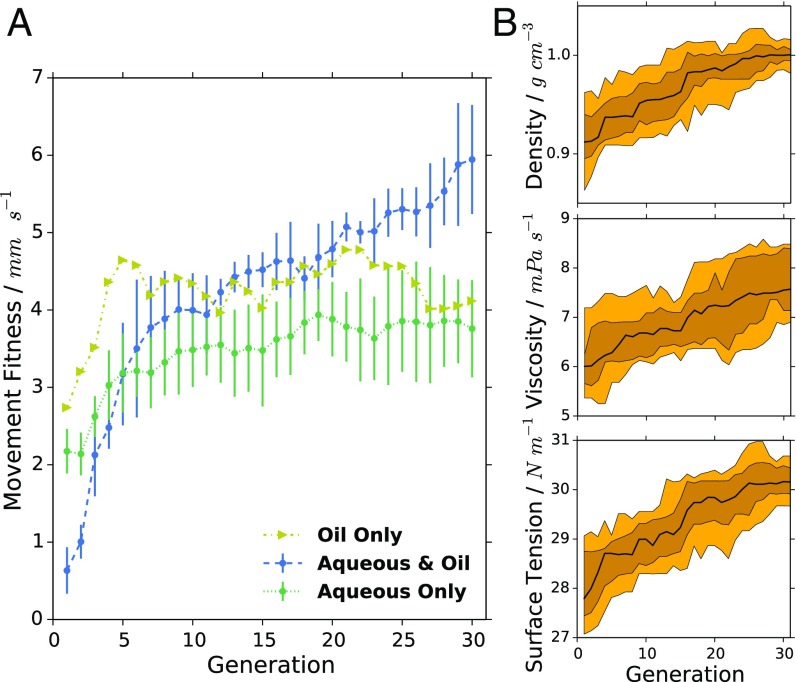
Having identified the behaviors possible in this system, a genetic algorithm optimization was then carried out for movement using all 10 components. CTAB and Brij-O10 were quickly optimized out almost entirely (SI Appendix, Fig. S10); thus, only the remaining four aqueous phases were subsequently used. It is very interesting to note that TTAB and CTAB, which differ only by two CH₂ groups to the surfactant tail, have such different effects on droplet behavior. The results of a genetic algorithm optimization for movement (average speed of the droplets) with these eight parameters are shown in Fig. 7A. With these eight inputs there are 9.2 × 10¹⁵ possible recipes, a space unfeasible to search exhaustively. The genetic algorithm was run for 30 generations, with 10 new recipes each generation, taking ∼80 h for a complete optimization. The optimization was repeated in triplicate from random starting recipes, and compared with the maximum fitness values observed in the oil-only experiments. The final median fitness value of each individual genetic algorithm run surpassed 5.37 mm s⁻¹, while the maximum fitness value achieved was 9.59 mm s⁻¹. This compares to the oil-only optimizations which achieved a maximum droplet speed of 7.17 mm s⁻¹ and a median of up to 4.78 mm s⁻¹. The large increase in median fitness from less than 1.0 up to 5.37–6.93 mm s⁻¹ showed that the environment in which the droplets are placed has a considerable influence on their movement, and that the higher number of parameters used in the optimization enabled even higher fitnesses to be observed. SI Appendix, Fig. S13 shows the evolution of the composition of both the aqueous and oil phases during the evolutionary experiments. Overall, the compositional trajectories and final values differ significantly between runs while the upward trend in fitness is conserved, illustrating the complexity of the system and why it is beneficial to optimize the aqueous and oil phases together. Interestingly, as SI Appendix, Fig. S14 shows, the physical properties of the oil phase are fairly consistent throughout the runs, despite this compositional variation.

Fig. 7.

(A) Comparison of median fitness values for each generation between the oil-only, aqueous-only, and simultaneous aqueous and oil optimizations. Error bars show SD. (B) Change in physical properties of the oil mixture vs. generation for the aqueous- and oil-phase optimization (run 1). The black line corresponds to the median for each generation, the dark yellow area shows the distribution between the 75th and 25th percentile, and the pale yellow area shows the distribution between the 90th and the 10th percentile.

To investigate whether such high fitnesses could be observed by first optimizing the oil phase and then the aqueous phase, instead of optimizing them simultaneously, evolution experiments were carried out with a predefined high-fitness oil formulation optimized in the TTAB-only aqueous phase (SI Appendix, Fig. S15). The recipe chosen had a high, reproducible movement fitness value of 5.96 mm s⁻¹. The oil droplet fitness again increased throughout the optimization, but only by 1–2 mm s⁻¹, in contrast to ∼6.0 mm s⁻¹ in the case of the eight-parameter evolution experiment. Only one of the three runs surpassed the fitness previously observed with 100% TTAB aqueous phase, suggesting that 100% TTAB was close to the optimal aqueous phase for this oil formulation, even though much higher fitnesses are attainable with different oil–aqueous formulations. Movie S6 compares the fastest-moving droplets from each of these evolution experiments.

The evolutionary trajectories were compared between the oil-only, aqueous-only, and combined optimizations (Fig. 7A). The oil-only optimization began from the highest fitness value compared with the others, closely followed by the aqueous-only optimization. In contrast, the combined optimization of aqueous and oil phases began at a fitness value of below 1.0 mm s⁻¹, far lower than the other runs, which both began with one phase closer to optimal. With the composition of both phases completely randomized for all individuals in the first generation, the low median fitness demonstrates that the eight-parameter space is vast and contains many more poor formulations for a given fitness criterion than good ones. The increase in fitness over successive generations is rapid, and leads to a much higher final fitness than for either of the separate optimizations. This demonstrates the complexity of the formulation space––an oil phase which is optimal for one aqueous phase may give poor results in another aqueous phase, and vice versa, yet when both phases are optimized together, the full range of effects of each component on the others is taken into account, and therefore a greater space is available to the algorithm for exploration.

Discussion

Herein, we believe we have illustrated how the combination of automated experimentation and data generation, physicochemical analysis, and “big-data” statistics has a unique potential to complement traditional analytical chemistry tools as we aim to understand complex chemical systems. Three analytical methods have been developed for the analysis of oil-in-water droplet systems––formulation physical property prediction based on machine-learning methods, quantification of oil dissolution using ¹H NMR spectroscopy, and the use of a pH indicator to visualize phase mixing and flows. Through density, viscosity, and surface tension prediction, correlations have been identified between physical properties and droplet behaviors. This also allowed the prediction of recipes exhibiting a rare cooperative droplet behavior––swarming. Without the ability to both generate and analyze this quantity of data, these insights would have been impossible, leading both to a weaker general understanding of the system and no ability to predict such rare behaviors. This also illustrates how smart automation cannot only help with exploration, optimization, and discovery but also be used for developing fundamental understanding of such systems. Despite a massive range of droplet behaviors, ¹H NMR spectroscopy has shown that the levels of oil dissolution are generally constant for all recipes. This implies that oil dissolution is not the key factor defining droplet behavior. It is our intention, however, to further develop this method via sampling at different times and locations––maybe dissolution kinetics vary in a way not captured by our end-point method. Finally, the use of a pH indicator has opened a window into the droplet and aqueous-phase dynamics. Specifically, long-range tethering interactions have been identified between droplets, which seems to be linked to octanoic acid dissolution in the aqueous phase. Notably, the three analytical methods developed complement each other; one is a measure of bulk properties, one is a measure of the state of the system, and the other allows visualization of spatiotemporal variations within the system. Particularly, the NMR and indicator studies fill a gap in the physical property prediction in that they study dynamic processes occurring, not just bulk properties. These three techniques are also all suitable for analyzing other dynamic droplet systems.

By expanding our droplet system to include the aqueous phase, using different surfactant types and modifiers, various droplet behaviors were observed. The increased speed of the droplets accessible when both phases (eight parameters) were optimized together (over oil or aqueous phase in isolation) sheds light on the complexity and intertwined physicochemical properties of our droplet system. The larger parameter space gave a far lower first-generation fitness than either four-parameter space, with the fitness subsequently rising rapidly during evolutionary exploration, showing that for systems such as ours, such an increase in parameter space can produce impressive results with a genetic algorithm. With eight parameters a complete exploration of all possible combinations would take 2.1 × 10¹¹ years with our platform, making artificial intelligence an indispensable tool. Evolution in materio, using artificial intelligence in combination with a liquid-handling robot for autonomous exploration of chemical spaces, is rapidly proving its utility for tackling wider chemical problems. Over and above work utilizing oil-in-water droplets, we believe that cheap, robust, and customizable automated platforms, in conjugation with advanced computer science methods, represent a hugely underdeveloped opportunity for chemists to apply to a wide range of research areas including complex systems, chemical synthesis, and materials chemistry. Of particular interest are recent developments in novelty-seeking and curiosity-driven algorithms that open the way to the genuine autonomous exploration of what can be done with a new system rather than a more directed optimization of a specific property (32, 33). In the future, we hope to apply these methods to other systems, to further show the benefits possible via the interaction of these fields.

Materials and Methods

Detailed materials and methods are given in SI Appendix. The robotic platform used within this work is based upon that previously reported by this group, modified to allow the use of multiple aqueous-phase constituents (2). Due to the need for maximum consistency throughout experiments, standard operating procedures were developed for oil- and aqueous-phase preparation which are shown in SI Appendix. Aqueous phases were prepared with a 20 mM concentration of the given modifier at a pH of approximately 13 while the oils were dyed with 0.25 mg mL⁻¹ Sudan III dye. For each droplet experiment, 4 × 4 µL droplets were placed into 3.5 mL of mixed aqueous phase and a 1-min movie recorded for analysis via computer vision.

Experiments Based on Physical Property Prediction.

For physical property prediction, the viscosity and density of 81 formulations were measured, while the surface tensions of 69 oil formulations were measured using the Du Noüy ring method. A weighted mean was then deemed sufficient for density prediction, while a support vector machine (SVM) regressor using a radial basis function (RBF) kernel was used for viscosity and surface tension prediction. For the discovery of swarming formulations the density, viscosity, and surface tension of five known swarming formulations were calculated. The range of physical properties from each group of swarming formulations was used to find formulations within them that could be tested and analyzed for swarming behaviors. Fifty-three formulations were tested in duplicate, of which 20 exhibited swarming in both repeats, with a further 10 showing swarming in one of the two repeats.

Random Matrix Screen.

A proximity-limited random search was carried out in 10 dimensions (6 aqueous, 4 oils); using a threshold factor to ensure formulations generated were sufficiently different, 393 random formulations were tested.

Genetic Algorithm Explorations.

A genetic algorithm was used with a genome length equal to the number of components for the mixture. Twenty-four random combinations were tested to form generation 1, then roulette wheel selection was used to select individuals carried over to undergo cross-over and random mutation––forming the next generation of 10 individuals. The experiment was continued for 30 generations. An individual’s fitness was quantified using the previously published methodology (2).