Pulsating dissolution of crystalline matter

Significance

The reaction of crystalline material with fluids is of relevance for natural and technical processes. A basic assumption has been that the reaction products are continuously released from the crystal surface. New experimental and analytical results show something fundamentally different: Material is released in a series of reaction pulses. Applied and theoretical implications impact both the upscaling of crystal dissolution kinetics, and more importantly, the problem of how dissolution and growth are connected via the equilibrium state. These results challenge the prevailing view that crystal dissolution is simply the inverse process of continuous crystal growth at crystal dislocations. Consequently, we need to examine how macroscopic crystal equilibrium reflects continuous or discontinuous processes in the microscopic state.

Abstract

Fluid–solid reactions result in material flux from or to the solid surface. The prediction of the flux, its variations, and changes with time are of interest to a wide array of disciplines, ranging from the material and earth sciences to pharmaceutical sciences. Reaction rate maps that are derived from sequences of topography maps illustrate the spatial distribution of reaction rates across the crystal surface. Here, we present highly spatially resolved rate maps that reveal the existence of rhythmic pulses of the material flux from the crystal surface. This observation leads to a change in our understanding of the way crystalline matter dissolves. Rhythmic fluctuations of the reactive surface site density and potentially concomitant oscillations in the fluid saturation imply spatial and temporal variability in surface reaction rates. Knowledge of such variability could aid attempts to upscale microscopic rates and predict reactive transport through changing porous media.

The dissolution of crystalline matter plays a critical role in technical and natural processes such as corrosion (1, 2), cement hydration (3, 4), nuclear waste management (5, 6), carbon sequestration (7, 8), and pharmaceutical bioavailability (9, 10). Reliable predictions of resulting material fluxes require a mechanistic understanding that includes both the dominant pattern and heterogeneous distribution of surface reactivity. However, a consistent dissolution model that includes such knowledge is still missing (8, 11–13). Understanding the mechanisms requires spatially and temporally resolved observations of reacting surfaces. Numerous dissolution studies using laboratory experiments and surface-sensitive methods have supported the conclusion of a continuous surface step movement that results in the removal of crystal layers via surface steps (e.g., refs. 14 and 15), as summarized in review articles (e.g., refs. 16 and 17).

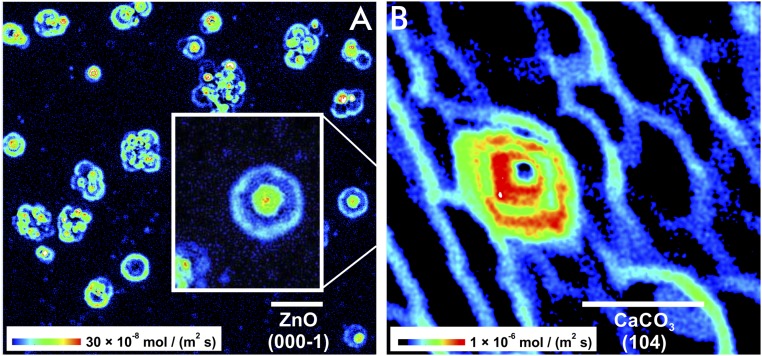
The interpretation that crystal moieties (e.g., atoms or molecules) are continuously removed during dissolution is now challenged by observations made possible through the analysis of reacting surfaces of high lattice symmetry and slow reaction kinetics. Zinc oxide (ZnO) is an example that allows for a “slow-motion” analysis of its dissolution kinetics. When we analyzed the measured rate distribution on (000-1) crystal surfaces of dissolving ZnO (18), we made a striking observation: the concentric distribution of rate pulses at and around etch pits (Fig. 1A).

Fig. 1.

Dissolution rate maps show quantitatively the spatial distribution of the time-normalized material flux. Note the intervals between two reaction fronts. Such surface areas are free of any material flux or show significantly lowered reactivity. The initially isolated rate pulses occur at etch pits that are formed around the outcrops of line defects. The locally regular material release is complicated after spatial superimposition of rate pulses. Rate maps of two dissolving crystal surfaces are shown. (A) ZnO (000-1) with concentric and equidistant rate pulses. (B) CaCO₃ (104) with repeated rate pulses (red) at a screw dislocation and single stepwave fronts (blue) originating from point defects. (Scale bar length: 10 µm.)

Conceptually, we base surface reactivity of crystalline matter on the dissolution stepwave model (14). This model describes the relationship between crystal lattice defects and the formation of reactive surface sites that drive the dissolution process. These kink sites are self-replicating, that is, the removal of a kink atom turns the adjacent atom into a kink atom. Repeated removal of kink atoms accounts for the spatial motion of steps across the crystal surface (see Supporting Information, Fig. S6 for more details). This continuous process results in the surface-normal retreat, and ultimately, in the destruction of any dissolving crystal. The stepwave model predicts an initial decrease in velocity close to a defect structure and an increase in velocity far from the defect. The absolute values of the velocity and acceleration of a step are controlled by the saturation state or local deviation from equilibrium (i.e., ΔG values) of the system. As a result, an initial decrease and increase in velocity, that is, the pulsation of local surface rates close to the defect, is implicit.

Lateral variations in reaction rate are also expected by considerations that focus on nucleation-driven surface reaction phenomena (4, 19, 20). However, a quantitative model of kink-site nucleation will require a more detailed and dynamic treatment with respect to single-surface sites and therefore further development of the existing stepwave model. Recent probabilistic kinetic Monte Carlo models incorporate such attempts, for example, via the dynamic interaction of surface steps (e.g., ref. 21).

As a general observation, the dissolution processes do not produce smooth surfaces with some etch pits (e.g., refs. 22 and 23). Instead, dissolution leads to the formation of highly complex, rough topographies. This complexity is an important constraint to the reactive flow conditions, providing feedback to crystal surface reactivity (24, 25).

Typically, there is a substantial heterogeneity in the surface reactivity that we can quantify and illustrate through spatially resolved rate maps (Fig. 1). A sequence of such maps also shows the time-resolved material flux from the reacting surface (22). Techniques such as atomic force microscopy (AFM) and vertical scanning interferometry (VSI) provide the data for these maps (for details see SI Text and Fig. S1). The overall rate is not just the mean but the complex interplay of all rate contributors. These rate components are identified from rate spectra in the frequency domain of the rate-map data (26).

Our ZnO rate map above shows pulsed surface rates (Fig. 1A). Are those pulses, over several micrometers in lateral distance, ZnO-specific or a general trait of dissolving crystalline matter? To answer this question, we also analyzed calcite (CaCO₃) rate maps (Fig. 1B). Cleaved (104) surfaces of calcite have been well studied with respect to their dissolution kinetics. Investigations mostly conducted with AFM techniques have focused on the velocity of reacting surface steps (16, 27). However, rate maps of sufficiently large field-of-view size of AFM data have either not been published or have not been analyzed for such features. We have now produced rate maps of sufficient size by using interferometry techniques. They show rate distributions on the carbonate surface that are indeed reminiscent of the concentric flux pulses of ZnO (Fig. 1A).

While the hexagonal lattice symmetry of ZnO parallel to the (000-1) face causes an almost circular shape of the equidistant pulsed reaction fronts, the calcite symmetry causes the expected rhombic, nonequidistant shape (28, 29). The complexity of calcite rate maps suggests the reason why the rate pulses have been missed before. The spatial superimposition of multiple rate pulses results fairly quickly in an irregular pattern of the material flux map (Fig. 1A and Supporting Information). Such patterns obstruct the identification of the initial pulse generator. Another critical factor for the detection of rate pulses is the specific dissolution rate of the material. Reaction rates on the order of 10⁻⁶ mol⋅m⁻²⋅s⁻¹ are representative for calcite and result in complex interferences of pulses. Fig. 1B shows an example of calcite with a low density in line defects, thus illustrating an undisturbed pulsation of a single screw dislocation. In any case, our results indicate that the occurrence of rate pulses is not limited to ZnO but a likely general mechanism of crystal dissolution. Therefore, it makes sense to further investigate the pulsed behavior of crystal dissolution and its implications.

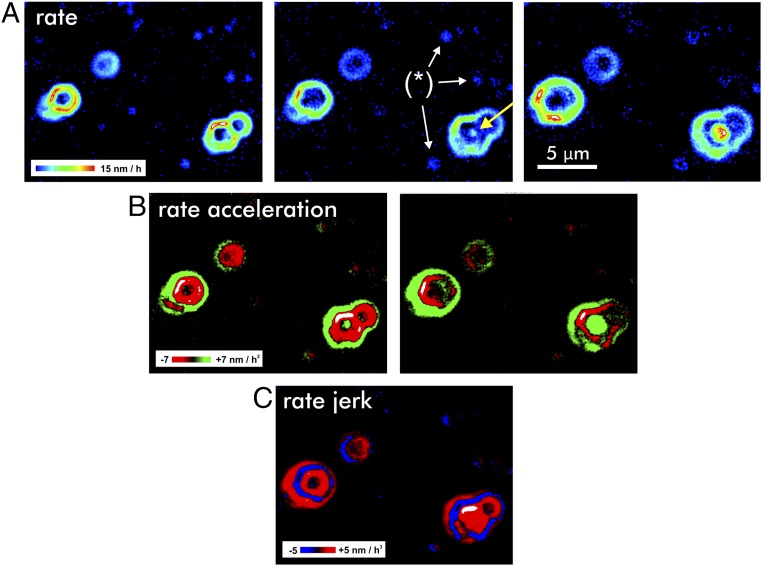
By using VSI techniques, we generated a time-lapse sequence of maps that quantify the development of the ZnO topography over a time span of 12 h. The resulting topography maps were used to generate a sequence of rate maps, that is, the first temporal derivative of the reacting crystal topography. Calculations of the second and third temporal derivatives then provide the maps of the rate acceleration and the so-called rate jerks (Fig. 2). The rate maps (Fig. 2A) show that higher rates are associated with the outcrops of screw dislocation defects. The sequence of maps illustrates the spatial development of the concentric rate pulses, manifested by the growth of their diameter. Note the occurrence of a new rate pulse in the center image of Fig. 2A (arrow). Previous theoretical considerations of the propagation of stepwaves (14) did not explicitly predict such behavior.

Fig. 2.

Surface reactivity maps illustrate the dynamics of the reacting crystal. The maps are based on difference calculations, that is, the temporal derivative. Three rate maps (Upper) result in two rate acceleration maps (Middle) and, subsequently, in a single map quantifying the change of the rate acceleration, the jerk (Lower). (A) Rate maps of a dissolving (000-1) ZnO face show the pulsed material flux from the surface and the lateral spread of reactive surface area. Note the onset of a new rate pulse (arrow) at a screw dislocation. Dissolution at point defects [examples are indicated by (*)] results in comparatively very low rate contributions (dark-blue color, no higher rate portions) and affect only a minor area of the reacting surface. (B) Rate-acceleration maps indicate regions that are subject of increasing (green) or decreasing (red) surface reactivity. (C) The rate-jerk map visualizes the emerging increase (red) versus decrease (blue) of surface reactivity.

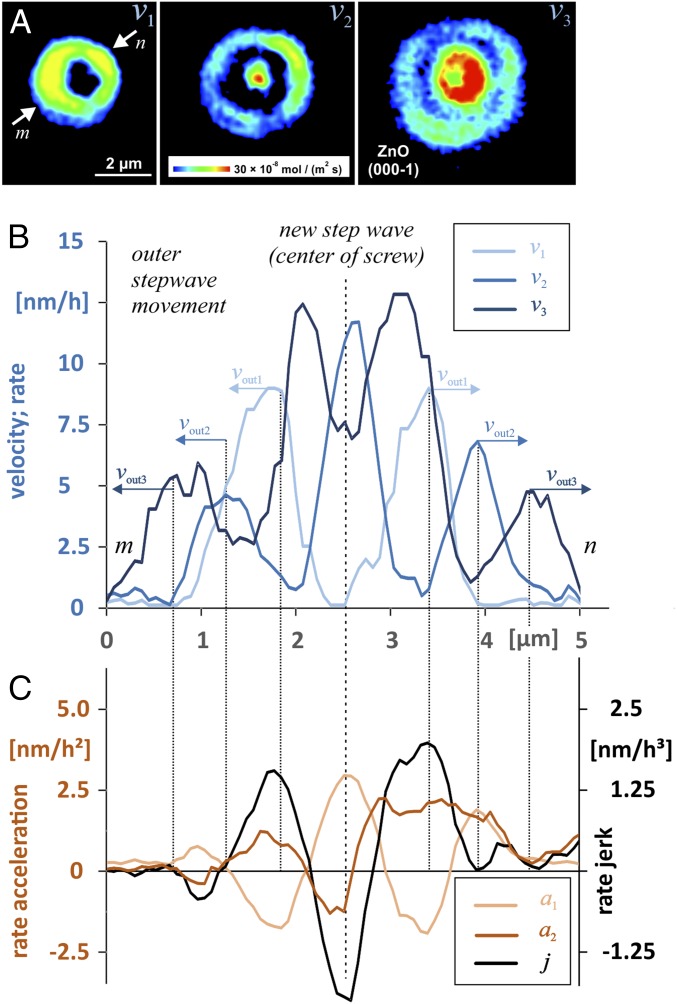
Many rate pulses interfere with other pulses emanated from neighboring pits. This leads quickly to complex interference patterns, as are visible for most reacting surface portions in Fig. 1A. Even the more regular-shaped pulses are often impacted by nearby pulses, causing a deformation of the symmetric shape of a pulse. In Fig. 2, the velocity patterns are modified by nearby pulse sources, from either a point defect (small features with very low rate) or an adjacent screw dislocation (higher rates). For a detailed analysis of rate, acceleration, and jerk profiles, we utilized a single and undisturbed pit as a source of rate pulses (Fig. 3). For comparison, details from partly superimposed pulses as well as an example of a long-term superimposition are available in Supporting Information.

Fig. 3.

(A) Sequence of rate maps analyzed for the evolution of ZnO dissolution rates at a screw defect via rate profiles (B). (C) Profiles compare the evolution of rate acceleration and rate jerk. The rate profiles v₁–v₃ visualize the reaction velocity over a reaction period of 4 h each. Integration time is 8 h for acceleration and 12 h for rate-jerk measurements.

As mentioned above, the second and third temporal derivatives of the surface-height change provide detailed information on the rate acceleration (Fig. 2B) and the rate jerk (Fig. 2C). Note that both parameters consist of positive and negative values, in contrast to the reaction rates. Due to this behavior of acceleration and jerk, the reaction rate is laterally fluctuating as a function of time. In general, the acceleration data explain both the onset and the spatial spread of rate pulses, which are constrained by periodic changes in the rate acceleration. Details of the rate jerk are presented in Fig. 2C. The strong pulsation of the jerk during the entire reaction period produces a periodic, oscillating formation (red) and destruction (blue) of reactive surface area. The term “reactive surface area” was previously introduced to provide a measure of the reacting surface. In contrast to the overall Brunauer–Emmett–Teller (BET) adsorption surface area that is typically applied for normalization purposes (30, 31), the surface reactivity is now interpreted as a time-dependent, transient state that is highly variable and described by the movement of crystal surface steps. On the atomic scale, this motion is quantified by circular dissolution stepwaves emanating from an etch pit, that is, the stepwave model (14), and Eq. 1 quantifies the related step velocity at a distance r from the crystal defect:

$$v\left(r\right)=v_{step}\left(1-\frac{e^{-\left[\sigma \overline{V}/rkT\right]}{e}^{[u\left(r\right)\overline{V}/kT]}}{1-e^{\mathrm{\Delta }G/kT}}\right),$$ [1]

where $v_{step}$ [m·s⁻¹] is the velocity of straight steps, σ [J·m⁻²] is the surface free energy, $\overline{V}$ is the molecular volume [m³·mol⁻¹], $u\left(r\right)$ [J·m⁻³] is the strain field of dislocation defects, k [J·K⁻¹⋅mol⁻¹] is Boltzmann’s constant, T [K] is temperature, and ΔG (<0) [J·mol⁻¹] is the Gibbs free energy of the dissolution reaction. Resulting step-velocity profiles show a maximum close to the center of a pit followed by a steep decrease with a minimum at the pit wall, $v\left(r_{pit}\right)$. For larger distances r beyond the pit wall, that is, after several nanometers, the dissolution stepwave then proceeds to expand and the velocity becomes $v_{step}$ (14). Thus, the steady-state separation $\mathrm{\Delta }r$ of the waves is

$$\mathrm{\Delta }r=a\frac{v_{step}}{v\left(r\right)},$$ [2]

with the molecular distance a as a prefactor. In this case, the undisturbed stepwave-related dissolution rate [m·s⁻¹] is defined by the velocity and spacing of the stepwaves:

$$rate\left(r\right)=\frac{a}{\mathrm{\Delta }r}{v}_{step}=v\left(r\right).$$ [3]

Thus, any rate change or rate acceleration during lateral stepwave movement is defined by the derivative of the velocity $v\left(r\right)$ of the curved step, that is, by changes in $\mathrm{\Delta }r$. Using Eq. 1, we get

$$\frac{dv}{dr}=-\frac{v_{step}\left(\frac{\sigma \overline{V}}{r^{2}kT}-\frac{2C\overline{V}r}{{\left(r_h^2+r^2\right)}^{2}kT}\right)e^{\left[C\overline{V}/\left(kT\left(r^2+r_h^2\right)\right)\right]-\left[\sigma \overline{V}/rkT\right]}}{1-e^{\mathrm{\Delta }G/kT}},$$ [4]

where C combines parameters of the strain field of the dislocation defect (details in ref. 32) and r_h is the size of the hollow core. The application of Eq. 4 produces negative values as a result of the strong deceleration of the step velocity close to the outcrop of the defect. Positive values for the acceleration are obtained at larger distances. A key piece of information from this equation is the occurrence of minimum values close to zero or zeros, that is, minimum values or intercepts with the length axis as shown from experimental results in Fig. 3. The calculation of zeros of Eq. 4 shows a single solution only:

$$r=0\hspace{0.17em}\text{at}\frac{2C}{\sigma },$$ [5]

depending on parameters of the strain field and the surface free energy (Eq. 5; details in Supporting Information). This agrees with the experimental findings about the lateral (spatial) evolution of stepwaves, as illustrated in Fig. 4, and is identical to the solution of zeros of the second derivative after r. Additional zeros or minimum values close to zero imply the vertical dynamics and, thus, temporal discontinuity of the stepwave generation. Specifically, the acceleration and deceleration at r = const. (Fig. 4, Left) are not part of the current stepwave equation and derivative. While the current stepwave equation explains only the outward movement of steps, the quantitative observations on larger scales are more complex. Even at spatial scales that are covered by kinetic Monte Carlo (KMC) simulations (33, 34), isotach maps show remarkable fluctuations and spatial heterogeneity of the stepwave velocity that are not averaged out over the crystal surface (23). Instead, such heterogeneity underscores the accumulation or bunching of surface steps (35, 36). Studies on crystal growth have shown that such fluctuations in step motion may originate from either the atomic processes at the steps or the transport processes at the crystal surface (37). KMC dissolution studies show how such heterogeneities are accompanied by periodic fluctuations of the kink-site density of the reacting surface (23). Such fluctuations are found to occur periodically, thus indicating a periodic increase or decrease in the number of highly reactive surface sites. The resulting temporal and spatial accumulation or consumption of surface kink sites provides a connection between the stepwave motion, according to Eq. 1 and the large-scale observations of rate pulses (Fig. 3).

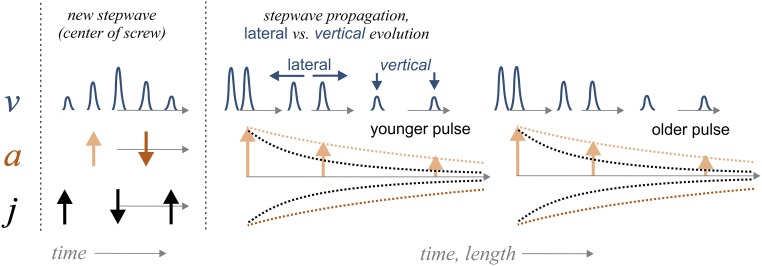
Fig. 4.

Generalization of the results of rate v, rate acceleration a, and rate jerk j as reported in Fig. 3. (Left) The picture illustrates the dynamics of the temporal evolution of a rate pulse, that is, the increase and decrease of the local rate in the central part of an etch pit. (Right) The side of this scheme illustrates the evolution of pulses during outward motion. While the lateral velocity of a single pulse (or ring) is constant, the vertical velocity decays. Subsequent pulses show an identical pattern.

In our experimental data, a sequence of rate profiles shows the formation and outward motion of rate pulses starting from the center of an etch pit (Fig. 3 A and B). On larger spatial scales, the observations away from the pit’s center, that is, at the current reaction front, provide quantitative insight into the dissolution pulses. First, their lateral spread is constant, as indicated by the lateral distances between v_out1–3. Thus, the periodic fluctuations of the step bunches are constrained by a maximum velocity as a result of Eq. 1. According to Eq. 1, the maximum velocities of all rate-map snapshots are observed in the central part of the pit. An interesting analytical result is the periodic or pulsating increase and decrease of the velocity in close proximity to the defect outcrop. Such behavior is not predicted by the stepwave model (14), where the step motion simply approaches a steady-state velocity as a function of distance from the center of the dislocation. In contrast, the results show that periods without any stepwave emanation (Fig. 3A, v₁) are followed by a periodic increase and decrease in the reaction velocity (compare reaction periods of v₂ and v₃), thus suggesting no steady-state behavior. A sketch (Fig. 4) summarizes the contrasting lateral (const.) versus vertical (pulsating) velocity evolution. Such behavior, however, provides an explanation for the existence of rate pulses. We assume a reaction period with rates $v\left(r_{pit}\right)$ and a given bulk undersaturation that drives the dissolution process under surface-controlled conditions. Transport-controlled conditions are ruled out, based on the experimental design and fluid-flow velocities according to analytical observations of step velocities as a function of solution flow rate for calcite (38). Now, the local release of dissolved matter is responsible for a local decrease of undersaturation in the deep central cone of the pit only. Such inhomogeneities that develop in the solution as a result of highly anisotropic dissolution reactions are reported from dissolution experiments, based on detailed topography analyses of etched surfaces (39). However, we did not observe any step-bunching features at the flat reacting surface surrounding the etch pits, according to the flow conditions (38). The concentration of dissolved ions is likely to increase in the deeper part of the etch pit cone. Such localized variations in concentration are observed in studies using AFM techniques (e.g., refs. 40 and 41). Because of the local decrease in undersaturation, $v\left(r_{pit}\right)$ drops in the following reaction period with lower surface reactivity up to a minimum rate. A potential explanation for the next rate pulse that emanates from the pit would be the decay of the local chemical inhomogeneity via diffusion (42). Rate acceleration and rate jerk exhibit such behavior accordingly (Fig. 3C). The emanation of a new rate pulse in the pit center is controlled by an increase in rate acceleration (Fig. 3 and Fig. S4B). Reactive surface portions emerge significantly at this site during the reaction period, as illustrated by the rate-jerk distribution. Simultaneously, the shift of the current reaction front is traced by the first maximum of the rate acceleration function. Contrarily, the decrease in the reaction rate is indicated by a negative rate acceleration; compare rate acceleration arrows, as generalized in Fig. 4.

In addition to this general picture, Fig. 3A also provides insight into vertical and lateral fluctuations of the step movement. Variations in the width of a rate pulse refer to a higher density of steps, that is, a smaller Δr. Locally faster step retreat, however, is indicated by local rate fluctuations. As an example, the rate map in the center of Fig. 3A shows a rate pulse of almost constant lateral extension. The observed rate variability, however, refers to a faster step retreat that occurs locally (greenish-yellow vs. blue color).

The reported dynamics of crystal surface reactivity requires new theoretical and analytical treatment focusing on specific sites of the reacting surface. We expect modifications of the stepwave model that implement the observed dynamics in rate acceleration. Computer simulation techniques provide “snapshots” of the reacting surface. Thus, KMC simulation techniques are promising tools for the quantitative analysis of the rate acceleration and jerk distribution on crystal surfaces.

Mechanistic analysis of the second and third temporal derivatives of surface changes requires datasets that provide insight into fast processes at larger fields of view. This and the lack of any disturbances by signal noise are beneficial aspects of KMC datasets. The major relevance of our results is their impact on strategies for the upscaling of surface reactivity and application in reactive transport models (43).

Further experiments are needed to address the impact of the driving force, that is, the distance from equilibrium on the rate pulses. By varying the experimental conditions over a range of undersaturations, we expect to obtain insights into the variability of the observed rate acceleration and jerk behavior, in particular near the critical ΔG required for etch pit opening (44). Additional investigations should focus on rate maps that are collected during reaction periods of different duration. These results could identify the potential impact of local fluctuations of reaction kinetics at surface steps on the acceleration or deceleration of step velocities. Recent observations of growth kinetics at steps highlight such impact on the evolution and growth kinetics of macrosteps (45).

We have no reason to assume that the observed pulsation could occur synchronously over an entire crystal surface or even a larger part of it, because the pulsed rate variation has not yet been reported in any bulk dissolution experiments. Furthermore, the retreat of macrosteps that controls the surface reaction kinetics at larger distances to the defects is unlikely to be directly influenced by small-scale rate variations that occur close to a defect structure and do not work in concert for multiple defects. We conclude, however, that potential consequences of such pulsation are rather linked to the formation of rough crystal topographies. Nanoscale roughness is a key factor that controls kink-site distribution and density and therefore may help explain why laboratory (bulk) dissolution rates are so variable (17). Thus, the temporal acceleration or deceleration of the kink-site replication as well as the superimposition of neighbored stepwaves may lead to contrasting interference patterns of step waves. We expect our results will lead to a further improvement of the stepwave model with respect to the quantitative treatment of macroscopic crystal surface evolution during dissolution processes. This includes the treatment of local chemical gradients and does thus imply local diffusion mechanisms. More specifically, such an approach will include information about specific surface sections with contrasting kink-site densities and step-bundle geometries as a quantitative key for the prediction of material fluxes. While most reacting crystal surfaces are not atomically flat, the impact of superimposing rate pulses will be of critical importance for many applications. Such superimposition patterns, combined with variations in defect density of a crystal, occur on a length scale of several tens of micrometers (see an example in Supporting Information). The observed contrasts in reaction velocity are responsible for specific surface topography alterations. Ultimately, they predefine the evolution of pore structures within crystalline matter. Lateral and vertical heterogeneity of reacting surfaces are important constraints to reactive transport modeling and specific parameterization, thus providing boundary conditions for reactive transport models on the pore scales and larger.

Materials and Methods

A cleaved calcite sample was partially masked with a gold layer of 550-nm thickness using the physical vapor deposition technique. The chemically inert, masked surface section served as a height reference for height difference calculations after dissolution reactions. Dissolution experiments were performed in a flow-through cell. The fluid volume in the cell was 300 µL. The volumetric flow rate was 30 mL/h, and the reaction period was 2 h. We used a 2.2 mMol Na₂CO₃ solution, equilibrated with air to obtain constant pCO₂ at pH 9.2 for the dissolution experiments. The detailed experimental setup for the ZnO single-crystals dissolution experiments is described in the literature (18).