Emergent chirality in the electric polarization texture of titanate superlattices

Significance

Many natural structures exhibit chirality that is essential to their functional interactions, yet the chiral electronic structures found in condensed matter systems have been primarily limited to magnetic materials. Notably, the electric dipole equivalent of magnetic skyrmions has remained conspicuously elusive. However, recent theoretical predictions and experimental observations of the continuous rotation of electric polarization in titanate superlattices suggests that such complex oxide nanocomposites are ideal candidates for realizing chiral electric dipole configurations. Here we present the results from superlattices of PbTiO₃ and SrTiO₃ using a combination of resonant soft X-ray diffraction and second-principles simulations. We observe chiral arrays of polar line defects, spontaneously formed by the complex interactions in these artificial superlattices constructed from two nonchiral lattices.

Abstract

Chirality is a geometrical property by which an object is not superimposable onto its mirror image, thereby imparting a handedness. Chirality determines many important properties in nature—from the strength of the weak interactions according to the electroweak theory in particle physics to the binding of enzymes with naturally occurring amino acids or sugars, reactions that are fundamental for life. In condensed matter physics, the prediction of topologically protected magnetic skyrmions and related spin textures in chiral magnets has stimulated significant research. If the magnetic dipoles were replaced by their electrical counterparts, then electrically controllable chiral devices could be designed. Complex oxide BaTiO₃/SrTiO₃ nanocomposites and PbTiO₃/SrTiO₃ superlattices are perfect candidates, since “polar vortices,” in which a continuous rotation of ferroelectric polarization spontaneously forms, have been recently discovered. Using resonant soft X-ray diffraction, we report the observation of a strong circular dichroism from the interaction between circularly polarized light and the chiral electric polarization texture that emerges in PbTiO₃/SrTiO₃ superlattices. This hallmark of chirality is explained by a helical rotation of electric polarization that second-principles simulations predict to reside within complex 3D polarization textures comprising ordered topological line defects. The handedness of the texture can be topologically characterized by the sign of the helicity number of the chiral line defects. This coupling between the optical and novel polar properties could be exploited to encode chiral signatures into photon or electron beams for information processing.

Superlattices composed of thin layers of ABO₃ perovskite oxides have attracted substantial interest in recent years because of the exotic phenomena that emerge (1–3) entirely from interfacial or confinement effects and the competition between various energies, leading to topological features such as vortex structures. Electric polarization vortices were theoretically predicted in BaTiO₃ quantum dots and nanowires (4), where the local dipoles continuously rotate to minimize depolarizing fields. Such rotational structures have recently been experimentally observed in PbTiO₃/SrTiO₃ superlattices (5), an intensively studied system since the emergence of improper ferroelectricity in short-period superlattices (6). The so-called “polar vortex” phase is characterized by the spontaneous formation of tube-like textures with laterally alternating clockwise and counterclockwise rotations of electric polarization (7). Such a polar configuration would be potentially chiral (8, 9) with natural optical activity (10) if additional symmetry lowering were permitted.

We have discovered that the polar textures in PbTiO₃/SrTiO₃ superlattices indeed exhibit emergent chirality, the fingerprints of which are imprinted onto its interactions with polarized light. Here, chirality of the polar textures is observed as circular dichroism in the resonant soft X-ray diffraction (RSXD) pattern, i.e., as the difference in diffracted intensities when the circular polarization of incident X-rays is reversed. Atomistic simulations of the superlattices reveal a complex energy surface. The symmetry of some atomic configurations is lowered to a chiral structure, directly related to the appearance of an antiparallel axial polarization at the cores of neighboring polar tubes, which is consistent with the experimentally observed circular dichroism. Within this framework of chiral polarization tubes, these axially polarized cores may be regarded as topological line defects (11). Moreover, the ordering of these chiral line defects within the 3D polar texture leads to a helical rotation of electric polarization along the ordering direction (Fig. S1).

Results and Discussion

(PbTiO₃)_n/(SrTiO₃)_n superlattices were grown epitaxially by pulsed laser deposition on DyScO₃ (001)_pc substrates (pc indicates pseudocubic indices) as described previously (Materials and Methods). For n = 10 to 16, the balance of elastic, electrostatic, and gradient (or anisotropy) energies forms the curled polar textures (5). X-ray diffraction (XRD) and high-resolution scanning transmission electron microscopy (HR-STEM) confirmed sharp interfaces and coherent atomic layers, as well as highly aligned superlattices of polar cores, both vertically and laterally (Materials and Methods). Within the film plane, the periodic cores of curled polar texture define a lateral repeat direction (designated [100]_χ in Fig. 1A, where χ denotes the chiral phase) along one of the principal axes of the pseudocubic perovskite cell.

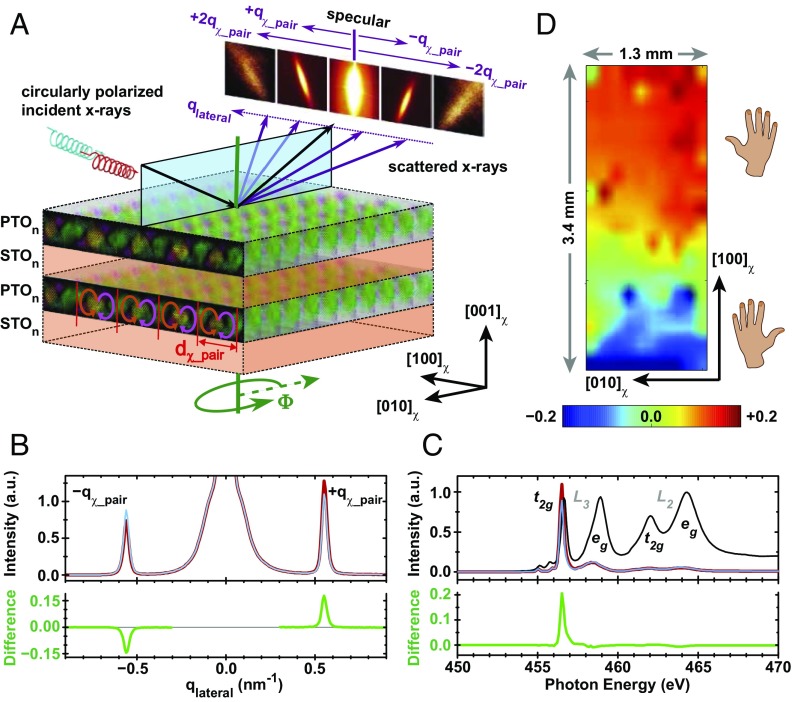
Fig. 1.

Self-organized arrays of electric polarization textures in (PbTiO₃)_n/(SrTiO₃)_n superlattices exhibit a chiral RSXD pattern. (A) These polar arrays produce diffraction satellites that decorate the specular reflection along the lateral direction, [100]_χ, for X-rays tuned near the titanium L₃ edge. Specular scattering plane is shown in blue. Red and blue helices illustrate opposing circular polarizations of incident X-rays. Sample azimuth is indicated by Φ. (B) (Upper) Line cut of scattered intensity versus lateral momentum transfer (q_lateral) using right- (red) and left-circularly (blue) polarized X-rays for n = 16. (Lower) XCD is the difference in intensity for the two helicities. (C) (Upper) Resonance profiles through the titanium L_3,2 edges at q_lateral = +q_{χ_pair} for both X-ray helicities (red and blue) and (Lower) their XCD (green) for n = 14. Fluorescence absorption spectrum (black curve in Upper) shows electronic states similar to that of Pb(Zr_0.2Ti_0.8)O₃ (14). (D) Map of XCD intensity at q_lateral = +q_{χ_pair} across an n = 14 sample. Regions of positive (negative) XCD indicate where chiral polar arrays have positive (negative) helicity.

We have performed RSXD (12, 13) on PbTiO₃/SrTiO₃ superlattices. The soft X-ray wavelengths (∼2 nm to 3 nm) are well matched to the periodicity of the lateral modulations in the polar texture, leading to satellites that decorate the 00ℓ_χ diffraction rod (Fig. 1A). Fig. 1B shows a line cut through the lateral satellite peaks in proximity to ℓ = 0. Peak positions (q_lateral = ±q_{χ_pair} = ±2π/d_{χ_pair}) indicate a lateral period equal to that of a pair of counterrotated polar cores, d_{χ_pair}, which is 11.4 nm for n = 16.

By tuning the X-ray energy within the vicinity of resonant electronic transitions from the titanium 2p_3/2 (L₃) and 2p_1/2 (L₂) core levels into empty 3d valence states, we directly probe the anisotropic electronic structure of distorted TiO₆ octahedra. Indeed, the intensity of the lateral satellites at q_lateral = ±q_{χ_pair} has a remarkable dependence on the photon energy of the incoming X-rays (Fig. 1C), predominantly concentrated at t_2g-like states near the L₃ edge. In X-ray absorption studies of ferroelectric Pb(Zr_0.2Ti_0.8)O₃, the same t_2g feature highlights the anisotropy of the polar TiO₆ distortion (14). The resonant behavior in Fig. 1C can be understood (ATS Diffraction) by considering that the supermodulation diffraction peaks are due to anisotropic tensor susceptibility (ATS) scattering (15, 16), driven by periodic rotational patterns of electric polarization in the textured arrays (Fig. S1).

Strikingly, the diffraction peaks of the polar texture exhibit pronounced X-ray circular dichroism (XCD), with intensity differing on the order of ∼20% when the circular polarization of incident X-rays is reversed. XCD in resonant diffraction peaks can contain contributions from a number of mechanisms, including chiral motifs (17), scattering from ordered magnetic moments (18), and dynamical effects (19–21). The antisymmetric XCD signal in Fig. 1B is a hallmark of chirality in magnetic materials such as those with chiral domain walls (18). However, no magnetism is expected nor found in the d⁰ configuration of PbTiO₃/SrTiO₃ superlattices. Rather, XCD here must be generated by a chiral rotation of electric polarization within the textured arrays (Fig. 2), as is expected for ATS diffraction peaks from chiral structures (16, 22–24). In these materials, the polarity of the XCD signal reverses when either the chirality of the crystal structure or the direction of the diffraction vector is independently inverted. The latter is observed in Fig. 1B by reversal of the lateral component of the diffraction vector, q_lateral, and Fig. 1D shows evidence of the former.

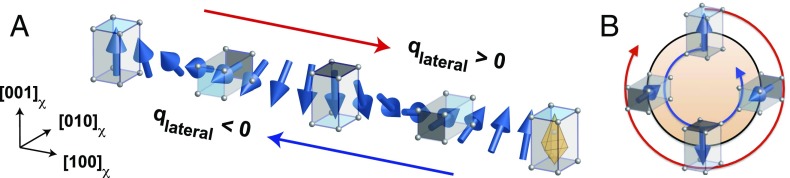
Fig. 2.

Mirrored diffraction vectors detect opposite rotational patterns in chiral textures. RSXD is sensitive to anisotropic TiO₆ distortions, so that a helical rotation of the electric polarization can produce RSXD peaks with antisymmetric XCD. (A) Conical blue arrows indicate the direction of polarization, which rotates helically along the lateral direction, [100]_χ. The distorted perovskite cell is depicted for several orientations, as is the distorted TiO₆ octahedron for an up-polarized unit cell. (B) The cyclic modulation of polarization for this same helix is highlighted by folding the lateral dimension into a circle. The diffraction vector with q_lateral > 0 (red arrow) senses a clockwise helical rotation of polarization, whereas the diffraction vector with q_lateral < 0 (blue arrow) detects a counterclockwise rotation.

One must also consider dynamical effects in resonant X-ray scattering, such as the refraction and polarization rotation of both incident and diffracted X-rays, which have been shown in antiferromagnetic ordering diffraction peaks to produce significant XCD in addition to the XCD expected from kinematical models (19–21). The kinematical scattering amplitude is the Fourier transform of the material’s effective electronic density, directly linked to the ordered state being studied (13). The results of dynamical effects also reveal information about material properties, but are strongly dependent on the particular geometry of each diffraction experiment (25). However, these components can be principally distinguished via their azimuthal dependence, in particular by the reversal (or not) of XCD. We next demonstrate that the azimuthal pattern of XCD (Fig. 3A) measured in the q_lateral = ±q_{χ_pair} diffraction peaks from PbTiO₃/SrTiO₃ superlattices is indicative of the chiral electric dipole configuration in the textured arrays, and that it is also distinct from that of other systems whose XCD is dominated by dynamical effects. Finally, we have also confirmed that XCD is essentially negligible (XCD of Ordered Phases, Fig. 4, and Fig. S2) in thinner (PbTiO₃)_n/(SrTiO₃)_n superlattices (e.g., n = 4), which have no curled polar structure but which still possess periodic arrays of ferroelectric a domains that exhibit resonant diffraction peaks (Phase Coexistence). Thus, the dramatic difference in XCD between samples with and without curled polar textures directly points to the chiral structure of the arrays, rather than dynamical effects, as the primary origin of XCD.

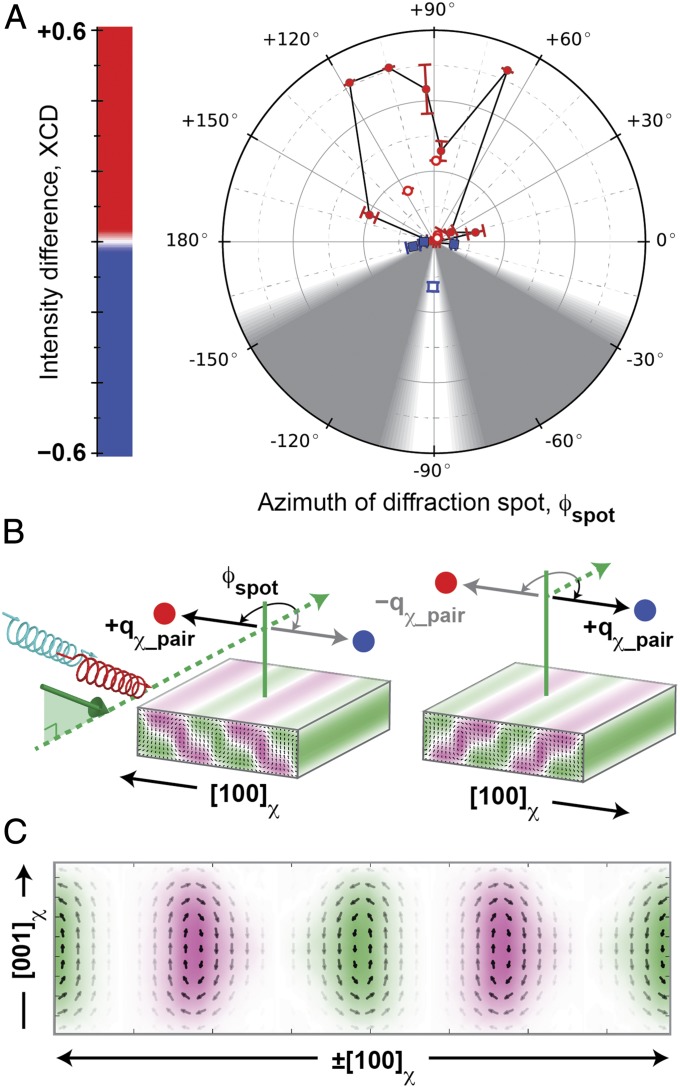
Fig. 3.

Rotational symmetry of chiral polar arrays observed in azimuthal pattern of XCD. (A) XCD intensity plotted versus azimuth, ϕ_spot, for each diffraction spot from the polar arrays. Red circles indicate XCD > 0; blue squares indicate XCD < 0. Filled markers were measured at n_SL = 4; hollow markers were measured at n_SL = 3. Gray regions show experimentally inaccessible sample geometries. (B) Diffraction patterns for two sample orientations (separated by 180° azimuthally) exhibit similar XCD (red and blue circles) relative to the scattering geometry: Φ = 0° (Left) and 180° (Right). Curved arrows indicate ϕ_spot, measured from the in-plane projection (dashed green arrow) of the incoming X-rays. Sample is depicted with counterrotated polarization cores (small black arrows) and alternating axial polarization (green and magenta) domains. (C) Polarization structure is averaged over both orientations in the (010)_χ cross-section. These polar cores possess a chiral texture that is robust versus a twofold rotation. Error bars in A represent uncertainty in fitting the XCD spectra at each azimuth (Azimuthal XCD Measurements).

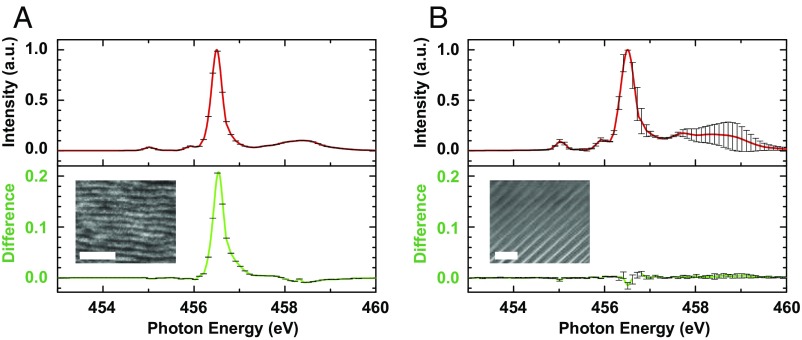
Fig. 4.

Resonance profiles for (PbTiO₃)_n/(SrTiO₃)_n superlattices through the titanium L₃ edge at (A) q_lateral = +q_{χ_pair} for n = 14 and (B) q_lateral = +q_a-domain = +2π/d_a-domain for n = 4, where d_a-domain ∼ 70 nm. (Upper) The polarization-averaged diffraction intensity (red) for both X-ray helicities, and (Lower) XCD (green). Insets show planar view HR-STEM images of (A) an array of polar cores ordered along [100]_χ (horizontal scale bar: 50 nm) and (B) an array of ferroelectric a domains ordered along [110]_χ (horizontal scale bar: 200 nm). Superlattices with chiral polar arrays exhibit strong XCD in A that is characteristic of the chiral arrangement of electric polarization in the texture. In superlattices with smaller layer thickness, the polarization arranges into periodic a domains only, with no chiral structure and correspondingly negligible XCD.

The helical polarization structure depicted in Fig. 2A and its inherent broken mirror symmetry along q_lateral will produce a resonant ATS diffraction pattern whose peaks, q_lateral = ±q_helix = ±2π/d_helix (d_helix is the period of the helix), have opposite XCD, similar to Fig. 1B. The twofold symmetry of the helix implies that its diffraction pattern after a 180° rotation is indistinguishable from the diffraction pattern of the original orientation. Notably, however, because q_lateral is fixed to the sample (by construction), the peak with positive dichroism in the original orientation is located at q_lateral = +q_helix, whereas, after rotation, it is located at q_lateral = −q_helix. We observe similar behavior from the PbTiO₃/SrTiO₃ polar arrays, as seen in Fig. 3.

Fig. 3A shows that, for a single diffraction spot with q_lateral = +q_{χ_pair}, XCD is large and positive (red) across a range of azimuths, ϕ_spot near +90°. XCD in that same spot is strongly negative (blue) for ϕ_spot near −90°, and, in between these extremes, the XCD tends toward zero at ϕ_spot near 0° or 180°. Similar azimuthal patterns were measured for multiple diffraction spots from the polar arrays (Materials and Methods), and have been overlaid in Fig. 3A to highlight this commonality via judicious selection of the origin, ϕ_spot = 0°. Here the azimuth, ϕ_spot, has been defined for each diffraction spot, to measure the in-plane projection of its scattering vector relative to the projection of incident X-rays onto the sample surface (dashed green line in Fig. 3B). The cartoon in Fig. 3B illustrates the data in Fig. 3A, to emphasize that either diffraction spot exhibits positive XCD (red disk) when its in-plane scattering vector is +90° from the dashed green reference line. This condition is fulfilled for q_lateral = +q_{χ_pair} (thick black arrow, parallel to [100]_χ) in Fig. 3B, Left and also by a 180° azimuthal rotation of the sample for q_lateral = −q_{χ_pair} (thick gray arrow, antiparallel to [100]_χ) in Fig. 3B, Right. For a fixed sample orientation, however, the mirrored diffraction spots (q_lateral = ±q_{χ_pair}) have XCD with opposite polarity, as in Fig. 1B. Indeed, the inversion of XCD polarity with reversal of q_lateral persists at all azimuths, as deduced from Fig. 3A, and is a defining feature that points toward the chiral origin of this XCD signal.

This azimuthal pattern of XCD in the polar array diffraction spots is functionally similar to that of the ideal electric polarization helix. In the reference frame of the diffractometer, this twofold rotation of the sample results in a similar (albeit not identical) XCD diffraction pattern from the polar texture. An immediate implication of this XCD pattern is that the electric polarization of the chiral array must possess a broken mirror symmetry along q_lateral, with an additional restriction that the electric polarization texture must be considerably unchanged by a 180° azimuthal rotation. These constraints extracted from experimental results help to identify the most likely candidate structures calculated from second-principles atomistic simulations, which are discussed in Calculation of Polarization Textures.

The XCD pattern of PbTiO₃/SrTiO₃ superlattices is not perfectly antisymmetric with respect to azimuth, largely because the magnitude is smaller for azimuths with negative XCD. This indicates that the chiral arrays do not perfectly mimic the ideal helix in their polarization configuration. This might arise, in part, due to a skewing of the atomic positions, which leads to a systematic asymmetric offset (i.e., buckling) of the polar core positions, as seen in Fig. S3. Skewed profiles of periodic structures are well known to produce asymmetric intensity in the mirrored diffraction spots of, e.g., surface gratings made of patterned lines with asymmetric cross-section (26). Dynamical effects might also partially contribute to the XCD signal, causing it to deviate from an idealized antisymmetric azimuthal pattern. In studies where dynamical modulation of dichroism [either XCD or X-ray linear dichroism (XLD)] in the diffraction peaks was found to be significant (20, 21), the azimuthal patterns possess twofold symmetry or else mirror symmetry that deviates only slightly from twofold symmetry (Fig. S4). This is in stark contrast to the inversion of XCD polarity that we observe with a 180° azimuthal rotation.

Our current analysis focuses on the general trend that positive XCD is observed at positive azimuths, while negative XCD is measured at negative azimuths. Other features of the azimuthal pattern in Fig. 3A could be manifestations of dynamical effects (Azimuthal XCD and Chirality), including fine intensity modulations and a notable imbalance of intensity between the azimuthal lobe of positive XCD and the lobe with negative XCD. Regardless, these two primary lobes of XCD with opposite polarization are clearly visible in the azimuthal pattern, even though some regions of the azimuthal circle are inaccessible due to geometrical constraints of the experimental setup. Based on this distinct azimuthal pattern, we can rule out dynamical effects as the principal source of XCD in the polar array diffraction spots. Also, in the absence of magnetic order, we conclude that XCD in these diffraction patterns is primarily the result of a chiral configuration of electric polarization in the curled textures of PbTiO₃/SrTiO₃ arrays.

Calculation of Polarization Textures

To ascertain more specifically the structure that produces the observed XCD signal, we have performed second-principles (27, 28) simulations, which allow for the treatment of thermal effects and larger systems than standard first-principles calculations. Structural relaxations (Materials and Methods) yield different atomic geometries (Fig. 5 A–C) that are very close in energy. Pairs of clockwise and counterclockwise rotation patterns alternating along [100]_χ are clearly visible, with a period of ∼8 nm for n = 10, closely matching experimental observations (Fig. S5). Amazingly, these simulations also reveal that the previously reported characterization (5) as “alternately rotating vortices” is only a partially complete description of the polarization texture.

Fig. 5.

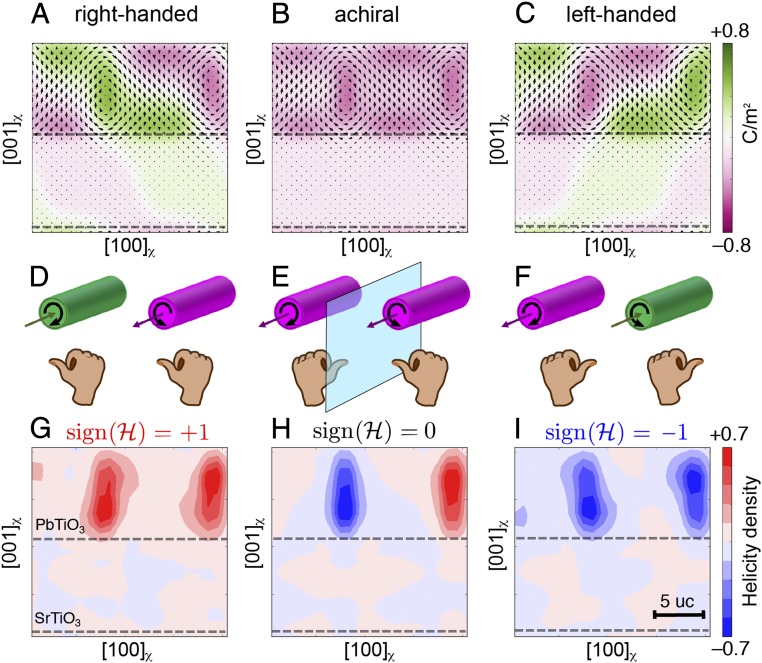
Second-principles calculations of electric polarization textures and their topological properties for n = 10. (A–C) Three different local minima, degenerate in energy. Each texture contains a pair of counterrotated cores yet has different chiral properties. Black arrows indicate the local dipoles, projected onto the (010)_χ plane. A large axial component of the polarization along ±[010]_χ, represented by the green and magenta domains, is observed. (D–F) Simplified cartoon with cylinders representing the cores and arrows that show their rotational and axial polarization components. A right-hand rule reveals the chirality of each cylinder. By curling one’s fingers in the direction of polar rotation around the core, the thumb points (anti-)parallel to the axial polarization for a (left-) right-handed core. (G–I) Maps of helicity. When the handedness of the two cores is the same, the system as a whole is chiral and the enantiomers can be distinguished by the sign of the integrated helicity (ℋ). Results obtained at temperature of 10 K.

Superimposed onto this curled polar texture, we observe the condensation of a robust polarization component along the axial direction of the polar cores (29, 30), [010]_χ, that triggers the appearance of chiral geometries (Fig. S6). Simulations at low temperature (10 K) predict the stabilization of enantiomers where the axial component points in opposite directions at the center of the clockwise and counterclockwise cores (Fig. 5 A and C). Our second-principles calculations also find an achiral structure, where the axial component is parallel throughout the structure (Fig. 5B). The difference in energy between these configurational states is small. This therefore requires that we look at these calculated results within the context of our experimental data to identify the most likely ground states. Furthermore, ab initio calculations do not overtly include the consequence of finite size effects, because of the periodic boundary conditions used. The net component of polarization along [010]_χ in the achiral structure would lead to polarization charges at the surfaces of a real sample, destabilizing this achiral state with respect to the chiral geometries. Polar reconstructions at the lateral surfaces by mobile carriers are unlikely because the superlattices are highly insulating. Even though we cannot rule out all screening mechanisms that might help stabilize achiral textures, we emphasize that only the chiral polar textures are compatible with the experimental XCD results presented earlier. The calculated chiral structures are stable up to higher temperatures, where a transition toward dynamically changing polar textures is predicted (Fig. S7).

The helicity density (31), defined as $\mathit{\mathscr{H}}={{\displaystyle \int }}^{}\overrightarrow{p}\cdot \left(\overrightarrow{\nabla }\times \overrightarrow{p}\right)d^{3}r$, and the sign of this scalar field, γ = sign(ℋ), allow an unambiguous classification of the handedness of a given polar core (Fig. 5 D–F), and its volume integral over the clockwise and anticlockwise pair defines the overall chirality of the system. The handedness is identical for both cores in Fig. 5A, leading to a net positive helicity (Fig. 5G), and positive XCD for positive ϕ_spot in Fig. 3A. Spatial agreement between Fig. 5G and the azimuthally robust polarization texture (averaged for Φ = 0 and 180° in Fig. 3C) identifies the helicity of alternating polar cores as the primary source of XCD. Within the central PbTiO₃ layers of these chiral arrays, the electric polarization forms a helical structure (Fig. S1) similar to Fig. 2A. In this context, the helicity number simultaneously describes the handedness of the individual cores and the handedness of the collective helical rotation within each layer (Helicity of Calculated Polarization Textures).

The polarization texture in Fig. 5C is a mirror image of Fig. 5A, with opposite handedness, net negative helicity, and an XCD signal that must be opposite in sign. Both enantiomers coexist as macroscale domains in the XCD map shown in Fig. 1D. The axial components of polarization in Fig. 5 could potentially be visible in planar view HR-STEM or dark-field transmission electron microscopy (TEM) images. In practice, however, variations in the strength and orientation of the axial polarization as a function of depth act to dilute the signal below detection limits (Fig. S8).

This discovery of chirality in PbTiO₃/SrTiO₃ superlattices stemming from helicity of the modulated polar arrays is of profound fundamental importance and poses new lines of inquiry. The most exciting discovery is the design of an emergent chirality into a material using building blocks that do not by themselves exhibit chirality. In contrast to other chiral crystals with a well-defined handedness that cannot be changed, such as α-quartz, here it should be possible to switch between the two energy-degenerate enantiomers. Such control could be intrinsically affected by a yet unrealized electrical analog to the Dzyaloshinskii−Moriya interaction, or extrinsically by electrically poling the cores of the chiral textures on a local scale to reverse their axial components. By extension, one might also control optical (32) or magnetic (33, 34) properties of other materials coupled to the polar textures. Additionally, there is reason to believe that these chiral structures could possess a negative index of refraction (28), applicable in tunable frequency oscillators and filters for communication devices.

Materials and Methods

Deposition and Structural Characterization of Thin Film Superlattices.

Superlattices of (SrTiO₃)_n/(PbTiO₃)_n were synthesized on DyScO₃ (110)_O substrates by pulsed laser deposition. Here n refers to the thickness in unit cells of respective materials oriented along the [001]_pc (pseudocubic) direction, defined relative to the orthorhombic substrate as [001]_pc//[110]_O; [100]_pc//${\left[\overline{1}10\right]}_O$; and [010]_pc//[001]_O. Superlattice films were grown (Synthesis and Structural Characterization) to a total thickness of 100 nm and were monitored throughout using Reflection High Energy Electron Diffraction (RHEED) in situ characterization; they exhibited Frank−van der Merwe growth mode. Various characterization techniques such as XRD, Rutherford back scattering (RBS), and TEM were employed to ensure structural and chemical homogeneity of superlattice films (5). For each superlattice, the lateral period of the counterrotated pair of polar cores (d_{χ_pair}) is well defined, ranging from ∼8 nm (n = 10) to 11.4 nm (n = 16).

Detecting Chirality by RSXD.

Synchrotron-based resonant diffraction experiments were performed at the Advanced Light Source, using the scattering endstation at beamline 4.0.2. Polarization and photon energy of the X-ray source were tuned by an elliptically polarizing undulator. Intensity of X-rays scattered by the sample were measured using an in-vacuum CCD, and background dark counts were removed (RSXD Measurements). The CCD detector was also used to record X-ray absorption spectra via fluorescence (RSXD Measurements) and monitor small shifts in the diffraction peak position as a function of photon energy due to dynamical scattering effects (RSXD Peak Shifts and Fig. S9).

Resonance profiles were measured by tuning the photon energy through the titanium L_3,2 edges (∼450 eV to 470 eV), while sample and detector angles were adjusted to maintain the Bragg condition for each energy. The satellite features have an out-of-plane modulation along ℓ, commensurate with the superlattice peaks observed in a specular θ–2θ XRD scan. The Bragg condition in Fig. 1C is (+q_{χ_pair}, n_SL = 3); i.e., the lateral component of the wavevector was set to +q_{χ_pair}, and the out-of-plane component was set to the third-order superlattice peak (and the axial component was zero). All spectra have been corrected for the energy-dependent intensity of the incoming beam (I₀) and are normalized to the maximum intensity of the polarization-averaged spectrum, after subtracting the nonresonant intensity in the preedge region (RSXD Measurements).

Line cuts through reciprocal space were measured at fixed photon energy, while adjusting sample and detector angles to vary q_lateral (q_out-of-plane) at a fixed value of q_out-of-plane (q_lateral). Fig. 1B shows a line cut parallel to q_lateral with fixed q_out-of-plane corresponding to n_SL = 3. Data were normalized to the average intensity at q_lateral = ±q_{χ_pair} for the polarization-averaged curve. Photon energy was fixed at the most intense feature in the resonance profile, identified as having t_2g character (∼456.5 eV).

All measurements were performed with nearly 100% circularly polarized X-rays. Data were collected in pairs, with helicity of the circular polarization reversed for each energy (resonance profiles) or momentum vector (reciprocal space line cuts). XCD (RSXD Measurements) was calculated as the difference of the scattered intensity for the two helicities; subtraction was performed after normalizing the scattered intensities.

Azimuthal data in Fig. 3A were collected from three diffraction spots, two of which were q_lateral = ±q_{χ_pair} for the primary ordering direction, [100]_χ//[001]_O (Azimuthal XCD Measurements and Fig. S10 A–C). The third diffraction spot was q_lateral = +q_{χ_pair} for the secondary ordering direction, [100]_χ//${\left[\overline{1}10\right]}_O$. The sample azimuth (Φ) was adjusted to vary the azimuth (ϕ_spot) of each diffraction spot, as depicted in Fig. S10 D–F. XCD resonance profiles were collected at each azimuth, then normalized and fitted by a reference spectrum (Azimuthal XCD Measurements).

The chirality map in Fig. 1D displays the XCD measured in the primary diffraction spot, q_lateral = +q_{χ_pair}, with ϕ_spot fixed near +90°. XCD intensity was recorded at fixed diffraction geometry while scanning the sample, with the effect of rastering the X-ray beam across the surface of the sample.

Second-Principles Simulations of PbTiO₃/SrTiO₃ Superlattices.

The superlattice potentials are identical to those used in ref. 28. We assume in-plane lattice constants of a = b = 3.901 Å and γ = 90°. To counteract the underestimate of the lattice constant due to the well-known overbinding error of the local density approximation, which is the first-principles theory used to compute the parameters of our model, an external expansive hydrostatic pressure of −11.2 GPa is imposed.

For computational feasibility, we have focused on a simulation supercell made from a periodic repetition of 2n × n × 2n elemental perovskite unit cells, sufficiently large to simulate domains in the n = 10 superlattice. We solved the models by running Monte Carlo simulations typically comprising 10,000 thermalization sweeps, followed by 40,000 sweeps to compute thermal averages. We ran Monte Carlo simulated annealings down to very low temperatures to perform structural relaxations and find the ground state or metastable solutions. Additional details of the simulation parameters and the resulting structures are discussed in Second-Principles Calculations.

Local polarizations are computed within a linear approximation of the product of the Born effective charge tensor times the atomic displacements from the reference structure positions divided by the volume of the unit cell. From the complex polarization texture, we can compute the helicity density as proposed by Moffatt (31). A detailed description of the helicity calculations and the polar texture chirality is found in Helicity of Calculated Polarization Textures.