Communication in context: Interpreting promises in an experiment on competition and trust

Significance

Does competition increase deception? Competition is likely to induce inflated promises, but are these promises believed, and are they followed through? We argue that the question requires care in the definition of deception. We report on an experiment where competition does indeed inflate promises, but the promises are neither believed literally nor discarded. Bigger promises are interpreted by both sides as signals of equitable intentions, without being meant or read literally. Behavior does not follow the letter of the promise, but we argue that the deviation is not perceived as deception—the language code has changed. Analyses of competition, deception, and trust need to take into account the shared understanding of the message itself.

Abstract

How much do people lie, and how much do people trust communication when lying is possible? An important step toward answering these questions is understanding how communication is interpreted. This paper establishes in a canonical experiment that competition can alter the shared communication code: the commonly understood meaning of messages. We study a sender–receiver game in which the sender dictates how to share $10 with the receiver, if the receiver participates. The receiver has an outside option and decides whether to participate after receiving a nonbinding offer from the sender. Competition for play between senders leads to higher offers but has no effect on actual transfers, expected transfers, or receivers’ willingness to play. The higher offers signal that sharing will be equitable without the expectation that they should be followed literally: Under competition “6 is the new 5.”

During the 2016 presidential campaign, in an interview that became justly famous, Anthony Scaramucci argued that the media were misinterpreting Donald Trump’s statements: “No, no, no, no, don’t take him literally, take him symbolically,” Scaramucci—later, if only briefly, White House Communication director—told MSNBC (1). Whether appropriate or not, the comment highlights an important point: Judgments about trustworthiness and truth telling rest on one’s belief about the code of communication, the mapping from words to their meaning in the context in which they are used.

The theoretical literature on cheap talk communication is careful to stress the importance of the code through which a message is expressed and interpreted (2–5). Experimental studies of communication and trust, on the other hand, measure trust as believing the letter of the message and trustworthiness as following through with the letter of the message (6–11). This paper exploits an experimental design with a rich set of messages and choices to study the impact of a change in context on communication, trust, and trustworthiness. The data lead us to conclude that context determines how a message is interpreted—the action expected after the message is sent.

The change in context we study is the introduction of competition. In social environments, the decision to trust someone is typically accompanied by the question of whom to trust—trust is naturally paired with competition. Indeed, a sizable literature studies the impact of competition on trust (9, 12–14). We find that competition carries with it a change in language: Not only are new messages used, but also the interpretation of the messages changes. Truthfulness has been found to be context dependent (15). Our thesis is that such dependence is commonly understood and shapes not only the content of messages, but also their expected reading and thus their contextual meaning. Framing has been shown to affect beliefs about beliefs (16); our evidence can be understood as showing that competition is a change in frame that alters the shared communication code.

Methods

Experimental Design.

The experiment is a variation on classic trust games (17, 18), designed as a one-shot dictator game with an outside option and preceded by one-sided, nonbinding communication (7). We ran two treatments. In the one-sender treatment (1S), two partners, a sender and a receiver, are matched randomly and anonymously. The receiver can choose whether to play the game or not. If the receiver chooses not to play, both subjects receive $2. If the receiver chooses to play, the sender is given $10 to divide freely between herself and the receiver in any integer split. Before the receiver decides whether to play, the sender sends the receiver a nonbinding message of the form “If you decide to play with me, I will give you x dollars,” where x can be any integer between 0 and 10.

In the two-sender treatment (2S)—the competition treatment—one receiver and two senders are matched randomly and anonymously. The receiver receives messages (nonbinding and private, of the same form as above) from both senders, identified solely as sender 1 and sender 2. If the receiver chooses not to play the game, all three players receive $2; if the receiver chooses to play, he must also indicate with which sender. The selected sender is then given $10 to share with the receiver as desired; the sender who is not selected receives $2.

Implementation.

We ran the experiment on two different platforms: in the laboratory and online, via Amazon’s Mechanical Turk. The laboratory experiment was approved by both Columbia University and New York University Institutional Review Boards. The Mechanical Turk experiment was approved by Columbia University Institutional Review Board. Informed consent was obtained in all cases.

The laboratory experiment was programmed in ZTree (19) and took place at the Center for Experimental Social Science (CESS) at New York University, with enrolled students recruited from the whole campus through the laboratory’s website. Each experimental session consisted of a single treatment. The terminology and the sequence of moves in the laboratory followed the description above, with the following caveats. After sending her message, each sender was asked how much she would transfer if the receiver chose to play with her, without being informed of the receiver's actual choice. (Asking senders’ choices via this “strategy method” allowed us to reduce confounding effects of learning and to increase the number of data points.) In addition to messages, participation decisions, and transfers, we also elicited beliefs. After having decided whether or not to play, the receiver was asked what he expected the sender(s) to transfer, given the(ir) message(s): These are the receiver’s first-order beliefs. After having indicated her transfer, each sender was asked what she believed the receiver expected her to transfer, given her message: These are the sender’s second-order beliefs. We incentivized the reporting of beliefs through a procedure used in closely related studies (7, 8, 20): In the calculation of each round’s payoff, a subject earned an extra $2 if the subject’s stated beliefs were within $1 of the mean of the relevant variable in the session, given the specific message. The main purpose of eliciting beliefs was to directly study whether senders and receivers shared a common understanding of the messages, as elaborated in our analysis below.

For both treatments, we ran eight rounds without feedback, with random assignment of roles and random rematching after each round. The only information revealed during the experiment consisted of the messages sent to the receiver (which were revealed to the receiver only). Each subject was paid his earnings over two random rounds, in addition to a $10 show-up fee. Sessions lasted between 30 min and 40 min, with average earnings of $20 in the 1S treatment and $19.50 in the 2S treatment. A copy of the instructions for the 2S treatment is in SI Appendix.

The second implementation of the experiment was via an online survey run on Qualtrics, with participants recruited from Amazon’s Mechanical Turk (MTurk) service. The experimental game, its terminology, and the structure of payoffs were identical to those we used in the laboratory, but monetary payoffs were reduced and the experiment was much shorter. Each subject played only one round, and the survey took about 3.5 min, on average, for average earnings of 110 cents. The survey included comprehension quizzes, and subjects who failed to reply correctly were prevented from proceeding. We divided the survey into four waves over an interval of three days. The first two waves were run simultaneously and collected data from senders, one wave for the 1S treatment and one for 2S. The second two waves of the survey, again run simultaneously, collected receivers’ data for the two treatments. Each receiver was shown one (1S) or two (2S) senders’ messages, randomly drawn from the responses to the survey’s first two waves. Payoffs were calculated ex post, after all surveys were received, by randomly matching senders and receivers, respecting the specific messages that had been drawn for each receiver. Both the messages and the payoff-relevant matchings were generated by sampling with replacement, which allowed us to overcome the discrepancy in the exact number of respondents between the sender(s) and the receiver surveys. A copy of the 2S survey for senders is in SI Appendix.

The design of the experiment is summarized in Table 1. We collected more data for 2S because in 2S only one of the three partners is a receiver. All data are available from a link in SI Appendix.

Table 1.

Experimental design: Condition (C), number of sessions (T), subjects, senders (S), receivers (R), rounds, and total number of observations for senders (S obs) and receivers (R obs) in the laboratory and in the MTurk survey

C	T	Subjects	S	R	Rounds	S obs	R obs
Laboratory
1S	6	78	39	39	8	312	312
2S	7	111	74	37	8	592	296
Mechanical Turk
1S	1	399	201	198	1	201	198
2S	1	595	595	200	1	595	200

We organize the data collected in the laboratory in two series: first-round data only and data aggregated over all rounds. We thus describe all results in terms of three data series: the two series collected in the laboratory and the data from the MTurk survey. (In all descriptions that follow, the MTurk data have been normalized to lie between 0 and 10, as opposed to between 0 and 100 cents, the actual range in the survey).

Each of the three series has strengths and weaknesses: First-round laboratory data are more directly comparable to data collected in the experiments that are closest to ours (7–9), but they are few in number—a particular problem because our subjects face more finely grained choices—and may reflect some confusion with the setting and the game; all-round experimental data are more numerous but are not independent—the same subjects make multiple decisions—and may be affected by learning, even in the absence of feedback; MTurk data are numerous, independent, and free from learning, but much less controlled. Most of our results are consistent across the three series, giving us confidence in their robustness.

Statistical tests for laboratory all-round data are complicated by the lack of independence. All SEs and test significance levels that refer to laboratory all-round data are calculated via bootstrapping, allowing for arbitrary correlation among choices made by the same individual. The methodology is described in detail in SI Appendix.

In both the laboratory and the MTurk survey, the messages sent by the senders were identified in the instructions as “messages.” In our description below, we refer to them interchangeably as either “messages” or “offers.”

Results

Competition Induces Higher Messages.

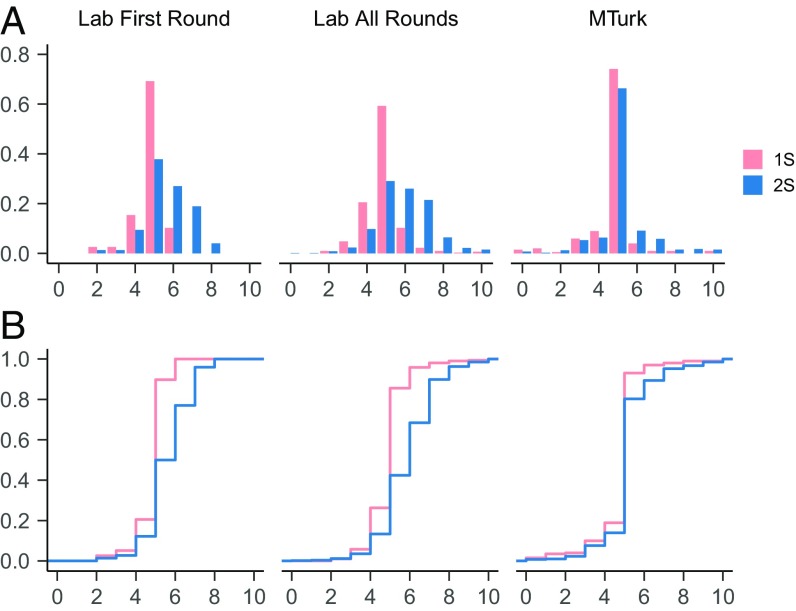
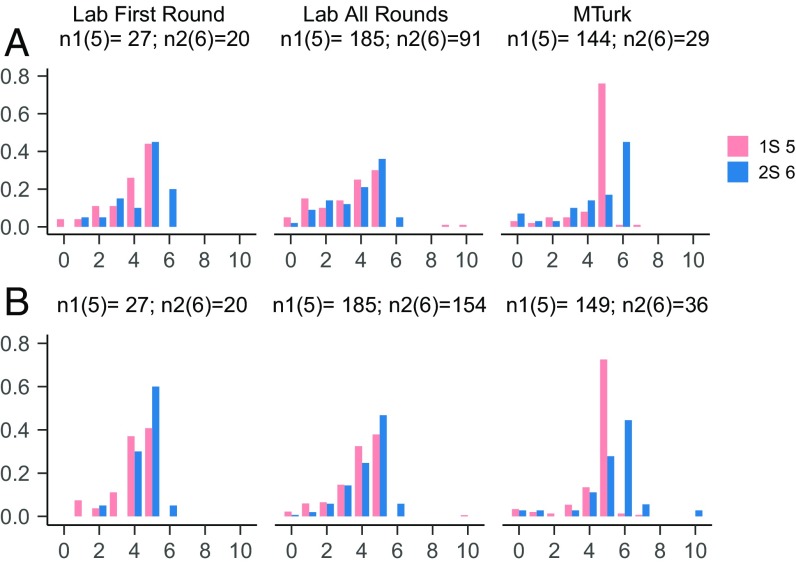
In all three data series, senders’ messages show three regularities (Fig. 1). First, there is a clear spike in the distributions at 5, the modal offer in both treatments. Second, the spike is more pronounced in 1S. Third, the empirical distribution in 2S is shifted to the right (i.e., upward), relative to 1S: Competition tends to increase the senders’ offers. A Kolmogorov–Smirnov test, adjusted for discreteness, strongly rejects the assumption of equal distributions across the two treatments (P < 0.001 in all three series) and fails to reject the one-sided alternative that the distribution in 2S first-order stochastically dominates the one in 1S (P = 1.000 for laboratory one round and MTurk, P = 0.902 for laboratory all rounds). [The adjustment for discreteness is based on ref. 21 and implemented with the ks.boot() function from the “Matching” R package. It is described in more detail in SI Appendix.]

Fig. 1.

Histograms of offers (A) and cumulative distribution functions (B). In all three series the frequency of offer 5 decreases in 2S, relative to 1S, while the frequencies of offers 6 and 7 increase. Writing P values for laboratory first round, laboratory all rounds, and MTurk, in order, the hypothesis of equal proportions of offer 5, against the one-sided alternative of a decline in 2S, is rejected with P = 0.001, P < 0.001, P = 0.032; the hypotheses of equal proportions of offer 6 and of offer 7, against the one-sided alternative of an increase in 2S, are rejected with P = 0.034, P < 0.001, P = 0.002 and P = 0.005, P < 0.001, P = 0.005, respectively [χ² test of proportions for laboratory first round and MTurk, bootstrapped simulations for laboratory all rounds (SI Appendix)].

The shift upward of the offer distribution in 2S arises because the decline in the frequency of offers 5 in 2S is accompanied by an increase in offers 6 and 7. The magnitude of the shift is less pronounced in the MTurk data, but in all three data series the changes in the frequencies of the offers have the same sign and are statistically significant (Fig. 1).

As a result of these changes in the offer distribution, average offers are higher in 2S than in 1S in all three data series. In all three the difference is statistically significant. Writing values in order for laboratory first round, laboratory all rounds, and MTurk, mean offers go from {4.8, 4.9, 4.75} in 1S to {5.6, 5.9, 5.15} in 2S. A t test rejects the hypothesis that the difference is zero (P < 0.001 in all three data series).

... But Not Higher Transfers or Higher Expected Transfers.

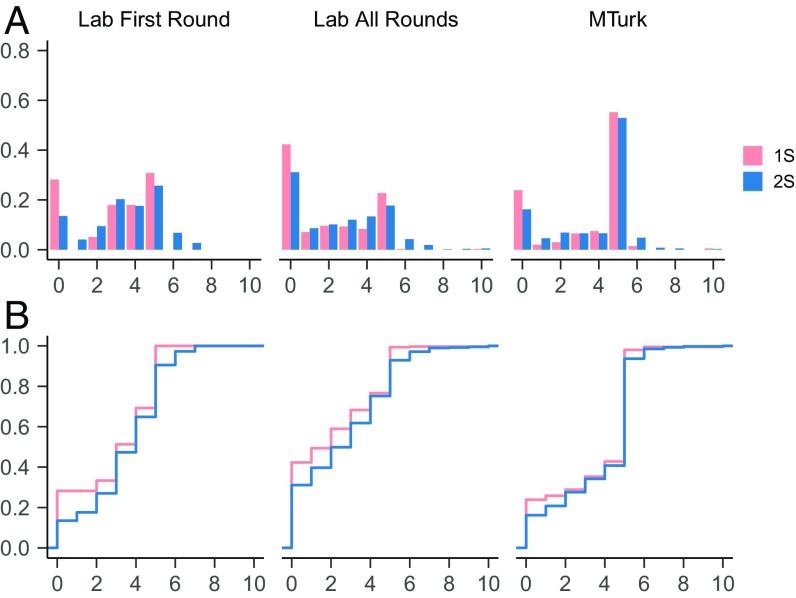
The noticeable shift upward in the distribution of offers induced by competition has no parallel in the (unconditional) distribution of transfers. Transfers move up only slightly, too slightly for statistical significance (Fig. 2). The two most frequent transfers in 1S—5 and 0 in all three data series—remain the most frequent in 2S in laboratory all rounds and MTurk. In all three series, however, their frequency declines, with intermediate transfers becoming more common.

Fig. 2.

Histograms of transfers (A) and cumulative distribution functions (B). A two-sided Kolmogorov–Smirnov test adjusted for discreteness cannot reject the hypothesis that the distributions are equal (P = 0.283 for laboratory first round, P = 0.164 for laboratory all round, and P = 0.129 for MTurk).

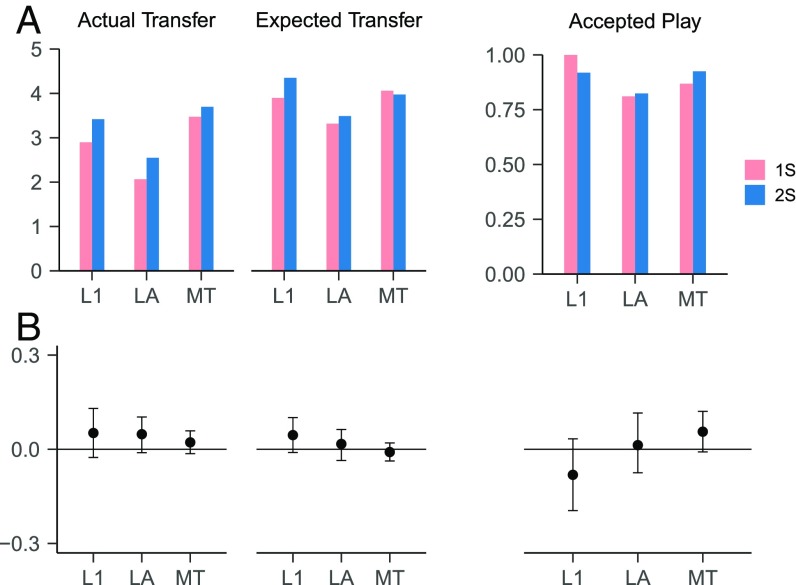
At the aggregate level, mean transfers are slightly higher in 2S, but the difference is not statistically significant in any series (Fig. 3 A and B, Left). Moreover, while competition shifted the offers upward, receivers did not expect higher transfers on average nor were they more willing to play: In all three data series, we find no significant differences in these variables between our two treatments (Fig. 3 A and B, Center and Right).

Fig. 3.

Transfers, expected transfers, and frequency of accepted play for 1S and 2S: point values (A) and normalized percentage differences (2S − 1S) with 95% confidence intervals (B). The three data series are identified as L1 (laboratory first round), LA (laboratory all rounds), and MT (MTurk). The normalized difference is expressed as share of the maximal possible difference. In all cases, the 95% confidence interval includes zero. One-sided tests (against the alternative that the relevant variable is higher in 2S) lend marginally higher statistical significance to the differences between the two treatments. Reporting results in order (L1, LA, MT), P = 0.094, P = 0.049, P = 0.114 (for transfers); P = 0.054, P = 0.215, P = 0.720 (for expected transfers); and P = 0.890, P = 0.374, P = 0.046 (for frequency of accepted play) [one-sided t test of means and χ² test of proportions for L1 and MT, bootstrapped simulations for LA (SI Appendix)].

How does one reconcile the higher offers with the essentially unchanged transfers and participation? Apparently, higher offers were not believed and thus did not result in higher expected transfers. But neither did they induce higher mistrust and thus lower participation and lower expected transfers.

“6 Is the New 5.”

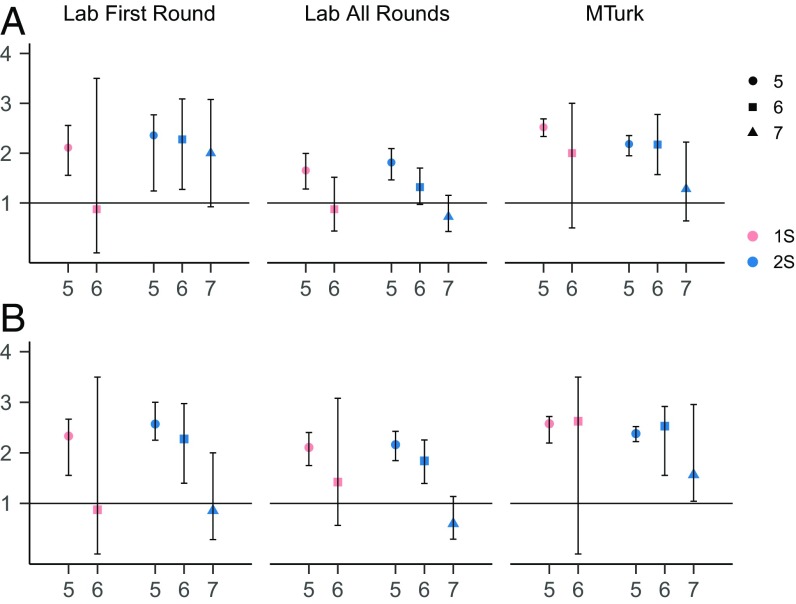
Across all three data series, offers of 6 in 1S are rare (Fig. 1A). They are also associated with lower transfers than offers of 5 (Fig. 4). Together, low frequency and low transfers suggest that an offer of 6 in 1S is a signal of low trustworthiness. In 2S, on the other hand, offers of 6 are effectively indistinguishable from offers of 5: In the laboratory, although not in MTurk, they are almost as frequent (Fig. 1A), and in all three series the average transfers following either offer are equivalent (Fig. 4). Offers of 7 are absent in 1S but appear in 2S, although they remain scarcer than either 5 or 6 (Fig. 1A). In all three series, offers of 7 in 2S are associated with low transfers, transfers that are statistically indistinguishable from those following offers of 6 in 1S (Fig. 4).

Fig. 4.

Mean transfers, conditional on offers 5, 6, and 7: point values and 95% confidence intervals. All confidence intervals are calculated via bootstrapping to account for the nonnegativity constraints and are centered on the empirical observation; in some cases the intervals are not symmetric because of the skewness of the data. We do not report transfers after offer 7 in 1S because the occurrences are too few to be meaningful: 0 such offers in laboratory first round; 7 (2%) in laboratory all rounds, and 2 (1%) in MTurk. The corresponding numbers in 2S are 7 (9%), 127 (21%), and 23 (6%). In 1S, offers of 6 are also rare (the numbers of offers 6 are reported in Fig. 5). However, the hypothesis of equal transfers in 1S and 2S following offers 6 (against the one-side alternative of higher transfers in 2S) is strongly rejected in both laboratory data series and marginally fails to be rejected in MTurk: P = 0.011, P = 0.001, P = 0.053 [for laboratory first round, laboratory all rounds, and MTurk, in order; one-sided t test for laboratory first round and MTurk, bootstrapped simulations for laboratory all rounds (SI Appendix)].

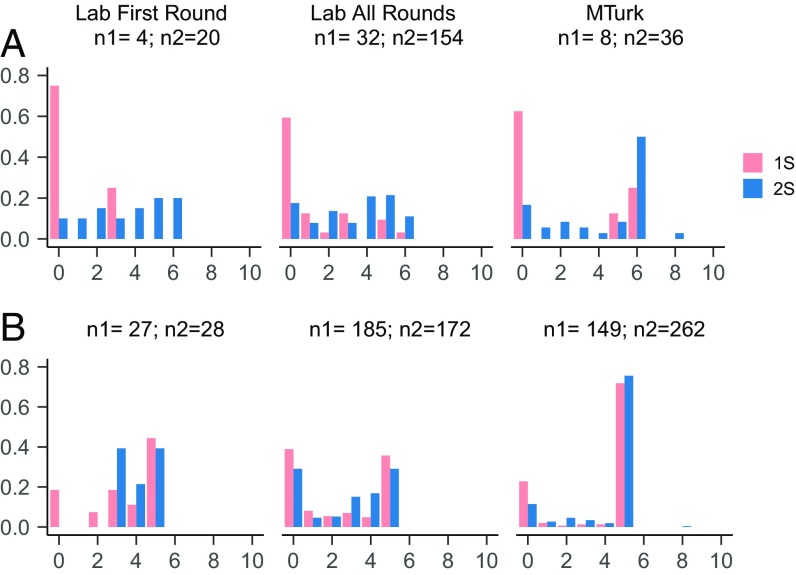
The data indicate different follow-through for offer 6 in the two treatments, with the caveat of few such data points in 1S. In all data series more than 50% of offers 6 are followed by a zero transfer in 1S, vs. less than 20% in 2S; in all data series, following offer 6, the fraction of transfers 6 is at least double in 2S relative to 1S (Fig. 5A).

Fig. 5.

Histograms of transfers conditional on offer 6 (A) and offer 5 (B). Each panel also reports the number of data points: n1 refers to 1S, n2 to 2S. Following offer 6, the data in 1S are too few to test for equality of the distributions in laboratory first round and MTurk; in laboratory all rounds a Kolmogorov–Smirnov test corrected for discreteness strongly rejects the hypothesis of equal distribution in 1S and 2S (P = 0.0032). Following offer 5, the test cannot reject equality of the distributions in laboratory first round and laboratory all rounds (P = 0.091 and P = 0.253), but rejects it in MTurk (P = 0.019).

Is the higher follow-through of offer 6 in 2S matched by different beliefs? In all three data series and for both receivers’ and senders’ beliefs, mean beliefs after offer 6 are higher in 2S than in 1S. However, all differences are small and none is statistically significant (SI Appendix, Fig. S1). It is plausible that mean beliefs do not differ much because subjects hold relatively diffuse beliefs: Instead of believing that a sender will transfer only either the offer itself or zero, receivers may assign positive probability to a variety of transfers. We can translate this perspective into a quantitative measure.

Because the term “credible” is ambiguous when meaning can depend on context, we use instead the word “persuasive”. According to the data, senders do not send and are not expected to send more than their offer. We thus define as nonpersuasive an offer of x that conveys no more information than that: It induces the receiver to assign positive probability to any transfer between 0 and x and zero probability to transfers above x. A persuasive offer is instead one that generates first-order beliefs in the neighborhood of the offer. Both to allow for some dispersion in beliefs and because the belief elicitation procedure rewarded subjects for being within $1 of the realized average value, we say that an offer of x is persuasive if it induces beliefs that the transfer will be only either x or (x − 1).

We evaluate whether offer x is persuasive by testing whether the realized fraction of beliefs at either x or (x − 1) is significantly higher than the expected fraction at such values if any belief between 0 and x is equally probable, i.e., under a uniform distribution from 0 to x (Fig. 6). According to this measure, in 1S only offer 5 is persuasive to receivers in all three data series and in all three data series is believed to be persuasive by senders (in MTurk only, offer 6 is also believed to be persuasive by the senders). In 2S, however, both offer 5 and offer 6 are persuasive to receivers in all three data series and are expected to be so by senders. No offer besides 5 or 6 satisfies the test for either order of beliefs in either 1S or 2S.

Fig. 6.

Receivers’ (A) and senders’ (B) beliefs at x or (x − 1), following offer x. Each point is normalized by the expected mass of reported beliefs at x or (x − 1) if any belief between 0 and x is equally likely. An offer is persuasive if the ratio is higher than 1. For receivers' beliefs (A), in 1S the ratio is significantly higher than 1 only for offer 5 (P < 0.001 for all three data series); in 2S the ratio is significantly higher than 1 for offer 5 (P < 0.001 for all data series) and for offer 6 (P = 0.001 for laboratory first round, P = 0.040 for laboratory all rounds, and P < 0.001 for MTurk), and for no other offer. For senders' beliefs (B), in 1S the ratio is significantly higher than 1 only for offer 5 (P < 0.001 for all data series) and for offer 6 in the MTurk data only (P = 0.004); in 2S the ratio is significantly higher than 1 for both offer 5 and offer 6 (P < 0.001 in both cases for all data series), and for no other offer. In B, MTurk data, offers 6 and 7, apparent contradictions between the confidence intervals and the bootstrapping P values are due to the scarcity of data and sparsity of the distributions. See SI Appendix for details on the test.

We interpret these results as supporting the hypothesis that an offer of 6 in 2S is interpreted differently from an offer of 6 in 1S. We also know that the offer is followed by different transfers in the two treatments (Figs. 4 and 5). The phrase “6 is the new 5” conveys these two points. However, the statement is stronger: It says that competition makes an offer of 6 equivalent to an offer of 5 in the absence of competition. As we noted, the hypothesis of equal mean transfers following offer 5 in 1S and offer 6 in 2S cannot be rejected in any of the three data series (Fig. 3), nor can the hypothesis of equal mean beliefs for both senders and receivers, although mean beliefs do not vary enough across offers to attribute much significance to the lack of rejection (SI Appendix, Fig. S1).

A more powerful test of beliefs compares the full distributions of expected transfers (for receivers) and beliefs about expected transfers (for senders), conditional on offer 5 in 1S and offer 6 in 2S (Fig. 7). For both receivers’ and senders’ beliefs, formal tests confirm that the distributions are not statistically different in the laboratory-first round and laboratory-all rounds series. In both laboratory series, beliefs peak at 5, in response to both offer 5 in 1S and offer 6 in 2S. In the MTurk data too, there is substantive shading down of beliefs following offer 6 in 2S: Only 44% of receivers’ beliefs are at 6, following offer 6 in 2S, vs. 73% at 5 following offer 5 in 1S; for senders’ beliefs the numbers are very similar: 45% at 6, after offer 6 in 2S, vs. 76% at 5 following offer 5 in 1S. However, in the MTurk data beliefs peak at the literal offers, and equality of the distributions is rejected for both receivers and senders. Although “6 is the new 5” applies to the MTurk data too when interpreted in terms of mean values (mean transfers and mean expected transfers), the histograms of beliefs suggest a more literal interpretation of offers. It is interesting to recall that the shift in offers induced by competition is also less pronounced in MTurk (Fig. 1A). Lower sensitivity to subtle changes in stimuli in MTurk, relative to laboratory experiments, has been documented in other studies (22, 23). It could be that the change in context is less salient in the less interactive, less controlled, and faster web-based environment.

Fig. 7.

Histograms of receivers’ (A) and senders’ (B) beliefs, conditional on offer 5 in 1S and offer 6 in 2S. Each panel also reports the number of data points as n1(5) for offer 5 in 1S and n2(6) for offer 6 in 2S. A two-sided Kolmogorov–Smirnov test, adjusted for discreteness, cannot reject equality of the two distributions for laboratory first round (P = 0.269 for receivers and P = 0.1285 for senders) and laboratory all rounds (P = 0.631 for receivers and P = 0.168 for senders), but rejects it for MTurk (P < 0.001 for both receivers and senders).

Discussion

Our best synthetic reading of the data is that messages are used and understood differently when senders compete for trust (in 2S), relative to the baseline treatment (1S). What drives the change in the communication code?

In the economic literature, the interaction between communication, trust, and trustworthiness has been studied through many different models (ref. 24 analyzes 24 of them), but explanations for the effectiveness of nonbinding promises come down to one of two mechanisms: guilt aversion (6, 7, 25–27), the aversion to disappointing others’ expectations, and lie aversion (28, 29), the aversion to not keeping one’s word. In our context, guilt arises from disappointing receivers’ expectations of the transfer they will receive; a lie amounts to transferring less than one has offered. Both mechanisms are psychologically interesting and parsimonious, and distinguishing between them can be subtle (20, 27, 29–32).

When we want to understand changes in communication codes across contexts, however, guilt aversion faces a challenge. The problem is that, akin to the standard theory of cheap talk communication (33), nothing in the theory anchors messages—a sender does not care intrinsically about messages, only about the expectations they induce in the receiver. Thus, while guilt aversion can explain why nonbinding promises are trustworthy, there is arbitrariness in which message is used to convey which expectation. This arbitrariness applies in any particular context, and a fortiori, across contexts.

Models of lie aversion, by contrast, define lies relative to messages’ literal or conventional meaning, which is exogenous to any particular context. The approach restricts the choice of messages, while allowing for a distinction between literal meaning and contextual meaning—how the message is understood. As incentives vary across contexts, not only may different messages be used, but also the contextual meaning attached to the same literal message can change. Importantly, how it changes is pinned down by context.

Consider the following minimal conceptual framework, where we impose the discipline of equilibrium reasoning—behavior optimally responds to correct beliefs about the behavior of others. We describe briefly its logic here, relegating a more detailed analysis to SI Appendix.

Suppose a fraction of subjects, call it θ, have high costs of lying: They always transfer what they have offered. A fraction (1 − θ) have low cost of lying and transfer 0 no matter their offer. In the 1S game, the model predicts concentration of messages at some unique offer x, supported by the belief that any sender offering x′ ≠ x must be untruthful, and a bimodal pattern of transfers, a fraction θ of the senders transferring x and the remainder transferring 0. [Given the outside option of 2, x must be acceptable to the receiver (xθ ≥ 2) and to the sender (x ≤ 8), but any x ∈ [2/θ,8] could be observed.] The experimental data in 1S are broadly consistent with this prediction, with offer 5 being focal. The data show high concentration of offers at 5 in all datasets (Fig. 1) and, conditional on offer 5, a bimodal pattern of transfers at 5 and 0 (Fig. 5B).

In 2S, the data show that offers are more dispersed (Fig. 1). Our bare-bones model can rationalize such dispersion under competition. Suppose multiple offers, all belonging to a set X, are observed in equilibrium, again supported by the belief that any x ∉ X is sent only by untruthful senders. For simplicity suppose X = {x₁, x₂} with 2 < x₁ < x₂. An offer cannot be accepted with positive probability unless it is sent by some truthful senders (more precisely, by enough truthful senders to induce an expected transfer superior to the outside option of 2). With x₁ < x₂, a truthful sender sends x₂ only if it is accepted with higher probability than x₁. But if x₂ is accepted with higher probability, then all untruthful senders send x₂. Thus, x₂ is sent by a mixture of truthful and untruthful senders, while x₁ is sent by truthful senders only. We show in SI Appendix that with competition both the receiver and truthful senders can be indifferent between the two different offers, and thus both offers can coexist in equilibrium.

The interesting finding is not merely that dispersion of offers can be supported in equilibrium; rather it is that such dispersion can be supported only with competition. Consider a candidate equilibrium identical to the one just discussed, but in the 1S game. Since the lower offer, x₁, is offered by truthful senders only, it is accepted by receivers with probability 1. But then truthful senders have no reason to offer x₂. In the 2S game, by contrast, the lower offer of x₁ may be matched with an offer of x₂ by the competing sender and thus may indeed be accepted with lower probability than x₂.

These predictions match well the concentration of offers we see in the data: the single spike of offers 5 in 1S and the larger share of offers 6 in 2S. They are also consistent with the frequencies of acceptance of offers 5 and 6 in 2S: When the two offers compete, 6 is accepted more frequently than 5 in all three data series [the ratio of the frequencies of acceptance is 2 in laboratory first round, 1.25 in laboratory all rounds, and 2.33 in MTurk, but in part because the data points are few, only the latter is significantly different from 1 (P < 0.001)].

The theory also rationalizes the change in the contextual meaning of message 6. In 1S, if message 5 is the equilibrium message, then message 6 is not used. It is associated with zero expected and realized transfers. In experimental data with some noise, message 6 may appear, but we would expect it to be used rarely and to be associated with low transfers. In 2S, both messages 5 and 6 can be sent in equilibrium. The expected and realized transfer following message 5 should be 5; following message 6, it cannot be smaller than 5, but it need not be higher. Even in noisy experimental data, message 6 in 2S would then be as persuasive as message 5 and be associated with similar mean transfers. Our experimental data fit these predictions well (Figs. 1, 4, and 5).

Not all predictions, however, are borne out: In 2S, especially but not exclusively in the laboratory data, transfers are more dispersed following both offer 5 and offer 6 (Fig. 5) than the theory predicts. And how should we interpret the increase in offers 7 that we observe in 2S in the laboratory data (Fig. 1)? If it is an off-equilibrium offer, as the lack of persuasiveness (Fig. 6) and low conditional transfers (Fig. 4) suggest, why is it so (relatively) common?

But the model with lying aversion sketched above is truly minimal. A more ambitious theory could add lying costs that depend on the magnitude of the lie (28, 34), possibly idiosyncratically, as well as heterogeneous innate altruism—the amount a sender would transfer in the absence of communication. Senders would then want to convince the receiver of their high altruism and/or high lying costs, but high offers would muddle higher altruism with lower lying costs. The multidimensional signaling game (35, 36) can rationalize greater dispersion in transfers after any offer, while still predicting the desired change in the contextual meaning of messages when competition increases.

We do not pursue this richer model here partly because it is less transparent, but mostly because our goal is not to calibrate a specific model to the data. Rather it is to stress, more broadly, the possible gap between literal and contextual meaning of messages and to highlight how models of lying aversion can generate predictions about such a gap and help us to understand it. (Of course, other theories, including guilt aversion, provide important insights into social behavior. Our emphasis here is on the contextual meaning of messages.) Our experiment is useful because it anchors the change in meaning on a structural change—competition—that is unambiguous and important. Others have found that competition can alter what is judged equitable behavior (37). We find that it can alter how communication is interpreted. The main message of this paper is that analyses of competition, communication, and trust can be made richer by incorporating the endogeneity of the language code.

We close with a question. In models of lying aversion, lying costs are sustained if behavior deviates from the literal meaning of the message. But why are lying costs sustained at all, if the contextual meaning is understood by the receiver? Philosophers have debated the moral standing of lies that do not intend to deceive (38, 39). We hope that future economic research too—theoretical and empirical—will pursue this direction.