Flexibility of thought in high creative individuals represented by percolation analysis

Significance

Creative thinking requires flexibility, which facilitates the creation of novel and innovative ideas. However, so far its role in creativity has been measured via indirect measures. We propose a quantitative measure of flexibility based on the robustness of semantic memory networks to attack, assuming that the higher robustness, the higher the flexibility of the network. We show how the semantic network of high creative individuals is more robust to attack, thus more flexible. This is a direct computational investigation on flexibility of semantic memory and creativity. Our approach can be applied to more general questions such as high-level cognitive capacities and clinical populations suffering from atypical thought processes.

Abstract

Flexibility of thought is theorized to play a critical role in the ability of high creative individuals to generate novel and innovative ideas. However, this has been examined only through indirect behavioral measures. Here we use network percolation analysis (removal of links in a network whose strength is below an increasing threshold) to computationally examine the robustness of the semantic memory networks of low and high creative individuals. Robustness of a network indicates its flexibility and thus can be used to quantify flexibility of thought as related to creativity. This is based on the assumption that the higher the robustness of the semantic network, the higher its flexibility. Our analysis reveals that the semantic network of high creative individuals is more robust to network percolation compared with the network of low creative individuals and that this higher robustness is related to differences in the structure of the networks. Specifically, we find that this higher robustness is related to stronger links connecting between different components of similar semantic words in the network, which may also help to facilitate spread of activation over their network. Thus, we directly and quantitatively examine the relation between flexibility of thought and creative ability. Our findings support the associative theory of creativity, which posits that high creative ability is related to a flexible structure of semantic memory. Finally, this approach may have further implications, by enabling a quantitative examination of flexibility of thought, in both healthy and clinical populations.

A defining feature of creativity is flexibility of thought, the ability to create and use new mental categories and concepts to reorganize our experiences (1, 2). Flexibility in creativity has been related to originality of ideas and the ability to break apart from mental fixations (3). However, the investigation of flexibility of thought in creativity has been done so far only through indirect behavioral measures, such as task switching (4, 5). An approach to quantify flexibility of thought in creativity is still missing. We propose a computational approach to quantify and study flexibility of thought, based on network analysis and percolation theory.

Percolation theory examines the robustness of complex networks under targeted attacks or random failures (6, 7). This is achieved by examining the effect of removing nodes or links from a network and how that removal affects the giant component (the largest connected group of nodes) in the network (6, 8). As a result of such removal process, groups of nodes disconnect from the network. The groups that separate from the network are the network percolation components, and the remaining group of nodes is the giant component in the network. The robustness of a network is its ability to withstand such failures and targeted attacks, evident in relative little effect on the giant component of the network. Here we examine and compare the robustness of the semantic networks of low and high creative individuals, as a quantitative measure of their flexibility of thought. This is based on the associative theory of creativity, which relates individual differences in creative ability to the flexibility of semantic memory structure (2). Semantic networks represent the structure of semantic memory, which allows us to quantitatively examine differences related to semantic memory between low and high creative individuals. We assume that the higher the robustness of a semantic network, the higher its flexibility. Thus, according to the associative theory of creativity, we hypothesize that the semantic network of high creative individuals is more robust.

Recent cognitive studies adopt methods from network science to directly examine theories that view semantic memory structure as a network (9, 10). Network science is based on mathematical graph theory, providing quantitative methods to investigate complex systems as networks (11). A network is composed of nodes, which represent the basic units of the system (e.g., semantic memory), and links, which signify the relations between them (e.g., semantic similarity). At the cognitive level, network research demonstrates how these computational tools can directly examine cognitive phenomena such as language development, individual differences in creativity, and memory retrieval (12–16). Although percolation theory is a powerful tool that can be used to study semantic memory, currently, only two such studies have been conducted. These studies examined how semantic memory is affected by failures (as exhibited in patients with Alzheimer’s disease; ref. 17) or how it facilitates dynamical processes operating upon it (such as memory retrieval; ref. 18). For example, Arenas et al. (18) used percolation theory to examine both structural and dynamical robustness at the semantic network level. This was done by examining how removal of links with an increasing threshold (all links with a weight lower than a specific threshold value) breaks apart the giant component and how this affects dynamical search processes operating on a semantic network. These studies demonstrate the potential of applying percolation theory in the study of semantic memory. Such an application can be used to quantitatively examine cognitive phenomena related to decline in memory structure, such as in dementia (17) or typical age-related memory decline that can lead to retrieval failures (19). In such conditions, it is assumed that degradation of links between concepts in semantic memory leads to a transmission deficit, which inhibits the spread of information in the network and may lead to insufficient activation, leading to retrieval failures (14). However, so far no study has applied such tools to quantify flexibility of thought or to examine individual differences in creativity.

We demonstrate the feasibility of using percolation analysis to study high-level cognition. We show how percolation theory can be harnessed to examine cognitive theory on the relation of creativity and flexibility of thought and to examine the mechanism that differentiates flexibility of thought in low and high creative individuals. Specifically, we test the hypothesis that the semantic network of high creative individuals is more flexible than that of low creative individuals, thus more robust. To test this hypothesis, we conduct a percolation analysis on the semantic networks of low semantic creative (LSC) and high semantic creative (HSC) individuals, data previously collected by Kenett et al. (15). Further, our current study allows us a detailed analysis of the structure and substructures of these networks, by examining how they break apart into components of similar words.

The LSC and HSC semantic networks are composed of 96 cue words, divided into groups of four concrete words from 24 categories (fruits, musical instruments, vehicles, etc.; Table S1), which represent a priori components of these networks. Kenett et al. (15) found differences in general network characteristics between the two groups, namely, the HSC network exhibiting lower average shortest path length (shortest path between any pair of nodes in the network) and a lower modularity (the extent to which the network breaks into smaller components) than the LSC network. These findings directly supported the associative theory of creativity that posits that low and high creative individuals differ in the structure of their semantic memory (15). The authors interpreted their results as indicating that the semantic network of HSC individuals is more flexible than that of LSC individuals. However, this was only indirectly inferred from the general network measures that were computed.

In the present study we directly examine the flexibility of the LSC and HSC semantic networks, using percolation analysis. Such an approach allows us to quantitatively examine an important feature of creative ability and directly examine the relation between creativity and flexibility of thought. To this end, we modify the approach used by ref. 15 to better represent the semantic networks of the LSC and HSC groups. Our modified approach also controls for the higher amount of associative responses generated by the HSC group to the cue words (Materials and Methods). We then conduct a percolation analysis, by removing links of strength below a given increasing threshold, and compare the giant component of the two networks. This analysis reveals that the HSC network is significantly more robust to network percolation, as indicated by its giant components breaking in higher thresholds and by a higher integral (which measures the robustness of the network). We then test and verify the significance of our results by examining how the percolation analysis is affected by adding noise to the link weights in the two networks and its validity by shuffling the links in the networks. Finally, we examine the mechanism that differentiates the robustness between the two groups, by comparing links that connect between or within components in the two networks. This analysis reveals that what contributes to the higher robustness of the HSC network is stronger links between components in their network and better separation into the a priori components. Both of these factors contribute to the robustness of the HSC network and may facilitate spread of cognitive activation in the network, an important aspect of the creative process (1, 2).

Results

Using free association data collected from LSC and HSC individuals (33 in each group), we developed an improved approach to construct the weighted semantic networks of each group and conduct percolation analysis on these networks (Materials and Methods). Furthermore, we control for the higher amount of associative responses generated by the HSC group for the different cue words by normalizing the weights of the links in the HSC network by a factor of 1.3 (the ratio between the average amount of responses of both groups; SI Network Construction). In the percolation analysis, we examine the percolation of both networks by removing links with weight strength below an increasing threshold (percolation step; Fig. 1). In each percolation step, we measure the size of the giant component and whether any and which component of nodes break from it (Fig. 2A). To examine the significance of our percolation process, we examine how it is affected by the addition of noise to the links in each network (Fig. 2B) and by shuffling the links in each network (Fig. 2C). Finally, we examine the specific mechanism that differentiates the network robustness between the two networks, by comparing the links between matched components in both networks (Fig. 3). Such analyses allow us to examine the specific property of flexibility of thought as related to creativity and also shed further light on the difference in semantic memory structure between low and high creative individuals.

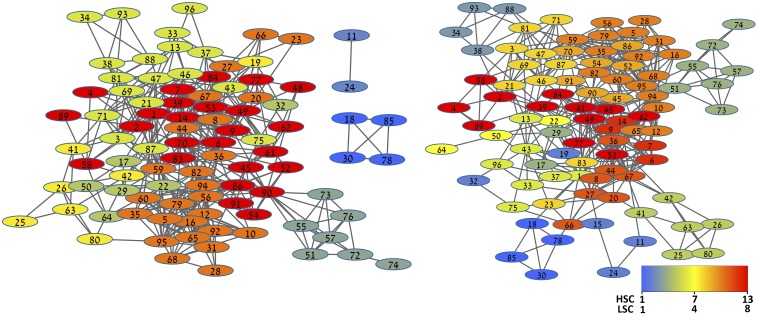
Fig. 1.

(Left) LSC and (Right) HSC networks with links above TH = 0.1. The nodes are numbered according to their labels (Table S1) and colored from blue to red according to their percolation order. The colder (blue) the node is, the earlier it was disconnected from the giant component, and therefore, it is weaker connected to the entire network. Because the number of components is different in both networks, the scales are different.

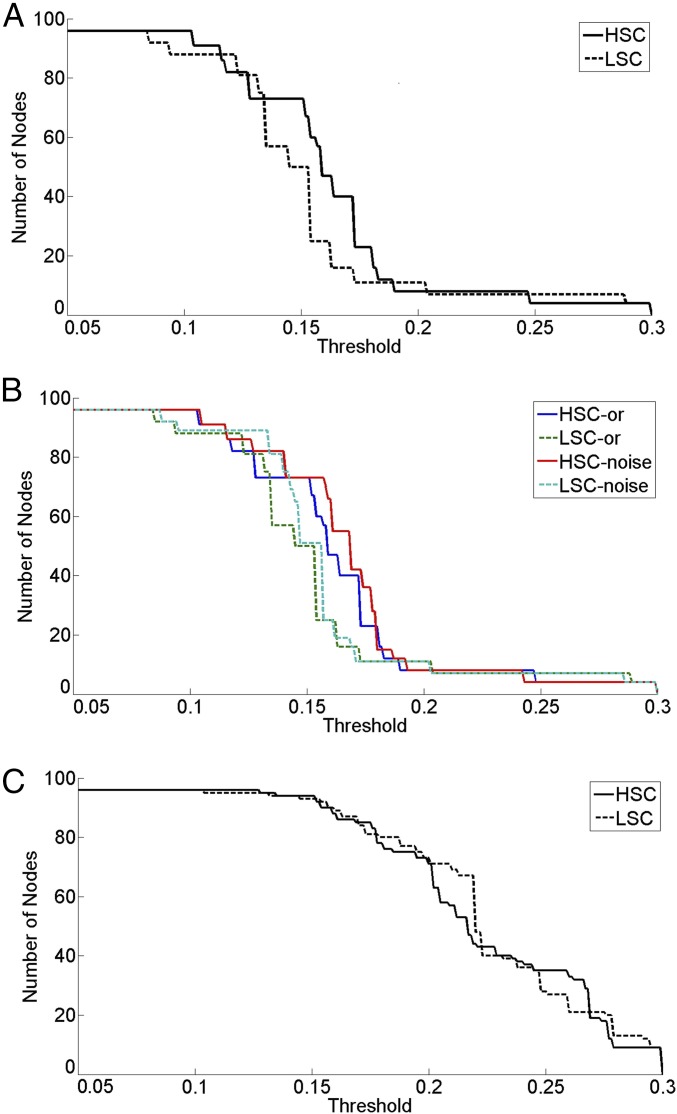
Fig. 2.

(A) Percolation analysis of the empirical networks of the LSC and HSC networks. (B) Effect of noise on the percolation analysis of the LSC and HSC networks, with addition of noise with SD of 0.01 (LSC/HSC-noise) or without addition of noise (LSC/HSC-or). (C) An example of typical iteration of the percolation analysis on the shuffled links analysis in both networks.

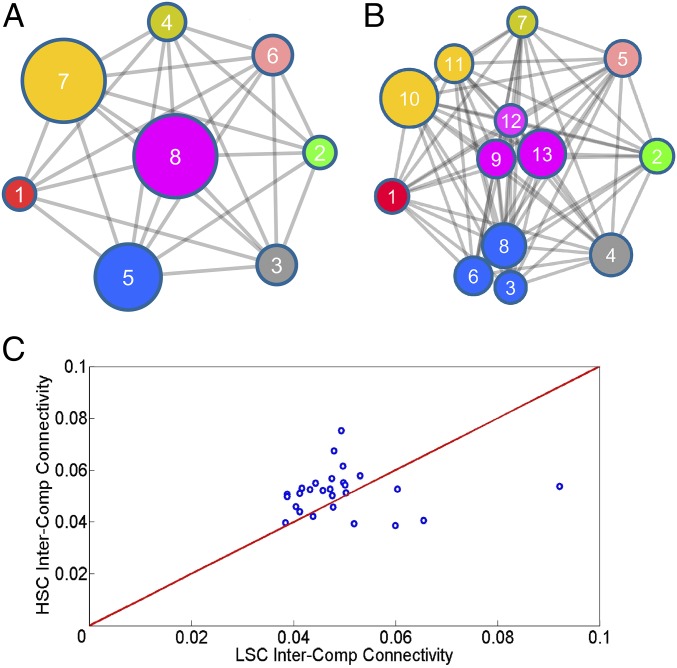
Fig. 3.

Interlinks analysis for the LSC and HSC groups. (A) LSC and (B) HSC percolated components network layout. The components are sized according to the number of nodes in the component and numbered according to their disconnection order from the giant component. (C) Scatterplot of the matched interlinks of the two groups, where each circle represents an interlink between two matched components in both networks. Circles above/below the diagonal indicate that this interlink is stronger in the HSC/LSC network compared with the LSC/HSC network.

Percolation Analysis.

Assuming that the semantic network of HSC individuals is more flexible than the LSC network, we hypothesize that their network will be more robust to percolation analysis and thus break apart slower than the LSC network. We therefore conduct the percolation analysis on the networks of the two groups. The result of this process is percolated components—a cluster of nodes in the network that break apart together at a certain threshold.

In Fig. 1 we demonstrate the percolation analysis on the LSC and HSC networks, for threshold value of 0.1 (all links with weights smaller than 0.1 are removed). The nodes are colored according to their percolation order, after completion of the percolation process where there is no more a giant component (Materials and Methods). This visualization illustrates that both networks break apart into mostly similar components (albeit at different thresholds). Further, it demonstrates how, for the same threshold value (0.1), the LSC network breaks apart into three components, whereas the HSC network does not break apart at all. For example, one percolated component that first breaks apart from the LSC network is the component of musical instruments (flute, clarinet, piano, and guitar), which also corresponds to the relevant a priori component (Table S1). In the LSC network, this percolated component breaks apart from the giant component already at a threshold value of 0.085. In the HSC network, however, this similar component breaks apart only at a threshold value of 0.104. This analysis also identifies how strong the different percolated components are connected to the network, according to the order in which they break apart from the giant component. For example, the musical instruments percolated component is the first to break because it has the weakest connecting links to the giant component in both networks.

This analysis reveals that the giant component of the LSC network breaks apart faster (at lower thresholds) compared with the HSC network (Fig. 2A). For the same threshold values the LSC giant component is mostly smaller than the HSC giant component, indicating that the HSC network is more robust and its components are better connected than in the LSC network. To quantify the difference in percolation between the two groups, we calculate the percolation integral of the percolation analysis for both groups (over curves like Fig. 2). This analysis finds that the percolation integral of the LSC group is smaller than that of the HSC group (14.76 vs. 15.64), providing further evidence that the LSC network breaks apart quicker than the HSC network. Finally, we find that the empirical critical percolation thresholds are different from a theoretical random network with the same average degree (SI Network Construction). To test the significance of our finding, we next examine how the percolation analysis is affected by adding noise to the weights of the links and examine its validity by shuffling between the links in the networks.

Effect of Noise Analysis.

We examine the significance of our finding by adding noise to the link weights and analyzing how this affects our conclusions. If our results are significant, adding noise to the link weights will not change the conclusions (the HSC network being more robust than the LSC network). To conduct this analysis, we analyzed 500 realizations of the percolation analysis, where in each realization a Gaussian noise was added to the network links with a mean value of zero and a varied standard variation, of ${10}^{-4}$ to ${10}^{-2}$. This range is chosen to examine the effect of noise with one and even two orders of magnitude above the noise level expected if the weights of the links were randomly distributed (${10}^{-4}$; Methods and Materials). We conduct an independent samples t test analysis to examine the effect of different distributions of noise on the percolation analysis. Examining the effects of different noise variance on the percolation integral of both groups and in particular the small SDs found for the robustness of the giant component supports our finding. The percolation integral of the HSC network is higher than that of the LSC network for the three different Gaussian noise distributions (Table 1). Furthermore, the integral values for link noise variance between ${10}^{-4}$ to ${10}^{-2}$ do not change drastically from the empirical percolation integral value of the two groups (Fig. 2B). Thus, both the LSC and HSC groups have a stable percolation process with significant different integrals (see also Table S3).

Table 1.

The effect of varied amount of noise on link weights on the percolation analysis for the two groups

Noise SD	LSC	HSC	t test
0.0001	14.76 (0.002)	15.64 (0.006)	−2,790.59***
0.001	14.76 (0.031)	15.65 (0.024)	−507.56***
0.01	15.10 (0.200)	15.81 (0.176)	−59.35***

The calculation of the integral is repeated 500 times for each of the different noise variances added to the link weights in the two networks (SD in parentheses). An independent samples t test statistically examined the difference between the two distributions with the different noise Gaussians. Noise SD, SD of noise Gaussian added to link weights; LSC, low semantic creative individuals; HSC, high semantic creative individuals; ***P < 0.001.

Link Shuffling Analysis.

Our finding on the difference in network robustness between the two groups may stem from the difference in link weights (and not the network structure) between the two networks. To test this alternative explanation, we conducted in each network a link shuffling analysis. This analysis is equivalent to randomly removing links in the network. To perform this analysis, we randomly shuffle links between pairs of nodes in each network. To maximize the fraction of links in the network that will be shuffled, we randomly shuffled 40,000 links in the network (there are about 4,500 links in each network). The shuffling analysis was conducted for each network independently and reiterated 500 times. In each iteration, we calculated the percolation integral for both networks (Fig. 2C presents one such iteration). We then conducted an independent samples t test analysis on the distribution of percolation integrals of the LSC group compared with the HSC group. This analysis reveals that the percolation shuffled integral of the LSC group (21.45; SD = 0.75) is even slightly larger than that of the HSC group (20.55; SD = 0.72), t(998) = 19.25, P < 0.001. Thus, it seems that the robustness of the HSC network is more affected by the shuffling of its structure, compared with the LSC network, leading to a larger shuffled percolation integral for the LSC network. This finding strongly suggests that the difference between the empirical percolation integral of the two groups is driven by the structure of the networks and not by the link weights.

Link Type Analysis.

Finally, we examine the mechanism contributing to the difference in network robustness between the two groups, by examining differences in the weights of the links connecting between components in the two groups. The components are those that become disconnected from the giant component during the percolation process. For each network we independently classify each of the links as either connecting different components in the network (interlinks) or as connecting nodes within components (intralinks). This is achieved after completing the network percolation analysis and then reverse-engineering each of the links in the networks (Materials and Methods).

To compare intralinks and interlinks between the two groups requires matching the links between the two groups, independently for the two types of links. This is due to the difference in the structure of the two networks. To achieve this, we remove links that appear in only one of the two groups. This resulted in 3,676 mutual interlinks and 348 mutual intralinks. Due to the skewness of the distributions, we conduct a Mann–Whitney U independent samples test. This analysis reveals only a significant difference between the strength of the interlinks between the two groups, U = 5,226,777, P < 0.001: the HSC group (0.04, SD = 0.02) has stronger interlinks than the LSC group (0.03, SD = 0.02). No significant difference is found for the difference in intralink strength between the HSC (0.15, SD = 0.09) and LSC (0.15, SD = 0.10) network (P < 0.7). Based on the significant difference between groups found only for the interlinks, and on the theory that creativity is related to the spread of information throughout the semantic network (15), we focus our attention on the differences between similar interlinks in the two groups. This is achieved by computing a component connectivity (interlink) measure between each pair of components for both networks, which indicates how strongly two components are connected to each other. This connectivity measure is the average interlink strength, i.e., the ratio of the sum of the interlinks and the number of interlinks between two components (Methods and Materials). We then compare the interlinks strength between similar pairs of components in both HSC and LSC networks.

This connectivity measure allows us to examine the general structure of the network. As seen in Fig. 3 A and B, the LSC and HSC networks have different structures. The HSC network has more components with smaller size, whereas the LSC network has fewer yet larger components (component number 4, 18 nodes; components number 6 and 7, 25 nodes). The components in the LSC and HSC networks are colored according to their nodes. For example, component 7 in the LSC network is composed from the same nodes as in components 10 and 11 in the HSC network. Similarly, most of the components in LSC match a single or few components in the HSC network. The overlap between the components is about 87% (Table S6). Furthermore, this indicates that in the LSC network, the groups of nodes are not as well separated into the a priori components as in the HSC network. To compare the connectivity measurement between the two groups, we match the components by compiling together small components in the HSC network that together match a larger component in the LSC network (Table S7). This results in eight matched components for both groups, with 28 matched interlinks. Plotting these matched interlinks for the two groups demonstrates that most of these matched links are stronger in the HSC network compared with the LSC network (Fig. 3C). It is seen that out of these 28 matched links, 21 links (75%) are stronger in the HSC network. Thus, the HSC group has mostly stronger interlinks between components, which increases their robustness and facilitates spread of information in the network.

Discussion

Flexibility of Thought from a Percolation Theory Perspective.

In this study, we provide a quantitative measure of flexibility of thought, based on the robustness of a semantic network to attack. Such an approach provides a unique way to examine flexibility of thought as related to high-level cognition (e.g., creativity), which is currently examined only via indirect behavioral methods (4, 5). According to the associative theory of creativity, high creative individuals have a more flexible semantic memory structure, which facilitates their ability to search through their memory and connect weakly related concepts together (2). We use percolation analysis to examine this higher flexibility, by examining the robustness of the semantic networks of low and high creative individuals to attack. Formulating flexibility of thought in creativity as the robustness of a semantic network to network percolation allows us to quantitatively and directly examine this theory. We conduct network percolation analysis on the semantic networks of LSC and HSC individuals, data previously collected by Kenett et al. (15). This is performed by using percolation theory to remove links with increasing weight strengths and examining how this affects the robustness of the semantic networks of low and high creative individuals. Such degradation of links is grounded in cognitive theory on memory phenomena such as dementia and retrieval failures (14, 17, 19). Thus, this analysis serves as a quantitative measure of flexibility of thought, assuming that the higher the robustness of the semantic network, the higher its flexibility.

Our analysis sheds further light on the difference in network structure between the LSC and HSC groups, by examining how they break apart. Although prior work examined the modularity of the LSC and HSC networks (15), only percolation analysis applied here allows studying the robustness of the networks and highlights the higher robustness exhibited by HSC individuals. This is achieved by measuring the effect of link removal on the size of the giant component in both networks. Furthermore, percolation analysis allows us to examine the importance of interlinks and intralinks and examine the hierarchy in which components break apart from the giant component in the network order (Fig. 1). Such information cannot be derived from modularity analysis, which only provides a global measure of the network.

We demonstrate that the semantic network of HSC individuals is more robust to network percolation, as exhibited by a higher percolation integral. This analysis is validated by adding noise to the link weights and statistically examining the significance of the difference in network percolation between the two groups. This analysis reveals that the empirical percolation integral is hardly affected by adding noise and that the difference between the networks robustness is highly significant. Next, we conduct a link shuffling analysis, to examine what contributes to the difference in network robustness between the two groups. This analysis reveals that the topological structure of the networks and not the link weights is the determining factor in the higher robustness of the HSC group to network percolation: the results of this shuffle disrupt the robustness of the HSC network. Finally, we conduct a more fine-grained analysis to examine the specific mechanism that is differentiating the robustness between the two groups. Specifically, we examine whether this difference is related to removal of links that connect components (interlinks) or links that connect nodes within components (intralinks) in the network. We show that this structural difference between the two networks lies in the HSC network having stronger interlinks than the LSC network. This difference in interlinks between the two groups may facilitate spread of activation in the HSC network, an important aspect of the creative process (1, 2): it facilitates spread of activation between components in the network, thus making it possible to break free from a component in the network and lead to novel combinations.

Methodological Considerations.

We examine the robustness of the semantic networks of LSC and HSC to network percolation. However, creativity is a continuous construct and not a categorical one (low versus high). Future research should examine network percolation of semantic networks in individuals (20, 21) to provide a better understanding of flexibility of thought as related to creativity. Furthermore, some researchers have argued against semantic networks estimated from free association data (22). Future research should replicate our findings based on further data and alternative methods to represent semantic networks. Finally, we only provided initial analytical insight to our findings. Future research is needed to conduct a more rigorous analytical analysis to strengthen and replicate our findings.

Implications for High-Level Cognitive Research.

From a more general perspective, the approach used in this study offers a powerful tool to quantitatively study flexibility of thought in both typical and clinical populations. Although percolation theory is an attractive tool in examining flexibility of thought, currently, only a handful of studies have used this approach in studying the robustness of cognitive systems (17, 18). For example, Borge-Holthoefer et al. (17) have used network degradation analysis to simulate the progression of Alzheimer’s disease. The present study demonstrates how percolation theory can be used to quantify and examine the more general capacity of thought flexibility. Such an approach can strongly contribute to operationalize and measure the construct of flexibility, which is integral in both creativity and intelligence research. To this end, a future comparison of our method to behavioral measures of flexibility in low and high creative individuals could replicate and demonstrate the strength of our quantitative approach. Finally, such an approach can be used to examine atypical thought processes in clinical populations suffering from cognitive network degradation, such as schizophrenia (23).

Materials and Methods

Creativity Assessment.

Participants (n = 140) were recruited as part of a larger research study on individual differences in creative ability (15). This study was approved by the Bar-Ilan University Institutional Review Board. First, all participants signed a consent form. They then completed the following creativity tasks: the remote association test, which measures associative thought related to creative ability (24); Tel Aviv University creativity test (25); a battery of divergent thinking tests; and the comprehension of metaphors task (26), which compares processing of word pairs that have different semantic relations. Participants were classified as low semantic creative (LSC) or high semantic creative (HSC) individuals (n = 33 participants in both groups) based on a statistical decision tree approach, using these scores (see ref. 15 for more details).

Network Construction.

The representation of the semantic networks of the LSC and HSC groups was based on a modified version of the method developed by ref. 15. Our revised method takes into account not only the correlation of associations, based on the overlap of associative features to a pair of cue words, but also the number of participants generating these overlapping associative features (SI Network Construction). Specifically, we also take into account the number of participants generating the associative features which determine the strength of semantic similarity between the cue words. The more similar associative response generated and the larger number of participants generating these association responses to a pair of cue words, the stronger the link between this pair of cue words is. The links in each network were normalized according to the mean number of associations per cue word. The normalization purpose was to remove the effect of the HSC individuals generating a higher number of associations per cue words, compared with the LSC individuals (SI Network Construction). The links between all pairs of cue words define a symmetric correlation matrix whose (i, j) element denotes the semantic similarity between cue words i and j. This matrix can be studied in terms of an adjacency matrix of a weighted, undirected network, where each cue word is a node, and a link between two nodes (cue words) represents the semantic weight between them.

Network Percolation Analysis.

The network percolation analysis is achieved by removing the links in the network according to an increasing threshold (all links with weight smaller than a threshold TH value; percolation step) while measuring the size (number of nodes) of the giant component in the network and identifying the detached components. The threshold was varied from the smallest weight in the network (initial TH) to a weight strength in which the giant component is smaller than three nodes (final TH). The threshold resolution was chosen according to the smallest difference between the sorted weights. In that way the percolation process is more accurate and allows us to understand better the order of components disconnection. The percolation analysis has different step sizes (number of nodes of a component that disconnects from the giant component in a specific percolation step); few of them are of size one, which means that only one node is disconnected at that specific degradation step, but most of them are groups of several nodes. Because we are examining the behavior of connected components, we smoothed the steps sized one to the nearest step. These smoothed components are referred to as percolated components.

The percolation integral is a good measure of the percolation stability because it measures how fast the giant component is breaking. For example, a network that breaks at low threshold values and has a steep percolation curve will have a lower integral than a network (with the same size of giant component) that breaks with high threshold values and a flat percolation curve. The integral calculation of the percolation analysis for each network is computed by summing the multiplication of the mean value of the giant component size (in its threshold value) and the threshold resolution $\text{PI}={\displaystyle {\int }_{\text{start\_TH}}^{\text{end\_TH}}\text{GC}\left(x\right)\mathit{dx}}={\displaystyle {\sum }_{\text{TH-start\_TH}}^{\text{end\_TH}}\text{GC}\left(\text{TH}\right)*\text{TH\_res}}$, where PI is the percolation integral, GC is the giant component, start/end_TH are the initial and final TH values, and TH_RES is the TH resolution.

Effect of Noise Analysis.

To test the significance of our results, the percolation integral is calculated after adding noise to the links in the two networks. This noise may change the links’ weights, i.e., making weaker weights stronger and vice versa. If this process changes the percolation integral dramatically, it means that our percolation process is not significant. The percolation integral is calculated over 500 realizations of the percolation analysis. In each realization, a Gaussian noise was added to the network with a mean value of zero and a variable SD ranging between ${10}^{-4}$ and ${10}^{-2}$. This range is chosen to examine the effect of noise with one and even two orders of magnitude above the noise level expected if the weights of the links were randomly distributed. Both LSC and HSC networks have ∼4,000 links, with a strength varying from zero to one. Thus, the mean strength between a pair of links in the network will be about $1/\mathrm{4,000}=2.5*{10}^{-4}$. This gives an estimation of a noise in a random network of the same size. Adding this noise to a random network will have a meaningful effect on the links. In the LSC and HSC networks this and higher noise may be used as a test for the network ability to withstand noise. The small effect of noise in our study supports the significant difference between the robustness of LSC and HSC networks.

Link Shuffling Analysis.

Link shuffling analysis is done to examine the structure of the network and its effect on the percolation process. In the shuffling process, two links in the network are randomly chosen (from two pairs of nodes) and exchanged. For example, nodes a and b with link strength 0.5 and nodes c and d with link strength 0.7 are exchanged in a way that the new network topology would be that a and c are connected with 0.5 and b and d with 0.7. This process is reiterated 10 times the number of links in the network to ensure that most of the links in the network are replaced (40,000 shuffles). This is reiterated to have 500 realizations, where in each realization the percolation integral of the shuffled network is calculated for both groups. In this shuffling analysis, we only change the structure of the network and not the number or weights of the links in the network.

Link Type Analysis.

Link type analysis is done to better understand the network structure and to investigate the mechanism that differentiates the network robustness of the two groups. This is done by classifying each of the links in the network as either links that connect between components (interlinks) or links that connect within components (intralink) in the network. This is achieved after completing the network percolation process. We then reverse engineer the links, going backward in the network percolation process and classifying the links based on whether they connect nodes within or between percolated components.

Based on the interlinks we compute for each pair of percolated componentsxa connectivity measure $C\left(i,j\right)={{\displaystyle \sum }}_{k=1}^{N_{i\text{,}j}}\text{interlinks}\left(i,j\right)/\text{Number\_Of\_Links}\left({\text{Comp}}_i,{\text{Comp}}_j\right)$, where $N_{i\text{,}j}$ is the number of interlinks between the percolated components i and j, Number_Of_Links(i,j) is the number of links between pair of components i and j. This measure allows us to examine the structure of the two networks (Fig. 3 A and B). In these networks, nodes represent the percolated components, and their size is in accordance with the size of the component they represent. Links in these networks represent the interlink connectivity measurement. To compare between the connectivity measure across the two networks, we matched the connectivity links by merging small components in the HSC network that together match a larger component in the LSC network (SI LSC and HSC Percolated Components Overlap Analysis). We then plotted the matched connectivity links of the two groups as a scatterplot (Fig. 3C). Finally, we conduct a Mann–Whitney U independent samples test to examine the difference in the matched connectivity links strength between the two networks.