Influence of water and enzyme SpnF on the dynamics and energetics of the ambimodal [6+4]/[4+2] cycloaddition

Significance

The investigation of time-resolved mechanisms of enzymatic reaction with accurate quantum-mechanics method is a holy grail of computational chemistry, and we now develop an efficient method, environment-perturbed transition-state sampling, to study single-molecule trajectories in enzymes and calculate activation barriers. In 2011, the Liu group published evidence for the first monofunctional Diels–Alderase, SpnF, in the biosynthetic pathway of Spinosyn A. We discovered later that the reaction bifurcates to the [4+2] and [6+4] adduct through a single ambimodal transition state. We now elucidate in detail the mechanism of the reaction and show how the SpnF enzyme dynamically controls product formation. Our method will find great application in the design of enzymes to control selectivity, particularly for reactions involving ambimodal transition states.

Abstract

SpnF is the first monofunctional Diels–Alder/[6+4]-ase that catalyzes a reaction leading to both Diels–Alder and [6+4] adducts through a single transition state. The environment-perturbed transition-state sampling method has been developed to calculate free energies, kinetic isotope effects, and quasi-classical reaction trajectories of enzyme-catalyzed reactions and the uncatalyzed reaction in water. Energetics calculated in this way reproduce the experiment and show that the normal Diels–Alder transition state is stabilized by H bonds with water molecules, while the ambimodal transition state is favored in the enzyme SpnF by both intramolecular hydrogen bonding and hydrophobic binding. Molecular dynamics simulations show that trajectories passing through the ambimodal transition state bifurcate to the [6+4] adduct and the Diels–Alder adduct with a ratio of 1:1 in the gas phase, 1:1.6 in water, and 1:11 in the enzyme. This example shows how an enzyme acts on a vibrational time scale to steer post-transition state trajectories toward the Diels–Alder adduct.

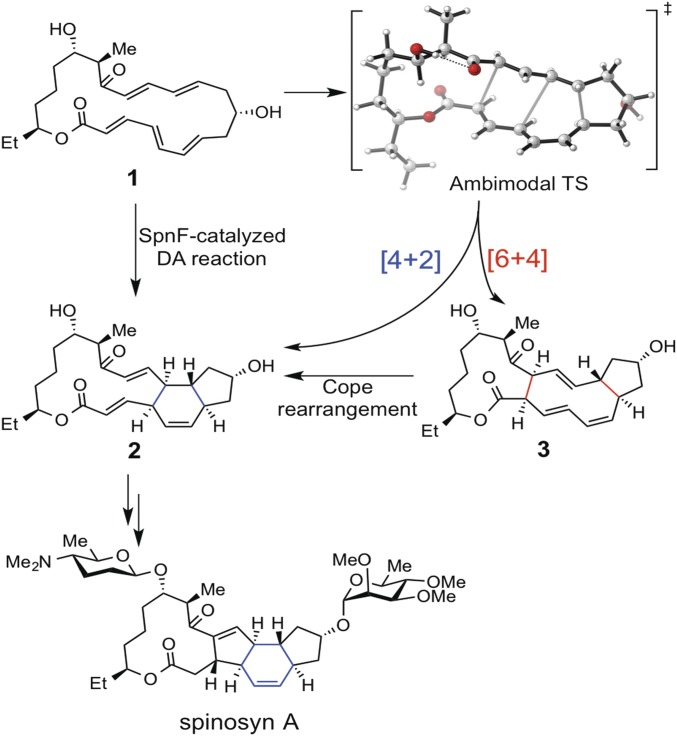
The enzyme SpnF catalyzes the transannular Diels–Alder (DA) reaction that converts 1 to 2 (Fig. 1) in the biosynthesis of spinosyn A, a major component of the insecticide spinosad (1). Previous dynamics simulations of this reaction in the gas phase (2) show that the reaction occurs via an ambimodal (3) transition state (TS), and a path that bifurcates to form two products: the experimentally observed DA ([4+2]) adduct 2 and an unobserved [6+4] adduct 3. The initial product ratio of 2 to 3 in the gas phase was predicted to be 2:5. The transition state is highly asynchronous, and the first C–C bond is formed 140–170 fs before the second (2). The selectivity of the reaction is governed not by TS partition functions but by dynamics that are sensitive to the environment (4, 5). We have now explained how the intrinsic mechanism is modified, energetically and dynamically, by aqueous solution and by the SpnF enzyme. In particular, our developed method, environment-perturbed transition-state sampling, enables the discovery of single-molecule time-resolved reaction pathways in condensed media.

Fig. 1.

SpnF-catalyzed transannular DA reaction of 1 to form 2. This is a step in the biosynthesis of spinosyn A.

Background

The wide applications of the DA reaction (6, 7) inspire the identification of natural enzymes that catalyze DA reactions (Diels–Alderases or DAases) (8). While extensive surveys of secondary metabolites indicate that hundreds of natural products are potentially biosynthesized by DAases (9), only a handful of purified enzymes have been demonstrated to catalyze DA reactions. These enzymes often catalyze other reactions, such as oxidations or degradations, thus leaving uncertain their specific influence on the DA reactions (10). In 2011, Liu and coworkers discovered the first monofunctional DAase, SpnF, which catalyzes a DA reaction in the biosynthetic pathway of spinosyn A. Although the crystal structure of SpnF was reported in 2015 (11), the mechanism by which the enzyme catalyzes the DA reaction is still largely unknown.

Computational simulations have been employed to rationalize the reaction mechanism (12), but accurate mechanistic studies in solvent and in enzyme remain challenging (13), because these require both accurate description of interatomic interactions and extensive sampling of molecular conformations (14). For instance, the recent study of AbyU-catalyzed DA reaction by Race and coworkers (15) has shown that the proposed DA reaction likely proceeds via a concerted, yet highly asynchronous transition state in the active site of the enzyme AbyU. However, the calculated potential of mean force (PMF) barrier using a hybrid quantum-mechanics classical molecular mechanics method severely underestimates the experimental barrier.

Additionally, as single-molecule experimental techniques to study reactions advance (16), mechanistic studies are no longer limited to the description of ensemble-average thermodynamics and kinetics. The explorations of chemical reactions now extend to the atomic level and femtosecond–picosecond time scale, which informs how atomic motions, conformational fluctuations, and solvent effects alter the reaction pathways of single molecules (17). This accordingly calls for the development of computational tools that investigate the energetics and dynamics of single molecules in condensed media.

We have developed an environment-perturbed transition-state sampling (EPTSS) method for individual trajectories. The EPTSS method has also been used for free-energy calculations and kinetic isotope effect calculations in solvents and enzymes. This enables the unraveling of the role of solvents and enzymes on control of single-molecule reaction pathways involving ambimodal transition states and potential energy surface (PES) bifurcations (5, 18). Quasi-classical trajectories have been employed previously in the gas phase to understand and predict selectivities of reactions with post-TS bifurcations on the PES (5, 19–21), such as for the cationic rearrangements occurring in terpene biosynthesis (22, 23). We report how solvent and enzyme influence the dynamical behavior of a bifurcating reaction path in the SpnF-catalyzed DA reaction.

Results and Discussion

Using quantum mechanics/molecular mechanics (QM/MM) methods (24, 25), we have examined the effect of water and SpnF on the dynamics and initial product ratios of the transannular cycloadditions of 1. We extended our previously described solvent-perturbed TS sampling method (26) to carry out quasi-classical normal-mode sampling of the ensemble of TS in enzymes. The method is now called the EPTSS to reflect its generality.

Conformational Ensembles for Reactant, Ambimodal TS-A, and DA TS-B.

The substrate 1 is a conformationally flexible 22-membered polyene lactone. The conformation complexity was thoroughly analyzed by Medvedev et al. (27). We find that the conformers of 1 consist mainly of two clusters represented in Fig. 2 by the gas-phase conformers R-A and R-B. They differ mainly in the presence or absence of an intramolecular hydrogen bond. This is reflected in the highlighted dihedral angle Φ. R-A has an intramolecular hydrogen bond (H bond) and R-B does not (Fig. 3). TS-A is more stable than TS-B by 3.3 kcal/mol in the gas phase (SI Appendix, Fig. S1) and by 0.9 kcal/mol in implicit water (SI Appendix, Fig. S10).

Fig. 2.

Ensembles of reactants from classical MD in water and in the enzyme. Water molecules and enzyme residues are not displayed. R-A and R-B are two representative conformations optimized in the gas phase. The dihedral angle used for discriminating between the two conformations is highlighted.

Fig. 3.

Ensembles of ambimodal TS-A and DA TS-B in enzyme. Ambimodal TS-A and DA TS-B are representative conformations for their corresponding ensembles. The dihedral angle used for discriminating two conformations is highlighted.

Classical molecular dynamics (MD) equilibrations in water and SpnF predict an 80:20 equilibrium mixture of R-B:R-A in both water and SpnF. This contrasts with the gas phase, where R-A is 5.2 kcal/mol below R-B, largely due to the intramolecular H bond. In water and in SpnF, hydrogen bonds to the carbonyl of R-B (Q148, I40 in SpnF) stabilize R-B (detailed in SI Appendix, section 5).

MD simulations with restrained TS (28) geometries were conducted separately on both TS conformers in water and enzyme SpnF. Ensembles for ambimodal TS-A and for DA TS-B were constructed separately by taking 100 snapshots of the solvent box containing the constrained TSs with a 100-ps interval in water and a 1-ns interval in the enzyme. For each ensemble, subsequent QM/MM calculations were conducted to optimize the reactant and the ambimodal TS-A or DA TS-B in the perturbing environment. The free energies of each were computed by averaging over the entire ensemble.

Computed Free Energies of Activation.

Table 1 shows the averaged free-energy barriers for ambimodal TS-A and DA TS-B in water and in the enzyme SpnF. Averages for different numbers of snapshots are shown in SI Appendix, Fig. S5. The averages based on a small number of snapshots have large SEs. The SEs decrease, and the energetics converge after including a large number of snapshots. Sufficient conformational sampling is essential for the free-energy calculations of reactions in condensed media (29, 30) (SI Appendix, section 4).

Table 1.

Free-energy barriers for cycloadditions of 1 in water and SpnF enzyme

Medium	Ambimodal TS-A, kcal/mol	DA TS-B, kcal/mol	Experiment, kcal/mol*	Experiment, min−1
Water	27.8 ± 1.9†	22.9 ± 2.1†	22.0	0.288 ± 0.0004
Enzyme	18.8 ± 1.0†	23.4 ± 1.1†	18.3	14 ± 1.6

^*Barrier obtained from experimental rate via the Eyring equation.

^†SE after averaging over 100 snapshots.

The DA TS-B is preferred in water, while the ambimodal TS-A is favored in the enzyme. This is a dramatic difference between the reaction in water and in SpnF enzyme. The computed barriers are consistent with the experimental values of 22.0 ± 0.01 kcal/mol in water and 18.3 ± 0.1 kcal/mol in SpnF, calculated from rates measured at 25 °C (1). The QM/MM umbrella sampling calculation has been recently performed by Zheng and Thiel (31). These simulations show a free-energy barrier of 22 kal/mol for D TS-B in the SpnF enzyme. This is also consistent with our result. We have also computed the secondary kinetic isotopic effect (KIE) for the reaction in water and in enzyme, and compared with the experimental results (32), as shown in SI Appendix, Table S3. Given experimental errors and statistical errors due to our limited computational sampling, the results are in reasonable agreement. The EPTSS KIEs are averaged over the entire TS ensemble. Both experiment and theory establish a significant inverse k_H/k_D at C7–C11, in the rate-determining TSs in both water and enzyme, indicating bond formation. Nearly negligible KIE are found experimentally and computationally at C4, C12, C2, and C14 (SI Appendix, Table S3). The only exception is for C4, where both experiment and theory predict no KIE in water, but small inverse in the enzyme. These results support that TS-B is favored in water, while TS-A in preferred in the enzyme.

The elucidation of hydrogen-bonding patterns gives insight into the origins of catalysis. In water, TS-B is better stabilized than TS-A by forming more intermolecular H bonds with water molecules. TS-A already has an intramolecular H bond and forms fewer H bonds with water. Additionally, TS-B is more polarized than TS-A (SI Appendix, sections 5 and 8.1).

The hydrogen bonds measured in the reactant and two conformers of the TS in the enzyme are shown in Table 2. H bonds between substrate and H42, E152 (to the TS), and A252 (to the reactant) stabilize the binding configuration of the TS and the reactant. Two typical snapshots are also shown for ambimodal TS-A and DA TS-B with H bonding to their surrounding residues. H bonds between the residues and the highlighted C=O decrease the energy barriers of the cycloadditions (33).

Table 2.

Percentage of structures that have H-bond interactions with enzyme residues in ensembles of reactant, TS-A, and TS-B after QM/MM optimizations. A H bond is defined as having a H–O bond length shorter than 2.25 Å and an O–H–O bond angle greater than 150°

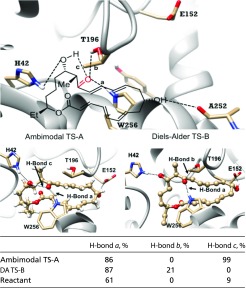In 100 snapshots in the enzyme, H bonds to W256 are present in 61% of the reactant snapshots, and in 86% and 87% of the ambimodal TS and DA TS, respectively. From reactant to TS, the ambimodal TS-A experiences an enhancement of H-bond c (intramolecular H bond) from 9 to 99%, while DA TS-B shows only a small increase in H-bond b (to T195) percentage from 0 to 21%. This explains in part why the ambimodal TS is more favorable in the enzyme. The protein pocket is highly hydrophobic, and only 0.2 water molecules are detected that bind to the hydroxyl and carbonyl group of the DA TS-B during the MD (as shown in SI Appendix, Fig. S14). The DA TS-B in the enzyme is not well stabilized by intermolecular H bonds provided by water or protein residues. This is in direct contrast to the previous computation by Gordeev and Ananikov (34) based on a theozyme model where all polar functional groups of the substrate bind to the amino acids.

Reaction Dynamics Simulations.

Enzymes can bind reactants and TS by both electrostatic and hydrophobic interactions. These interactions may favor certain TS geometries, and influence reaction dynamics as well.

The role of dynamics on catalysis by enzymes has been a significant topic of discussion ever since Falzone, Wright, and Benkovic reported correlations between dynamical motions of remote residues and changes in rate by mutation of these residues (35). After considerable debate, the current consensus is that relatively slow (millisecond–microsecond) motions of loops and remote residues do indeed alter the structure of the active site and the rate of reaction (36), but fast (picosecond–femtosecond) couplings of vibrational motions to motions along the reaction coordinate have little or no influence on the rate of reactions. We note that residues in contact with the reactant as they vibrate through the transition zone can influence energetics, and the femtosecond motions of these residues can be coupled to the reaction event, while even nanosecond loop motion is too slow to influence reaction dynamics.

Fig. 4 shows the distribution of sampled geometries for the DA TS-B in water (Fig. 4A), and the ambimodal TS-A in the gas phase (Fig. 4B), in water (Fig. 4C) and in SpnF enzyme (Fig. 4D). Bonds 2 and 3 are formed in the [4+2] and the [6+4] adducts, respectively. For DA TS-B in water, the distribution of bond 2 is 2.62 ± 0.42 Å, and that of bond 3 is 3.65 ± 0.51 Å. The two bonds on average differ by ∼1 Å. The formation of the [4+2] adduct is almost always observed in dynamics from this TS (vide infra). In contrast, the ambimodal TS-A in enzyme shows that bonds 2 and 3 are much closer in length with 2.96 ± 0.25 Å for bond 2 and 3.12 ± 0.26 Å for bond 3. In the gas phase, the difference between bonds 2 and 3 is further narrowed, making the formation of [6+4] adduct more likely. These results indicate that the nature of the TS varies in the gas, water, and enzyme environment. This is a result of the average dynamical environment and alters the TS geometries. Reaction dynamics simulations are essential to elucidate how these environment perturbations change the pathways that trajectories have to take to achieve product formation.

Fig. 4.

Distribution of bonds 2 and 3 in 240 TS geometries for (A) DA TS-B in water, (B) ambimodal-A TS in the gas phase, (C) ambimodal TS-A in water, and (D) ambimodal TS-A in the enzyme. Bond 2 in blue leads to the [4+2] adduct, while bond 3 in red leads to the [6+4] adduct. For A, C, and D, TS geometries were sampled by using normal-mode sampling on 60 transition structures optimized in various snapshots of enzyme or of water.

Reaction dynamics trajectories were initiated from TS geometries after normal-mode sampling to explore the dynamics of product formation. Each reactive trajectory was propagated for 300 fs using the QM/MM method (Methods).

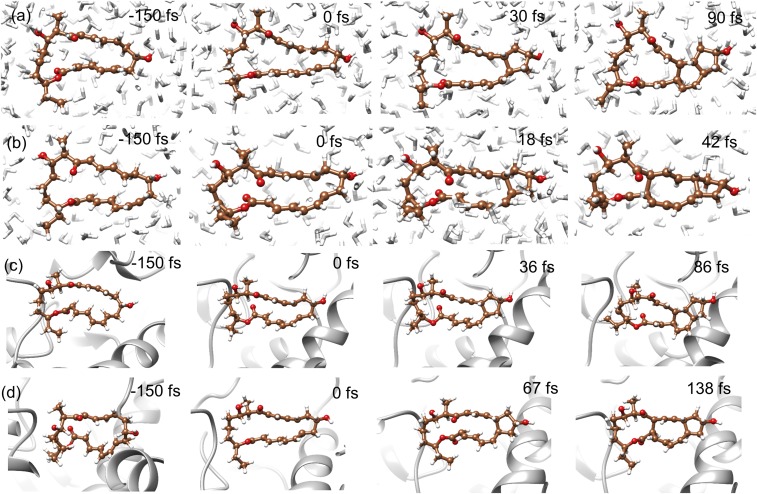
Fig. 5 displays typical trajectories propagated in water and in the enzyme. The third and fourth panels in each row indicate the time at which bond 1 and either bonds 2 or 3 are formed, defined as achieving a distance of 1.6 Å (37). (Bonds 1, 2, and 3 are labeled in Fig. 4.) Bond 1 forms in both adducts. Bond 2 forms in the [4+2] adduct, while bond 3 forms in the [6+4] adduct. Fig. 5 A and B shows the production of [4+2] adduct and [6+4] adduct, respectively. In Fig. 5A, bond 1 forms at 30 fs, then bond 2 forms at 90 fs. In Fig. 5B, bond 1 forms at 18 fs, then bond 3 forms at 42 fs. Likewise, Fig. 5 C and D represents the formation of [4+2] adduct and [6+4] adduct, respectively, in the enzyme, with two bonds forming at 36 and 86 fs for the formation of the [4+2] adduct, and at 67 and 138 fs for the formation of the [6+4] adduct. The full movies of these trajectories are included in SI Appendix.

Fig. 5.

Typical trajectories for the formation of (A) [4+2] adduct in water, (B) [6+4] adduct in water, (C) [4+2] adduct in enzyme, (D) [6+4] adduct in enzyme. We define 1.6 Å as the criterion for C–C bond formation.

Fig. 6 shows overlays of 100 trajectories plotted according to lengths of forming bonds 1, 2, and 3. The ratios of [4+2]:[6+4] products are also presented. In water, the DA TS leads almost exclusively to DA adduct, with only 1 out of 100 trajectories leading to a [6+4] adduct. For trajectories passing through the ambimodal TS, bifurcation to form both products is observed; [4+2]:[6+4] ratios of 11:1 in enzyme, 1.6:1 in water, and 1:1.1 in the gas phase are completed. The selectivity for [4+2] and [6+4] adduct results from the competition between the formation of bond 2 and bond 3. From gas phase to water, a trend toward [4+2] adduct was observed, even though the distributions of the transition state geometries for ambimodal TS-A are very similar in both media. The dipole moment of the [4+2] adduct is 4.74 debye, while that of the [6+4] adduct is 3.46 debye (SI Appendix, Fig. S9), and the [4+2] adduct is better stabilized by polar solvent. In addition, trajectories were propagated in implicit solvents [solvation model density (SMD) model (38)] to explore how the polarity of the medium influences the product distribution. The [4+2]:[6+4] ratio is 1:1 in implicit hexane and 1.5:1 in implicit water. This further supports that increase in solvent polarity promotes the formation of the [4+2] adduct over the [6+4] adduct.

Fig. 6.

Distributions of reactive trajectories initiated from DA TS in water, ambimodal TS in the gas phase, in water, and in enzyme. One hundred randomly chosen trajectories were plotted in each case. Trajectories leading to [4+2] adduct are shown in blue, and those leading to [6+4] adduct are shown in red.

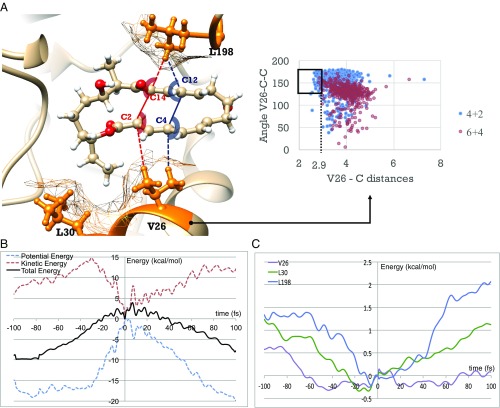
Fig. 7A shows how the hydrophobic residue valine V26 influences the formation of the two adducts through interactions with bond 2 (C4–C12) and bond 3 (C2–C14). The distribution of hydrophobic contacts shows a stronger compression on bond 2 than bond 3, as framed on the graph. This leads to relatively larger difference of lengths of partial bond 2 and 3 in the ambimodal TS in the enzyme compared with the gas phase and in water, which favors the formation of the [4+2] adduct. Leucine L198, the other residue nearby the TS, involves similar hydrophobic interactions with the two bonds, as illustrated in SI Appendix, Fig. S11.

Fig. 7.

(A) Hydrophobic interactions in SpnF–TS complex. The distance is measured from the closest H on V26 or L30 (depending which residue is closer in the snapshot) to C4 or C2, and the angle is the closest H–C4–C14 or H–C2–C14. Framed are the strong hydrophobic contacts, defined as the angle larger than 150° and the distance shorter than 2.9 Å. (B) Average of potential energy, kinetic energy, and total energy of the substrate versus time. (C) Average of kinetic energy for residues V26, L30, and L198 versus time. Energies are averaged from 159 trajectories leading to the [4+2] adduct. The energy at 0 fs are set as zero.

We analyzed the evolution of averaged potential energy (PE), kinetic energy (KE), and total energy (KE+PE) for 159 reactive trajectories leading to the [4+2] adduct (Fig. 7B). From −100 to −30 fs, KE increases by about 10 kcal/mol while PE remains relatively unchanged. This is a phase of thermal activation of the substrate to achieve reactive conformations. Subsequently, 15 kcal/mol KE is transferred into PE to form the TS at 0 fs (SI Appendix, Fig. S12). After passing the TS, the product is gradually formed with KE increasing and PE decreasing. The formation of bond 2 takes relatively longer time than bond 1, and PE and KE change smoothly. Fig. 7C displays the decreases of the kinetic energies for the three hydrophobic residues (V26, L30, and L198) surrounding the reacting molecule from −100 to 0 fs. Their kinetic energy in total decreases by ∼3 kcal/mol. We found that the KEs for polar residues that form H bonds to the substrate are always within 0.5 kcal/mol (SI Appendix, Fig. S13). These results indicate a kinetic energy transfer from the hydrophobic residues to the reacting substrate by vibrational collisions on a femtosecond time scale.

Conclusion

The EPTSS method (26) has been developed and applied to compute free-energy barriers and quasi-classical dynamics in aqueous solution and in the enzyme SpnF. Using this method, we investigated medium effects and femtosecond dynamics of SpnF-catalyzed transannular DA reactions. Two distinct TS were found for the reaction in water and in the enzyme. The computed reaction barriers are in good agreement with the experimentally measured rates of reaction. Important residues that contribute to the overall catalytic process and product distributions were identified. Our study shows how water and enzyme residues influence the rates of reaction and the distributions of products in a dynamically controlled ambimodal reaction mechanism.

Methods

The EPTSS method consists of four major steps. (i) Construction of the reaction/medium models. Initial structures of reactants and transition states were optimized in the gas phase at the M06-2X/6–31G(d) level of theory (39), using Gaussian 09 (40). The optimized structures were then solvated in a water box using AmberTools 14 (41) for the aqueous system. For the reaction in enzyme, the substrate or TS were docked into the enzyme active site using AutoDock Vina. (ii) Configuration Sampling. Separate ensembles of R-A and R-B reactants were constructed by carrying out classical MD equilibrations in water and SpnF using MM for reactant and environment. Classical MD was performed using Amber 14 on the substrate and the transition state for 10 ns in water and for 500 ns in SpnF. The FF99SBildn force field was used for protein residues. General Amber Force Field was used for reactant and transition structures. During the classical MD on the TS, restraining potentials of 500 kcal/mol/Ų were applied to the reaction coordinates in the TS. Snapshots (typically 100) of reactant and TS were sampled from production MD runs at 5-ps intervals in water and 1-ns intervals in SpnF. (iii) Free-energy calculations. To compute the QM/MM free-energy differences, we used a modified form of the ensemble-averaged variational transition state theory (EA-VTST) of Truhlar et al. (27, 42), which incorporates vibrational contributions to the PMF in condensed phase. For each snapshot, the coordinates of the environment (water or SpnF) were frozen, the geometry of 1 was optimized with QM/MM with M06-2X/6–31G(d) as QM, and the free energy was computed from harmonic vibrational partition functions at the stationary point. Free energies of TS-A and TS-B were computed similarly, using conventional TST instead of locating the TS variationally (VTST). This form of the theory is called EA-TST. In our previous study, the reaction-path VTST calculation is performed along the intrinsic reaction coordinate initiated from the ambimodal TS-A in the gas phase. The rate-determining VTS highly resembles the TS, which justifies the EA-TST we used here. In the TS equilibrations, reacting bond lengths were restrained as described in Methods. Free-energy barriers were computed as 〈E(TS-A)〉 – 〈E(R)〉 and 〈E(TS-B)〉 – 〈E(R)〉, where angle brackets indicate an ensemble average over 100 snapshots. Our free-energy scheme assumes that enzyme is well preorganized. The assumption has been justified in other studies (22). On the other hand, for reactions without large charge separation, the preorganization energy is relatively trivial. The SpnF-catalyzed DA reaction was shown to involve very little charge separation by Medvedev et al. (27). This also justifies our method used here. Further details are given in SI Appendix, section 4. (iv) Reaction dynamics. Reactive trajectory simulations were initiated from the random normal-mode sampled TS in water or in enzyme. Normal-mode sampling was conducted at 300 K for each sampled TS structure to obtain coordinates and momenta in a quasi-classical manner. These trajectories were propagated forward and backward for 150 fs each. A detailed description of each step of S/EPTSS can be found in SI Appendix, section 6.

Online Content.

Methods, along with any additional Extended Data display items and Source Data, are available in the online version of the paper; references unique to these sections appear only in the online paper.

SI Appendix is available in the online version of the paper.